- Research Article
- Open access
- Published:
A Reinforcement Learning Based Framework for Prediction of Near Likely Nodes in Data-Centric Mobile Wireless Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 319275 (2010)
Abstract
Data-centric storage provides energy-efficient data dissemination and organization for the increasing amount of wireless data. One of the approaches in data-centric storage is that the nodes that collected data will transfer their data to other neighboring nodes that store the similar type of data. However, when the nodes are mobile, type-based data distribution alone cannot provide robust data storage and retrieval, since the nodes that store similar types may move far away and cannot be easily reachable in the future. In order to minimize the communication overhead and achieve efficient data retrieval in mobile environments, we propose a reinforcement learning-based framework called PARIS, which utilizes past node trajectory information to predict the near likely nodes in the future as the best content distributee. Our framework can adaptively improve the prediction accuracy by using the reinforcement learning technique. Our experiments demonstrate that our approach can effectively and efficiently predict the future neighborhood.
1. Introduction
The development of data-centric storage has enabled efficient data dissemination of wireless networks. In data-centric storage, data is stored by attributes or types (e.g., geographic location and event type) at nodes within the network [1–3]. Queries for data with a particular attribute will be sent directly to the relevant node(s) instead of performing flooding throughout the network, thereby data-centric storage enables efficient data dissemination/access.
In data-centric storage of wireless networks, wireless devices that collect the data are called collector nodes. Whereas the data can be stored on other nodes, called storage nodes [3–5], based on their attributes or types. Most existing data-centric storage models can only deal with static wireless networks. However, with the increasing deployment of wireless devices, there are emerging pervasive applications that rely on the mobility of wireless device. Two representative examples are: ( ) sensors are used for animal migration tracking, and (
) sensors are used for animal migration tracking, and ( ) wireless devices are equipped with police officers to monitor their daily patrol routes, collect crime information by areas, and record corresponding law enforcement actions. In these two scenarios, efficient data retrieval can be achieved if the data-centric storage is enabled, that is, the data is stored by the types of animals, by the activities performed by the animals, or by the tasks that are carried out by the police officers. The challenge is to design schemes that can support data-centric storage when all the nodes are moving around. In this paper, we consider a fully distributed network, in which there is no node playing the sole role as storage; each node can act as both the collector and storage node. For instance, a wireless node, playing the role of a collector node, can collect data of more than one type, but usually it only stores one type of data and transfers the rest of data of other data types to other nodes, which are the storage nodes corresponding to this collector node. Further, to reduce the communication overhead, the storage nodes are picked from the neighborhood, that is, the nodes in the transmission range, of the collector node.
) wireless devices are equipped with police officers to monitor their daily patrol routes, collect crime information by areas, and record corresponding law enforcement actions. In these two scenarios, efficient data retrieval can be achieved if the data-centric storage is enabled, that is, the data is stored by the types of animals, by the activities performed by the animals, or by the tasks that are carried out by the police officers. The challenge is to design schemes that can support data-centric storage when all the nodes are moving around. In this paper, we consider a fully distributed network, in which there is no node playing the sole role as storage; each node can act as both the collector and storage node. For instance, a wireless node, playing the role of a collector node, can collect data of more than one type, but usually it only stores one type of data and transfers the rest of data of other data types to other nodes, which are the storage nodes corresponding to this collector node. Further, to reduce the communication overhead, the storage nodes are picked from the neighborhood, that is, the nodes in the transmission range, of the collector node.
However, in mobile wireless networks, it is possible that both storage and collector nodes move in a broad area, which brings the possibility that the storage nodes that are currently in the neighborhood of the collector nodes may move far away and cannot be easily reached in the future. Thus, when a user sends queries to the collector nodes, the queries need to be redirected to those storage nodes with much communication overhead. Therefore, it is desirable that the collector nodes migrate their data to the storage nodes that not only possess similar data types but also highly likely to travel with them in the future. We define this kind of storage nodes as near likely nodes, which are the nodes that are in the neighborhood (i.e., near) and carry the same type of data that needs to be stored (i.e., likely). In this paper, we propose mechanisms to predict near likely nodes for data-centric mobile wireless networks to achieve efficient data storage and retrieval. More specifically, we propose PARIS, a fully distributed neighborhood prediction framework based on reinforcement learning techniques that utilize past node trajectory information to determine the best content distributee for the future. We first define a probability-based neighborhood prediction model. We then propose two approaches, namely point-based and traced-based, that predict the future neighborhood based on the correlations of the past trajectories. Moreover, we develop WINTER (WINdow adjusTment with Expanding and shRinking) algorithm, which can perform adaptive adjustment during runtime and improve the prediction accuracy by using the reinforcement learning technique. In addition, a probability-based metric is developed to measure the accuracy of prediction. Our approach of data transfer based on neighbor prediction helps to reduce communication overhead and consequently the overall energy consumption during data retrieval because the storage nodes most likely move together.
To evaluate the effectiveness and efficiency of our scheme, we conducted experiments using mobile wireless networks simulated based on a city environment and its vicinity in Germany [6, 7]. By examining two representative scenarios, walking scenario, and vehicular driving scenario, our experimental results show high-prediction accuracy and low-computational time when using PARIS, thereby providing strong evidence of the effectiveness of using data-centric approach through the prediction of near likely nodes in mobile wireless applications.
The rest of the paper is organized as follows. We place our work in the context of the related research in Section 2. In Section 3, we provide an overview of our problem and formulate our probability-based neighborhood prediction model. We next discuss the likelihood of neighborhood by presenting our two prediction approaches and the new metric for measuring accuracy prediction in Section 4. Further, we present the protocols of data transfer and data retrieval and our adaptive accuracy adjustment using reinforcement learning under the PARIS framework in Section 5. We present the experimental evaluation of our approach in Section 6. Finally, we conclude our work in Section 7.
2. Related Work
There has been active work on data-centric storage in sensor networks. In addition to the approaches of global data storage in which the wireless device data is aggregated to be stored at external central servers, algorithms of local information processing [8], and wide-area data dissemination [9, 10] are proposed. Reference [8] used signal processing techniques to collaborate among local nodes for information processing. References [9, 10] proposed directed diffusion algorithms that implement in-network aggregation and allow nodes to access data by name across wireless networks. Further, recent work is more focused on data-centric storage [1–3, 5], where the data is stored decentralized by attributes and types. Reference [1] achieved data-centric storage based on the GPSR routing algorithm and an efficient peer-to-peer lookup system. Reference [2] developed schemes for resilient data-centric storage from the viewpoint of energy savings and scalability in wireless networks. Whereas the security and privacy concerns in data-centric storage are addressed in [3]. Most of these current works only deal with static sensor networks. In this paper, we study data-centric storage in mobile wireless networks.
To detect mobility of wireless nodes, [11] used received signal strength in wireless LAN to detect wireless device mobility. Reference [12] determined mobility from GSM traces using different metrics. In [13] signal variance is used with Hidden Markov Model (HMM) to eliminate oscillations between the static and mobile states for mobility detection. Further, [14] proposed to use correlation coefficients on RSSI traces to detect wireless devices that are moving together.
The works that are most closely related to ours are [15–17]. A user-centric approach was proposed in [15] for colocation prediction that is used for media sharing based on repeating similar journeys in the urban transportation environment. Unlike [15], our approach does not require repeated trajectory patterns, and thus is more generic and can be applied to a broad array of pervasive applications involving mobile devices. References [16, 17] addressed the detection of nodes of similar mobility patterns in group caching in MANET. However, these works do not support fully distributed models. Further, their work focused on current neighbors, not the prediction of future ones. Our work is novel in that we utilize the past node trajectories to predict the future co-movement of nodes for data-centric storage in mobile environments.
3. Problem Overview
In this section, we first present our assumptions. We then provide an overview of PARIS and define our probability model for neighborhood prediction.
3.1. Assumptions
When considering data-centric mobile wireless networks, we have the following assumptions.
-
(i)
Mobility. Wireless device are moving, randomly or in some pattern, in a well-defined area, though the nodes are not aware of their moving patterns, if there is any. There are no predefined trajectories for each node. However, we assume that there exists a comovement pattern within nodes, that is, group of nodes may travel together to common destinations. For example, a group of tourists in New York City may travel to visit the Metropolitan Museum together and they use their mobile phones to take pictures, shoot videos, and write multimedia blogs on the way.
-
(ii)
Location-Aware. We assume that the nodes know their physical locations at all time points during moving. It is a reasonable assumption because in many cases the data is useful only if the location of its source is known. For example, knowing that a crime occurred, which requires a law enforcement action, but without knowing where it occurred is useless. Localization of the mobile nodes can be achieved through the use of GPS or some other approximates but less burdensome localization algorithms [18, 19].
-
(iii)
Neighborhood. Each node has a short communication range and can communicate only with nodes within its transmission range. We call the nodes in the transmission range the neighbors. Mobility of wireless devices may result in the change of the neighborhood. However, we assume that for every node, it has a stable neighborhood within a period of time. For example, police officers who carry out the same tasks are kept in neighborhood while they are on duty.
-
(iv)
Data-centric storage. We assume that the storage is data-centric, that is, the particular node that stores a given data object is determined by the object's type such as event type [1, 2]. Hence, all data with the same type will be stored at the same node (not necessarily the collector node), so that the subsequent data retrieval requests could be efficiently directed. In particular, we propose to transfer data of the same type to a node's near likely nodes. The subsequent data queries will reach a collector node first through routing protocols for mobile wireless networks [20] and will then be redirected to the corresponding storage nodes.
3.2. Overview of PARIS
Data-centric approaches provide low-communication overhead and efficient search, however applying data-centric mechanisms to mobile environments brings new challenges. Since mobility of nodes can change the reachability of nodes and consequently affect the routing decision and long-term storage capability, data-centric storage in mobile wireless networks must take mobility into consideration. In mobile wireless networks, when a node stores its data on other nodes [1, 2], it is desirable that the chosen nodes are in the neighborhood in the future, so that when there come the requests for the data, the collector node can efficiently redirect the requests to its near likely nodes that store the data in its neighborhood.
In PARIS, we study how to store and retrieve data efficiently by making use of neighborhood predication for data-centric storage in mobile wireless networks. In addition, PARIS can be easily extended to help in load balancing when a node exceeds its storage. The main logical components in PARIS are on-demand data transfer, runtime update of near likely node (for efficient data retrieval), and adaptive adjustment through reinforcement learning. By on-demand data transfer, each collector node calculates its near likely node only when it needs to transfer its data to another node. During data retrieval, the collector node is responsible to redirect the corresponding queries to its near likely node. If at a later time, the near likely node that carries the data from a collector node is moving out of the neighborhood of the collector node, the collector node will run the neighborhood prediction process again and perform a runtime update to transfer the data from the storage node to its current near likely node. As it is only performed at certain time points, the on-demand data transfer mechanism reduces both the communication overhead and energy consumption in the neighborhood prediction procedure. Additionally, the WINTER algorithm based on the reinforcement learning technique is developed to adaptively improve the accuracy of neighborhood prediction in each prediction round. The details of PARIS will be presented in Section 5.
3.3. Probability Model
Generally, with mobile devices, the neighborhood may change over time. Some nodes may move into or move out of the transmission range periodically. To predict the future neighborhood, we utilize the trajectory of the mobile devices. We assume the position of the nodes at each time point is in a  -dimensional space. We note that our results can be easily extended to more than two dimensions. We denote the location of mobile node
-dimensional space. We note that our results can be easily extended to more than two dimensions. We denote the location of mobile node  at time
at time  as
as  , where
, where  and
and  denote the
denote the  - and
- and  -coordinates of
-coordinates of  at time point
at time point  . Then given a time window
. Then given a time window  that consists of
that consists of  time points, the trajectory of node
time points, the trajectory of node  of
of  is denoted as
is denoted as  . Given a set of trajectories
. Given a set of trajectories  of
of  nodes, our goal is to use
nodes, our goal is to use  to predict the neighborhood of
to predict the neighborhood of  at a future time point
at a future time point  . To achieve this goal, we define a probability model of prediction that quantifies the likelihood of the future neighborhood. Since we assume that for every node, it has a stable neighborhood within a period of time, our prediction is based on the principle that the nodes that are not only the neighbors in the past but also moving in the same direction are highly likely to be neighbors in the near future. Based on this, we define two probability parameters.
. To achieve this goal, we define a probability model of prediction that quantifies the likelihood of the future neighborhood. Since we assume that for every node, it has a stable neighborhood within a period of time, our prediction is based on the principle that the nodes that are not only the neighbors in the past but also moving in the same direction are highly likely to be neighbors in the near future. Based on this, we define two probability parameters.
-
(1)
Neighbor probability
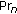 : it is used to reflect the belief from the trajectories
: it is used to reflect the belief from the trajectories  that a node
that a node 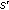 is in the same neighborhood of the node
is in the same neighborhood of the node  .
. -
(2)
Direction probability
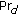 : it is used to measure the likelihood from the trajectories
: it is used to measure the likelihood from the trajectories 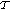 that two nodes
that two nodes 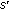 and
and  are moving in the same direction.
are moving in the same direction.
We further define the belief probability that node  is in the neighborhood of
is in the neighborhood of  in the future as
in the future as  expressed by
expressed by

Given the time window  , a collector node
, a collector node  and its neighbor nodes, if
and its neighbor nodes, if  needs to store its data on its near likely node, then from its neighbor nodes that have available storage and store the same type of data that needs to be transferred from
needs to store its data on its near likely node, then from its neighbor nodes that have available storage and store the same type of data that needs to be transferred from  ,
,  picks the node that is of the maximum
picks the node that is of the maximum  . Our model can be easily extended to choose
. Our model can be easily extended to choose  nodes that are of top-
nodes that are of top-
 .
.
4. Neighborhood Likelihood
In this section, we first explain how to compute the neighbor probability  . We then propose two approaches, namely, trace-based and point-based, to calculate the direction probability
. We then propose two approaches, namely, trace-based and point-based, to calculate the direction probability  . We next develop a new metric that measures the prediction accuracy.
. We next develop a new metric that measures the prediction accuracy.
4.1. Neighbor Probability
Given a node  within a time window
within a time window  , for any node
, for any node  , let
, let  =
=  ,
,  and
and  are neighbors at time point
are neighbors at time point  . Then the neighbor probability
. Then the neighbor probability

Intuitively at more time points that  is in the neighborhood of
is in the neighborhood of  in the past, it will be more likely that
in the past, it will be more likely that  remains as the neighbor of
remains as the neighbor of  in the future.
in the future.
4.2. Direction Probability
If two nodes are moving in the same direction, they should have similar trajectories and their  - and
- and  -coordinates must follow the similar traces, and consequently may result in a strong correlation between their
-coordinates must follow the similar traces, and consequently may result in a strong correlation between their  - and
- and  -coordinates, respectively, and vice versa. Figure 1 shows an example of the coordinates versus time series when two nodes move together. We observed that the two nodes have highly-correlated traces in both
-coordinates, respectively, and vice versa. Figure 1 shows an example of the coordinates versus time series when two nodes move together. We observed that the two nodes have highly-correlated traces in both  and
and  dimensions.
dimensions.
Thus, to measure whether two nodes are moving in the same direction, we use the Pearson correlation coefficient [21]. In general, the Pearson correlation coefficient is a statistical method that measures the strength and direction of a linear relationship between two given random variables. More specifically, given two random variables  and
and  , the Pearson correlation coefficient
, the Pearson correlation coefficient  is defined as
is defined as

where  (
( , resp.) and
, resp.) and  (
( , resp.) are the mean and standard deviation of
, resp.) are the mean and standard deviation of  and
and  . The
. The  value ranges from
value ranges from  1 to +1. Correlation +1/
1 to +1. Correlation +1/ 1 means that there is a perfect positive/negative linear relationship between
1 means that there is a perfect positive/negative linear relationship between  and
and  . In Figure 1, the high
. In Figure 1, the high  value 0.96 for both the
value 0.96 for both the  dimension and the
dimension and the  dimension shows high correlation between the coordinates of two nodes that are moving together.
dimension shows high correlation between the coordinates of two nodes that are moving together.
Further, to measure the direction probability, we develop two schemes, point-based and trace-based, based on the Pearson correlation coefficient. These two schemes consider both spatial and temporal changes of nodes in mobile environments.
4.2.1. Point-Based Scheme
This approach utilizes the moving direction of the node  and
and  at each time point
at each time point  within a time window
within a time window  to determine whether two nodes are moving together. The key idea is that the collector node computes the moving directions of the neighbor nodes at all time points in the time window
to determine whether two nodes are moving together. The key idea is that the collector node computes the moving directions of the neighbor nodes at all time points in the time window  and measures the Pearson correlation coefficients of the moving directions.
and measures the Pearson correlation coefficients of the moving directions.
Given the node  and its trajectory
and its trajectory  , where
, where  and
and  are the
are the  and
and  coordinates of the node at each time point
coordinates of the node at each time point  respectively, we define the gradient
respectively, we define the gradient to measure the moving direction at the time point
to measure the moving direction at the time point 

As defined, the gradient quantifies the direction that the node moves from the time point  to
to  . Figure 2 illustrates an example. Although the gradient
. Figure 2 illustrates an example. Although the gradient  may not be accurate when the trajectory between the time points
may not be accurate when the trajectory between the time points  and
and  is not linear, we argue that we can always reduce the error by adding more time points on the nonlinear trajectories, so that the subtrajectories are close to linear format. For example, as shown in Figure 2 we can split the non-linear trajectories between
is not linear, we argue that we can always reduce the error by adding more time points on the nonlinear trajectories, so that the subtrajectories are close to linear format. For example, as shown in Figure 2 we can split the non-linear trajectories between  and
and  into smaller units by adding a time point
into smaller units by adding a time point  between
between  and
and  , as a result the trajectories between
, as a result the trajectories between  and
and  as well as between
as well as between  and
and  are close to linear.
are close to linear.
Given two nodes  and
and  , let
, let  and
and  be the trajectories of
be the trajectories of  and
and  of the time window
of the time window  . For both
. For both  and
and  , the collector node
, the collector node  computes
computes  at each time point
at each time point  and put them into two vectors
and put them into two vectors  and
and  , with
, with  from trajectory
from trajectory  in
in  and from
and from  in
in  . It is straightforward that with
. It is straightforward that with  time points in
time points in  , there are
, there are 
 s in
s in  and
and  . Finally, we measure the Pearson correlation coefficient of
. Finally, we measure the Pearson correlation coefficient of  and
and  . If the coefficient is positive, we take it as the direction probability
. If the coefficient is positive, we take it as the direction probability  of node
of node  and
and  . Otherwise, we value
. Otherwise, we value  as
as  .
.

4.2.2. Trace-Based Scheme
In this approach, opposite to the point-based approach, the collector node does not calculate the moving direction at each time point. Instead, it measures the Pearson correlation coefficients of two trajectories. To be more specific, given two trajectories  and
and  of two nodes
of two nodes  and
and  , first, the collector node
, first, the collector node  computes the Pearson correlation coefficient between the
computes the Pearson correlation coefficient between the  -coordinates of
-coordinates of  and that of
and that of  and collects the positive coefficients
and collects the positive coefficients  . Similarly, it calculates the Pearson correlation coefficient of the
. Similarly, it calculates the Pearson correlation coefficient of the  -coordinates of
-coordinates of  and that of
and that of  . Let the set of positive coefficients be
. Let the set of positive coefficients be 

As illustrated in Figure 1, when two nodes are moving together, the values of correlation coefficients are high in both  and
and  dimensions. Since the correlation coefficients on
dimensions. Since the correlation coefficients on  and
and  dimensions are independent, we multiply
dimensions are independent, we multiply  and
and  as the direction probability
as the direction probability

Moreover,  is normalized as needed.
is normalized as needed.
4.3. Measurement of Accuracy of Neighborhood Prediction
One challenge of data-centric mobile wireless networks is the efficiency of data retrieval, which highly depends on the accuracy of neighborhood prediction results. Wrong prediction results may cause data to be stored on unreachable nodes and thus incur expensive communication overhead and consume more energy. Therefore, it is necessary to measure the accuracy of neighborhood prediction and evaluate the effectiveness of our prediction schemes. In this section, we present our new metric Prediction Accuracy in measuring neighborhood prediction accuracy.
In Prediction Accuracy metric, the time points are split into two time windows, past  and future
and future  . The window of past
. The window of past  is used as the "training set" to predict the near likely nodes, whereas the window of future
is used as the "training set" to predict the near likely nodes, whereas the window of future  , is used as the "test set" to verify the accuracy of the prediction. We choose
, is used as the "test set" to verify the accuracy of the prediction. We choose  nodes, denoted as
nodes, denoted as  , as the "test participants". Our accuracy measurement consists of two steps.
, as the "test participants". Our accuracy measurement consists of two steps.
Step 1 (Training).
For each node  in
in  , we find its near likely node
, we find its near likely node  that is of the maximum
that is of the maximum  in the time window
in the time window  . For
. For  nodes, we collect
nodes, we collect  such neighbor nodes and put their
such neighbor nodes and put their  into a vector
into a vector  . Thus
. Thus  consists of
consists of  probability values.
probability values.
Step 2 (Testing).
For each near likely neighbor  from Step 1, we calculate its
from Step 1, we calculate its  of the window
of the window  and store
and store  in a vector
in a vector  , which is also a set of
, which is also a set of  probability values. Our measurement of accuracy is based on the distance of
probability values. Our measurement of accuracy is based on the distance of  and
and  . The smaller the distance is, the more accurate the prediction result will be.
. The smaller the distance is, the more accurate the prediction result will be.
To measure the distance of two probability distribution  and
and  , our metric of Prediction Accuracy is based on KL-divergence. KL-divergence is a noncommutative measure of the difference between two probability distributions in probability theory and information theory [22]. Specifically, for probability distributions
, our metric of Prediction Accuracy is based on KL-divergence. KL-divergence is a noncommutative measure of the difference between two probability distributions in probability theory and information theory [22]. Specifically, for probability distributions  and
and  , the KL-divergence of
, the KL-divergence of  from
from  is defined as
is defined as

The smaller the value of  is, the more
is, the more  is similar to
is similar to  , which consequently indicates that our prediction of future near likely node is more accurate.
, which consequently indicates that our prediction of future near likely node is more accurate.
Intuitively, for the nodes that are predicted as near likely neighbors, if in the future window, their belief probability increases, it indicates that the neighborhood of these nodes is not changing in the future window and our prediction correctly captures their neighborhood. On the other hand, if their probability decreases in the future window, it shows that the neighborhood of these nodes is changing in the future window. Since KL-divergence only shows the aggregate result of the difference of two probabilities, to study the prediction error at a more detailed level, we use Cumulative Distribution Function (CDF). Specifically, given the probability distributions  from the past window and
from the past window and  from the future window, we compute the positive and negative probability difference vectors
from the future window, we compute the positive and negative probability difference vectors  and
and  :
:

The nodes in  (
( , resp.) are the ones whose probabilities are increasing (decreasing, resp.). We measure CDF of both
, resp.) are the ones whose probabilities are increasing (decreasing, resp.). We measure CDF of both  and
and  . Intuitively, the closer the distributions of
. Intuitively, the closer the distributions of  and
and  to the value 0 are, the more accurate the prediction is.
to the value 0 are, the more accurate the prediction is.
5. Framework of PARIS for Data Transfer and Data Retrieval
In this section, we describe the three main logical components in PARIS framework, on-demand data transfer, runtime update of near likely nodes, and adaptive adjustment through reinforcement learning.
5.1. On-Demand Data Transfer
In PARIS, data transfer happens on-demand, that is, when a collector node  needs to transfer its data to other nodes, and the communication between nodes is only performed at the specific time point. Thus, the on-demand scheme reduces the communication overhead and energy consumption incurred from frequent information exchange. There are two requirements when choosing the nodes that the data will be transferred to
needs to transfer its data to other nodes, and the communication between nodes is only performed at the specific time point. Thus, the on-demand scheme reduces the communication overhead and energy consumption incurred from frequent information exchange. There are two requirements when choosing the nodes that the data will be transferred to
-
(i)
Following the data-centric requirement, the collector node picks the neighbor nodes that have not only sufficient storage but also the matching type of data that will be transferred.
-
(ii)
If there are multiple nodes that satisfy the first requirement, the collector node will pick the node with the largest
 .
.
The on-demand data transfer procedure consists of three steps.
-
(1)
A collector node
 sends a request to all the nodes in its neighborhood. The request consists of the inquiry of the allowed data type, the size of the available storage, and the trajectory of the next
sends a request to all the nodes in its neighborhood. The request consists of the inquiry of the allowed data type, the size of the available storage, and the trajectory of the next 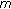 time points in the time window
time points in the time window  . The neighbor nodes reply the request of
. The neighbor nodes reply the request of  with proper information.
with proper information. -
(2)
The collector node
 collects the answers and picks the node that satisfies the above two requirements as the near likely node
collects the answers and picks the node that satisfies the above two requirements as the near likely node 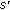 .
. -
(3)
The collector node
 sends its data to its near likely node
sends its data to its near likely node 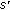 , and updates its data track table. The data track table consists of entries in the format of
, and updates its data track table. The data track table consists of entries in the format of 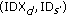 , with each entry used for tracking which node the data is stored on, so that when there is a user query for the data, node
, with each entry used for tracking which node the data is stored on, so that when there is a user query for the data, node  can efficiently redirect the query. The
can efficiently redirect the query. The 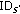 is the node identity of the near likely node that stores data with index
is the node identity of the near likely node that stores data with index  in the data track table.
in the data track table.
5.2. Runtime Update of Near Likely Node
Given the fact that the estimated near likely node has a belief probability to be in the neighborhood in the future, it is possible that when a data query arrives at a future time point, the near likely node has already moved out of the neighborhood of the collector node. This will increase the communication overhead in order to locate the "previous" near likely node for data retrieval. In order to minimize the communication overhead, it is desirable to always keep the transferred data in the neighborhood of the collector node in a mobile wireless network environment.
We propose runtime update of the near likely node in PARIS. Usually in wireless networks each node keeps a list of its neighbors and update the list periodically based on the communication of beacon packets [23]. Upon each neighbor update, the node checks its data track table. If a node identity, which appears in the data track table, has disappeared from its neighbor list, the node needs to perform a runtime update to find its current near likely node. To avoid frequent runtime updates and consequently much update overhead, it is desirable to look for the current near likely node of the same data type as the replacement. The following steps will take place:
-
(1)
The collector node
 runs step 1 and 2 from the on-demand data transfer procedure for the corresponding type of data with
runs step 1 and 2 from the on-demand data transfer procedure for the corresponding type of data with 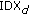 and identifies a new near likely node
and identifies a new near likely node 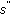 .
. -
(2)
The collector node
 then sends a request to the previous near likely node
then sends a request to the previous near likely node 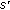 and asks
and asks  to transfer the data with
to transfer the data with  to node
to node  .
. -
(3)
Once the collector node
 receives the confirmation from
receives the confirmation from 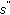 that the data transfer is successful, it updates its data track table by replacing
that the data transfer is successful, it updates its data track table by replacing 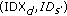 with
with 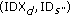 .
.
A node may be identified as a near likely node for more than one collector nodes. In PARIS, the near likely node is stateless, whereas the collector nodes keep a data track table to maintain the data transfer information. The advantage of the runtime update of near likely node is that the data is stored on either the collector node itself or its near likely nodes. Thereby no flooding messages are needed during data retrieval, and thus reduce the overall communication overhead.
5.3. Adaptive Adjustment by Reinforcement Learning
Although runtime update always keeps data close, it may incur expensive energy consumption and increased communication overhead if the update is frequent. The reason for such frequent update is the prediction of near likely neighbors that is not accurate enough. As shown in Section 4.3, the prediction accuracy is affected by the configuration of time windows that are used to collect the past trajectories of a node. Time windows that are too small cannot capture the correct neighborhood and cause inaccurate neighbor prediction, while time windows that are too large will consume more energy on each neighboring nodes for collecting trajectory traces and increase the communication overhead when sending the trajectory traces to the collector node. Therefore, the appropriate time window will allow PARIS to be effective for neighborhood prediction.
To improve the neighbor prediction accuracy, we adaptively adjust the time windows by applying the reinforcement learning mechanism from the beginning of the whole procedure. Reinforcement learning is a machine learning technique that deals with sequential control problems [24].
Our goal is that according to the current state, that is, the current neighborhood prediction, determines how to revise the size of the time window to reach a better neighborhood prediction in the next round. The revision of the time windows consists of two operations: expanding, that is, increasing the window size by one time point, and shrinking, that is, decreasing the window size by one time point. The collector node  keeps an observation of the change of KL-divergence incurred by expansion/shrinkage of the time window. We say the prediction accuracy falls if the KL-divergence increases. Otherwise, we say the prediction accuracy improves. Based on this, we developed an algorithm based on reinforcement learning, called WINTER (WINdow adjusTment with Expanding and shRinking), which adaptively adjusts the time window size by the following:
keeps an observation of the change of KL-divergence incurred by expansion/shrinkage of the time window. We say the prediction accuracy falls if the KL-divergence increases. Otherwise, we say the prediction accuracy improves. Based on this, we developed an algorithm based on reinforcement learning, called WINTER (WINdow adjusTment with Expanding and shRinking), which adaptively adjusts the time window size by the following:
-
(i)
If the prediction accuracy falls from time window
 to
to  , then for time window
, then for time window 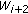 , we "reverse" the operation, that is, if the operation on
, we "reverse" the operation, that is, if the operation on  is expansion/shrinkage, we shrink/expand for
is expansion/shrinkage, we shrink/expand for  .
. -
(ii)
Otherwise, the prediction accuracy improves from time window
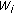 to
to 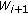 . Then we repeat the same operation on
. Then we repeat the same operation on 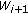 for
for  .
.
After a sequence of expansions and shrinkages, it is possible that different collector nodes have time windows of different sizes.
The pseudocode that implements WINTER is shown in Algorithm 1.
Algorithm 1: The WINTER algorithm.
( ) Let
) Let  and
and  be the collector node and its predicted near likely neighbor;
be the collector node and its predicted near likely neighbor;
( )
)  ;
;
( )repeat
)repeat
( ) Let
) Let  and
and  be the KL-divergence measured from time window
be the KL-divergence measured from time window  and
and  ;
;
( ) Let
) Let  be the operation (expansion or shrinkage) on time window
be the operation (expansion or shrinkage) on time window  ;
;
( ) if (
) if ( ) then
) then
( ) //KL-divergence improves;
) //KL-divergence improves;
( ) if
) if == "expansion" then
== "expansion" then
( ) The size of the next time window
) The size of the next time window  ;
; 
( ) else
) else
( ) The size of the next time window
) The size of the next time window  ;
;  1;
1; 
( ) end if
) end if
( ) else
) else
( ) //KL-divergence falls;
) //KL-divergence falls;
( ) if
) if == "expansion" then
== "expansion" then
( ) The size of the next time window
) The size of the next time window  ;
;
( )
)  "shrinkage";
"shrinkage"; 
( ) else
) else
( ) The size of the next time window
) The size of the next time window  ;
;
( )
)  "expansion";
"expansion"; 
( ) end if
) end if
( ) end if
) end if
( )
)  ;
;
( ) until The time points are exhausted;
) until The time points are exhausted;
6. Experimental Evaluation
In this section, we describe our experimental methodology and present the results that evaluate the effectiveness of our approaches.
6.1. Methodology
We would like to evaluate the feasibility of our approach in an environment close to real applications (e.g., status monitoring of patrol officers). Using mobile wireless networks, we conducted experiments based on mobile devices generated from a city environment and its vicinity in Germany [6, 7] as shown in Figure 3. The size of the area is 25000 m  25000 m. We created two simulation scenarios, one is in walking speed of 4 ft/s, and the other is in vehicular driving speed of 50 ft/s. For the walking scenario, two data sets, we call
25000 m. We created two simulation scenarios, one is in walking speed of 4 ft/s, and the other is in vehicular driving speed of 50 ft/s. For the walking scenario, two data sets, we call  and
and  , are obtained using this simulation environment with 1000 and 5000 nodes generated, respectively, and placed randomly inside the city.
, are obtained using this simulation environment with 1000 and 5000 nodes generated, respectively, and placed randomly inside the city.
For the vehicular driving scenario, one data set is created through the simulation environment with 1000 nodes generated and placed randomly inside the city. For the duration of our study, some new nodes may move into the city environment and some existing nodes may move out the city environment. There are no pre-defined trajectories for each node. However, group of nodes may travel together to common destinations (e.g., the city center). Figure 4 presents the average number of neighbors when using the small data set in walking scenario for the duration of our study time, shown as percentage from 0 to 1, for 600 nodes and 100 nodes, respectively.
The 100 nodes are randomly chosen from 600 nodes. We observed that the average number of neighbors increases from a few nodes to around 14 nodes as the study time moves along, indicating that groups of nodes are gradually formed and traveling together to the similar destinations. The vehicular driving scenario has the similar trend as the walking scenario. This is in line with our co-movement assumption. Thus, these datasets are suitable for our neighborhood prediction study.
6.2. Metrics
We will utilize the following performance metrics to evaluate the effectiveness of PARIS in terms of prediction of near likely nodes.
Prediction Accuracy
As described in Section 4.3, the Prediction Accuracy metric measures the statistical characteristics of neighborhood prediction based on the Cumulative Distribution Function (CDF) of the difference of the future probability  to the past probability
to the past probability  of the near likely node on top of the KL-divergence. We split our study time to a past time window for prediction and a future time window to evaluate our prediction. In the following discussion, we use the percentage of study time as the measurement of window size.
of the near likely node on top of the KL-divergence. We split our study time to a past time window for prediction and a future time window to evaluate our prediction. In the following discussion, we use the percentage of study time as the measurement of window size.
We investigate the impact of different window sizes of the past as well as the future on the prediction accuracy using both point-based and trace-based schemes.
Time Performance
By measuring the time that each scheme needs to provide the prediction results, we evaluate the feasibility of applying these schemes to nodes that usually have limited computational power and memory. The Time Performance metric helps to benchmark our approaches in the simulation environment and further indicates the possibility to implement them in real wireless device.
6.3. Results
KL-Divergence
We first study the neighborhood prediction accuracy in our proposed mechanism for both walking and vehicular speed scenarios. Figure 5 presents values of KL-divergence versus different past window sizes when fixing the future window size, whereas Figure 6 presents values of KL-divergence versus different future window sizes when fixing the past window size for both point-based as well as trace-based schemes under the case when the average number of neighbors is 5.
KL-divergence: fixed future window size; (a) and (b) the future window size is set to 0. 2 and 0.4 of the total study time, respectively, when the average number of neighbors is 5; (c) the future window size is set to 0.4 of the total study time when the average number of neighbors is 15.Walking Scenario: Future window 0.2Walking Scenario: Future window 0.4Vehicular Scenario: Future window 0.4
KL-divergence: fixed past window size; (a) and (b) the past window size is set to 0. 2 and 0.4 of the total study time, respectively, when the average number of neighbors is 5; (c) the past window size is set to 0.4 of the total study time when the average number of neighbors is 15.Walking Scenario: Past window 0.2Walking Scenario: Past window 0.4Vehicular Scenario: Past window 0.4
For the walking speed scenario, we observed small KL-divergence values that are always less than 0.5. This is encouraging as the smaller KL-divergence values indicate that the distribution of the belief probability in the future is close to the distribution of that in the past. Further, as shown in Figures 5(a) and 5(b), when fixing the time window of the future, 0.2 and 0.4 of the total study time, respectively, as the size of the past time window increases, the KL-divergence value presents an overall decreasing trend for the point-based scheme. This means that by using the point-based scheme, the larger the past window size, the more accurate the prediction of near likely node can become. However, for the trace-based scheme, we observed that the KL-divergence value fluctuates. This is interesting since it shows that for the trace-based scheme, simply increasing the past window size does not increase the accuracy, which indicates that we need both expansion and shrinkage for adaptive adjustment of window sizes.
On the other hand, when fixing the time window of the past, 0.2 and 0.4 of the total study time, respectively, as presented in Figures 6(a) and 6(b), we observed an increasing trend of the KL-divergence value for both schemes as the window size of future is increasing when the average number of neighbors is 5, indicating that the near likely node may gradually move away from the collector node when the future is long enough.
We also investigate the neighbor prediction accuracy in our proposed mechanism for the vehicular driving scenario. Figures 5(c) and 6(c) present the neighborhood prediction accuracy in the vehicular-driving scenario. First, similar to the walking scenario, the values of KL-divergence are less than 0.5, which indicates that our scheme obtains accurate prediction accuracy in the vehicular driving scenario as in the walking scenario. We also observed similar changing trend as the result of walking scenario.
In particular, as shown in Figure 5(c), when fixing the future window size to 0.4 of the total study time, as the size of the past window size increases, the KL-divergence value presents an overall decreasing trend, which is similar to the trend in Figure 5(b). While fixing the past window size to 0.4 as shown in Figure 6(c), we also observed similar increasing trend and KL-divergence value as in Figure 6(b). Further, the increased amount of the KL-divergence values is always small (around 0.05). These results indicate that our proposed schemes are appropriate for different mobility scenarios.
In general, we found that the KL-divergence values of trace-based scheme is smaller than those using point-based scheme for both walking and vehicular driving scenarios. Moreover, for the walking scenario, we observed similar results when the average number of neighbors increases to 15 and 45. Due to space limitation, the results are omitted. Therefore, the trace-based scheme has better prediction accuracy than the point-based scheme.
Further, we compared the values of KL-divergence between the small and the large data sets in Figure 7. In order to compare these two different data sets directly, we used the same transmission range of the nodes in each data set, which is under 300 m and 600 m, respectively.
We observed similar behavior for both large data set and small data set as the KL-divergence value presents an obvious decreasing trend when increasing the past window size and decreasing the future window size simultaneously. Furthermore, the KL-divergence values are smaller for the large data set. This is because there are more nodes in the large dataset, which form larger neighborhood and thereby provides better prediction result. In the sequel, due to the space limit, we will only present the results obtained from the small data set.
Cumulative Distribution Function (CDF)
Turning to studying the CDF of the difference of the future probability  to the past probability
to the past probability  of the near likely node. Figure 8 presents the CDF of the probability difference for both point-based and trace-based schemes when the window size of the future is fixed as 0.2 of the total study time, whereas the window size of the past changes from 0.2 to 0.4 of the total study time. We found that for both the positive difference
of the near likely node. Figure 8 presents the CDF of the probability difference for both point-based and trace-based schemes when the window size of the future is fixed as 0.2 of the total study time, whereas the window size of the past changes from 0.2 to 0.4 of the total study time. We found that for both the positive difference  and the negative difference
and the negative difference  , the CDF curve of the trace-based scheme lies to the left side of the point-based scheme.
, the CDF curve of the trace-based scheme lies to the left side of the point-based scheme.
Cumulative Distribution Function (CDF) of the difference of the future probability  to the past probability
to the past probability  of the near likely node under the case of the average number of neighbors is 15 in walking scenario. Positive difference (0.2, 0.2)Positive difference (0.4, 0.2)Negative difference (0.2, 0.2)Negative difference (0.4, 0.2)
of the near likely node under the case of the average number of neighbors is 15 in walking scenario. Positive difference (0.2, 0.2)Positive difference (0.4, 0.2)Negative difference (0.2, 0.2)Negative difference (0.4, 0.2)
This shows that in terms of neighborhood prediction accuracy, the trace-based scheme outperforms the point-based scheme, which is inline with the results obtained from the KL-divergence.
Moreover, we investigated the prediction accuracy under the cases of different average number of neighbors, that is, 5, 15, and 45, respectively, in the neighborhood. Figure 9 presents the CDF of  for both of our schemes. We observed that for each scheme, the curves of different average number of neighbors are close to each other, suggesting that the prediction accuracy is not sensitive to different average number of neighbors. These results are very encouraging as it indicates that given a prediction scheme the prediction accuracy only relies on the window size.
for both of our schemes. We observed that for each scheme, the curves of different average number of neighbors are close to each other, suggesting that the prediction accuracy is not sensitive to different average number of neighbors. These results are very encouraging as it indicates that given a prediction scheme the prediction accuracy only relies on the window size.
Impact of the number of neighbors: Cumulative Distribution Function (CDF) of the positive difference of the future probability  to the past probability
to the past probability  of the near likely node under different average number of neighbors in walking scenario: 5, 15, and 45. Point-based scheme (0.4, 0.4)Trace-based scheme (0.4, 0.4)
of the near likely node under different average number of neighbors in walking scenario: 5, 15, and 45. Point-based scheme (0.4, 0.4)Trace-based scheme (0.4, 0.4)
Reinforcement Learning
We next examine the effects of reinforcement learning on prediction accuracy using WINTER algorithm. Figure 10 presents the expansion/shrinkage of the prediction window (i.e., the past window) according to the obtained KL-divergence value. In Figure 10(a), we observed that when fixing the future testing window to 0.12, the prediction window size is adjusted adaptively based on the KL-divergence values; when the KL-divergence value decreases from 0.043 to 0.02, the size of the prediction window expands from 0.12 to 0.2, while the prediction window shrinks from 0.2 to 0.08 when the KL-divergence value increases from 0.02 to 0.039. We observed the similar window adjustment behavior in Figure 10(b). Further, we found that by adaptive adjustment, the KL-divergence values are always less than 0.05 (even less than 0.016 in Figure 10(b)). These results are encouraging as it indicates that our approach of adaptive adjustment through reinforcement learning is effective in improving prediction accuracy during runtime.
We further investigate the behavior of adaptive adjustment through reinforcement learning by doubling the study time. Figure 11 presents how the KL-divergence values change during the expansion/shrinkage of the prediction window. First, we observed that the KL-divergence values are always less than 0.05. This proves the effectiveness of our adaptive adjustment approach. Second, we observed that although the study time in both Figures 11(a) and 11(b) is scaled from 0 to 1, the similar window size adjustment behavior presents as with shorter study time (Figure 10). For example, in Figure 11(a), when fixing the size of the future testing window as 0.12, when the KL-divergence value increases from 0.02 to 0.038, the size of the prediction window shrinks from 0.12 to 0.08, while the prediction window expands from 0.08 to 0.16 when the KL-divergence value decreases from 0.038 to 0.022. This demonstrates that our adaptive adjustment approach through reinforcement learning works in larger time windows as well.
Time Performance
Figure 12 presents the comparison of time measurements under various setups including different average number of neighbors and various window sizes for both small and large data sets. We found that the time to perform neighborhood prediction is in the order of milliseconds for both schemes.
We observed that the point-based scheme runs at about two times faster than the trace-based scheme constantly under different average number of neighbors and various window sizes. This is because the trace-based scheme needs to calculate correlation coefficients for both  and
and  dimensions, whereas the point-based scheme only calculates the correlation coefficient for gradient. Further, the time measurements of the large data set are also in the order of milliseconds as shown in Figure 12(b). This indicates that even when a node has large number of neighbors, our schemes can efficiently predict the near likely nodes.
dimensions, whereas the point-based scheme only calculates the correlation coefficient for gradient. Further, the time measurements of the large data set are also in the order of milliseconds as shown in Figure 12(b). This indicates that even when a node has large number of neighbors, our schemes can efficiently predict the near likely nodes.
Communication Overhead
Next, we measure the communication overhead incurred by collecting the trajectory information from a collector's neighbors. Let us consider the transmission packets of 512 bytes [25]. We assume that each trajectory record consists of a pair of ( ) coordinates and a timestamp, each of float type. In other words, each trajectory record consists of 12 bytes. Therefore, one transmission packet can contain at most 42 trajectories. If one node records its trajectory every
) coordinates and a timestamp, each of float type. In other words, each trajectory record consists of 12 bytes. Therefore, one transmission packet can contain at most 42 trajectories. If one node records its trajectory every  seconds, then the trajectory information of
seconds, then the trajectory information of  seconds can be stored in
seconds can be stored in  packets.
packets.
Moreover, we assume that for every  seconds, to apply the neighborhood prediction mechanism, the collector node needs to collect the trajectory of
seconds, to apply the neighborhood prediction mechanism, the collector node needs to collect the trajectory of  seconds from its
seconds from its  neighbors. Therefore, there are
neighbors. Therefore, there are  packets transmitted to the collector node from its neighbors. Assume the collector node needs to transfer its data of size
packets transmitted to the collector node from its neighbors. Assume the collector node needs to transfer its data of size  to the storage node within these
to the storage node within these  seconds. Then the size of the transmission packets needed for collecting trajectory information is
seconds. Then the size of the transmission packets needed for collecting trajectory information is  of the data sent to the identified near likely node by the collector node. We assume that
of the data sent to the identified near likely node by the collector node. We assume that  is less than 1.
is less than 1.
Based on our analysis, we can see that both the packet size  and the percentage of transmission packets
and the percentage of transmission packets  are not affected by the moving speed of the mobile nodes. Thus, the communication overhead incurred from the trajectory information exchange in our approach is not sensitive to the mobility model.
are not affected by the moving speed of the mobile nodes. Thus, the communication overhead incurred from the trajectory information exchange in our approach is not sensitive to the mobility model.
We further study how the overhead for collecting trajectory information varies with the changing amount of data size under different network sizes. The results are shown in Figure 13. It presents that the overhead is negligible compared with the size of the transferred data. In particular, Figure 13(a) presents the results with the number of neighbors  = 5, the trajectories of
= 5, the trajectories of  of seconds to be collected, the data size
of seconds to be collected, the data size  varying from 1 MB to 5 MB, and each node recording its trajectories every
varying from 1 MB to 5 MB, and each node recording its trajectories every  seconds. We observed that small overhead fraction values in percentage that are always less than 0.7%. Specifically, it is as small as 0.05% for the data size of 5 MB and trajectory of 60 seconds. Furthermore, we noticed that the larger the data size is, the smaller the fraction will be. The same trend is also observed in Figure 13(b), which presents a larger network with 15 neighbors. These results showed that the communication overhead incurred by collecting the trajectory information is negligible compared with the total size of the transferred data.
seconds. We observed that small overhead fraction values in percentage that are always less than 0.7%. Specifically, it is as small as 0.05% for the data size of 5 MB and trajectory of 60 seconds. Furthermore, we noticed that the larger the data size is, the smaller the fraction will be. The same trend is also observed in Figure 13(b), which presents a larger network with 15 neighbors. These results showed that the communication overhead incurred by collecting the trajectory information is negligible compared with the total size of the transferred data.
Furthermore, we realized that there exists a tradeoff between the communication overhead and the frequency of data update. The higher frequency the data is updated, the higher prediction accuracy may be achieved, however, higher communication overhead can occur. We note that in our scheme the data update is performed on-demand, and thus the frequency of data update can be configured.
Finally, we study the communication overhead incurred in terms of hop counts during data retrieval. Figure 14 presents the number of hops traveled with and without using the scheme we proposed over the study time. We found that under our proposed scheme the number of hops traveled for data retrieval is less than half of that without using it, indicating that using our scheme can significantly reduce the communication overhead and thus reduce the overall energy consumption of wireless devices. We will quantify the savings of energy consumption in our future work.
In summary, our experimental evaluation in prediction accuracy, time performance, and communication overhead is highly encouraging as they clearly indicate that our prediction schemes of near likely nodes can not only effectively but also efficiently perform future neighborhood prediction. Our results also point out that there is a tradeoff between the prediction accuracy and the time efficiency when choosing prediction schemes—the scheme that provides better prediction accuracy runs slower.
7. Conclusion
The development of data-centric networks has enabled efficient data dissemination and access when the increasing large volume of data is spread across the networks. New challenges arise when there is a demand of implementing data-centric approaches in mobile wireless applications. In this paper, we proposed PARIS, a fully distributed framework based on reinforcement learning technique for data-centric storage in mobile wireless networks. PARIS is based on neighborhood prediction and utilizes the past node trajectory information to predict the near likely node that stores the same type of data and will most likely to remain in the neighborhood in the near future. These near likely nodes are chosen as the content distributee so that the later data retrieval is only needed in the neighborhood and is thus more efficient in terms of communication overhead and energy consumption. We proposed two schemes to predict the future neighborhood, point-based and trace-based. We derived a probability-based metric to measure the accuracy of prediction. Further, we developed WINTER (WINdow adjusTment with Expanding and shRinking) algorithm to adaptively improve the prediction accuracy using the reinforcement learning technique. Additionally, we derived a probability-based metric to measure the accuracy of prediction. Our results using simulation data generated from mobile wireless networks in a city environment show that our prediction schemes of near likely nodes can both effectively as well as efficiently perform future neighborhood prediction.
There are several avenues for future work. Since it is possible that multiple collector nodes choose the same nodes as the near likely nodes, it is interesting to study how to balance the load of the "popular" near likely nodes with others based on data types. Further, as energy-efficiency being an important feature of wireless networks, we want to quantify the energy consumption model in PARIS.
References
Shenker S, Ratnasamy S, Karp B, Govindan R, Estrin D: Data-centric storage in sensornets. Proceedings of the ACM SIGCOMM Computer Communication Review (ACM SIGCOMM '03), January 2003 33: 137-142.
Ghose A, Grossklags J, Chuang J: Resilient data-centric storage in wireless Ad-Hoc sensor networks. Proceedings of the 4th International Conference on Mobile Data Management (MDM '03), 2003, Lecture Notes in Computer Science 2574: 45-62.
Shao M, Zhu S, Zhang W, Cao G: pDCS: security and privacy support for data-centric sensor networks. Proceedings of the IEEE International Conference on Computer Communications (INFOCOM '07), 2007 1298-1306.
Krishnamachari DEB, Wicker S: Modelling data-centric routing in wireless sensor networks. Proceedings of the IEEE International Conference on Computer Communications (INFOCOM '02), 2002
Ratnasamy S, Karp B, Yin L, Yu F, Estrin D, Govindan R, Shenker S: GHT: a geographic hash table for data-centric storage. Proceedings of the 1st ACM International Workshop on Wireless Sensor Networks and Applications, September 2002 78-87.
Brinkhoff T: Generating network-based moving objects. Proceedings of the 12th International Conference on Scientific and Statistical Database Management (SSDBM '00), July 2000 253-255.
Brinkhoff T: A framework for generating network-based moving objects. GeoInformatica 2002, 6(2):153-180. 10.1023/A:1015231126594
Yao K, Hudson RE, Reed CW, Chen D, Lorenzelli F: Blind beamforming on a randomly distributed sensor array system. IEEE Journal on Selected Areas in Communications 1998, 16(8):1555-1566. 10.1109/49.730461
Heidemann J, Silva F, Intanagonwiwat C, Govindan R, Estrin D, Ganesan D: Building efficient wireless sensor networks with low-level naming. Proceedings of the ACM Symposium on Operating Systems Review (OSR '01), 2001 146-159.
Intanagonwiwat C, Govindan R, Estrin D: Directed diffusion: a scalable and robust communication paradigm for sensor networks. Proceedings of the 6th Annual International Conference on Mobile Computing and Networking (MOBICOM '), August 2000, Boston, Mass, USA 56-67.
Muthukrishnan K, Lijding M, Meratnia N, Havinga P: Sensing motion using spectral and spatial analysis of WLAN RSSI. Proceedings of the 2nd European Conference on Smart Sensing and Context (EuroSSC '07), October 2007, Lecture Notes in Computer Science 4793: 62-76.
Sohn T, Varshavsky A, LaMarca A, Chen MY, Choudhury T, Smith I, Consolvo S, Hightower J, Griswold WG, De Lara E: Mobility detection using everyday GSM traces. Proceedings of the 8th International Conference of Ubiquitous Computing (UbiComp '06), September 2006, Lecture Notes in Computer Science 4206: 212-224.
Krumm J, Horvitz E: Locadio: inferring motion and location from Wi-Fi signal strengths. Proceedings of the 1st Annual International Conference on Mobile and Ubiquitous Systems (MOBIQUITOUS '04), August 2004 4-13.
Chandrasekaran G, Ergin MA, Gruteser M, Martin R, Yang J, Chen Y: Decode: detecting co-moving wireless devices. Proceedings of the 5th IEEE International Conference on Mobile Ad-Hoc and Sensor Systems (MASS '08), 2008 315-320.
McNamara L, Mascolo C, Capra L: Media sharing based on colocation prediction in urban transport. Proceedings of the ACM International Conference on Mobile Computing and Networking (MOBICOM '08), September 2008 58-69.
Huang J-L, Chen M-S: On the effect of group mobility to data replication in Ad Hoc networks. IEEE Transactions on Mobile Computing 2006, 5(5):492-507.
Chow C-Y, Leong HV, Chan ATS: GroCoca: group-based peer-to-peer cooperative caching in mobile environment. IEEE Journal on Selected Areas in Communications 2007, 25(1):179-191.
Langendoen K, Reijers N: Distributed localization in wireless sensor networks: a quantitative comparison. Computer Networks 2003, 43(4):499-518. 10.1016/S1389-1286(03)00356-6
Priyantha NB, Miu AKL, Balakrishnan H, Teller S: The cricket compass for context-aware mobile applications. Proceedings of the 7th Annual ACM/IEEE International Conference on Mobile Computing and Networking (MOBICOM '01), 2001 1-14.
Akkaya K, Younis M: A survey on routing protocols for wireless sensor networks. Ad Hoc Networks 2005, 3(3):325-349. 10.1016/j.adhoc.2003.09.010
Casella G, Berger RL: Statistical Inference. Duxbury Press, Belmont, Calif, USA; 1990.
Kullback S, Leibler RA: On information and sufficiency. Annals of Mathematical Statistics 1951, 22(1):79-86. 10.1214/aoms/1177729694
Borbash SA, Ephremides A, McGlynn MJ: An asynchronous neighbor discovery algorithm for wireless sensor networks. Ad Hoc Networks 2007, 5(7):998-1016. 10.1016/j.adhoc.2006.04.006
Kaelbling LP, Littman ML, Moore AW: Reinforcement learning: a survey. Journal of Artificial Intelligence Research 1996, 4: 237-285.
Perkins CE, Royer EM, Das SR, Marina MK: Performance comparison of two on-demand routing protocols for Ad Hoc networks. IEEE Personal Communications 2001, 8(1):16-28. 10.1109/98.904895
Chen Y, Wang Hui(Wendy), Zheng X, Yang J: Prediction of near likely nodes in data-centric mobile wireless networks. Proceedings of the IEEE Military Communications Conference (MILCOM '09), 2009
Acknowledgment
This paper was supported in part by NSF Grant CNS-0954020. The preliminary results have been published in "Prediction of Near Likely Nodes in Data-Centric Mobile Wireless Networks" [26] in MILCOM 2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, Y., Wang, H., Zheng, X. et al. A Reinforcement Learning Based Framework for Prediction of Near Likely Nodes in Data-Centric Mobile Wireless Networks. J Wireless Com Network 2010, 319275 (2010). https://doi.org/10.1155/2010/319275
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/319275
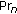 : it is used to reflect the belief from the trajectories
: it is used to reflect the belief from the trajectories  that a node
that a node 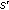 is in the same neighborhood of the node
is in the same neighborhood of the node  .
.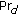 : it is used to measure the likelihood from the trajectories
: it is used to measure the likelihood from the trajectories 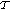 that two nodes
that two nodes 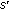 and
and  are moving in the same direction.
are moving in the same direction.
 and
and  coordinates versus time series for nodes 0 and 442 when they are moving together.
coordinates versus time series for nodes 0 and 442 when they are moving together. dimension, PCC = 0.96
dimension, PCC = 0.96 dimension, PCC = 0.96
dimension, PCC = 0.96
 .
. sends a request to all the nodes in its neighborhood. The request consists of the inquiry of the allowed data type, the size of the available storage, and the trajectory of the next
sends a request to all the nodes in its neighborhood. The request consists of the inquiry of the allowed data type, the size of the available storage, and the trajectory of the next 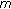 time points in the time window
time points in the time window  . The neighbor nodes reply the request of
. The neighbor nodes reply the request of  with proper information.
with proper information. collects the answers and picks the node that satisfies the above two requirements as the near likely node
collects the answers and picks the node that satisfies the above two requirements as the near likely node 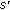 .
. sends its data to its near likely node
sends its data to its near likely node 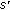 , and updates its data track table. The data track table consists of entries in the format of
, and updates its data track table. The data track table consists of entries in the format of 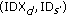 , with each entry used for tracking which node the data is stored on, so that when there is a user query for the data, node
, with each entry used for tracking which node the data is stored on, so that when there is a user query for the data, node  can efficiently redirect the query. The
can efficiently redirect the query. The 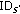 is the node identity of the near likely node that stores data with index
is the node identity of the near likely node that stores data with index  in the data track table.
in the data track table. runs step 1 and 2 from the on-demand data transfer procedure for the corresponding type of data with
runs step 1 and 2 from the on-demand data transfer procedure for the corresponding type of data with 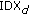 and identifies a new near likely node
and identifies a new near likely node 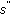 .
. then sends a request to the previous near likely node
then sends a request to the previous near likely node 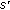 and asks
and asks  to transfer the data with
to transfer the data with  to node
to node  .
. receives the confirmation from
receives the confirmation from 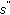 that the data transfer is successful, it updates its data track table by replacing
that the data transfer is successful, it updates its data track table by replacing 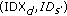 with
with 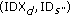 .
. to
to  , then for time window
, then for time window 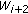 , we "reverse" the operation, that is, if the operation on
, we "reverse" the operation, that is, if the operation on  is expansion/shrinkage, we shrink/expand for
is expansion/shrinkage, we shrink/expand for  .
.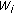 to
to 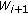 . Then we repeat the same operation on
. Then we repeat the same operation on 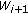 for
for  .
.










