- Research Article
- Open access
- Published:
Primal Decomposition-Based Method for Weighted Sum-Rate Maximization in Downlink OFDMA Systems
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 324780 (2010)
Abstract
We consider the weighted sum-rate maximization problem in downlink Orthogonal Frequency Division Multiple Access (OFDMA) systems. Motivated by the increasing popularity of OFDMA in future wireless technologies, a low complexity suboptimal resource allocation algorithm is obtained for joint optimization of multiuser subcarrier assignment and power allocation. The algorithm is based on an approximated primal decomposition-based method, which is inspired from exact primal decomposition techniques. The original nonconvex optimization problem is divided into two subproblems which can be solved independently. Numerical results are provided to compare the performance of the proposed algorithm to Lagrange relaxation based suboptimal methods as well as to optimal exhaustive search-based method. Despite its reduced computational complexity, the proposed algorithm provides close-to-optimal performance.
1. Introduction
Orthogonal Frequency Division Multiple Access (OFDMA) plays a major role in the physical layer specifications of future wireless technologies (e.g., 3G-LTE, WIMAX, IMT-A) [1–4]. In OFDMA systems, the transmit power and subcarriers are dynamically assigned to the users, based on their channel state information (CSI) to optimize a certain performance criteria [5–22]. In general, this process requires solving combinatorial optimization problems. Thus, the existing convex optimization techniques cannot be directly applied, and the complexity of the problem increases exponentially with the number of subcarriers.
Two main radio resource allocation (RRA) problems have been addressed in the literature. The first ones, consist of maximizing an increasing function of the user rates [5–13] subject to different power constraints, whilst the second ones consist of minimizing the transmit power subject to constraints on the minimum user rates [13–17]. A suboptimal greedy method for maximizing the smallest rate among the users has been proposed in [5]. A branch-and-bound based algorithm for sum-rate maximization has been proposed in [6]. However, in practice the branch-and-bound method is still too computationally heavy for finding the global solution [23]. Computationally efficient algorithms for maximizing the sum-rate have been developed in [7, 8]. A suboptimal method for characterizing the achievable rate region of the two-users frequency division multiple access (FDMA) channel have been presented in [10]. The general weighted sum-rate maximization problem has been used in [9] to characterize FDMA capacity region for a broadcast channel. Due to the nontractability of the original problem, a modified convex problem formulation, FDMA-time division multiple access (TDMA) was proposed (i.e., time sharing among users). Authors also considered algorithms to obtain optimal and suboptimal solutions to a particular variation of the original problem where the total power is evenly divided among the used set of subcarriers. Lagrangian relaxation-based approaches to obtain suboptimal algorithms for the weighted sum-power minimization problem has been introduced in [13, 14]. A greedy algorithm is proposed in [15] to obtain and approximate solutions for the same problem. Recently, a Lagrangian relaxation-based method has been proposed in [13] for the weighted sum-rate maximization problem. A bisection search method was used to update the dual variable until the algorithm converges. Due to the nonconvexity of the optimization problem the optimality of the algorithm is not guaranteed.
In this paper, we propose an alternative method based on the primal decomposition technique [24, 25]. Using numerical simulations, its performance is compared to Lagrangian relaxation based algorithm [13] as well as to the optimal exhaustive search algorithm. Numerical results show that the proposed algorithm converges very fast. Although, the optimality of the final value cannot be guaranteed due to the nonconvexity of the problem, the simulations show that rate-region achieved by the proposed algorithm exactly matches with the one obtained using optimal exhaustive search algorithm.
The rest of the paper is organized as follows. In Section 2 we present the system model and problem formulation. The proposed algorithm is presented in Section 3 and convergence properties are discussed in Section 4. Section 5 compares the complexity of the proposed algorithm to Lagrangian relaxation-based algorithm in [13] as well as to the optimal exhaustive search based method. The numerical simulation results are presented in Sections 6, and 7 concludes our paper.
Notations
 denotes the absolute value of complex number
denotes the absolute value of complex number  .
.  represents the transpose of vector
represents the transpose of vector  and
and  denotes the
denotes the  th standard unit vector.
th standard unit vector.  stands for circularly symmetric complex Gaussian distribution with mean
stands for circularly symmetric complex Gaussian distribution with mean  , variance
, variance  per dimension. For any real number
per dimension. For any real number  ,
,  denotes
denotes  .
.
2. System Model and Problem Formulation
Consider a single antenna (Note that, under OFDMA assumption, extension to the multiple antennas case is straightforward [26].) OFDMA downlink transmission with  users and
users and  subcarriers as shown in Figure 1. The signal received by user
subcarriers as shown in Figure 1. The signal received by user  in subcarrier
in subcarrier  can be expressed as
can be expressed as

where  is the user index,
is the user index,  is the subcarrier index,
is the subcarrier index,  denotes the set of subcarriers allocated to user
denotes the set of subcarriers allocated to user  ,
,  is the transmitted signal,
is the transmitted signal,  is the power allocated,
is the power allocated,  is channel frequency response, and
is channel frequency response, and  is the received noise. We assume that
is the received noise. We assume that  is time-invariant and its value is available at the base station. The noise samples are assumed to be independent and identically distributed as
is time-invariant and its value is available at the base station. The noise samples are assumed to be independent and identically distributed as  . We denote by
. We denote by  the channel signal-to-noise ratio (SNR) of
the channel signal-to-noise ratio (SNR) of  th user in subcarrier
th user in subcarrier  and by
and by  the weight associated with the rate of user
the weight associated with the rate of user  . The weighted sum-rate maximization problem subject to a sum-power constraint
. The weighted sum-rate maximization problem subject to a sum-power constraint  can be formulated as [13]
can be formulated as [13]

where variables are  and
and  .
.
It is also useful to introduce a virtual system where each subcarrier can be used by all users in the same time. This results in a general OFDMA downlink channel where the signal received by user  in subcarrier
in subcarrier  is given by
is given by

and the second term in the right-hand side represents the interference from other users. Assuming independent channel coding across users at the transmitter and independent decoding at receivers, the weighted sum-rate maximization problem for the virtual system can be formulated as

where the optimization variables are  . The constraints associated with orthogonal subcarrier allocations in problem (2) have been dropped out and the interference among users allocated to the same subcarrier is reflected in the objective.
. The constraints associated with orthogonal subcarrier allocations in problem (2) have been dropped out and the interference among users allocated to the same subcarrier is reflected in the objective.
Here we can make several observations. First, any solution of problem (4) is such that the second constraint in problem (2) is automatically satisfied, for reasons that will be explained in the beginning of Section 3.2. In other words, any solution of problem (4) is feasible for problem (2). Moreover, at any of these solutions the objective function of problem (4) will be exactly the same as the objective function of problem (2). Based on these observations it can be concluded that any solution of the auxiliary problem (4) is a solution for the original problem (2) as well.
The original problem (2) is combinatorial and it requires exponential complexity to find a global optimum. Although problem (4) is still nonconvex it is noncombinatorial. Thus, in the following, we focus on solving problem (4) instead of solving the original problem (2). A similar approach has been used in [7] to solve the (nonweighted) sum-rate maximization problem, that is, for the particular case  ,
, . However, the methods proposed there do not apply to the general case of arbitrary weights, for reasons that will become clear in Section 3.3. Due to the nonconvexity of problem (4) finding the global optimum is intractable. Thus, an approximative method inspired from the primal decomposition technique is presented in Section 3.
. However, the methods proposed there do not apply to the general case of arbitrary weights, for reasons that will become clear in Section 3.3. Due to the nonconvexity of problem (4) finding the global optimum is intractable. Thus, an approximative method inspired from the primal decomposition technique is presented in Section 3.
3. Approximated Primal Decomposition- (APD-) Based Algorithm
3.1. Primal Decomposition
To reveal the complicating constraints [24], we introduce  new variables
new variables  ,
,  , and reformulate the problem (4) as follows:
, and reformulate the problem (4) as follows:

where the optimization variables are  and
and  . Note that
. Note that  represents the total power on subcarrier
represents the total power on subcarrier  . Treating
. Treating  as complicating variables, problem (5) can be decomposed [24, 25] into a master problem and
as complicating variables, problem (5) can be decomposed [24, 25] into a master problem and  subproblems, one subproblem for each subcarrier
subproblems, one subproblem for each subcarrier  . For a given subcarrier
. For a given subcarrier  , the subproblem is given by
, the subproblem is given by

where variables are  ,
,  . The master problem can be expressed as
. The master problem can be expressed as

where variables are  and
and  represents the optimal value of subproblem (6) for fixed
represents the optimal value of subproblem (6) for fixed  .
.
3.2. Algorithm Derivation
Let us denote by  the feasible set of problem (6). Note that subproblem (6) is not a convex optimization problem (Since we maximize a convex function.). However, its objective function is convex with respect to (w.r.t.) optimization variables
the feasible set of problem (6). Note that subproblem (6) is not a convex optimization problem (Since we maximize a convex function.). However, its objective function is convex with respect to (w.r.t.) optimization variables  , its feasible set is a nonempty convex polyhedral set (i.e., a simplex [27]) and its objective is bounded above on
, its feasible set is a nonempty convex polyhedral set (i.e., a simplex [27]) and its objective is bounded above on  . Thus, by following the approach of [7, Section
. Thus, by following the approach of [7, Section  ], from [28, Corollary
], from [28, Corollary  ] (If a convex function
] (If a convex function  is bounded above on a convex set
is bounded above on a convex set  , then the maximum of
, then the maximum of  relative to
relative to  is attained at one of the finitely many extreme points of
is attained at one of the finitely many extreme points of  .) it follows that the solutions of subproblems (6) must be achieved at one of the vertices of the polyhedral set
.) it follows that the solutions of subproblems (6) must be achieved at one of the vertices of the polyhedral set  . Consequently, the solutions of the
. Consequently, the solutions of the  subproblems can be expressed as
subproblems can be expressed as

where  represents the index of the user allocated to
represents the index of the user allocated to  th subcarrier, that is,
th subcarrier, that is,

Solution (8) confirms that, even though in subproblems (6) all users are allowed to use all subcarriers, the optimal power allocation consists of allocating only one user per subcarrier. This guarantees that solution (8) is feasible for the original problem (2).
By substituting (8) and (9) in the objective of (6),  can be expressed as
can be expressed as


We note that the index  depends on
depends on  according to (9) and the function
according to (9) and the function  is the pointwise maximum of a set of concave functions. Therefore
is the pointwise maximum of a set of concave functions. Therefore  is not a concave function w.r.t.
is not a concave function w.r.t.  [27] in general. Thus, standard convex optimization tools (e.g., subgradient-based methods) cannot be directly applied to solve master problem (7).
[27] in general. Thus, standard convex optimization tools (e.g., subgradient-based methods) cannot be directly applied to solve master problem (7).
We propose an iterative method, where at each iteration  we first solve the
we first solve the  subproblems (6) to obtain an user-to-carrier allocation
subproblems (6) to obtain an user-to-carrier allocation  for a given subcarrier power allocation
for a given subcarrier power allocation  ,
,  . Then, the objective of the master problem is approximated by the following lower bound
. Then, the objective of the master problem is approximated by the following lower bound

where  denotes the feasible set of the master problem (7). The lower bound is concave w.r.t.
denotes the feasible set of the master problem (7). The lower bound is concave w.r.t.  and the solution of the approximated master problem can be found by multilevel waterfilling algorithm [9]. The resulting solution is used as subcarrier power allocation for the next iteration. The proposed algorithm can be summarized as follows.
and the solution of the approximated master problem can be found by multilevel waterfilling algorithm [9]. The resulting solution is used as subcarrier power allocation for the next iteration. The proposed algorithm can be summarized as follows.
Algorithm 1.
Approximated primal decomposition (APD) for OFDMA weighted sum-rate maximization.
-
(1)
initialization:
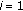 ,
, 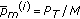 .
. -
(2)
solve the
 subproblems (6) for
subproblems (6) for 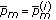 and return
and return  ,
,  computed according to (9).
computed according to (9). -
(3)
solve the following approximation of master problem (7)
 (13)
(13)and return the solution
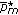 ; let
; let  .
. -
(4)
check a stopping criteria; if it is satisfied EXIT, otherwise let
 and go to step (
and go to step ( ).
).
The solution of problem (13) solved at step ( ) is given by the following multilevel waterfilling expression [9]:
) is given by the following multilevel waterfilling expression [9]:

where  is chosen such that the power constraint is satisfied with equality, that is,
is chosen such that the power constraint is satisfied with equality, that is,

3.3. Particularization to the Sum-Rate Maximization
The problem of the sum-rate maximization (i.e.,  for all
for all  ) in downlink OFDMA systems is solved in [7, Section
) in downlink OFDMA systems is solved in [7, Section  ]. The solution method is exactly equivalent to only one iteration of the APD algorithm. Unlike the general weighted sum-rate maximization, in which user weights
]. The solution method is exactly equivalent to only one iteration of the APD algorithm. Unlike the general weighted sum-rate maximization, in which user weights  's are different, in the sum-rate maximization (i.e.,
's are different, in the sum-rate maximization (i.e.,  for all
for all  ) the index
) the index  will not depend on
will not depend on  according to (9). Thus, by using (10) and (11) the function
according to (9). Thus, by using (10) and (11) the function  can be found as
can be found as  which is concave w.r.t.
which is concave w.r.t.  (recall that the function
(recall that the function  is not concave w.r.t.
is not concave w.r.t.  when the user weights
when the user weights  's are different). As a result, the inequality given in (12) holds with equality and solving problem (7) gives the optimal subcarrier power allocation [7, Section
's are different). As a result, the inequality given in (12) holds with equality and solving problem (7) gives the optimal subcarrier power allocation [7, Section  ].
].
4. Convergence Behavior and Exit Criterion
In this section, we start by investigating the monotonicity of the proposed algorithm. Then we provide a specific exit criterion which certifies that algorithm converged to a fixed power and subcarrier allocation followed by a simple graphical illustration.
4.1. Monotonic Behavior
The following theorem states the monotonic behavior of the proposed algorithm.
Theorem 1.
For any iteration  ,
,

that is, the proposed APD method is an ascent algorithm.
Proof.
From (10) and (11), it follows that the solution of (6) in iteration  is given by,
is given by,

Now we can write the following chain of relations,

where the first inequality follows from (13), the second one follows trivially from the maximization over the users, and the last equality follows from (11) and (10), respectively.
4.2. Exit Criterion
The exit criterion for such ascent algorithm is typically chosen heuristically, for example, the increasing in the objective between two successive iterations is below a certain predefined threshold. However, for the proposed algorithm we are able to find an exit criterion which certifies that algorithm converged to a fixed power and subcarrier allocation and further improvement is not possible. This is described by the following theorem.
Theorem 2.
If at iteration  , (
, ( ) we have
) we have  ,
,  then the following holds:
then the following holds:
-
(1)
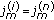 , for all
, for all 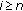 ,
,  ,
, -
(2)
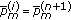 , for all
, for all 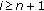 ,
,  ,
, -
(3)
 , for all
, for all  .
.
That is, the algorithm converges to a fixed power and subcarrier allocation.
Proof.
Since  's are continuous random variables, the probability to have multiple solutions for (9) is zero. Thus, in the following we assume that
's are continuous random variables, the probability to have multiple solutions for (9) is zero. Thus, in the following we assume that  given by (9) is unique (Equation (9) has multiple solutions if and only if
given by (9) is unique (Equation (9) has multiple solutions if and only if  for some
for some  . When
. When  we assign
we assign  any arbitrarily user index.).
any arbitrarily user index.).
Note that the objective function of (13) is strictly concave. Thus it has a unique solution [27]. Therefore, for all  ,
, implies that
implies that . Since (9) has a unique solution as well,
. Since (9) has a unique solution as well, further implies that
further implies that . Since we have shown that
. Since we have shown that implies that
implies that , item (
, item ( ) follows directly by induction. Furthermore, item (
) follows directly by induction. Furthermore, item ( ) follows from item (
) follows from item ( ) by the uniqueness of the solution of problem (13). Finally, item (
) by the uniqueness of the solution of problem (13). Finally, item ( ) follows trivially from item (
) follows trivially from item ( ).
).
Thus the exit criterion checks if the subcarrier allocation between two successive iterations remains unchanged. Such point is a local optimum (possible global) in the sense that the objective cannot be increased by changing the power allocation or subcarrier allocation only.
As a specific example, consider the simple OFDMA system with two subcarriers (i.e.,  ). By performing the variable transformations
). By performing the variable transformations and
and ,
, , we can express the variation of
, we can express the variation of on
on as,
as,

which is plotted in Figure 2. According to Figure 2(a) global optimal is achieved at the iteration  . Achieving global optimality is not always possible because, quasiconcavity [27] of
. Achieving global optimality is not always possible because, quasiconcavity [27] of  cannot be guaranteed with random channel SNR,
cannot be guaranteed with random channel SNR,  . Consequently the APD algorithm can converge to a local optimal solution as shown in Figure 2(b).
. Consequently the APD algorithm can converge to a local optimal solution as shown in Figure 2(b).
5. Complexity Analysis
In this section, we analyze and compare the computational complexity of the proposed APD algorithm to Lagrangian relaxation-based algorithm [13] as well as to the optimal exhaustive search algorithm. With  users and
users and  subcarriers, altogether we have
subcarriers, altogether we have  user-subcarrier combinations. Therefore finding optimal subcarrier and power assignment requires
user-subcarrier combinations. Therefore finding optimal subcarrier and power assignment requires  searches. Combined with multilevel waterfilling at each instance of subcarrier assignment,
searches. Combined with multilevel waterfilling at each instance of subcarrier assignment,  operations are required to find the solution. The algorithm proposed in [13] for the weighted sum-rate maximization problem requires
operations are required to find the solution. The algorithm proposed in [13] for the weighted sum-rate maximization problem requires  operations to obtain a suboptimal solution. The proposed APD algorithm described in Section 3 requires
operations to obtain a suboptimal solution. The proposed APD algorithm described in Section 3 requires  operations in step (
operations in step ( ) and
) and operations (This is the number of operations required in ordering.) in step (
operations (This is the number of operations required in ordering.) in step ( ). In practice, it is reasonable to assume that
). In practice, it is reasonable to assume that (The assumption is reasonable since the number of users simultaneously serviced by the system can be very large. For example, in a Wi-Max system
(The assumption is reasonable since the number of users simultaneously serviced by the system can be very large. For example, in a Wi-Max system  can be up to
can be up to  [29]. However, the value of
[29]. However, the value of  will not become very large (in a WiMax system
will not become very large (in a WiMax system at most).). Therefore the complexity of the APD algorithm can be approximated by
at most).). Therefore the complexity of the APD algorithm can be approximated by  .
.
6. Numerical Results
The performance of the proposed APD algorithm is compared to the dual decomposition-based algorithm proposed in [13], denoted as WSRmax, as well as to the optimal algorithm based on exhaustive search. The WSRMax algorithm uses a bisection search method to update the dual variable  [13, Section IV]. For initializing the bisection search interval,
[13, Section IV]. For initializing the bisection search interval,  , we exploit the fact that the subgradient of the dual function can be analytically computed. Since the dual function is convex, the sign of its subgradients changes as we pass through the minimum point of the dual function [13, equation (
, we exploit the fact that the subgradient of the dual function can be analytically computed. Since the dual function is convex, the sign of its subgradients changes as we pass through the minimum point of the dual function [13, equation ( )]. Therefore, we use a grid search (with step size
)]. Therefore, we use a grid search (with step size  ) to identify the interval in which the subgradient of dual function changes its sign, and it is used as initial bisection search interval. Thus, the interval
) to identify the interval in which the subgradient of dual function changes its sign, and it is used as initial bisection search interval. Thus, the interval  is guaranteed to contain the optimal value of the the dual function and the width of the initial interval is one, that is,
is guaranteed to contain the optimal value of the the dual function and the width of the initial interval is one, that is,  . The proposed APD algorithm is initialized by allocating equal power to all subcarriers.
. The proposed APD algorithm is initialized by allocating equal power to all subcarriers.
In what follows, we compare the convergence behavior of the APD and the WSRMax algorithms. For a fair comparison, we define the following metric:

the average normalized weighted sum-rate deviation, where  is the optimal weighted sum-rate value obtained using optimal exhaustive search,
is the optimal weighted sum-rate value obtained using optimal exhaustive search,  is the estimated objective value from either the APD algorithm or the WSRMax algorithm, and expectation
is the estimated objective value from either the APD algorithm or the WSRMax algorithm, and expectation  is taken w.r.t. channel realization. An OFDMA system with
is taken w.r.t. channel realization. An OFDMA system with  subcarriers and a uniform power delay profile with
subcarriers and a uniform power delay profile with  channel taps is considered. We assume
channel taps is considered. We assume ,
, ,
, and define SNR per subcarrier as
and define SNR per subcarrier as .
.
Figure 3 shows the convergence behavior of the considered algorithms with SNR dB for
dB for  and
and  users. The weights of the users are
users. The weights of the users are  for
for  and
and  for
for  . The floor of the curves is due to the suboptimality of the algorithms. The results show that the APD algorithm converges faster than the WSRMax algorithm and provides smaller average normalized weighted sum-rate deviations. Specifically, for both cases,
. The floor of the curves is due to the suboptimality of the algorithms. The results show that the APD algorithm converges faster than the WSRMax algorithm and provides smaller average normalized weighted sum-rate deviations. Specifically, for both cases,  and
and  , the APD algorithm requires only
, the APD algorithm requires only  iterations on average to achieve an average normalized weighted sum-rate deviation of
iterations on average to achieve an average normalized weighted sum-rate deviation of  whilst the WSRMax algorithm requires around
whilst the WSRMax algorithm requires around  iterations to reach the same accuracy level. It is intuitively obvious that the number of iterations required by the APD algorithm is sensitive to the nature of the surface of the objective function
iterations to reach the same accuracy level. It is intuitively obvious that the number of iterations required by the APD algorithm is sensitive to the nature of the surface of the objective function  of problem (7), for example, see Figure 2. In general, it is a hard to quantify the number of iterations before convergence (or any bounds on the number of iterations) due to the nonconvexity of problem (5). However, the numerical results suggest that the APD algorithm often converges very fast in practice. It should be emphasized that the number of iterations required in the initialization of the WSRmax algorithm (i.e., the number of iterations required to find the initial bisection search interval) is not considered when drawing the curves. In particular, for the initialization process, the WSRMax algorithm requires a several number of steps (each step has complexity of
of problem (7), for example, see Figure 2. In general, it is a hard to quantify the number of iterations before convergence (or any bounds on the number of iterations) due to the nonconvexity of problem (5). However, the numerical results suggest that the APD algorithm often converges very fast in practice. It should be emphasized that the number of iterations required in the initialization of the WSRmax algorithm (i.e., the number of iterations required to find the initial bisection search interval) is not considered when drawing the curves. In particular, for the initialization process, the WSRMax algorithm requires a several number of steps (each step has complexity of  ) and the proposed APD algorithm requires none. Moreover, it is hard to find good initialization methods for the WSRMax algorithm (i.e., initialization for bisection search method) compromising between the number of steps required in the initialization and the width of the initial searching interval
) and the proposed APD algorithm requires none. Moreover, it is hard to find good initialization methods for the WSRMax algorithm (i.e., initialization for bisection search method) compromising between the number of steps required in the initialization and the width of the initial searching interval  . Consequently, additional precautions are required and therefore, in practical implementations the APD algorithm is more favorable compared to the WSRMax algorithm.
. Consequently, additional precautions are required and therefore, in practical implementations the APD algorithm is more favorable compared to the WSRMax algorithm.
In the sequel, we compare the behavior of the APD and the WSRMax algorithms using the following metric:

the probability of missing the global optimal, where  is a small number which quantifies the maximum admissible deviation between
is a small number which quantifies the maximum admissible deviation between  and
and  . It is considered that the global optimum is missed if
. It is considered that the global optimum is missed if  is more than
is more than  away from
away from  .
.
Figure 4 uses the same simulation setup as that in Figure 3 and depicts the variation of probability of missing the global optimal,  with the number of iterations. The floor of probability
with the number of iterations. The floor of probability  is again due to the suboptimality of both algorithms. The influence of
is again due to the suboptimality of both algorithms. The influence of  on
on  is totally indistinguishable in case of the APD algorithm. This behavior shows that the proposed algorithm APD can arrive very close-to-optimal solutions within a very small number of iterations and then it remains there. The results further show that the
is totally indistinguishable in case of the APD algorithm. This behavior shows that the proposed algorithm APD can arrive very close-to-optimal solutions within a very small number of iterations and then it remains there. The results further show that the  evaluated using the WSRMax algorithm is highly dependent on
evaluated using the WSRMax algorithm is highly dependent on  . That is, the smaller the deviations in the
. That is, the smaller the deviations in the  from the optimal
from the optimal  , the larger the number of iterations required by the WSRMax algorithm to reach the expected target value
, the larger the number of iterations required by the WSRMax algorithm to reach the expected target value  . Therefore, independent from the
. Therefore, independent from the  , the APD algorithm allows to find a suboptimal solution within a small number of iterations at the expense of a slight increase in
, the APD algorithm allows to find a suboptimal solution within a small number of iterations at the expense of a slight increase in  . These observations are very useful in practice since they carry significant information in the system design point of view. For example, consider a design requirement
. These observations are very useful in practice since they carry significant information in the system design point of view. For example, consider a design requirement  . Here, the WSRmax algorithm requires 18 iterations. If we tight more the design requirement as
. Here, the WSRmax algorithm requires 18 iterations. If we tight more the design requirement as  , then the number of iterations required by the WSRmax increases to 24. In contrast, the APD algorithm always requires just one iteration.
, then the number of iterations required by the WSRmax increases to 24. In contrast, the APD algorithm always requires just one iteration.
Figure 5 shows the rate region (The standard way to characterize the boundary points in the 2-user rate region is by solving problem (4) for  and
and  , where
, where  [30].) computed by using all considered algorithms. The same simulation setup as in [13] was used where
[30].) computed by using all considered algorithms. The same simulation setup as in [13] was used where  ,
,  ,
,  and the channel SNR vectors for users
and the channel SNR vectors for users  and
and  are
are  and
and  , respectively. Although the computational complexity of the proposed algorithm is much smaller compared to that of optimal exhaustive search-based method, Figure 5 indicates that the rate region obtained by the APD algorithm almost coincides with the optimal rate region. This behavior is expected since the average normalized weighted sum-rate deviation, (20) is in the order of
, respectively. Although the computational complexity of the proposed algorithm is much smaller compared to that of optimal exhaustive search-based method, Figure 5 indicates that the rate region obtained by the APD algorithm almost coincides with the optimal rate region. This behavior is expected since the average normalized weighted sum-rate deviation, (20) is in the order of  as shown in Figure 3.
as shown in Figure 3.
In the following we compare the behavior of the APD and the WSRmax algorithm for large number of subcarriers and users. Since, for large number of users and subcarriers the complexity of evaluating  is prohibitively high, the metrics defined in (20) and (21) are not used. The behavior of the APD algorithm is compared with that of the WSRmax algorithm.
is prohibitively high, the metrics defined in (20) and (21) are not used. The behavior of the APD algorithm is compared with that of the WSRmax algorithm.
In Figure 6, the evolution of the expected weighted sum-rate provided by the APD algorithm is compared to the resulting expected weighted sum-rate from the WSRmax algorithm, where the expectation is taken w.r.t. channel realization. An OFDMA system with  subcarriers, a uniform power delay profile with
subcarriers, a uniform power delay profile with  channel taps, and
channel taps, and  users is considered. The weights of the users are taken from the sequence
users is considered. The weights of the users are taken from the sequence  , (e.g., when
, (e.g., when  , weights are [
, weights are [ ]). The SNR is assumed to be
]). The SNR is assumed to be  dB. The results show that even for a large number of carriers, the APD algorithm converges very fast as compared to the WSRMax algorithm independent of the number of users.
dB. The results show that even for a large number of carriers, the APD algorithm converges very fast as compared to the WSRMax algorithm independent of the number of users.
7. Conclusions
A joint subcarrier and power allocation algorithm which is inspired from primal decomposition techniques has been proposed for maximizing the weighted sum-rate in multiuser OFDMA downlink systems. Although the original problem is nonconvex, the proposed APD algorithm finds fast a suboptimal, but still very close-to-optimal solution with very high probability (i.e., more than  of the time). Unlike the recently proposed WSRMax algorithm [13], the APD algorithm requires no additional precautions in the initialization, and convergence to a suboptimal solution is possible within a very small number of iterations. Although the proposed primal decomposition-based solution method does not rely on zero duality gap for proving the optimality in the case of large number of subcarriers, our computational experience with larger number of subcarriers suggests that the proposed APD algorithm is capable of finding the same solution as the WSRmax algorithm (which is asymptotically optimal when the number of carriers grows to
of the time). Unlike the recently proposed WSRMax algorithm [13], the APD algorithm requires no additional precautions in the initialization, and convergence to a suboptimal solution is possible within a very small number of iterations. Although the proposed primal decomposition-based solution method does not rely on zero duality gap for proving the optimality in the case of large number of subcarriers, our computational experience with larger number of subcarriers suggests that the proposed APD algorithm is capable of finding the same solution as the WSRmax algorithm (which is asymptotically optimal when the number of carriers grows to  ) even with very few iterations.
) even with very few iterations.
References
Sesia S, Toufic I, Baker M: LTE—The UMTS Long Term Evolution. John Wiley & Son, Oxford, UK; 2009.
Ali SH, Lee K-D, Leung VCM: Dynamic resource allocation in OFDMA wireless metropolitan area networks [Radio Resource Management and Protocol Engineering for IEEE 802.16]. IEEE Wireless Communications 2007, 14(1):6-13.
Kwon T, Lee H, Choi S, et al.: Design and implementation of a simulator based on a cross-layer protocol between MAC and PHY layers in a WiBro compatible. IEEE Communications Magazine 2005, 43(12):136-146.
Huang CY, Juan H-H, Lin M-S, Chang C-J: Radio resource management of heterogeneous services in mobile WiMAX systems. IEEE Wireless Communications 2007, 14(1):20-26.
Rhee W, Cioffi M: Increase in capacity of multiuser OFDM system using dynamic subchannel allocation. Proceedings of the IEEE Vehicle Technology Conference, May 2000, Tokyo, Japan 2: 1085-1089.
Mao Z, Wang X: Branch-and-bound approach to OFDMA radio resource allocation. Proceedings of the IEEE Vehicle Technology Conference, September 2006, Montreal, Canada 1-5.
Li G, Liu H: On the optimality of the OFDMA network. IEEE Communications Letters 2005, 9(5):438-440. 10.1109/LCOMM.2005.1431164
Jang J, Lee KB: Transmit power adaptation for multiuser OFDM systems. IEEE Journal on Selected Areas in Communications 2003, 21(2):171-178. 10.1109/JSAC.2002.807348
Hoo LMC, Halder B, Tellado J, Cioffi JM: Multiuser transmit optimization for multicarrier broadcast channels: asymptotic FDMA capacity region and algorithms. IEEE Transactions on Communications 2004, 52(6):922-930. 10.1109/TCOMM.2004.829570
Yu W, Cioffi JM: FDMA capacity of Gaussian multiple-access channels with ISI. IEEE Transactions on Communications 2002, 50(1):102-111. 10.1109/26.975766
Bae CS, Cho D-H: Fairness-aware adaptive resource allocation scheme in multihop OFDMA systems. IEEE Communications Letters 2007, 11(2):134-136.
Shen Z, Andrews JG, Evans BL: Adaptive resource allocation in multiuser OFDM systems with proportional rate constraints. IEEE Transactions on Wireless Communications 2005, 4(6):2726-2736.
Seong K, Mohseni M, Cioffi JM: Optimal resource allocation for OFDMA downlink systems. Proceedings of the IEEE International Symposium on Information Theory, July 2006, Seattle, Wash, USA 1394-1398.
Wong CY, Cheng RS, Letaief KB, Murch RD: Multiuser OFDM with adaptive subcarrier, bit, and power allocation. IEEE Journal on Selected Areas in Communications 1999, 17(10):1747-1758. 10.1109/49.793310
Zhang G: Subcarrier and bit allocation for real-time services in multiuser OFDM systems. Proceedings of the IEEE International Conference on Communications, June 2004, Paris, France 5: 2985-2989.
Kivanc D, Li G, Liu H: Computationally efficient bandwidth allocation and power control for OFDMA. IEEE Transactions on Wireless Communications 2003, 2(6):1150-1158. 10.1109/TWC.2003.819016
Ho WWL, Liang Y-C: Optimal resource allocation for multiuser MIMO-OFDM systems with user rate constraints. IEEE Transactions on Vehicular Technology 2009, 58(3):1190-1203.
Wong CY, Cheng RS, Letaief KB, Murch RD: Multiuser OFDM with adaptive subcarrier, bit, and power allocation. IEEE Journal on Selected Areas in Communications 1999, 17(10):1747-1758. 10.1109/49.793310
Ergen M, Coleri S, Varaiya P: QoS aware adaptive resource allocation techniques for fair schesuling in OFDMA based broadband wireless access systems. IEEE Transactions on Broadcasting 2003, 49(4):362-370. 10.1109/TBC.2003.819051
Li G, Liu H: Downlink radio resource allocation for multi-cell OFDMA system. IEEE Transactions on Wireless Communications 2006, 5(12):3451-3459.
Li G, Liu H: Resource allocation for OFDMA relay networks with fairness constraints. IEEE Journal on Selected Areas in Communications 2006, 24(11):2061-2068.
Kim I, Park I-S, Lee YH: Use of linear programming for dynamic subcarrier and bit allocation in multiuser OFDM. IEEE Transactions on Vehicular Technology 2006, 55(4):1195-1207. 10.1109/TVT.2006.877490
Bertsekas DP: Network Optimization Continuous and Discrete Models. Athens Scientific, Belmont, Mass, USA; 1999.
Boyd S: Primal and dual decomposition. Course reader for convex optimization II, Stanford. 2007, http://www.stanford.edu/class/ee364b/
Palomar DP, Chiang M: Alternative distributed algorithms for network utility maximization: framework and applications. IEEE Transactions on Automatic Control 2007, 52(12):2254-2269.
Tse D, Viswanath P: Fundamentals of Wireless Communication. Cambridge University Press, Cambridge, UK; 2005.
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, UK; 2004.
Rockafellar RT: Convex Analysis. Princeton University Press, Prinston, NJ, USA; 1970.
Nuaymi L: WiMax Technology for Broadband Wireless Access. John Wiley & Sons publication, Oxford, UK; 2007.
Tse DN: Optimal power allocation over parallel Gaussian broadcast channels. Proceedings of the IEEE International Symposium on Information Theory, 1997, Ulm, Germany 27.
Acknowledgment
This research was supported by the Finnish Funding Agency for Technology and Innovation (Tekes), Academy of Finland, Nokia, Nokia Siemens Networks, Elektrobit, Graduate School in Electronics, Telecommunications and Automation (GETA) Foundations, Nokia Foundation, and Tauno Tönning Foundation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Weeraddana, C., Codreanu, M., Li, W. et al. Primal Decomposition-Based Method for Weighted Sum-Rate Maximization in Downlink OFDMA Systems. J Wireless Com Network 2010, 324780 (2010). https://doi.org/10.1155/2010/324780
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/324780

 users and
users and
 subcarriers.
subcarriers.
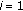 ,
, 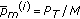 .
. subproblems (6) for
subproblems (6) for 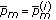 and return
and return  ,
,  computed according to (9).
computed according to (9).
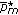 ; let
; let  .
. and go to step (
and go to step ( ).
).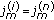 , for all
, for all  ,
,  ,
,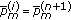 , for all
, for all 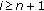 ,
,  ,
, , for all
, for all  .
.

 and
and
 users,
users,
 subcarriers, and SNR = 10 dB.
subcarriers, and SNR = 10 dB.

 users,
users,
 subcarriers, and SNR = 10 dB.
subcarriers, and SNR = 10 dB.

 users and
users and
 subcarriers.
subcarriers.

 = 8,16,32,64 users,
= 8,16,32,64 users,
 subcarriers, and SNR = 10 dB.
subcarriers, and SNR = 10 dB.