- Research Article
- Open access
- Published:
Combined Distributed Turbo Coding and Space Frequency Block Coding Techniques
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 327041 (2010)
Abstract
The distributed space-time (frequency) coding and distributed channel turbo coding used independently represent two cooperative techniques that can provide increased throughput and spectral efficiency at an imposed maximum Bit Error Rate (BER) and delay required from the new generation of cellular networks. This paper proposes two cooperative algorithms that employ jointly the two types of techniques, analyzes their BER and spectral efficiency performances versus the qualities of the channels involved, and presents some conclusions regarding the adaptive employment of these algorithms.
1. Introduction
Most of the services that should be provided by future wireless networks require low or very low  and delay values and high data rates. The cooperative transmission techniques represent one of the most promising solutions in wireless networks for provisioning the increased capacity, extended coverage, and improved fairness [1–3] required by such services. They could ensure low
and delay values and high data rates. The cooperative transmission techniques represent one of the most promising solutions in wireless networks for provisioning the increased capacity, extended coverage, and improved fairness [1–3] required by such services. They could ensure low  , while still inserting limited transmission delays, and also significantly improve the spectral efficiency of wireless systems.
, while still inserting limited transmission delays, and also significantly improve the spectral efficiency of wireless systems.
Another technique that could fulfill the above requirements is the Multiple Input Multiple Output-Orthogonal Frequency Division Multiplexing (MIMO-OFDM) [4, 5], which has already been adopted in high rate wireless communications standards, such as WiMAX and LTE. However, considering a conventional cellular architecture with colocated antennas, there is significant correlation between channels in some environments; moreover, the use of an antenna array at the user terminals (UTs) may not be feasible due to size, cost, and hardware limitations. The OFDM-MIMO could be also implemented through cooperation of users, which share their antennas and thereby create a Virtual Antenna Array (VAA) or a Virtual MIMO (VMIMO) system. In this context, the concept of Distributed Space-Time Coding (DSTC) was introduced in [6, 7]. This approach allows single-antenna devices to gain some benefits from spatial diversity without the need for physical antenna arrays. Several recent works [8, 9] have considered either the design of DSTC or Distributed Space-Frequency Coding (DSFC) or the application of the existing space-time/frequency codes in a distributed manner for the wireless relay-based systems. The use of Space-Time Block Coding (STBC) based on Alamouti schemes [10] implemented in a distributed manner in OFDM-based cooperative schemes has been discussed in [11, 12], while a full-rate and full-diversity quasiorthogonal STBC scheme to be applied in virtual antenna arrays was proposed in [13]. In [14], Distributed Space-Frequency Block Coding (DSFBC) schemes for OFDM-based cellular systems which use an antenna array at the BS and a single antenna at both the UT and RN have been proposed.
Another cooperative approach that aims at exploiting diversity is the Distributed Forward Error Correction Coding (DFEC). Such a cooperation scheme, proposed in [15], was intended initially to create transmit diversity in the uplink of a wireless system. Using standard FEC, partitioning of code words and transmitting these parts by the cooperating partners, together with error detection at each partner, could overcome the drawbacks of a simple cooperation based on repetition coding. The performances of FEC-based cooperation schemes were investigated under various channel conditions and power allocation modes in [16, 17], while some algorithms are provided in [18] and throughput maximization methods are provided in [19]. Niu and Lu [20] have combined the OFDM flexible subcarrier allocation with distributed coding, extending the cooperative communication strategy from the time domain to the time-frequency domain, by incorporating the Orthogonal Frequency-Division Multiple Access (OFDMA) concept. Practical distributed coding protocols that use Rate-Compatible Punctured Convolutional Codes (RCPCC) were proposed and investigated in [21]. This approach ensures high performances both for Amplify & Forward (AF) and Decode & Forward (DF) relaying schemes, while maintaining a low complexity.
One step further is the joint use of cooperative techniques, such as DST(F)BC or DFEC, with Network Coding (NC), which combines the advantages provided by each of the involved techniques and diminishes their shortcomings. Recent papers, such as [22–25], propose various versions of combining these techniques which provide results that are more than promising. Nevertheless, the employment of NC-based techniques involves more elaborate cluster-selection techniques which seem to be difficult to implement in the present mobile cellular systems.
Therefore, this paper proposes two cooperation algorithms, serving one UT, that employ in a joint manner the distributed space frequency coding and distributed FEC, analyzes their performances and compares these performances with those of DSFC and DFEC cooperation algorithms used independently. The paper is structured as follows: Section 2 explains briefly the motivation of this study, while Section 3 presents the cooperation protocol and topologies used and briefly arguments their selection. Section 4 describes the DSFC and DFEC cooperative algorithms and the proposed combined DSFC+DFEC cooperation algorithms, while Section 5 briefly discusses the evaluation of their spectral efficiency. Section 6 describes the performance metrics employed and the test scenarios used for performance evaluation; it presents the simulation results obtained and analyzes these results. Finally, Section 7 presents some conclusions regarding the selection of the cooperative algorithm according to the given topology, scenario, and type of service that has to be provided.
2. Motivation and Objectives
The performances of the cooperative algorithms,  , Bloc Error Rate (BLER), and spectral efficiency, are strongly affected by the combining method of the signals received on the source—destination and on the relay (relays)—destination links. Two main categories of message-combining methods could be used:
, Bloc Error Rate (BLER), and spectral efficiency, are strongly affected by the combining method of the signals received on the source—destination and on the relay (relays)—destination links. Two main categories of message-combining methods could be used:
-
(i)
symbol-level combining, which is specific to space-time/space-frequency coding and to maximum ratio combining. These message combining techniques provide diversity gain,
-
(ii)
bit-level combining, that is, bit-LLRs addition and/or concatenation, which is characteristic to distributed FEC. These message combining techniques provide less diversity gain, but they provide coding gain.
These combining methods exhibit different degrees of flexibility, when employed in different cooperative transmission scenarios. Symbol-level combining requires the same constellation on each transmission link, regardless of the significantly different qualities of the channels employed by each cooperation phase. Bit-level combining has a greater flexibility, allowing the use of different constellations on different transmission links, according to each channel state, fact that has significant impact upon the spectral efficiency.
The joint use of the two types of message combining could ensure both improved  and flexibility, thus providing greater spectral efficiency. One way to achieve this mix of message combining in cooperative networks would be to employ in a joint manner distributed FEC and distributed diversity techniques, thus providing both coding and diversity gains.
and flexibility, thus providing greater spectral efficiency. One way to achieve this mix of message combining in cooperative networks would be to employ in a joint manner distributed FEC and distributed diversity techniques, thus providing both coding and diversity gains.
The main objective of the paper is to analyze the performances of some particular cooperation algorithms combining DSFC and DFEC within a topology containing a virtual MIMO scheme that uses the antennae of one or two relay nodes (RNs), to compare their  and spectral efficiency performances to those of cooperation schemes using independently either the DSFC or DFEC techniques, and to identify scenarios within which these combined distributed coding schemes provide greater spectral efficiencies at an imposed
and spectral efficiency performances to those of cooperation schemes using independently either the DSFC or DFEC techniques, and to identify scenarios within which these combined distributed coding schemes provide greater spectral efficiencies at an imposed  . The applicability of these algorithms to several types of services, according to the
. The applicability of these algorithms to several types of services, according to the  and spectral efficiency requirements, will also be briefly considered.
and spectral efficiency requirements, will also be briefly considered.
3. Cooperation Protocol and Topologies
This paper considers a test topology, with single-antenna equipments, where two dedicated relay nodes (RN1, RN2), fixed or nomadic, assist the communication between the Base Station (BS) and the UT. The access scheme is OFDMA, the constellations used are QPSK, 16, and 64 QAM and all point-to-point transmissions are Single Input Single Output (SISO) ones.
The cooperative algorithms studied employ the classical two-phase cooperation protocol, which are supposed to occur successively in time, but might not use the same signal constellation.
-
(1)
In the "broadcast phase", the source node (BS or UT) sends its message to the RN and to the destination node (UT or BS, resp.). The content of the broadcast message is specific to the cooperation algorithm employed.
-
(2)
In the "relaying phase", the RNs decode the received message, perform the processing specific to the cooperation algorithm employed and send their messages to destination (UT or BS).
The destination jointly decodes the information received from the RNs or both from the source and RNs, according to the cooperation algorithm.
The two phases of the cooperation protocol applied to this topology are illustrated in Figure 1 for the downlink (DL) connection; that is, the broadcast message is transmitted to the RNs and UT, while the relay message, which depends on the DFEC algorithm employed, is transmitted jointly by the two RNs using a cooperative diversity scheme, like DSTC or DSFC. The message sent during the broadcast phase might be employed or not by the destination's receiver.
Since the number of RNs is limited by relay assignment, resource allocation and signaling issues, the test topology can be simplified by imposing the source to act as one of the RNs and transmit both during the broadcast phase, as source, and during the relaying phase, as one of the RNs, as shown in Figure 1.
The asymmetrical two-RN topology, with different  ratios received from the two RNs, could be transformed into a symmetrical topology for easier analysis and simulation, by considering an equivalent
ratios received from the two RNs, could be transformed into a symmetrical topology for easier analysis and simulation, by considering an equivalent  value that is received from each RN on the RN-destination links, as shown in Figure 2.
value that is received from each RN on the RN-destination links, as shown in Figure 2.
4. Cooperative Distributed Coding Algorithms
This section gives a short overview of the cooperation algorithms employing Alamouti-based DSFC and Turbo Coding (TC)-based DFEC techniques and describes the proposed combined DSFC-DFEC cooperation algorithms.
4.1. Distributed Space-Frequency Coding (DSFC)
The topology with two RNs contains five links; namely, the direct BS-UT link, defined by the  channel, the BS-RN
i
links
channel, the BS-RN
i
links  , defined by the
, defined by the 
 channels, and the RNi-UT links, defined by channels
channels, and the RNi-UT links, defined by channels 
 , as shown in Figure 1. Within the topology with one RN, the BS-RN2 link is an ideal one, while the RN2-UT link is represented by another realization of the
, as shown in Figure 1. Within the topology with one RN, the BS-RN2 link is an ideal one, while the RN2-UT link is represented by another realization of the  channel.
channel.
The operations performed by this DSFC algorithm during cooperation are briefly described below.
-
(1)
In the broadcast phase, the source node transmits the coded block (
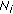 information bits and
information bits and 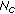 check bits) towards the RNs and destination, using a modulation adapted to the channels involved.
check bits) towards the RNs and destination, using a modulation adapted to the channels involved. -
(2)
In the relaying phase, the RNs decode and re-encode the message with the same FEC code, apply a DSFC-Alamouti scheme [10] and transmit their perfectly synchronized messages on the RN i -destination channels using the same signal constellation (not necessarily the same as in the first phase).
-
(3)
At the destination end, the DSFC-decoded symbols and the ones received from the source during the broadcast phase are MRC-combined to provide the symbols that are fed to the FEC decoder. Because this algorithm uses at destination signals received both from RNs and the source, it will be denoted as the composed DSFC, c-DSFC. Since the messages received during the cooperation phases are combined at QAM-symbol level, all links should use the same modulation.
To point out the effects of the direct link transmission upon the performance of the DSFC scheme, an alternative version, called simple DSFC (s-DSFC), which does not use the direct link at the receiver's end, is also considered. Hence, different signal constellations might be used during the two cooperation phases.
In the subsequent sections, we consider that all channels involved are complex flat Rayleigh-faded channels, and the noise samples have zero-mean and variance equaling  . We also consider that the OFDM subcarrier separation is significantly lower than the channel's coherence bandwidth, and so, the fading over two adjacent subcarriers can be considered flat.
. We also consider that the OFDM subcarrier separation is significantly lower than the channel's coherence bandwidth, and so, the fading over two adjacent subcarriers can be considered flat.
Considering the c-DSFC algorithm, the instantaneous  on subcarrier
on subcarrier  obtained after the MRC-combining performed at destination between the symbols received on the direct link and those provided by the Alamouti decoding of the DSFC signals on the RNi-destination links is [14, 26]
obtained after the MRC-combining performed at destination between the symbols received on the direct link and those provided by the Alamouti decoding of the DSFC signals on the RNi-destination links is [14, 26]

where  represents the complex coefficient of the flat Rayleigh faded BS-UT channel, during the broadcast phase, for the
represents the complex coefficient of the flat Rayleigh faded BS-UT channel, during the broadcast phase, for the  th subcarrier with an average power
th subcarrier with an average power  ,
,  denotes the RNi-UT channel during relaying phase, for the
denotes the RNi-UT channel during relaying phase, for the  th subcarrier with an average power of
th subcarrier with an average power of  , in the assumption that the fading over two adjacent subcarriers can be considered flat; that is,
, in the assumption that the fading over two adjacent subcarriers can be considered flat; that is,  is equal to
is equal to  . We also assume that the noise variance of the signals received at the UT during the two phases to be equal, that is,
. We also assume that the noise variance of the signals received at the UT during the two phases to be equal, that is,  .
.
If the topology with one RN is considered, see Figure 1, then the BS acts as the second RN (in the DL), and therefore, in relation (1),  should be replaced by
should be replaced by  , the complex flat Rayleigh BS-UT channel's realization for the
, the complex flat Rayleigh BS-UT channel's realization for the  th subcarrier during the relaying phase.
th subcarrier during the relaying phase.
If the direct link is not used in the decoding process at the receiving end (the s-DSFC algorithm) the instantaneous  on subcarrier
on subcarrier  is expressed in a similar manner by (2) [14, 26] and is smaller that the one ensured by the c-DSFC algorithm, see(1)
is expressed in a similar manner by (2) [14, 26] and is smaller that the one ensured by the c-DSFC algorithm, see(1)

If the channels are correctly equalized, we may assume that the LLRs of all bits of the FEC codeword are extracted from the same equivalent channel, with SNRs expressed by (1) for the algorithm which employ the source-destination link, respectively, by (2) for topologies which do not employ this link.
4.2. Distributed FEC Cooperation Algorithms
Distributed FEC algorithms use the classical two-phase cooperation protocol [16, 17], applied within a topology with one RN, for example, RN1, which is particularized in Figure 3. Most of distributed FEC algorithms use the same encoder both at source and at RN, some of them employing different puncturing patterns for the two transmissions. Usually, Convolutional Turbo Codes (CTCs) or Low Density Parity Check (LDPC) codes are employed to implement the distributed FEC.
4.2.1. Distributed FEC with Incremental Redundancy
The Incremental Redundancy DFEC (IR-DFEC) algorithm that uses CTCs is briefly described below and represented in Figure 3.
-
(i)
Broadcast Phase
The UT (or the BS) encodes the  information bits using a CTC code with a coding rate
information bits using a CTC code with a coding rate  (the mother code rate). The resulted check bits are appropriately punctured according to a rate matching algorithm [27], to obtain a desired coding rate
(the mother code rate). The resulted check bits are appropriately punctured according to a rate matching algorithm [27], to obtain a desired coding rate  . The resulted coded blocks of length
. The resulted coded blocks of length  are then sent by the source (UT or BS) over the source-destination and source-RN links.
are then sent by the source (UT or BS) over the source-destination and source-RN links.
-
(ii)
Relaying Phase
The RN decodes the received block, using a turbo decoder, and it re-encodes these bits using the same CTC encoder. Then, it selects a number of additional check bits  , by using a different puncturing pattern corresponding to a coding rate
, by using a different puncturing pattern corresponding to a coding rate  , and these bits are transmitted over the RN-destination link. The two coding rates
, and these bits are transmitted over the RN-destination link. The two coding rates  and
and  are chosen so that the global coding rate,
are chosen so that the global coding rate,  , which is expressed by (3), would equal the rate of the mother code
, which is expressed by (3), would equal the rate of the mother code

-
(iii)
Decoding
At destination, before turbodecoding, the blocks received both from source and RN are assembled and completed according to the employed puncturing rules. The  information and the
information and the  check bits generated by the source are received at smaller equivalent
check bits generated by the source are received at smaller equivalent  values,
values,  , than the
, than the  check bits generated by the relay,
check bits generated by the relay,  , as shown by (4), fact that represents the main disadvantage of IR-DFEC
, as shown by (4), fact that represents the main disadvantage of IR-DFEC

The advantage of the IR-DFEC scheme consists of the relatively small amount of time-frequency resources required by the relaying phase, which increase the spectral efficiency, and the possibility to build distributed Hybrid Automatic Repeat Request (H-ARQ) schemes based on this cooperation scheme.
4.2.2. Hybrid Distributed FEC with Incremental Redundancy
The effects of small SNRs on the direct link might be overcome by a Hybrid IR-DFEC (HIR-DFEC) algorithm based both on repetition and incremental redundancy encoding. The HIR-DFEC algorithm is similar to the IR-DFEC one, see Figure 3, but in the relaying phase the RN sends, besides the  check bits, the decoded information bits
check bits, the decoded information bits  . The coding rate obtained in the relaying phase is
. The coding rate obtained in the relaying phase is  .
.
The decoding performed at the destination node is schematically represented in Figure 4. The destination node combines the LLRs corresponding to the information bits received over the direct and relay links, then it reorders the check bits received on the two links and concatenates them in order to restore the LLR-flow of the complete  -rate codeword, which is fed into the turbo decoder.
-rate codeword, which is fed into the turbo decoder.
The global coding rate  is the same as the one of the IR-DFEC algorithm, (3), but this algorithm involves the transmission of two sets of
is the same as the one of the IR-DFEC algorithm, (3), but this algorithm involves the transmission of two sets of  information bits, and therefore, in the computation of the payload bit rate and spectral efficiency, a transmission rate,
information bits, and therefore, in the computation of the payload bit rate and spectral efficiency, a transmission rate,  , given by (5) should be considered
, given by (5) should be considered

The spectral efficiency of this algorithm is smaller, but the  information bits are better protected, since they are transmitted both on the direct and on the relay links, and therefore, they are received under an equivalent
information bits are better protected, since they are transmitted both on the direct and on the relay links, and therefore, they are received under an equivalent  ,
,  , expressed by (6), which is greater than the one ensured by the IR-DFEC for these bits. As for the
, expressed by (6), which is greater than the one ensured by the IR-DFEC for these bits. As for the  and
and  check bits, they are received on similar conditions as in the IR-DFEC algorithm
check bits, they are received on similar conditions as in the IR-DFEC algorithm

4.2.3. Combined DSFC+DFEC Cooperation Algorithms
Distributed turbo coding algorithms (IR-DFEC or HIR-DFEC) are able to provide increased spectral efficiency, system flexibility but also significant coding gains if the source-RN and RN-destination links have good qualities. These conditions cannot be ensured only by positioning the relay, while the employment of powerful channel codes decreases the spectral efficiency and increases the complexity.
The quality of the transmission between the RN and destination can be significantly improved by using one or two RNs to implement a DSFC (or DSTC) algorithm, due to the diversity provided on the uncorrelated RNi-destination links. In the same time, a small  could be ensured in the broadcast phase by placing the RNs closer to the source. Therefore, the combined use of DFEC and DSFC algorithms could provide improved performances and allow the use of simplified relay selection algorithms.
could be ensured in the broadcast phase by placing the RNs closer to the source. Therefore, the combined use of DFEC and DSFC algorithms could provide improved performances and allow the use of simplified relay selection algorithms.
The combined s-DSFC+DFEC algorithms proposed are schematically represented in Figure 1 for the DL connection in the particular case when only 2 relays are used to implement the s-DSFC in the relaying phase. A brief description of the operations performed is presented below.
-
(i)
Broadcast phase. The source (BS) broadcasts the
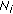 information bits encoded with a CTC of rate
information bits encoded with a CTC of rate 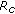 (
(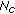 check bits) over the BS-UT and BS-RNi links.
check bits) over the BS-UT and BS-RNi links. -
(ii)
Relaying phase. The RNs performs the DFEC decoding, followed by the HIR-DFEC or IR-DFEC encoding. Then, the two RNs perform the DSFC encoding, that is, Alamouti scheme, described in Section 4.1, using the same QAM constellation, which might be different from the one employed during the broadcast phase.
-
(iii)
Decoding at destination. The destination performs the following operations:
-
(1)
demodulates and extracts the LLRs of the
 bits transmitted during the broadcast phase,
bits transmitted during the broadcast phase, -
(2)
extracts the symbols transmitted during relay phase by SFC-decoding and extracts the LLRs of the
 (for HIR-DFEC) or
(for HIR-DFEC) or 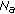 (for IR-FEC) received bits; note that the message received on the direct link, during the broadcast phase, is not used in this operation,
(for IR-FEC) received bits; note that the message received on the direct link, during the broadcast phase, is not used in this operation, -
(3)
combines the LLRs of the
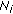 bits received on both broadcast and relay phase (only for HIR-DFEC),
bits received on both broadcast and relay phase (only for HIR-DFEC), -
(4)
reorders the LLRs of the received bits and performs the DFEC decoding.
-
(1)
4.3. Some Considerations Regarding the Effects of the Errors on the Source-Relays Links
The qualities of the source-relay links have a significant effect upon the global  provided by the cooperative algorithms. In order to evaluate their effects upon the
provided by the cooperative algorithms. In order to evaluate their effects upon the  performance of the proposed algorithms, we assume that if the block received by the one of the RNs is decoded with errors, the RN re-encodes the decoded bits and apply the corresponding cooperation algorithm. Another option would be to make the RN stop transmitting any message and to signalize this fact to destination. But this second approach would require additional signaling and adaptive use of the cooperation algorithm at destination.
performance of the proposed algorithms, we assume that if the block received by the one of the RNs is decoded with errors, the RN re-encodes the decoded bits and apply the corresponding cooperation algorithm. Another option would be to make the RN stop transmitting any message and to signalize this fact to destination. But this second approach would require additional signaling and adaptive use of the cooperation algorithm at destination.
Denoting by  the block error probability at destination provided by the algorithm
the block error probability at destination provided by the algorithm  , if the messages transmitted by RNs are correct, and by
, if the messages transmitted by RNs are correct, and by  and
and  the block error probabilities after the RNi decoding, the global block error probability of the whole cooperative algorithm,
the block error probabilities after the RNi decoding, the global block error probability of the whole cooperative algorithm,  , can be expressed using the probability of a correct decoding at destination
, can be expressed using the probability of a correct decoding at destination  , by
, by

The values of  and
and  differ for the two ways of transmission. For the DL connection, due to the higher BS antenna and to the possibility to employ RNs that have Line Of Sight (LOS) channels to the BS, the two
differ for the two ways of transmission. For the DL connection, due to the higher BS antenna and to the possibility to employ RNs that have Line Of Sight (LOS) channels to the BS, the two  , and the corresponding
, and the corresponding  , can be considered negligible and the global
, can be considered negligible and the global  is established by the
is established by the  provided by the cooperative algorithm
provided by the cooperative algorithm  at the UT. For the UL connection, the error probabilities of the UT-RNi links cannot be neglected and the global
at the UT. For the UL connection, the error probabilities of the UT-RNi links cannot be neglected and the global  and
and  are dictated by both the cooperative decoding in the BS (destination), that is,
are dictated by both the cooperative decoding in the BS (destination), that is,  and
and  , and by the error probabilities of the UT-RNi links, that is,
, and by the error probabilities of the UT-RNi links, that is,  and
and  . Therefore, the
. Therefore, the  and
and  are expected to be greater on the UL than on the DL connection, in such a topology.
are expected to be greater on the UL than on the DL connection, in such a topology.
5. Computation of the Spectral Efficiency Provided by the Proposed Algorithms
The spectral efficiency is one of the main criteria used to select the appropriate cooperative transmission algorithm. The spectral efficiency  provided by the cooperative algorithm
provided by the cooperative algorithm  is expressed by (8) in terms of the nominal bit rate
is expressed by (8) in terms of the nominal bit rate  , bit error probability
, bit error probability  , which define the throughput
, which define the throughput  , and the employed bandwidth
, and the employed bandwidth 

The nominal bit rate and the bandwidth are dependent on the cooperation algorithm's structure and the parameters of the transmission scheme. The bit error probability is expressed in terms of an equivalent  at the decoder's input, which includes the values of the
at the decoder's input, which includes the values of the  on the source-destination and RN-destination channels. This equivalent
on the source-destination and RN-destination channels. This equivalent  depends on the cooperation algorithm and on the combining method employed.
depends on the cooperation algorithm and on the combining method employed.
5.1. Spectral Efficiency of the IR-DFEC Algorithm
We consider that during the broadcast phase the number of bits/QAM symbol is  , while during the relaying phase it is
, while during the relaying phase it is  . Then, the number
. Then, the number  of QAM symbols required to transmit the messages during the two cooperation phases is computed using the considerations of Section 4.2.1 and is expressed by
of QAM symbols required to transmit the messages during the two cooperation phases is computed using the considerations of Section 4.2.1 and is expressed by

We assume that the  symbols are transmitted in an OFDM system that has
symbols are transmitted in an OFDM system that has  subcarriers and
subcarriers and  OFDM-symbol periods per resource allocation unit, with an
OFDM-symbol periods per resource allocation unit, with an  separation frequency between subcarriers and a guard interval of g% of the symbol period. Considering further that the nominal bit rate is obtained by dividing the number of information bits
separation frequency between subcarriers and a guard interval of g% of the symbol period. Considering further that the nominal bit rate is obtained by dividing the number of information bits  to the time required to transmit all coded bits and that the bandwidth occupied equals
to the time required to transmit all coded bits and that the bandwidth occupied equals  the spectral efficiency provided by this algorithm is given by, as shown in [28]
the spectral efficiency provided by this algorithm is given by, as shown in [28]

The  factor expresses the fact that during the two phases different QAM constellations are used, while
factor expresses the fact that during the two phases different QAM constellations are used, while  indicates that in the relaying phase only a fraction of the first message's length is transmitted.
indicates that in the relaying phase only a fraction of the first message's length is transmitted.
5.2. Spectral Efficiency of the HIR-DFEC Algorithm
Assuming again that during the broadcast phase, the number of bits/QAM symbol is  , and during the relaying phase, it is
, and during the relaying phase, it is  , and using the considerations of Section 4.2.2, the number
, and using the considerations of Section 4.2.2, the number  of QAM symbols required transmitting the messages during the two cooperation phases equals
of QAM symbols required transmitting the messages during the two cooperation phases equals

Then, using a similar reasoning as above, the spectral efficiency of the transmission that employs HIR-DFEC is expressed by

The nominal spectral efficiency of the IR-DFEC is greater than the one of HIR-DFEC due to the smaller number of additional bits transmitted during the relaying phase. Nevertheless, the spectral efficiency is also influenced by  , which should be smaller for the HIR-DFEC.
, which should be smaller for the HIR-DFEC.
5.3. Spectral Efficiency of the DSFC Algorithms
The spectral efficiency of the s-DSFC algorithm could be derived by using the same reasoning as for the HIR-DFEC algorithm. The spectral efficiency  has expressions similar to (12), in which the bit error rate should be the one provided by this algorithm, that is, BERs-DSFC.
has expressions similar to (12), in which the bit error rate should be the one provided by this algorithm, that is, BERs-DSFC.
For the c-DSFC algorithm, since the combining is performed at QAM symbol-level, the two phases of cooperation should employ the same number  of bits/QAM symbol. The spectral efficiency
of bits/QAM symbol. The spectral efficiency  of this algorithm can be computed using (13), where
of this algorithm can be computed using (13), where  denotes the coding rate of the FEC used
denotes the coding rate of the FEC used

5.4. Spectral Efficiency of the Combined DSFC+DFEC Algorithms
Since the two combined DSFC-DFEC algorithms are obtained superimposing the s-DSFC over the IR-DFEC or HIR-DFEC algorithms, their spectral efficiencies should be computed using (10) for DSFC+IR-DFEC and (12) for the DSFC+HIR-DFEC. In these relations, the  used should be the one provided by the respective combined algorithm.
used should be the one provided by the respective combined algorithm.
6. Performance Evaluation of the DSFC and DFEC Cooperation Algorithms
This section presents a comparative performance evaluation of the coded cooperative algorithms described in the previous section. The performances are evaluated in the assumption that the RNs are perfectly synchronized and that perfect Channel State Information (CSI) is available in all network nodes.
6.1. Performance Metrics and Simulation Scenarios
The performance metrics employed are the  and the spectral efficiency. The global
and the spectral efficiency. The global  of the studied algorithms is obtained by computer simulations, while the spectral efficiency is obtained by computation using the relations presented in Section 5. Both performance metrics provided by each algorithm are evaluated in terms of
of the studied algorithms is obtained by computer simulations, while the spectral efficiency is obtained by computation using the relations presented in Section 5. Both performance metrics provided by each algorithm are evaluated in terms of  of the direct BS-UT link, while the
of the direct BS-UT link, while the  of the other links are equal to, or greater with a constant value than the current value of
of the other links are equal to, or greater with a constant value than the current value of  of the direct link.
of the direct link.
The channel model employed on all links is briefly summarized below:
-
(i)
propagation loss with a path loss exponent of 2,
-
(ii)
multipath propagation power delay profile: ITU-T pedestrian B,
-
(iii)
quasistatic Rayleigh small scale fading,
-
(iv)
the additive noise is complex Gaussian noise with zero mean value (AWGN).
The broadcast phase uses QPSK, while the relaying phase uses either QPSK or 16 QAM or 64 QAM. The channel codes employed by the DFEC algorithms are obtained by puncturing a mother turbo code of rate  defined in [27], generated by the feedback polynomial 138 and the feedforward polynomial 158. For the c-DSFC algorithm, the FEC code employed has a rate
defined in [27], generated by the feedback polynomial 138 and the feedforward polynomial 158. For the c-DSFC algorithm, the FEC code employed has a rate  . The coded block is 7200-bit long, with 3600 information bits. The IR-DFEC and HIR-DFEC transmissions use additionally a group of 3600 check bits computed and transmitted by the RN (or RNs), the global coding rate being
. The coded block is 7200-bit long, with 3600 information bits. The IR-DFEC and HIR-DFEC transmissions use additionally a group of 3600 check bits computed and transmitted by the RN (or RNs), the global coding rate being  .
.
The scenarios selected for performance evaluation consider the cooperative topologies with two RNs and with one RN (see Figure 1) and are described below; they are meant to point out the differences between the performances provided in the DL and UL connections. The relations between the  values of the component channels are presented in Table 1.
values of the component channels are presented in Table 1.
-
(1)
Scenario D1 is defined for the DL connection; it considers that the qualities of the RNi-UT links are comparable to the one of the direct BS-UT link, while the BS-RNi links have better qualities due to the higher BS antenna and appropriate selection of the fixed and dedicated RNs.
-
(2)
Scenario D2 is also defined for the DL connection, but it is an asymmetrical one which considers that one of the RNi-UT links has better quality than the direct BS-UT link. This scenario describes a situation when one of the relays could be better positioned relatively to the destination. The same scenario could be employed for the topology with one RN, as well.
-
(3)
Scenario U, is defined to point out the effects of potential shadowing that might affect the UT-RNi transmissions, upon the UL cooperative connection. Therefore, the
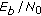 values of both UT-RNi channels (Scenario U1), or the
values of both UT-RNi channels (Scenario U1), or the 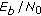 value of one of these channels (Scenario U2), were set to be smaller than that the one of the RNi-BS channels.
value of one of these channels (Scenario U2), were set to be smaller than that the one of the RNi-BS channels.
 link parameters of the defined test scenarios.
link parameters of the defined test scenarios.In all scenarios, the DFEC algorithms (using one RN) employ the UT-RNi link that has the highest  .
.
6.2. 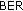 Performances on the Downlink Connection
Performances on the Downlink Connection
The  provided by the studied algorithms in the DL connection within scenarios D1 and D2 are shown in Figures 5 and 6. These results, obtained from extensive computer simulations, lead to the following conclusions.
provided by the studied algorithms in the DL connection within scenarios D1 and D2 are shown in Figures 5 and 6. These results, obtained from extensive computer simulations, lead to the following conclusions.
-
(1)
The c-DSFC cooperative algorithm, using the signal received on the direct BS-UT link in the combined MRC decoding, ensures a significantly smaller
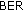 (see Figure 5). This can be explained by the greater equivalent
(see Figure 5). This can be explained by the greater equivalent 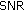 , see (1), provided by the use of the BS-UT signal in the combing process at destination.
, see (1), provided by the use of the BS-UT signal in the combing process at destination.
The increase of the  of the RNi-UT links, scenario D2, leads to a small influence of the direct link for low values of the reference
of the RNi-UT links, scenario D2, leads to a small influence of the direct link for low values of the reference  , while for greater values of the reference
, while for greater values of the reference  the influence of the direct link increases, as results from comparing the c-DSFC and s-DSFC curves between (−4; 0) dB and above 2 dB, respectively, in Figure 6. This behavior is explained by (1).
the influence of the direct link increases, as results from comparing the c-DSFC and s-DSFC curves between (−4; 0) dB and above 2 dB, respectively, in Figure 6. This behavior is explained by (1).
There should also be noted the decrease of the  provided by the s-DSFC algorithm in scenario D2, compared to scenario D1, due to the increased equivalent
provided by the s-DSFC algorithm in scenario D2, compared to scenario D1, due to the increased equivalent  , see (2).
, see (2).
-
(2)
The DFEC algorithms, when are not combined with DSFC, provide poorer
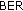 performance than the c-DSFC algorithm, and in some cases (see Figure 6) poorer performances than the simple DSFC. This is mainly explained by three facts:
performance than the c-DSFC algorithm, and in some cases (see Figure 6) poorer performances than the simple DSFC. This is mainly explained by three facts: -
(i)
DFEC algorithms employ only one RN, so there is no diversity for the
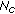 and
and 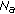 check bits (see Figures 3 and 4), while for the
check bits (see Figures 3 and 4), while for the 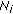 information bits only the HIR-DFEC provides diversity,
information bits only the HIR-DFEC provides diversity, -
(ii)
the turbo-decoder "combines" the LLRs of all received bits, providing only a coding gain,
-
(iii)
the LLRs of the bits within a coded block have different levels of reliability since they are obtained from two different links, with different
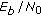 , and by different processing.
, and by different processing.
As expected, HIR-DFEC ensures smaller  than IR-DFEC. A comparison between Figures 5 and 6 shows that the improvement of the RNi-UT links does not bring significant decrease of the
than IR-DFEC. A comparison between Figures 5 and 6 shows that the improvement of the RNi-UT links does not bring significant decrease of the  provided by the DFEC algorithms.
provided by the DFEC algorithms.
-
(3)
The use of s-DSFC algorithm in the relaying phase of the DFEC algorithms; that is, s-DSFC+IR-DFEC or HIR-DFEC leads to a significant improvement of their
 performances. The s-DSFC provides diversity for the bits transmitted during the relaying phase, that is,
performances. The s-DSFC provides diversity for the bits transmitted during the relaying phase, that is, 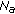 or
or 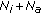 , which is transformed by the bit-level combining and by the turbodecoder into an additional coding gain. The improvement of the RNi-UT links in scenario D2 (see Figure 6) brings no significant variation of the
, which is transformed by the bit-level combining and by the turbodecoder into an additional coding gain. The improvement of the RNi-UT links in scenario D2 (see Figure 6) brings no significant variation of the 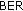 provided by these algorithms compared to the ones of Figure 5. This could be explained by the fact that only a part of the coded bits are transmitted on the better RNi-UT channels, and their more reliable LLRs do not improve significantly the performance of the FEC turbo decoding process.
provided by these algorithms compared to the ones of Figure 5. This could be explained by the fact that only a part of the coded bits are transmitted on the better RNi-UT channels, and their more reliable LLRs do not improve significantly the performance of the FEC turbo decoding process.
The  performances of the combined algorithms are still poorer than the ones of c-DSFC because the use of s-DSFC improves only the quality of the
performances of the combined algorithms are still poorer than the ones of c-DSFC because the use of s-DSFC improves only the quality of the  (IR) or
(IR) or  and
and  (HIR) received LLRs. Still, due to the bit-level combining and especially to the effects of the poorly received
(HIR) received LLRs. Still, due to the bit-level combining and especially to the effects of the poorly received  bits, the coding gain brought is smaller than the diversity gain provided by the c-DSFBC algorithm, which uses the direct link.
bits, the coding gain brought is smaller than the diversity gain provided by the c-DSFBC algorithm, which uses the direct link.
6.3. 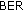 Performances on the Uplink Connection
Performances on the Uplink Connection
The  performances provided by the studied cooperative algorithms within scenario U1 are presented in Figure 7 and lead to the following conclusions.
performances provided by the studied cooperative algorithms within scenario U1 are presented in Figure 7 and lead to the following conclusions.
-
(1)
The c-DSFC algorithm provides lower
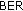 than s-DSFC, due to the same reasons as for the DL connection. Nevertheless, the values of
than s-DSFC, due to the same reasons as for the DL connection. Nevertheless, the values of 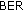 provided by the two algorithms for the same
provided by the two algorithms for the same 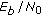 values of the component channels are significantly greater than the ones provided in the D1 scenario, see Figure 5. These poorer performances are due to the worse source (UT)-RNi links and could be explained by using relation (7), where probabilities
values of the component channels are significantly greater than the ones provided in the D1 scenario, see Figure 5. These poorer performances are due to the worse source (UT)-RNi links and could be explained by using relation (7), where probabilities 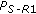 and
and 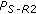 are no longer negligible and so the global
are no longer negligible and so the global 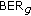 and
and 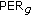 are not depending only on the
are not depending only on the 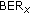 (or
(or 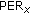 ) provided by the DSFC decoder at destination. Another effect of the errors on the UT-RNi links is the decrease of the diversity gain, expressed by a smaller slope of the
) provided by the DSFC decoder at destination. Another effect of the errors on the UT-RNi links is the decrease of the diversity gain, expressed by a smaller slope of the 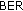 versus
versus 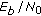 curves of these algorithms.
curves of these algorithms. -
(2)
The DFEC algorithms provide
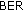 values that are comparable to the ones of the s-DSFC, but greater than the ones of the c-DSFC. The differences in the
values that are comparable to the ones of the s-DSFC, but greater than the ones of the c-DSFC. The differences in the 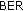 performances are significantly smaller than in the downlink case.
performances are significantly smaller than in the downlink case. -
(3)
The combination of the DFEC techniques with the s-DSFC leads to lower
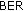 values, due to the same reasons as in the DL case, but the performance improvement brought by this combination is significantly smaller than in the DL connection, due to the poorer source (UT)-RNi links. The improvement of the UT-RN2 channel, scenario U2, leads to slightly smaller
values, due to the same reasons as in the DL case, but the performance improvement brought by this combination is significantly smaller than in the DL connection, due to the poorer source (UT)-RNi links. The improvement of the UT-RN2 channel, scenario U2, leads to slightly smaller 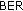 values for all algorithms than the ones provided in scenario U1, as results from the comparison between Figure 7 and Figure 8. The major characteristic of this scenario is that the DFEC algorithms provide better performances if they are not combined with s-DSFC. This is because they need to use only the good UT-RN2 link during the relaying phase, while the s-DSFC employs both UT-RNi links, out of which one is of poor quality. The
values for all algorithms than the ones provided in scenario U1, as results from the comparison between Figure 7 and Figure 8. The major characteristic of this scenario is that the DFEC algorithms provide better performances if they are not combined with s-DSFC. This is because they need to use only the good UT-RN2 link during the relaying phase, while the s-DSFC employs both UT-RNi links, out of which one is of poor quality. The 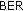 increase can be explained by using (7).
increase can be explained by using (7).
The main conclusion is that in the UL connection, the insertion of the s-DSFC in the DFEC algorithms is beneficial only if the two UT-RNi links have about the same quality; otherwise, the DFEC algorithms used alone could provide smaller  , because they could employ only the best UT-RNi link.
, because they could employ only the best UT-RNi link.
6.4. Spectral Efficiency Performances
The spectral efficiency performances of the studied algorithms were evaluated only for the DL connection, since according to (10), (12), and (13), the only factor differing for the two ways of transmission is the bit error rate, which was analyzed in the previous section. Figure 9 shows the spectral efficiencies computed for the studied algorithms in the D1 scenario when  . The main conclusions drawn are the following.
. The main conclusions drawn are the following.
(i)The two algorithms that use the IR-DFEC (combined or not with s-DSFC) provide the highest spectral efficiencies due to the small redundancy inserted, see (10). The HIR-DFEC-based algorithms provide smaller spectral efficiencies due to their greater redundancy during the relaying phase, which cannot be compensated by the smaller  provided, see (12). The flat parts (zones) of the curves exhibited by DFEC algorithms are extended with approximately 2 dB by combining them with the s-DSFC algorithm.
provided, see (12). The flat parts (zones) of the curves exhibited by DFEC algorithms are extended with approximately 2 dB by combining them with the s-DSFC algorithm.
(ii)The c-DFSC algorithm ensures about the same spectral efficiency as the HIR-DFEC algorithm, because they both transmit about the same redundancy, see (13) and (12), while the differences in  are not big enough to affect significantly the spectral efficiency. The s-DSFC provides a narrower flat zone, due to the greater
are not big enough to affect significantly the spectral efficiency. The s-DSFC provides a narrower flat zone, due to the greater  needed to ensure a negligible
needed to ensure a negligible  , for example, 10‒ 3, as shown in Figure 5.
, for example, 10‒ 3, as shown in Figure 5.
Concluding, the IR-DFEC algorithm provides the greatest spectral efficiency and should be preferred for applications where the target  is not set to small values, while the c-DSFC should be used in applications which require small
is not set to small values, while the c-DSFC should be used in applications which require small  values.
values.
The spectral efficiencies of all algorithms described above, except for the c-DSFC, can be increased by using a higher modulation on the RNi-destination link(s) during the relaying phase, as results by increasing  in (10) or (12). For a fair comparison, the increase of
in (10) or (12). For a fair comparison, the increase of  requires that the higher constellation should ensure the same
requires that the higher constellation should ensure the same  on the RNi-UT links as the one ensured by QPSK. This would require an
on the RNi-UT links as the one ensured by QPSK. This would require an  increased with 4 dB for 16 QAM
increased with 4 dB for 16 QAM  and with 8.3 dB for 64 QAM
and with 8.3 dB for 64 QAM  . Such an improvement of the RN-UT channels could be accomplished either by changing the positions of the two RNs or by increasing the RN's transmitted power or by both. The spectral efficiencies provided by the studied algorithms versus
. Such an improvement of the RN-UT channels could be accomplished either by changing the positions of the two RNs or by increasing the RN's transmitted power or by both. The spectral efficiencies provided by the studied algorithms versus  within the D1 scenario modified according to the above values, are presented in Figures 10 and 11. The figures also present the spectral efficiency provided by c-DSFC algorithm for
within the D1 scenario modified according to the above values, are presented in Figures 10 and 11. The figures also present the spectral efficiency provided by c-DSFC algorithm for  and
and  , as reference.
, as reference.
The major difference between Figures 10 and 11 and the curves of Figure 9 lies in the greater values of the spectral efficiencies in the flat zones, due to the higher  which ensures about the same
which ensures about the same  . Compared to the spectral efficiency of c-DSFC with
. Compared to the spectral efficiency of c-DSFC with  , the spectral efficiency of IR-DFEC-based algorithms is increased in the flat zones by a factor
, the spectral efficiency of IR-DFEC-based algorithms is increased in the flat zones by a factor  expressed by (14a). The values of
expressed by (14a). The values of  equal 1.6 for
equal 1.6 for  and 1.72 for
and 1.72 for  . A similar factor for the algorithms that use the HIR-DFEC, computed using (12) and (13) is expressed by (14b); it equals 1.33 for
. A similar factor for the algorithms that use the HIR-DFEC, computed using (12) and (13) is expressed by (14b); it equals 1.33 for  and 1.5 for
and 1.5 for 


The spectral efficiencies provided by these cooperative algorithms in the D2 scenario are presented in Figure 12, for  . The significant extension of the flat zone of the s-DSFC algorithm, compared to Figure 9, can be explained by its significantly smaller
. The significant extension of the flat zone of the s-DSFC algorithm, compared to Figure 9, can be explained by its significantly smaller  (see Figure 6) though the maximum value of its spectral efficiency has not changed, see (12). The rest of the algorithms exhibit similar performances to the ones provided for poorer RNi-UT channels of scenario D1, Figure 9, but their flat zones are slightly extended due to the better RN-UT channel available in this scenario.
(see Figure 6) though the maximum value of its spectral efficiency has not changed, see (12). The rest of the algorithms exhibit similar performances to the ones provided for poorer RNi-UT channels of scenario D1, Figure 9, but their flat zones are slightly extended due to the better RN-UT channel available in this scenario.
Finally, Figures 13 and 14 show the spectral efficiencies provided in the modified D2 scenarios defined above, when higher order modulations, that is,  and
and  , are used in the relaying phase. Due to the employment of a larger constellation on the RNi-UT links with correspondingly increased
, are used in the relaying phase. Due to the employment of a larger constellation on the RNi-UT links with correspondingly increased  , the values of the spectral efficiencies of all algorithms are greater than the ones of Figure 12, except for c-DSFC algorithm which should use
, the values of the spectral efficiencies of all algorithms are greater than the ones of Figure 12, except for c-DSFC algorithm which should use  .
.
The spectral efficiencies provided by these algorithms in UL connections, scenarios U1 and U2, have similar behaviors in terms of the  of the direct link, but their flat zones are narrower than the corresponding ones in the DL, due to the greater
of the direct link, but their flat zones are narrower than the corresponding ones in the DL, due to the greater  values occurring in the uplink, see Section 6.3.
values occurring in the uplink, see Section 6.3.
7. Conclusions
This paper has studied the  and spectral efficiency performances provided in some relevant DL and UL scenarios by two algorithms that employ in a joint manner the DSFC and DFEC cooperation algorithms. Their performances were compared to the ones provided by the constituent DSFC and, respectively, DFEC algorithms used independently. The combination of these two types of cooperation algorithms exploits both the flexibility of DFEC and the diversity provided by DSFC, while simplifying the relay assignment issue. The diversity provided by DSFC on the RN-destination links allows the placement of the RNs closer to the source and so the source-RN transmissions would not require the high redundancy of small-rate channel codes. The use of DFEC algorithms involves the direct link that brings an extra coding gain to compensate the decrease of the RN-destination link's quality due to the positioning of the relay closer to the source.
and spectral efficiency performances provided in some relevant DL and UL scenarios by two algorithms that employ in a joint manner the DSFC and DFEC cooperation algorithms. Their performances were compared to the ones provided by the constituent DSFC and, respectively, DFEC algorithms used independently. The combination of these two types of cooperation algorithms exploits both the flexibility of DFEC and the diversity provided by DSFC, while simplifying the relay assignment issue. The diversity provided by DSFC on the RN-destination links allows the placement of the RNs closer to the source and so the source-RN transmissions would not require the high redundancy of small-rate channel codes. The use of DFEC algorithms involves the direct link that brings an extra coding gain to compensate the decrease of the RN-destination link's quality due to the positioning of the relay closer to the source.
The results obtained in scenarios with good source-RN and relatively poor RN-destination channels, that is, scenario D1, show that combined s-DSFC+DFEC algorithms could provide the best tradeoff between  and spectral efficiency performances. This tradeoff could be "fine-tuned" by the amount of redundancy employed in the relaying phase of cooperation, by using either the HIR-DFEC algorithm that provides lower
and spectral efficiency performances. This tradeoff could be "fine-tuned" by the amount of redundancy employed in the relaying phase of cooperation, by using either the HIR-DFEC algorithm that provides lower  values, or the IR-DFEC one, which provides the greatest spectral efficiency. Even if the c-DSFC algorithm, which uses the direct link at destination, provides the smallest
values, or the IR-DFEC one, which provides the greatest spectral efficiency. Even if the c-DSFC algorithm, which uses the direct link at destination, provides the smallest  out of all studied algorithms in all scenarios considered, its spectral efficiency and link-adaptation flexibility are small due to the combining at symbol level, which in its turn provides a greater diversity gain. If the RN-destination link's quality could be improved by relay-assignment while still ensuring good source-RN links, for example, scenario D2, the s-DSFC algorithm is the best choice considering both
out of all studied algorithms in all scenarios considered, its spectral efficiency and link-adaptation flexibility are small due to the combining at symbol level, which in its turn provides a greater diversity gain. If the RN-destination link's quality could be improved by relay-assignment while still ensuring good source-RN links, for example, scenario D2, the s-DSFC algorithm is the best choice considering both  and spectral efficiency performances, but the greatest spectral efficiency could be provided by IR-DFEC algorithms.
and spectral efficiency performances, but the greatest spectral efficiency could be provided by IR-DFEC algorithms.
For scenarios with poor source-RN links, for example, scenarios U1 and U2, all DFEC algorithms analyzed present comparable  performances to the ones of the c-DSFC algorithm. In such scenarios, the s-DSFC+DFEC or even only DFEC algorithms are the best choice if both
performances to the ones of the c-DSFC algorithm. In such scenarios, the s-DSFC+DFEC or even only DFEC algorithms are the best choice if both  and spectral efficiency performances and system flexibility are to be taken into account.
and spectral efficiency performances and system flexibility are to be taken into account.
The results obtained also indicate how these cooperative algorithms should be used adaptively to match the performance requirements ( and spectral efficiency) of various services. For highly interactive applications which require low or very low
and spectral efficiency) of various services. For highly interactive applications which require low or very low  values and not a great spectral efficiency, for example, video conferences, the best option would be the c-DSFC, due to its symbol-level combining. For widely used applications requiring relatively low
values and not a great spectral efficiency, for example, video conferences, the best option would be the c-DSFC, due to its symbol-level combining. For widely used applications requiring relatively low  , for example, audio and video streaming, the s-DSFC+HIR-DFEC algorithm is one of the best options, since it ensures a relatively low
, for example, audio and video streaming, the s-DSFC+HIR-DFEC algorithm is one of the best options, since it ensures a relatively low  and a high spectral efficiency. For popular applications that accept higher
and a high spectral efficiency. For popular applications that accept higher  values, for example, telephony or messaging, the IR-DFEC combined with s-DSFC on the RNi-destination links would be advisable, since it ensures the highest spectral efficiency, which is an important factor for this type of services.
values, for example, telephony or messaging, the IR-DFEC combined with s-DSFC on the RNi-destination links would be advisable, since it ensures the highest spectral efficiency, which is an important factor for this type of services.
References
Fitzek FHP, Katz MD (Eds): Cooperation in Wireless Networks: Principles and Applications. Springer, New York, NY, USA; 2006.
Ray Liu KJ, Sadek AK, Su W, Kwasinski A: Cooperative Communications and Networking. Cambridge University Press, New York, NY, USA; 2009.
CODIV- Enhanced Wireless Communication Systems Employing Cooperative Diversity FP7-ICT-2007-215477-CODIV project, http://www.ict-codiv.eu/
Foschini GJ, Gans MJ: On limits of wireless communications in a fading environment when using multiple antennas. Wireless Personal Communications 1998, 6(3):311-335. 10.1023/A:1008889222784
Liu H, Li G: OFDM-Based Broadband Wireless Networks. John Wiley & Sons, Hoboken, NJ, USA; 2005.
Dohler M: Virtual antenna arrays, Ph.D. thesis. King's College London, London, UK; November 2003.
Laneman JN, Wornell GW: Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks. IEEE Transactions on Information Theory 2003, 49(10):2415-2425. 10.1109/TIT.2003.817829
Jing Y, Hassibi B: Distributed space-time codes in wireless relay networks. Proceedings of Sensor Array and Multichannel Signal Processing Workshop (SAM '04), July 2004, Barcelona, Spain 249-253.
Kiran T, Rajan BS: Distributed space-time codes with reduced decoding complexity. Proceedings of IEEE International Symposium on Information Theory (ISIT '06), July 2006, Seatle, Wash, USA 542-546.
Alamouti SM: A simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998, 16(8):1451-1458. 10.1109/49.730453
Sirkeci-Mergen B, Scaglione A: Randomized distributed space-time coding for cooperative communication in self organized networks. Proceedings of the 6th IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '05), June 2005, New York, NY, USA 500-504.
Shin OS, Chan AM, Kung HT, Tarokh V: Design of an OFDM cooperative space-time diversity system. IEEE Transactions on Vehicular Technology 2007, 56(4):2203-2215.
Hayes M, Kassim SK, Chambers JA, Macleod MD: Exploitation of quasi-orthogonal space time block codes in virtual antenna arrays—part I—theoretical capacity and throughput gains. Proceedings of the 67th IEEE Vehicular Technology Conference-Spring (VTC '08), May 2008, Singapore 349-352.
Teodoro S, Silva A, Gil JM, Gameiro A: Virtual MIMO schemes for downlink space-frequency coding OFDM systems. Proceedings of the 20th Personal, Indoor and Mobile Radio Communications Symposium (PIMRC '09), September 2009, Tokyo, Japan
Hunter TE, Nosratinia A: Cooperative diversity through coding. Proceedings of IEEE International Symposium on Information Theory (ISIT '02), July 2002, Lausanne, Switzerland
Hunter TE, Nosratinia A: Coded cooperation under slow fading, fast fading, and power control. Proceedings of the 36th Asilomar Conference on Signals Systems and Computers, November 2002, Pacific Grove, Calif, USA 1: 118-122.
Lin Z, Erkip E, Stefanov A: An asymptotic analysis on the performance of coded cooperation systems. Proceedings of the 60th IEEE Vehicular Technology Conference (VTC '04), September 2004, Los Angeles, Calif, USA 1333-1337.
Kim SJ, Mitran P, Tarokh V: Performance bounds for bidirectional coded cooperation protocols. IEEE Transactions on Information Theory 2008, 54(11):5235-5241.
Lin Z, Erkip E, Ghosh M: Adaptive modulation for coded cooperative systems. Proceedings of the 6th IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '05), June 2005, New York, NY, USA 615-619.
Niu J, Lu I-T: Coded cooperation in OFDMA systems. Proceedings of the 40th Annual Conference on Information Sciences and Systems (CISS '06), March 2006, Princeton, NJ, USA 300-305.
Noh K-L, Suter B, Serpedin E: A practical cooperative coding scheme and its optimum level of cooperation for wireless ad-doc networks. Proceedings of Texas Wireless Symposium, 2005, Austin, Tex, USA
Yuen C, Chin WH, Guan YL, Chen W, Tee T: Bi-directional multi-antenna relay communications with wireless network coding. Proceedings of the 67th IEEE Vehicular Technology Conference-Spring (VTC '08), May 2008, Singapore 1385-1388.
Cui T, Gao F, Ho T, Nallanathan A: Distributed space-time coding for two-way wireless relay networks. IEEE Transactions on Signal Processing 2009, 57(2):658-671.
Kuek SK, Yuen C, Chin WH: Four-node relay network with Bi-directional traffic employing wireless network coding with pre-cancellation. Proceedings of the 67th IEEE Vehicular Technology Conference-Spring (VTC '08), May 2008, Singapore 1201-1205.
Eslamifar M, Chin WH, Yuen C, Liang GY: Performance analysis of two-way multiple-antenna relaying with network coding. Proceedings of the 70th IEEE Vehicular Technology Conference Fall (VTC '09), September 2009, Barcelona, Spain
Castelain D, et al.: Preliminary advanced PHY layer algorithm selection and results. Deliverable 3.3a, FP7-ICT-2007-215477-CODIV "Enhanced Wireless Communication Systems Employing COoperative DIVersity", pp. 14–42, 2009, http://www.ict-codiv.eu/deliverables/D3.3a.pdf Deliverable 3.3a, FP7-ICT-2007-215477-CODIV "Enhanced Wireless Communication Systems Employing COoperative DIVersity", pp. 14–42, 2009,
Technical Specification Group Radio Access Network, Multiplexing and Channel Coding 3GPP Standard TS 25.212 V6.3.0, 2004
Castelain D, et al.: Final advanced PHY layer algorithm selection and results. Deliverable 3.3b, FP7-ICT-2007-215477-CODIV "Enhanced Wireless Communication Systems Employing COoperative DIVersity", pp. 56–60, 2009, http://www.ict-codiv.eu/deliverables/D3.3b.pdf Deliverable 3.3b, FP7-ICT-2007-215477-CODIV "Enhanced Wireless Communication Systems Employing COoperative DIVersity", pp. 56–60, 2009,
Acknowledgment
The authors wish to acknowledge the support of the ICT-FP7 European project "Enhanced Wireless Communication Systems Employing Cooperative Diversity—CODIV", FP7/ICT/2007/215477.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bota, V., Polgar, Z.A., Silva, A. et al. Combined Distributed Turbo Coding and Space Frequency Block Coding Techniques. J Wireless Com Network 2010, 327041 (2010). https://doi.org/10.1155/2010/327041
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/327041


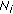 information bits and
information bits and 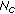 check bits) towards the RNs and destination, using a modulation adapted to the channels involved.
check bits) towards the RNs and destination, using a modulation adapted to the channels involved.

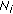 information bits encoded with a CTC of rate
information bits encoded with a CTC of rate 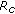 (
(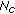 check bits) over the BS-UT and BS-RNi links.
check bits) over the BS-UT and BS-RNi links. bits transmitted during the broadcast phase,
bits transmitted during the broadcast phase, (for HIR-DFEC) or
(for HIR-DFEC) or 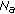 (for IR-FEC) received bits; note that the message received on the direct link, during the broadcast phase, is not used in this operation,
(for IR-FEC) received bits; note that the message received on the direct link, during the broadcast phase, is not used in this operation,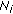 bits received on both broadcast and relay phase (only for HIR-DFEC),
bits received on both broadcast and relay phase (only for HIR-DFEC),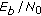 values of both UT-RNi channels (Scenario U1), or the
values of both UT-RNi channels (Scenario U1), or the 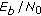 value of one of these channels (Scenario U2), were set to be smaller than that the one of the RNi-BS channels.
value of one of these channels (Scenario U2), were set to be smaller than that the one of the RNi-BS channels. Performances on the Downlink Connection
Performances on the Downlink Connection
 versus
versus  ; DSFC, DFEC, and DSFC+DFEC algorithms—scenario D1.
; DSFC, DFEC, and DSFC+DFEC algorithms—scenario D1.
 versus
versus  ; DSFC, DFEC, and DSFC+DFEC algorithms—scenario D2.
; DSFC, DFEC, and DSFC+DFEC algorithms—scenario D2.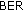 (see Figure
(see Figure 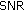 , see (1), provided by the use of the BS-UT signal in the combing process at destination.
, see (1), provided by the use of the BS-UT signal in the combing process at destination.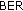 performance than the c-DSFC algorithm, and in some cases (see Figure
performance than the c-DSFC algorithm, and in some cases (see Figure 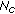 and
and 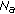 check bits (see Figures
check bits (see Figures 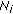 information bits only the HIR-DFEC provides diversity,
information bits only the HIR-DFEC provides diversity,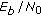 , and by different processing.
, and by different processing. performances. The s-DSFC provides diversity for the bits transmitted during the relaying phase, that is,
performances. The s-DSFC provides diversity for the bits transmitted during the relaying phase, that is, 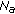 or
or 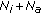 , which is transformed by the bit-level combining and by the turbodecoder into an additional coding gain. The improvement of the RNi-UT links in scenario D2 (see Figure
, which is transformed by the bit-level combining and by the turbodecoder into an additional coding gain. The improvement of the RNi-UT links in scenario D2 (see Figure 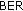 provided by these algorithms compared to the ones of Figure
provided by these algorithms compared to the ones of Figure 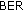 Performances on the Uplink Connection
Performances on the Uplink Connection
 versus
versus
 ; DSFC, DFEC, and DSFC+DFEC algorithms—scenario U1.
; DSFC, DFEC, and DSFC+DFEC algorithms—scenario U1.
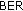 than s-DSFC, due to the same reasons as for the DL connection. Nevertheless, the values of
than s-DSFC, due to the same reasons as for the DL connection. Nevertheless, the values of 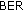 provided by the two algorithms for the same
provided by the two algorithms for the same 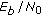 values of the component channels are significantly greater than the ones provided in the D1 scenario, see Figure
values of the component channels are significantly greater than the ones provided in the D1 scenario, see Figure 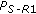 and
and 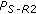 are no longer negligible and so the global
are no longer negligible and so the global 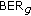 and
and 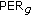 are not depending only on the
are not depending only on the 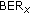 (or
(or 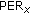 ) provided by the DSFC decoder at destination. Another effect of the errors on the UT-RNi links is the decrease of the diversity gain, expressed by a smaller slope of the
) provided by the DSFC decoder at destination. Another effect of the errors on the UT-RNi links is the decrease of the diversity gain, expressed by a smaller slope of the 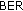 versus
versus 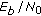 curves of these algorithms.
curves of these algorithms.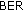 values that are comparable to the ones of the s-DSFC, but greater than the ones of the c-DSFC. The differences in the
values that are comparable to the ones of the s-DSFC, but greater than the ones of the c-DSFC. The differences in the 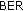 performances are significantly smaller than in the downlink case.
performances are significantly smaller than in the downlink case.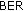 values, due to the same reasons as in the DL case, but the performance improvement brought by this combination is significantly smaller than in the DL connection, due to the poorer source (UT)-RNi links. The improvement of the UT-RN2 channel, scenario U2, leads to slightly smaller
values, due to the same reasons as in the DL case, but the performance improvement brought by this combination is significantly smaller than in the DL connection, due to the poorer source (UT)-RNi links. The improvement of the UT-RN2 channel, scenario U2, leads to slightly smaller  values for all algorithms than the ones provided in scenario U1, as results from the comparison between Figure
values for all algorithms than the ones provided in scenario U1, as results from the comparison between Figure  increase can be explained by using (7).
increase can be explained by using (7).
 versus
versus
 ; DSFC, DFEC, and DSFC+DFEC algorithms—scenario U2.
; DSFC, DFEC, and DSFC+DFEC algorithms—scenario U2.

 —scenario D1—
—scenario D1— .
.
 —modified D1—
—modified D1— ,
,  .
.
 —modified D1—
—modified D1— ,
,  .
.
 —scenario D2—
—scenario D2— .
.
 —modified D2—
—modified D2— ,
,  .
.
 —modified D2—
—modified D2— ,
,  .
.