- Research Article
- Open access
- Published:
Collaborative Event-Driven Coverage and Rate Allocation for Event Miss-Ratio Assurances in Wireless Sensor Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 345052 (2010)
Abstract
Wireless sensor networks are often required to provide event miss-ratio assurance for a given event type. To meet such assurances along with minimum energy consumption, this paper shows how a node's activation and rate assignment is dependent on its distance to event sources, and proposes a practical coverage and rate allocation (CORA) protocol to exploit this dependency in realistic environments. Both uniform event distribution and nonuniform event distribution are considered and the notion of ideal correlation distance around a clusterhead is introduced for on-duty node selection. In correlation distance guided CORA, rate assignment assists coverage scheduling by determining which nodes should be activated for minimizing data redundancy in transmission. Coverage scheduling assists rate assignment by controlling the amount of overlap among sensing regions of neighboring nodes, thereby providing sufficient data correlation for rate assignment. Extensive simulation results show that CORA meets the required event miss-ratios in realistic environments. CORA's joint coverage scheduling and rate allocation reduce the total energy expenditure by 85%, average battery energy consumption by 25%, and the overhead of source coding up to 90% as compared to existing rate allocation techniques.
1. Introduction
Wireless sensor networks usually consist of a large number of sensor nodes that collaboratively gather data from a target region of interest. A sensor network is expected to provide event miss-ratio guarantees, while minimizing the energy consumption of its sensor nodes. The miss-ratio for an event is equal to the fraction of those occurrences that are missed by wireless sensor nodes in a given time interval. While a sensor network can dynamically adapt its aggregate coverage in response to event misses, providing such assurances with minimum energy consumption is not easy due to the following problems. First, event occurrences may follow a nonuniform distribution. Consequently, two sensor nodes may detect a different number of events in a given interval even though their contribution to aggregate coverage of the network is the same. Second, minimizing the number of active nodes by reducing the overlapping areas among sensing regions of neighboring nodes often sacrifices their correlation. However, sensor data correlation can be exploited by distributed source coding for reducing the energy spent for data transmission which is a major component in overall system energy consumption [1, 2]. Inspired by these problems, this paper is the first of its kind to exploit the relationship between coverage scheduling (i.e., deciding which sensing unit(s) of each node should be activated) and source coding rate allocation (i.e., determining the number of bits that a sensor node should transmit for its sensor reading), and to show how they should cooperate. The main contributions of this research include the following.
We demonstrate the existence of an ideal correlator radius within cluster of sensor nodes around which on-duty node selection will minimize the amount of data sensed and transmitted under both uniform and nonuniform event distributions.
CORA (COverage and Rate Allocation) Protocol is proposed to exploit ideal correlator radius concept via cooperation between event-based scheduling and rate allocation. CORA schedules on-duty nodes to achieve better accuracy on the coverage of the monitored area than existing algorithms and provides event miss-ratio assurances even when nodes have no location information and there's noise in sensing ranges of nodes.
This paper develops a novel technique called differential data transmission to remove those data redundancies which cannot be eliminated via distributed source coding. Nonredundant data gathered by distributed source coding are compared with known reference data and then only its difference from the reference data are transmitted to the clusterhead.
We noticed that certain cluster members are critical for meeting the required event miss-ratios energy efficiently due to their following two features. First, by taking advantage of their location in cluster topology, they can apply distributed source coding for other cluster members and significantly reduce data redundancy. Second, due to their proximity to the hotspots (i.e., regions with high event occurrence probabilities), they can detect majority of the event occurrences which are condensed around hotspots. Therefore, in CORA, rate allocation requests coverage scheduling to activate such critical cluster members within the ideal proximity of the clusterhead which we refer as correlator radius. Similarly, coverage scheduling helps rate allocation assign various rates to sensor nodes by determining which neighboring sensor nodes of a given sensor node should be put in sleep mode.
CORA's rate allocation first identifies the uniform/nonuniform distribution of event occurrences using a continuously updated histogram. Under nonuniform event distribution, those hotspot locations where the event occurrence probability is very high are determined. For both uniform and nonuniform event distributions, we then demonstrate the existence of an ideal radius around the clusterhead where the source coding gain is maximized. At the distance of ideal radius from clusterhead, our rate allocation algorithm forms groups of active nodes. Each group has a so-called correlator node that gathers data from its group members and transmits the aggregated data to its clusterhead. To further improve data reduction, we propose a new differential data transmission technique for correlator nodes. To the best of our knowledge, there is no previously known technique that assigns rates in accordance with the occurrence of the observed phenomena.
CORA's coverage scheduling is unique of its kind in guaranteeing the miss-ratio required for each event without any need for location information of nodes. While activating less number of nodes than existing coverage scheduling algorithms to provide such assurances, coverage scheduling also relieves sensor nodes computation and storage overhead. To be of practical value, the coverage scheduling algorithm takes into account the effects of realistic environments on coverage such as the changes in sensing ability of nodes and the noise in distance measurements between node pairs.
The preliminary results of this research have appeared in [3, 4]. The rest of the paper is organized as follows. The related work is presented in Section 2. In Section 3, system model and assumptions are given. The problem we tackle is formally described in Section 4. Section 5 presents the CORA protocol. The performance evaluation of CORA is discussed in Section 6. The concluding remarks are made in Section 7.
2. Related Work
Coverage scheduling algorithms and distributed source coding techniques are usually addressed as two separate research fronts in the literature. CORA distinguishes itself from the existing solutions in closing the loop between these two research fronts.
Coverage Scheduling
Coverage scheduling in wireless sensor networks has received increasing attention in the recent years [5–15]. Some research efforts have considered coverage scheduling in conjunction with connectivity requirements [16, 17], bandwidth constraints [18], and target localization [19]. But, in none of the previously known coverage scheduling techniques, the impact of coverage scheduling on distributed source coding is addressed, even though distributed source coding efficiency depends on which set of sensor nodes gather data for an event. In comparison, CORA identifies the nodes that are critical for distributed source coding by keeping track of the event distribution. Then, only such critical nodes are put on duty to provide the variable coverage needed over the monitored area for minimizing event misses. CORA also uses less number of active nodes to meet the coverage needed than existing coverage scheduling techniques [5].
Rate Allocation
Distributed source coding [20, 21] and explicit communication [22] reduce the amount of data transmitted by taking advantage of the correlation structure between the sensor measurements. Let  and
and  be the data sources at two neighboring sensor nodes that have overlapping sensing areas and belong to the same cluster. In case of distributed source coding, the data of
be the data sources at two neighboring sensor nodes that have overlapping sensing areas and belong to the same cluster. In case of distributed source coding, the data of  are sent as
are sent as  to the clusterhead which then informs
to the clusterhead which then informs  about the correlation structure between the data of
about the correlation structure between the data of  and
and  . Finally, the data of
. Finally, the data of  are encoded as
are encoded as  with side information
with side information  in accordance with the Slepian-Wolf theorem [20]. In case of explicit communication, the node with source
in accordance with the Slepian-Wolf theorem [20]. In case of explicit communication, the node with source  receives explicit side information
receives explicit side information  from the node with source
from the node with source  and decodes
and decodes  . Then, the data of
. Then, the data of  is encoded as
is encoded as  and sent to their clusterhead in addition to
and sent to their clusterhead in addition to  .
.
Recently, rate assignment algorithms are developed to determine the coding rates to be used by each sensor node [22–24]. These rate assignment algorithms usually focus on minimizing energy consumption and do not consider the overhead of distributed source coding. In CORA however, cooperative coverage scheduling and rate assignment activates and maintains correlation information only for those critical nodes that would maximize the energy saving of distributed source coding.
The main drawback of aforementioned existing rate allocation algorithms is that they usually assume uniform distribution of event occurrences. In our work, we address both uniform and nonuniform event distributions and show the ideal correlator radius for each case. In light of the ideal correlator radius, our rate allocation algorithm partitions on duty nodes into groups, each with a designated correlator node, and assigns rates within each group in response to the uniform/nonuniform distribution of event occurrences.
Rate allocation and network lifetime are very related to each other. For instance, in [25], rate allocation in wireless sensor networks is addressed under a given network lifetime requirement. This research work advocates the use of lexicographical max-min rate allocation for all sensor nodes in order to avoid a severe bias in rate allocation when the objective is to maximize the sum of rates of all nodes.
Event Miss-Ratio Assurances
The problem of event-misses have been addressed by several node level scheduling algorithms [26–29]. The objective of such research efforts is to keep a node in low power modes as much as possible while processing event occurrences within their deadlines. However, these existing techniques do not provide any event miss-ratio assurances and schedule events at a sensor node separately from its neighboring nodes. Such algorithms can not relieve a sensor node from processing those events that are also detected by its neighboring nodes. In comparison, CORA assigns each event only to some sensor nodes within a group of cluster members. Therefore, CORA significantly reduces the event processing load at each node.
3. System Model and Terminology
Network and Node Model
This paper focuses on dense wireless sensor networks which consists of multiple clusters that are formed based on node residual energy levels. We consider single hop clusters where each cluster member is within the direct transmission range of the clusterhead. The sensor nodes are static and have the same hardware capabilities. The distance between any two sensor nodes within a cluster is assumed to be known based on standard methods such as Received-Signal-Strength-Indicator (RSSI) and Time of Arrival (ToA).
We consider the recent commercial off-the-shelf sensor nodes that have multiple sensing units [30]. The sensor nodes do not have an attached GPS device but their positions within a cluster are estimated based on internode distances. The power control circuit of each sensing unit enables putting it in sleep or active mode [31]. The sensing unit consumes constant power level in active mode. The radio unit has dynamic transmission power control capability which enables sensor nodes to control their transmission range under the effect of environmental factors and multipath propagation. In order to transmit  bits between two sensor nodes separated by a distance
bits between two sensor nodes separated by a distance  , the required power is modeled as
, the required power is modeled as  for transmission and
for transmission and  for reception where
for reception where  and
and  are constants [32].
are constants [32].
Coverage and Event Model
In sensor networks, different types of coverage models exist, (i) the monitored area consists of a discrete set of points and each point should be within the sensing region of at least one active node [12], (ii) the monitored area is a predefined contiguous region and the active sensor nodes should be covering each point within this region [10], and (iii) the monitored area is a contiguous region defined by the union of all individual nodes' sensing regions, and a subset of active nodes should cover the sensing regions of others [11]. In this paper, we focus on the third coverage model. We consider both uniform and nonuniform event distribution models. In uniform case, each node has the same event occurrence probability. To model nonuniform event distribution, however, random hotspot locations are created within the monitored area, and event occurrences follow the Gaussian distribution around these hotspot locations.
Data Correlation Model
For  active sensor nodes that participate in source coding within the same group, a vector
active sensor nodes that participate in source coding within the same group, a vector  of
of  entries keeps the mean values of their sensor readings and an
entries keeps the mean values of their sensor readings and an  matrix
matrix  maintains their correlation.
maintains their correlation.  , where the random variable
, where the random variable  corresponds to the source sensor readings at
corresponds to the source sensor readings at  active cluster member for
active cluster member for  .
.  denotes the correlation degree between
denotes the correlation degree between  and
and  active cluster member for
active cluster member for  .
.
The existing research efforts consider only internode distances while modeling sensor data correlation [33]. Given a set of nodes  , their model calculate the nonredundant data produced by node
, their model calculate the nonredundant data produced by node  based on the minimum Euclidean distance between node
based on the minimum Euclidean distance between node  and any node
and any node  for
for  . However, this distance-based approach faces problems when node
. However, this distance-based approach faces problems when node  is very close to more than one member of the node set
is very close to more than one member of the node set  . In this case, the amount of nonredundant data generated by
. In this case, the amount of nonredundant data generated by  is actually much less than the amount that is approximated by their model. To address such cases and represent correlation more accurately, this paper models the data correlation among sensor nodes based on the overlapping area of their sensing regions. Specifically, the data correlation of active cluster members
is actually much less than the amount that is approximated by their model. To address such cases and represent correlation more accurately, this paper models the data correlation among sensor nodes based on the overlapping area of their sensing regions. Specifically, the data correlation of active cluster members  and
and  is expressed as
is expressed as  , where
, where  and
and  denote the sensing regions of
denote the sensing regions of  and
and  active cluster members, respectively, for
active cluster members, respectively, for  and
and  is the sensing range.
is the sensing range.
The total number of bits in the sensed data of a group of  sensor nodes is expressed based on their aggregate coverage. Specifically, if the entropy [34] of the source at a single cluster member is
sensor nodes is expressed based on their aggregate coverage. Specifically, if the entropy [34] of the source at a single cluster member is  bits then the sensor nodes produce
bits then the sensor nodes produce  bits of nonredundant data where
bits of nonredundant data where  is the sensing region of node
is the sensing region of node  sensor node for
sensor node for  . The number of entries in
. The number of entries in  and
and  indicate the storage overhead of source coding which is equal to
indicate the storage overhead of source coding which is equal to  . The update overhead of source coding is determined by the modifications made on
. The update overhead of source coding is determined by the modifications made on  and
and  for each new event occurrence. Table 1 lists most of the notation used in the rest of the paper.
for each new event occurrence. Table 1 lists most of the notation used in the rest of the paper.
4. Problem Statement
Let us consider an event type  to be sensed by a wireless sensor network. Let us assume that a discrete set of
to be sensed by a wireless sensor network. Let us assume that a discrete set of  sensor nodes' sensing areas define the monitored area. Also let
sensor nodes' sensing areas define the monitored area. Also let  denote the point where
denote the point where  sensor node is located for
sensor node is located for  . Let us consider a short interval where at most one event can occur at location
. Let us consider a short interval where at most one event can occur at location  . We define two random variables
. We define two random variables  and
and  that correspond to the total number of event occurrences and the total number of event detections, respectively, within the monitored area. When the monitored area has total
that correspond to the total number of event occurrences and the total number of event detections, respectively, within the monitored area. When the monitored area has total  event occurrences,
event occurrences, assumes the value
assumes the value  for
for  . Similarly,
. Similarly, takes the value
takes the value  when total
when total  event occurrences are detected among
event occurrences are detected among  number of event occurrences for
number of event occurrences for  . Also let us define the inputs and outputs of the problem as follows.
. Also let us define the inputs and outputs of the problem as follows.
-
(i)
Inputs:
-
(a)
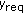 : the required event miss-ratio threshold for event
: the required event miss-ratio threshold for event  ,
, -
(b)
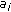 : the sensing area of sensor node at location
: the sensing area of sensor node at location  for
for 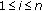 ,
, -
(c)
 : probability of event occurrence at
: probability of event occurrence at 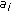 for
for  ,
, -
(d)
 : probability that
: probability that  takes value
takes value  for
for  .
.
-
(a)
-
(ii)
Outputs:
-
(a)
 : the observed (actual) event miss-ratio for event
: the observed (actual) event miss-ratio for event  ,
, -
(b)
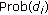 : probability of event detection at
: probability of event detection at  for
for 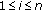 ,
, -
(c)
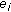 : the energy consumption of active sensor nodes for data transmission with their assigned rates at location
: the energy consumption of active sensor nodes for data transmission with their assigned rates at location 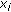 for
for 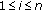 ,
, -
(d)
 : probability that
: probability that  takes value
takes value  for
for  .
.
-
(a)
The problem of this paper is to show that the proposed protocol CORA guarantees that the observed event miss-ratio  is less than or equal to the required event miss-ratio
is less than or equal to the required event miss-ratio 

and minimize the total energy consumption of all active sensor nodes

where  and
and  (i.e., the expected values of
(i.e., the expected values of  and
and  , resp.) are written as
, resp.) are written as

There are two extreme cases for  . At one extreme, the observed event miss-ratio is becoming equal to one when all event occurrences are missed. The other extreme occurs when all event occurrences are detected, thereby making the observed event miss-ratio equal to zero.
. At one extreme, the observed event miss-ratio is becoming equal to one when all event occurrences are missed. The other extreme occurs when all event occurrences are detected, thereby making the observed event miss-ratio equal to zero.
Among the aforementioned probability values, depends on the distribution of event occurrences.
depends on the distribution of event occurrences.  is controlled by the aggregate coverage of active sensor nodes.
is controlled by the aggregate coverage of active sensor nodes.  is computed by considering all possible combinations of the
is computed by considering all possible combinations of the  locations for having total
locations for having total  events in the monitored area for
events in the monitored area for  . As an example, let us derive a close expression for
. As an example, let us derive a close expression for  where there exists a single event in the entire monitored area. The probability, say
where there exists a single event in the entire monitored area. The probability, say  , that a single event occurs at location
, that a single event occurs at location  is equal to the probability of event occurrence at location
is equal to the probability of event occurrence at location  times the product of all those probabilities of not having event occurrences at the remaining
times the product of all those probabilities of not having event occurrences at the remaining  grid locations for
grid locations for  .
.  is equal to the sum of all
is equal to the sum of all  s over
s over  locations. Thus,
locations. Thus,

Since there is no close formula for  for
for  we provide Algorithm Probability Computation for
we provide Algorithm Probability Computation for  to express
to express  .
.  is computed similar to
is computed similar to  with the exception that it depends on not only the probability of event occurrences but also their probability of detection. For example,
with the exception that it depends on not only the probability of event occurrences but also their probability of detection. For example, is expressed as
is expressed as

where

5. CORA Protocol for Event Miss-Ratio Assurances
We first give in this section an overview of how CORA provides event miss-ratio assurances with minimum energy consumption. The network lifetime is divided into consecutive rounds and CORA performs coverage scheduling and rate assignment at the beginning of each round. The round-based operation enables CORA to take the recent node residual energy information into account. At each location  , coverage scheduling and rate assignment control
, coverage scheduling and rate assignment control  and
and  respectively, for
respectively, for  . Meanwhile, CORA enables event-driven cooperation of coverage scheduling and rate assignment in two phases.
. Meanwhile, CORA enables event-driven cooperation of coverage scheduling and rate assignment in two phases.
In Phase I, event distribution is identified using a continuously updated histogram. Depending on whether the event distribution is uniform or nonuniform, the ideal correlator radius is found for each cluster. As we will show, there exists a single correlator radius within the cluster for uniform event distribution such as the one depicted in Figure 1. For nonuniform event distributions as illustrated in Figure 2, a local correlator radius exists for each hotspot. The local correlator radii of all hotspots are combined to find the cluster level global correlator radius. Under the guidance of the correlator radius, correlator nodes are selected and cluster members form groups around correlator nodes for rate assignment.
In Phase II, those critical nodes which significantly improve the energy consumption of the cluster are identified from their assigned rates. Coverage scheduling then activates only those critical nodes for improving energy consumption and meeting the required event miss-ratios. Since Phase I differs for uniform and nonuniform event distributions, the steps of Phase I are described next separately for uniform and nonuniform event distributions.
5.1. Phase I for Uniform Event Distribution
The expected amount of data generated by each node is the same under uniform event distribution. Therefore, the locations of sensor nodes within the cluster topology plays the key role for overall energy consumption. In this section, we study how distance of correlator nodes to the clusterhead affects the energy expenditure. Let us refer to this distance as  where the subscript denotes the correlator radius and
where the subscript denotes the correlator radius and  . Let
. Let  be the ideal
be the ideal value which maximizes the energy gain of distributed source coding by correlator nodes relative to the case when cluster members transmit data directly to the clusterhead. In what follows, we will explain how
value which maximizes the energy gain of distributed source coding by correlator nodes relative to the case when cluster members transmit data directly to the clusterhead. In what follows, we will explain how  is found in Step I of Protocol CORA by formulating this energy gain as a function of
is found in Step I of Protocol CORA by formulating this energy gain as a function of  . We will then describe the allocation of coding rates in accordance with
. We will then describe the allocation of coding rates in accordance with  .
.
We now analyze the energy consumption for a cluster of wireless sensor nodes when distributed source coding is applied at a given distance  from the clusterhead (i.e., when correlator nodes have distance
from the clusterhead (i.e., when correlator nodes have distance  to the clusterhead). The first question we answer in this analysis is the following: For which cluster members would correlator nodes yield any improvement in energy consumption? Especially within the close proximity of the clusterhead, transmitting data directly to the clusterhead (i.e., bypassing the correlators) should be preferable over sending data through the correlator nodes.
to the clusterhead). The first question we answer in this analysis is the following: For which cluster members would correlator nodes yield any improvement in energy consumption? Especially within the close proximity of the clusterhead, transmitting data directly to the clusterhead (i.e., bypassing the correlators) should be preferable over sending data through the correlator nodes.
Let us call the union of those locations from where the sensed data should be sent directly to the clusterhead as Direct Transmission Region (DTR). Let  denote the radius of
denote the radius of  where the subscript
where the subscript  refers to direct data transmission. The donut shaped region obtained by excluding the
refers to direct data transmission. The donut shaped region obtained by excluding the  from the clusterhead transmission region is referred to as Distributed Source Coding Region (DSCR). Figure 3 illustrates
from the clusterhead transmission region is referred to as Distributed Source Coding Region (DSCR). Figure 3 illustrates  and
and  in blue and red colors, respectively.
in blue and red colors, respectively.
A correlator node  is illustrated with its members
is illustrated with its members  , and
, and  . The ideal correlator radius
. The ideal correlator radius  guides the formation of such rate assignment groups in Distributed Source Coding Region (
guides the formation of such rate assignment groups in Distributed Source Coding Region ( ) shaded in red color. The cluster members such as node
) shaded in red color. The cluster members such as node  in blue colored Direct Transmission Region (
in blue colored Direct Transmission Region ( ) send data directly to the clusterhead.
) send data directly to the clusterhead.
To identify  , we find the relationship between
, we find the relationship between  and
and  . Specifically, we consider the energy consumed for gathering data from any cluster member
. Specifically, we consider the energy consumed for gathering data from any cluster member  with distance
with distance  to the clusterhead where
to the clusterhead where  . Note that the energy consumption of node
. Note that the energy consumption of node  should be the same in direct data transmission and distributed source coding cases since node
should be the same in direct data transmission and distributed source coding cases since node  is located on the boundary of
is located on the boundary of  . Let us refer to the energy consumption of node
. Let us refer to the energy consumption of node  when it uses direct transmission to the clusterhead as
when it uses direct transmission to the clusterhead as  . Let
. Let  be the energy consumption of
be the energy consumption of  when its data reach the clusterhead indirectly through correlator nodes.
when its data reach the clusterhead indirectly through correlator nodes.
When node  bypasses the correlators, the entropy of the source at node
bypasses the correlators, the entropy of the source at node  is transmitted over distance
is transmitted over distance  to the clusterhead. Based on the energy model given in Section 3,
to the clusterhead. Based on the energy model given in Section 3, would be
would be

When correlator nodes apply distributed source coding at distance  from the clusterhead,
from the clusterhead, sends only nonredundant data to the correlator node which are then forwarded to the clusterhead. Thus, we next consider the expected amount of data transmitted by node
sends only nonredundant data to the correlator node which are then forwarded to the clusterhead. Thus, we next consider the expected amount of data transmitted by node  when data redundancy is eliminated by distributed source coding.
when data redundancy is eliminated by distributed source coding.
The redundancy in node  's data is attributed to the overlap of node
's data is attributed to the overlap of node  's sensing region with the sensing regions of its neighboring nodes. Consequently, we need to find how much of the area within the sensing range of a node is covered only by the node itself. When there is coverage redundancy within the cluster, the expected size of the common area covered by node
's sensing region with the sensing regions of its neighboring nodes. Consequently, we need to find how much of the area within the sensing range of a node is covered only by the node itself. When there is coverage redundancy within the cluster, the expected size of the common area covered by node  with its neighboring nodes is
with its neighboring nodes is

where  refers to the coverage area of the cluster and the term
refers to the coverage area of the cluster and the term  denotes the maximum area that can be covered by cluster members. If there is no coverage redundancy (i.e., no overlap among sensing regions of neighboring nodes), then the size of the common area becomes zero. Following these observations, let us define
denotes the maximum area that can be covered by cluster members. If there is no coverage redundancy (i.e., no overlap among sensing regions of neighboring nodes), then the size of the common area becomes zero. Following these observations, let us define  as the ratio of a node's sensing region that is covered exclusively by the node itself where
as the ratio of a node's sensing region that is covered exclusively by the node itself where  . With the assumption that coverage redundancy is uniformly distributed among cluster members,
. With the assumption that coverage redundancy is uniformly distributed among cluster members, is expressed as
is expressed as

Let us also assume that the task of covering the common areas (i.e., the regions that are covered by at least two cluster members) is evenly distributed among all cluster members. We introduce the variable  as the expected ratio of the common areas covered by a sensor node to its overall sensing region where
as the expected ratio of the common areas covered by a sensor node to its overall sensing region where  . Since any area within the cluster that is not covered only by a single sensor node belongs to the common area,
. Since any area within the cluster that is not covered only by a single sensor node belongs to the common area, is expressed as
is expressed as

From the exclusive and common areas covered by node  , we can now determine the amount of nonredundant data transmitted by node
, we can now determine the amount of nonredundant data transmitted by node  and express
and express  . Specifically,
. Specifically,

where  represents the ratio of the rate control message size to the data message size. First, rate information is transmitted from the correlator to node
represents the ratio of the rate control message size to the data message size. First, rate information is transmitted from the correlator to node  over distance
over distance  . Then, node
. Then, node  codes sensor data with the assigned rate. The data received by the correlator node are transmitted to the clusterhead over distance
codes sensor data with the assigned rate. The data received by the correlator node are transmitted to the clusterhead over distance  .
.
Let  refer to the
refer to the  value substitution of which to (7) and (11) yields the same energy consumption for
value substitution of which to (7) and (11) yields the same energy consumption for  and
and  , respectively. The term
, respectively. The term  is included in
is included in  subscript to indicate that
subscript to indicate that  is dependent on the
is dependent on the  value. Since
value. Since  refers to the radius of
refers to the radius of  , a cluster member uses direct data transmission to the clusterhead if its distance to the clusterhead is less than
, a cluster member uses direct data transmission to the clusterhead if its distance to the clusterhead is less than  . Otherwise, the data of the cluster member are sent to its designated correlator node. In light of this selection criteria for data transmission, we next define the energy gain function of correlator nodes for any given
. Otherwise, the data of the cluster member are sent to its designated correlator node. In light of this selection criteria for data transmission, we next define the energy gain function of correlator nodes for any given  value.
value.
Let  denote the energy consumption for gathering data from the cluster members when they bypass the correlator nodes and transmit their data directly to the clusterhead with the subscript referring to no source coding. Let
denote the energy consumption for gathering data from the cluster members when they bypass the correlator nodes and transmit their data directly to the clusterhead with the subscript referring to no source coding. Let  be the energy expenditure for the case where cluster members use correlator nodes with the subscript denoting distributed source coding.
be the energy expenditure for the case where cluster members use correlator nodes with the subscript denoting distributed source coding.  is a function of
is a function of  and is defined within the interval
and is defined within the interval  while
while  is independent from
is independent from  . Then, the energy gain due to the correlator nodes is defined as
. Then, the energy gain due to the correlator nodes is defined as  where
where

By incorporating each possible location of a cluster member within the cluster, is expressed as
is expressed as

where  and
and  refer to the expected energy consumption of cluster members in
refer to the expected energy consumption of cluster members in  and
and  , respectively. Specifically,
, respectively. Specifically,

where  that is the probability of having a sensor node with distance
that is the probability of having a sensor node with distance  to the clusterhead. The first and second terms of (14) represent the energy consumption of cluster members in
to the clusterhead. The first and second terms of (14) represent the energy consumption of cluster members in  that are closer to and farther from the clusterhead than correlator nodes, respectively. On the other hand,
that are closer to and farther from the clusterhead than correlator nodes, respectively. On the other hand, is defined by considering the direct transmission from each cluster member as
is defined by considering the direct transmission from each cluster member as

By subtracting  from
from  is determined and the ideal correlator radius is found as the
is determined and the ideal correlator radius is found as the  value which yields the maximum
value which yields the maximum  . Specifically,
. Specifically, is a dome-shaped function of
is a dome-shaped function of  with its derivative having value zero at point
with its derivative having value zero at point  . Figure 4 illustrates the behavior of
. Figure 4 illustrates the behavior of  along with the ideal correlator radius
along with the ideal correlator radius  .
.
Algorithm Coding Rate Assignment describes how rate allocation groups are formed under guidance of  and rates are assigned to group members at Step II and Step III of Protocol CORA, respectively. To select the correlator nodes, the average residual energy of cluster members is calculated first. A cluster member within
and rates are assigned to group members at Step II and Step III of Protocol CORA, respectively. To select the correlator nodes, the average residual energy of cluster members is calculated first. A cluster member within  becomes a correlator node if (i) it has higher residual energy than the average residual energy, and (ii) its distance to the clusterhead is closer to
becomes a correlator node if (i) it has higher residual energy than the average residual energy, and (ii) its distance to the clusterhead is closer to  than any one of its neighboring nodes. The remaining active nodes join the group of the closest correlator node.
than any one of its neighboring nodes. The remaining active nodes join the group of the closest correlator node.
Within each group, the data transmissions from group members to the correlator node are ordered in descending order of node residual energy levels. Thus, a sensor node uses the data of other group members that have higher residual energy as side information. Note that, having a high residual energy node transmit data earlier than others does not guarantee that it will use the highest coding rate. This is especially true when such a node has highly overlapping sensing region with other high energy nodes that have already transmitted data. However, when a high energy node uses low coding rate, its residual energy would not change significantly while other nodes would be spending more energy. Consequently, CORA would schedule such group members to transmit data earlier than others in the following rounds.
The correlator node applies the proposed differential data transmission technique to further reduce the size of the data before sending it to the clusterhead. The basic motivation behind differential data transmission is that the data gathered from group members exhibit not only spatial correlation but also temporal correlation. To exploit the correlation in temporal domain, both clusterhead and correlator node maintain a common reference data which captures the characteristic values of last  data values transmitted from the correlator node to the clusterhead.
data values transmitted from the correlator node to the clusterhead.
Let  be the reference data and
be the reference data and  be the raw nonredundant data gathered at the correlator node. Let
be the raw nonredundant data gathered at the correlator node. Let  denote the difference operator and
denote the difference operator and  refer to its inverse. As an example, if the sensor readings are mapped to numbers than
refer to its inverse. As an example, if the sensor readings are mapped to numbers than  and
and  may correspond to the subtraction and addition, respectively. Then, the correlator node transmits the differential data
may correspond to the subtraction and addition, respectively. Then, the correlator node transmits the differential data  with the value
with the value  . After receiving
. After receiving  , the clusterhead recovers the original raw data
, the clusterhead recovers the original raw data  .
.
5.2. Phase I for Nonuniform Event Distribution
CORA determines the ideal rate assignment for a nonuniform event distribution by considering all hotspots of event occurrences. For each hotspot, a local ideal correlator radius is computed first. Then, local ideal correlator radii for different hotspots are combined to determine the global ideal correlator radius for the cluster. In the following analysis, we describe the computation of the ideal correlator radius  for a hotspot with distance
for a hotspot with distance  to the clusterhead as shown in Figure 5.
to the clusterhead as shown in Figure 5.
In the analysis, we do not follow a particular event distribution but assume that event occurrence probabilities are nonzero within the local proximity of hotspots only. In particular, let  be the event occurrence probability at a point with distance
be the event occurrence probability at a point with distance  to the hotspot center.
to the hotspot center.  can be calculated either by using exponential and Pareto distributions depending on the nature of the event occurrences. In exponential distribution, the probability density function is
can be calculated either by using exponential and Pareto distributions depending on the nature of the event occurrences. In exponential distribution, the probability density function is  where the event occurrence probability decreases rapidly as the distance to the hotspot center increases. For those hotspots with a slowly decreasing effect, Pareto distribution is more suitable due to its density function
where the event occurrence probability decreases rapidly as the distance to the hotspot center increases. For those hotspots with a slowly decreasing effect, Pareto distribution is more suitable due to its density function  where
where  is the shape parameter and
is the shape parameter and  is the initial value.
is the initial value.
As in uniform event distribution analysis, we will express the energy gain function  in terms of
in terms of  where
where  . However, unlike the uniform event distribution case, the analysis is shaped by those locations near hotspots that have nonzero event occurrence probabilities rather than all cluster locations. Let us refer to the maximum distance between the center of the hotspot and any node within the hotspot as the hotspot range and denote it by
. However, unlike the uniform event distribution case, the analysis is shaped by those locations near hotspots that have nonzero event occurrence probabilities rather than all cluster locations. Let us refer to the maximum distance between the center of the hotspot and any node within the hotspot as the hotspot range and denote it by  .
.
In computation of both  and
and  , we will consider each possible distance
, we will consider each possible distance  that a sensor node can have to the hotspot center where
that a sensor node can have to the hotspot center where  . In Figure 5, a red circle labeled
. In Figure 5, a red circle labeled  illustrates the possible node locations with distance
illustrates the possible node locations with distance  to the hotspot center. For the upper semicircle of
to the hotspot center. For the upper semicircle of  as an example, such locations are defined by the coordinates
as an example, such locations are defined by the coordinates  where
where  and
and  . Let
. Let  denote the expected energy consumption of the nodes located on
denote the expected energy consumption of the nodes located on  when they use correlator nodes. Let
when they use correlator nodes. Let  refer to the expected energy expenditure of the same nodes on
refer to the expected energy expenditure of the same nodes on  when they apply direct data transmission to the clusterhead. We will integrate
when they apply direct data transmission to the clusterhead. We will integrate  and
and  over all
over all  within the hotspot to find
within the hotspot to find  and
and  , respectively.
, respectively.
To compute  , we break up
, we break up  into small segments
into small segments  with each segment representing a possible location of a sensor node on
with each segment representing a possible location of a sensor node on  . For each one of these segments, the event occurrence probability is the same and is equal to
. For each one of these segments, the event occurrence probability is the same and is equal to  . From Figure 5, it can be observed that
. From Figure 5, it can be observed that

Therefore,

where

and  . In words, when there is a sensor node on
. In words, when there is a sensor node on  , the probability of event data transmission from
, the probability of event data transmission from  is equal to the probability that the node is placed at
is equal to the probability that the node is placed at  (i.e.,
(i.e., ) and the probability that an event occurs (i.e.,
) and the probability that an event occurs (i.e., ). The energy consumption for sending data from
). The energy consumption for sending data from  to the clusterhead consists of two components. First, the data are transmitted from
to the clusterhead consists of two components. First, the data are transmitted from  to the correlator node over distance
to the correlator node over distance  , and then sent by correlator node to the clusterhead over distance
, and then sent by correlator node to the clusterhead over distance  .
.
To determine  , we follow the same segment-based division of
, we follow the same segment-based division of  but assume that any sensor node on
but assume that any sensor node on  bypasses the correlator nodes. Thus,
bypasses the correlator nodes. Thus,

where  .
.
To express  and
and  , we integrate over each
, we integrate over each  and incorporate the expected number of nodes to be located on
and incorporate the expected number of nodes to be located on  for
for  . Specifically,
. Specifically,

Finally, we take the derivative of the energy gain function  where
where  . The ideal correlator radius
. The ideal correlator radius  makes the derivative function
makes the derivative function  equal to zero at point
equal to zero at point  .
.
Given a set of  hotspots with the local ideal correlator radius for the
hotspots with the local ideal correlator radius for the  hotspot referred to as
hotspot referred to as  , the global ideal correlator radius is set as
, the global ideal correlator radius is set as  where
where  . Once the value of
. Once the value of  is obtained, the selection of correlator nodes and their group members are the same with the uniform event distribution case. Within a group however, the rates are allocated based on the proximity of nodes to the hotspots. Specifically, a sensor node uses the data of other group members that have larger distances to the hotspot as side information. The motivation here is that those group members that are near the hotspots consume more energy due to their high event detection activity. Thus, CORA alleviates the burden on such nodes by increasing their side information in distributed source coding.
is obtained, the selection of correlator nodes and their group members are the same with the uniform event distribution case. Within a group however, the rates are allocated based on the proximity of nodes to the hotspots. Specifically, a sensor node uses the data of other group members that have larger distances to the hotspot as side information. The motivation here is that those group members that are near the hotspots consume more energy due to their high event detection activity. Thus, CORA alleviates the burden on such nodes by increasing their side information in distributed source coding.
5.3. Phase II for Both Uniform and Nonuniform Event Distributions
This section presents the steps of Phase II that are implemented in the same way for both uniform and nonuniform event distributions. CORA employs a priority-based coverage scheduling technique to select the active sensor nodes for each event  . In coverage scheduling, a node that is considered earlier for activation has better chance of going to sleep mode since those nodes that are waiting to be activated can still meet the required event miss-ratio. Based on this observation, CORA implements node priorities to have critical nodes considered later in coverage scheduling, thereby forcing them to remain active. In Step IV, each cluster member
. In coverage scheduling, a node that is considered earlier for activation has better chance of going to sleep mode since those nodes that are waiting to be activated can still meet the required event miss-ratio. Based on this observation, CORA implements node priorities to have critical nodes considered later in coverage scheduling, thereby forcing them to remain active. In Step IV, each cluster member  is associated with a score
is associated with a score  that reveals how much it improves the energy expenditure of the cluster for
that reveals how much it improves the energy expenditure of the cluster for  .
.  is computed by estimating the rates within the neighborhood of node
is computed by estimating the rates within the neighborhood of node  for the following two cases:
for the following two cases:
Case I.
Node  participates in distributed source coding.
participates in distributed source coding.
Case II.
Node  is excluded from distributed source coding.
is excluded from distributed source coding.
The rate predictions are made according to the proposed rate assignment algorithms. Then, is set as the ratio of the expected average residual energy of the neighboring nodes for Case I to the one for Case II. Consequently, the critical nodes get assigned the highest scores.
is set as the ratio of the expected average residual energy of the neighboring nodes for Case I to the one for Case II. Consequently, the critical nodes get assigned the highest scores.
Algorithm Coverage Scheduling implements Step V of Protocol CORA for the assignment of events to cluster members. The clusterhead first sorts the nodes in ascending order of their scores such that low score nodes are considered first. Then, each node  is evaluated for coverage scheduling in the order of its score where
is evaluated for coverage scheduling in the order of its score where  . The status of node
. The status of node  for event
for event  is determined according to its sensing region's overlap with the sensing regions of its neighboring nodes. To control event misses, either (i) node
is determined according to its sensing region's overlap with the sensing regions of its neighboring nodes. To control event misses, either (i) node  remains active and covers the physical area within its sensing region on its own, or (ii) node
remains active and covers the physical area within its sensing region on its own, or (ii) node  goes to sleep mode and lets its neighboring nodes provide coverage over its sensing region.
goes to sleep mode and lets its neighboring nodes provide coverage over its sensing region.
Let  denote the set of neighboring nodes for
denote the set of neighboring nodes for  that can contribute to the coverage of
that can contribute to the coverage of  's sensing region where
's sensing region where  . Based on the evaluation of scores, the clusterhead creates an eligible set of neighboring nodes
. Based on the evaluation of scores, the clusterhead creates an eligible set of neighboring nodes  for coverage of node
for coverage of node  's sensing region where
's sensing region where  . Each neighboring node
. Each neighboring node  satisfies either one of the following conditions where
satisfies either one of the following conditions where  and
and  .
.
-
(i)
 .
. -
(ii)
 and node
and node  has already been scheduled as an active node or has not announced its status yet for
has already been scheduled as an active node or has not announced its status yet for 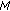 .
. -
(iii)
 and node
and node 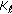 has already been scheduled as an active node for
has already been scheduled as an active node for  .
.
Once its eligible set of neighboring nodes are identified, node  computes the uncovered part of its sensing region for event
computes the uncovered part of its sensing region for event  denoted by
denoted by  where
where  . If
. If  , then node
, then node  goes to sleep mode for event
goes to sleep mode for event  since its sensing region is covered sufficiently by neighboring nodes that would remain active. Otherwise, node
since its sensing region is covered sufficiently by neighboring nodes that would remain active. Otherwise, node  is scheduled active to preserve
is scheduled active to preserve  for event
for event  .
.
To ensure that  , each cluster member
, each cluster member  identifies its
identifies its  from
from  and event distribution such that
and event distribution such that  . Let us define
. Let us define  and
and  as the maximum and minimum probability of an event occurrence, respectively, for
as the maximum and minimum probability of an event occurrence, respectively, for  at any point within the monitored region. Specifically,
at any point within the monitored region. Specifically, and
and  for
for  where
where  is the sensor locations in the monitored region. For node
is the sensor locations in the monitored region. For node  located at
located at  is set as
is set as

where  . Consequently, CORA provides variable coverage over the monitored area with the worst and best coverage defined by the following two cases. When
. Consequently, CORA provides variable coverage over the monitored area with the worst and best coverage defined by the following two cases. When  is equal to
is equal to  , node
, node  meets the required event miss-ratio threshold by setting
meets the required event miss-ratio threshold by setting  . On the other hand, if
. On the other hand, if  is equal to
is equal to  , then node
, then node  detects all event occurrences by using
detects all event occurrences by using  .
.
Lemma 1.
The variable coverage provided by CORA guarantees that  for any given event
for any given event  .
.
Proof of Lemma 1.
The proof is given in the Appendix.
We next present an efficient algorithm to compute the area covered within a node's sensing region by its neighboring nodes. The coverage computation is used to verify that a node's sensing region has sufficient overlap with its neighboring nodes before the node goes to sleep mode. While computing coverage, a sensor node considers its neighboring nodes in ascending order of their identifiers. For each neighboring node, the area of intersection that's not covered by lower id nodes is determined. This helps the overlapping areas between the sensing regions of neighboring nodes to be considered only once.
Algorithm Coverage Computation describes the steps taken for finding the area of overlap a node has with its neighboring nodes. The sensing region of each node is represented as a set of  segments
segments  as shown in Figure 6 where
as shown in Figure 6 where  . Each segment has the same thickness
. Each segment has the same thickness  and the union of all segments is equal to the node's sensing region where
and the union of all segments is equal to the node's sensing region where  . The segments are numbered in increasing order from the center of the sensing region towards its boundary.
. The segments are numbered in increasing order from the center of the sensing region towards its boundary.
For a given neighboring node, the segment with the lowest id that intersects with the sensing region of the neighboring node is determined. Then, for each segment with a higher id than the lowest id segment, the covered part of the segment by the neighboring node is represented with an angle  . This angle is defined with respect to the intersection points of the segment and the neighboring node's sensing region as illustrated in Figure 6. By finding the overlap with the sensing regions of all neighboring nodes, the covered portions of any given segment
. This angle is defined with respect to the intersection points of the segment and the neighboring node's sensing region as illustrated in Figure 6. By finding the overlap with the sensing regions of all neighboring nodes, the covered portions of any given segment  are represented with a set of angles
are represented with a set of angles  where
where  . The covered portion of segment
. The covered portion of segment  is found based on the comparison of
is found based on the comparison of  and the sum of magnitudes for the angles in
and the sum of magnitudes for the angles in  . The total covered portion of the sensing region is determined by incorporating each segment in proportion with its area.
. The total covered portion of the sensing region is determined by incorporating each segment in proportion with its area.
Example 1.
Let us consider a particular segment  within the sensing region of node
within the sensing region of node  for which the neighboring nodes
for which the neighboring nodes  , and
, and  can contribute to its coverage. Suppose
can contribute to its coverage. Suppose

initially based on the contributions of nodes  and
and  to the coverage of the
to the coverage of the  segment. If the angle obtained for the coverage contribution of node
segment. If the angle obtained for the coverage contribution of node  is found to be
is found to be  , then
, then  is updated as
is updated as

Finally, based on the magnitudes of each angle, the covered area of segment  is determined as
is determined as

where  refers to sum of the magnitudes of angles in any given set
refers to sum of the magnitudes of angles in any given set  .
.
The accuracy of the proposed coverage computation technique improves with increasing number of segments. However, using a large number of segments also comes at the expense of higher computational and storage overhead. We next describe how the overhead of the segment-based representation is minimized. The key idea is to limit the application of segment-based division scheme to specific parts of the sensing region only. The remaining parts of the sensing region are divided into subregions at a higher level of granularity than segments, specifically into four quadrants. These quadrants have the special property that the full coverage of each quadrant can be verified in a very simple manner. The segment-based representation is then applied only within those quadrants for which the full coverage cannot be verified.
Let us now focus on the coverage of any given quadrant within a node's sensing region by the neighboring sensor nodes. We refer to the four quadrants within the sensing region as  (upper left),
(upper left), (down left),
(down left), (upper right),
(upper right), (down right) as shown in Figure 7(b). Without loss of generality, let us consider the full coverage of
(down right) as shown in Figure 7(b). Without loss of generality, let us consider the full coverage of  , the upper left quadrant, shown in Figure 7(a). In order to lay down the placement constraints of neighboring sensor nodes for the full coverage of quadrant
, the upper left quadrant, shown in Figure 7(a). In order to lay down the placement constraints of neighboring sensor nodes for the full coverage of quadrant  , we first address the random placement of a single neighboring node within quadrant
, we first address the random placement of a single neighboring node within quadrant  . In any outcome of this experiment, the extreme points at which the neighboring node can be located are
. In any outcome of this experiment, the extreme points at which the neighboring node can be located are  and
and  shown as dots in Figure 7(a). The circles with dashed lines in the figure indicate the sensing region of the neighboring node when it would be located at
shown as dots in Figure 7(a). The circles with dashed lines in the figure indicate the sensing region of the neighboring node when it would be located at  and
and  . These boundary cases are important in the sense that they reveal the field
. These boundary cases are important in the sense that they reveal the field  in which the placement of the neighboring node yields the full coverage of the quadrant.
in which the placement of the neighboring node yields the full coverage of the quadrant.
The division of a node's sensing region into four quadrants to analyze its coverage. The derivation of the fields  , and
, and  for quadrant
for quadrant  of a sensor node located at point
of a sensor node located at point  . The solid and dashed circles represent the sensing regions of the node and its neighboring node, respectivelyThe fields in each quadrant are distinguished by appending the quadrant name
. The solid and dashed circles represent the sensing regions of the node and its neighboring node, respectivelyThe fields in each quadrant are distinguished by appending the quadrant name  to the end of the field name
to the end of the field name
Figure 7(a) shows field  along with fields
along with fields  and
and  which together form the quadrant. Specifically
which together form the quadrant. Specifically

Figure 7(b) shows these three fields separately for each one of the quadrants where the quadrant name is indicated in parentheses and appended to the field name.
Let us also consider the random placement of more than one neighboring node over the quadrant. In this case, either one of the conditions below satisfies full coverage of the quadrant.
Condition 1.
At least one of the neighboring nodes should be located in the field  .
.
Condition 2.
There should be at least one neighboring node in each one of the fields  and
and  .
.
These conditions apply to all quadrants since each one of them has its own  , and
, and  fields.
fields.
We next give an important lemma which describes the coverage relationship between different quadrants of the same sensing region. The key observation here is that the existence of active neighboring nodes in a quadrant can compensate for the uncovered parts of its adjacent quadrants. Two quadrants are referred to as adjacent if they have a common boundary of length  and they constitute a contiguous
and they constitute a contiguous  .
.
Example 2.
The quadrant  is adjacent to
is adjacent to  and
and  but not
but not  .
.
Lemma 2.
Let  and
and  be the set of active nodes that are located over the adjacent quadrants
be the set of active nodes that are located over the adjacent quadrants  and
and  , respectively, where
, respectively, where  , and
, and  . An element of
. An element of  placed in
placed in  field has an equal coverage effect on
field has an equal coverage effect on  as compared to an element of
as compared to an element of  placed in
placed in  . This property is also symmetric and is applicable to
. This property is also symmetric and is applicable to  fields of adjacent quadrants.
fields of adjacent quadrants.
Proof of Lemma 2.
The proof is available in the Appendix.
From Lemma 2, Condition 2 for the full coverage of each quadrant is rephrased as follows. Let the neighboring subregions of  be denoted by
be denoted by  and
and  according to the type of adjacent field that
according to the type of adjacent field that  has with its neighboring quadrant where
has with its neighboring quadrant where  and
and  .
.
Example 3.
If  is equal to
is equal to  then
then  and
and  since the quadrants
since the quadrants  and
and  have adjacent
have adjacent  fields while quadrants
fields while quadrants  and
and  have neighboring
have neighboring  fields.
fields.
Then, for the full coverage of  , Condition 2 requires the existence of at least one neighboring node in each one of the following fields.
, Condition 2 requires the existence of at least one neighboring node in each one of the following fields.
-
(i)
 or
or  .
. -
(ii)
 or
or  .
.
The remaining question that needs to be answered is how to determine the field and the quadrant that a neighboring is located.
Let us consider a node  with coordinates
with coordinates  which computes the covered portion of its sensing region. Let node
which computes the covered portion of its sensing region. Let node  be one of neighboring nodes of node
be one of neighboring nodes of node  with coordinates
with coordinates  where
where  . Table 2 gives a set of simple conditions that can be checked by node
. Table 2 gives a set of simple conditions that can be checked by node  to identify the particular quadrant and field at which node
to identify the particular quadrant and field at which node  is located. In these conditions, if node
is located. In these conditions, if node  is located at the boundary of two quadrants, it is assumed to belong to the right quadrant in clockwise order. The conditions are expressed in terms of distance of node
is located at the boundary of two quadrants, it is assumed to belong to the right quadrant in clockwise order. The conditions are expressed in terms of distance of node  to the points
to the points  , and
, and  that are illustrated in Figure 7(b). Once the exact quadrant and field information for each neighboring node is determined, the sensor node verifies whether each one of its quadrants is covered completely by checking Condition 1 and Condition 2.
that are illustrated in Figure 7(b). Once the exact quadrant and field information for each neighboring node is determined, the sensor node verifies whether each one of its quadrants is covered completely by checking Condition 1 and Condition 2.
 to be placed in a specific quadrant and field over node
to be placed in a specific quadrant and field over node  's sensing region.
's sensing region.We next address the effect of environmental factors on coverage computation. The changes in weather and ground status result in differences between the effective sensing ranges of nodes and their nominal sensing ranges. To incorporate effective sensing ranges into coverage computation, CORA considers both single-node detectable and multi-node detectable environmental factors such as humidity level and rain, respectively. Let  denote the set of all such environmental factors taken into account by the sensor nodes. For each sensing unit, a correction constant
denote the set of all such environmental factors taken into account by the sensor nodes. For each sensing unit, a correction constant is associated with
is associated with  environmental factor for
environmental factor for  where
where  . The magnitude and sign of each correction constant is determined by experimental evaluation with sensor hardware and different settings for the environmental factor it is associated with. The negative and positive sign for
. The magnitude and sign of each correction constant is determined by experimental evaluation with sensor hardware and different settings for the environmental factor it is associated with. The negative and positive sign for  represents the degradation and improvement in the sensing ability of the sensing unit due to the
represents the degradation and improvement in the sensing ability of the sensing unit due to the  environmental factor, respectively, [35].
environmental factor, respectively, [35].
The effective sensing range of a sensing unit  is obtained by adjusting its nominal sensing range
is obtained by adjusting its nominal sensing range  as
as

Once the effective sensing range is determined, it is broadcast to the neighboring nodes at the beginning of each round before the coverage scheduling takes place. In order to check the full coverage of its quadrants, a sensor node compares its distance to each one of its neighboring nodes with its effective sensing range. Then, among those neighboring nodes within the sensing region, the sensor node considers only the ones which have larger effective sensing ranges than itself while checking Condition 1 and Condition 2. For the quadrants that are not fully covered, the coverage of the segments are determined based on the intersection of effective sensing ranges of the node itself and its neighboring node.
5.3.1. Noise in Internode Distance Measurements
The clusterhead uses the distances between pairs of cluster members to create a local coordinate system. The coordinate assigned to each cluster member is not exact and has an error margin [36]. This section considers how such errors in node location estimates can be incorporated into coverage computation. In the absence of exact node coordinate information, we express coverage and event miss-ratio in terms of expected values rather than absolute values.
Let us represent the maximum deviation on the  and
and  coordinates of sensor nodes as
coordinates of sensor nodes as  and
and  , respectively. A cluster member with coordinate estimates
, respectively. A cluster member with coordinate estimates  may be located at any point within the ellipsis bounded by a box of width
may be located at any point within the ellipsis bounded by a box of width  and of height
and of height  . In what follows, we denote the set of all candidate points for the exact location of the node in this ellipsis by
. In what follows, we denote the set of all candidate points for the exact location of the node in this ellipsis by  .
.
Let us now consider the coverage of any given cluster member  's sensing area by its neighboring nodes where
's sensing area by its neighboring nodes where  . We refer to node
. We refer to node  's location as
's location as  and the neighboring nodes that can contribute to the coverage of its sensing region as the set
and the neighboring nodes that can contribute to the coverage of its sensing region as the set  . In the case of location errors, we define two sets of angles for the coverage of each segment within
. In the case of location errors, we define two sets of angles for the coverage of each segment within  's sensing region. These sets of angles, namely,
's sensing region. These sets of angles, namely,  and
and  , represent the worst and best possible cases for the coverage of the
, represent the worst and best possible cases for the coverage of the  segment by the neighboring sensor nodes in
segment by the neighboring sensor nodes in  , respectively, where
, respectively, where  .
.
Let  represent one of the neighboring nodes in
represent one of the neighboring nodes in  with coordinates
with coordinates  that covers a part of
that covers a part of  segment within node
segment within node  's sensing region where
's sensing region where  and
and  . Now consider the possible cases for the actual locations of nodes
. Now consider the possible cases for the actual locations of nodes  and
and  that minimizes and maximizes the covered part of the node
that minimizes and maximizes the covered part of the node  's sensing region by node
's sensing region by node  , respectively. For the worst case placement in terms of coverage, let us assume that node
, respectively. For the worst case placement in terms of coverage, let us assume that node  's coordinates are
's coordinates are  and node
and node  is located at
is located at  where
where  and
and  . Similarly, also assume that when node
. Similarly, also assume that when node  is positioned at
is positioned at  and
and  has coordinates
has coordinates  , the best case for the coverage of the
, the best case for the coverage of the  segment is achieved where
segment is achieved where  and
and  .
.  and
and  the following condition holds
the following condition holds

Let the pair of angles  represent the worst and best case contribution of node
represent the worst and best case contribution of node  for the coverage of the
for the coverage of the  segment, respectively.
segment, respectively.  and
and  are updated with the addition of
are updated with the addition of  and
and  , respectively. The same coverage computation is applied for each neighboring node in set
, respectively. The same coverage computation is applied for each neighboring node in set  in addition to node
in addition to node  . Once the coverage contribution of all neighboring nodes is determined, we define
. Once the coverage contribution of all neighboring nodes is determined, we define  as the expected covered portion of
as the expected covered portion of  segment where
segment where

and  represents the sum of the magnitudes of angles in a set
represents the sum of the magnitudes of angles in a set  . From the coverage of each segment
. From the coverage of each segment  for
for  , the uncovered portion of node
, the uncovered portion of node  's sensing region is determined as
's sensing region is determined as

6. Performance Evaluation
CORA is evaluated in terms of event miss-ratios, total energy expenditure, average node battery consumption, and the storage/update overhead for the application of source coding. In the simulations, we consider sensor networks with multiple clusters in which the clusters are formed based on residual energy of sensor nodes. Each network is simulated for a single round with  data gatherings. For uniform event distribution, every sensor node within a cluster is assumed to detect an event per data gathering. For nonuniform event distribution, we have randomly selected hotspot centers. At each data gathering, the event occurrences are modeled around these hotspot centers following the Gaussian distribution.
data gatherings. For uniform event distribution, every sensor node within a cluster is assumed to detect an event per data gathering. For nonuniform event distribution, we have randomly selected hotspot centers. At each data gathering, the event occurrences are modeled around these hotspot centers following the Gaussian distribution.
In the simulation graphs, the results for uniform and nonuniform event distributions are illustrated with solid and dashed lines, respectively. Each point shown in the graphs is obtained by averaging the simulation outcomes from a large number sensor networks. The sensor networks are deployed randomly over a target area of side length 100 m. The number of sensor nodes in each network is selected from the interval [ ] to control node/coverage redundancy. As network population increases, the sensing ranges of nodes overlap more, thereby increasing both the number of nodes redundant for coverage and the data correlation among neighboring sensor nodes.
] to control node/coverage redundancy. As network population increases, the sensing ranges of nodes overlap more, thereby increasing both the number of nodes redundant for coverage and the data correlation among neighboring sensor nodes.
The sensing range and transmission range of the nodes are set to 10 m and 30 m, respectively. The initial residual energy level of each node is assigned as 10 Joules. To calculate the energy expenditure, we have used the radio power consumption model described in Section 3 with settings  and
and  . The entropy of the source at a single cluster member is modeled as
. The entropy of the source at a single cluster member is modeled as  bits. The ratio of the control message size to the data message size is set to
bits. The ratio of the control message size to the data message size is set to  . Unless specified otherwise, the required event miss-ratio threshold is equal to
. Unless specified otherwise, the required event miss-ratio threshold is equal to  .
.
Figure 8(a) shows the results of the experiments in which we've considered sensor nodes equipped with four sensing units for event types  . CORA exploits the increase in node redundancy and required event miss-ratio thresholds to minimize the average number of events scheduled to each sensor node. As simulation results indicate, CORA enables a node to keep only one of its sensing units active at any time with sufficient node redundancy. It is possible that a node keeps its sensing unit active for event type
. CORA exploits the increase in node redundancy and required event miss-ratio thresholds to minimize the average number of events scheduled to each sensor node. As simulation results indicate, CORA enables a node to keep only one of its sensing units active at any time with sufficient node redundancy. It is possible that a node keeps its sensing unit active for event type  while its neighboring node might activate the sensing unit for a different event type
while its neighboring node might activate the sensing unit for a different event type  . Meanwhile, CORA's distributed coverage scheduling ensures that event miss-ratio assurances are met for every event types
. Meanwhile, CORA's distributed coverage scheduling ensures that event miss-ratio assurances are met for every event types  and
and  .
.
Performance evaluation of coverage scheduling. CORA takes advantage of the increase in network population and the required event miss-ratio thresholds to reduce the number of events to be sensed by each nodeThe experimental validation of the event miss-ratio assurancesCORA uses less number of active nodes to meet a given coverage requirement than the sponsored sector based coverage ( ) scheduling technique proposed in [5]
) scheduling technique proposed in [5]
Figure 8(b) illustrates the empirical verification of the assurances provided by CORA under different event miss-ratio requirements. For a particular  value, a large number of simulations are run while keeping the network population constant. The observed event miss-ratios
value, a large number of simulations are run while keeping the network population constant. The observed event miss-ratios  (shown in
(shown in  axis of Figure 8(b)) always remain below the required event miss-ratios
axis of Figure 8(b)) always remain below the required event miss-ratios  (illustrated in
(illustrated in  axis of Figure 8(b)).
axis of Figure 8(b)).
CORA assigns rates to the active nodes only and therefore is highly scalable. Figure 8(c) shows the results of the simulations that are run with the same required event miss-ratio value but with varying number of nodes. Even though the network population increases, CORA limits the number of nodes that are scheduled active and get assigned rates. Having only a smaller set of nodes active prolong the time event miss-ratio assurances can be met as those sensor nodes which are put in off-duty mode can save their energy to go active in the subsequent scheduling phases.
The simulations in Figure 8(c) also evaluate the accuracy of Algorithm Coverage Computation. For comparison, we have used the sponsored sector-based coverage computation technique proposed in [5] which we refer to as  in the results.
in the results.  considers those neighboring nodes that are located within the sensing region of a node while checking whether the node's sensing region is covered by its neighboring nodes. If the node's sensing region overlaps sufficiently by its neighboring nodes, then it becomes eligible to go off-duty. In particular, for a neighboring node with distance closer than the sensing range
considers those neighboring nodes that are located within the sensing region of a node while checking whether the node's sensing region is covered by its neighboring nodes. If the node's sensing region overlaps sufficiently by its neighboring nodes, then it becomes eligible to go off-duty. In particular, for a neighboring node with distance closer than the sensing range  represents the region covered by the neighboring sensor node with a central angle
represents the region covered by the neighboring sensor node with a central angle  which is referred to as the sponsored sector where
which is referred to as the sponsored sector where  . If the union of sponsored sectors by all neighboring nodes is equal to
. If the union of sponsored sectors by all neighboring nodes is equal to  , then the sensing region of the node is covered completely by its neighboring nodes and the node becomes eligible for going to sleep mode.
, then the sensing region of the node is covered completely by its neighboring nodes and the node becomes eligible for going to sleep mode.
Figure 8(c) shows that CORA approximates the coverage of the monitored area with better accuracy than  and hence activates less number of nodes to meet the same coverage requirement. This is attributed to the fact that, CORA can consider
and hence activates less number of nodes to meet the same coverage requirement. This is attributed to the fact that, CORA can consider  neighboring nodes of a sensor node during coverage computation, including those with a distance to the sensor node larger than the sensing range
neighboring nodes of a sensor node during coverage computation, including those with a distance to the sensor node larger than the sensing range  . While achieving more accurate coverage computation, CORA introduces little overhead with the help of its quadrant-based and segment-based coverage computation techniques described in Section 5.3.
. While achieving more accurate coverage computation, CORA introduces little overhead with the help of its quadrant-based and segment-based coverage computation techniques described in Section 5.3.
Figure 9(a) and Figure 9(b) show that CORA is a good cross-layer combination. In these simulations, Cooperative CORA refers to the proposed collaboration where rate assignment helps coverage scheduling by identifying which critical nodes should be activated for minimizing data redundancy in transmission. On the other hand, Noncooperative CORA describes the case when coverage scheduling is applied before the rate assignment, however without any interaction between the two. In noncooperative case, as coverage scheduling does not have feedback on those critical nodes for reducing data redundancy, it is possible that such critical nodes are put in sleep mode just by checking their residual energy and coverage of their sensing area by their neighbor sensor nodes. As simulation results indicate, the increase in node density improves the amount of side data available to a sensor node and decreases the average battery consumption. However, by identifying the critical nodes and only letting them participate in source coding, Cooperative CORA yields better energy consumption and battery usage than Noncooperative CORA.
Performance evaluation of the collaboration between the proposed coverage scheduling and rate assignment techniques and the energy gains obtained from the differential data transmission technique. The contribution of the collaboration between the proposed coverage scheduling and rate assignment techniques to the total energy consumption of the sensor nodesThe improvement in average battery consumption of sensor nodes due to the collaboration between the proposed coverage scheduling and rate assignment techniquesThe energy savings due to differential data transmission between correlator nodes and their clusterhead
To evaluate the performance of differential data transmission, we consider the energy spent for gathering data from the correlator nodes to their clusterhead. We model the sensor data sent by correlator nodes as numbers, and define arithmetic subtraction ( ) as the difference operator and arithmetic addition (
) as the difference operator and arithmetic addition ( ) as its reverse. The reference data used between the clusterhead and a particular correlator node is calculated based on the arithmetic average of the data values transmitted by that correlator node. The data value to be transmitted from a correlator node is selected as 100 plus a random differential data value for each data gathering. The upper bound used in each experiment for the differential data values are shown in the
) as its reverse. The reference data used between the clusterhead and a particular correlator node is calculated based on the arithmetic average of the data values transmitted by that correlator node. The data value to be transmitted from a correlator node is selected as 100 plus a random differential data value for each data gathering. The upper bound used in each experiment for the differential data values are shown in the  axis of Figure 9(c). When upper bound value is 40 as an example, the sensor data sent by correlator nodes are selected randomly from the range [
axis of Figure 9(c). When upper bound value is 40 as an example, the sensor data sent by correlator nodes are selected randomly from the range [ ].
].
Let us consider a scenario where the reference data value used by a particular correlator node is 110, and the correlator node has sensor data value of 130. The correlator node would apply the difference operator (subtraction) with respect to the reference data and would send 20 as the differential data value. Clusterhead would then recover the original data 130 using the same reference data value by applying the inverse operator (addition) to the reference data value 110 and the differential data 20 received from the correlator node. CORA in Figure 9(c) refers to the energy consumption when original data values, such as 130 in the example above, are sent by the correlator nodes without any differential data transmission. As simulation results show, differential data transmission takes advantage of the temporal correlation of data sent by correlator nodes to the clusterhead for reducing energy consumption.
The performance of CORA is also evaluated with respect to the existing rate assignment schemes. For comparison, we have chosen Master-Slave and Clustered Slepian-Wolf rate assignment techniques [24] due to their following special feature. These rate assignment schemes represent the two extreme cases for the tradeoff between the efficiency of rate allocation and overhead of source coding. Following the notation in Table 1, let us consider a cluster of  active sensor nodes with
active sensor nodes with  referring to
referring to  active sensor node.
active sensor node.
-
(i)
Master-Slave Rate Assignment. This rate allocation represents the low efficiency, low-overhead end of all possible rate assignments to sensor nodes. The cluster members code their data according to their correlation with the data of the clusterhead. For clarity, let us label active node
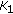 as the clusterhead. Then, master-slave rate assignment allocates rate
as the clusterhead. Then, master-slave rate assignment allocates rate 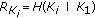 to active node
to active node 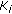 for
for  . This rate allocation has low storage overhead as only the correlation between the data of each cluster member and the clusterhead needs to be maintained. However, while being scalable, Master-Slave scheme sacrifices the potential gains achievable from the correlation of a cluster member
. This rate allocation has low storage overhead as only the correlation between the data of each cluster member and the clusterhead needs to be maintained. However, while being scalable, Master-Slave scheme sacrifices the potential gains achievable from the correlation of a cluster member 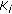 with other cluster members
with other cluster members 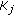 for
for  .
. -
(ii)
Clustered Slepian-Wolf Rate Assignment. This rate assignment has the characteristic of efficient rate allocation at the cost of high storage overhead of correlation information. The cluster members code their data based on their correlation with the cluster members that have higher residual energy. Let us consider active nodes as labeled in descending order of their residual energy where active node
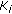 has more remaining energy than
has more remaining energy than 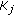 for
for 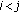 with clusterhead
with clusterhead 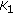 having the highest residual energy. Slepian-Wolf Rate Assignment then assigns rate
having the highest residual energy. Slepian-Wolf Rate Assignment then assigns rate 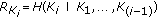 to active node
to active node 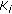 . To achieve this rate allocation, data correlation need to be maintained between node
. To achieve this rate allocation, data correlation need to be maintained between node 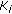 and node(s)
and node(s) 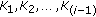 . Consequently, clustered Slepian-Wolf brings significant storage/update overhead in order to increase the side data available to sensor nodes.
. Consequently, clustered Slepian-Wolf brings significant storage/update overhead in order to increase the side data available to sensor nodes.
As Figures 10(a)–10(c) show, CORA possesses the desirable features of both Clustered Slepian-Wolf (efficiency) and Master-Slave (low-overhead) rate assignment schemes. In particular, CORA would first identify critical nodes within the cluster for source coding gain and coverage scheduling then activates only those critical nodes for ensuring that the required event miss-ratios are met. For clarity of discussion, let us assume there are  such critical nodes which are scheduled active and label them as
such critical nodes which are scheduled active and label them as  where
where  . CORA puts noncritical nodes
. CORA puts noncritical nodes  in sleep mode, thereby assigning rates to and maintaining correlation between node
in sleep mode, thereby assigning rates to and maintaining correlation between node  and other critical nodes only.
and other critical nodes only.
Performance evaluation of CORA with respect to existing rate assignment schemes. The total energy consumed by sensor nodes when coding rates are assigned by CORA, Master-Slave and Clustered Slepian-Wolf rate assignment schemesThe gains in average battery consumption of the nodes achieved by CORA as compared to the existing rate assignment techniquesWhile achieving better energy savings than Clustered Slepian-Wolf rate assignment scheme, CORA introduces very low overhead that is close to the overhead of Master-Slave rate assignment technique
Figure 10(a) shows the total energy consumption of sensor nodes when CORA Protocol, Master-Slave, and Clustered Slepian-Wolf schemes are applied on the same network instances. As node redundancy increases, CORA's ability to identify noncritical sensor nodes and to put them off duty yields better energy consumption than Clustered Slepian-Wolf. As expected from the increase in side data, Figure 10(b) shows that node redundancy improves the average battery consumption for both CORA and Clustered Slepian-Wolf. For Master-Slave, the battery consumption of nodes remains almost the same since data is coded at each cluster member without considering its correlation with other cluster members. In terms of storage/update overhead, CORA gets close to Master-Slave with the increase in node density as illustrated in Figure 10(c).
7. Conclusions
In this paper, we have addressed the problem of meeting event miss-ratio requirements with minimum energy expenditure. We identify a graceful cooperation between coverage scheduling and rate allocation techniques, which are addressed separately in the literature. For both uniform/ nonuniform (hotspot) event distributions, we show the existence of a radius within the cluster for ideal application of distributed source coding. With the help of this radius, rate allocation guides coverage scheduling to activate only those cluster members that are critical for minimizing energy consumption. The coverage scheduling technique of the proposed protocol CORA assists rate assignment by enabling overlapping sensing regions and correlation among neighboring nodes while minimizing the overhead of distributed source coding. In comparison with existing rate allocation algorithms, CORA significantly improves energy expenditure by 85%, node battery energy consumption up to 25% and source coding overhead by 90%.
This paper has addressed the impact of environmental factors on the size of circular-shaped sensing regions. As for future work, identifying the irregular-shaped sensing regions due to environmental factors and considering their effect on event miss-ratio assurances remain interesting and challenging problems.
Algorithm 1: Probability computation for  .
.
Require: : The case of having total
: The case of having total  event occurrences in the monitored area where
event occurrences in the monitored area where  and
and  is the number of sensor locations.
is the number of sensor locations.
Ensure: is computed.
is computed.
-
1:
Initialize
 .
. -
2:
Determine the set
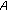 of all possible combinations of
of all possible combinations of 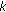 events that occur in any
events that occur in any  out of
out of  network locations.
network locations. -
3:
while the set
 is not empty do
is not empty do -
4:
Remove a combination from
 and denote it by
and denote it by  .
. -
5:
Find out the product of the event occurrence probabilities at the locations selected by combination
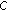 and probabilities of not having any event occurrences at the remaining locations of the network.
and probabilities of not having any event occurrences at the remaining locations of the network. -
6:
Multiply the product from the previous step with the probability of having combination
 and add the result of multiplication to
and add the result of multiplication to  .
. -
7:
end while
Algorithm 2: Protocol CORA.
Require:  : An event to be sensed by sensor nodes in a cluster-based wireless sensor network.
: An event to be sensed by sensor nodes in a cluster-based wireless sensor network.
 : The required event miss-ratio threshold.
: The required event miss-ratio threshold.
Ensure:  The event miss-ratio assurance
The event miss-ratio assurance  is met.
is met.

 is minimized.
is minimized.
 PHASE I
PHASE I
-
StepI:
Each clusterhead finds its correlator radius.
-
StepII:
Those cluster members that are located around the correlator radius form rate assignment groups, each consisting of a correlator node and a number of sensor nodes.
-
StepIII:
Each correlator node assigns the source coding rates to its group members in order to minimize
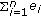 .
. PHASE II
PHASE II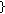
-
StepIV:
Each clusterhead identifies the critical nodes of rate assignment groups, based on their assigned rates.
-
StepV:
The members of each cluster perform coverage scheduling by activating critical nodes, in order to meet the required event miss-ratio threshold
 .
.
Algorithm 3: Coding rate assignment.
Require: A cluster of sensor nodes that produce correlated data for a given event  .
.
Ensure: The coding rates are allocated for event  to minimize the energy consumption.
to minimize the energy consumption.
-
1:
The ideal correlator radius
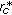 is determined by the clusterhead for uniform event distribution.
is determined by the clusterhead for uniform event distribution. -
2:
for all Active node
 do
do -
3:
if
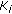 is located within
is located within 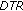 then
then -
4:
Use coding rate
 and transmit data directly to the clusterhead.
and transmit data directly to the clusterhead. -
5:
else
-
6:
Check whether node
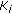 should become a correlator node by verifying the residual energy requirement and comparing its distance to the clusterhead with
should become a correlator node by verifying the residual energy requirement and comparing its distance to the clusterhead with  .
. -
7:
if
 is selected as correlator then
is selected as correlator then -
8:
Code data at rate
 and apply differential data transmission for group members.
and apply differential data transmission for group members. -
9:
else
-
10:
Use coding rate
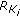 =
= 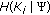 and send data to the correlator node where the set
and send data to the correlator node where the set 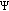 contains the group members with higher residual energy.
contains the group members with higher residual energy. -
11:
end if
-
12:
end if
-
13:
end for
Algorithm 4: Coverage scheduling.
Require: A cluster of wireless sensor nodes to be scheduled for sensing event  .
.
 : The required event miss-ratio threshold for event
: The required event miss-ratio threshold for event  .
.
 : The scores assigned to cluster members based on coding rate estimates.
: The scores assigned to cluster members based on coding rate estimates.
Ensure: Each cluster member is selected either as an active node or a sleeping node for event  .
.
-
1:
The set
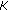 of cluster members are sorted in ascending order of their scores in
of cluster members are sorted in ascending order of their scores in  .
. -
2:
for all Node
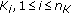 do
do -
3:
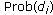 is identified from
is identified from 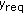 and event distribution for
and event distribution for 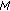 .
. -
4:
if
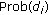 is met by neighboring nodes of node
is met by neighboring nodes of node  then
then -
5:
Node
 goes to sleep mode.
goes to sleep mode. -
6:
else
-
7:
Node
 is activated for
is activated for  .
. -
8:
end if
-
9:
end for
Algorithm 5: Coverage computation.
Require: Any given cluster member that has overlapping sensing regions with the set neighboring nodes  where the
where the 
neighboring node is referred to as  .
.
Ensure: : The area within the cluster member's sensing region that is not covered by the neighboring nodes from the set
: The area within the cluster member's sensing region that is not covered by the neighboring nodes from the set  is
is
computed.
-
1:
Initialize
 to zero.
to zero. -
2:
Divide the node's sensing region into
 segments each of width
segments each of width 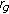 .
. -
3:
Let
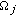 be the set of angles that represent the covered portions of the
be the set of angles that represent the covered portions of the 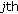 segment. Initialize
segment. Initialize 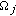 to
to  for
for 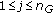 .
. -
4:
Sort the set of neighboring nodes
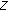 in ascending order of node identifiers.
in ascending order of node identifiers. -
5:
for all
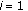 to
to 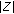 do
do -
6:
Identify the lowest id segment that intersects with node
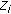 's sensing region.
's sensing region. -
7:
for all
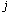 = lowest id segment to
= lowest id segment to  do
do -
8:
Determine the portion of segment
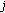 that is covered by node
that is covered by node 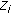 but not by any other node
but not by any other node 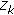 and represent this covered portion with the angle
and represent this covered portion with the angle 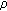 where
where 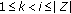 .
. -
9:
Add
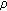 as an element to the set
as an element to the set  .
. -
10:
end for
-
11:
end for
-
12:
for all
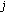 =
= 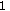 to
to  do
do -
13:
Add
 to
to  where
where 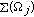 denote the sum of magnitudes of the angles in
denote the sum of magnitudes of the angles in  .
. -
14:
end for
-
15:
return

References
Feeney LM, Nilsson M: Investigating the energy consumption of a wireless network interface in an ad hoc networking environment. Proceedings of the 20th Annual Joint Conference of the IEEE Computer and Communications Societies, April 2001 1548-1557.
Jones CE, Sivalingam KM, Agrawal P, Chen JC: A survey of energy efficient network protocols for wireless networks. Wireless Networks 2001, 7(4):343-358. 10.1023/A:1016627727877
Sanli HO, Cam H: Event-driven coverage and rate allocation for providing miss-ratio assurances in wireless sensor networks. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007 1134-1138.
Sanli HO, Cam H: Adaptive task scheduling for providing event miss-ratio statistical assurances in wireless sensor networks. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '06), April 2006 445-450.
Tian D, Georganas ND: A node scheduling scheme for energy conservation in large wireless sensor networks. Wireless Communications and Mobile Computing 2003, 3(2):271-290. 10.1002/wcm.116
Tian W, Liu J: A novel approach for the maximum coverage sets of WSN based on immune clone selection algorithm. Proceedings of the 2nd International Symposium on Electronic Commerce and Security (ISECS '09), May 2009, Nanchang, China 1: 275-279.
Chen UR, Chiou BS, Chen JM, Lin W: An adjustable target coverage method in directional sensor networks. Proceedings of the 3rd IEEE Asia-Pacific Services Computing Conference (APSCC '08), December 2008, Pisa, Italy 174-180.
Wang X, Xing G, Zhang Y, Lu C, Pless R, Gill C: Integrated coverage and connectivity configuration in wireless sensor networks. Proceedings of the 1st International Conference on Embedded Networked Sensor Systems (SenSys '03), November 2003 28-39.
Yan T, He T, Stankovic JA: Differentiated surveillance for sensor networks. Proceedings of the 1st International Conference on Embedded Networked Sensor Systems (SenSys '03), November 2003 51-62.
Gupta H, Das SR, Gu Q: Connected sensor cover: Self-organization of sensor networks for efficient query execution. Proceedings of the 4th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MOBIHOC '03), June 2003 189-200.
Carle J, Simplot-Ryl D: Energy-efficient area monitoring for sensor networks. IEEE Computer 37(2):40-46.
Cardei M, Wu J: Energy-efficient coverage problems in wireless ad-hoc sensor networks. Computer Communications 2006, 29(4):413-420. 10.1016/j.comcom.2004.12.025
Slijepcevic S, Potkonjak M: Power efficient organization of wireless sensor networks. Proceedings of International Conference on Communications (ICC '01), June 2001 472-476.
Sanli HO, Poornachandran R, Çam H: Collaborative two-level task scheduling for wireless sensor nodes with multiple sensing units. Proceedings of the 2nd Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks (SECON '05), September 2005 350-361.
Cǎrbunar B, Grama A, Vitek J, Cǎrbunar O: Redundancy and coverage detection in sensor networks. ACM Transactions on Sensor Networks 2006, 2(1):94-128. 10.1145/1138127.1138131
Liu C, Wu K, Xiao Y, Sun B: Random coverage with guaranteed connectivity: joint scheduling for wireless sensor networks. IEEE Transactions on Parallel and Distributed Systems 2006, 17(6):562-575.
C. F. Huang, Y.C. Tseng, and H. L. Wu, “Distributed protocols for ensuring both coverage and connectivity of a wireless sensor network,” ACM Transactions on Sensor Networks, vol. 3, no. 1, artile 5, 2007.
M. X. Cheng, L. Ruan, and W. Wu, “Coverage breach problems in bandwidth-constrained sensor networks,” ACM Transactions on Sensor Networks, vol. 3, no. 2, article 12, 2007.
Wang W, Srinivasan V, Wang B, Chua KC: Coverage for target localization in wireless sensor networks. Proceedings of the 5th International Conference on Information Processing in Sensor Networks (IPSN '06), April 2006 118-125.
Slepian D, Wolf JK: Noiseless coding of correlated information sources. IEEE Transactions on Information Theory 1973, 19(4):471-480. 10.1109/TIT.1973.1055037
Pradhan SS, Ramchandran K: Distributed source coding using syndromes (DISCUSS): design and construction. Proceedings of the Data Compression Conference (DCC '99), March 1999 158-167.
Cristescu R, Beferull-Lozano B, Vetterli M: On network correlated data gathering. Proceedings of the 23rd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '04), March 2004 2571-2582.
Baek SJ, de Veciana G, Su X: Minimizing energy consumption in large-scale sensor networks through distributed data compression and hierarchical aggregation. IEEE Journal on Selected Areas in Communications 2004, 22(6):1130-1140. 10.1109/JSAC.2004.830934
Marco D, Neuhoff DL: Reliability vs. efficiency in distributed source coding for field-gathering sensor networks. Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks (IPSN '04), April 2004 161-168.
Hou YT, Shi Y, Sherali HD: Rate allocation and network lifetime problems for wireless sensor networks. IEEE/ACM Transactions on Networking 2008, 16(2):321-334.
Poornachandran R, Ahmad H, Çam H: Energy-efficient task scheduling for wireless sensor nodes with multiple sensing units. Proceedings of the 24th IEEE International Performance, Computing, and Communications Conference (IPCCC '05), April 2005 409-414.
Sinha A, Chandrakasan A: Operating system and algorithmic techniques for energy scalable wireless sensor networks. Proceedings of the 2nd International Conference on Mobile Data Management (MDM ' 05), January 2001 1987: 199-209.
McIntyre GA, Hintz KJ: Sensor measurement scheduling: an enhanced dynamic, preemptive algorithm. Optical Engineering 1998, 37(2):517-523. 10.1117/1.601640
Goel S, Imielinski T: Prediction-based monitoring in sensor networks: taking lessons from MPEG. Computer Communication Review 2001, 31(5):82-98. 10.1145/1037107.1037117
Mica Motes, http://www.xbow.com/
MTS400CA and MTS420CA (with GPS module) Environmental Sensor Boards http://www.xbow.com/
Heinzelman WR, Chandrakasan A, Balakrishnan H: Energy-efficient communication protocol for wireless microsensor networks. Proceedings of the 33rd Annual Hawaii International Conference on System Siences (HICSS-33 '00), January 2000, Maui, Hawaii, USA 8020.
Pattem S, Krishnamachari B, Govindan R: The impact of spatial correlation on routing with compression in wireless sensor networks. Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks (IPSN '04), April 2004 28-35.
Cover T, Thomas J: Elements of Information Theory, Wiley Series in Telecommunications. John Wiley & Sons, New York, NY, USA; 1991.
Casalegno JW: All-weather ground sensor system with possible law enforcement applications. Enabling Technologies for Law Enforcement and Security, February 2001, Proceedings of SPIE 4232: 359-366.
Oliveira HABF, Nakamura EF, Loureiro AAF, Boukerche A: Error analysis of localization systems for sensor networks. Proceedings of the 13th ACM International Workshop on Geographic Information Systems (GIS '05), November 2005 71-78.
Author information
Authors and Affiliations
Corresponding author
Appendix
Proof of Lemma 1. Considering  , we need to prove that
, we need to prove that  , specifically
, specifically


Without loss of generality, let us consider the terms  and
and  in expansion of
in expansion of  and
and  , respectively, where
, respectively, where  . To identify the value of
. To identify the value of  and
and  , we consider every possible division of
, we consider every possible division of  network locations into two subsets, namely,
network locations into two subsets, namely,  and
and  , such that
, such that  and
and  . If
. If  , then we assume that an event occurs at
, then we assume that an event occurs at  and an event gets detected at
and an event gets detected at  . Otherwise, it is assumed that there is not any event occurrence or event detection at
. Otherwise, it is assumed that there is not any event occurrence or event detection at  . For a
. For a  combination among all such possible divisions, the probability of having
combination among all such possible divisions, the probability of having  event
event  over the monitored area is calculated as
over the monitored area is calculated as


On the other hand, the probability of having  event
event  is expressed as
is expressed as


By replacing the probability of event detections in accordance with the variable coverage provided by CORA, (A.3) becomes


Note that our objective is to show that  , thus we multiply
, thus we multiply  and every other term in
and every other term in  with the constant
with the constant  and get
and get


Let us now compare the coefficients of the first term  for
for  from (A.5), specifically
from (A.5), specifically

 from (A.4), that is equal to
from (A.4), that is equal to


Even in the case of single event occurrence and single event detection (i.e., ), the coefficient in (A.6) is less than the coefficient in (A.7) since the largest value the expression
), the coefficient in (A.6) is less than the coefficient in (A.7) since the largest value the expression  can assume is 1. Further, it is easy to see that the second term
can assume is 1. Further, it is easy to see that the second term


 . Considering that the selection of
. Considering that the selection of  and the combination for
and the combination for  event occurrences/detections were arbitrary, one can conclude that
event occurrences/detections were arbitrary, one can conclude that  .
.

Proof of Lemma 2. Without loss of generality, let us focus on quadrants  and
and  in Figure 7(b). We refer to the set of active nodes covering the upper left (
in Figure 7(b). We refer to the set of active nodes covering the upper left ( ) and upper right (
) and upper right ( ) quadrant as
) quadrant as  and
and  , respectively. For the worst-case analysis let us make the following assumptions.
, respectively. For the worst-case analysis let us make the following assumptions.
-
(i)
 does not satisfy Condition 2 for the quadrant
does not satisfy Condition 2 for the quadrant  with the active nodes placed in
with the active nodes placed in  only.
only. -
(ii)
All active nodes from the set
 are placed at point
are placed at point  within
within  .
. -
(iii)
All active nodes from the set
 are placed at point
are placed at point  within
within  .
.
In order to prove that active nodes at  can compensate for the uncovered portion of the subregion
can compensate for the uncovered portion of the subregion  , that is
, that is  , it is necessary to show that
, it is necessary to show that
-
(i)
 ,
, -
(ii)
 .
.
The condition (i) is trivial based on the disk equation itself. The condition (ii) can be proved by placing an imaginary active node at each one of the points  and
and  . The points
. The points  can then be defined as the intersection of the node's sensing region centered at
can then be defined as the intersection of the node's sensing region centered at  with the imaginary active nodes centered at
with the imaginary active nodes centered at  , respectively.Let
, respectively.Let  be the projection point of
be the projection point of  online segment
online segment  which is indicated as a red dot in Figure 7(b). The equality
which is indicated as a red dot in Figure 7(b). The equality  holds due to the fact that the sensing regions are congruent. Similarly, the equation
holds due to the fact that the sensing regions are congruent. Similarly, the equation  also holds from the symmetry where
also holds from the symmetry where  is the projection point of
is the projection point of  on line segment
on line segment  shown as a red point in Figure 7(b).It can be concluded from these equalities that
shown as a red point in Figure 7(b).It can be concluded from these equalities that  . This proves that
. This proves that  can be covered by active nodes placed at
can be covered by active nodes placed at  even in worst-case placement of active nodes. Similarly, the members of
even in worst-case placement of active nodes. Similarly, the members of  placed at
placed at  can cover the field
can cover the field  completely.
completely.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ozgur Sanli, H., Çam, H. Collaborative Event-Driven Coverage and Rate Allocation for Event Miss-Ratio Assurances in Wireless Sensor Networks. J Wireless Com Network 2010, 345052 (2010). https://doi.org/10.1155/2010/345052
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/345052
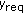 : the required event miss-ratio threshold for event
: the required event miss-ratio threshold for event  ,
,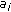 : the sensing area of sensor node at location
: the sensing area of sensor node at location  for
for 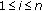 ,
, : probability of event occurrence at
: probability of event occurrence at 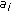 for
for  ,
, : probability that
: probability that  takes value
takes value  for
for  .
. : the observed (actual) event miss-ratio for event
: the observed (actual) event miss-ratio for event  ,
,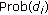 : probability of event detection at
: probability of event detection at  for
for 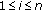 ,
,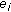 : the energy consumption of active sensor nodes for data transmission with their assigned rates at location
: the energy consumption of active sensor nodes for data transmission with their assigned rates at location 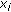 for
for 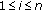 ,
, : probability that
: probability that  takes value
takes value  for
for  .
.



 is shown for a cluster of
is shown for a cluster of  sensor nodes with settings
sensor nodes with settings  m.,
m., m. (i.e., cluster range),
m. (i.e., cluster range), bits and
bits and  . The ideal correlator radius
. The ideal correlator radius  within the interval
within the interval  is indicated with the dashed blue line.
is indicated with the dashed blue line.
 to the clusterhead and correlator radius
to the clusterhead and correlator radius  is used within the cluster.
is used within the cluster. .
. and node
and node  has already been scheduled as an active node or has not announced its status yet for
has already been scheduled as an active node or has not announced its status yet for 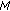 .
. and node
and node 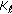 has already been scheduled as an active node for
has already been scheduled as an active node for  .
.
 segments. The covered portion of each segment by neighboring nodes is represented with an angle. In the figure,
segments. The covered portion of each segment by neighboring nodes is represented with an angle. In the figure, corresponds to the covered portion of the lowest id segment,
corresponds to the covered portion of the lowest id segment, , of node
, of node  's sensing region by its neighboring node
's sensing region by its neighboring node  .
.
 or
or  .
. or
or  .
.

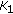 as the clusterhead. Then, master-slave rate assignment allocates rate
as the clusterhead. Then, master-slave rate assignment allocates rate 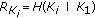 to active node
to active node 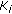 for
for  . This rate allocation has low storage overhead as only the correlation between the data of each cluster member and the clusterhead needs to be maintained. However, while being scalable, Master-Slave scheme sacrifices the potential gains achievable from the correlation of a cluster member
. This rate allocation has low storage overhead as only the correlation between the data of each cluster member and the clusterhead needs to be maintained. However, while being scalable, Master-Slave scheme sacrifices the potential gains achievable from the correlation of a cluster member 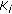 with other cluster members
with other cluster members 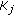 for
for  .
.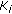 has more remaining energy than
has more remaining energy than 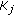 for
for 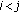 with clusterhead
with clusterhead 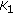 having the highest residual energy. Slepian-Wolf Rate Assignment then assigns rate
having the highest residual energy. Slepian-Wolf Rate Assignment then assigns rate 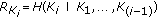 to active node
to active node 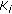 . To achieve this rate allocation, data correlation need to be maintained between node
. To achieve this rate allocation, data correlation need to be maintained between node 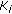 and node(s)
and node(s) 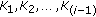 . Consequently, clustered Slepian-Wolf brings significant storage/update overhead in order to increase the side data available to sensor nodes.
. Consequently, clustered Slepian-Wolf brings significant storage/update overhead in order to increase the side data available to sensor nodes.
 .
.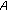 of all possible combinations of
of all possible combinations of 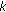 events that occur in any
events that occur in any  out of
out of  network locations.
network locations. is not empty do
is not empty do and denote it by
and denote it by  .
.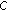 and probabilities of not having any event occurrences at the remaining locations of the network.
and probabilities of not having any event occurrences at the remaining locations of the network. and add the result of multiplication to
and add the result of multiplication to  .
.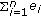 .
. PHASE II
PHASE II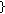
 .
.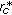 is determined by the clusterhead for uniform event distribution.
is determined by the clusterhead for uniform event distribution. do
do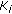 is located within
is located within 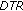 then
then and transmit data directly to the clusterhead.
and transmit data directly to the clusterhead.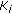 should become a correlator node by verifying the residual energy requirement and comparing its distance to the clusterhead with
should become a correlator node by verifying the residual energy requirement and comparing its distance to the clusterhead with  .
. is selected as correlator then
is selected as correlator then and apply differential data transmission for group members.
and apply differential data transmission for group members.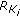 =
= 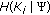 and send data to the correlator node where the set
and send data to the correlator node where the set  contains the group members with higher residual energy.
contains the group members with higher residual energy. of cluster members are sorted in ascending order of their scores in
of cluster members are sorted in ascending order of their scores in  .
.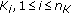 do
do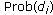 is identified from
is identified from 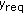 and event distribution for
and event distribution for 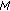 .
.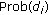 is met by neighboring nodes of node
is met by neighboring nodes of node  then
then goes to sleep mode.
goes to sleep mode. is activated for
is activated for  .
.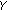 to zero.
to zero. segments each of width
segments each of width 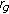 .
.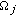 be the set of angles that represent the covered portions of the
be the set of angles that represent the covered portions of the 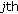 segment. Initialize
segment. Initialize 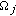 to
to 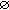 for
for 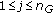 .
.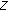 in ascending order of node identifiers.
in ascending order of node identifiers.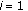 to
to 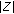 do
do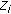 's sensing region.
's sensing region.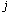 = lowest id segment to
= lowest id segment to  do
do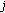 that is covered by node
that is covered by node 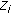 but not by any other node
but not by any other node 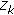 and represent this covered portion with the angle
and represent this covered portion with the angle 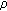 where
where 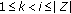 .
.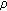 as an element to the set
as an element to the set  .
.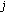 =
= 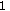 to
to  do
do to
to  where
where 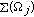 denote the sum of magnitudes of the angles in
denote the sum of magnitudes of the angles in  .
.
 does not satisfy Condition 2 for the quadrant
does not satisfy Condition 2 for the quadrant  with the active nodes placed in
with the active nodes placed in  only.
only. are placed at point
are placed at point  within
within  .
. are placed at point
are placed at point  within
within  .
. ,
, .
.