- Research Article
- Open access
- Published:
A Dynamic Utility Adaptation Framework for Efficient Multimedia Service Support in CDMA Wireless Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 375410 (2010)
Abstract
In this paper the problem of channel-aware opportunistic resource allocation for the downlink in CDMA wireless networks supporting simultaneously real-time multimedia and non-real-time data services is addressed. In order to treat different types of services with diverse QoS prerequisites through common optimization formulation a utility-based power and rate allocation framework is adopted. Emphasis is placed on real-time services' strict short-term QoS prerequisites, the fulfillment of which requires a significantly different treatment than the use of static utility functions, traditionally used to address long-term QoS or fairness prerequisites of delay-tolerant data services. To that end, we introduce a novel framework that enables the dynamic adaptation of real-time multimedia users' utilities as the system evolves, with respect to the corresponding short-term throughput service performance variations. The corresponding non-convex network utility maximization (NUM) problem is then formulated and solved, to obtain optimal power and rate allocation. Via simulation and analysis it is demonstrated that significant performance improvements are achieved in terms of real-time user's short-term throughput requirement satisfaction, without any considerable loss in total system throughput. Finally, essential tradeoffs between fulfilling real-time services' short-term QoS prerequisites and maximizing system performance, under an opportunistic scheduling wireless environment, are revealed and quantified.
1. Introduction
With the growing demand for high data rate and support of multiple services with various quality of service (QoS) requirements, the scheduling policy plays a key role in the efficient resource allocation process in future wireless networks. Moreover, users' time and location-dependent channel conditions limit the system's available resources and hence its ability to satisfy their QoS properties. Therefore, a flexible power and rate allocation scheme is essential for optimizing the system's performance.
Considerable research efforts have been devoted to the combined problem of power and rate allocation for the downlink of a code division multiple access (CDMA) system (e.g., [1–3]) aiming at the exploitation of multiuser diversity (i.e., users' time-varying channel conditions) towards optimizing the system's performance, while satisfying various QoS constraints [4–9]. Moreover, due to the heterogeneity of the wireless environment and the need for the support of diverse QoS requirements, the concept of utilities from the field of economics has been adopted for devising proficient opportunistic resource allocation algorithms. A utility function reflects a users' degree of satisfaction with respect to their service performance in a normalized and transparent way, allowing services with assorted QoS prerequisites to be represented, by forming appropriate utilities [10–15], under a common utility-based optimization framework. Hence, Network Utility Maximization (NUM) theory provides the foundations and mathematical tools for setting and treating such problems.
In a typical NUM formulation, user's utilities are static, predetermined functions, associated to specific services or service classes, emphasizing mainly on the support of non-real-time users' long-term requirements. Therefore, users' utilities mainly define a continuous relationship between their service performance and their actual achieved throughput (i.e., goodput that reflects the number of reliable bits transmitted) over the wireless opportunistic CDMA paradigm, while considering long-term user's fairness issues [16], minimum performance requirements [17] and/or appropriate constraints imposed by the devices' physical limitations [18].
On the other hand, the delay-sensitive nature of real-time multimedia services poses additional demands on accessing the system resourses within short time intervals. Therefore, the adoption of probabilistic short-term delay [19, 20] or throughput [21, 22] constraints have been proposed towards efficiently expressing real-time services' QoS prerequisites over a time-varying wireless environment. However, the conventional use of static predefined users utilities does not permit the efficient integration of the latter probabilistic short-term constraints within a NUM problem formulation and thus in the system's resource scheduling policy.
In this paper, we study the problem of jointly scheduling multiple services, that is, delay-sensitive, real-time, and delay-tolerant high-throughput non-real-time services, over a heterogeneous CDMA wireless system via NUM optimization. Towards achieving our goal, this paper makes the following contributions.
-
(a)
We design real-time users' utilities that dynamically adjust with respect to users' service short-term QoS satisfaction levels fulfillment, enabling them to efficiently reflect real-time services strict, instantaneous resource demands at the scheduling policy. We refer to the above novel approach as Dynamic Utility Adaptation (DUA) framework. DUA serves as an extension to current NUM theory in order to mainly treat and overcome issues that arise from the use of static utilities, when aiming at introducing users' short-term goals or prerequisites under a NUM optimization setting.
-
(b)
We adopt and exploit probabilistic short-term throughput constraints, instead of myopic probabilistic delay constraints, in order to introduce the essential requirements of real-time users (requesting multimedia services) in the resource allocation process of a CDMA wireless network.
-
(c)
Through the proper use of static and dynamic utilities according to the respective service types, we aim at:(a) meeting various types of user services' QoS requirements, namely, real-time and non-real-time, under a common optimization framework and (b) exploiting the benefits emerging by the scheduler's opportunistic character, not only individually per type of users but also in a collaborative manner as well. In this way, a scheduling policy is devised that avoids the problem where the optimization of the performance of users of a specific type of service leads to the corresponding degradation of the performance of other types of services. Thus, several inherent system and users' limitations in satisfying services' short-term QoS requirements, caused by the corresponding physical hardware constraints, under an interference limited opportunistic wireless environment are highlighted and discussed.
-
(d)
Finally, two simple iterative algorithms are proposed. The first one, residing at the base station, attains an asymptotically optimal (in the number of users) power and rate allocation of systems' non-convex optimization problem, which is continuously reset at the beginning of each time slot with respect to users' utilities adaptation. The second one, residing at the mobile node, dynamically adapts a real-time user's utility by realizing a control loop which: (a) constantly monitors a user's service performance, (b) analyzes its current status with respect to QoS requirements, and (c) reacts to QoS triggering events via the dynamic alteration of the user's utility. It is demonstrated via modeling and simulation that our proposed scheme achieves to the fulfillment of real-time users' short-term prerequisites without any considerable loss in the system's total achieved throughput. The obtained results allow to reveal and quantify the inherent tradeoff between efficiently fulfilling real-time services' demanding short-term QoS prerequisites and maximizing overall system performance, under an opportunistic wireless environment.
The rest of the paper is organized as follows. In Section 2, the system model and definitions are presented. In Section 3, the proposed dynamic users' utility adaptation framework is first analyzed, and its application on real-time services is presented. Then, the corresponding utility-based optimization problem is formulated, and its solution is derived. In Section 4, real-time users' self-adaptation mechanism in Q S-triggered events is described, and an enhanced power and rate allocation scheme is proposed. Numerical results and relevant discussions are provided in Section 5, while Section 6 concludes the paper.
S-triggered events is described, and an enhanced power and rate allocation scheme is proposed. Numerical results and relevant discussions are provided in Section 5, while Section 6 concludes the paper.
2. System Model and Definitions
In this paper, we consider the downlink of a single cell time-slotted CDMA wireless system with N continuously backlogged users at time slot t. A time slot is a fixed interval of time and could consist of one or several packets. User-channel conditions, which are affected by shadow fading and long-time scale variations, are assumed to be fixed within the duration of a time slot. The scheduler is assumed to resign at the base station, and hence it can make decisions on users' power and rate allocation at the beginning of each time slot. Let us denote by  the downlink transmission rate at which the base station transmits to user
the downlink transmission rate at which the base station transmits to user  in the slot under consideration and by
in the slot under consideration and by  the maximum rate at which they can receive data (due to physical hardware limitations). Let us also denote by
the maximum rate at which they can receive data (due to physical hardware limitations). Let us also denote by  the bit energy-to-interference density ratio for user
the bit energy-to-interference density ratio for user  at their mobile device receiver, by
at their mobile device receiver, by  the path gain from the base station to mobile user
the path gain from the base station to mobile user  and by
and by  the transmission power allocated at a given slot to user
the transmission power allocated at a given slot to user  , which, however, is limited by the base station's maximum downlink power
, which, however, is limited by the base station's maximum downlink power  The received
The received  for each user
for each user  is given [16–18] by
is given [16–18] by

where  denotes the orthogonality factor,
denotes the orthogonality factor,  is the system's spreading bandwidth,
is the system's spreading bandwidth,  denotes the users' power allocation vector,
denotes the users' power allocation vector,  includes the background noise and intercell interference at user
includes the background noise and intercell interference at user  determines the intracell interference at user
determines the intracell interference at user  and
and  denotes the transmission environment between user
denotes the transmission environment between user  and the base station.
and the base station.
In our system, we consider two basic types of users, namely, non-real-time users (NRT) requesting delay-tolerant high-throughput services and real-time  users with strict short-term QoS constraints. Throughout the rest of the paper we denote by
users with strict short-term QoS constraints. Throughout the rest of the paper we denote by  the number of non-real-time users (real-time users) and by
the number of non-real-time users (real-time users) and by  the corresponding set. Due to the variety of the supported services' QoS prerequisites, each mobile user is associated with a proper utility function
the corresponding set. Due to the variety of the supported services' QoS prerequisites, each mobile user is associated with a proper utility function  which represents his degree of satisfaction in accordance to his actual expected downlink throughput and can be expressed as
which represents his degree of satisfaction in accordance to his actual expected downlink throughput and can be expressed as

where  represents a function for the probability of a successful packet transmission for user
represents a function for the probability of a successful packet transmission for user  and is an increasing function of their bit energy to interference ratio
and is an increasing function of their bit energy to interference ratio  at any time slot. A user's function for the probability of a successful packet transmission at fixed data rates depends on the transmission scheme (modulation and coding) being used and can be represented by a sigmoidal-like function of their power allocation for various modulation schemes [18]. Therefore, a user
at any time slot. A user's function for the probability of a successful packet transmission at fixed data rates depends on the transmission scheme (modulation and coding) being used and can be represented by a sigmoidal-like function of their power allocation for various modulation schemes [18]. Therefore, a user  efficiency function
efficiency function  has the following properties.
has the following properties.
-
(1)
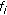 is an increasing function of
is an increasing function of 
-
(2)
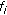 is a continuous, twice differentiable sigmoidal function with respect to
is a continuous, twice differentiable sigmoidal function with respect to 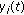 .
. -
(3)
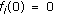 to ensure that
to ensure that  when
when  (t)
(t) 0.
0. -
(4)
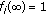 .
.
Moreover, we define as  the two tunable parameters of the sigmoidal function
the two tunable parameters of the sigmoidal function that determine function's
that determine function's steepness and unique inflection point, respectively [24] (generic definition:
steepness and unique inflection point, respectively [24] (generic definition:  where c
where c  and
and  . Intuitively, since parameter a controls the slope of the sigmoidal function, it determines a user's tolerance in power deviations (in the region of functions
. Intuitively, since parameter a controls the slope of the sigmoidal function, it determines a user's tolerance in power deviations (in the region of functions  inflection point), while parameter
inflection point), while parameter  , controls the relative place of the inflection point of function
, controls the relative place of the inflection point of function  (at the access of
(at the access of  ), and thus the power level upon which a user's successful packet receive probability increases rapidly (for small deviations of the allocated power), following a concave form [18, 23]). Without loss of generality, we assume that all users have the same value for their parameter
), and thus the power level upon which a user's successful packet receive probability increases rapidly (for small deviations of the allocated power), following a concave form [18, 23]). Without loss of generality, we assume that all users have the same value for their parameter  i,
(i.e.,
i,
(i.e., ). The validity of the above properties has been demonstrated in several practical scenarios with reasonably large packet sizes M (i.e.,
). The validity of the above properties has been demonstrated in several practical scenarios with reasonably large packet sizes M (i.e., ) [25, 26].
) [25, 26].
Observing a user's utility as defined in (2), we can point out that the main factors that affect its values are a user's transmission environment  , transmission rate
, transmission rate  and transmission scheme (parameter
and transmission scheme (parameter  of function
of function ). For delay-tolerant non-real-time users, the maximization of their utility corresponds to their desired goodput maximization, and as a result, the corresponding utility is suitable for reflecting their desired throughput maximization at the system's resource allocation optimization problem. On the other hand, real-time users' degree of satisfaction does not increase in a linear or concave way along with their throughput maximization (as in the case of NRT users), but according to their fixed data rate expectation fulfillment, as well as their short-term QoS requirements satisfaction due to their delay sensitive nature (e.g., sigmoidal form).
). For delay-tolerant non-real-time users, the maximization of their utility corresponds to their desired goodput maximization, and as a result, the corresponding utility is suitable for reflecting their desired throughput maximization at the system's resource allocation optimization problem. On the other hand, real-time users' degree of satisfaction does not increase in a linear or concave way along with their throughput maximization (as in the case of NRT users), but according to their fixed data rate expectation fulfillment, as well as their short-term QoS requirements satisfaction due to their delay sensitive nature (e.g., sigmoidal form).
2.1. Real-Time Services' QoS Requirements
A real-time user's requirements consist mainly of a constant downlink rate and short-term delay and throughput guaranties [21, 22]. Therefore, we consider as a real-time user's performance indicator, the achieved probability of receiving an amount of service, in terms of data units, smaller than a predefined threshold within successive short observation time intervals, which is expressed as follows:

where denotes a RT user i observation time interval in terms of slots,
denotes a RT user i observation time interval in terms of slots, his predefined data units threshold, and
his predefined data units threshold, and  the amount of data they received within a specific time interval from slot
the amount of data they received within a specific time interval from slot  to slot t. The smaller the achieved value of an RT user's short-term throughput probability (3), the greater is their degree of satisfaction. Given a real-time user i requiring downlink rate,
to slot t. The smaller the achieved value of an RT user's short-term throughput probability (3), the greater is their degree of satisfaction. Given a real-time user i requiring downlink rate,  we can estimate their data units threshold as
we can estimate their data units threshold as

where  denotes the duration of a time slot. It has been shown in [22] that short-term throughput constraints can more efficiently and comprehensively reflect the essential requirements of RT users (i.e., both delay and throughput expectations) compared to myopic probabilistic delay constraints. This is due to the fact that the adoption of the latter over a time-varying wireless environment may often cause RT users' throughput rates dissatisfaction, within either small or long time intervals, due to their potentially bad channel conditions and variations, leading to their service QoS-aware performance degradation.
denotes the duration of a time slot. It has been shown in [22] that short-term throughput constraints can more efficiently and comprehensively reflect the essential requirements of RT users (i.e., both delay and throughput expectations) compared to myopic probabilistic delay constraints. This is due to the fact that the adoption of the latter over a time-varying wireless environment may often cause RT users' throughput rates dissatisfaction, within either small or long time intervals, due to their potentially bad channel conditions and variations, leading to their service QoS-aware performance degradation.
The previous  users' QoS quarantines, as defined in (3) and (4), are suitable for Constant Bit Rate (CBR) real-time traffic (e.g., video conferencing, telephony (voice services), etc.). To incorporate the QoS prerequisites of other types of real-time services such as real-time Variable Bit Rate (VBR) traffic (e.g., compressed video streams) in the proposed probabilistic short-term throughput framework, the ability to dynamically adjust the requested downlink data rate,
users' QoS quarantines, as defined in (3) and (4), are suitable for Constant Bit Rate (CBR) real-time traffic (e.g., video conferencing, telephony (voice services), etc.). To incorporate the QoS prerequisites of other types of real-time services such as real-time Variable Bit Rate (VBR) traffic (e.g., compressed video streams) in the proposed probabilistic short-term throughput framework, the ability to dynamically adjust the requested downlink data rate,  , and thus their data units threshold
, and thus their data units threshold  , at the corresponding RT user
, at the corresponding RT user should be provided. Therefore, in this case, we define
should be provided. Therefore, in this case, we define . The adopted short-term throughout prerequisites inherent attribute of fulfilling the requested data rate of an RT user within short-term time intervals, instead of converging to it within long-term intervals (as in [16–18]), allows the efficient support of both CBR and VBR traffic.
. The adopted short-term throughout prerequisites inherent attribute of fulfilling the requested data rate of an RT user within short-term time intervals, instead of converging to it within long-term intervals (as in [16–18]), allows the efficient support of both CBR and VBR traffic.
In order to guarantee short-term throughput requirements satisfaction for all RT users (i.e., achieve small values for their probabilities defined in (3)), we aim at providing them with the flexibility of dynamically affecting the priorities of being selected for receiving service according to their corresponding short-term throughput performance, through the introduction of an appropriate user-centric dynamic behavior which drives their ability to dynamically adapt their utility functions, as detailed in the following section.
3. Dynamic Utility Adaptation (DUA) Frame Work—Problem Formulation and Solution
In this section, we first detail and analyze a novel framework for reflecting users' short-term QoS requirements at their utility functions under a NUM problem formulation. This is achieved via the dynamic alteration of the utilities' properties in accordance to generic short-term time-varying QoS performance metrics—we refer to this framework as Dynamic Utility Adaptation (DUA). Emphasizing on multimedia services and their corresponding QoS prerequisites, a methodology for dynamically adapting RT users' utility parameters in accordance to their short-term throughput requirements is examined. Then, the overall utility-based optimization problem is formulated, considering both NRT and RT users' performance expectations, and its solution is derived. Finally, following a pure optimization theoretic analysis, the design properties of the proposed DUA framework are examined by determining the way users' utilities parameters deviations affect their priority of accessing system resources.
3.1. Dynamic Utility Adaptation Framework
Towards optimizing system's performance, a scheduling policy should allocate wireless network resources, in terms of transmission powers and corresponding rates, in a way that not only maximizes users' utilities and hence their degree of satisfaction in each time slot, but also satisfies their QoS prerequisites. The use of fixed predefined utility functions enables the reflection of users' long-term performance expectations at the scheduler and is in line with its opportunistic channel-aware nature [24]. On the other hand, RT users' short-term QoS demands require the scheduler's response within short-time intervals in the light of short-term QoS violations; therefore, the latter should also be reflected in their utilities.
With respect to the previous discussion and analysis, we introduce the dynamic adaptation of RT users' utilities  by allowing them to properly and dynamically adjust the values of their utility parameter
by allowing them to properly and dynamically adjust the values of their utility parameter  . Moreover, we redefine RT users' utility function as follows:
. Moreover, we redefine RT users' utility function as follows:

where  denotes a user's utility tunable parameter b
i
at time slot t and is defined as
denotes a user's utility tunable parameter b
i
at time slot t and is defined as

where  is RT user
is RT user  proper parameter in accordance to his transmission scheme (i.e., function's
proper parameter in accordance to his transmission scheme (i.e., function's initial fixed
initial fixed  parameter) and
parameter) and  is the factor that dynamically adjusts parameter's b
i
overall value in accordance to user's short-term performance. Thus,
is the factor that dynamically adjusts parameter's b
i
overall value in accordance to user's short-term performance. Thus,  is fixed within the duration of a time-slot. Let us underline that when RT users adjust their
is fixed within the duration of a time-slot. Let us underline that when RT users adjust their  parameter does not actually select a different modulation scheme, defined only by the fixed part of (6) (i.e.,
parameter does not actually select a different modulation scheme, defined only by the fixed part of (6) (i.e., ), but aim at reflecting in the scheduling policy (via their utility function) their expectations in system resources with respect to their current short-term QoS performance and thus, affecting their priority in accessing system's resources. In general, as
), but aim at reflecting in the scheduling policy (via their utility function) their expectations in system resources with respect to their current short-term QoS performance and thus, affecting their priority in accessing system's resources. In general, as  decreases a user's lack of resources is mirrored to his utility and consequently their need for having high priority in accessing system resources is revealed, a desirable property that justifies its selection, as it is shown via the solution of the corresponding utility-based system optimization problem.
decreases a user's lack of resources is mirrored to his utility and consequently their need for having high priority in accessing system resources is revealed, a desirable property that justifies its selection, as it is shown via the solution of the corresponding utility-based system optimization problem.
Parameters and
and  are the upper and lower bounds of a RT user's parameter
are the upper and lower bounds of a RT user's parameter  in each time slot t, respectively. As it is analyzed later in this paper (Appendix A), the existence of these bounding parameters restricts a user's ability to self-optimize their QoS performance over a time-varying wireless environment, due to the potentially bad channel conditions or lack of available system radio resources.
in each time slot t, respectively. As it is analyzed later in this paper (Appendix A), the existence of these bounding parameters restricts a user's ability to self-optimize their QoS performance over a time-varying wireless environment, due to the potentially bad channel conditions or lack of available system radio resources.
3.2. Adjusting the Properties of Real-Time Users' Utilities
In order real-time users to efficiently adjust their utility parameter  for all
for all  at the beginning of each time slot t, according to their short-term throughput requirements, the introduction of their actual short-term throughput performance information into the tuning procedure of their utility
at the beginning of each time slot t, according to their short-term throughput requirements, the introduction of their actual short-term throughput performance information into the tuning procedure of their utility  parameter is essential. Therefore, let us define the actual amount of data units that a real-time user
parameter is essential. Therefore, let us define the actual amount of data units that a real-time user  received within his observation time interval
received within his observation time interval  from slot
from slot to slot
to slot  as follows:
as follows:

where  denotes the actual amount of data that a real-time users
denotes the actual amount of data that a real-time users  received at time slot t and
received at time slot t and  ,
, denote his corresponding transmission rate and power allocation at the under consideration time slot, respectively. By using the above information and comparing it with a portion of his predefined short-term data units threshold
denote his corresponding transmission rate and power allocation at the under consideration time slot, respectively. By using the above information and comparing it with a portion of his predefined short-term data units threshold  an RT users can adjust their utility
an RT users can adjust their utility  parameter as
parameter as

where  and
and  are two normalized indicators that reflect a real-time user's need for accessing the system resources at time slot t, when they have shortage or excess of data units received within their current short observation time interval, respectively. Furthermore, parameter
are two normalized indicators that reflect a real-time user's need for accessing the system resources at time slot t, when they have shortage or excess of data units received within their current short observation time interval, respectively. Furthermore, parameter  (
( ), referred as the system's triggering parameter, determines the system's degree of preemption. Large values for the system's triggering parameter will make the scheduling policy react in a more preemptive way to real-time users' short-term throughput performance deviations, and therefore the achieved probabilities of not satisfying their short-term QoS requirements values will decrease.
), referred as the system's triggering parameter, determines the system's degree of preemption. Large values for the system's triggering parameter will make the scheduling policy react in a more preemptive way to real-time users' short-term throughput performance deviations, and therefore the achieved probabilities of not satisfying their short-term QoS requirements values will decrease.
In accordance to (8), when a real-time user has received till time slot
has received till time slot  less amount of data units than his predefined threshold, then in order to accomplish his short-term throughput QoS requirements satisfaction, the value of his utility
less amount of data units than his predefined threshold, then in order to accomplish his short-term throughput QoS requirements satisfaction, the value of his utility  parameter decreases and thus, his probability of being selected at current slot t increases. Furthermore, the reduction of a real-time user's
parameter decreases and thus, his probability of being selected at current slot t increases. Furthermore, the reduction of a real-time user's utility
utility  parameter from its corresponding value
parameter from its corresponding value  is determined by his normalized indicator
is determined by his normalized indicator  at that time slot. A RT user's
at that time slot. A RT user's  indicator reflects his need of accessing the system resources, according to the weighted distribution of his received data within his observation time interval, and therefore is defined as
indicator reflects his need of accessing the system resources, according to the weighted distribution of his received data within his observation time interval, and therefore is defined as

It is noted that represents a weight related to each time slot within the last
represents a weight related to each time slot within the last successive slots of an RT user
successive slots of an RT user  observation interval
observation interval that determines the importance of the user
that determines the importance of the user  received amount of service at that slot (i.e., time slot
received amount of service at that slot (i.e., time slot  on his estimated indicator. Moreover, the values of an RT user slots weights, as well as the importance of his information, are linearly inversely proportional to his distance
on his estimated indicator. Moreover, the values of an RT user slots weights, as well as the importance of his information, are linearly inversely proportional to his distance from the current slot t, since we want the information of the most distant slots to play a more important role on the degree of his need in accessing the system's resources. For instance, even if two real-time users
from the current slot t, since we want the information of the most distant slots to play a more important role on the degree of his need in accessing the system's resources. For instance, even if two real-time users  have received the same amount of data within the same observation time intervals (i.e.,
have received the same amount of data within the same observation time intervals (i.e.,  when
when  ), but user
), but user  has received service in slots more recent to the current than user j, then their indicator's
has received service in slots more recent to the current than user j, then their indicator's value will be smaller than user j indicator value
value will be smaller than user j indicator value  according to his slots' weights, since his tolerance for not accessing the system's resources is greater. Thus, user
according to his slots' weights, since his tolerance for not accessing the system's resources is greater. Thus, user utility
utility  parameter will be smaller than user
parameter will be smaller than user  corresponding parameter, and therefore they will have higher priority on accessing the system's resources at the current slot.
corresponding parameter, and therefore they will have higher priority on accessing the system's resources at the current slot.
On the other hand, when a real-time user has received a larger amount of data units than the predefined threshold within the last  successive time slots of his observation interval
successive time slots of his observation interval  then their utility
then their utility  parameter increases according to (8), and their priority in being served decreases. The larger RT user
parameter increases according to (8), and their priority in being served decreases. The larger RT user  received amount of data within their observation interval
received amount of data within their observation interval is, the lower their selection priority should be, and therefore their normalized indicator can be defined as follows:
is, the lower their selection priority should be, and therefore their normalized indicator can be defined as follows:

where the denominant denotes the maximum weighted amount of data units an RT user
denotes the maximum weighted amount of data units an RT user can receive within any time interval of
can receive within any time interval of  time slots, due to their downlink rate limitation
time slots, due to their downlink rate limitation . Such a design attribute allows the reallocation of excess system resources to NRT users towards the desirable optimization of their throughput performance [21, 22].
. Such a design attribute allows the reallocation of excess system resources to NRT users towards the desirable optimization of their throughput performance [21, 22].
Concluding this section's analysis, let us underline that the methodology expressed via (8), (9), and (10) applies in the most demanding case where the objective is to minimize RT users' probabilistic throughput constraints (i.e.,  ). Moreover, in the special case where an upper bound is set for RT users probabilistic prerequisites, that is,
). Moreover, in the special case where an upper bound is set for RT users probabilistic prerequisites, that is,  , then the two normalized parameters
, then the two normalized parameters  are defined as
are defined as


towards reflecting RT user's need for accessing the system resources at time slot t, when they are accomplishing or not the requested bound  respectively, under the assumption of the system's feasibility (i.e., there always exists at least one power and rate vector that leads to the satisfaction of all RT users' probabilistic throughput constraints).
respectively, under the assumption of the system's feasibility (i.e., there always exists at least one power and rate vector that leads to the satisfaction of all RT users' probabilistic throughput constraints).
3.3. Problem's Formulation, Transformation, and Solution
In order to optimize the overall system performance as well as users' degree of satisfaction, the following utility-based power and rate allocation optimization problem must be solved at the scheduler at every time slot

where  denotes NRT users' fixed parameter of their
denotes NRT users' fixed parameter of their function in accordance to the used modulation and coding scheme and
function in accordance to the used modulation and coding scheme and  is obtained via (8). Intuitively, (13) aims at jointly fulfilling and optimizing both NRT and RT users' QoS-aware degree of satisfaction, via maximizing the actual achieved throughput of the first (i.e., expressed via utility (2)) and via fulfilling the probabilistic short-term throughput prerequisites of the second (i.e., expressed via utility (5) and (6)). In the rest of the paper, for simplicity in the presentation, we omit the notation of the specific slot t in the notations of the system's and users' variables that remain fixed within the duration of a time slot.
is obtained via (8). Intuitively, (13) aims at jointly fulfilling and optimizing both NRT and RT users' QoS-aware degree of satisfaction, via maximizing the actual achieved throughput of the first (i.e., expressed via utility (2)) and via fulfilling the probabilistic short-term throughput prerequisites of the second (i.e., expressed via utility (5) and (6)). In the rest of the paper, for simplicity in the presentation, we omit the notation of the specific slot t in the notations of the system's and users' variables that remain fixed within the duration of a time slot.
Following the approach in [24], the optimal solution of the above problem is achieved when the base station transmits with its maximum power level  (i.e.,
(i.e.,  ), and hence a user
), and hence a user utility defined in (2) or (5) is adjusted according to the following expression:
utility defined in (2) or (5) is adjusted according to the following expression:

where  ,
,  is the break point of function
is the break point of function  and
and  when
when  , or
, or  otherwise. For
otherwise. For ,
,  is a convex function of
is a convex function of  and for
and for  is a sigmoidal function. Therefore,
is a sigmoidal function. Therefore,  is a sigmoidal function of
is a sigmoidal function of  at his maximum transmission rate
at his maximum transmission rate , with inflection point denoted as
, with inflection point denoted as (specifically,
(specifically, ,
,  and
and  ). Furthermore, the optimization problem (13) can be transformed to the following:
). Furthermore, the optimization problem (13) can be transformed to the following:

Towards solving the non-convex optimization (15), a pricing-based algorithm was developed in [18], and its asymptotic optimality, when the number of users is large, has been proven. Initially, the scheduler selects users to which nonzero power will be allocated by using the information of their parameters'  values. Parameter
values. Parameter  represents user
represents user maximum willingness to pay per unit power
maximum willingness to pay per unit power

In other words,  is the price
is the price  that maximizes user
that maximizes user  net utility
net utility (i.e., the utility minus the cost) and can be calculated as follows:
(i.e., the utility minus the cost) and can be calculated as follows:

where  is the unique solution of
is the unique solution of

Moreover, if for any two users  andj
andj for
for , then
, then  , and therefore user
, and therefore user  is more likely to be selected than userj. Hence, the scheduler selects users in a decreasing order of their maximum willingness to pay from
is more likely to be selected than userj. Hence, the scheduler selects users in a decreasing order of their maximum willingness to pay from  to
to  satisfying
satisfying

Finally, for the selected users the base station updates and broadcasts  till finding a unique equilibrium price
till finding a unique equilibrium price  that satisfies
that satisfies  [18]. Knowing
[18]. Knowing λ*, selected users' transmission powers and rates can be easily derived.
λ*, selected users' transmission powers and rates can be easily derived.
In accordance to the previous analysis, the price of a users' willingness to pay  plays a key role in their selection priority and, moreover, in the portion of total system's resources a user will finally occupy in the subsequent time slot. The following proposition shows that by allowing RT user to adapt their utility properties via adjusting his
plays a key role in their selection priority and, moreover, in the portion of total system's resources a user will finally occupy in the subsequent time slot. The following proposition shows that by allowing RT user to adapt their utility properties via adjusting his  parameter, they gain the enhanced flexibility of controlling the priority of being selected in accessing system resources among the others, towards optimizing their service performance.
parameter, they gain the enhanced flexibility of controlling the priority of being selected in accessing system resources among the others, towards optimizing their service performance.
Proposition 1.
If  and
and , then if
, then if
 .
.
Proof.
see Appendix B.
Proposition 1 asserts that if all other conditions are equivalent, a user  with smaller parameter
with smaller parameter  has a higher priority in being selected than a user j with larger value for his parameter
has a higher priority in being selected than a user j with larger value for his parameter . Moreover, if smaller values of an RT user's expected throughput within their observation time interval are observed, then lower values of his
. Moreover, if smaller values of an RT user's expected throughput within their observation time interval are observed, then lower values of his  parameter will result to higher probability in being selected, and vise versa. Essentially, the above proposition can be generalized for more than two users, revealing not only a relational dependency among users' utilities properties and his allocated resources, when the latter are derived through the solution of the system's utility-based optimization problem, defined in (13), but also the validity of the proposed DUA methodology expressed via (8), (9), and (10).
parameter will result to higher probability in being selected, and vise versa. Essentially, the above proposition can be generalized for more than two users, revealing not only a relational dependency among users' utilities properties and his allocated resources, when the latter are derived through the solution of the system's utility-based optimization problem, defined in (13), but also the validity of the proposed DUA methodology expressed via (8), (9), and (10).
4. Proposed Scheduling Policy—Towards Node's QoS-Aware Self-Optimization
Nodes' QoS-aware self-optimization refers to the ability of sensing his service performance variations as well as his environment changes, and then reacting to QoS triggering events towards optimizing his service performance. Such a behavior is revealed through the solution of the corresponding power and rate allocation optimization problem in CDMA networks when both NRT and RT services require access at system resources. Users requesting real-time services can monitor his services' performance, analyze and compute their resource expectations in a normalized way according to their short-term QoS prerequisites, and then adapt their utility functions' properties in order to affect their selection priority in the scheduling policy as well as the amount of anticipated resources. Moreover, at the base station, the system scheduler interacts with the mobile nodes towards solving the corresponding optimization problem, as defined in (13).
In the rest of this section, we present a Dynamic Utility Adaptation-based Users' Power and Rate Allocation (DUA_UPRA) scheme, which is realized by the efficient collaboration of two low complexity algorithms residing at the mobile nodes and base station, respectively. From mobile nodes perspective, DUA_UPRA introduces a control loop towards enabling their QoS-aware self-optimization, while at the base station, DUA_UPRA realizes a flexible algorithm, executed at the end of each time slot, to obtain optimal users' power and rate vectors for the subsequent time slot via obtaining the solution of (13).
DUA_UPRA Scheme
At Mobile Nodes [A Control Loop]
Step 1 (Information Monitoring).
A user computes the actual amount of data units that has received within his current observation timeinterval according to (7).
Step 2 (Information Analysis).
Determines his need for accessing system resources with respect to his QoS prerequisites (3), in accordance to (9) or (10).
Step 3 (Decision Making Towards Self-Optimization).
Reflects his QoS requirements and resources expectation at the scheduler by adjusting his utility function following (8) and then, disseminates this information at the base station.
At Base Station (A Resource Scheduler)
Step 1.
The scheduler requests users' utility functions.
Step 2.
The non-convex power and rate optimization problem (13) is redefined with respect to the current users' utilities (i.e.,  , and
, and  .
.
Step 3.
Users' selection is performed for the current optimization problem, according to the mobile selection procedure in (17)–(19).
Step 4.
Users' downlink allocated paower and throughput are estimated for non-real-time users from  and for real-time users from
and for real-time users from  , according to the power and rate allocation algorithm (PAA) in [18]. Let us underline, that a real-time user i actual downlink power and rate estimation is a function only of
, according to the power and rate allocation algorithm (PAA) in [18]. Let us underline, that a real-time user i actual downlink power and rate estimation is a function only of  parameter in Step 4 and hence of his corresponding transmission scheme.
parameter in Step 4 and hence of his corresponding transmission scheme.
In the following, the complexity of DUA_UPRA scheme is discussed. We initially place emphasis on DUA_UPRA scheme at the mobile node, due to the low computational power of mobile devices. Specifically, the proposed control loop needs to perform the following computations to obtain: (a) a finite summation (7), (b) one normalized real number via (9) or (10) (a summation and a deviation), and then (c) an additional sum in (8). The latter requires the computation of the upper and lower bounds of  via the algorithms provided in Appendix A. The maximum upper-bounded number
via the algorithms provided in Appendix A. The maximum upper-bounded number  of iterations required to obtain the above bounds is also justified in Appendix A. Apart from the time complexity, due to mobile devise hardware limitations, space considerations are also important. For the implementation of our proposed approach, the mobile device needs to store
of iterations required to obtain the above bounds is also justified in Appendix A. Apart from the time complexity, due to mobile devise hardware limitations, space considerations are also important. For the implementation of our proposed approach, the mobile device needs to store  (i.e., maintained on its memory) real numbers in order DUA_UPRA scheme at the mobile node to operate (i.e.,
(i.e., maintained on its memory) real numbers in order DUA_UPRA scheme at the mobile node to operate (i.e.,  real numbers for computing its short-term throughput performance (7),
real numbers for computing its short-term throughput performance (7),  real numbers for the corresponding slots weights and 1 for maintaining the value of
real numbers for the corresponding slots weights and 1 for maintaining the value of  ). Finally, concerning DUA_UPRA scheme at the base station, we adopt the low complexity algorithms provided in [18] towards obtaining the solution of non-convex optimization problem (14) (a simple shorting and a simple bisection algorithms with overall upper-bounded number of iterations to convergence).
). Finally, concerning DUA_UPRA scheme at the base station, we adopt the low complexity algorithms provided in [18] towards obtaining the solution of non-convex optimization problem (14) (a simple shorting and a simple bisection algorithms with overall upper-bounded number of iterations to convergence).
5. Numerical Results and Discussions
In this section, the operation and performance of the proposed dynamic utility adaptation-based users' power and rate allocation scheme DUA_UPRA is evaluated via modeling and simulation. In order to better illustrate the performance and the efficacy of the proposed scheme, in terms of average achieved actual downlink throughput and RT users' short-term throughput constraints satisfaction, we compare it against the performance of a fundamental utility-based power and rate allocation scheme [24] (in the following, we refer to it as UPRA algorithm) which only aims at optimizing users' actual throughput performance, without considering RT users' QoS prerequisites; therefore serving the purpose of system's performance benchmark.
Throughout our study, we considered a single cell time-slotted CDMA system. The duration of a slot is assumed to be  msec and the simulation lasts for 10,000 slots. We assume that the base station is located at the cell's center and that its maximum transmission power is
msec and the simulation lasts for 10,000 slots. We assume that the base station is located at the cell's center and that its maximum transmission power is  (Watts). We model the path gain from the base station to user
(Watts). We model the path gain from the base station to user as
as (Rayleigh channels), where
(Rayleigh channels), where  is the distance of user
is the distance of user from the base station,
from the base station,  is the distance loss exponent
is the distance loss exponent  , and
, and is the log-normal distributed random variable with mean 0 and variance
is the log-normal distributed random variable with mean 0 and variance (dB), which represents the shadowing [27].
(dB), which represents the shadowing [27].
We assumed that the system's spreading bandwidth is  and that the maximum downlink rate for all users is
and that the maximum downlink rate for all users is  Kbps. The total number of continuously backlogged users in the system is
Kbps. The total number of continuously backlogged users in the system is  and we considered two types of users, namely, non-real-time users
and we considered two types of users, namely, non-real-time users and real-time users
and real-time users  . Unless otherwise explicitly indicated, in the following, we consider that real-time users require constant downlink rates of
. Unless otherwise explicitly indicated, in the following, we consider that real-time users require constant downlink rates of (i.e., CBR real-time traffic) while their corresponding observation time intervals were set to
(i.e., CBR real-time traffic) while their corresponding observation time intervals were set to slots for all
slots for all  , and therefore an RT user's short-term data units threshold is set equal to
, and therefore an RT user's short-term data units threshold is set equal to . We consider saturated NRT users requesting best effort NRT services, aiming at maximizing the achieved actual downlink throughput. The system's triggering parameter is
. We consider saturated NRT users requesting best effort NRT services, aiming at maximizing the achieved actual downlink throughput. The system's triggering parameter is  . Both types of users are assumed to have the same transmission scheme. Therefore, we considered that their
. Both types of users are assumed to have the same transmission scheme. Therefore, we considered that their functions' parameters are
functions' parameters are  [18] and
[18] and ,
, . In order to compute real-time users' minimum and maximum values for their parameter
. In order to compute real-time users' minimum and maximum values for their parameter  in each time slot t, according to the algorithms proposed in Appendix A, we considered that
in each time slot t, according to the algorithms proposed in Appendix A, we considered that  and
and  .
.
With the objective of better evaluating the performance of the proposed DUA_UPRA scheme, we considered four basic scheduling scenarios. In the first scenario, referred to as SC1, in order to explore our scheme's behavior in terms of satisfying RT and NRT service QoS requirements and to gratify that the proposed dynamic users' utilities adaptation framework DUA reflects correctly their corresponding degree of satisfaction, we assumed that all users have the same average channel conditions. In the second and the third scenarios (SC2 and SC3), we evaluate the performance of our proposed scheduler when users with different average channel conditions are served, considering, respectively, only RT users (SC2) and both NRT and RT users (SC3) at the system in order to demonstrate our schemes' flexibility in adapting the resource allocation process according not only to users' various QoS requirements but also to their average channel conditions, aiming at reducing the drawbacks emerging from the users' "near-far" effect. Finally, the fourth scheduling scenario (SC4) aims at demonstrating and revealing DUA_UPRA algorithms efficacy in supporting variable rate real-time traffic users.
5.1. Scheduling Scenario 1 (SC1)
Figure 1 illustrates the total system's actual average throughput as a function of the number of  users in the system (i.e.,
users in the system (i.e., and therefore
and therefore  users' percentage in the system ranges from 16.67% to 100%, resp.), while Figure 2 presents RT users' probabilities of not satisfying their short-term throughput requirements (i.e.,
users' percentage in the system ranges from 16.67% to 100%, resp.), while Figure 2 presents RT users' probabilities of not satisfying their short-term throughput requirements (i.e.,  ) as a function of their number in the system under UPRA algorithm (black columns) and DUA_UPRA scheme (blue columns). All users average channel conditions are similar (i.e., are placed at same distances from the cell's center), therefore, only their fast fading attribute affects their instantaneous values.
) as a function of their number in the system under UPRA algorithm (black columns) and DUA_UPRA scheme (blue columns). All users average channel conditions are similar (i.e., are placed at same distances from the cell's center), therefore, only their fast fading attribute affects their instantaneous values.
We can clearly observe from Figure 2 that RT users' probabilities of not satisfying their short-term throughput requirements are significantly reduced under DUA_UPRA scheme, compared to the UPRA algorithm, even for large numbers of RT users in the system. Furthermore, our scheduling scheme's efficacy in satisfying RT users' QoS requirements is obtained without any considerable loss in the system's average (per user) achieved throughput, since as shown in Figure 1 system's average achieved throughput under DUA_UPRA scheme remains very close to the optimal one achieved by a pure opportunistic utility-based algorithm (UPRA). The observed loss in overall system's average throughput under DUA_UPRA is due to RT users slight overprovisioning of available resources towards maintaining their strict short-term throughout prerequisites (i.e., fixed amount of data per short-term windows). On the other hand, the latter resources are allocated to NRT users under UPRA, which are purely opportunistically served and, therefore, obtain increased average actual throughout (leading to better overall system throughput), at the expense of high RT user's short-term throughput failure probabilities (i.e., high RT users' performance degradation). The latter tradeoff is revealed in more detail in the following scenarios as well.
Moreover, by closely observing the allocation of system resources, in terms of actual average throughput for each one of the considered types of users individually, we can further see our scheme's property of exploiting the opportunistic nature individually for each type of users in order to optimize their diverse QoS requirements. Therefore, Figure 3 illustrates  users' actual average throughput as a function of their number in the system under DUA_UPRA. Specifically, it can be observed that an RT user's average received throughput remains almost constant, independent of their number in the system, due to DUA_UPRA scheme's property of allocating system resources to RT users up to the point where their required streaming throughput is satisfied. It is noted that, as observed in Figure 3, RT users' average achieved throughput is slightly larger than their predefined fixed downlink transmission rate, due to the system's preemptive nature when supporting RT services (determined by the values of triggering parameter
users' actual average throughput as a function of their number in the system under DUA_UPRA. Specifically, it can be observed that an RT user's average received throughput remains almost constant, independent of their number in the system, due to DUA_UPRA scheme's property of allocating system resources to RT users up to the point where their required streaming throughput is satisfied. It is noted that, as observed in Figure 3, RT users' average achieved throughput is slightly larger than their predefined fixed downlink transmission rate, due to the system's preemptive nature when supporting RT services (determined by the values of triggering parameter  ). On the other hand, an NRT user's average received throughput increases as the number of NRT users in the system decreases because the degree of competition among them for the excess system resources decreases as well, which is an inherent characteristic of any opportunistic scheduler.
). On the other hand, an NRT user's average received throughput increases as the number of NRT users in the system decreases because the degree of competition among them for the excess system resources decreases as well, which is an inherent characteristic of any opportunistic scheduler.
With the presentation of the following two figures (Figures 4 and 5), we focus on DUA_UPRA scheme's performance under the most demanding case in  in terms of RT users' short-term throughput QoS requirements satisfaction, where all the users in the system are RT users (i.e.,
in terms of RT users' short-term throughput QoS requirements satisfaction, where all the users in the system are RT users (i.e.,  ). We aim at demonstrating that DUA_UPRA scheme's enhanced performance, with respect to RT services QoS properties, asserts and affects all RT users and not only a portion of them, despite the large fluctuations on their channel conditions (due to fast fading). Specifically in Figure 4, we present each RT user's average actual achieved throughput, for all thirty users in the system, while in Figure 5 their corresponding short-term throughput failure probabilities under DUA_UPRA scheme (black dots) and UPRA algorithm (gray square) are depicted.
). We aim at demonstrating that DUA_UPRA scheme's enhanced performance, with respect to RT services QoS properties, asserts and affects all RT users and not only a portion of them, despite the large fluctuations on their channel conditions (due to fast fading). Specifically in Figure 4, we present each RT user's average actual achieved throughput, for all thirty users in the system, while in Figure 5 their corresponding short-term throughput failure probabilities under DUA_UPRA scheme (black dots) and UPRA algorithm (gray square) are depicted.
We observe that all users' probabilities of not satisfying their short-term throughput constraints are very small (maximum value: 0.7% average: 0.19%) under DUA_UPRA, while under UPRA they are high and diverse (maximum value: 20.7% average: 9.8%). Furthermore, under DUA_UPRA real-time users' average achieved throughput remains very high compared to the one achieved under UPRA that exploits optimally system's throughput abilities without, however, providing short-term throughput constraints. Thus, all real-time users' average actual received throughput is almost the same under DUA_UPRA.
5.2. Scheduling Scenario 2 (SC2)
In the second scheduling scenario SC2, we also considered a system with users (i.e.,
users (i.e., ), however, separated into two classes: good users and bad users with good and bad average channel conditions, respectively. Good users' average channel conditions are assumed to be 7 dB larger than bad users. For each type of users in the system, we evaluate their average probabilities of not satisfying their short-term throughput constraints (illustrated in Figure 6), as well as their throughput performance (presented in Figure 7), as a function of the number of RT bad users in the system, under DUA_UPRA (blue columns, solid for bad users and stripes for good users) and UPRA (black columns, solid for bad users and stripes for good users) algorithms.
), however, separated into two classes: good users and bad users with good and bad average channel conditions, respectively. Good users' average channel conditions are assumed to be 7 dB larger than bad users. For each type of users in the system, we evaluate their average probabilities of not satisfying their short-term throughput constraints (illustrated in Figure 6), as well as their throughput performance (presented in Figure 7), as a function of the number of RT bad users in the system, under DUA_UPRA (blue columns, solid for bad users and stripes for good users) and UPRA (black columns, solid for bad users and stripes for good users) algorithms.
The corresponding results demonstrate that under UPRA algorithm (black solid columns) bad users are strongly unfavored, not only in terms of their short-term throughput constraints dissatisfaction (Figure 6) but also due to their low throughput performance (Figure 7), especially when their number in the system is low. This mainly occurs due to UPRA goal of maximizing the system's total utility. Bad users' contribution to the maximization of the system's total utility is very low (i.e., they practically contribute only when their channels are very good compared to good users' average channel conditions), and therefore they are rarely selected by UPRA algorithm, which leads to their throughput performance degradation. On the other hand, under DUA_UPRA scheme bad users' short-term throughput performance is highly improved (Figure 7, solid blue columns). Especially, when their number in the system is small, the percentage of their short-term throughput dissatisfaction decreases even 75% compared with the corresponding one achieved under UPRA (solid black columns). Moreover, we observe that bad users' average downlink throughput takes the same values independently of their number in the system under DUA_UPRA scheme (Figure 7, solid blue columns).
Observing good users' performance metrics, we notice that their probabilities of not satisfying their short-term throughput constraints are highly improved under DUA_UPRA scheme (Figure 6 striped blue columns (last)) (i.e., always smaller than 0.18%), especially when their number in the system is high (number of bad users is small). On the other hand, under UPRA algorithm, due to the high competition, their short-term throughput constraints are still not satisfied (Figure 6 striped black columns). Finally, the downlink throughput performance reduction of good RT users under DUA_UPRA scheme, when compared to the one achieved under UPRA algorithm, is not only harmless (Figure 7 striped blue and black columns) since good RT users' required downlink rate is still achieved and satisfied, but rather desired since the excess system resources can be efficiently allocated to bad RT users in order to improve their short-term throughput requirements, as well as to other NRT users.
5.3. Scheduling Scenario 3 (SC3)
With this scenario (SC3), we aim at studying DUA_UPRA scheme's ability to efficiently treat "near-far" effect in a more pragmatic wireless setting, as well as quantifying the tradeoff between RT users short-term throughput satisfaction fulfillment and system's overall achieved throughout. To that end, we consider  active users in the system, where five
active users in the system, where five  request real-time traffic
request real-time traffic  512 Kbps,
512 Kbps,  slots,
slots, ) for all
) for all , while the rest are considered as NRT users
, while the rest are considered as NRT users  . NRT users constantly maintain their position with respect to cell's center, placed in groups of five NRT users in the following distances
. NRT users constantly maintain their position with respect to cell's center, placed in groups of five NRT users in the following distances  (Figure 8). On the other hand, the set of RT users in the system is gradually moving away from cell's center (per case), as shown in Figure 8, in order to better simulate the fact that RT users experience Rayleigh fast fading channels with various average quality conditions, due to their corresponding distance to cell's base station. Thus, RT users' distances from cell's centre per case are provided in Table 1.
(Figure 8). On the other hand, the set of RT users in the system is gradually moving away from cell's center (per case), as shown in Figure 8, in order to better simulate the fact that RT users experience Rayleigh fast fading channels with various average quality conditions, due to their corresponding distance to cell's base station. Thus, RT users' distances from cell's centre per case are provided in Table 1.
Figure 9, illustrates overall system downlink average throughput (black columns), as well RT and NRT users' average throughput (gray and dotted columns, resp.) for each one of the simulated cases (horizontal axis). Furthermore, the corresponding RT users' average short-term throughput failure probabilities are presented in Figure 10. The results show that the proposed DUA_UPRA scheme efficiently overcomes the problem of "near-far" effect, since RT users QoS prerequisites are fulfilled, in terms of achieved average actual throughout larger than 512 kbps and short-term throughput failure probabilities less than 0.8%, even under the most demanding scenario that is, . On the other hand, a significant tradeoff is revealed. As the average channel quality of RT users decreases (i.e., RT users are moving away from cell's center) then, the system increases the number of slots allocated to them, in order to balance between their short-term throughput requirements fulfillment and their inevitable actual throughput degradation (due to their bad channel quality). Therefore, RT users' average throughput deceases (Figure 9, grey columns) but their short-term throughput failure probabilities remain very low (Figure 10). At the end, RT users QoS prerequisites are preserved, but, at the cost of low NRT users' throughput as well as overall system throughout. That is due to the small number of system slots allocated to NRT users. The latter, leads only to a small increment of NRT users' average throughput (as RT users are moving away from cell's center), even if their instantaneous achieved rates are increased, due to their good channel conditions (Figure 9, dotted columns).
. On the other hand, a significant tradeoff is revealed. As the average channel quality of RT users decreases (i.e., RT users are moving away from cell's center) then, the system increases the number of slots allocated to them, in order to balance between their short-term throughput requirements fulfillment and their inevitable actual throughput degradation (due to their bad channel quality). Therefore, RT users' average throughput deceases (Figure 9, grey columns) but their short-term throughput failure probabilities remain very low (Figure 10). At the end, RT users QoS prerequisites are preserved, but, at the cost of low NRT users' throughput as well as overall system throughout. That is due to the small number of system slots allocated to NRT users. The latter, leads only to a small increment of NRT users' average throughput (as RT users are moving away from cell's center), even if their instantaneous achieved rates are increased, due to their good channel conditions (Figure 9, dotted columns).
5.4. Scheduling Scenario 4 (SC4)
In this final set of simulations (SC4), we explore the service performance of a RT user requesting variable rate traffic under the proposed DUA_UPRA scheme, as the system evolves. To that end, we consider a scenario with  real-time users, with the same average channel conditions (with fast-fading Rayleigh channels). All users except one user (user j) are assumed to have the same QoS prerequisites (i.e., CBR traffic of
real-time users, with the same average channel conditions (with fast-fading Rayleigh channels). All users except one user (user j) are assumed to have the same QoS prerequisites (i.e., CBR traffic of ). User j traffic is considered to be of variable rate as follows: from
). User j traffic is considered to be of variable rate as follows: from , from
, from  (Kbps) and from
(Kbps) and from  to
to  timeslot,
timeslot, 
Figure 11 illustrates the variable rate RT user's instantaneous actual throughput as a function of time, while Figure 12 their corresponding short-term throughput probability (i.e., at timeslot t) as a function of time, under DUA_UPRA scheme. In both figures, the timeslots at which user j required throughput alters are marked with vertical red lines, while the corresponding requested rates are presented with gray horizontal lines in Figure 11. The results show that the dynamic adaptation of the under consideration user's requested actual throughput is fulfilled under DUA_UPRA, and thus the timeframe required to complete a new request is less than 50 timeslots (i.e., less than
at timeslot t) as a function of time, under DUA_UPRA scheme. In both figures, the timeslots at which user j required throughput alters are marked with vertical red lines, while the corresponding requested rates are presented with gray horizontal lines in Figure 11. The results show that the dynamic adaptation of the under consideration user's requested actual throughput is fulfilled under DUA_UPRA, and thus the timeframe required to complete a new request is less than 50 timeslots (i.e., less than  ). Moreover, during the latter transition period (i.e., after a change of the requested throughput), the RT user's short-term throughput failure probabilities slightly increases (maximum value
). Moreover, during the latter transition period (i.e., after a change of the requested throughput), the RT user's short-term throughput failure probabilities slightly increases (maximum value  %) and then starts dropping again, due to algorithms adaptation to the new request (Figure 12). Finally, we can observe that the user's actual throughput always remains slightly higher that the required (Figure 11), since in order to always fulfill their short-term throughput requirements (per time slot), the system slightly overprovides them with resources.
%) and then starts dropping again, due to algorithms adaptation to the new request (Figure 12). Finally, we can observe that the user's actual throughput always remains slightly higher that the required (Figure 11), since in order to always fulfill their short-term throughput requirements (per time slot), the system slightly overprovides them with resources.
6. Concluding Remarks
In this paper, we studied the combined problem of allocating system resources, in terms of power assignment and transmission rate, in the downlink of a CDMA wireless system, where multiple services with various QoS requirements are simultaneously requested. We expressed users' degree of satisfaction with respect to their QoS demands fulfillment (non-real-time and real-time services) through a common utility-based framework which provides us with the enhanced flexibility of effectively influencing the opportunistic scheduler to meet their various QoS prerequisites.
Emphasis was placed on RT users' probabilistic short-term throughput requirements satisfaction. Specifically, in order to dynamically and accurately affect their selection priority with respect to their QoS prerequisites satisfaction, we introduced the information of their short-term received data distribution into the proposed methodology of tuning their utility functions' properties. Through modeling and simulation under various scheduling scenarios, we demonstrated that significant performance improvements are achieved in terms of real-time user's short-term throughput requirement satisfaction and non-real-time users actual throughput maximization, without any considerable loss in the total system throughput.
It should be noted that in this work, we considered linear relationship between users' assigned data rates and their corresponding degree of satisfaction. However, the degree of a user's satisfaction with respect to their service quality can be more efficiently expressed by applying other than linear utility functions of their actual throughput rates [11]. The mathematical formulation and the analytical solution of the above utility optimization problem provide a first step towards the realization of autonomic wireless network where hybrid data flows are simultaneously supported, and therefore is an issue of a great importance and part of our current research work.
References
Lu S, Bharghavan V, Srikant R: Fair scheduling in wireless packet networks. IEEE/ACM Transactions on Networking 1999, 7(4):473-489. 10.1109/90.793003
Lee T, Lin J, Su YT: Downlink power control algorithms for cellular radio systems. IEEE Transactions on Vehicular Technology 1995, 44(1):89-94. 10.1109/25.350273
Bender P, Black P, Grob M, Padovani R, Sindhushayana N, Viterbi A: CDMA/HDR: a bandwidth-efficient high-speed wireless data service for nomadic users. IEEE Communications Magazine 2000, 38(7):70-77. 10.1109/35.852034
Borst S, Whiting P: Dynamic rate control algorithms for HDR throughput optimization. Proceedings of the 20th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '01), April 2001 976-985.
Andrews M, Qian L, Stolyar A: Optimal utility based multi-user throughput allocation subject to throughput constraints. Proceedings of the Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '05), March 2005 2415-2424.
Berggren F, Jäntti R: Asymptotically fair transmission scheduling over fading channels. IEEE Transactions on Wireless Communications 2004, 3(1):326-336. 10.1109/TWC.2003.821147
Liu Y, Gruhl S, Knightly EW: WCFQ: an opportunistic wireless scheduler with statistical fairness bounds. IEEE Transactions on Wireless Communications 2003, 2(5):1017-1028. 10.1109/TWC.2003.816777
Liu X, Chong EKP, Shroff NB: A framework for opportunistic scheduling in wireless networks. Computer Networks 2003, 41(4):451-474. 10.1016/S1389-1286(02)00401-2
Kim JB, Honig ML: Resource allocation for multiple classes of DS-CDMA traffic. IEEE Transactions on Vehicular Technology 2000, 49(2):506-519. 10.1109/25.832982
Meshkati F, Goldsmith AJ, Vincent Poor H, Schwartz SC: A game-theoretic approach to energy-efficient modulation in CDMA networks with delay constraints. Proceedings of the IEEE Radio and Wireless Symposium (RWS '07), January 2007 11-14.
Harks T: Utility proportional fair bandwidth allocation: an optimization oriented approach. In Proceedings of the 3rd International Workshop on QoS in Multiservice IP Networks, 2005, Catania, Italy, Lecture Notes in Computer Science. Volume 3375. Springer; 61-74.
Hande P, Zhang S, Chiang M: Distributed rate allocation for inelastic flows. IEEE/ACM Transactions on Networking 2007, 15(6):1240-1253.
Dianati M, Shen X, Naik K: Cooperative fair scheduling for the downlink of CDMA cellular networks. IEEE Transactions on Vehicular Technology 2007, 56(4 I):1749-1760.
Duan X, Niu Z, Zheng J: Utility optimization and fairness guarantees for multimedia traffic in the downlink of DS-CDMA systems. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '03), December 2003 940-944.
Duan X, Niu Z, Zheng J: A dynamic utility-based radio resource management scheme for mobile multimedia DS-CDMA systems. Proceedings of the of IEEE Global Telecommunications Conference (GLOBECOM '02), November 2002, Taipei, Taiwan
Lee J-W, Mazumdar RR, Shroff NB: Opportunistic power scheduling for dynamic multi-server wireless systems. IEEE Transactions on Wireless Communications 2006, 5(6):1506-1515.
Lee J-W, Mazumdar RR, Shroff NB: Opportunistic power scheduling for multi-server wireless systems with minimum performance constraints. Proceedings of the 23rd Conference of the IEEE Communications Society (INFOCOM '04), March 2004 1067-1077.
Lee J-W, Mazumdar RR, Shroff NB: Downlink power allocation for multi-class wireless systems. IEEE/ACM Transactions on Networking 2005, 13(4):854-867.
Shakkotai S, Stolyar A: Scheduling for multiple flows sharing a time-varying channel: the exponential rule. American Mathematical Society Translations 2002., 207:
Kastrinogiannis T, Papavassiliou S: Satisfying elastic short term fairness in high throughput wireless communication systems with multimedia services. Proceedings of the IEEE International Conference on Communications (ICC '07), June 2007 5064-5069.
Kastrinogiannis T, Papavassiliou S, Kastrinogiannis K, Soulios D: A utility-based resource allocation approach for the downlink in CDMA wireless networks with multimedia services. Proceedings of the 18th Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007 1-5.
Kastrinogiannis T, Papavassiliou S: Utility based short-term throughput driven scheduling approach for efficient resource allocation in CDMA wireless networks. Wireless Personal Communications 2010, 52(3):517-535. 10.1007/s11277-008-9632-9
Xiao M, Shroff NB, Chong EKP: A utility-based power-control scheme in wireless cellular systems. IEEE/ACM Transactions on Networking 2003, 11(2):210-221. 10.1109/TNET.2003.810314
Lee J-W, Mazumdar RR, Shroff NB: Joint resource allocation and base-station assignment for the downlink in CDMA networks. IEEE/ACM Transactions on Networking 2006, 14(1):1-14.
Meshkati F, Poor HV, Schwartz SC: A non-cooperative power control game in delay-constrained multiple-access networks. Proceedings of IEEE International Symp. on Information Theory (ISIT '05), September 2005, Adelaide, Australia
Meshkati F, Goldsmith AJ, Vincent Poor H, Schwartz SC: A game-theoretic approach to energy-efficient modulation in CDMA networks with delay constraints. Proceedings of the IEEE Radio and Wireless Symposium (RWS '07), January 2007 11-14.
Stuber G: Principles of Mobile Communication. Kluwer Academic, Norwell, Mass, USA; 1996.
Shewchuck JR: An Introduction to the Conjugate Gradient Method Without the Agonizing Pain. 1.25th edition. School of Computer Science, Carnegie Mellon University, Pittsburg, Pa, USA; 1994.
Acknowledgment
This work has been partially supported by EC FP7 EFIPSANS Project (INFSO-ICT-215549).
Author information
Authors and Affiliations
Corresponding author
Appendices
A. Limitations on Controlling Users' Selection Priorities
In the following, we rigorously define the lower and upper bounds of real-time users'  parameter (i.e.,
parameter (i.e., , resp.) and justify their role in the proposed scheduling policy as well as the way they restrict users' ability to self-optimize their services' QoS performance. It is shown that even if RT users' introduced self-optimization behavior enhances their ability to self-optimize their QoS-aware performance, mobile nodes' potential bad channel conditions, the system's lack of available resources, as well as their physical limitations may prevent the fulfillment of their short-term QoS requirements. Moreover, we provide low complexity algorithms for computing the above boundary values.
, resp.) and justify their role in the proposed scheduling policy as well as the way they restrict users' ability to self-optimize their services' QoS performance. It is shown that even if RT users' introduced self-optimization behavior enhances their ability to self-optimize their QoS-aware performance, mobile nodes' potential bad channel conditions, the system's lack of available resources, as well as their physical limitations may prevent the fulfillment of their short-term QoS requirements. Moreover, we provide low complexity algorithms for computing the above boundary values.
As analyzed in the previous sections, a real-time user's utility function parameter  plays a key role in the selection priority of accessing system's resources at each time slot, since it affects the corresponding value of their willingness to pay
plays a key role in the selection priority of accessing system's resources at each time slot, since it affects the corresponding value of their willingness to pay  . On the other hand, the appropriate values for
. On the other hand, the appropriate values for should be such that for any further decrement or increment in the value of
should be such that for any further decrement or increment in the value of  (with respect to these bounds) the corresponding value of parameter
(with respect to these bounds) the corresponding value of parameter  is not affected. Consequently, parameter
is not affected. Consequently, parameter  should be bounded among them. Therefore, we use the following condition for identifying an RT user
should be bounded among them. Therefore, we use the following condition for identifying an RT user  bounds of their
bounds of their  parameter
parameter


where  represents RT users' maximum willingness as a function of his parameter
represents RT users' maximum willingness as a function of his parameter  .
.
Definitions of 
 Following a pure functions theoretic analysis, the lower bound of an RT user's utility function parameter
Following a pure functions theoretic analysis, the lower bound of an RT user's utility function parameter  can be formally defined as follows.
can be formally defined as follows.
Proposition 2 (Definition of  ).
).
We defines as  for all
for all  the maximum value of a RT user
the maximum value of a RT user  utility function parameter
utility function parameter  at slot t, such that
at slot t, such that


where  Thus, when
Thus, when  then
then  .
.
Proof.
See Appendix C.
The existence of such a lower bound reveals an inherent users' limitation on controlling their services' short-term QoS requirements when operating over a time-varying wireless environment; the reason is twofold. On the one hand, due to its opportunistic nature, the scheduler in the sight of low available resources may potentially unfavor some user's towards optimizing overall system's welfare. On the other hand, even when plethora of system resources is available, RT users' potential bad instantaneous channel condition and their physical limitations may make the goal of their short-term QoS prerequisites fulfillment unreachable.
The following proposition defines an RT user's utility function parameter  upper bound.
upper bound.
Proposition 3 (Definition of  ).
).
One defines as  the maximum value of a real-time user
the maximum value of a real-time user  utility function parameter
utility function parameter  at time slot t such that
at time slot t such that


where is a large positive number and
is a large positive number and  . Thus,
. Thus,


Proof.
See Appendix D.
From the definition of  we can observe that the worse RT user's channel conditions are (i.e., parameter A
i
increases), the smaller is our ability of influencing their selection priority, since the range of their utility function parameter
we can observe that the worse RT user's channel conditions are (i.e., parameter A
i
increases), the smaller is our ability of influencing their selection priority, since the range of their utility function parameter  decreases as well.
decreases as well.
Algorithms for Computing 
We conclude this section by introducing two low complexity algorithms for computing RT users' parameters  lower and upper bounds at each time slot. Initially, by using Proposition 2, we provide a "divide and conquer"-based algorithm for computing a real-time user's parameter
lower and upper bounds at each time slot. Initially, by using Proposition 2, we provide a "divide and conquer"-based algorithm for computing a real-time user's parameter  lower bound
lower bound 
Algorithm for Computing ( )
)
Let us refer to  and
and  as conditions A and B, respectively.
as conditions A and B, respectively.
-
(i)
Set
 ,
,  ,
, 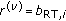 and
and 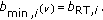
-
(ii)
If
 AND
AND  are true then
are true then  ,
,  and
and 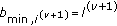 else
else  ,
, 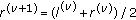 and
and 
-
(iii)
If
 OR
OR ,
, 
-
(iv)
If NOT (
 ) is true then
) is true then 
The maximum number of algorithm's iterations ν * is  , where ε is a small positive constant. Finally, with respect to Proposition 3, we propose the adoption of a "Steepest Descent"-based algorithm for computing at every time slot t, a real-time user
, where ε is a small positive constant. Finally, with respect to Proposition 3, we propose the adoption of a "Steepest Descent"-based algorithm for computing at every time slot t, a real-time user  parameter
parameter  upper bound,
upper bound,  .
.
Algorithm for Computing ( )
)
-
(i)
Let
 be a large positive constant.
be a large positive constant. -
(ii)
 = 0,
= 0,  .
. -
(iii)
For
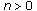 then
then 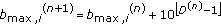 where:
where: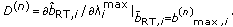
-
(iv)
If
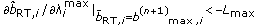 , go to (vii)
, go to (vii) -
(iv)
If
 , then go to (vii)
, then go to (vii) -
(vi)
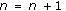 and go to (iii).
and go to (iii). -
(vii)
Stop.
The previous algorithm is a modified "Steepest Descent"-based algorithm, adapted to the needs of our problem (Proposition 3). Specifically, in our case, we are not interested in finding the minimum of the function  , but in accordance to (A.1), in finding a large value of b at which the absolute values of gradient
, but in accordance to (A.1), in finding a large value of b at which the absolute values of gradient  are very large (for practical considerations, we approximate infinite with a large number
are very large (for practical considerations, we approximate infinite with a large number Therefore, to improve convergence time, we use as a step the corresponding power of 10 (in step iii). It is easy to show, considering the complexity of the "Steepest Descent" [28], that the maximum number of iterations required for convergence are
Therefore, to improve convergence time, we use as a step the corresponding power of 10 (in step iii). It is easy to show, considering the complexity of the "Steepest Descent" [28], that the maximum number of iterations required for convergence are  , where
, where  .
.
Finally, the total maximum number of iterations required to compute the minimum and the maximum values of is
is  , where ε and
, where ε and  are a small and a large positive constants, respectively.
are a small and a large positive constants, respectively.
B. Proof of Proposition 1
From (14), we can observe that when for two users  then the only parameters that are affected by variations in the value of parameters
then the only parameters that are affected by variations in the value of parameters and hence determine the properties of their utility functions
and hence determine the properties of their utility functions  and
and  are
are  ,
,  and the corresponding values of their
and the corresponding values of their  functions, respectively. Therefore, we first provide the following two lemmas that determine the way that a user
functions, respectively. Therefore, we first provide the following two lemmas that determine the way that a user parameter
parameter  affects his
affects his function and his
function and his  parameter.
parameter.
Lemma 4.
If  then
then  for all
for all
Proof.
If one sets as  in the generic definition of a sigmoidal function:
in the generic definition of a sigmoidal function:


where  and
and  , one can rewrite itas
, one can rewrite itas . Thus, if
. Thus, if then
then  and
and 
Lemma 5.
If  and
and , if
, if  then
then  .
.
Proof.
From (14), one can compute a user i, parameter  value as follows:
value as follows:  where
where  . Let one defines as
. Let one defines as  and as
and as  . When
. When  , then
, then  since
since  is maximum and
is maximum and


Thus, if then
then since
since


If there exists  ,
,  such that
such that  , and
, and 
 such that
such that  , then if
, then if  , from (B.3), one has
, from (B.3), one has  , and hence
, and hence  . Thus, since
. Thus, since  and
and  , from (B.2) one has
, from (B.2) one has  .
.
Finally, since if  then
then  , and when
, and when  then
then concludes that if
concludes that if  then
then  . Finally, based on Lemmas 4 and 5 one proves Proposition 1. From Remark
. Finally, based on Lemmas 4 and 5 one proves Proposition 1. From Remark (Proposition 3, [24]) one has seen that if for any two users
(Proposition 3, [24]) one has seen that if for any two users , j
, j for
for  , then
, then  . Therefore one has to prove that if
. Therefore one has to prove that if  then
then  for
for  . By the definition of a user
. By the definition of a user  utility in (14), and Lemma 5, let one defines:
utility in (14), and Lemma 5, let one defines:


Furthermore, there are three possible cases for the value of parameter P, when  .
.
Case 1.
If  then from (14) if
then from (14) if  then
then  , and hence it easily follows that
, and hence it easily follows that  .
.
Case 2.
If  and
and  , then from Lemma 4 if
, then from Lemma 4 if  we have
we have  , and it follows that
, and it follows that  .
.
Case 3.
If  and
and  , then since
, then since  and (as in Case 1)
and (as in Case 1)  , we can conclude that
, we can conclude that  .
.
Finally, since when for
for  , the proof is completed.
, the proof is completed.
C. Proof of Proposition 2
In order to determine a lower bound of an RT user's parameter , we first identify some of the main properties of his utility function with respect to
, we first identify some of the main properties of his utility function with respect to  . The following lemma defines the relationship between the inflection point of a user's sigmoidal-like utility function and its parameter
. The following lemma defines the relationship between the inflection point of a user's sigmoidal-like utility function and its parameter  .
.
Lemma 6.
For any two values  ,
,  , of user
, of user  utility parameter
utility parameter  such that
such that  , it holds that
, it holds that  where
where  ,
,  are the inflection points of their corresponding utilities
are the inflection points of their corresponding utilities  and
and  , respectively.
, respectively.
Proof.
See Appendix E.
Furthermore, we can also prove that when  , then a user's utility function inflection point has always smaller value than his utility separation point,
, then a user's utility function inflection point has always smaller value than his utility separation point,  .
.
Lemma 7.
When  ,
,  .
.
Proof.
See Appendix F.
Based on the two previous lemmas, we can see that there always exists a value  for a user
for a user utility function parameter
utility function parameter  when
when  , such that for smaller than
, such that for smaller than  values of
values of  , the inflection point of function
, the inflection point of function  is always smaller that its separation point (i.e.,
is always smaller that its separation point (i.e.,  ). Therefore, we can provide the following proposition.
). Therefore, we can provide the following proposition.
Proposition 8.
There always exists a value of a real-time user i utility function parameter  when
when  , denoted as
, denoted as  , such that
, such that  , and hence
, and hence  when
when  .
.
Proof.
See Appendix H.
We can now proceed to prove that when , there always exists a value for a user
, there always exists a value for a user utility function parameter
utility function parameter  denoted as
denoted as such that when
such that when  then their maximum willingness to pay is calculated by the second part of (17), because
then their maximum willingness to pay is calculated by the second part of (17), because  in (18) does not exist and hence, condition (A.1) is fulfilled. Towards that, we first provide the following proposition.
in (18) does not exist and hence, condition (A.1) is fulfilled. Towards that, we first provide the following proposition.
Proposition 9.
There always exists a value for a real-time user  utility function parameter
utility function parameter  when
when  , indicated as
, indicated as  such that when
such that when  then there is no
then there is no  such that
such that


Proof.
See Appendix I.
According to Proposition 8, there always exists a value for a real-time user utility function parameter
utility function parameter  (i.e.,
(i.e.,  ) when
) when  such that for
such that for  then
then


and in accordance to Proposition 9, there always exists a value for a real-time user utility function parameter
utility function parameter  (i.e.,
(i.e.,  ) when
) when  such that for
such that for  then
then


and hence (18) has no solution. Therefore, there always exist a value for parameter  when
when  , denoted as
, denoted as  , such that both (C.2) and (C.3) are satisfied. Specifically,
, such that both (C.2) and (C.3) are satisfied. Specifically,  . Moreover, since when
. Moreover, since when  then, (18) has no solution, and by (17), we have
then, (18) has no solution, and by (17), we have  , where
, where . Furthermore, since
. Furthermore, since  , we conclude that when
, we conclude that when  then
then  and hence
and hence  .
.
Moreover, the proof is completed.
D. Proof of Proposition 3
In the following, we determine the sufficient conditions that will allow us to define an upper bound of an RT user's utility parameter  when
when  and to justify its purpose with respect to condition (A.1). Moreover, since
and to justify its purpose with respect to condition (A.1). Moreover, since , then without loss of generality in the rest of this subsection, we assume that a user
, then without loss of generality in the rest of this subsection, we assume that a user  function
function parameters
parameters  and
and  have fixed values independent from the value of parameter
have fixed values independent from the value of parameter .
.
Initially, we determine an upper bound of a real-time user's parameter , denoted as
, denoted as
 , without considering the satisfaction of condition (A.1). The existence of such an upper bound is based on the base station's total downlink power limitation, as explained in the following lemma.
, without considering the satisfaction of condition (A.1). The existence of such an upper bound is based on the base station's total downlink power limitation, as explained in the following lemma.
Lemma 10.
There always exists an upper bound of a real-time user's  utility function parameter
utility function parameter  , when
, when  , denoted as
, denoted as  , where
, where


due to the power limitations of the base station  and the corresponding user's channel conditions per time slot (i.e., Ai ). Specifically, if
and the corresponding user's channel conditions per time slot (i.e., Ai ). Specifically, if  then
then  where
where  is the solution of (18).
is the solution of (18).
Proof.
See Appendix I
Moreover, we have already proven that  is a continuous and decreasing function of
is a continuous and decreasing function of  (in Proposition 1) and vice versa. Furthermore, the following lemma states that when
(in Proposition 1) and vice versa. Furthermore, the following lemma states that when  ,
, is also a concave up function of
is also a concave up function of  .
.
Lemma 11.
When  an
an  user's
user's  utility function parameter
utility function parameter  is a concave up function of his parameter
is a concave up function of his parameter  , since
, since  .
.
Proof.
See Appendix J.
Based on the previous lemmas, we can now formally define an upper bound for a real-time user's parameter  , with respect to (A.1), as follows. Let
, with respect to (A.1), as follows. Let be a positive constant such as when
be a positive constant such as when  ,
,  . Moreover, for a user's parameter
. Moreover, for a user's parameter  , which is a function of their maximum willingness to pay
, which is a function of their maximum willingness to pay  , we have proven the following properties:
, we have proven the following properties:
 (in Lemma 10).
(in Lemma 10).
For  :
:
-
(a)
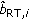 is a continuously decreasing function of parameter
is a continuously decreasing function of parameter 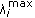 (in Proposition 1).
(in Proposition 1). -
(b)
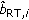 is a concave up function of parameter
is a concave up function of parameter 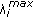 (in Lemma 11).
(in Lemma 11).
Therefore, we can conclude that there always exists a  , denoted as
, denoted as  , such that
, such that


which completes the proof.
E. Proof of Lemma 6
If  is the inflection point of the sigmoid like function
is the inflection point of the sigmoid like function  (for simplicity in the presentation, in this proof, we denote
(for simplicity in the presentation, in this proof, we denote  as
as  ) the following equation must be satisfied
) the following equation must be satisfied


Moreover, we can compute the second derivative of a users' utility function in accordance to the partial derivatives chain rule as follows,  and after mathematical manipulations, we can conclude that
and after mathematical manipulations, we can conclude that


where  . Furthermore, with respect to (B.1) we can easily derive that
. Furthermore, with respect to (B.1) we can easily derive that


Let us further define as


where  in order (E.1) to be satisfied when
in order (E.1) to be satisfied when  . Function
. Function  is an increasing function of variable b
i
is an increasing function of variable b
i
 since
since


and a decreasing function of variable γ
i
 since
since


Now, let us consider the case where  ,
,  and with respect to (E.1) and (E.4),
and with respect to (E.1) and (E.4),  = 0 since
= 0 since  is the inflection point of user
is the inflection point of user utility function
utility function  when
when  (i.e.,
(i.e.,  ). Then, if we increase the value of user
). Then, if we increase the value of user parameter b
i
from
parameter b
i
from  to
to  , where
, where  , then
, then


since  is an increasing function of parameterb
i
and the value of parameter
is an increasing function of parameterb
i
and the value of parameter  is fixed (i.e.,
is fixed (i.e.,  ). Furthermore, with respect to (E.1) and (E.4), there must also exist a value of parameter
). Furthermore, with respect to (E.1) and (E.4), there must also exist a value of parameter  regarding the inflection point of function
regarding the inflection point of function  and hence
and hence


According to (E.7) and (E.8), and since  is a decreasing function of parameter
is a decreasing function of parameter we can easily conclude that,
we can easily conclude that,  when
when  . Finally, since γ
i
is an increasing function of P
i
we proved that if
. Finally, since γ
i
is an increasing function of P
i
we proved that if  ,
, .
.
F. Proof of Lemma 7
It can be easily shown that


Moreover, we can see from (14) that when  then
then


Thus, if  , then
, then  belongs to the concave part of the sigmoid-like function
belongs to the concave part of the sigmoid-like function  , and hence
, and hence  . Towards that and in accordance to (E.3) in Lemma 6, when
. Towards that and in accordance to (E.3) in Lemma 6, when  we have
we have


In order (F.3) to have negative values for and
and the following inequality must be asserted,
the following inequality must be asserted,  , which is true.
, which is true.
G. Proof of Proposition 8
In accordance to Lemma 6 the inflection point of a user
of a user  sigmoidal like utility function is an increasing function of his utility parameter
sigmoidal like utility function is an increasing function of his utility parameter  when
when  . Therefore, since when
. Therefore, since when  = 0
= 0 then
then  according to Lemma 7, and when
according to Lemma 7, and when  then
then  according to the definition of a user's utility function, we can conclude that there always exists a value of a real-time user
according to the definition of a user's utility function, we can conclude that there always exists a value of a real-time user  utility function parameter
utility function parameter  where
where  , (i.e.,
, (i.e.,  ) such that
) such that  and hence when
and hence when  , then
, then  .
.
H. Proof of Proposition 9
Let us define


Moreover, as it has been proved in [24], Lemma 6, a user  net utility
net utility  is maximized only when their power allocation value is in the concave part of their utility function (i.e.,
is maximized only when their power allocation value is in the concave part of their utility function (i.e.,  ). Therefore, we search for the solution of
). Therefore, we search for the solution of  only within the range
only within the range , as it further can be observe from (18). Furthermore, since from Proposition 2 when
, as it further can be observe from (18). Furthermore, since from Proposition 2 when  , then
, then  , the concave part of a user's utility function is for
, the concave part of a user's utility function is for  within the range of
within the range of  to
to and if
and if  then
then


When  then
then  because
because  for all
for all  therefore is an increasing function ofP and
therefore is an increasing function ofP and  . Furthermore, if we prove that there exists
. Furthermore, if we prove that there exists  such that
such that  when
when  we will have conclude the proof of the proposition, since
we will have conclude the proof of the proposition, since will not exist. After some algebra, we have from (H.1) that
will not exist. After some algebra, we have from (H.1) that


where we have denote  for presentation purposes. Since the denominator in (H.3) takes no negative values, we must examine the properties of the numerator. Therefore, let us define the following function
for presentation purposes. Since the denominator in (H.3) takes no negative values, we must examine the properties of the numerator. Therefore, let us define the following function


Thus,


By (H.5), we can prove that since the numerator of  is an decreasing function of b,
is an decreasing function of b,  and the denominator of
and the denominator of  is always positive, then if we decrease a real time user's utility function parameter
is always positive, then if we decrease a real time user's utility function parameter  from
from  to 0, then there always exists a value for parameter
to 0, then there always exists a value for parameter  , namely,
, namely,  , such that
, such that  and when
and when  then
then  , therefore, when
, therefore, when  there is no
there is no  such
such 
 .
.
I. Proof of Lemma 10
In accordance to (17) and (18), a real-time user's willingness to pay can be estimated when  as
as


Moreover, we have that  and after some mathematical manipulations, we conclude
and after some mathematical manipulations, we conclude


and finally that


Moreover, we have that


and hence after some algebra with respect to  , we can see that
, we can see that


 ,
,
 ,
,
 , where
, where  .
.
In order (I.5) to have a real solution,  , when
, when  , and thus
, and thus  , the following two conditions must be satisfied (without loss of generality and for simplicity in the presentation since
, the following two conditions must be satisfied (without loss of generality and for simplicity in the presentation since  in the following, we set
in the following, we set
 and after some algebra we can conclude that the following inequality has to be satisfied
and after some algebra we can conclude that the following inequality has to be satisfied


 , and thus, in accordance to (I.5)
, and thus, in accordance to (I.5)


Furthermore, since  and
and  , in order
, in order  the following inequality must be satisfied
the following inequality must be satisfied


and after some algebra we conclude that


Finally, from (I.3) and (I.9), we can determine the upper bound of a real-time  user's
user's  utility function parameter
utility function parameter  as follows:
as follows:


J. Proof of Lemma 11
In accordance to (I.3) and (I.7) in Lemma 10, we have that when  then
then


Finally, we can also easily compute  , since
, since  and hence
and hence  (since from (I.9) in Lemma 10, we proved that when
(since from (I.9) in Lemma 10, we proved that when then
then  ) which concludes the proof.
) which concludes the proof.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kastrinogiannis, T., Papavassiliou, S. A Dynamic Utility Adaptation Framework for Efficient Multimedia Service Support in CDMA Wireless Networks. J Wireless Com Network 2010, 375410 (2010). https://doi.org/10.1155/2010/375410
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/375410
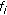 is an increasing function of
is an increasing function of 
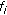 is a continuous, twice differentiable sigmoidal function with respect to
is a continuous, twice differentiable sigmoidal function with respect to 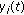 .
.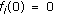 to ensure that
to ensure that  when
when  (t)
(t) 0.
0.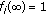 .
.



 .
.
 .
.






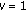 ,
, 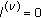 ,
, 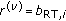 and
and 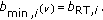
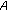 AND
AND 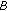 are true then
are true then  ,
,  and
and 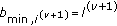 else
else  ,
, 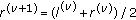 and
and 
 OR
OR ,
, 
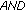
 ) is true then
) is true then 
 be a large positive constant.
be a large positive constant. = 0,
= 0,  .
.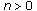 then
then 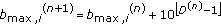 where:
where: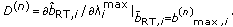
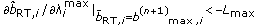 , go to (vii)
, go to (vii) , then go to (vii)
, then go to (vii)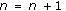 and go to (iii).
and go to (iii).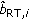 is a continuously decreasing function of parameter
is a continuously decreasing function of parameter  (in Proposition 1).
(in Proposition 1).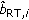 is a concave up function of parameter
is a concave up function of parameter 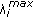 (in Lemma 11).
(in Lemma 11).