- Research Article
- Open access
- Published:
Master Synchronization in Physical-Layer Communications of Wireless Sensor Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 382570 (2011)
Abstract
Synchronization in physical layer of wireless sensor networks is critical in restricting complexity of tag node and power consumption. Considering the master-to-tag communication (i.e., receiving signal from a master or anchor node by tag nodes), we propose a scheme on the basis of the principles of feedback control, to transfer the signal acquisition functionality from the tag receivers to the master nodes in a cluster. Furthermore, the algorithm of timing acquisition and phase adjustment do work in the master transmitter, and the tag nodes just need feedback results of the phase detection. The tag nodes do not require complicated clock or phase adjustment circuit any more or estimation in synchronization either. Thus, this master synchronization method reduces the complexity of tag nodes and power consumption. Due to the large random time delay in the wireless feedback loop, there exists the problem of stability and convergence in the acquisition. We analyze it and present a feasible scheme for the proposed master synchronization. In order to reduce acquisition time and cost in feedback, a two-step master acquisition algorithm is proposed. The acquisition performance under nonideal channel is analyzed, and further verified by simulations.
1. Introduction
Recent years, the research on wireless sensor networks (WSNs) has attracted many focuses from academic, military, and industrial community. In many cases, including outdoor applications, a large amount of sensor tags not only sense but also exchange the gathered information. Thus, how to satisfy the requirement of the sensor tags, including small size, low complexity, and low-power consumption to ensure a long-time maintenance-free work, becomes a primary challenge in practice [1]. The development of physical-layer technologies is still required for further reducing power consumption in sensor nodes. In this area, the conventional timing recovery in a receiver costs significant power and complexity. On account of this, this paper introduces a master synchronization differing from the traditional mechanism in wireless communication to simplify transceiver and lower the power consumption in tag nodes. Its feasibility and performance are studied in this paper.
At present, the reduction of power consumption in nodes communication process is mostly considered by the methods in Medium-Access Layer (MAC) designs. Literatures have contributed several energy-efficient MAC protocols [2–4]. In addition, the low-power wireless passive sensor networks (WPSN) are attracting considerable attention due to the low-cost tags [5]. To supply the energy source of transceiver, the cluster node feeds the passive RFID tags with RF power. Even so, the absorbed energy can just offer temporary and close interaction between nodes. It is difficult to meet the requirement of communication distance and data rate in common applications [6].
Carrier acquisition, bit, and frame synchronization process are the essential conditions in physical layer of wireless data communication [7]. However, the low-power research for synchronization subsystem is often overlooked, ignoring that it comprises over 15% of the physical layer die area in several common wireless standards, such as Bluetooth and 802.11. In WSNs, the acquisition and tracking scheme implemented in receiver is commonly adopted to physical-layer communication as it used to be [8, 9]. It has the advantages of fast acquisition and high synchronization precision, but a shortcoming that the receiver must have a significant chip area, controllable clock (such as voltage-controlled oscillator, VCO), or a high-rate sampler and signal processor, which cost more than 15% system power. In ultrawideband communications, the high-precision controllable delay line is even required in receiver for acquiring narrow pulses which also leads to high circuit complexity and power consumption [10].
Shown in Figure 1, there are two examples including a large amount of sprinkled sensor tags exchanging information with master node in aircraft, and tag nodes in warehouse reporting humidity and temperature to anchors. The hierarchical or cluster structure is designed for the large-scale WSNs [1], and its master nodes have remarkable ability for communication and information processing. Most sensor tags, whose major task is to collect sensing information, work under the low-power mode even in a sleep state. To wake up the nodes along with communications, each tag node has to equip full-function wireless communication module [11]. The nodes communicate small amount of data in low burst rate in numerous situations, including various-distance links from tens of meters to a kilometer. There is no requirement for establishing a link within a few microseconds. Meanwhile, the master nodes need no more consideration for their power consumption and complexity due to their dominant roles in WSNs. To simplify the receiver in tags, this paper develops a synchronization mechanism using the feedback control principles to reduce the complexity and power consumption in tag nodes, where there is no or little timing recovery circuits required. The method can not only be applied to the interaction among low-complexity and high-power efficiency nodes, but also provides a flexible communication by combining the advantages of WPSN.
The analog or digital methods are utilized for synchronization acquisition in a conventional receiver. The analog phase-locked loop (PLL) using feedback control is to achieve the carrier and phase synchronization. Timing recovery by adaptive digital signal processing adopts the open-loop frequency or phase offset estimation which still use the principles of feedback iteration on the received cyclostationary signal. Different from traditional acquisition, the proposed master synchronization transfers the timing recovery and clock control to the master node, while the tag receiver only requires to generate and feedback the error control signals. That distributes the synchronization functionality into transmitter and receiver to meet the low-complexity and low-power consumption requirements of a tag node. Since the error control information can be fed back only through a wireless channel, shortening acquisition time and lowering the power consumption of tag nodes are the key issues to the proposed synchronization scheme. Due to the large time delay caused by feedback loop in wireless link, the stability of the proposed distributed feedback-control synchronization may be influenced greatly. The stability analysis and a feasible protocol is given below.
The outline of this paper is as follows. In Section 2 the master synchronization models and three algorithms for wireless sensor networks are introduced. In Section 3, the stability of these distributed feedback control methods are analyzed, and a stable acquisition is proposed in Section 4. The performance of the single-step pulse master synchronization is also deduced in Section 4. In Section 5, a two-step master synchronization is given to reduce the acquisition time, and its performance is analyzed either. Numerical results are presented in Section 6, and conclusions are drawn in Section 7.
2. Master Synchronization Modeland Algorithm
The master synchronization presented in this paper aims at the synchronization problem when a master sends commands or messages to tag nodes. This synchronization method is based on feedback control principles. Since the phase-locked loop is the most classical feedback control method, we analyze the master synchronization by using the similar model of phase-locked loop at first [12, 13].
Figure 2 is a block diagram of the common PLL scheme with a feedback structure. Considering a case of noiseless environment, the equivalent phase differential equation of the first-order sampling PLL is given by

where  is the equivalent function of phase detection,
is the equivalent function of phase detection,  is the feedback delay,
is the feedback delay,  is the carrier phase of received signal,
is the carrier phase of received signal,  is the local acquired phase of receiver, and
is the local acquired phase of receiver, and  is the loop gain consistent with the phase adjustment stepsize factor of the first-order PLL. In master synchronization,
is the loop gain consistent with the phase adjustment stepsize factor of the first-order PLL. In master synchronization,  is regarded as the phase of local oscillator in the tag receiver, and
is regarded as the phase of local oscillator in the tag receiver, and  as adjustable phase of transmitter. Since the proposed feedback loop bridges over the transmitter and the receiver, the delays in forward and reverse wireless link should be both considered for its performance.
as adjustable phase of transmitter. Since the proposed feedback loop bridges over the transmitter and the receiver, the delays in forward and reverse wireless link should be both considered for its performance.
Considering first-order loop model above, where there is no loop filter, the total delay in forward and reverse link is equivalent to  . Consistent with the conventional principles of PLL, the phase of signal received in tag node has a
. Consistent with the conventional principles of PLL, the phase of signal received in tag node has a  difference from its local phase at the locked status. To achieve acquisition by this loop, the signal of local oscillator in receiver is requested with a same period as the received signal. The stability and performance of synchronization is also impacted by loop gain
difference from its local phase at the locked status. To achieve acquisition by this loop, the signal of local oscillator in receiver is requested with a same period as the received signal. The stability and performance of synchronization is also impacted by loop gain  , and feedback delay
, and feedback delay  .
.
Except for the sampling feedback loop based on sinusoidal wave, the sawtooth and the pulse waveforms are generally employed as reference signals in feedback control systems. Because of the linear relation between the phase error and feedback control signal, the sawtooth reference signal is able to obtain a better stability. The phase differential equation of such a feedback loop is presented as

Defining  as the periodic narrow pulse signal with width
as the periodic narrow pulse signal with width  , the sampling phase detection in tag receiver is obtained by pulse coherent detection. Comparing the correlation output with the preset threshold, we can determined whether the receiver has achieved synchronization or not. In order to simplify the analysis, we adopt a rectangle pulse given by
, the sampling phase detection in tag receiver is obtained by pulse coherent detection. Comparing the correlation output with the preset threshold, we can determined whether the receiver has achieved synchronization or not. In order to simplify the analysis, we adopt a rectangle pulse given by

where  is the pulse width. Thus, the equivalent phase differential equation of the feedback synchronization loop is given by
is the pulse width. Thus, the equivalent phase differential equation of the feedback synchronization loop is given by

When the correlation output exceeds the threshold, that is to say, the phase difference between received pulse and local phase in tag node is less than a pulse width, it can be determined that the acquisition is achieved. The phase detector is a gated on-off control function. The advantage of pulse synchronization feedback loop is obvious that the tag receiver transmits no feedback when correlation output is lower than threshold, that is  , and the master adjusts its phase by itself until it receives a feedback from tag receiver. That means tag receiver will not consume energy until the condition of synchronization acquisition is satisfied. Assisted by the multiple access code, the above scheme can not only achieve synchronization acquisition, but also activate a mass of tag receivers. It is intelligible that such a master synchronization has the advantages of low-power consumption and low complexity for the tag nodes in WSNs.
, and the master adjusts its phase by itself until it receives a feedback from tag receiver. That means tag receiver will not consume energy until the condition of synchronization acquisition is satisfied. Assisted by the multiple access code, the above scheme can not only achieve synchronization acquisition, but also activate a mass of tag receivers. It is intelligible that such a master synchronization has the advantages of low-power consumption and low complexity for the tag nodes in WSNs.
3. Stability Analysis
The master synchronization separates feedback control into two parts in transmitter and receiver. However, the stability of this feedback loop is affected by adding the long delay caused by the forward and reverse wireless link. Since the phase detector is often a nonlinear feedback unit with respect to the phase, it is hard to obtain a closed-form solution of determining stability or convergence under most situations.
The stability analysis of sampling phase-locked loop (SPLL) is given in [12, 13]. At first, the transfer function of SPLL should be obtained. According to (1), the Z-transform of the transfer function near the locked status that  can be derived:
can be derived:

The stability criteria for a feedback system is whether or not all the poles of the transfer function (or the roots of characteristic equation) lie in the unit circle. Once there is a pole outside the unit circle, the system is unstable. According to this principle, the stability boundary of the stepsize, that is, the adjustment gain  , is derived as
, is derived as

Obviously, the analysis of sawtooth-waveform-based system is similar with that of SPLL based. Because of linear output of the sampling phase detector  , its stability analysis result is closer to above theoretical value.
, its stability analysis result is closer to above theoretical value.
Since the pulse-based master synchronization adopts decision feedback, its stability analysis involves the control theory. In the control theory, it is called as an act-and-wait type time-periodic control, where a more comprehensive analysis is presented in [14–16]. The stability boundaries for the given three master synchronization are analyzed and simulated. Suppose the signal period is  , Figure 3 shows the stability margin with respect to the feedback loop gain
, Figure 3 shows the stability margin with respect to the feedback loop gain  and the delay
and the delay  . The stable region is on the left-hand side of figure relative to the thick curve, and the right-hand side is unstable. The stability boundaries of sawtooth-waveform- and sine-waveform-based master synchronization is close to the result of analysis in (6). When the feedback delay increases, the gain
. The stable region is on the left-hand side of figure relative to the thick curve, and the right-hand side is unstable. The stability boundaries of sawtooth-waveform- and sine-waveform-based master synchronization is close to the result of analysis in (6). When the feedback delay increases, the gain  should be decreased to ensure the stability of the feedback loop. If we consider the fading of wireless links in practice, the above result limits the range of the stepsize of phase adjustment in master node.
should be decreased to ensure the stability of the feedback loop. If we consider the fading of wireless links in practice, the above result limits the range of the stepsize of phase adjustment in master node.
The stability of pulse-based master synchronization is not only a function of loop gain  and feedback delay
and feedback delay  , but also the pulse width
, but also the pulse width  . To ensure the necessary acquisition precision, the width of the narrow pulse is set as
. To ensure the necessary acquisition precision, the width of the narrow pulse is set as  in analysis. According to the stability boundaries chart shown in Figure 3, the available margin of pulse master synchronization is much smaller than the other two types given above. Furthermore, Figure 4 illustrates the stability boundary with pulse width
in analysis. According to the stability boundaries chart shown in Figure 3, the available margin of pulse master synchronization is much smaller than the other two types given above. Furthermore, Figure 4 illustrates the stability boundary with pulse width  and loop gain
and loop gain  at
at  . When the pulse width is greater than a threshold, the system is always stable at a comprehensible
. When the pulse width is greater than a threshold, the system is always stable at a comprehensible  .
.
4. Applying Master Synchronization in WSNs
In order to reduce the power consumption of tag nodes, unnecessary feedback must be avoided in the master synchronization. In our proposed scheme, the acknowledgements are just transmitted at the time of satisfying the timing condition in tag receiver. That means a little energy may be cost in feedback. Therefore, it may be very beneficial to low-power working of the tag receiver. However, there are some problems to be solved in the following aspects. First, the stability of the mast synchronization is influenced by the long-delay feedback. Second, the precise synchronization required a small loop gain  which leads to large acquisition time. Third, the detection probability
which leads to large acquisition time. Third, the detection probability  and the false-alarm probability
and the false-alarm probability  caused by the wireless channel increase the average acquisition time and the transmitted energy in tag nodes obviously.
caused by the wireless channel increase the average acquisition time and the transmitted energy in tag nodes obviously.
4.1. Stable Acquisition
The intuitive reason of instability in master synchronization is that the feedback control error departs from the right phase in master node due to the large delay. A simple method to ensure the stability of pulse master synchronization is by modulating the phase information into corresponding phase signal transmitted to tag node. After the tag node acquires this phase signal, that is, correlation exceeds the preset threshold, the carried phase information is fed back by the acknowledgement. Accepting the acknowledgement, the master node adjusts the VCO or NCO according to the phase information. Consequently, the phase of received signal would just agree with the phase of local oscillator in tag receiver.
Figure 5 shows the signaling procedure mentioned above. When there is burst data to the tag node  , the master node transmits the synchronization signaling to the tag receiver and adjusts its phase step by step. When the tag receiver
, the master node transmits the synchronization signaling to the tag receiver and adjusts its phase step by step. When the tag receiver  acquires the signal at the phase
acquires the signal at the phase  , it demodulates the carried phase information and feeds it back to the master node by acknowledgement, or directly relays it back. Acknowledged by the tag node
, it demodulates the carried phase information and feeds it back to the master node by acknowledgement, or directly relays it back. Acknowledged by the tag node  , the master adjusts transmitter to the phase
, the master adjusts transmitter to the phase  , and starts sending data.
, and starts sending data.
Considering the multiple access problem in the WSN with a mass of nodes, we can substitute the simple pulse signal with a pseudorandom multiaccess coded PCM signal. Adopting the multi-access code with a certain length not only resolves the problems of multi-access communication to tag nodes, but also reduces the synchronization false alarm probability  . Figure 6 shows the block diagram of symbol-level master synchronization system. Here, the integral window
. Figure 6 shows the block diagram of symbol-level master synchronization system. Here, the integral window  of the tag correlator, is the length of multi-access code, not the pulse width.
of the tag correlator, is the length of multi-access code, not the pulse width.
4.2. Performance Analysis
The master synchronization is similar to the process of single dwell serial acquisition. In the traditional serial acquisition, the receiver needs to adjust the phase of local correlation template until it reaches consensus with that of the received signal. Different from serial acquisition, the adjustment of signal phase is transferred to the master transmitter in WSNs and the feedback has to be sent in wireless link. If the master synchronization requires a precision in the interval of  , the searching stepsize requires to be less than
, the searching stepsize requires to be less than  . Noting that the synchronization accuracy of ultra-wideband impulse is affected by many factors, such as the searching stepsize, impulse waveform, multipath environment, modulation scheme, and decision threshold [17, 18], it is out of the range of this paper and should be further studied for the proposed scheme.
. Noting that the synchronization accuracy of ultra-wideband impulse is affected by many factors, such as the searching stepsize, impulse waveform, multipath environment, modulation scheme, and decision threshold [17, 18], it is out of the range of this paper and should be further studied for the proposed scheme.
The serial searching period, which is also the maximum searching time without considering the missed detections, is  . The initial phase difference between the local phase of the tag receiver and that of the received signal corresponds to the uniform distribution. The time delay in feedback is denoted by
. The initial phase difference between the local phase of the tag receiver and that of the received signal corresponds to the uniform distribution. The time delay in feedback is denoted by  . In an ideal communication channel, apparently, the average acquisition time of the pulse master synchronization is
. In an ideal communication channel, apparently, the average acquisition time of the pulse master synchronization is

In the case that there are error decisions of acquisition, the master synchronization has a problem of mistaking non-synchronous status as synchronous status, which is defined by false alarm probability. On the contrary, the synchronous status may be detected as non-synchronous status either. Its probability is  , where
, where  is the detection probability. By repeatedly sending
is the detection probability. By repeatedly sending  -periodic synchronization signaling for confirmation, the false alarm is eliminated with a penalty of
-periodic synchronization signaling for confirmation, the false alarm is eliminated with a penalty of  delay. If the synchronization is not confirmed, the serial search continues. Missing synchronization, the feedback system has to achieve acquisition in the next period of the serial search, which results in a long acquisition time.
delay. If the synchronization is not confirmed, the serial search continues. Missing synchronization, the feedback system has to achieve acquisition in the next period of the serial search, which results in a long acquisition time.
In the communication of wireless sensor networks, the acknowledgement has to be delivered through wireless links. Not only should the false alarms and missed detections caused by the wireless fading and noise be considered, but also the feedback delay and the loss of acknowledgement in wireless channel may increase the acquisition time. Suppose  is the probability that the acknowledgement is correctly received, the Markov chain acquisition model can be applied to analyze the average acquisition time [19]. Using standard signal flow graph reduction techniques, one arrives at the desired result, namely,
is the probability that the acknowledgement is correctly received, the Markov chain acquisition model can be applied to analyze the average acquisition time [19]. Using standard signal flow graph reduction techniques, one arrives at the desired result, namely,

If in addition  , the variance of acquisition time is obtained as
, the variance of acquisition time is obtained as

In the ideal case, the pulse master synchronization needs only the acquisition and confirmation acknowledgements. However, the false alarms may cause unnecessary feedbacks transmitted by the tag node. Apparently, the power consumption will increase with the increasing feedback times in the acquisition. Therefore, the average feedback time is an important parameter in the proposed master synchronization. Similar to the analysis above, it can be analyzed by the probability methods. The average initial clock difference is  . When there is no missed detection and no lost synchronization acknowledgement in the first search period, the times of extra feedbacks are
. When there is no missed detection and no lost synchronization acknowledgement in the first search period, the times of extra feedbacks are  . When there is a missed detection or a lost acknowledgement in the first search period and no false in the second period, the extra feedbacks are
. When there is a missed detection or a lost acknowledgement in the first search period and no false in the second period, the extra feedbacks are  . When the acquisition is arrived in the third search period, the extra feedbacks are
. When the acquisition is arrived in the third search period, the extra feedbacks are  . The average feedback times can be deduced by analogy
. The average feedback times can be deduced by analogy

Disregarding the lose of the synchronization acknowledgement, the average feedback times is inversely proportional to the detection probability  and directly proportional to the false alarm probability
and directly proportional to the false alarm probability  . However, with the common threshold decision in acquisition, the relationship between
. However, with the common threshold decision in acquisition, the relationship between  and
and  is given by [19]
is given by [19]

where  is the signal bandwidth,
is the signal bandwidth,  is the signal-to-noise ratio (SNR), and
is the signal-to-noise ratio (SNR), and  is the inverse function of
is the inverse function of  function. According to the equation, the false alarm probability decreases when the detection probability decreases. Obviously, a minimum feedback times can be obtained with the small detection and false alarm probabilities. Unfortunately, the small detection probability would also greatly extend the acquisition time.
function. According to the equation, the false alarm probability decreases when the detection probability decreases. Obviously, a minimum feedback times can be obtained with the small detection and false alarm probabilities. Unfortunately, the small detection probability would also greatly extend the acquisition time.
Under a certain  and channel environment, it can be seen that there is a minimum average acquisition time according to (8) and (11). Suppose that
and channel environment, it can be seen that there is a minimum average acquisition time according to (8) and (11). Suppose that  ,
,  ,
,  , and an additive-white-Gaussian-noise (AWGN) channel with
, and an additive-white-Gaussian-noise (AWGN) channel with  , the analysis results are illustrated in Figure 7. At
, the analysis results are illustrated in Figure 7. At  , there exists a minimum value of average acquisition time. It is worth noting that this minimum point varies at different SNR and
, there exists a minimum value of average acquisition time. It is worth noting that this minimum point varies at different SNR and  .
.
5. Two-Step Acquisition
The pulse master synchronization has the advantages that single feedback and low complexity in tag receiver are required under ideal condition. At the same time, a main problem of master acquisition is that a highly precise synchronization with narrow pulse signal costs long time to be achieved. Take the ultra-wideband pulse for example, the longest acquisition time is  . In this view, we propose a two-step acquisition scheme to limit acquisition time and feedback times in master synchronization, while guaranteeing the precision.
. In this view, we propose a two-step acquisition scheme to limit acquisition time and feedback times in master synchronization, while guaranteeing the precision.
The two-step acquisition consists of two master acquisition processes. The main difference between the two steps is the widths of synchronization pulses transmitted by master node. The two processes are as follows.
(1)In the first step of acquisition, the master node transmits periodic synchronization pulses with width  that
that  to the tag node. The stepsize of phase adjustment in master is
to the tag node. The stepsize of phase adjustment in master is  . We also call it as search stepsize. The correlation pulse generated in the tag receiver keeps constant width
. We also call it as search stepsize. The correlation pulse generated in the tag receiver keeps constant width  . The search process is the same as the pulse master synchronization described in Section 2. Thus, the search period in the first step is
. The search process is the same as the pulse master synchronization described in Section 2. Thus, the search period in the first step is  , and acquisition precision is
, and acquisition precision is  .
.
-
(2)
The width of synchronization pulse sent by the master node changes to
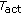 in the second step. In a phase range acquired by first step, master node adjusts the phase of transmitting pulses by stepsize
in the second step. In a phase range acquired by first step, master node adjusts the phase of transmitting pulses by stepsize  . With the same acquisition described in Section 2, the search period in this stage is
. With the same acquisition described in Section 2, the search period in this stage is 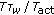 .
.
Although the two-step acquisition scheme may increase the feedback times and power consumption, the cost is acceptable and the reduction of acquisition time is remarkable. Suppose that the detection probability  and false alarm probability
and false alarm probability  remain unchanged in the two steps of master synchronization, the acquisition time can be further derived by the fact of the same processes in the two search steps. The two-step acquisition time is given by (12).
remain unchanged in the two steps of master synchronization, the acquisition time can be further derived by the fact of the same processes in the two search steps. The two-step acquisition time is given by (12).
In the proposed two-step acquisition, the optimum pulse width transmitted by master node in the first step

is chosen by minimizing acquisition time. From (12), we obtain


where  denotes the integer ceiling operation and
denotes the integer ceiling operation and  is the average acquisition time function of
is the average acquisition time function of  . From the cost function (13), we can illustrate the optimum curve in Figure 8. The optimum pulse width corresponding to the minimum point of
. From the cost function (13), we can illustrate the optimum curve in Figure 8. The optimum pulse width corresponding to the minimum point of  is derived that
is derived that  . Since
. Since  is an integer multiple of
is an integer multiple of  and
and  has a less increment at
has a less increment at  , we have
, we have  .
.
The average feedback times of the two-step master acquisition is an accumulation with feedback times of the two search stages. Therefore, it can be obtained that

In exactly the same manner as described above, the optimum  according to (14) also satisfies the request by the minimum feedback times.
according to (14) also satisfies the request by the minimum feedback times.
By assigning  as in (14), Figure 7 also illustrates the two-step acquisition curves of average acquisition time and average feedback times. The average acquisition time of the proposed two-step scheme is much less than that of the single-step master acquisition with a same
as in (14), Figure 7 also illustrates the two-step acquisition curves of average acquisition time and average feedback times. The average acquisition time of the proposed two-step scheme is much less than that of the single-step master acquisition with a same  . At the same time, the difference of feedback times between the single-step and two-step master acquisitions is small at the region of short acquisition time. With a big
. At the same time, the difference of feedback times between the single-step and two-step master acquisitions is small at the region of short acquisition time. With a big  , the feedback times of two-step search is even less than that of the single-step acquisition.
, the feedback times of two-step search is even less than that of the single-step acquisition.
6. Simulations
In this section, the feasibility of the proposed master synchronization and the correctness of the analysis are demonstrated by simulations. We implement point-to-point simulations because the master synchronization is a physical-layer method in wireless sensor networks. The research of the proposed master synchronization mainly focuses on three contents including the stability, the acquisition time, and the feedback time (power consumption). The stability margins of master synchronization is obtained and analyzed. To break the stability constraint of the pulse master synchronization, the phase information is proposed to be carried by acknowledgement. The simulations of the acquisition time and the feedback time to verify the analysis are mentioned in the following part.
The simulation condition includes the period of pulses denoted by  , the pulse width
, the pulse width  , and the feedback delay
, and the feedback delay  . Suppose that the false alarm probability in tag receivers and the feedback detection probability are
. Suppose that the false alarm probability in tag receivers and the feedback detection probability are  and
and  , respectively. In the two-step scheme, the optimum width of transmitted pulses in first step is
, respectively. In the two-step scheme, the optimum width of transmitted pulses in first step is  according to (14). That determines the phase search range of the second step.
according to (14). That determines the phase search range of the second step.
Figure 9 is the comparison among the simulations of acquisition time and the analysis for single-step and two-step pulse master synchronization. Shown in the figure, the acquisition time reduces when the detection probability  of the tag node increases at a certain
of the tag node increases at a certain  . The proposed two-step acquisition time is much less than that of the single-step scheme as expected. The consistency between the analytical curve and the results of simulations proves the correctness of the analysis. The feedback times with respect to
. The proposed two-step acquisition time is much less than that of the single-step scheme as expected. The consistency between the analytical curve and the results of simulations proves the correctness of the analysis. The feedback times with respect to  is shown in Figure 10. Since that feedback consumes the energy of tag node, fewer feedback times are able to maintain longer lifecycle in the proposed master synchronization. Shown as the curves, the two-step master acquisition requires much fewer feedback times than single-step acquisition. Besides, this conclusion is consistent with the theoretical results shown in the figure. Thus, the analysis illustrated in Figure 7 is credible. The limited feedbacks of two-step scheme illuminates the feasibility of proposed pulse master synchronization in WSNs.
is shown in Figure 10. Since that feedback consumes the energy of tag node, fewer feedback times are able to maintain longer lifecycle in the proposed master synchronization. Shown as the curves, the two-step master acquisition requires much fewer feedback times than single-step acquisition. Besides, this conclusion is consistent with the theoretical results shown in the figure. Thus, the analysis illustrated in Figure 7 is credible. The limited feedbacks of two-step scheme illuminates the feasibility of proposed pulse master synchronization in WSNs.
Due to the limited transmitting power by a tag node, the wireless fading, and the interference in reverse link, the feedback signal may be lost more probable by master node than that in master-to-tag link. Therefore, the low  is nonnegligible according to the acquisition time analyzed in (8) and (12). Supposing an ideal environment in master-to-tag link, that is,
is nonnegligible according to the acquisition time analyzed in (8) and (12). Supposing an ideal environment in master-to-tag link, that is,  and
and  , and the loop gain
, and the loop gain  . We simulate and compare the acquisition times
. We simulate and compare the acquisition times  with different
with different  . The simulation and analysis results from the single-step and two-step acquisitions are depicted in Figure 11. Sawtooth-waveform- and sine-waveform- (SPLL-) based master synchronization are also compared in the figure for their high convergence rate. From the results illustrated, the two-step pulse master synchronization still has a much faster acquisition than the single-step scheme. The theoretical curves are consistent with the simulations. At a low
. The simulation and analysis results from the single-step and two-step acquisitions are depicted in Figure 11. Sawtooth-waveform- and sine-waveform- (SPLL-) based master synchronization are also compared in the figure for their high convergence rate. From the results illustrated, the two-step pulse master synchronization still has a much faster acquisition than the single-step scheme. The theoretical curves are consistent with the simulations. At a low  , the acquisition time of the two-step pulse scheme is even shorter than those of the sawtooth waveform and sine waveform-based acquisitions. Only in high
, the acquisition time of the two-step pulse scheme is even shorter than those of the sawtooth waveform and sine waveform-based acquisitions. Only in high  , the former has a little longer acquisition time, but much shorter than others as expected. Considering that the feedbacks are required in every signal period by the sawtooth and sine synchronization, their power consumptions by the tag node are much larger than that of the pulse master synchronization.
, the former has a little longer acquisition time, but much shorter than others as expected. Considering that the feedbacks are required in every signal period by the sawtooth and sine synchronization, their power consumptions by the tag node are much larger than that of the pulse master synchronization.
7. Conclusion
Even though the proposed synchronization may be unsuitable for the conventional transceivers due to its slow acquisition and feedback requirement, it significantly reduce the complexity and power consumption in physical-layer communication of tag nodes. Aiming at the case that low burst data rate and existing master node in cluster of a WSN, the pulse master acquisition presents feasibility and a longer communication distance than the RFID-based techniques. From the analysis and simulation results, the two-step pulse scheme has a better performance for the acquisition time and power consumption in tag node. It is an interesting method in physical-layer synchronization of wireless sensor networks. And what is more, the synchronization tracking is another problem to be solved even in low burst-rate communications. Fast estimation algorithms may be implemented to further reduce the complexity and power consumption with this distributed synchronization architecture.
References
Yick J, Mukherjee B, Ghosal D: Wireless sensor network survey. Computer Networks 2008, 52(12):2292-2330. 10.1016/j.comnet.2008.04.002
Kohvakka M, Suhonen J, Hämäläinen TD, Hännikäinen M: Energy-efficient reservation-based medium access control protocol for wireless sensor networks. EURASIP Journal on Wireless Communications and Networking 2010, 2010:-22.
Zhao L, Guo L, Cong L, Zhang H: An energy-efficient MAC protocol for WSNs: game-theoretic constraint optimization with multiple objectives. Wireless Sensor Networks 2009, 1: 358-364. 10.4236/wsn.2009.14044
Pantazis NA, Vergados DD: A survey on power control issues in wireless sensor networks. IEEE Communications Surveys & Tutorials 2007, 9(4):86-107.
Akan OB, Isik MT, Baykal B: Wireless passive sensor networks. IEEE Communications Magazine 2009, 47(8):92-99.
Isik MT, Akan OB: PADRE: modulated backscattering-based PAssive data REtrieval in wireless sensor networks. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '09), April 2009 1-6.
Mengali U, D'Andrea A: Synchronisation Techniques for Digital Receivers. Kluwer Academic, Boston, Mass, USA; 1997.
Ammer J, Rabaey J: Low power synchronization for wireless sensor network modems. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '05), March 2005 670-675.
McEwen NC, et al.: A low-power, digital transceiver for wireless sensor networks. Proceedings of the 2nd IEE/EURASIP Conference on DSPenabled Radio, September 2005, London, UK 18-23.
Xu H, Yang L: Ultra-wideband technology: yesterday, today, and tomorrow. Proceedings of the IEEE Radio and Wireless Symposium (RWS '08), January 2008 715-718.
Demirkol I, Ersoy C, Onur E: Wake-up receivers for wireless sensor networks: benefits and challenges. IEEE Wireless Communications 2009, 16(4):88-96.
Gardner FM: Phase-Locked Techniques. 3rd edition. John Wiley & Sons, New York, NY, USA; 2005.
Zheng J: Principles and Applications of Phase-Locked Loop. 2nd edition. People's Posts and Telecommunications Press, China; 1984.
Insperger T, Wahi P, Colombo A, Stépán G, Di Bernardo M, Hogan SJ: Full characterization of act-and-wait control for first-order unstable lag processes. Journal of Vibration and Control 2010, 16(7-8):1209-1233. 10.1177/1077546309341135
Insperger T: Act-and-wait concept for continuous-time control systems with feedback delay. IEEE Transactions on Control Systems Technology 2006, 14(5):974-977.
Insperger T, Stépán G: Act-and-wait control concept for discrete-time systems with feedback delay. IET Control Theory and Applications 2007, 1(3):553-557. 10.1049/iet-cta:20060051
He N, Tepedelenlioglu C: Performance analysis of non-coherent UWB receivers at different synchronization levels. IEEE Transactions on Wireless Communications 2006, 5(6):1266-1273.
Xu H, Yang L: Timing with dirty templates for low-resolution digital UWB receivers. IEEE Transactions on Wireless Communications 2008, 7(1):54-59.
Simon MK, Omura JK, Scholtz RA, Levitt BK: Spread Spectrum Communications Handbook. McGraw-Hill, New York, NY, USA; 1994.
Acknowledgments
This work was supported by National Natural Science Foundation (project 60962001, project 61071088) of China, and Guangxi Nature Science Foundation (project 0731026) in China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zheng, L., Ge, W. & Qiu, H. Master Synchronization in Physical-Layer Communications of Wireless Sensor Networks. J Wireless Com Network 2010, 382570 (2011). https://doi.org/10.1155/2010/382570
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/382570




 .
.


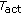 in the second step. In a phase range acquired by first step, master node adjusts the phase of transmitting pulses by stepsize
in the second step. In a phase range acquired by first step, master node adjusts the phase of transmitting pulses by stepsize  . With the same acquisition described in Section 2, the search period in this stage is
. With the same acquisition described in Section 2, the search period in this stage is 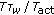 .
.
 as a function of
as a function of  .
.
 in forward channel.
in forward channel.

 in forward channel.
in forward channel.

 in reverse link.
in reverse link.