- Research Article
- Open access
- Published:
A Novel Method for Improving Fairness over Multiaccess Channels
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 395763 (2010)
Abstract
It is known that the orthogonal multiple access (OMA) guarantees for homogeneous networks, where all users have almost the same received power, a higher degree of fairness (in rate) than that provided by successive interference cancellation (SIC). The situation changes in heterogeneous networks, where the received powers are very disparate, and SIC becomes superior to OMA. In this paper, we propose to partition the network into (almost) homogeneous subnetworks such that the users within each subnetwork employ OMA, and SIC is utilized across subnetworks. The newly proposed scheme is equivalent to partition the users into ordered groups. The main contribution is a practical algorithm for finding the ordered partition that maximizes the minimum rate. We also give a geometrical interpretation for the rate-vector yield by our algorithm. Experimental results show that the proposed strategy leads to a good tradeoff between fairness and the asymptotic multiuser efficiency.
1. Introduction and Preliminaries
Rate allocation in multiuser communication systems is an important task which should consider simultaneously the fairness and the spectral efficiency. This paper is focused on fairness of multiple-access (MA) schemes working under maximum spectral efficiency evaluated in terms of sum rate. The state of art is the method recently introduced in [1]. However, the main drawback of this algorithm is a significant decrease of the asymptotic multiuser efficiency (AME) [2–4]. We propose a new strategy that combines the strengths of two different MA schemes such that to guarantee a good tradeoff between fairness and AME.
1.1. System Model
Consider a single-antenna Gaussian MA channel with  users transmitting to the base station (BS). The system model can be written as [1, Example 1]
users transmitting to the base station (BS). The system model can be written as [1, Example 1]

where  is the received signal,
is the received signal,  models the fading channel from the
models the fading channel from the  th user to the BS, and
th user to the BS, and  is the symbol transmitted by the
is the symbol transmitted by the  th user. The additive noise
th user. The additive noise  is assumed to be white circular Gaussian with variance
is assumed to be white circular Gaussian with variance  for each real and imaginary component. Under the hypothesis that the transmitting powers of the users are constrained such that
for each real and imaginary component. Under the hypothesis that the transmitting powers of the users are constrained such that  ,
,  , we have
, we have


where  is the rate of the
is the rate of the  th user and
th user and  . The interested reader can find in [5, Chapter 6] a comprehensive discussion on the significance of (2) and (3). The following two methods can be applied to achieve equality in (2):
. The interested reader can find in [5, Chapter 6] a comprehensive discussion on the significance of (2) and (3). The following two methods can be applied to achieve equality in (2):
-
(1)
OMA: orthogonal multiple-access with degrees of freedom (DOF) allocated proportional to users' received powers;
-
(2)
SIC: successive interference cancellation.
We refer to [5, Chapter 6] for more details on OMA, SIC, and the definition of DOF.
It is also pointed out in [5] that, whenever the received power is almost the same for all users, that is, the network is homogeneous, OMA guarantees a higher degree of fairness (in rate) than that provided by SIC. The situation changes in heterogeneous networks, where the received powers are very disparate: if the decoding is performed in the decreasing order of the received powers, then SIC becomes superior to OMA. However, the SIC systems have drawbacks which do not exist for OMA. Because the signals received from the users are estimated and subtracted from the composite signal one after the other, the inaccurate estimation for the current user makes the next users decoded unreliably. This deficiency becomes more severe when the number of users increases. In fact, it is known that SIC works well only when a specific disparity of the powers is enforced (see, e.g., [6, 7] and Chapter 5 in [8]).
To measure the fairness and the performance, we employ two criteria that have been used frequently in the past. For instance, it is customary to evaluate the fairness with the following max-min criterion: a rate vector is called max-min fair (MMF) if and only if an increase in the rate of one user results in the decrease in the rate of one or more users who have smaller or equal rates [1, 9]. Additionally, we consider the AME. Note that AME quantifies the loss of performance when the interferer users are present and the background noise vanishes [2–4]. More precisely, AME is a measure of degradation in bit error rate because of the presence of multiple-access interference in a white Gaussian channel.
1.2. Basics of the New Method
Our approach exploits the beneficial aspects of both OMA and SIC. Because we do not aim to improve fairness by sacrificing the throughput, we assume that (2) is satisfied with equality.
The key idea is to partition the network into (almost) homogeneous subnetworks such that the users within each subnetwork employ OMA, and SIC is utilized across subnetworks. Since OMA is applied to (almost) homogeneous subnetworks, it is likely that the degree of fairness is not deteriorated. The application of SIC to subnetworks and not directly to users allows to decrease the number of decoding stages, which potentially improves the performance.
Given that the number of users is  , we assume that the number of subnetworks is
, we assume that the number of subnetworks is  . The newly proposed scheme is equivalent to partition the
. The newly proposed scheme is equivalent to partition the  users into
users into  ordered groups. Note that the order matters because it corresponds to the order in which the groups are decoded. Remark for
ordered groups. Note that the order matters because it corresponds to the order in which the groups are decoded. Remark for  that the grouping method is the same with OMA. Moreover, the grouping method is identical with SIC for
that the grouping method is the same with OMA. Moreover, the grouping method is identical with SIC for  . Similarly to conventional SIC, the max-min rate achieved in this case depends on the order in which the groups are decoded. We consider the family of all ordered partitions of the
. Similarly to conventional SIC, the max-min rate achieved in this case depends on the order in which the groups are decoded. We consider the family of all ordered partitions of the  users into
users into  nonempty groups. Then we pick up the ordered partition for which the minimum rate is maximized, and we name it
nonempty groups. Then we pick up the ordered partition for which the minimum rate is maximized, and we name it  (basic ordered grouping of
(basic ordered grouping of users into
users into groups). Conventionally,
groups). Conventionally,  coincides with OMA, and we write
coincides with OMA, and we write  . Obviously,
. Obviously,  .
.
Furthermore, one can select again from  the ordered partition which maximizes the minimum rate. The new selection is dubbed
the ordered partition which maximizes the minimum rate. The new selection is dubbed  . Remark that the rate vector which corresponds to
. Remark that the rate vector which corresponds to  is not necessarily the same with the max-min fair rate vector that was defined in Section 1.1. However,
is not necessarily the same with the max-min fair rate vector that was defined in Section 1.1. However,  is guaranteed to be max-min fair among all possible user groupings for which the sum capacity is achieved.
is guaranteed to be max-min fair among all possible user groupings for which the sum capacity is achieved.
We investigate how the fairness can be evaluated for OMA, SIC, and BORG. In this context we demonstrate for  a fundamental property, which allows us to introduce a low-complexity search method for choosing
a fundamental property, which allows us to introduce a low-complexity search method for choosing  from all ordered partitions of
from all ordered partitions of  users into
users into  groups.
groups.
We give also a geometrical interpretation for the rate-vector yield by our algorithm. More exactly, we point out the connections between the outcome of the proposed method and the polymatroid structure of the capacity region as it is used in multiuser information theory [1, 10, 11].
During recent years, several works have exploited the polymatroid structure for optimizing the fairness in multiaccess systems [1, 12]. The main idea is based on the fact that particular points within the sum capacity facet of the polymatroid can be achieved by successive decoding and time sharing. Then, the effort is focused on finding the time-sharing coefficients which give the fairest point. For the sake of comparison, we pick up the method from [1], which is based on time sharing, and we name it TS. It is clear that TS cannot be inferior to our method if the criterion is the fairness in the multiaccess system. But since TS is a linear combination of successive decoders with different decoding orders, it suffers from the same deficiencies like the ones mentioned earlier for SIC.
The rest of the paper is organized as follows. Section 2 contains the main contribution, where we show how a low-complexity search algorithm can be devised to find the ordered partition which maximizes the minimum rate. The geometrical interpretation of the result is included. In Section 3, the newly proposed method is compared with OMA, SIC, and TS in a simulation study which comprises four different network models. In all cases, the new strategy provides the best tradeoff between fairness and AME.
2. Fairness
2.1. Formulas for OMA and SIC
It is well known for OMA method that the degree of fairness among users is lowered when their received powers are very disparate [5]. This drawback can be easily understood from the formula which gives the rate of the  th user [5, Chapter 6]:
th user [5, Chapter 6]:

where  . From the identity above, we have
. From the identity above, we have  for all
for all  , where
, where  . Hence, the rates are as disparate as the received powers are, which leads to unfair rates in heterogeneous networks. For example, if
. Hence, the rates are as disparate as the received powers are, which leads to unfair rates in heterogeneous networks. For example, if  , then the minimum rate
, then the minimum rate  tends also to zero.
tends also to zero.
When SIC is applied, the fairest rate vector is obtained by decoding the users in the decreasing order of their received powers [1]. Consequently, the rate of the  th user has the expression [5]
th user has the expression [5]

With the convention that  denotes the number of users whose received power is smaller than
denotes the number of users whose received power is smaller than  , the following inequality is readily obtained:
, the following inequality is readily obtained:  . It shows that, as long as
. It shows that, as long as  is not much smaller than
is not much smaller than  , then
, then  does not tend to zero when
does not tend to zero when  . Hence, it is likely that SIC has a higher degree of fairness than OMA when the received powers are very disparate.
. Hence, it is likely that SIC has a higher degree of fairness than OMA when the received powers are very disparate.
2.2. BORG and Its Low-Complexity Implementation
Consider the following scenario:  users are divided into nonempty groups
users are divided into nonempty groups  . For an arbitrary
. For an arbitrary  , we use
, we use  to denote the sum of the received powers for the users that belong to the group
to denote the sum of the received powers for the users that belong to the group  . It is clear that
. It is clear that  and
and  .
.
To be in line with the previous literature, we adopt the convention that the order of the groups in the successive decoding is  , where
, where  is a permutation of the set
is a permutation of the set  . For simplicity, we denote by ORG the ordered partition which is given by the sequence of subsets
. For simplicity, we denote by ORG the ordered partition which is given by the sequence of subsets  . By combining the results from (4) and (5), we get the rate of the
. By combining the results from (4) and (5), we get the rate of the  th user
th user

For writing the equation above more compactly, we have assumed that the  th user belongs to the group
th user belongs to the group  .
.
The naive approach for finding  when
when  is to search among all ordered partitions of the
is to search among all ordered partitions of the  users into
users into  groups, then to compute the minimum rate in each case, and eventually to pick up the partition which maximizes the minimum rate. This leads to a huge computational burden and makes the method unpractical. We show below how the number of ordered partitions to be considered can be reduced significantly.
groups, then to compute the minimum rate in each case, and eventually to pick up the partition which maximizes the minimum rate. This leads to a huge computational burden and makes the method unpractical. We show below how the number of ordered partitions to be considered can be reduced significantly.
We need some more definitions. Let  be a vector of strictly positive integers whose sum is equal to
be a vector of strictly positive integers whose sum is equal to  . The ordered partition
. The ordered partition  is of type
is of type  if for all
if for all  the cardinality of
the cardinality of  is
is  . Given
. Given  and
and  , we denote by
, we denote by  the family of all ordered partitions of type
the family of all ordered partitions of type  . It is important to remark that for all partitions within this family we have that (i) the order of the subsets is the same and is given by the reverse order of the permutation
. It is important to remark that for all partitions within this family we have that (i) the order of the subsets is the same and is given by the reverse order of the permutation  ; (ii) the cardinality of the
; (ii) the cardinality of the  th subset is the same, namely,
th subset is the same, namely,  .
.
Additionally, for two arbitrary subsets  and
and  , we write
, we write  if the received powers of all users within
if the received powers of all users within  are greater than those of the users within
are greater than those of the users within  . When the condition is not satisfied, we write
. When the condition is not satisfied, we write  .
.
Theorem 1.
Let  . For fixed
. For fixed  and
and  , consider all ordered partitions that belong to
, consider all ordered partitions that belong to  . In this class, the ordered partition that maximizes the minimum rate for a given set
. In this class, the ordered partition that maximizes the minimum rate for a given set  is the one which satisfies the condition
is the one which satisfies the condition

The proof is deferred to the appendix.
Now we are prepared to formalize the result which shows the decrease in computational complexity.
Corollary 2.
For  , we have the following.
, we have the following.
-
(i)
To select
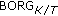 by brute-force search amounts to compute the minimum rate for
by brute-force search amounts to compute the minimum rate for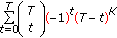 (8)
(8)different ordered partitions.
-
(ii)
Theorem 1 allows to reduce to
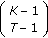 (9)
(9)the number of ordered partitions that are considered in the evaluation process.
Proof.
-
(i)
In the case of brute-force search, it is easy to note that the rate vector must be computed for all ordered partitions of the
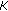 users into
users into 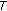 nonempty subsets. Hence, the number of partitions to be considered equals
nonempty subsets. Hence, the number of partitions to be considered equals 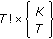 , where
, where 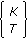 is the Stirling number of the second kind, and its closed-form expression is given by
is the Stirling number of the second kind, and its closed-form expression is given by 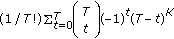 [13]. This proves the result in (8).
[13]. This proves the result in (8). -
(ii)
From Theorem 1, we know that for all permutations
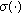 there exists a single ordered partition of type
there exists a single ordered partition of type  that must be considered, namely, the one which satisfies (7). For finding
that must be considered, namely, the one which satisfies (7). For finding 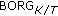 , we must evaluate a single rate vector for each vector type. This implies that the number of partitions which are investigated equals the number of ways that the integer
, we must evaluate a single rate vector for each vector type. This implies that the number of partitions which are investigated equals the number of ways that the integer 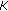 can be written as a sum of
can be written as a sum of 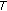 strictly positive integers. According to [13], this number is given by (9).
strictly positive integers. According to [13], this number is given by (9).
To gain more insight, let us suppose that  users and
users and  groups. Corollary 2 points out that the number of competing partitions for the selection of
groups. Corollary 2 points out that the number of competing partitions for the selection of  can be reduced from 55980 to 36, which implies a significant decrease of the computational complexity. However, by using the result from (9), it is easy to verify that the number of rate vectors which must be evaluated for selecting
can be reduced from 55980 to 36, which implies a significant decrease of the computational complexity. However, by using the result from (9), it is easy to verify that the number of rate vectors which must be evaluated for selecting  is
is  .
.
2.3. Geometrical Interpretation
We resort to the polymatroid structure of the capacity region [1, 10, 11], to give a new interpretation of BORG. The object of interest is the polyhedron defined by

where the set function  is a mapping for all subsets of
is a mapping for all subsets of  to the positive real numbers. For the problem that we study, it is convenient to choose
to the positive real numbers. For the problem that we study, it is convenient to choose

Then, it is a simple exercise to verify that the set function defined in (11) satisfies (i)  (normalized); (ii)
(normalized); (ii)  if
if  (increasing); (iii)
(increasing); (iii)  (submodular). Thus, according to the definition from [14],
(submodular). Thus, according to the definition from [14],  is a polymatroid. Moreover, the hyperplane given by
is a polymatroid. Moreover, the hyperplane given by  is the sum-capacity facet of
is the sum-capacity facet of  [1]. We analyze next the points within the sum-capacity facet that correspond to OMA, SIC, and ORG. To get the point which corresponds to OMA, we rewrite the identity in (4) as
[1]. We analyze next the points within the sum-capacity facet that correspond to OMA, SIC, and ORG. To get the point which corresponds to OMA, we rewrite the identity in (4) as

For SIC, we take  to be an arbitrary permutation of the set
to be an arbitrary permutation of the set  , and we assume that the users are decoded in the reverse order of
, and we assume that the users are decoded in the reverse order of  . Therefore, the rate of the
. Therefore, the rate of the  th user is
th user is

The formula in (5) is easily obtained from (13) for the particular case when  is chosen such that
is chosen such that  . More importantly, (13) shows that, for each permutation
. More importantly, (13) shows that, for each permutation  ,
,  is a corner point of the polymatroid
is a corner point of the polymatroid  (see [10, 14] for more details).
(see [10, 14] for more details).
With the convention that the  th user belongs to
th user belongs to  , where
, where  is a permutation of
is a permutation of  , the expression in (6) is equivalent to
, the expression in (6) is equivalent to

Observe that, in general, the rate vector given by (14) does not correspond to a corner of  .
.
To enhance intuition, we depict in Figure 1(a) the polymatroid  for
for  when the two users have equal received powers (
when the two users have equal received powers ( ). Similarly, in Figure 1(b), it is shown
). Similarly, in Figure 1(b), it is shown  for the case when
for the case when  . In both cases, the sum-capacity facet is the segment whose endpoints are the corners
. In both cases, the sum-capacity facet is the segment whose endpoints are the corners  and
and  .
.
Because  , the number of groups for the BORG method can be either
, the number of groups for the BORG method can be either  or
or  . Thus, we are interested in the points within the sum-capacity facet that correspond to
. Thus, we are interested in the points within the sum-capacity facet that correspond to  and
and  , respectively. As we already know,
, respectively. As we already know,  is the same with OMA, and
is the same with OMA, and  coincides with SIC, where
coincides with SIC, where  with
with  . Consequently,
. Consequently,  is chosen by selecting between OMA and
is chosen by selecting between OMA and  the one which maximizes the minimum rate. For completeness, we consider also the point TS that corresponds to the degree of fairness provided by the method from [1], which finds optimum weights for the time sharing between
the one which maximizes the minimum rate. For completeness, we consider also the point TS that corresponds to the degree of fairness provided by the method from [1], which finds optimum weights for the time sharing between  and
and  .
.
Note in Figure 1(a) that the OMA point is the fairest on the sum-capacity facet. In this case, it is obvious that also  corresponds to the fairest point. Moreover, the method from [1] gives the same weight to both
corresponds to the fairest point. Moreover, the method from [1] gives the same weight to both  and
and  , which makes the TS point coincide with the OMA point. The situation changes in Figure 1(b), where
, which makes the TS point coincide with the OMA point. The situation changes in Figure 1(b), where  and
and  . This leads to
. This leads to  . Remark also in Figure 1(b) that, even if
. Remark also in Figure 1(b) that, even if  is the best among OMA and SIC, the minimum of its rate vector is slightly smaller than the minimum rate for TS.
is the best among OMA and SIC, the minimum of its rate vector is slightly smaller than the minimum rate for TS.
Next, we demonstrate by simulations the capabilities of various MA schemes.
3. Simulation Results
3.1. Evaluation Criteria
As it was already mentioned, the fairest rate vector is obtained by applying TS or, equivalently, by time sharing between the corner points of the sum-capacity facet. To find the fairest rate vector and also the optimal time-sharing coefficients, we have implemented in Matlab the algorithms III and IV from [1].
Let us assume that the number of runs for a specified set of experimental conditions is  . An arbitrary method, say MET, is compared with TS by computing the Normalized Min-Rate with formula
. An arbitrary method, say MET, is compared with TS by computing the Normalized Min-Rate with formula

where  is the minimum of the rate-vector yield by MET in the
is the minimum of the rate-vector yield by MET in the  th run. Similarly,
th run. Similarly,  is the minimum of the TS rate vector in the
is the minimum of the TS rate vector in the  th run.
th run.
The second figure of merit that we consider for evaluating the MA schemes is the AME, which is generally denoted by  . AME takes values in the interval
. AME takes values in the interval  and attains its maximum when OMA is utilized. Therefore, we have
and attains its maximum when OMA is utilized. Therefore, we have  for all
for all  (see Chapter 5 in [3]).
(see Chapter 5 in [3]).
To keep SIC inline with what we have in the corner points of the sum-capacity facet, we assume that all cancellations are perfect, and what is forwarded to the next decoder has no residual error from the already decoded users [15]. Furthermore, suppose that in each step a matched filter is used as decoder such that for computing the AME of the  th user we can apply the formula (3.123) from [3]:
th user we can apply the formula (3.123) from [3]:

Note that the expression above takes into consideration the system model from (1). Additionally, it is assumed that the users are decoded in the decreasing order of the received powers. We emphasize that we do not use formula (7.31) from [3] because it was derived for SIC with residual errors propagated from previous steps.
It is clear that, for  , we do not need to compute AME for all ordered partitions of the
, we do not need to compute AME for all ordered partitions of the  users into
users into  subgroups but only for
subgroups but only for  . With slight abuse of notation, we assume that
. With slight abuse of notation, we assume that  is the ordered partition
is the ordered partition  , where
, where  .
.
More importantly, the BORG method combines the features of both OMA and SIC such that (i) the users within each group are orthogonal one to each other; (ii) the groups share the entire channel. It is evident that only the second characteristic determines the degradation of the AME. Hence, the expression of AME can be derived straightforwardly from (16) by taking into account that, when decoding the group  , the role of interferer is played by the groups
, the role of interferer is played by the groups  . If the
. If the  th user belongs to the group
th user belongs to the group  , then we have
, then we have

Remark in the expression above that AME is the same for all the users within the  -group.
-group.
It is worth mentioning here that  does not necessarily coincide with the grouping that maximizes the AME. For example, if the received powers are
does not necessarily coincide with the grouping that maximizes the AME. For example, if the received powers are  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  , then the optimum AME is produced by the ordered partition
, then the optimum AME is produced by the ordered partition  , where
, where  ,
,  , and
, and  . The inequality
. The inequality  implies
implies  , which shows clearly that
, which shows clearly that  cannot be the ordered partition
cannot be the ordered partition  .
.
We conclude the short discussion on the second figure of merit, by noticing that, whenever an experiment is repeated  times, we calculate for each method MET the Average AME
times, we calculate for each method MET the Average AME

where  is the AME for the
is the AME for the  th user in the
th user in the  th run.
th run.
In the examples outlined below, the Normalized Min-Rate and the Average AME are employed to compare the performance of the following MA schemes: TS,  ,
,  ,
,  ,
,  , and
, and  . In our settings, the number of users is
. In our settings, the number of users is  , and the number of runs for each set of experimental conditions is
, and the number of runs for each set of experimental conditions is  . Additionally, the power of the Gaussian noise is taken to be one (
. Additionally, the power of the Gaussian noise is taken to be one ( ). Four different network models are considered.
). Four different network models are considered.
3.2. Examples
Model I
To quantify the degree of network heterogeneity, we consider the ratio between the power of the strongest user and the power of the weakest user:  . The larger is
. The larger is  , the more heterogeneous is the network. For a fixed value
, the more heterogeneous is the network. For a fixed value  , we take
, we take  and
and  . The powers
. The powers  are chosen to be outcomes from a uniform distribution on
are chosen to be outcomes from a uniform distribution on  , and the experiment is repeated
, and the experiment is repeated  times. This selection guarantees that the mean power
times. This selection guarantees that the mean power  is equal to 100. When
is equal to 100. When  , a single realization is considered, namely,
, a single realization is considered, namely,  .
.
We plot in Figure 2(a) the Normalized Min-Rate obtained for various MA schemes when  increases from 0 dB to 30 dB. Due to the definition in (15), the graph for TS is a straight line parallel to
increases from 0 dB to 30 dB. Due to the definition in (15), the graph for TS is a straight line parallel to  -axis. Note in the same figure that the degree of fairness is very high for OMA when
-axis. Note in the same figure that the degree of fairness is very high for OMA when  is close to 0 dB, but it decreases rapidly when the heterogeneity of the network increases. By contrast, SIC has a very low degree of fairness in homogeneous networks, but it improves with the increase of the network heterogeneity such that for
is close to 0 dB, but it decreases rapidly when the heterogeneity of the network increases. By contrast, SIC has a very low degree of fairness in homogeneous networks, but it improves with the increase of the network heterogeneity such that for  dB, SIC is clearly superior to OMA.
dB, SIC is clearly superior to OMA.
The beneficial effects of the newly proposed strategy can be observed for  , which performs as well as OMA for small
, which performs as well as OMA for small  , but surpasses both OMA and SIC for large
, but surpasses both OMA and SIC for large  . More interestingly, good results are obtained not only when searching for the optimum
. More interestingly, good results are obtained not only when searching for the optimum  , but also when the number of groups is kept fixed. Remark for the heterogeneous networks that
, but also when the number of groups is kept fixed. Remark for the heterogeneous networks that  performs very similarly with
performs very similarly with  .
.
In Figure 2(b), we show the Average AME for the six methods which are compared. As it was already pointed out previously, OMA achieves always the maximum possible AME. We can notice from Figure 2(b) that SIC and TS yield the poorest Average AME. This drawback appears for the two schemes because the firstly decoded users receive high interference, which makes their AME close to zero. It is remarkable that  and
and  have AME superior to that of SIC. Moreover, the performance of
have AME superior to that of SIC. Moreover, the performance of  approaches the Average AME of OMA when
approaches the Average AME of OMA when  increases.
increases.
Experimental results for Model I: (a) Normalized Min-Rate versus  ; (b) Average AME versus
; (b) Average AME versus  . The number of users is
. The number of users is  . Note that
. Note that  is expressed in dB, and for each
is expressed in dB, and for each  the reported results are obtained from
the reported results are obtained from  runs. The following MA methods are compared (for each method we indicate the color and the marker symbol used in plots): TS (black left-pointing triangle),
runs. The following MA methods are compared (for each method we indicate the color and the marker symbol used in plots): TS (black left-pointing triangle),  (blue asterisk),
(blue asterisk),  (magenta right-pointing triangle),
(magenta right-pointing triangle),  (green diamond),
(green diamond),  (red square), and
(red square), and  (brown circle).
(brown circle).
Model II
Let  ,
,  ,
,  , and
, and  . We simulate a network such that
. We simulate a network such that  are uniformly distributed on
are uniformly distributed on  , and
, and  are uniformly distributed on
are uniformly distributed on  . The parameter
. The parameter  controls the degree of heterogeneity of the network. When
controls the degree of heterogeneity of the network. When  , all the users belong to a single cluster, and the increase of
, all the users belong to a single cluster, and the increase of  makes the network to consist of two disjoint clusters.
makes the network to consist of two disjoint clusters.
The results plotted in Figure 3 are obtained by varying the value of  from 0 to 180. For each value of
from 0 to 180. For each value of  ,
,  different realizations of
different realizations of  are generated. In terms of fairness and AME, the performance of
are generated. In terms of fairness and AME, the performance of  is the same with that of
is the same with that of  for
for  . Remark in Figure 3(a) that the graph of
. Remark in Figure 3(a) that the graph of  coincides with that of
coincides with that of  when
when  is larger than 100. A similar fact can be also observed in Figure 3(b). So,
is larger than 100. A similar fact can be also observed in Figure 3(b). So,  automatically adapts to the topology of the network.
automatically adapts to the topology of the network.
Experimental results for Model II: (a) Normalized Min-Rate versus  ; (b) Average AME versus
; (b) Average AME versus  . Note that
. Note that  is not expressed in dB. The number of users (
is not expressed in dB. The number of users ( ), the number of runs (
), the number of runs ( ), and all graphical conventions are the same like in Figure 2.
), and all graphical conventions are the same like in Figure 2.
Model III
We consider again a network including two clusters. This time, the received powers of the users are generated as suggested in [16]. Let  such that
such that  . We take
. We take  , where
, where  if
if  and
and  if
if  . The distribution of the random variable
. The distribution of the random variable  is Chi-Square with two degrees of freedom.
is Chi-Square with two degrees of freedom.
Remark that the heterogeneity of the network is measured by the difference  , which we increase from 0 to 90. The Normalized Min-Rate and the Average AME calculated for each
, which we increase from 0 to 90. The Normalized Min-Rate and the Average AME calculated for each  based on
based on  runs are shown in Figure 4. It is easy to observe the following outcome of the experiment. Because the Chi-Square distribution has infinite support, OMA does not provide fairness in rate allocation when
runs are shown in Figure 4. It is easy to observe the following outcome of the experiment. Because the Chi-Square distribution has infinite support, OMA does not provide fairness in rate allocation when  . Due to the same reason, for all values of
. Due to the same reason, for all values of  , the degree of fairness yield by
, the degree of fairness yield by  is inferior to that of
is inferior to that of  even if, for
even if, for  , the number of groups equals the "true" number of clusters. However, when comparing the Average AME,
, the number of groups equals the "true" number of clusters. However, when comparing the Average AME,  is ranked the second after OMA which achieves the maximum possible value.
is ranked the second after OMA which achieves the maximum possible value.
Experimental results for Model III: (a) Normalized Min-Rate versus  ; (b) Average AME versus
; (b) Average AME versus  . Note that
. Note that  is not expressed in dB. The number of users (
is not expressed in dB. The number of users ( ), the number of runs (
), the number of runs ( ), and all graphical conventions are the same like in Figure 2.
), and all graphical conventions are the same like in Figure 2.
Model IV
Following the suggestion of one of the reviewers, we briefly investigate the case of  users uniformly distributed over a two-dimensional area. For the sake of concreteness, let
users uniformly distributed over a two-dimensional area. For the sake of concreteness, let  be the distances from the BS to the users. According to the large-scale model, we have
be the distances from the BS to the users. According to the large-scale model, we have  , where
, where  is the received power from the
is the received power from the  th user,
th user,  is the received power from a transmitter located at distance one from the BS,
is the received power from a transmitter located at distance one from the BS,  is the distance from the
is the distance from the  th user to the BS, and
th user to the BS, and  is the path loss exponent [17, 18].
is the path loss exponent [17, 18].
It is widely accepted that  for urban area cellular radio [18, Table 3.2]. In our settings, we choose the path loss exponent to be
for urban area cellular radio [18, Table 3.2]. In our settings, we choose the path loss exponent to be  and
and  . For two arbitrary bounds
. For two arbitrary bounds  and
and  with property
with property  , the squared distances
, the squared distances  are selected to be uniformly distributed on
are selected to be uniformly distributed on  . Hence, the mean power has the expression
. Hence, the mean power has the expression  . Let us consider various values of
. Let us consider various values of  between 1.2 and 3.0, and for each
between 1.2 and 3.0, and for each  we choose
we choose  such that
such that  . Conventionally we take
. Conventionally we take  . It is easy to verify that
. It is easy to verify that  implies
implies  , or equivalently all the users are located on a circle whose center coincides with the BS. Obviously, this corresponds to the case of a homogeneous network. In fact, for all
, or equivalently all the users are located on a circle whose center coincides with the BS. Obviously, this corresponds to the case of a homogeneous network. In fact, for all  , the quantity
, the quantity  can be used to measure the heterogeneity of the network: the bigger is
can be used to measure the heterogeneity of the network: the bigger is  , the larger is the difference
, the larger is the difference  , which makes the values of
, which makes the values of  ,
,  , more disparate.
, more disparate.
In Figure 5, we plot the Normalized Min-Rate and the Average AME. They are computed for each  based on
based on  runs, while for
runs, while for  one single realization is considered. By comparing the results within Figure 5 with those from Figure 2, we can observe that the multiaccess schemes have a similar behavior for Model IV and Model I.
one single realization is considered. By comparing the results within Figure 5 with those from Figure 2, we can observe that the multiaccess schemes have a similar behavior for Model IV and Model I.
As a final remark, we note that for all four network models, finding the partition which corresponds to  is faster than applying the TS optimization strategy. In all runs, the execution time for
is faster than applying the TS optimization strategy. In all runs, the execution time for  was at about
was at about  of the execution time for TS. When the number of users is very large, the computational complexity can be decreased by searching for
of the execution time for TS. When the number of users is very large, the computational complexity can be decreased by searching for  with a fixed
with a fixed  , instead of finding the partition
, instead of finding the partition  . We observe from the numerical examples that
. We observe from the numerical examples that  and
and  have an acceptable level of performance.
have an acceptable level of performance.
Experimental results for Model IV: (a) Normalized Min-Rate versus  ; (b) Average AME versus
; (b) Average AME versus  . Note that
. Note that  is not expressed in dB. The number of users (
is not expressed in dB. The number of users ( ), the number of runs (
), the number of runs ( ), and all graphical conventions are the same like in Figure 2.
), and all graphical conventions are the same like in Figure 2.
4. Conclusion
In this paper, we investigated how OMA and SIC can be combined to improve fairness in Gaussian wireless networks. The newly proposed method divides the network into (almost) homogeneous subnetworks such that the users within each subnetwork employ OMA, and SIC is utilized across subnetworks. Equivalently, the  users are partitioned into
users are partitioned into  ordered groups. The main theoretical result which we proved for any
ordered groups. The main theoretical result which we proved for any  shows that the ordered partition which maximizes the minimum rate can be found with a low-complexity algorithm. Moreover, it was demonstrated experimentally that the user grouping strategy guarantees a good tradeoff between fairness and the asymptotic multiuser efficiency.
shows that the ordered partition which maximizes the minimum rate can be found with a low-complexity algorithm. Moreover, it was demonstrated experimentally that the user grouping strategy guarantees a good tradeoff between fairness and the asymptotic multiuser efficiency.
References
Maddah-Ali MA, Mobasher A, Khandani AK: Fairness in multiuser systems with polymatroid capacity region. IEEE Transactions on Information Theory 2009, 55(5):2128-2138.
Verdu S: Optimum multiuser asymptotic efficiency. IEEE Transactions on Signal Processing 1986, 34: 890-897.
Verdu S: Multiuser Detection. Cambridge University Press, Cambridge, UK; 1998.
Yang B, Danilo-Lemoine F: Asymptotic multiuser efficiency of a decorrelator based successive interference cancellation DS-CDMA multiuser receiver. Proceedings of Military Communications Conference (MILCOM '06), 2006-7.
Tse D, Viswanath P: Fundamentals of Wireless Communications. Cambridge University Press, Cambridge, UK; 2005.
Viterbi AJ: Very low rate convolutional codes for maximum theoretical performance of spread-spectrum multiple-access channels. IEEE Journal on Selected Areas in Communications 1990, 8(4):641-649. 10.1109/49.54460
Warrier D, Madhow U: On the capacity of cellular CDMA with successive decoding and controlled power disparities. Proceedings of the 48th IEEE Vehicular Technology Conference (VTC '98), May 1998, Ottawa, Canada 3: 1873-1877.
Buehrer RM: Code Division Multiple Access(CDMA). Synthesis Lectures on Communications 2006, 2: 1-192.
Bertsekas DP, Gallager RG: Data Networks. Prentice-Hall, Upper Saddle River, NJ, USA; 1987.
Tse DNC, Hanly SV: Multiaccess fading channels-part I: polymatroid structure, optimal resource allocation and throughput capacities. IEEE Transactions on Information Theory 1998, 44(7):2796-2815. 10.1109/18.737513
Zhang X, Chen J, Wicker SB, Berger T: Successive coding in multiuser information theory. IEEE Transactions on Information Theory 2007, 53(6):2246-2254.
Shum KW, Sung CW: Fair rate allocation in some Gaussian multiaccess channels. Proceedings of IEEE International Symposium on Information Theory (ISIT '06), July 2006, Seattle, Wash, USA 163-167.
Flajolet P, Sedgewick R: Analytic Combinatorics. Cambridge University Press, Cambridge, UK; 2009.
Edmonds J: Submodular functions, matroids, and certain polyhedra. Proceedings of Calgary International Conference on Combinatorial Structures and Applications, 1970, Calgary, Canada 69-87.
Cover T, Thomas J: Elements of Information Theory. John Wiley & sons, New York, NY, USA; 2006.
Jagannathan K, Borst S, Whiting P, Modiano E: Scheduling of multi-antenna broadcast systems with heterogeneous users. IEEE Journal on Selected Areas in Communications 2007, 25(7):1424-1434.
Pahlavan K, Krishnamurthy P: Principles of Wireless Networks: A Unified Approach. Prentice-Hall, Upper Saddle River, NJ, USA; 2002.
Rappaport TS: Wireless Communications: Principles and Practice. Prentice-Hall, Upper Saddle River, NJ, USA; 2002.
Cloud M, Drachman B: Inequalities: With Applications to Engineering. Springer, Berlin, Germany; 1998.
Acknowledgment
This work was supported by the Academy of Finland, Project nos. 113572, 118355, 134767, and 213462.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Theorem 1
First we demonstrate two auxiliary results that are instrumental in proving Theorem 1.
Lemma 3.
-
(i)
Let
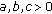 with
with 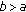 . The following inequality holds:
. The following inequality holds: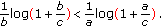 (A1)
(A1) -
(ii)
For
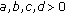 that satisfy simultaneously the conditions
that satisfy simultaneously the conditions 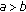 and
and 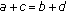 , we have
, we have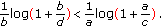 (A2)
(A2)
Proof.
For an arbitrary  , the following inequality is well known [19]:
, the following inequality is well known [19]:

where  denotes the natural logarithm. By using this result together with some elementary calculations, the inequalities in (A.1) and (A.2) are readily obtained.
denotes the natural logarithm. By using this result together with some elementary calculations, the inequalities in (A.1) and (A.2) are readily obtained.
-
(i)
Since
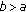 , there exists
, there exists 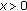 such that
such that 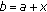 . So, the left-hand side of (A.1) can be expressed as
. So, the left-hand side of (A.1) can be expressed as 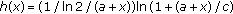 . It is easy to check that the first derivative of
. It is easy to check that the first derivative of 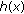 is strictly negative for all
is strictly negative for all 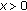 :
: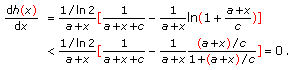 (A4)
(A4)Note that the inequality in (A.4) is a straightforward consequence of (A.3). The fact that
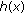 is a monotonically decreasing function proves the inequality in (A.1).
is a monotonically decreasing function proves the inequality in (A.1). -
(ii)
The inequality
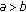 guarantees that there exists
guarantees that there exists 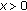 such that
such that 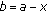 . Moreover, we have
. Moreover, we have  because
because 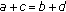 . For all
. For all 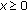 , we define
, we define 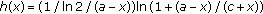 . In (A.2), the left-hand side is equal to
. In (A.2), the left-hand side is equal to  with
with 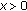 , whereas the right-hand side coincides with
, whereas the right-hand side coincides with 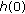 . To prove the inequality, it is enough to show that
. To prove the inequality, it is enough to show that 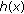 is a monotonically decreasing function or, equivalently, to verify that the first derivative of
is a monotonically decreasing function or, equivalently, to verify that the first derivative of  is strictly negative:
is strictly negative: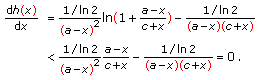 (A5)
(A5)The inequality in (A.5) was obtained by applying (A.3).
Lemma 4.
For a given set  , let
, let  and
and  be two ordered partitions from
be two ordered partitions from  . If there exists
. If there exists  such that
such that
(C1)  for all
for all  ,
,
(C2)  ,
,
(C3)  ,
,
then the minimum rate corresponding to  is not larger than the minimum rate corresponding to
is not larger than the minimum rate corresponding to  .
.
Proof.
Without loss of generality, we assume  for all
for all  . Additionally, we make the assumption that do not exist two different users for which the received powers are the same. With the exception of the symbol
. Additionally, we make the assumption that do not exist two different users for which the received powers are the same. With the exception of the symbol  , all the notations employed in connection with the ordered partition
, all the notations employed in connection with the ordered partition  are the same with those utilized for
are the same with those utilized for  .
.
The formula in (6) leads to the following expression of the minimum rate for the users within  :
:

where  is the received power of the weakest user within
is the received power of the weakest user within  and
and  . The equation above together with condition (
. The equation above together with condition ( ) lead to the identity
) lead to the identity  for all
for all  . Hence, for proving Lemma 4, it is enough to show that
. Hence, for proving Lemma 4, it is enough to show that

This inequality can be obtained from the three results which are outlined below.
Result 1.
 .
.
To verify the inequality, we note that




In (A.9), we use the fact that  , which is a consequence of (
, which is a consequence of ( )–(
)–( ). The inequality in (A.10) is derived by applying (A.2) with
). The inequality in (A.10) is derived by applying (A.2) with  ,
,  ,
,  , and
, and  .
.
Result 2.
If  , then
, then  .
.
First we consider the case  for which we get:
for which we get:





Because  contains the weakest users of
contains the weakest users of  , condition
, condition  implies
implies  , which leads to the identity in (A.13). The inequality in (A.14) can be verified by operating in (A.1) the following substitutions:
, which leads to the identity in (A.13). The inequality in (A.14) can be verified by operating in (A.1) the following substitutions:  ,
,  , and
, and  . It is easy to check that
. It is easy to check that  . Hence,
. Hence,  , which proves the inequality in (A.15).
, which proves the inequality in (A.15).
Under the hypothesis  , we have
, we have




The identity in (A.17) is the same with the one from (A.13). Then we write the inequality in (A.2) for the particular case when  ,
,  ,
,  ,
,  , and we get (A.18). Observe that
, and we get (A.18). Observe that  . Additionally,
. Additionally,  implies
implies  , which yields the inequality in (A.19).
, which yields the inequality in (A.19).
Result 3.
If  , then
, then  . Note that
. Note that





The identity in (A.22) is obtained by applying the same type of reasoning like the one used to demonstrate (A.13). Then we focus on (A.23), which is proved by choosing  ,
,  ,
,  in (A.1). Furthermore, we get (A.24) from
in (A.1). Furthermore, we get (A.24) from  .
.
The inequalities in (A.11), (A.16), (A.20), and (A.25) lead to (A.7), which concludes the proof of Lemma 4.
Now we give the proof of the theorem.
Proof of Theorem 1.
Given  , we consider the ordered partition
, we consider the ordered partition  that belongs to
that belongs to  . For an arbitrary
. For an arbitrary  , we define the following elementary transformation, which is denoted by
, we define the following elementary transformation, which is denoted by  :
:
-
(i)
if
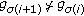 , then
, then 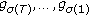 is transformed to another ordered partition from
is transformed to another ordered partition from 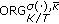 , say
, say 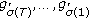 , such that the conditions (
, such that the conditions (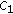 ) and (
) and (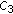 ) from Lemma 4 are satisfied;
) from Lemma 4 are satisfied; -
(ii)
otherwise, the ordered partition
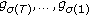 remains unchanged.
remains unchanged.
Assume that we apply  to
to  . The newly obtained ordered partition is then transformed by
. The newly obtained ordered partition is then transformed by  , and the process continues until
, and the process continues until  is applied. Due to the definition of
is applied. Due to the definition of  , the resulting ordered partition is guaranteed to contain the strongest user in the group which is decoded first. If the type-vector
, the resulting ordered partition is guaranteed to contain the strongest user in the group which is decoded first. If the type-vector  has the property that
has the property that  and the second strongest user was not yet included in the group which is decoded first, then we move it to this group by iterating again from
and the second strongest user was not yet included in the group which is decoded first, then we move it to this group by iterating again from  to
to  . When
. When  , the second strongest user can be moved to the second decoded group by using similar transformations.
, the second strongest user can be moved to the second decoded group by using similar transformations.
Based on the observations above, we remark that each ordered partition from  can be transformed, in a finite number of steps, to the unique partition from
can be transformed, in a finite number of steps, to the unique partition from  which satisfies the condition in (7). Each step consists in transforming the current ordered partition to a new one by applying
which satisfies the condition in (7). Each step consists in transforming the current ordered partition to a new one by applying  , where
, where  . We conclude the proof by mentioning that, at each step, the minimum rate increases or remains constant (see Lemma 4).
. We conclude the proof by mentioning that, at each step, the minimum rate increases or remains constant (see Lemma 4).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Razavi, S.A., Giurcăneanu, C.D. A Novel Method for Improving Fairness over Multiaccess Channels. J Wireless Com Network 2010, 395763 (2010). https://doi.org/10.1155/2010/395763
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/395763
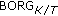 by brute-force search amounts to compute the minimum rate for
by brute-force search amounts to compute the minimum rate for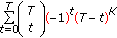
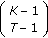
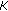 users into
users into 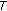 nonempty subsets. Hence, the number of partitions to be considered equals
nonempty subsets. Hence, the number of partitions to be considered equals 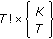 , where
, where  is the Stirling number of the second kind, and its closed-form expression is given by
is the Stirling number of the second kind, and its closed-form expression is given by 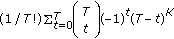 [
[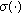 there exists a single ordered partition of type
there exists a single ordered partition of type  that must be considered, namely, the one which satisfies (7). For finding
that must be considered, namely, the one which satisfies (7). For finding 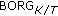 , we must evaluate a single rate vector for each vector type. This implies that the number of partitions which are investigated equals the number of ways that the integer
, we must evaluate a single rate vector for each vector type. This implies that the number of partitions which are investigated equals the number of ways that the integer 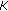 can be written as a sum of
can be written as a sum of 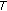 strictly positive integers. According to [
strictly positive integers. According to [
 when
when  users. The points marked on the sum-capacity facet correspond to various MA methods. Here,
users. The points marked on the sum-capacity facet correspond to various MA methods. Here,  means that user
means that user  is decoded before user
is decoded before user  . Two different cases are considered: (a) homogeneous network (
. Two different cases are considered: (a) homogeneous network ( ), (b) heterogeneous network (
), (b) heterogeneous network ( ).
).



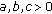 with
with 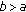 . The following inequality holds:
. The following inequality holds: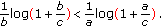
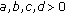 that satisfy simultaneously the conditions
that satisfy simultaneously the conditions 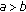 and
and 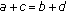 , we have
, we have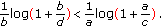
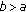 , there exists
, there exists 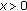 such that
such that 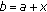 . So, the left-hand side of (A.1) can be expressed as
. So, the left-hand side of (A.1) can be expressed as 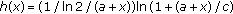 . It is easy to check that the first derivative of
. It is easy to check that the first derivative of 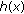 is strictly negative for all
is strictly negative for all 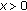 :
: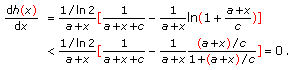
 is a monotonically decreasing function proves the inequality in (A.1).
is a monotonically decreasing function proves the inequality in (A.1). guarantees that there exists
guarantees that there exists  such that
such that 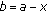 . Moreover, we have
. Moreover, we have  because
because 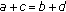 . For all
. For all 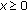 , we define
, we define 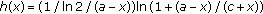 . In (A.2), the left-hand side is equal to
. In (A.2), the left-hand side is equal to  with
with 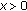 , whereas the right-hand side coincides with
, whereas the right-hand side coincides with 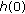 . To prove the inequality, it is enough to show that
. To prove the inequality, it is enough to show that 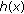 is a monotonically decreasing function or, equivalently, to verify that the first derivative of
is a monotonically decreasing function or, equivalently, to verify that the first derivative of  is strictly negative:
is strictly negative: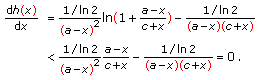
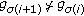 , then
, then 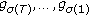 is transformed to another ordered partition from
is transformed to another ordered partition from 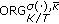 , say
, say 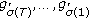 , such that the conditions (
, such that the conditions ( ) and (
) and ( ) from Lemma 4 are satisfied;
) from Lemma 4 are satisfied; remains unchanged.
remains unchanged.