- Research Article
- Open access
- Published:
Novel Precoded Relay-Assisted Algorithm for Cellular Systems
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 414657 (2010)
Abstract
Cooperative schemes are promising solutions for cellular wireless systems to improve system fairness, extend coverage and increase capacity. The use of relays is of significant interest to allow radio access in situations where a direct path is not available or has poor quality. A data precoded relay-assisted scheme is proposed for a system cooperating with 2 relays, each equipped with either a single antenna or 2-antenna array. However, because of the half-duplex constraint at the relays, relaying-assisted transmission would require the use of a higher order constellation than in the case when a continuous link is available from the BS to the UT. This would imply a penalty in the power efficiency. The simple precoding scheme proposed exploits the relation between QPSK and 16-QAM, by alternately transmitting through the 2 relays, achieving full diversity, while significantly reducing power penalty. Analysis of the pairwise error probability of the proposed algorithm with a single antenna in each relay is derived and confirmed with numerical results. We show the performance improvements of the precoded scheme, relatively to equivalent distributed SFBC scheme employing 16-QAM, for several channel quality scenarios.
1. Introduction
Multiple-input, multiple-output (MIMO) wireless communications are effective in mitigating channel fading, thus improving the cellular system capacity [1]. However, there is significant correlation between channels in some environments, and using an antenna array at the user terminal (UT) may not be feasible due to size, cost, and hardware limitations. Cooperative systems are promising solutions for wireless systems to overcome such limitations, when the direct link does not have good transmission conditions [2]. It can be achieved through cooperation of terminals (either dedicated or user terminals acting as relays), which share their antennas and thereby create a virtual antenna array (VAA) or a virtual MIMO (VMIMO) system [3]. These allow single antenna devices to benefit from spatial diversity without the need for colocated additional physical antenna arrays.
Several cooperative diversity protocols have been proposed and analysed to demonstrate the potential benefits of cooperation [4, 5]. In [6], a theoretical diversity-multiplexing trade-off study is presented regarding a cooperative system with 1 and 2 antennas in a single-relay scheme. Furthermore, in [7] the Rayleigh performance of a single-relay cooperative scenario with multiple-antenna nodes is investigated, deriving pairwise error probability (PEP) expressions. In order to get higher diversity orders, one can also consider the use of multiple-relay nodes [8]. However, increasing the number of relays reduces the bandwidth efficiency of the system, as the source uses only a fraction of the total available degrees of freedom to transmit the information.
In [9], the idea of space-time coding devised for point-to-point colocated multiple antenna systems is applied for a wireless relay network with single antenna nodes and PEP of such a scheme is derived. The authors show that in a relay network with a single source, a single destination with  single antenna relays, distributed space-time coding (DSTC) asymptotically approaches the diversity of a colocated multiple antenna system with
single antenna relays, distributed space-time coding (DSTC) asymptotically approaches the diversity of a colocated multiple antenna system with  transmit antennas and one receiving antenna. More recently, in [10], distributed orthogonal space-time block codes (DOSTBCs) achieving single-symbol decodability have been introduced for cooperative networks. The authors considered a special class of these codes (row monomial DOSTBCs), deriving upper-bounds on the maximum symbol-rate. In [11], single-symbol decodable (SSD) DSTBCs have been studied when the relay nodes are assumed to know the corresponding channel phase information. An upper bound on the symbol rate for such a set up is shown to be one half of the rate of the direct link transmission when this link is available, which is independent of the number of relays. In [12], a semi-orthogonal precoded DSTBC was proposed, wherein the source performs precoding on the information symbols before transmitting it to all the relays. Several relays are considered all equipped with a single antenna. A systematic construction of these codes is presented for more than 3 relays and the constructed codes are shown to have higher rates than those of DOSTBCs. Although achieving full diversity, these distributed orthogonal algorithms cannot achieve full spectral efficiency, since they use 2 phases for transmission. For this reason, these cooperative systems achieve half of the bandwidth efficiency of the equivalent non-cooperative systems.
transmit antennas and one receiving antenna. More recently, in [10], distributed orthogonal space-time block codes (DOSTBCs) achieving single-symbol decodability have been introduced for cooperative networks. The authors considered a special class of these codes (row monomial DOSTBCs), deriving upper-bounds on the maximum symbol-rate. In [11], single-symbol decodable (SSD) DSTBCs have been studied when the relay nodes are assumed to know the corresponding channel phase information. An upper bound on the symbol rate for such a set up is shown to be one half of the rate of the direct link transmission when this link is available, which is independent of the number of relays. In [12], a semi-orthogonal precoded DSTBC was proposed, wherein the source performs precoding on the information symbols before transmitting it to all the relays. Several relays are considered all equipped with a single antenna. A systematic construction of these codes is presented for more than 3 relays and the constructed codes are shown to have higher rates than those of DOSTBCs. Although achieving full diversity, these distributed orthogonal algorithms cannot achieve full spectral efficiency, since they use 2 phases for transmission. For this reason, these cooperative systems achieve half of the bandwidth efficiency of the equivalent non-cooperative systems.
Other works were developed with the objective of increasing capacity or diversity order of cooperative systems, using non-orthogonal protocols for cooperative systems with 2 or more relays, as in [13, 14]. In [13] a generalised non-orthogonal amplify-and-forward protocol is proposed with a low decoder complexity, achieving better error performances than in [9], depending on the coding. In [14] coding strategies are studied for non-orthogonal cooperative channels, using one or more designed space-time precoders, in a protocol where inter-relay communication is allowed, but again having no full spectral efficiency. In these non-orthogonal algorithms, transmission via an existing direct path is required. Thus, in situations with poor direct link conditions, performance is significantly degraded and in case of outage of one relay some information can be lost.
Further along the development of cooperative systems, some relay precoder designs were also proposed, however with different goals [15, 16]. In [15], the precoder maximizes the capacity between the source and destination nodes in a non-regenerative relay system, with a single relay node, considering all the nodes with multiple antennas. In [16], MIMO relay provides robustness against imperfect channel state information (CSI), for a multipoint-to-multipoint communication through the use of a relay precoder design.
Our previous work included a distributed space-frequency block coding (SFBC) scheme, designed for orthogonal frequency-division multiplexing-based cellular systems, requiring a direct path [17]. We have thereby considered the use of an antenna array at the base station (BS) and a single antenna at both the UT and relay node (RN). We observed better performances with the cooperative systems against the non-cooperative, when one has better link quality in the first hop to the relay than the direct link. However, as the other cooperative systems recently proposed, this scheme has also half of the spectral efficiency of the respective non-cooperative system. Because of the half-duplex constraint at the relays, transmission of a data rate equivalent to that of a modulation technique with  bits per symbol in the case the direct link would be available from the BS to the UT would require the use of a constellation with
bits per symbol in the case the direct link would be available from the BS to the UT would require the use of a constellation with  bits per symbol. This would imply a penalty in the power efficiency.
bits per symbol. This would imply a penalty in the power efficiency.
The aim of this paper is to propose a novel data-precoded relay-assisted (RA) algorithm, which can achieve full spatial diversity, obtaining a coding gain in comparison with the equivalent distributed SFBCs scheme, maintaining the same spectral efficiency of the non-cooperative system. Two RNs are used for cooperation, equipped with either 1 or 2 antennas. The simple precoding scheme proposed exploits the relation between QPSK and 16-QAM, by alternately transmitting through the 2 relays, achieving full diversity, while significantly reducing power penalty. Also there is no need to transmit through the direct link, in alternative to the non-orthogonal algorithms proposed previously. This is beneficial for most scenarios, since the direct link is usually strongly affected by path loss or shadowing. In this algorithm, we perform precoding of the data symbols prior to transmission and posterior decoding at the UT by using Viterbi algorithm [18]. Analysis of the pairwise error probability of the proposed algorithm with a single antenna in each relay is derived and confirmed with numerical results.
The remainder of the paper is organized as follows: in Section 2, a general description of the system model considered is presented; we then describe the proposed algorithm and derive the main link equations as well as compare the proposed scheme with the equivalent distributed SFBC system, for both cases of 1 and 2 antennas at relays, in Section 3; also, pairwise error probability derivation and diversity analysis is made for the proposed algorithm with 1 antenna at each relay, in the same section; then, in Section 4, we present the comparison between theoretical and simulation results, and the performance of the precoded algorithm is assessed and compared with the reference cooperative and non-cooperative systems; finally, main conclusions are pointed out in Section 5.
2. System Model
The system considered consists of 1 BS, 1 UT, and 2 RNs. BS is equipped with  antennas and the UT with a single antenna, whereas RNs have
antennas and the UT with a single antenna, whereas RNs have  antennas each, with
antennas each, with  , being referred as RA
, being referred as RA  (Figure 1). As we consider error-free BS-RN channels, the number of antennas at the base station is irrelevant. However, in practical systems using multiple antennas at the BS increases the probability of finding relays providing good BS-RN quality links. Channels are modelled by Rayleigh flat-fading channels and are represented by
(Figure 1). As we consider error-free BS-RN channels, the number of antennas at the base station is irrelevant. However, in practical systems using multiple antennas at the BS increases the probability of finding relays providing good BS-RN quality links. Channels are modelled by Rayleigh flat-fading channels and are represented by  for the link formed between the
for the link formed between the  th antenna of BS and the
th antenna of BS and the  th antenna of RN
l
, and by
th antenna of RN
l
, and by  for the link between the
for the link between the  th antenna of RN
l
and UT, with
th antenna of RN
l
and UT, with  ,
,  , and
, and  .
.
The fact that we have two independent paths from the relays to the destination allows us to achieve diversity, assuming error-free links from source to relays. We consider the case that the relays are half-duplex; that is, they cannot transmit and receive at the same time. Considering the half-duplex nature, we may have several options.
The relay nodes are allowed to simultaneously transmit over the same channel by emulating a space-frequency code. Concerning this scheme with single antenna relays, RA  system, Alamouti coding can be implemented in a distributed fashion by the 2 relay nodes [19]. Assuming now a system with 2 antennas in each relay, the quasi-orthogonal SFBC (QO-SFBC) proposed in [20] can also be implemented in a distributed manner.
system, Alamouti coding can be implemented in a distributed fashion by the 2 relay nodes [19]. Assuming now a system with 2 antennas in each relay, the quasi-orthogonal SFBC (QO-SFBC) proposed in [20] can also be implemented in a distributed manner.
Another case occurs when the relays receive and transmit alternately and the source is transmitting continuously, firstly sending the information to the RN1 and then repeating it to the RN2. In this approach, diversity is achieved without need for any extra processing at the relays and using maximum ratio combining at the UT.
In the above two approaches spatial diversity can be achieved, but because of the half-duplex constraints of relays, the information has to be transmitted in half of the time that would be needed in the case of a continuous link available from the source to the destination. This means that, assuming that a modulation scheme carrying  bits per symbol could be used in the case when continuous direct link was available, one would need to switch towards a modulation carrying
bits per symbol could be used in the case when continuous direct link was available, one would need to switch towards a modulation carrying  bits per symbol (if the symbol duration was kept identical), for example, going from QPSK to 16-QAM when 2 RNs are available. As a major consequence, increasing modulation order leads to a decrease of power efficiency. However, as we will show in the next sections, the relation between 16-QAM and QPSK defines an inherent trellis structure that can be used to bring the performance closer to the one that would be obtained with the more power efficient modulation scheme.
bits per symbol (if the symbol duration was kept identical), for example, going from QPSK to 16-QAM when 2 RNs are available. As a major consequence, increasing modulation order leads to a decrease of power efficiency. However, as we will show in the next sections, the relation between 16-QAM and QPSK defines an inherent trellis structure that can be used to bring the performance closer to the one that would be obtained with the more power efficient modulation scheme.
In another manner, the relays can receive and transmit alternately, while the source is transmitting continuously, according to Figure 2, maintaining spectral efficiency and modulation as compared to the non-cooperative scheme. However, no diversity can be achieved in this case. In order to get both full spectral efficiency and diversity, we propose a novel algorithm where the data symbols are precoded, prior to the source's transmission to the RNs. The data information received and transmitted in each time slot is exemplified in Figure 2, for the case of single antenna RNs (RA Precoded  ), where
), where  is the precoded symbol in time slot
is the precoded symbol in time slot  . Precoding is chosen so that diversity can be achieved without the need of exact duplication of the signal. In this cooperative algorithm for the 2-antenna's relays scheme (RA Precoded
. Precoding is chosen so that diversity can be achieved without the need of exact duplication of the signal. In this cooperative algorithm for the 2-antenna's relays scheme (RA Precoded  ), the signals transmitted by the 2 antennas are space-frequency encoded using the Alamouti coding, as we can see in Figure 3. In this table the pair of symbols (
), the signals transmitted by the 2 antennas are space-frequency encoded using the Alamouti coding, as we can see in Figure 3. In this table the pair of symbols ( ) represents two symbols transmitted or received in adjacent subcarriers: symbol
) represents two symbols transmitted or received in adjacent subcarriers: symbol  corresponds to subcarrier
corresponds to subcarrier  and
and  to subcarrier
to subcarrier  . The superscript in signals also refers to subcarrier position. Assuming uncorrelated antenna channels, a diversity order of 4 can be achieved.
. The superscript in signals also refers to subcarrier position. Assuming uncorrelated antenna channels, a diversity order of 4 can be achieved.
The rate of the proposed scheme is  , where
, where  is the number of symbols transmitted, which is close to 1 for large values of
is the number of symbols transmitted, which is close to 1 for large values of  .
.
We further assume that each relay node is capable of deciding whether or not it has decoded correctly. If an RN decodes correctly, it will forward the BS data in the second phase; otherwise it remains idle. This can be achieved through the use of cyclic redundancy check codes. This performance can also be approximated by setting a signal-to-noise ratio (SNR) threshold at both RNs; the RN will only forward the source data if the received SNR is larger than that threshold [9].
3. Data-Precoded Algorithm
Let us assume that the source produces a sequence of symbols  , each one carrying
, each one carrying  information bits. The BS transmitter precodes successive pairs of symbols
information bits. The BS transmitter precodes successive pairs of symbols  , using a bijective function
, using a bijective function  . The precoded symbols,
. The precoded symbols,  , are alternately transmitted to the two relays, allowing that each symbol reaches the UT through two independent links. When one of the links fails, the bijectivity allows to recover the original symbols QPSK, as shown in Figure 4.
, are alternately transmitted to the two relays, allowing that each symbol reaches the UT through two independent links. When one of the links fails, the bijectivity allows to recover the original symbols QPSK, as shown in Figure 4.
In the case that original symbols are QPSK, one can use a simple precoding operation that relates QPSK and 16-QAM, obtaining the symbols transmitted by the BS given by

where  is the
is the  th QPSK symbol of the original sequence information, with unitary power;
th QPSK symbol of the original sequence information, with unitary power;  is a normalization factor, so that the average transmitted power is 1, in this case being
is a normalization factor, so that the average transmitted power is 1, in this case being  . From (1), we can easily recognize that each symbol
. From (1), we can easily recognize that each symbol  is a 16-QAM symbol. However, the receiver will interpret it as a sum of 2 QPSK symbols, allowing, because of the fact that each QPSK symbol is received through two paths, to bring the performance close to the one that would be achieved if the QPSK symbols were transmitted continuously.
is a 16-QAM symbol. However, the receiver will interpret it as a sum of 2 QPSK symbols, allowing, because of the fact that each QPSK symbol is received through two paths, to bring the performance close to the one that would be achieved if the QPSK symbols were transmitted continuously.
In the proposed precoded algorithm, while BS transmits data continually to the RNs, relays transmit and receive alternately: RN1 transmits in even time slots, or symbol duration, while RN2 receives; RN2 transmits in odd time slots, during the reception period of RN1 (Figure 2). At the UT, we use the Viterbi decoding algorithm to separate the QPSK data symbols, since it is the optimal decoding method [21]. In the following the signal expressions and methods are presented in detail, separately for each scheme.
3.1. RA Scheme with 1 Antenna at Relays
The received signals at UT, when we have a single-antenna at each relay, in time slots  and
and  , are given by
, are given by

where  represents the cooperative channel for links RN
l
represents the cooperative channel for links RN
l
 UT;
UT;  is the complex flat-fading Rayleigh channel realization for time slot
is the complex flat-fading Rayleigh channel realization for time slot  , with unit average power and
, with unit average power and  represents the long-term channel power;
represents the long-term channel power;  and
and  are the zero mean complex additive white Gaussian noise samples with variance of
are the zero mean complex additive white Gaussian noise samples with variance of  .
.
It is easy to see that the proposed scheme has a trellis structure for the transmission of the QPSK symbols  . As the code is linear, we can assume that symbol
. As the code is linear, we can assume that symbol  (algebraically as
(algebraically as  ) is transmitted. An error event can be recovered in two steps as shown in Figure 5. The distance for the path that erroneously will recover
) is transmitted. An error event can be recovered in two steps as shown in Figure 5. The distance for the path that erroneously will recover  instead of
instead of  is given by (3), where
is given by (3), where  is the distance between the QPSK symbols
is the distance between the QPSK symbols  and
and  . The minimum distance between two diverging paths is
. The minimum distance between two diverging paths is

As the error events can start at an odd or even time slot, the minimum distance is given by

where  is the minimum distance of the QPSK constellation.
is the minimum distance of the QPSK constellation.
Assuming that we use the RA scheme with Alamouti, the minimum distance of the received 16-QAM constellation is given by

Let  be the ratio between the minimum and maximum of the channel power gains, that is,
be the ratio between the minimum and maximum of the channel power gains, that is,

Then, when the channel power gains exhibit an asymmetry with ratio  , the asymptotic channel coding power gain of the proposed scheme, relative to the distributed Alamouti, is given by
, the asymptotic channel coding power gain of the proposed scheme, relative to the distributed Alamouti, is given by

Therefore, the proposed scheme asymptotically achieves the performance of QPSK, in the case of high SNR and when the channels have equal average power gain, that is, an improvement of 4 dB relatively to 16-QAM; taking  to 0, the performance will be that of distributed Alamouti, as we have only one path, reducing to a 16-QAM demodulation situation.
to 0, the performance will be that of distributed Alamouti, as we have only one path, reducing to a 16-QAM demodulation situation.
The gain as a function of the channel power gains ratio is represented in Figure 6.
The trellis code of the proposed scheme is represented in Figure 7. According to (1), we have defined four states,  ,
,  , which are basically the QPSK symbols, whereas the transmitted QPSK symbols
, which are basically the QPSK symbols, whereas the transmitted QPSK symbols  are simply the scaled bipolar versions of
are simply the scaled bipolar versions of  , so that they have the required power.
, so that they have the required power.
The weight associated with a state transition from  to
to  is defined as
is defined as  . As we have alternate transmission through RN1 and RN2, the weights depend on the instant
. As we have alternate transmission through RN1 and RN2, the weights depend on the instant  and are given by
and are given by

with  if
if  is even and
is even and  if
if  is odd;
is odd;  represents the QPSK soft-symbol associated with
represents the QPSK soft-symbol associated with  , that is,
, that is,

For each state, there are 4 branches arriving at each symbol. The Viterbi algorithm is then used to find the most probable sequence [18], with the Euclidian-squared distance given by

3.2. RA Scheme with 2 Antennas at Relays
For the case of RNs being equipped with 2 antennas ( ), the signals transmitted in each relay are encoded in space-frequency using Alamouti code. The received signals at UT, in time slot
), the signals transmitted in each relay are encoded in space-frequency using Alamouti code. The received signals at UT, in time slot  , for adjacent subcarrier
, for adjacent subcarrier  and
and  , are given by
, are given by

with  in odd time slots and
in odd time slots and  in even time slots, where
in even time slots, where  represents the complex flat-fading cooperative Rayleigh channel of the
represents the complex flat-fading cooperative Rayleigh channel of the  th antenna of RN
l
and UT, on time slot
th antenna of RN
l
and UT, on time slot  and
and  th subcarrier position. Channels are considered flat for adjacent subcarriers; that is, the subcarrier separation is significantly lower than the coherence bandwidth of the channel.
th subcarrier position. Channels are considered flat for adjacent subcarriers; that is, the subcarrier separation is significantly lower than the coherence bandwidth of the channel.
At the UT, the SFBC decoding is performed, using coefficients  , as follows:
, as follows:

The obtained decoded symbols, expressed as

are then object of Viterbi decoding used to find the most probable sequence, similarly to the previous scheme, with the corresponding trellis code weights for time slot  given by (14), and with
given by (14), and with  represented in (9):
represented in (9):

3.3. Error Probability and Diversity Gain Analysis
Let us compute the probability of an error event as shown in Figure 5, that is, assuming that the transmitted symbols correspond to the all-zero path, the probability that in decoding an incorrect path is taken at time  and remerges at time
and remerges at time  . This represents a lower bound on the actual probability of error, which is accurate for medium to high SNRs. Dropping for simplicity the subscripts
. This represents a lower bound on the actual probability of error, which is accurate for medium to high SNRs. Dropping for simplicity the subscripts  in
in  and assuming without loss of generality
and assuming without loss of generality  , the minimum distance between the two segments is given by
, the minimum distance between the two segments is given by

where  is the minimum distance for QPSK modulation.
is the minimum distance for QPSK modulation.
The PEP for general QPSK modulation and coherent detection [22], under perfect synchronization, is given by

where  is the complementary error function.
is the complementary error function.
Replacing in (16)  by the expression in (15), we obtain the conditioned error probability for
by the expression in (15), we obtain the conditioned error probability for  :
:

where  ,
,  , and
, and  . The variables
. The variables  are i.i.d. and follow an exponential distribution with means
are i.i.d. and follow an exponential distribution with means  and
and  and the respective probability density function (pdf) is
and the respective probability density function (pdf) is

For the proposed scheme we then get the unconditioned probability of error as the following expression:

which, by replacing the pdf expressions of  and
and  in (19), can be simplified to
in (19), can be simplified to

Integrating the previous equation, the final expression for PEP of the proposed scheme is extracted:

Expressing the error probability expression as a function of  , a simplified form is obtained:
, a simplified form is obtained:

Expanding this expression as a Mac-Laurin series up to order 2, (22) reduces to

where  is the remainder term of order 2 [23].
is the remainder term of order 2 [23].
For the high SNR regime, that is, for  , we obtain an approximated expression for the proposed error probability:
, we obtain an approximated expression for the proposed error probability:

Diversity order, which is an important measure that we ultimately also need to keep track of, has been defined as the absolute values of the slopes of the error probability curve plotted on a log-log scale in high SNR regime [24]. From (24) we can see that the error probability decays as  , which means that our scheme achieves diversity order of 2.
, which means that our scheme achieves diversity order of 2.
4. Numerical Results
4.1. Assumptions and Conditions
Some assumptions were considered for this work, such as perfect CSI at the relays and at the UT, the transmitted power per time slot normalized to 1, and the distance between antenna elements of each BS and RNs large enough to assume uncorrelated antenna propagation channels. The block length used in the simulations,  , is of 3600 symbols.
, is of 3600 symbols.
In order to characterize propagation aspects as a whole, including the effects of path loss, shadowing, scattering, and others, we considered different link quality combinations, quantifying it in terms of SNR, given by the ratio between the link's received power and noise power. We define different SNRs for the second-hop cooperative links: RN1 UT and RN2
UT and RN2 UT, referred to as SNRc1 and SNRc2, respectively; and for the direct link (the alternative link between the BS and the UT of the non-cooperative systems) as SNRd. For simplicity and also assuming that the relays only forward BS data if decoding is correct, we do not refer to SNR differences in the first cooperative hop.
UT, referred to as SNRc1 and SNRc2, respectively; and for the direct link (the alternative link between the BS and the UT of the non-cooperative systems) as SNRd. For simplicity and also assuming that the relays only forward BS data if decoding is correct, we do not refer to SNR differences in the first cooperative hop.
Three propagation scenarios were accounted for, differing on those links' SNRs, as shown in Figure 8. In Scenario 1 we assume that all the links have the same quality conditions, that is, SNRd = SNRc1 = SNRc2. We also include scenarios where the cooperative links, that is, RN1 UT and RN2
UT and RN2 UT, have higher quality than the direct link. The choice of these scenarios derives from the fact that, in most real situations, the cooperative link has higher transmission quality conditions than the worse alternative direct link, since selection of relay nodes takes the transmission quality of both cooperative hops into account. We then define Scenario 2 where the link between RN1 and UT has an SNR 10 dB higher than the other two links, that is,
UT, have higher quality than the direct link. The choice of these scenarios derives from the fact that, in most real situations, the cooperative link has higher transmission quality conditions than the worse alternative direct link, since selection of relay nodes takes the transmission quality of both cooperative hops into account. We then define Scenario 2 where the link between RN1 and UT has an SNR 10 dB higher than the other two links, that is,  and
and  . Scenario 3 is our best quality cooperative scenario, where the entire cooperative path has better transmission quality conditions than the direct path, that is,
. Scenario 3 is our best quality cooperative scenario, where the entire cooperative path has better transmission quality conditions than the direct path, that is,  .
.
In all considered systems, two information bits are transmitted per symbol interval, and thus all of them have the same spectral efficiency. We considered that the BS is equipped with 2 or 4 antennas for the non-cooperative systems. In systems where a space-frequency code is needed for 2 transmitting antennas, the well-known Alamouti coding is implemented [19]. In systems with 4 antennas transmitting simultaneously, we implement the QO-SFBC code proposed by Tirkkonen, Boariu, and Hottinen (TBH) in [20].
The schemes considered in our evaluations are presented next, where the former bullet includes the proposed ones and the two last ones are used as references:
-
(i)
hereby proposed scheme, with precoded QPSK and Viterbi algorithm decoding, for 2 relays with 1 and 2 antennas (RA-Precoded
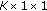 and RA-Precoded
and RA-Precoded 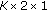 , resp.);
, resp.); -
(ii)
distributed SFBC for 2 relays with 1 and 2 antennas using 16-QAM modulation (RA Alamouti
 and RA TBH
and RA TBH  , resp.);
, resp.); -
(iii)
non-cooperative
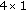 QPSK with QO-SFBC code with a continuous link available (Non-coop TBH 4×1);
QPSK with QO-SFBC code with a continuous link available (Non-coop TBH 4×1); -
(iv)
non-cooperative
 QPSK Alamouti coding with a continuous link available (Non-coop Alamouti 2×1).
QPSK Alamouti coding with a continuous link available (Non-coop Alamouti 2×1).
The results of the cooperative and non-cooperative schemes are presented in terms of bit error rate (BER) as a function of  of the direct link used for reference, where
of the direct link used for reference, where  is the received energy per bit at the UT and
is the received energy per bit at the UT and  is the bilateral noise power spectral density.
is the bilateral noise power spectral density.
4.2. PEP Analysis Validation
The analytical PEP derivation is corroborated by the BER performance obtained through Monte Carlo simulations, for the RA scheme with 1 antenna in each relay, assuming error-free transmission between BS and the RNs. Theoretical and simulated BER curves are shown in Figure 9, including the theoretical upper bound derived previously for high SNR regime. The simulation curve has approximately the same behaviour as that of the lower bound provided in (21), only differing for low SNRs. In real situations and at low SNRs, error events may correspond to paths that are not corresponding to the minimum distance, which results in the differences between the lower bound and simulated curves. These are anyhow lower than 1 dB and negligible for  dB. We can also observe that the simulated curve has the same linear decay as the asymptotic curve given by (24) for high SNRs, confirming the diversity order of 2.
dB. We can also observe that the simulated curve has the same linear decay as the asymptotic curve given by (24) for high SNRs, confirming the diversity order of 2.
4.3. Scheme with 1 Antenna in Each Relay
Cooperative and reference systems performances for the case of 1 antenna in each relay ( ) are shown in Figure 10 for Scenario 1. In this case, the reference systems presented are the non-cooperative Alamouti
) are shown in Figure 10 for Scenario 1. In this case, the reference systems presented are the non-cooperative Alamouti  and RA Alamouti
and RA Alamouti  ones.
ones.
When comparing the RA-Precoded scheme against RA Alamouti, we observe an improvement of 2.2 dB, for BER = 10−3. This, in turn, derives from the precoding used in the proposed scheme, which mitigates some of the penalty resultant from the half-duplex constraint at the relays, avoiding the use of a higher modulation order.
The proposed cooperative scheme has a penalty of about 1 dB from the best reference, that is,  QPSK Alamouti coding with a continuous link available, for the same BER conditions. It is however worthwhile to point out that in our reference we assume independence between the channels. In practice using colocated antennas inevitably leads to some correlation between the channels, in fact reducing such 1 dB of penalty, or even outperforming it in the case of high correlation.
QPSK Alamouti coding with a continuous link available, for the same BER conditions. It is however worthwhile to point out that in our reference we assume independence between the channels. In practice using colocated antennas inevitably leads to some correlation between the channels, in fact reducing such 1 dB of penalty, or even outperforming it in the case of high correlation.
In Figure 11, the performance of the same schemes in Scenario 2 is presented. In this scenario conditions the proposed precoded scheme outperform the equivalent non-cooperative system. Improvements of 4 dB are obtained in comparison with  Alamouti, for BER = 10−3. However, the RA Alamouti scheme is still worse than the non-cooperative scheme with 2 antennas in BS. The coding gain between the precoded scheme and the RA Alamouti is of 6 dB for the same BER conditions, which is higher than that in the previous scenario.
Alamouti, for BER = 10−3. However, the RA Alamouti scheme is still worse than the non-cooperative scheme with 2 antennas in BS. The coding gain between the precoded scheme and the RA Alamouti is of 6 dB for the same BER conditions, which is higher than that in the previous scenario.
In Figure 12, both links between relays and UT have SNRs 10 dB higher than the direct link (Scenario 3). In this case, the cooperative schemes have the same resulting behaviour as in the previous scenarios, although the cooperative schemes achieve better performances, as expected. The difference between non-cooperative  and the RA Precoded schemes is now more than 8 dB, for BER = 10−3 (for best visualisation purposes, the non-cooperative
and the RA Precoded schemes is now more than 8 dB, for BER = 10−3 (for best visualisation purposes, the non-cooperative  curve is not completely shown in the plot).
curve is not completely shown in the plot).
Comparing with the distributed RA Alamouti, we have an improvement of about 2.2 dB in using the proposed code, for BER = 10−3, which is the same difference than in Scenario 1.
4.4. Scheme with 2 Antennas in Each Relay
For the scheme with 2 antennas in RNs ( ), the same study was made, for the same scenarios. In this case, the chosen reference systems are the non-cooperative Alamouti
), the same study was made, for the same scenarios. In this case, the chosen reference systems are the non-cooperative Alamouti  and TBH
and TBH  systems and the RA scheme with the TBH code applied to the relay nodes.
systems and the RA scheme with the TBH code applied to the relay nodes.
In Figure 13, all the links have the same transmission conditions. In this scenario case, higher coding gains are obtained with the proposed algorithm than those in Figure 10, as expected, since we have now 2 antennas in each relay. An enhancement of about 4 dB is achieved with the RA Precoded scheme, compared with the cooperative scheme using TBH code, for BER = 10−3. Comparing with the non-cooperative systems, the proposed scheme outperforms the non-cooperative system  by about 2 dB, for the same BER. The performance of the new algorithm also overpasses the non-cooperative system
by about 2 dB, for the same BER. The performance of the new algorithm also overpasses the non-cooperative system  for high SNRs, specifically for
for high SNRs, specifically for  dB. This happens because, oppositely to the Alamouti coding, space-time codes for 4 antennas are not fully orthogonal, not achieving full diversity.
dB. This happens because, oppositely to the Alamouti coding, space-time codes for 4 antennas are not fully orthogonal, not achieving full diversity.
For Scenario 2 (results in Figure 14), as expected, the difference between the RA and non-cooperative systems is higher than that in the previous scenario. The RA-Precoded scheme has improvements of 6.2 dB and more than 15 dB in comparison with the non-cooperative  and
and  systems, respectively, for BER = 10−3. As in the RA
systems, respectively, for BER = 10−3. As in the RA  , the difference between the algorithms used in cooperative schemes is higher that than in the first scenario, differing by about 7.5 dB, for BER = 10−3.
, the difference between the algorithms used in cooperative schemes is higher that than in the first scenario, differing by about 7.5 dB, for BER = 10−3.
For Scenario 3 (in Figure 15), even higher coding gains are obtained with cooperative systems, in comparison with the non-cooperative ones. For example, the proposed algorithm in comparison with the equivalent non-cooperative  system has a gain higher than 10 dB. The difference between both RA schemes is similar to the one in Scenario 1.
system has a gain higher than 10 dB. The difference between both RA schemes is similar to the one in Scenario 1.
5. Conclusions
We proposed a novel data-precoded relay-assisted scheme, which ensures spatial diversity for cooperative systems with 2 relays, while ensuring spectral efficiency. Numerical results for the precoded scheme were computed, in scenarios with different link quality conditions, for the cases of each relay node being equipped with either 1 or 2 antennas.
The implemented precoding mitigates some of the penalty resulting from the half-duplex constraint at the relays. It brings the performance very close to the one achieved when a direct continuous link is available and SFBC coding is used at the BS. Actually, for the case of 2 antennas in each relay, the precoded scheme outperforms the non-cooperative one for high SNR regime, due to the non-orthogonality of space-frequency codes for 4 transmitting antennas. Improvements are obtained for scenarios where cooperative links have higher quality than the direct link, being more pronounced as the quality of the cooperative links increases.
We observe that, independently of the propagation scenario, both precoded schemes outperform the equivalent distributed SFBC cooperative schemes, achieving better performance due to the coding gain obtained with precoding. Even for the most probable situation of asymmetric quality conditions between cooperative links, results show that the proposed scheme is better than the reference cooperative ones. In these cases, the difference between the 2 cooperative schemes is higher. For example, it is of about 7.5 dB for BER = 10−3, considering the case of  .
.
We also observe that the extra antenna in each relay leads to a considerable improvement in the overall system performance, which is at least of 3 dB for BER = 10−3. Furthermore, the performance difference between the precoded schemes and the respective equivalent distributed SFBC schemes are higher for the case of having 2 antennas in each relay.
From the presented results, it is clear that the proposed cooperative schemes can be used to extend the coverage mainly in scenarios where the quality of the direct link is poor, as is the case of cluttered urban environments.
References
Foschini GJ, Gans MJ: On limits of wireless communications in a fading environment when using multiple antennas. Wireless Personal Communications 1998, 6(3):311-335. 10.1023/A:1008889222784
Fitzek FHP, Katz MD: Cooperation in Wireless Networks: Principles and Applications. Springer, Dordrechi, The Netherlands; 2006.
Dohler M: Virtual antenna arrays, Ph.D. thesis. King's College London, London, UK; 2003.
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part I: system description. IEEE Transactions on Communications 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Yuksel M, Erkip E: Diversity-multiplexing tradeoff in multiple-antenna relay systems. Proceedings of IEEE International Symposium on Information Theory (ISIT '06), July 2006, Seattle, Wash, USA 1154-1158.
Muhaidat H, Uysal M: Cooperative diversity with multiple-antenna nodes in fading relay channels. IEEE Transactions on Wireless Communications 2008, 7(8):3036-3046.
Liu KJR, Sadek AK, Su W, Kwasinski A: Cooperative Communications and Networking. Cambridge University Press, New York, NY, USA; 2009.
Jing Y, Hassibi B: Distributed space-time coding in wireless relay networks. IEEE Transactions on Wireless Communications 2006, 5(12):3524-3536.
Yi Z, Kim IM: Single-symbol ML decodable distributed STBCs for cooperative networks. IEEE Transactions on Information Theory 2007, 53(8):2977-2985.
Sreedhar D, Chockalingam A, Sundar Rajan B: Single-symbol ML decodable distributed STBCs for partially-coherent cooperative networks. Proceedings of IEEE International Symposium on Information Theory (ISIT '08), July 2008, Toronto, Canada 2672-2681.
Harshan J, Rajan BS: High-rate, single-symbol ML decodable precoded DSTBCs for cooperative networks. IEEE Transactions on Information Theory 2009, 55(5):2004-2015.
Rajan GS, Rajan BS: A non-orthogonal distributed space-time coded protocol—part I: signal model and design criteria. Proceedings of IEEE Information Theory Workshop (ITW '06), October 2006, Chegdu, China 385-389.
Kraidy GM, Gresset N, Boutros JJ: Coding for the non-orthogonal amplify-and-forward cooperative channel. Proceedings of the IEEE Information Theory Workshop (ITW '07), September 2007, Lake Tahoe, Calif, USA 626-631.
Tang X, Hua Y: Optimal design of non-regenerative MIMO wireless relays. IEEE Transactions on Wireless Communications 2007, 6(4):1398-1406.
Chalise BK, Vandendorpe L: MIMO relay design for multipoint-to-multipoint communications with imperfect channel state information. IEEE Transactions on Signal Processing 2009, 57(7):2785-2796.
Teodoro S, Silva A, Gil JM, Gameiro A: Virtual MIMO schemes for downlink space-frequency coding OFDM systems. Proceedings of the 20th IEEE Personal, Indoor and Mobile Radio Communications Symposium (PIMRC '09), September 2009, Tokyo, Japan
Viterbi AJ: Error bounds on convolutional codes and an asymptotically optimum decoding algorithms. IEEE Transactions on Information Theory 1967, 13(2):260-269.
Alamouti SM: A simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998, 16(8):1451-1458. 10.1109/49.730453
Tirkkonen O, Boariu A, Hottinen A: Minimal non-orthogonality rate 1 space-time block code for 3+ Tx antennas. Proceedings of the 6th IEEE International Symposium on Spread Spectrum Techniques and Applications (ISSSTA '00), September 2000, Parsippany, NJ, USA 429-432.
Teodoro S, Silva A, Gil JM, Gameiro A: Distributed space-time code using precoding for cellular systems. Proceedings of the 72nd IEEE Vehicular Technology Conference (VTC '10), September 2010, Ottawa, Canada
Goldsmith A: Wireless Communications. Cambridge University Press, New York, NY, USA; 2005.
James G, Burley D, Dyke P, Searl J, Clements D, Wright J: Modern Engineering Mathematics. 3rd edition. Prentice-Hall, Harlow, UK; 2001.
Simon MK, Alouini MS: Digital Communication over Fading Channels. 2nd edition. Wiley-Interscience, New York, NY, USA; 2005.
Acknowledgments
The work presented in this paper was supported by the European project CODIV, Portuguese projects CADWIN and AGILE, and by the Portuguese Foundation for Science and Technology (FCT) with a grant for the first author.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Teodoro, S., Silva, A., Gil, J.M. et al. Novel Precoded Relay-Assisted Algorithm for Cellular Systems. J Wireless Com Network 2010, 414657 (2010). https://doi.org/10.1155/2010/414657
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/414657

 antennas at each relay (RA
antennas at each relay (RA  ).
).
 scheme with Precoded algorithm.
scheme with Precoded algorithm.

 scheme with Precoded algorithm.
scheme with Precoded algorithm.

 .
.
 and
and  .
.
 system.
system.


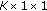 and RA-Precoded
and RA-Precoded 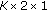 , resp.);
, resp.); and RA TBH
and RA TBH  , resp.);
, resp.);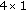 QPSK with QO-SFBC code with a continuous link available (Non-coop TBH 4×1);
QPSK with QO-SFBC code with a continuous link available (Non-coop TBH 4×1); QPSK Alamouti coding with a continuous link available (Non-coop Alamouti 2×1).
QPSK Alamouti coding with a continuous link available (Non-coop Alamouti 2×1).
 .
.




