- Research Article
- Open access
- Published:
Improved Design of Unequal Error Protection LDPC Codes
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 423989 (2010)
Abstract
We propose an improved method for designing unequal error protection (UEP) low-density parity-check (LDPC) codes. The method is based on density evolution. The degree distribution with the best UEP properties is found, under the constraint that the threshold should not exceed the threshold of a non-UEP code plus some threshold offset. For different codeword lengths and different construction algorithms, we search for good threshold offsets for the UEP code design. The choice of the threshold offset is based on the average a posteriori variable node mutual information. Simulations reveal the counter intuitive result that the short-to-medium length codes designed with a suitable threshold offset all outperform the corresponding non-UEP codes in terms of average bit-error rate. The proposed codes are also compared to other UEP-LDPC codes found in the literature.
1. Introduction
In many communication scenarios,such as wireless networks and transport of multimedia data, sufficient error protection is often a luxury. In these systems, it may be wasteful or even infeasible to provide uniform protection for all information bits. Instead, it is more efficient to protect the most important information more than the rest, by using a channel code with unequal error protection (UEP). This implies improving the performance of the more important bits by sacrificing some performance of the less important bits. This paper focuses on the design of UEP low-density parity-check (LDPC) codes with improved average bit-error rate (BER).
Several methods for designing UEP-LDPC codes have been presented, [1–11]. The irregular UEP-LDPC design schemes described in [1–7] are based on the irregularity of the variable and/or check node degree distributions. These schemes enhance the UEP properties of the code through density evolution methods. Vasic et al. proposed a class of UEP-LDPC codes based on cyclic difference families, [8]. In [9], UEP capability is achieved by a combination of two Tanner graphs of different rates. The UEP-LDPC codes presented in [10] are based on the algebraic Plotkin construction and are decoded in multiple stages. UEP may also be provided by nonbinary LDPC codes, [11].
In this work, we consider the flexible UEP-LDPC code design proposed in [3], which is based on a hierarchical optimization of the variable node degree distribution for each protection class. The algorithm maximizes the average variable node degree within one class at a time while guaranteeing a minimum variable node degree as high as possible. The optimization can be stated as a linear programming problem and can, thus, be easily solved. To keep the average performance of the UEP-LDPC code reasonably good, the search for UEP codes is limited to degree distributions whose convergence thresholds lie within a certain range  of the minimum threshold of a code with the same parameters. In the following, we call
of the minimum threshold of a code with the same parameters. In the following, we call  the threshold offset.
the threshold offset.
In the latest years, much effort has been spent on construction algorithms for short-to-medium-length LDPC codes, [12–14]. However, these algorithms rely on degree distributions optimized for infinitely long codes and focus on constructing LDPC code graphs with a small number of short cycles, thereby improving the performance in the error-floor region for short LDPC codes. In the design proposed here, we optimize the threshold offset given the construction algorithm used to specify the parity-check matrix of the code. The improved UEP codes have an average performance that is better than the corresponding non-UEP codes (with  dB), which may seem counter-intuitive. Typically, the reduced error rate of the most protected class is compensated for by an increased error rate of the other classes. Nonetheless, we show that with a good choice of the threshold offset and for several common code construction algorithms, the performance of the UEP code is significantly better than the performance of the corresponding non-UEP code. However, for long codes and a high number of decoder iterations, the UEP code design reduces the performance since the UEP codes have worse thresholds than the non-UEP codes. The performance for different values of the threshold offset is found in [3], which shows that a threshold offset of 0.1 dB is a good choice. This is true for the random construction used in [3], but it is not noted that the best choice of the threshold offset varies for different construction algorithms.
dB), which may seem counter-intuitive. Typically, the reduced error rate of the most protected class is compensated for by an increased error rate of the other classes. Nonetheless, we show that with a good choice of the threshold offset and for several common code construction algorithms, the performance of the UEP code is significantly better than the performance of the corresponding non-UEP code. However, for long codes and a high number of decoder iterations, the UEP code design reduces the performance since the UEP codes have worse thresholds than the non-UEP codes. The performance for different values of the threshold offset is found in [3], which shows that a threshold offset of 0.1 dB is a good choice. This is true for the random construction used in [3], but it is not noted that the best choice of the threshold offset varies for different construction algorithms.
Some intuition as to why UEP code design may increase the average performance can be gained by considering irregular LDPC codes, not designed for UEP, and their advantages compared to regular LDPC codes, [15]. In irregular codes, variable nodes with high degree typically correct their value quickly and these nodes can then help to correct lower degree variable nodes. Therefore, irregular graphs may lead to a wave effect, where the highest degree nodes are corrected first, then the nodes with slightly lower degree, and so on. The more irregular a code is, that is, the higher the maximum variable node degree, the faster the correction of the high degree variable nodes. There are reasons to believe that the code with the best threshold under an appropriate constraint on the allowed number of iterations, that is, a code with fast convergence, yields the best performance for finite-length codes also when the number of iterations is high, [16]. UEP code design is another way to achieve the differentiation between nodes that may lead to a wave effect and fast convergence. By allowing the code to have a worse threshold (as is the case in the UEP code design we consider), more differentiation between nodes in different classes can be achieved. It should also be noted that there is a trade-off between the maximum variable node degree and the codeword length. The maximum variable node degree should be lower for a short code to reduce the number of harmful cycles involving variable nodes of low degree. The wave effect achieved by the UEP design is accomplished without increasing the maximum variable node degree.
Let us recall some basic notation of LDPC codes. The sparse parity-check matrix  has dimension
has dimension  , where
, where  and
and  are the lengths of the information word and the codeword, respectively. We consider irregular LDPC codes with edge-based variable node and check node degree distributions defined by the polynomials [16]
are the lengths of the information word and the codeword, respectively. We consider irregular LDPC codes with edge-based variable node and check node degree distributions defined by the polynomials [16]  and
and  , where
, where  and
and  are the maximum variable and check node degree of the code, respectively. For UEP codes, we divide the variable nodes into several protection classes (
are the maximum variable and check node degree of the code, respectively. For UEP codes, we divide the variable nodes into several protection classes ( ) with degrading level of protection. The resulting variable node degree distribution is defined by the coefficients
) with degrading level of protection. The resulting variable node degree distribution is defined by the coefficients  , which denote the fractions of edges incident to degree-
, which denote the fractions of edges incident to degree- variable nodes of protection class
variable nodes of protection class  . The overall degree distribution is given by
. The overall degree distribution is given by  . In the following, we distinguish between code design, by which we mean the design of degree distributions that describe a code ensemble, and code construction, by which we mean the construction of a specific code realization (described by a parity-check matrix).
. In the following, we distinguish between code design, by which we mean the design of degree distributions that describe a code ensemble, and code construction, by which we mean the construction of a specific code realization (described by a parity-check matrix).
2. Design of Finite-Length UEP Codes
In [16], Richardson et al. state that for short LDPC codes, it is not always best to pick the degree distribution pair with the best threshold. Instead, it can be advantageous to look for the best possible threshold under an appropriate constraint on the allowed number of iterations. In this paper, we show that by searching among degree distributions designed for UEP with worse threshold than the corresponding non-UEP degree distributions, we may find degree distributions with significantly lower error rates for a finite length than the degree distributions with the best possible threshold. Well-designed UEP codes have faster convergence for all protection classes and thereby better performance for finite-length LDPC codes.
2.1. Detailed Mutual Information Evolution
An appropriate method for analyzing UEP codes is needed to choose a good value for the threshold offset  , without relying on time-consuming error rate simulations. We consider the theoretical mutual information (MI) functions, which are typically calculated from the degree distributions
, without relying on time-consuming error rate simulations. We consider the theoretical mutual information (MI) functions, which are typically calculated from the degree distributions  and
and  of a code. However, different LDPC codes with the same degree distributions can have very different UEP properties, [17]. The differences depend on how different protection classes are connected, which in turn depends on the code construction algorithm used to place the edges in the graph according to the given degree distributions. To observe the differences also between codes with equal degree distributions, a detailed computation of MI may be performed by considering the edge-based MI messages traversing the graph instead of node-based averages. This has been done for protographs in [18]. We follow the same approach, but use the parity-check matrix instead of the protograph base matrix. See [19, 20] for more details on MI analysis. The detailed MI evolution is described in detail in the appendix. In the following, we use the average a posteriori variable node MI denoted by
of a code. However, different LDPC codes with the same degree distributions can have very different UEP properties, [17]. The differences depend on how different protection classes are connected, which in turn depends on the code construction algorithm used to place the edges in the graph according to the given degree distributions. To observe the differences also between codes with equal degree distributions, a detailed computation of MI may be performed by considering the edge-based MI messages traversing the graph instead of node-based averages. This has been done for protographs in [18]. We follow the same approach, but use the parity-check matrix instead of the protograph base matrix. See [19, 20] for more details on MI analysis. The detailed MI evolution is described in detail in the appendix. In the following, we use the average a posteriori variable node MI denoted by  (calculated for each variable node in step (5) of the MI analysis in the appendix) to compare the convergence rates of different LDPC codes.
(calculated for each variable node in step (5) of the MI analysis in the appendix) to compare the convergence rates of different LDPC codes.
2.2. Design Procedure
For simplicity, a good value of  is found through an exhaustive search in a region of typical values. In the following section, we show that there is only a small difference in MI and BER for similar values of
is found through an exhaustive search in a region of typical values. In the following section, we show that there is only a small difference in MI and BER for similar values of  . It is therefore reasonable to consider only a few values of
. It is therefore reasonable to consider only a few values of  in the search and the best value among these is likely to give a BER result very close to what could be achieved by a more thorough search. For each value of
in the search and the best value among these is likely to give a BER result very close to what could be achieved by a more thorough search. For each value of  in the range of the search, three steps must be performed.
in the range of the search, three steps must be performed.
-
(1)
Design a UEP code following [3] for the
 under consideration, keeping
under consideration, keeping  ,
, 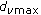 , and the proportions between the protection classes fixed. This step results in subdegree distributions for each protection class.
, and the proportions between the protection classes fixed. This step results in subdegree distributions for each protection class. -
(2)
Construct a parity-check matrix using an appropriate code construction algorithm.
-
(3)
Calculate the detailed MI evolution for a given
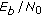 and a maximum number of decoder iterations. The code with the highest average
and a maximum number of decoder iterations. The code with the highest average  has the best overall performance within this family of codes.
has the best overall performance within this family of codes.
The value of the threshold offset  is optimized for a specific
is optimized for a specific  , which means that a code that is optimized for low
, which means that a code that is optimized for low  may perform worse for high
may perform worse for high  , and vice versa. For UEP codes, the proportions between the protection classes also affect the UEP properties of a code and thereby are also the best choice of
, and vice versa. For UEP codes, the proportions between the protection classes also affect the UEP properties of a code and thereby are also the best choice of  . In our simulations we have seen that with 20% of the information bits in the most protected class
. In our simulations we have seen that with 20% of the information bits in the most protected class  and 80% in a less protected class
and 80% in a less protected class  , good performance is achieved for rate 1/2 codes of different lengths. We therefore omit further investigations of the effect of different proportions between the protection classes.
, good performance is achieved for rate 1/2 codes of different lengths. We therefore omit further investigations of the effect of different proportions between the protection classes.
3. Design Examples
We design UEP codes of lengths  and
and  . All codes are designed using the check node degree distributions given in [16, Table II]. The performance of any UEP code is compared to the performance of a non-UEP code with the variable node degree distribution that gives the best threshold, also tabulated in [16, Table II]. A maximum of 100 decoder iterations is allowed. Except for the variable node degree distribution, the UEP codes and the corresponding non-UEP code have the same parameters. We consider only rate-1/2 LDPC codes. All UEP codes presented in this section have 20% of the information bits in
. All codes are designed using the check node degree distributions given in [16, Table II]. The performance of any UEP code is compared to the performance of a non-UEP code with the variable node degree distribution that gives the best threshold, also tabulated in [16, Table II]. A maximum of 100 decoder iterations is allowed. Except for the variable node degree distribution, the UEP codes and the corresponding non-UEP code have the same parameters. We consider only rate-1/2 LDPC codes. All UEP codes presented in this section have 20% of the information bits in  and the remaining 80% in
and the remaining 80% in  . A third protection class contains all parity bits. We first focus on design of generalized ACE constrained progressive edge-growth (PEG) codes [14] (in the following denoted by PEG-ACE codes) in Section 3.1. The random construction and the PEG construction algorithm [12] are considered in Section 3.2.
. A third protection class contains all parity bits. We first focus on design of generalized ACE constrained progressive edge-growth (PEG) codes [14] (in the following denoted by PEG-ACE codes) in Section 3.1. The random construction and the PEG construction algorithm [12] are considered in Section 3.2.
The progressive edge-growth (PEG) construction algorithm is an efficient algorithm for the construction of parity-check matrices with large girth (the length of the shortest cycle in the Tanner graph) by progressively connecting variable nodes and check nodes [12]. The approximate cycle extrinsic message degree (ACE) construction algorithm lowers the error floor by emphasizing both the number of edges from variable nodes in a cycle to nodes in the graph that are not part of the cycle as well as the length of cycles [13]. The PEG-ACE construction algorithm is a generalization of the popular PEG algorithm, that is shown to generate good LDPC codes with short and moderate block lengths having large girth [14]. If the creation of cycles cannot be avoided while adding an edge, the PEG-ACE construction algorithm chooses an edge that creates the longest possible cycle with the best possible ACE constraint.
3.1. Optimization of the Threshold Offset for PEG-ACE Codes
Six different PEG-ACE codes with varying  are designed and constructed according to the design procedure in Section 2.2 Non-UEP codes correspond to
are designed and constructed according to the design procedure in Section 2.2 Non-UEP codes correspond to  dB. These codes have length
dB. These codes have length  and allowed maximum variable node degree
and allowed maximum variable node degree  . Figure 1 shows the average a posteriori variable node MI as a function of decoder iterations at two different
. Figure 1 shows the average a posteriori variable node MI as a function of decoder iterations at two different  . For a low number of iterations, a large
. For a low number of iterations, a large  gives fast convergence for both
gives fast convergence for both  shown. This implies that for applications where only a small number of decoder iterations are allowed, a large
shown. This implies that for applications where only a small number of decoder iterations are allowed, a large  yields the best performance. The average
yields the best performance. The average  at
at  dB is maximized by
dB is maximized by  dB. After 100 iterations,
dB. After 100 iterations,  dB gives the highest average
dB gives the highest average  , but simulations show that the code with
, but simulations show that the code with  dB outperforms the code with
dB outperforms the code with  dB at low
dB at low  . At
. At  dB,
dB,  dB maximizes the average
dB maximizes the average  . The variable node degree distributions for the PEG-ACE codes with
. The variable node degree distributions for the PEG-ACE codes with  dB and
dB and  dB are tabulated in Table 1. The random code with
dB are tabulated in Table 1. The random code with  dB will be considered in Section 3.2.
dB will be considered in Section 3.2.
 dB and
dB and  dB) and the random
dB) and the random  dB code.
dB code.Average a posteriori variable node MI as a function of decoder iterations for six different PEG-ACE codes with and . For a low number of iterations, a large  gives fast convergence for both
gives fast convergence for both  shown. For a larger number of iterations (around 60),
shown. For a larger number of iterations (around 60),  dB gives the highest MI at
dB gives the highest MI at  dB, and
dB, and  dB gives the highest MI at
dB gives the highest MI at  dB.
dB.
Figure 2 shows the BER performance of the two protection classes containing information bits for  dB and
dB and  dB.The BER of the non-UEP code is shown for comparison. The figure shows that the code with
dB.The BER of the non-UEP code is shown for comparison. The figure shows that the code with  dB performs well for low
dB performs well for low  as expected, while the code with lower
as expected, while the code with lower  has less UEP capability but better average performance at high
has less UEP capability but better average performance at high  . The average BER is just slightly lower than the BER of
. The average BER is just slightly lower than the BER of  , since the average BER is calculated from the BERs of the two protection classes containing information bits, scaled with the proportions of the classes. Note that both classes of these UEP codes perform better than the comparable non-UEP code. In addition, the UEP codes offer a small difference in BER between the classes.
, since the average BER is calculated from the BERs of the two protection classes containing information bits, scaled with the proportions of the classes. Note that both classes of these UEP codes perform better than the comparable non-UEP code. In addition, the UEP codes offer a small difference in BER between the classes.
Figure 3 shows the performance of three PEG-ACE codes of length  and allowed maximum variable node degree
and allowed maximum variable node degree  . The non-UEP code is compared to a code optimized for low
. The non-UEP code is compared to a code optimized for low  (which gives
(which gives  dB) and a code optimized for high
dB) and a code optimized for high  (which gives
(which gives  dB). Both classes of the two UEP codes perform better than the non-UEP code. At
dB). Both classes of the two UEP codes perform better than the non-UEP code. At  dB, the UEP code with
dB, the UEP code with  dB has an average BER which is around one magnitude less than the non-UEP code.
dB has an average BER which is around one magnitude less than the non-UEP code.
3.2. Code Design for Other Construction Algorithms
For given degree distributions, it has been shown that the choice of the construction algorithm strongly affects the UEP properties of the LDPC code, [17]. For codes with little inherent UEP (e.g., PEG and PEG-ACE codes), the threshold offset  needs to be large to yield a code with good UEP capability. On the other hand, for codes with significant inherent UEP (e.g., randomly constructed codes), a high
needs to be large to yield a code with good UEP capability. On the other hand, for codes with significant inherent UEP (e.g., randomly constructed codes), a high  may make the less protected classes so badly protected that a wave effect does not occur. Figure 4 shows the performance of codes of length
may make the less protected classes so badly protected that a wave effect does not occur. Figure 4 shows the performance of codes of length  constructed by three different algorithms: the random construction, only avoiding cycles of length 4, the PEG construction algorithm, and the PEG-ACE construction algorithm. The figure shows the BER of the non-UEP codes as well as the BER of classes
constructed by three different algorithms: the random construction, only avoiding cycles of length 4, the PEG construction algorithm, and the PEG-ACE construction algorithm. The figure shows the BER of the non-UEP codes as well as the BER of classes  and
and  of the UEP codes. The variable node degree distributions of the UEP codes are given in Table 1. Note that the PEG
of the UEP codes. The variable node degree distributions of the UEP codes are given in Table 1. Note that the PEG  dB code has the same variable node degree distribution as the PEG-ACE
dB code has the same variable node degree distribution as the PEG-ACE  dB code.
dB code.
BER performance of non-UEP and UEP codes, constructed by three different construction algorithms. All codes have  and allowed
and allowed  . The random code has good UEP capability already for
. The random code has good UEP capability already for  dB, while the PEG code and the PEG-ACE code have less UEP capability for
dB, while the PEG code and the PEG-ACE code have less UEP capability for  dB. All UEP codes have better average performance than the corresponding non-UEP codes, except for the random code at low
dB. All UEP codes have better average performance than the corresponding non-UEP codes, except for the random code at low  .
.
For the random code, MI calculations at  dB show that the non-UEP code gives the highest MI, except at very few decoder iterations. At
dB show that the non-UEP code gives the highest MI, except at very few decoder iterations. At  dB, the code with
dB, the code with  dB is slightly better than other choices of
dB is slightly better than other choices of  after around 50 iterations. Thereby it can be assumed that the non-UEP random code will perform better at low
after around 50 iterations. Thereby it can be assumed that the non-UEP random code will perform better at low  , and the UEP random code with
, and the UEP random code with  dB will perform better at high
dB will perform better at high  . This is confirmed by the results shown in Figure 4. For the PEG and PEG-ACE code, the threshold offset
. This is confirmed by the results shown in Figure 4. For the PEG and PEG-ACE code, the threshold offset  dB used to design the codes gives the maximum MI at
dB used to design the codes gives the maximum MI at  dB. For both codes,
dB. For both codes,  dB gives higher MI at
dB gives higher MI at  dB, but for the PEG code there is only a slight difference in MI between these two values of
dB, but for the PEG code there is only a slight difference in MI between these two values of  .
.
The figure shows that both the PEG and the PEG-ACE UEP codes have significantly better performance than the corresponding non-UEP codes at low  . Remember that the PEG-ACE code with
. Remember that the PEG-ACE code with  dB performs better for high
dB performs better for high  . The PEG and PEG-ACE construction algorithms result in codes with little inherent UEP and the UEP capabilities gained by the relatively high
. The PEG and PEG-ACE construction algorithms result in codes with little inherent UEP and the UEP capabilities gained by the relatively high  give faster convergence of the codes. However, the random UEP code has only a slightly lower average BER than the non-UEP code at high
give faster convergence of the codes. However, the random UEP code has only a slightly lower average BER than the non-UEP code at high  . Note that the average performance of random codes with
. Note that the average performance of random codes with  dB is worse than for the non-UEP code. That is, for the random code with much inherent UEP there is not as much to gain by the UEP code design as for the PEG and the PEG-ACE codes, which have little inherent UEP.
dB is worse than for the non-UEP code. That is, for the random code with much inherent UEP there is not as much to gain by the UEP code design as for the PEG and the PEG-ACE codes, which have little inherent UEP.
These results show as expected that a PEG or PEG-ACE code should typically be chosen instead of a random code, even if the application benefits from UEP. For a large range of  , the most protected class of the PEG and PEG-ACE code has only slightly worse performance than the random code, while the average BER is much higher for the random code. This paper shows that we can improve both the average BER performance and the UEP capability by optimizing the threshold offset.
, the most protected class of the PEG and PEG-ACE code has only slightly worse performance than the random code, while the average BER is much higher for the random code. This paper shows that we can improve both the average BER performance and the UEP capability by optimizing the threshold offset.
3.3. Comparison to Other UEP-LDPC Codes
UEP-LDPC codes of similar length and rate as the codes presented here can be found in [6, 7]. Ma and Kwak [6] propose a partially regular code design, where all variable nodes in one protection class have the same degree. Good variable node degrees for each class are found through density evolution using the Gaussian approximation. Figures 5 and 6 show the performance of the code designed by Ma and Kwak together with the performance of two PEG-ACE codes (also shown in Figure 2). All these codes have  and
and  . The code designed by Ma and Kwak has 12.5% of the information bits in
. The code designed by Ma and Kwak has 12.5% of the information bits in  and 87.5% in
and 87.5% in  , compared to the codes proposed in this paper where 20% of the information bits belong to
, compared to the codes proposed in this paper where 20% of the information bits belong to  . Note that Ma and Kwak [6] present the performance after only 10 decoder iterations, so in Figure 5 we compare their code to the PEG-ACE codes after 10 iterations. Figure 6 demonstrates the performance of the same codes after 100 iterations. The performance of the Ma and Kwak code for 10 iterations is taken directly from [6]. To find the performance after 100 iterations, we have run simulations with a code constructed according to the specifications given in [6]. It has been verified that our simulations give the same result as shown in [6] after 10 iterations.
. Note that Ma and Kwak [6] present the performance after only 10 decoder iterations, so in Figure 5 we compare their code to the PEG-ACE codes after 10 iterations. Figure 6 demonstrates the performance of the same codes after 100 iterations. The performance of the Ma and Kwak code for 10 iterations is taken directly from [6]. To find the performance after 100 iterations, we have run simulations with a code constructed according to the specifications given in [6]. It has been verified that our simulations give the same result as shown in [6] after 10 iterations.
BER performance of the PEG-ACE  dB code and the code designed by Ma and Kwak [6] after 10 decoder iterations. Both codes have
dB code and the code designed by Ma and Kwak [6] after 10 decoder iterations. Both codes have  and
and  .
.
BER performance of two PEG-ACE codes and the code designed by Ma and Kwak [6] after 100 decoder iterations. Both codes have  and
and  . The PEG-ACE
. The PEG-ACE  dB code performs slightly better than the code designed by Ma and Kwak for both classes. The PEG-ACE
dB code performs slightly better than the code designed by Ma and Kwak for both classes. The PEG-ACE  dB code performs much better than the Ma and Kwak code for low
dB code performs much better than the Ma and Kwak code for low  , but
, but  has slightly higher BER at high
has slightly higher BER at high  .
.
Figure 5 shows that after only 10 decoder iterations, the PEG-ACE  dB code performs best at low
dB code performs best at low  . This is in accordance with Figure 1, which demonstrates that the code with the highest
. This is in accordance with Figure 1, which demonstrates that the code with the highest  has the best average MI when the number of decoder iterations is low. However, at high
has the best average MI when the number of decoder iterations is low. However, at high  , the code proposed by Ma and Kwak has a lower average BER (
, the code proposed by Ma and Kwak has a lower average BER ( performs better). The PEG-ACE
performs better). The PEG-ACE  dB code performs almost the same as the Ma and Kwak code, except at high
dB code performs almost the same as the Ma and Kwak code, except at high  , where
, where  of the PEG-ACE code has worse performance.
of the PEG-ACE code has worse performance.
After 100 decoder iterations, see Figure 6, the PEG-ACE  dB code performs well at low
dB code performs well at low  compared to the code designed by Ma and Kwak. Up to
compared to the code designed by Ma and Kwak. Up to  dB, there is a gain of around 0.13 dB for
dB, there is a gain of around 0.13 dB for  and around 0.1 dB for
and around 0.1 dB for  for the different BERs. At
for the different BERs. At  dB, the Ma and Kwak code performs slightly better than the PEG-ACE
dB, the Ma and Kwak code performs slightly better than the PEG-ACE  dB code. The PEG-ACE
dB code. The PEG-ACE  dB code has a little bit lower BERs than the Ma and Kwak code at all
dB code has a little bit lower BERs than the Ma and Kwak code at all  .
.
Note that there is a significant difference in BER between  and
and  after 10 iterations, while the difference is much smaller after 100 iterations. This is typical for codes constructed using the PEG or PEG-ACE algorithm [17]. However, if 100 iterations are allowed, both classes have a lower BER than the most protected class have after only 10 iterations. Thus, if a reasonably high number of iterations can be allowed in terms of time and complexity, it is better to run many iterations even if the difference in error protection between the classes is reduced.
after 10 iterations, while the difference is much smaller after 100 iterations. This is typical for codes constructed using the PEG or PEG-ACE algorithm [17]. However, if 100 iterations are allowed, both classes have a lower BER than the most protected class have after only 10 iterations. Thus, if a reasonably high number of iterations can be allowed in terms of time and complexity, it is better to run many iterations even if the difference in error protection between the classes is reduced.
Yang et al. [7] present simulation results for an irregular UEP-LDPC code of length  and
and  , which may be compared to the PEG-ACE codes proposed here with
, which may be compared to the PEG-ACE codes proposed here with  and
and  . Figure 7 shows the performance of these codes. Note that Yang et al. divide the information bits into three different protection classes, 1485 bits in
. Figure 7 shows the performance of these codes. Note that Yang et al. divide the information bits into three different protection classes, 1485 bits in  , 307 bits in
, 307 bits in  , and 3208 bits in
, and 3208 bits in  . The PEG-ACE
. The PEG-ACE  dB code performs best for high
dB code performs best for high  . At
. At  dB,
dB,  of the PEG-ACE
of the PEG-ACE  dB code has a lower BER than
dB code has a lower BER than  of the code designed by Yang et al. At low
of the code designed by Yang et al. At low  , the PEG-ACE
, the PEG-ACE  dB code has similar performance as the code designed by Yang et al. The PEG-ACE
dB code has similar performance as the code designed by Yang et al. The PEG-ACE  dB code has very good performance at low
dB code has very good performance at low  , and at
, and at  up to 0.7 dB the average BER is lower than the BER of the most protected class in the code designed by Yang et al.
up to 0.7 dB the average BER is lower than the BER of the most protected class in the code designed by Yang et al.
BER performance of two PEG-ACE codes with and and the code designed by Yang et al . [7]with  and
and  .
.
4. Conclusions
We have proposed an improved design algorithm for UEP-LDPC codes, resulting in codes with reduced average BER. The algorithm searches for good threshold offsets for the UEP design, given different codeword lengths and different construction algorithms. The choice of the threshold offset is based on the average a posteriori variable node MI of the codes. Simulations show that the codes designed with a suitable threshold offset all outperform the corresponding non-UEP codes in terms of average BER. We show that the average BER is reduced by up to an order of magnitude by the proposed code design.
References
Rahnavard N, Fekri F: Unequal error protection using low-density parity-check codes. Proceedings of the IEEE International Symposium on Information Theory (ISIT '04), July 2004 449.
Rahnavard N, Pishro-Nik H, Fekri F: Unequal error protection using partially regular LDPC codes. IEEE Transactions on Communications 2007, 55(3):387-391.
Poulliat C, Declercq D, Fijalkow I: Enhancement of unequal error protection properties of LDPC codes. Eurasip Journal on Wireless Communications and Networking 2007, 2007:-9.
Sassatelli L, Henkel W, Declercq D: Check-irregular LDPC codes for unequal error protection under iterative decoding. Proceedings of the 4th International Symposium on Turbo Codes & Related Topics, April 2006
Pishro-Nik H, Rahnavard N, Fekri F: Nonuniform error correction using low-density parity-check codes. IEEE Transactions on Information Theory 2005, 51(7):2702-2714. 10.1109/TIT.2005.850230
Ma P, Kwak KS: Unequal error protection low-density parity-check codes design based on gaussian approximation in image transmission. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '09), April 2009 1-6.
Yang X, Yuan D, Ma P, Jiang M: New research on unequal error protection (UEP) property of irregular LDPC codes. Proceedings of the 1st Consumer Communications and Networking Conference (CCNC '04), January 2004 361-363.
Vasic B, Cvetkovic A, Sankaranarayanan S, Marcellin M: Adaptive error protection low-density parity-check codes for joint source-channel coding schemes. Proceedings of the IEEE International Symposium on Information Theory (ISIT '03), July 2003 267-267.
Rahnavard N, Fekri F: New results on unequal error protection using LDPC codes. IEEE Communications Letters 2006, 10(1):43-45. 10.1109/LCOMM.2006.1576564
Kumar V, Milenkovic O: On unequal error protection LDPC codes based on plotkin-type constructions. IEEE Transactions on Communications 2006, 54(6):994-1005. 10.1109/TCOMM.2006.876842
Goupil A, Declercq D: UEP non-binary LDPC codes: a promising framework based on group codes. Proceedings of the IEEE International Symposium on Information Theory (ISIT '08), July 2008 2227-2231.
Hu XY, Eleftheriou E, Arnold DM: Regular and irregular progressive edge-growth tanner graphs. IEEE Transactions on Information Theory 2005, 51(1):386-398.
Tian T, Jones CR, Villasenor JD, Wesel RD: Selective avoidance of cycles in irregular LDPC code construction. IEEE Transactions on Communications 2004, 52(8):1242-1247. 10.1109/TCOMM.2004.833048
Vukobratović D, Šenk V: Generalized ACE constrained progressive edge-growth LDPC code design. IEEE Communications Letters 2008, 12(1):32-34.
Luby MG, Mitzenmacher M, Shokrollahi MA, Spielman DA: Improved low-density parity-check codes using irregular graphs. IEEE Transactions on Information Theory 2001, 47(2):585-598. 10.1109/18.910576
Richardson TJ, Shokrollahi MA, Urbanke RL: Design of capacity-approaching irregular low-density parity-check codes. IEEE Transactions on Information Theory 2001, 47(2):619-637. 10.1109/18.910578
Von Deetzen N, Sandberg S: On the UEP capabilities of several LDPC construction algorithms. IEEE Transactions on Communications 2010, 58(11):3041-3046.
Liva G, Chiani M: Protograph LDPC codes design based on EXIT analysis. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007 3250-3254.
Brink ST: Convergence behavior of iteratively decoded parallel concatenated codes. IEEE Transactions on Communications 2001, 49(10):1727-1737. 10.1109/26.957394
Ten Brink S, Kramer G, Ashikhmin A: Design of low-density parity-check codes for modulation and detection. IEEE Transactions on Communications 2004, 52(4):670-678. 10.1109/TCOMM.2004.826370
Chung SY, Richardson TJ, Urbanke RL: Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation. IEEE Transactions on Information Theory 2001, 47(2):657-670. 10.1109/18.910580
Author information
Authors and Affiliations
Corresponding author
Appendix
Detailed MI Evolution
Let  be the a priori MI between one input message and the codeword bit associated to the variable node.
be the a priori MI between one input message and the codeword bit associated to the variable node.  is the extrinsic MI between one output message and the codeword bit. Similarly on the check node side, we define
is the extrinsic MI between one output message and the codeword bit. Similarly on the check node side, we define  (
( ) to be the a priori (extrinsic) MI between one check node input (output) message and the codeword bit corresponding to the variable node providing (receiving) the message. The evolution is initialized by the MI between one received message and the corresponding codeword bit, denoted by
) to be the a priori (extrinsic) MI between one check node input (output) message and the codeword bit corresponding to the variable node providing (receiving) the message. The evolution is initialized by the MI between one received message and the corresponding codeword bit, denoted by  , which corresponds to the channel capacity. For the AWGN channel, it is given by
, which corresponds to the channel capacity. For the AWGN channel, it is given by  , where
, where


and  is the signal-to-noise ratio at which the analysis is performed. The function
is the signal-to-noise ratio at which the analysis is performed. The function  is defined by
is defined by


and computes the MI based on the noise variance. For a variable node with degree  , the extrinsic MI between the
, the extrinsic MI between the  -th output message and the corresponding codeword bit is [18]
-th output message and the corresponding codeword bit is [18]


where  is the a priori MI of the message received by the variable node on its
is the a priori MI of the message received by the variable node on its  -th edge. The extrinsic MI for a check node with degree
-th edge. The extrinsic MI for a check node with degree  may be written as
may be written as


where  is the a priori MI of the message received by the check node on its
is the a priori MI of the message received by the check node on its  -th edge. Note that the MI functions are subject to the Gaussian approximation (see [21]) and are not exact.
-th edge. Note that the MI functions are subject to the Gaussian approximation (see [21]) and are not exact.
The following algorithm describes the MI analysis of a given parity-check matrix. We denote element ( ) of the parity-check matrix by
) of the parity-check matrix by  .
.
-
(1)
Initialization
 (A.5)
(A.5) -
(2)
Check to variable update
-
(a)
For
 and
and  , if
, if  , calculate
, calculate (A.6)
(A.6) -
where
 is the set of check nodes incident to variable node
is the set of check nodes incident to variable node  .
. -
(b)
If
 ,
,  .
. -
(c)
For
 and
and  , set
, set  .
.
-
(a)
-
(3)
Variable to check update
-
(a)
For
 and
and 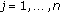 , if
, if  , calculate
, calculate (A.7)
(A.7) -
where
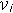 is the set of variable nodes incident to check node
is the set of variable nodes incident to check node  .
. -
(b)
If
 ,
,  .
. -
(c)
For
 and
and  , set
, set  .
.
-
(a)
-
(4)
A posteriori check node MI
-
For
 , calculate
, calculate (A.8)
(A.8) -
(5)
A posteriori variable node MI
-
For
 , calculate
, calculate (A.9)
(A.9) -
(6)
Repeat (2)–(5) until
 for
for  .
.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sandberg, S. Improved Design of Unequal Error Protection LDPC Codes. J Wireless Com Network 2010, 423989 (2010). https://doi.org/10.1155/2010/423989
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/423989
 under consideration, keeping
under consideration, keeping  ,
, 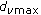 , and the proportions between the protection classes fixed. This step results in subdegree distributions for each protection class.
, and the proportions between the protection classes fixed. This step results in subdegree distributions for each protection class.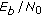 and a maximum number of decoder iterations. The code with the highest average
and a maximum number of decoder iterations. The code with the highest average  has the best overall performance within this family of codes.
has the best overall performance within this family of codes.

 and allowed
and allowed  . The average BER is shown for the non-UEP code, while the BERs of both
. The average BER is shown for the non-UEP code, while the BERs of both  and
and  are shown for the UEP codes. Both classes of the UEP codes perform better than the non-UEP code.
are shown for the UEP codes. Both classes of the UEP codes perform better than the non-UEP code.
 and
and  . Both classes of the two UEP codes have lower BER than the non-UEP code. The code optimized for a low
. Both classes of the two UEP codes have lower BER than the non-UEP code. The code optimized for a low  (0.5 dB) with
(0.5 dB) with  dB performs best at low
dB performs best at low  , while the code optimized for high
, while the code optimized for high  (1 dB) with
(1 dB) with  dB has a lower average BER at
dB has a lower average BER at  above 0.8 dB.
above 0.8 dB.




 and
and  , if
, if  , calculate
, calculate
 is the set of check nodes incident to variable node
is the set of check nodes incident to variable node  .
. ,
,  .
. and
and  , set
, set  .
. and
and 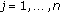 , if
, if  , calculate
, calculate
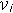 is the set of variable nodes incident to check node
is the set of variable nodes incident to check node  .
. ,
,  .
. and
and  , set
, set  .
. , calculate
, calculate
 , calculate
, calculate
 for
for  .
.