- Research Article
- Open access
- Published:
Data Dissemination in Wireless Sensor Networks with Network Coding
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 465915 (2010)
Abstract
In wireless sensor networks (WSNs), it is often necessary to update the software running on sensors, which requires reliable dissemination of large data objects to each sensor with energy efficiency. During data dissemination, due to sleep scheduling designed for energy efficiency, some sensors may not receive some packets at some time slots. In the meantime, due to the unreliability of wireless communication, a sensor may not successfully receive a packet even when it is in the active mode. Thus, retransmission of such packets to those sensors is necessary, which consumes more energy and increases the delay of data dissemination cycle. In this paper, we propose a network coding-based approach in data dissemination such that data dissemination can be accomplished at the earliest time. Thus, less energy is consumed and the delay can be decreased. The impact of packet loss probability and the sleep probability of sensors on the network coding gain is analyzed. A threshold is also given to decide whether the current sleep scheduling is effective on energy saving in data dissemination process or not. Simulation results demonstrate the effectiveness and scalability of the proposed work.
1. Introduction
Recently, more research attention has been directed towards wireless sensor networks. Once deployed, sensors are expected to operate for extended periods of time, and it is impractical to physically reach all sensors. However, it is quite often necessary to update the software running on those sensors or add new functionality to the sensors [1–3]. Reprogramming the network needs to reliably disseminate large data objects (50–100 KB) to every sensor in the network with energy efficiency [2].
Protocols for reliably disseminating large data objects in WSNs have been developed over years. Protocols in [1–4] achieve data dissemination reliability through different mechanisms such as hop-by-hop recovery, NACKs or ACKs mechanisms, while another requirement of disseminating large objects in WSNs, energy efficiency, has not been well studied.
In WSNs, energy consumption is a critical issue and sleep scheduling has been well studied as a conservative approach to minimize the energy consumption due to idle listening [5, 6]. Though sleep scheduling can save energy, sensors in sleep mode cannot receive data packets. In addition, due to the unreliability of wireless communication, a sensor may not receive the packet successfully even when it is in active mode [7]. Hence, a data packet may be transmitted several times in order to be disseminated to all sensors, which wastes energy and increases the delay of the whole data dissemination process. In other words, the data dissemination process consists of sending native data packets and recovering "wanted" packets that each sensor has not received due to sleep scheduling and/or link unreliability. In order to complete the data dissemination process in a timely manner and achieve energy efficiency, it is crucial to assure that the maximum number of "wanted" packets at all sensors can be recovered at each time slot.
Recently, network coding has become a promising approach to improve the system throughput in wireless networks. Network coding with XORs operation in wireless broadcast has been studied in [8], which shows the advantage of the proposed XORs coding scheme over the traditional wireless broadcast in the bandwidth efficiency through simulations and theoretical analysis. In XORs coding, a coded packet carries both the coding vector information and the encoded data. Thus, upon receiving a coded packet, the receiver knows which packets are encoded together and how to decode the packet with the available packets at the receiver. The work in [9] has proved that optimal XORs encoding decision for wireless broadcast, which decides the coding vector of each coded packet, is an NP-hard problem. Heuristic algorithms of encoding decision problem for wireless broadcast and multicast are proposed in [9, 10]. However, the proposed encoding decision approach can only be applied to the scenario where all receivers remain active during the whole time period of recovery. Such an approach can not be applied to WSNs with sleep scheduling because different sets of active sensors may be available at different time slots.
In this paper, given the sleep scheduling information at the sensors, we aim to determine an effective XORs encoding strategy such that the minimum number of transmissions is required in order for each sensor in the network to successfully receive the whole set of disseminated data packets. Thus, energy consumption can be reduced and the data dissemination process can be accomplished in a timely manner. To achieve such an objective, it is important to maximize the expected number of active sensors that can decode out one "wanted" data packet at each time slot in the recovery process, which is the focus of this paper. The contribution of the proposed work is summarized as follows.
-
(i)
The proposed work takes both link unreliability and sleep scheduling into consideration and proposes an XORs encoding decision algorithm to maximize the expected number of active sensors that can decode out one native packet in their "wanted" data packet sets at each time slot in the recovery process.
-
(ii)
We analyze the impact of each link's packet loss probability and each sensor's sleep probability at each time slot on the network coding gain, which is an extension of the analysis given in [8].
-
(iii)
We also study the effectiveness of sleep scheduling on energy saving, which is offsetted by the total number of active time slots consumed in the data dissemination process. A threshold is derived to decide whether the current sleep scheduling is effective on energy saving or not. The simulation results also confirm the accuracy of our analysis.
The rest of the paper is organized as follows. Related work is reviewed in Section 2. Section 3 introduces the system architecture and data dissemination schemes. The problem description and its complexity is presented in Section 4. Section 5 describes the algorithm design. Theoretical analysis is given in Section 6. Section 7 gives the simulation results. Finally, we conclude the paper in Section 8.
2. Related Work
In this section, we review the related work of network coding in WSNs. Network coding is originally proposed in information theory [11] and recently has become a promising approach to improve the system throughput in wireless networks [11–16]. Adaptive network coding is proposed in [17] to reduce traffic in the process of software updates where linear network coding technique is used. As computation ability and the memory at sensor nodes are very limited, the complexity of linear encoding and decoding introduces extra overhead. Thus, it is more appropriate to use XORs operation in WSNs since both encoding and decoding operations are much simpler. In fact, XORs coding has been widely used in wireless networks to reduce the complexity of linear network coding [8, 10, 18, 19].
COPE proposed in [18] improves the throughput of unicast with XORs coding. By exploiting the broadcast nature of wireless medium, each node buffers overheard packets for a short time and notifies its neighbors which packets it has heard. When a node transmits a packet, it uses its knowledge of what its neighbors have heard to perform opportunistic coding and XORs multiple packets to transmit them as a single packet while ensuring that each intended next-hop has enough information to decode the encoded packet.
Network coding with XORs operation in wireless broadcast has also been studied in [8], which shows the advantage of the proposed network coding scheme over traditional wireless broadcast in bandwidth efficiency through simulations and theoretical analysis. However, encoding decision has not been given in [8]. The work in [9] has proved that optimal XORs encoding decision problem for wireless broadcast is an NP-hard problem.
Several heuristic algorithms for encoding decision in wireless broadcast and multicast have been proposed in [9, 10]. With the knowledge of the "wanted" packet set at each receiver, an auxiliary graph is constructed. The encoding decision during the recovery process is then converted to a clique partition problem in the auxiliary graph. However, the proposed encoding decision algorithms can only be applied to the scenario where all receivers remain active during the time period of recovery. Such an approach cannot be applied to WSNs since different set of active sensors may be available at different time slots. Thus, encoding decision in WSNs with sleep scheduling cannot be converted into finding a minimum clique partition in the graph.
The work in [20] proposes a retransmission scheme, which only uses reception estimation to determine the coding set selection. However, the reception estimation at the source node may not be accurate enough, consequently, some receivers may not be able to decode useful information from the coded packet and more retransmissions will be needed. In addition, the coding decision based on reception estimation does not consider the impact of sleep scheduling, which affects the decoding probability at the receivers in low duty-cycled WSNs.
3. System Architecture and Data Dissemination with Network Coding
In this paper, we propose to use XORs coding in data dissemination in a large scale WSN which is organized as a multihop cluster hierarchy [21]. A multihop cluster hierarchical architecture consists of multiple layers as shown in Figure 1. In the lowest layer, all the nodes in the network are grouped into clusters. In addition, besides being a member in a cluster, a node may act as a cluster head in a down layer cluster, for example,  in the figure. Within each cluster, the cluster head communicates with its member sensors in a one-hop fashion [22]. We also assume that each sensor is aware of its one-hop neighbors' sleep scheduling and the reliability of the wireless links between the sensor to its neighbors. This can be easily accomplished by one-hop information exchange and link loss inference [23].
in the figure. Within each cluster, the cluster head communicates with its member sensors in a one-hop fashion [22]. We also assume that each sensor is aware of its one-hop neighbors' sleep scheduling and the reliability of the wireless links between the sensor to its neighbors. This can be easily accomplished by one-hop information exchange and link loss inference [23].
Our data dissemination process is conducted at each cluster head so as to make sure that finally all the sensors obtain the updating packets. In a multihop cluster hierarchy, if a cluster head in an intermediate layer starts to transmit the received packet immediately after receiving one fresh packet, the gain of network coding cannot be fully utilized. On the other hand, if a cluster head waits and starts to transmit packets until it receives all packets from the cluster head in the upper layer, it will waste bandwidth and introduce extra delay. In order to achieve the balance between bandwidth efficiency and network coding gain, we propose to use a threshold  to determine when the current cluster head starts to transmit the packets to its member nodes. Specifically, for each cluster head, after obtaining
to determine when the current cluster head starts to transmit the packets to its member nodes. Specifically, for each cluster head, after obtaining  fresh native packets, where
fresh native packets, where  and
and  is the number of native packets available at its upper-layer cluster head, it will conduct XORs coding scheme to transmit the packets to its member nodes. In the simulation part, we will study the impact of the threshold
is the number of native packets available at its upper-layer cluster head, it will conduct XORs coding scheme to transmit the packets to its member nodes. In the simulation part, we will study the impact of the threshold  on the delay and energy consumption.
on the delay and energy consumption.
In the rest of the paper, we focus on how a cluster head encodes the packets and transmits them to its member sensors. The coding decision at other cluster heads can use the same approach.
As we mentioned earlier, the data dissemination process consists of sending native data packets and recovering "wanted" packets for each receiver. We now give an example to show that network coding can indeed recover "wanted" packets for all neighbors more efficiently.
Suppose that four packets  , and
, and  need to be transmitted to sensors
need to be transmitted to sensors  and
and  as shown in Figure 2. The sleep scheduling at each receiver is given in Figure 2(a) where 1 denotes that this sensor is active at the current time slot, otherwise, it is in sleep mode. For the sake of simplicity, in this example, we assume that no packet is lost due to unreliable wireless communication, which means that a sensor can receive a packet successfully when it is in active mode. We also assume that an active sensor can only transmit or receive one packet at each time slot [5]. We show that different data dissemination approaches will lead to different finishing time of data dissemination.
as shown in Figure 2. The sleep scheduling at each receiver is given in Figure 2(a) where 1 denotes that this sensor is active at the current time slot, otherwise, it is in sleep mode. For the sake of simplicity, in this example, we assume that no packet is lost due to unreliable wireless communication, which means that a sensor can receive a packet successfully when it is in active mode. We also assume that an active sensor can only transmit or receive one packet at each time slot [5]. We show that different data dissemination approaches will lead to different finishing time of data dissemination.
-
(i)
Without network coding, 4 native packets will be sent firstly, followed by sending native packets to recover "wanted" packets at sensors. Figure 2(b) gives the "wanted" data packet set at each sensor after 4 native packets are sent out. Without network coding, it will take 10 time slots to finish the data dissemination process as shown in Figure 2(c).
-
(ii)
With network coding, 4 native packets can be sent at first followed by sending encoded packets to recover "wanted" packets at sensors. Assume that our coding strategy at each time slot is to maximize the number of active receivers that can decode the encoded packet. For example, at time
 , if
, if 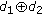 is sent, all four receivers can obtain a "wanted" packet by
is sent, all four receivers can obtain a "wanted" packet by 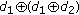 or
or 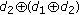 . Eventually, it will take 8 time slots to finish the data dissemination process as shown in Figure 2(d). Under such a data dissemination approach, as all native packets are sent at first, the available packets at sensors are most diversified. Thus, the best network coding gain can be achieved. This, however, means that each sensor needs to buffer all received native packets in order to decode out "wanted" packets, which might not be feasible in a WSN due to limited memories at sensors.
. Eventually, it will take 8 time slots to finish the data dissemination process as shown in Figure 2(d). Under such a data dissemination approach, as all native packets are sent at first, the available packets at sensors are most diversified. Thus, the best network coding gain can be achieved. This, however, means that each sensor needs to buffer all received native packets in order to decode out "wanted" packets, which might not be feasible in a WSN due to limited memories at sensors. -
(iii)
An alternative approach will be to divide the data dissemination process into several batches where in each batch,
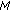 native packets are sent followed by the recovering process [24]. Once all
native packets are sent followed by the recovering process [24]. Once all 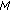 native packets are received by all sensors in the cluster, the cluster head proceeds to transmit the following batch of packets. The data dissemination is accomplished when all batches of packets are obtained by all sensor nodes in the network. In Figure 2(e), we send two native packets at first, followed by sending encoded packets to recover "wanted" packets of the first batch at sensors, then send the last two native packets followed by sending encoded packets to recover "wanted" packets of the second batch at sensors. It takes 9 time slots to finish the data dissemination process.
native packets are received by all sensors in the cluster, the cluster head proceeds to transmit the following batch of packets. The data dissemination is accomplished when all batches of packets are obtained by all sensor nodes in the network. In Figure 2(e), we send two native packets at first, followed by sending encoded packets to recover "wanted" packets of the first batch at sensors, then send the last two native packets followed by sending encoded packets to recover "wanted" packets of the second batch at sensors. It takes 9 time slots to finish the data dissemination process.
We now discuss how the cluster head can maintain "wanted" packet set at each member sensor. After sending out a packet, the cluster head needs to collect the "wanted" packet set at each member sensor. In order to reduce ACKs implosion, only the active receivers that have received a packet at current time slot successfully and can obtain/decode one "wanted" packet from the received packet will send an ACK message to the cluster head. Thus, according to ACKs from receivers, the cluster head can derive the "wanted" packet set for each active receiver.
With the information of "wanted" packet set of each receiver at each time slot in the recovery process, an encoding decision which aims to maximize the expected number of active sensors that can decode out one "wanted" packet at current time slot will be introduced in the following section.
4. Problem Description and Complexity
In this section, we first describe the encoding decision problem that aims to decide which native packets should be encoded at each time slot  in the recovering process such that the maximum expected number of active sensors at time slot
in the recovering process such that the maximum expected number of active sensors at time slot  can decode out one "wanted" native packet. Thus, we limit our discussion to the recovery process of one data dissemination batch in a cluster, which can also be applied to other batches in all other clusters.
can decode out one "wanted" native packet. Thus, we limit our discussion to the recovery process of one data dissemination batch in a cluster, which can also be applied to other batches in all other clusters.
Suppose that  is the set of data packets in a batch which need to be disseminated to all the sensors in a cluster. Let
is the set of data packets in a batch which need to be disseminated to all the sensors in a cluster. Let  be the set of active member sensors in the cluster at
be the set of active member sensors in the cluster at  th time slot At each time slot, the cluster head can obtain its neighbor sensors' "wanted" packet set based on ACKs feedback. Let
th time slot At each time slot, the cluster head can obtain its neighbor sensors' "wanted" packet set based on ACKs feedback. Let  be 1 if packet
be 1 if packet  is not available at active sensor
is not available at active sensor  at current time slot where
at current time slot where  , otherwise, let it be 0. Let
, otherwise, let it be 0. Let  and
and  be the "wanted" data packet set of active sensor
be the "wanted" data packet set of active sensor  at current time slot
at current time slot  as shown in Figure 2(b). Assume that
as shown in Figure 2(b). Assume that  is the probability that sensor
is the probability that sensor  can not successfully receive a packet from the cluster head when
can not successfully receive a packet from the cluster head when  is in active mode.
is in active mode.
Let  be 1 if native packet
be 1 if native packet  is combined in current encoded packet, otherwise, let it be 0. Let
is combined in current encoded packet, otherwise, let it be 0. Let  be 1 if active sensor
be 1 if active sensor  can decode out one "wanted" native packet
can decode out one "wanted" native packet  from the current encoded packet where
from the current encoded packet where  , otherwise, let it be 0. Considering unreliable wireless communication, the probability that an active sensor
, otherwise, let it be 0. Considering unreliable wireless communication, the probability that an active sensor  can successfully obtain one "wanted" packet at the current time slot is
can successfully obtain one "wanted" packet at the current time slot is  . Thus, at current time slot, the expected number of sensors that can decode out one "wanted" packet is
. Thus, at current time slot, the expected number of sensors that can decode out one "wanted" packet is  , which needs to be maximized in order to save energy.
, which needs to be maximized in order to save energy.
Still take Figure 2(d) as an example, after  , the cluster head starts to recover the "wanted" packets at its member sensors. At
, the cluster head starts to recover the "wanted" packets at its member sensors. At  , if the cluster head sends an encoded packet
, if the cluster head sends an encoded packet  , in an ideal condition where no packet will be lost, active receivers
, in an ideal condition where no packet will be lost, active receivers  can decode out one "wanted" packet by
can decode out one "wanted" packet by  or
or  . Assume that
. Assume that  ,
,  ,
,  ,
,  in a practical wireless network where the probability of successfully receiving a packet at
in a practical wireless network where the probability of successfully receiving a packet at  ,
,  ,
,  , and
, and  is
is  and
and  respectively due to unreliable wireless communication. Thus, the expected number of active receivers that can decode out one "wanted" packet after receiving the current encoded packet
respectively due to unreliable wireless communication. Thus, the expected number of active receivers that can decode out one "wanted" packet after receiving the current encoded packet  is
is  , which is maximum at the current time slot. Thus, the cluster head will send out
, which is maximum at the current time slot. Thus, the cluster head will send out  at the current time slot. In this paper, such an encoding decision problem using XORs coding is referred to as network coding based data dissemination (NCDD) problem.
at the current time slot. In this paper, such an encoding decision problem using XORs coding is referred to as network coding based data dissemination (NCDD) problem.
4.1. Problem Formulation
We can formally formulate the NCDD problem at time slot  in the recovery process as follows:
in the recovery process as follows:

subject to





In the above formulation, the term of the objective represents the expected number of active receivers that can decode out one "wanted" data packet from the encoded packet at the current time slot. Equations (2) and (6) ensure that each receiver can only decode out at most one "wanted" native packet from the encoded packet. Equations (3) and (4) give two requirements that active receiver  can decode out one "wanted" packet
can decode out one "wanted" packet  : (
: ( ) packet
) packet  is in
is in  's "wanted" packet set and
's "wanted" packet set and  is participated in the encoded packet; (
is participated in the encoded packet; ( ) all other combined native packets except
) all other combined native packets except  in the encoded packet have already been successfully received by receiver
in the encoded packet have already been successfully received by receiver  . Equation (5) guarantees that if packet
. Equation (5) guarantees that if packet  is available at all active receivers at current time slot
is available at all active receivers at current time slot  ,
,  must not be combined into the encoded packet.
must not be combined into the encoded packet.
4.2. Problem Complexity
Theorem 1.
NCDD problem is NP-hard.
Proof.
We prove the theorem by a reduction from MAXIMUM ONE-IN-THREE SAT problem which is a well known NP-hard problem in the strong sense.
MAXIMUM ONE-IN-THREE SAT: We are given a set  of
of  boolean variables and a collection
boolean variables and a collection  of clauses with exactly three literals. Each of these clauses is a boolean formula and it is true if and only if exactly one of its three literals is true. Without loss of generality, we assume that the three literals in
of clauses with exactly three literals. Each of these clauses is a boolean formula and it is true if and only if exactly one of its three literals is true. Without loss of generality, we assume that the three literals in  are
are  . The objective of MAXIMUM ONE-IN-THREE SAT is to find a truth assignment such that the maximum number of clauses is true. We use
. The objective of MAXIMUM ONE-IN-THREE SAT is to find a truth assignment such that the maximum number of clauses is true. We use  to denote the optimal solution of this problem.
to denote the optimal solution of this problem.
Given an instance of MAXIMUM ONE-IN-THREE SAT, we can construct an instance of the decision version of the NCDD problem in polynomial time as follows. Let there be  data packets needed to be disseminated from the cluster head to
data packets needed to be disseminated from the cluster head to  receiver nodes. If
receiver nodes. If  , packet
, packet  is participated in encoding, otherwise,
is participated in encoding, otherwise,  is not participated in encoding. For each clause
is not participated in encoding. For each clause  , if
, if  is a literal of
is a literal of  , then
, then  is a "wanted" packet at
is a "wanted" packet at  . In other words, each sensor
. In other words, each sensor  has lost exactly three packets and has all other packets. Let the probability that an active sensor can successfully receive a packet be
has lost exactly three packets and has all other packets. Let the probability that an active sensor can successfully receive a packet be  . Then, our objective is to maximize
. Then, our objective is to maximize  For a given encoded packet,
For a given encoded packet,  can decode a new native packet if and only if exactly one native packet in
can decode a new native packet if and only if exactly one native packet in  is encoded into the new encoded one. The problem is to find an encoding strategy to maximize the number of receivers which can decode out one "wanted" packet from the encoded packet. We use
is encoded into the new encoded one. The problem is to find an encoding strategy to maximize the number of receivers which can decode out one "wanted" packet from the encoded packet. We use  to refer to the result of this objective.
to refer to the result of this objective.
-
(i)
Suppose that there is a true assignment for MAXIMUM ONE-IN-THREE SAT with the maximum number of clauses. If
 is true, there must be exactly one true assignment for
is true, there must be exactly one true assignment for  . Without loss of generality, we assume that
. Without loss of generality, we assume that  is true while
is true while 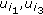 are both false. According to the construction of the instance, only
are both false. According to the construction of the instance, only 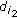 is participated in encoding while neither
is participated in encoding while neither  nor
nor 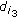 is participated in encoding. In other words, only one lost packet of
is participated in encoding. In other words, only one lost packet of 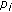 is participated in encoding and
is participated in encoding and 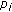 has all other packets involved in encoding, thus,
has all other packets involved in encoding, thus, 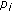 can decode out one "wanted" native packet
can decode out one "wanted" native packet 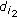 . Therefore, if there is a clause which is true in the MAXIMUM ONE-IN-THREE SAT problem, there must be a receiver which can obtain a "wanted" native packet. Then, we have
. Therefore, if there is a clause which is true in the MAXIMUM ONE-IN-THREE SAT problem, there must be a receiver which can obtain a "wanted" native packet. Then, we have 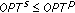 .
. -
(ii)
Suppose that there is an encoding strategy such that the maximum number of receivers can decode the new native packet. Assume that
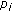 can decode a new native packet
can decode a new native packet 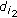 from the encoded one. According to the decoding strategy, the other two "wanted" packets
from the encoded one. According to the decoding strategy, the other two "wanted" packets  must not be encoded into the new one, that is,
must not be encoded into the new one, that is, 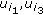 both have false assignment while
both have false assignment while 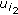 is true. In this assignment,
is true. In this assignment, 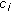 also has a true value. So, we have
also has a true value. So, we have 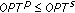 .
.
The above analysis shows that  . Thus NCDD problem is NP-hard.
. Thus NCDD problem is NP-hard.
5. Algorithm for NCDD Problem
In this section, we first introduce an auxiliary graph in which each vertex is assigned a weight. We then show that the proposed NCDD problem can be converted into finding a maximum weight clique problem in the auxiliary graph, based on which we develop a heuristic algorithm for the NCDD problem.
5.1. Model Design
At any  th time slot, let
th time slot, let  be the set of packets "wanted" by
be the set of packets "wanted" by  and
and  be the set of packets received by
be the set of packets received by  . We can construct an auxiliary graph
. We can construct an auxiliary graph  similar to [9] where
similar to [9] where  and
and  , which means that every "wanted" packet of each active sensor has a vertex in
, which means that every "wanted" packet of each active sensor has a vertex in  . Considering two receivers
. Considering two receivers  and
and  , if they have lost the same packet
, if they have lost the same packet  , then they can both recover
, then they can both recover  if only native packet
if only native packet  is encoded at current time slot. We use a link
is encoded at current time slot. We use a link  between
between  and
and  to denote such recoverability. If
to denote such recoverability. If  is a "wanted" packet of
is a "wanted" packet of  and
and  , while
, while  is a "wanted" packet of
is a "wanted" packet of  and
and  , then
, then  can recover
can recover  when it receives
when it receives  and
and  can recover
can recover  when it receives
when it receives  . We use a link
. We use a link  between
between  and
and  to denote such recoverability. In other words,
to denote such recoverability. In other words,  ,
,  or
or  ,
,  where
where  .
.
For a clique  in the graph, let
in the graph, let  be the sensors which have "wanted" packets in
be the sensors which have "wanted" packets in  and
and  be the set of "wanted" packets of those sensors in
be the set of "wanted" packets of those sensors in  . Suppose that there are
. Suppose that there are  packets in
packets in  . For any vertex
. For any vertex  , according to the edge assignment of
, according to the edge assignment of  ,
,  must have already successfully obtained the packets in
must have already successfully obtained the packets in  but still requires packet
but still requires packet  . Thus, if
. Thus, if  where
where  are encoded and sent at
are encoded and sent at  th time slot, each sensor in
th time slot, each sensor in  will be able to decode out one "wanted" packet if the encoded packet can be successfully received by all sensors in
will be able to decode out one "wanted" packet if the encoded packet can be successfully received by all sensors in  . To consider the unreliability of wireless communication, we assign weight
. To consider the unreliability of wireless communication, we assign weight  in the vertex
in the vertex  for any
for any  . Then the weight for clique
. Then the weight for clique  which is defined in
which is defined in

is equivalent to the expected number of active sensors which can successfully decode out one "wanted" packet if all packets in  are encoded together. Thus, our NCDD problem which aims to maximize the expected number of active sensors that can decode out one "wanted" packet is converted into finding a maximum weight clique in graph
are encoded together. Thus, our NCDD problem which aims to maximize the expected number of active sensors that can decode out one "wanted" packet is converted into finding a maximum weight clique in graph  .
.
For example, after the whole 4 native packets are sent, the "wanted" packet set in Figure 2(b) can be constructed into Figure 3. Thus, the encoding decision for recovery process at  is then converted into finding a maximum weight clique in such a graph. As shown in Figure 3, the clique that consists of
is then converted into finding a maximum weight clique in such a graph. As shown in Figure 3, the clique that consists of  is the clique with the maximum weight
is the clique with the maximum weight  . After the encoded packet
. After the encoded packet  is sent, active receivers
is sent, active receivers  can decode out
can decode out  , respectively, if all sensors successfully receive
, respectively, if all sensors successfully receive  .
.
5.2. Algorithm Design
Assume that the total number of vertices in  is
is  . We first sort all vertices into nonincreasing order according to
. We first sort all vertices into nonincreasing order according to  . For the example given in Figure 3, vertices in
. For the example given in Figure 3, vertices in  will be sorted into
will be sorted into  .
.
For the simplicity of presentation, we abuse the notation a little bit and assign a unique id  for each vertex in
for each vertex in  , which uses one-dimensional subscript for vertices in
, which uses one-dimensional subscript for vertices in  instead of using two-dimensional subscripts. Correspondingly, we use
instead of using two-dimensional subscripts. Correspondingly, we use  to denote the weight of
to denote the weight of  . Thus, for the example given in Figure 3, we have
. Thus, for the example given in Figure 3, we have 
 ,
,  . Without loss of generality, we assume that
. Without loss of generality, we assume that  where
where  .
.
Let  be the clique with maximum weight in the subgraph which only contains vertices of
be the clique with maximum weight in the subgraph which only contains vertices of  and let
and let  be the weight of clique
be the weight of clique  . In other words,
. In other words,  represents the maximum weight clique the algorithm has found considering of the subgraph consisting of vertices
represents the maximum weight clique the algorithm has found considering of the subgraph consisting of vertices  . The algorithm starts with
. The algorithm starts with  and iteratively considers more vertices until all vertices in
and iteratively considers more vertices until all vertices in  are considered. The algorithm stops when
are considered. The algorithm stops when  is found.
is found.
When we consider vertex  , there are two cases. If
, there are two cases. If  is also a clique, then
is also a clique, then  and
and  , otherwise, if
, otherwise, if  is not a clique, we need to find out a clique
is not a clique, we need to find out a clique  that includes
that includes  in the subgraph consisting of
in the subgraph consisting of  . Let
. Let  be the set of neighbors of vertex
be the set of neighbors of vertex  . Initially,
. Initially,  and
and  . If
. If  is not
is not  , let
, let  be the smallest
be the smallest  such that
such that  . We add
. We add  to the clique, that is,
to the clique, that is,  , and update
, and update  , that is,
, that is,  . If
. If  is still not
is still not  , we then add another vertex whose index is the smallest in
, we then add another vertex whose index is the smallest in  into the clique
into the clique  . We repeat this process until there is no vertex in
. We repeat this process until there is no vertex in  , that is,
, that is,  . By comparing the weight of the clique
. By comparing the weight of the clique  without including
without including  and the weight of the clique
and the weight of the clique  including
including  , the clique
, the clique  with maximum weight in the subgraph including vertices in
with maximum weight in the subgraph including vertices in  is set to be the one with the larger weight. The detail of the algorithm is given in Algorithm 1. After this algorithm,
is set to be the one with the larger weight. The detail of the algorithm is given in Algorithm 1. After this algorithm,  gives all vertices in the found maximum weight clique. All native packets involved in
gives all vertices in the found maximum weight clique. All native packets involved in  will be encoded together and be sent out at current time slot.
will be encoded together and be sent out at current time slot.
Algorithm 1: Maximum weight clique algorithm.
Function 
if 
if 
 ;
;
 ;
;
return
while 
 ;
;
 ;
;

 ;
;
if 
if 
 ;
; 
return
Function 
 ,
,  ;
;  ;
;
 ,
,  ;
;
 ;
;
 ;
;
 ,
,  ;
;
for  down to 1
down to 1
if  is also a clique;
is also a clique;
 ;
;
 ;
;
else
 ;
;
 ;
;
 ;
;
if 
 ;
;  ;
;
return
We now show how to find the maximum weight clique of the graph shown in Figure 3. Assume that  has been found, which consists of
has been found, which consists of  . Next, we will consider
. Next, we will consider  . Since
. Since  is not a clique, we need to find
is not a clique, we need to find  which includes vertex
which includes vertex  in the subgraph consisting of
in the subgraph consisting of  . The corresponding steps for finding such
. The corresponding steps for finding such  is given in Algorithm 2 where
is given in Algorithm 2 where  in
in  denotes that we use a unique id
denotes that we use a unique id  in the algorithm to replace the original vertex
in the algorithm to replace the original vertex  . After
. After  is found, we compare it with
is found, we compare it with  which has the weight
which has the weight  . Since
. Since  is larger than
is larger than  , the clique
, the clique  is the maximum weight clique found in graph
is the maximum weight clique found in graph  . Vertices in
. Vertices in  indicate that
indicate that  ,
,  and
and  lost packet
lost packet  and
and  lost packet
lost packet  . The encoding decision will be to send
. The encoding decision will be to send  .
.
Algorithm 2: The steps of finding  .
.

Step  :
:








Step  :
:





Step  :
:





Step  :
:


Terminate;
6. Analysis
In this section, we firstly analyze the impact of packet loss probability and sleep probability on network coding gain. Then, we derive a threshold to decide whether the current sleep scheduling can save energy compared with no sleep scheduling. We only limit the analysis to one cluster in the multihop cluster hierarchy.
6.1. Impact of Packet Loss Probability and Sleep Probability on Network Coding Gain
Suppose that  is the number of transmissions that the data dissemination process requires without coding and
is the number of transmissions that the data dissemination process requires without coding and  is the number of transmissions required with XORs coding. Assume that the probability that receiver
is the number of transmissions required with XORs coding. Assume that the probability that receiver  is in sleep mode is
is in sleep mode is  at each time slot, and
at each time slot, and  is the probability that receiver
is the probability that receiver  can not successfully receive a packet even when it is in active mode due to unreliable wireless communication. We have the following two lemmas.
can not successfully receive a packet even when it is in active mode due to unreliable wireless communication. We have the following two lemmas.
Lemma 1.
The total number of transmissions without coding required for transmitting sufficient large  packets to
packets to  receivers is
receivers is

where  and
and  ,
,  .
.
Proof.
See Appendix .
Lemma 2.
The total number of transmissions with XORs coding for transmitting sufficient large  packets to
packets to  receivers is
receivers is

Proof.
See Appendix .
With the analytical result of  and
and  , we can define analytical network coding gain as
, we can define analytical network coding gain as

Take two receivers as an example, assume that  ,
,  ,
,  ,
,  and
and  is sufficient large. According to (8) and (9), we can calculate that
is sufficient large. According to (8) and (9), we can calculate that  M,
M,  M. Then, the analytical network coding gain is
M. Then, the analytical network coding gain is  .
.
From Lemmas 1 and 2, we can also obtain the following corollary.
Corollary 1.
With two receivers, the maximum network coding gain  can be achieved if
can be achieved if  , that is,
, that is,  .
.
Proof.
See Appendix .
6.2. Impact of Sleep Probability on Energy Consumption
Though sleep scheduling can save energy consumption due to idle listening, sensors in sleep mode cannot receive data packets, which imposes retransmission and may consume more energy. If sensor  is active at
is active at  th time slot, we say that
th time slot, we say that  th time slot is an active time slot for sensor
th time slot is an active time slot for sensor  . We know that only at its active time slot, sensor
. We know that only at its active time slot, sensor  consumes its energy. Thus, we can use the total number of active time slots consumed for the sensors to successfully receive the whole set of packets as the energy consumption for data dissemination.
consumes its energy. Thus, we can use the total number of active time slots consumed for the sensors to successfully receive the whole set of packets as the energy consumption for data dissemination.
We define a threshold as follows:

where  .
.
Then, we have the following lemma.
Lemma 3.
In XORs coding, if  , the current sleep scheduling can save energy consumed by idle listening; otherwise, the current sleep scheduling has no contribution to energy saving.
, the current sleep scheduling can save energy consumed by idle listening; otherwise, the current sleep scheduling has no contribution to energy saving.
Proof.
See Appendix .
Take two receivers with  ,
,  ,
,  ,
,  as an example, according to (11), we have
as an example, according to (11), we have  . Thus, the energy saving with sleep scheduling is offsetted by more retransmissions. In this case, the cluster head should wake up more sensors. An interesting problem is how to design an optimal sleep scheduling such that energy saving of sleep scheduling will not be offsetted by more retransmission, which is out of the scope of this paper.
. Thus, the energy saving with sleep scheduling is offsetted by more retransmissions. In this case, the cluster head should wake up more sensors. An interesting problem is how to design an optimal sleep scheduling such that energy saving of sleep scheduling will not be offsetted by more retransmission, which is out of the scope of this paper.
7. Simulation Results
In this section, we demonstrate the effectiveness of our dissemination schemes through simulations using C simulator. In our simulations, a multihop cluster hierarchical WSN is randomly generated with the fixed value of the number of sensors if without specification. We group the packets required to send into batches, and each batch has
simulator. In our simulations, a multihop cluster hierarchical WSN is randomly generated with the fixed value of the number of sensors if without specification. We group the packets required to send into batches, and each batch has  packets. Recovery process with network coding starts after every
packets. Recovery process with network coding starts after every  native packets are transmitted. In a cluster, we randomly generate sensor
native packets are transmitted. In a cluster, we randomly generate sensor  's sleep scheduling according to its sleeping probability
's sleep scheduling according to its sleeping probability  .
.
To demonstrate the advantage of our coding scheme, we introduce two baseline algorithms, namely, dissemination without coding algorithm and dissemination with random_coding algorithm. Dissemination without coding algorithm randomly transmits a native "wanted" packet at each time slot until all receivers obtain their "wanted" data packets while dissemination with random_coding algorithm transmits an XORs packet which is randomly generated at each time slot until all receivers obtain their "wanted" packets.
In the simulation, we are interested in evaluating the performance of our coding schemes from the following perspectives.
-
(i)
The number of active receivers that can obtain a new "wanted" packet at one time slot and the total number of transmissions required in one batch data dissemination within one cluster.
-
(ii)
The impact of the number of receiver sensors
 , batch size
, batch size 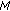 , sleep probability and packet loss probability on the network coding gain under different dissemination schemes within one cluster.
, sleep probability and packet loss probability on the network coding gain under different dissemination schemes within one cluster. -
(iii)
How close the performance of our proposed algorithms is to the derived analytical results within one cluster.
-
(iv)
The impact of the threshold
 on the delay and the total number of transmissions required in a multihop cluster hierarchy.
on the delay and the total number of transmissions required in a multihop cluster hierarchy.
For each setting, we simulate 150 instances and report the average performance.
7.1. Comparison with Different Data Dissemination Schemes
The effectiveness of our coding scheme for maximizing the expected number of sensors that can obtain one "wanted" packet at one time slot is demonstrated by comparing with dissemination without coding algorithm and dissemination with random_coding algorithm.
We evaluate the performance of our algorithms by varying the number of active sensors within a cluster at one time slot in the range of  for
for  , and
, and  . As shown in Figure 4, the number of active sensors that can obtain one "wanted" packet by our coding scheme is much more than that by dissemination without coding algorithm and dissemination with random_coding algorithm.
. As shown in Figure 4, the number of active sensors that can obtain one "wanted" packet by our coding scheme is much more than that by dissemination without coding algorithm and dissemination with random_coding algorithm.
For one batch data dissemination process within a cluster, to demonstrate the performance of our coding scheme, the total number of transmissions required is also compared with the other two baseline algorithms: dissemination without coding and dissemination with random_coding algorithms. We vary the number of packets needed to be sent in the range of  for
for  ,
,  ,
,  . As shown in Figure 5, the total number of transmissions required in one batch dissemination by our coding scheme is much less than that by dissemination without coding and dissemination with random_coding algorithms. Hence, for data dissemination with a large set of packets, our XORs coding scheme can efficiently decrease the number of transmissions required. Thus, more energy can be saved.
. As shown in Figure 5, the total number of transmissions required in one batch dissemination by our coding scheme is much less than that by dissemination without coding and dissemination with random_coding algorithms. Hence, for data dissemination with a large set of packets, our XORs coding scheme can efficiently decrease the number of transmissions required. Thus, more energy can be saved.
7.2. Network Coding Gain Comparison with Analytical Results
We demonstrate the effectiveness of the proposed network coding algorithm by comparing the network coding gain obtained through simulation with the analytical network coding gain.
We start with a simple experiment where there are only two members sensors in a cluster. We fix  to 0.2 and vary
to 0.2 and vary  in the range of
in the range of  for
for  . As shown in Figure 6(a), the network coding gain obtained by our simulation follows the same trend as the analytical results. In addition, the maximum network coding gain is achieved when
. As shown in Figure 6(a), the network coding gain obtained by our simulation follows the same trend as the analytical results. In addition, the maximum network coding gain is achieved when  with both our simulation results and analytical results, which verifies Corollary 1. When
with both our simulation results and analytical results, which verifies Corollary 1. When  , most likely the "wanted" packets at one receiver are the packets available at another receiver, thus, coding opportunity is high, which achieves maximum network coding gain.
, most likely the "wanted" packets at one receiver are the packets available at another receiver, thus, coding opportunity is high, which achieves maximum network coding gain.
We also extend the simulation to 10 receivers in a cluster. The loss probability of  is varied along the x-axis for
is varied along the x-axis for  ;
;  ,
,  ;
;  ,
,  and
and  ,
,  ,
,  ,
,  ,
,  . As shown in Figure 6(b), the simulation results are very close to the analytical results. In addition, Figure 6 verifies that network coding indeed can bring gains on reducing the number of transmissions required.
. As shown in Figure 6(b), the simulation results are very close to the analytical results. In addition, Figure 6 verifies that network coding indeed can bring gains on reducing the number of transmissions required.
In Figure 7, we vary the sleep probability at sensors, similar results as Figure 6 can be observed and the network coding gain obtained through simulations is quite close to the analytical results.
7.3. The Impact of Sleep Scheduling on Energy Saving
We now study the impact of sleep scheduling on the energy consumption. Our simulation is conducted within one cluster. We use the total number of active time slots consumed to denote the energy consumption in data dissemination process.
Suppose that XORs coding is applied. Let  be the total number of active time slots consumed for data dissemination with sleep scheduling and
be the total number of active time slots consumed for data dissemination with sleep scheduling and  be the total number of transmissions for data dissemination without sleep scheduling. The energy saving in XORs coding with sleep scheduling over that without sleep scheduling is
be the total number of transmissions for data dissemination without sleep scheduling. The energy saving in XORs coding with sleep scheduling over that without sleep scheduling is

For data dissemination without coding, we can define energy saving with sleep scheduling over that without sleep scheduling in a similar way.
We evaluate the performance of our algorithm by varying  in
in  for
for  ,
,  ,
,  ,
,  ,
,  . As shown in Figure 8, the simulation results are very close to the analytical results.
. As shown in Figure 8, the simulation results are very close to the analytical results.
For our XORs coding, from the figure, we know that the energy consumption with sleep scheduling is less than that without sleep scheduling when  is less than 0.15. When
is less than 0.15. When  , the energy consumption with sleep scheduling is equal to that without sleep scheduling. When
, the energy consumption with sleep scheduling is equal to that without sleep scheduling. When  is larger than 0.15, sleep scheduling has no contribution to the energy saving, it even incurs more energy consumption than that without sleep scheduling. This interesting result is plausible since when the number of sleep sensors becomes larger, more retransmissions are required, which imposes more energy consumption. In this case, the energy saving with sleep scheduling is offsetted by more retransmissions, which means that the threshold
is larger than 0.15, sleep scheduling has no contribution to the energy saving, it even incurs more energy consumption than that without sleep scheduling. This interesting result is plausible since when the number of sleep sensors becomes larger, more retransmissions are required, which imposes more energy consumption. In this case, the energy saving with sleep scheduling is offsetted by more retransmissions, which means that the threshold  and the cluster head should wake up more sensors to receive packets in order to save energy.
and the cluster head should wake up more sensors to receive packets in order to save energy.
7.4. The Impact of Threshold  on the Delay and the Total Number of Transmissions Required
on the Delay and the Total Number of Transmissions Required
We now study the impact of threshold  on the delay of the data dissemination process in a multihop cluster hierarchical WSN. The threshold
on the delay of the data dissemination process in a multihop cluster hierarchical WSN. The threshold  is varied in the range of
is varied in the range of  for
for  . Figure 9 gives the delay required for data dissemination when the number of layers is 5 and 6, respectively. We can see that the delay increases with the threshold
. Figure 9 gives the delay required for data dissemination when the number of layers is 5 and 6, respectively. We can see that the delay increases with the threshold  . This is because the cluster heads need to wait more time before they can transmit their available packets to their members with the increasing of
. This is because the cluster heads need to wait more time before they can transmit their available packets to their members with the increasing of  . Thus, the cluster heads in down layers can do nothing for a long time. Specifically, when
. Thus, the cluster heads in down layers can do nothing for a long time. Specifically, when  , each cluster head cannot transmit its available packets until receiving all
, each cluster head cannot transmit its available packets until receiving all  packets. In this case, concurrent transmissions cannot be allowed even if there is no collision between them, which thus increases the delay. From Figure 9, we can also see that the delay increases with the number of layers, because the number of receivers increases with the number of layers.
packets. In this case, concurrent transmissions cannot be allowed even if there is no collision between them, which thus increases the delay. From Figure 9, we can also see that the delay increases with the number of layers, because the number of receivers increases with the number of layers.
We further study the impact of the threshold  on the total number of transmissions required under a multihop cluster hierarchical WSN. The threshold
on the total number of transmissions required under a multihop cluster hierarchical WSN. The threshold  is also varied in the range of
is also varied in the range of  for
for  . As shown in Figure 10, the total number of transmissions required decreases with the threshold
. As shown in Figure 10, the total number of transmissions required decreases with the threshold  . When
. When  is small, the cluster heads transmit the packets to their members more quickly. Therefore, the number of fresh packets available at cluster heads is small, which can not fully utilize the network coding gain. Hence, the total number of transmissions required is more than with larger threshold
is small, the cluster heads transmit the packets to their members more quickly. Therefore, the number of fresh packets available at cluster heads is small, which can not fully utilize the network coding gain. Hence, the total number of transmissions required is more than with larger threshold  .
.
8. Conclusion
This paper studies data dissemination in wireless sensor networks with network coding to achieve energy efficiency. In order to quickly complete the whole process of data dissemination, at each time slot in the recovery process, we aim to transmit an encoded packet such that the expected number of active sensors that can decode out one "wanted" packet is maximized. A maximum weight clique model is proposed here to achieve such an objective. We further study the impact of packet loss probability and sleep probability on network coding gain. We also analyze the impact of sleep probability on energy saving gain and derive a threshold which can be used to decide whether the current sleep scheduling is effective on energy saving or not. The simulation results verify the work proposed in the paper.
References
Hui JW, Culler D: The dynamic behavior of a data dissemination protocol for network programming at scale. Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems (SenSys '04), November 2004, Baltimore, Md, USA 81-94.
Liang C-JM, Musǎloiu-E R, Terzis A: Typhoon: a reliable data dissemination protocol for wireless sensor networks. Proceedings of the 5th European Conference on Wireless Sensor Networks (EWSN '08), January 2008, Lecture Notes in Computer Science 4913: 268-285.
Wan C-Y, Campbell AT, Krishnamurthy L: PSFQ: a reliable transport protocol for wireless sensor networks. Proceedings of the 1st ACM International Workshop on Wireless Sensor Networks and Applications, September 2002, Atlanta, Ga, USA 1-11.
Kulkarni SS, Wang L: MNP: multihop network reprogramming service for sensor networks. Proceedings of the 25th IEEE International Conference on Distributed Computing Systems (ICDCS '05), June 2005 7-16.
Lu G, Sadagopan N, Krishnamachari B, Goel A: Delay efficient sleep scheduling in wireless sensor networks. Proceedings of the 24th IEEE Annual Joint Conference of the Computer and Communications Societies (INFOCOM '05), 2005, Miami, Fla, USA 4: 2470-2481.
Ye W, Heidemann J, Estrin D: An energy-efficient MAC protocol for wireless sensor networks. Proceedings of the 21st IEEE Annual Joint Conference of the Computer and Communications Societies (INFOCOM '02), 2002 3: 1567-1576.
Cerpa A, Wong JL, Kuang L, Potkonjak M, Estrin D: Statistical model of lossy links in wireless sensor networks. Proceedings of the 4th International Symposium on Information Processing in Sensor Networks (IPSN '05), 2005, Los Angeles, Calif, USA 81-88.
Nguyen D, Tran T, Nguyen T, Bose B: Wireless broadcast using network coding. IEEE Transactions on Vehicular Technology 2009, 58(2):914-925.
El Rouayheb SY, Chaudhry MAR, Sprintson A: On the minimum number of transmissions in single-hop wireless coding networks. Proceedings of the IEEE Information Theory Workshop (ITW '07), September 2007, Tahoe City, Calif, USA 120-125.
Zhan C, Xu Y, Wang J, Lee V: Reliable multicast in wireless networks using network coding. Proceedings of the 6th International Conference on Mobile Adhoc and Sensor Systems (MASS '09), 2009, Macau, China 506-515.
Ahlswede R, Cai N, Li S-YR, Yeung RW: Network information flow. IEEE Transactions on Information Theory 2000, 46(4):1204-1216. 10.1109/18.850663
Fragouli C, Soljanin E: Information flow decomposition for network coding. IEEE Transactions on Information Theory 2006, 52(3):829-848.
Fragouli C, Le Boudec J-Y, Widmer J: Network coding: an instant primer. Computer Communication Review 36(1):63-68.
Deb S, Effros M, Ho T: Network coding for wireless applications: a brief tutorial. Proceedings of the International Workshop on Wireless Adhoc Networks (IWWAN '05), May 2005
Ghaderi M, Towsley D, Kurose J: Reliability gain of network coding in lossy wireless networks. Proceedings of the 27th IEEE Conference on Computer Communications (INFOCOM '08), April 2008, Phoenix, Ariz, USA 2171-2179.
Lin Y, Liang B, Li B: Data persistence in large-scale sensor networks with decentralized fountain codes. Proceedings of the 26th IEEE International Conference on Computer Communications (INFOCOM '07), May 2007, Anchorage, Alaska, USA 1658-1666.
Hou I-H, Tsai Y-E, Abdelzaher TF, Gupta I: AdapCode: adaptive network coding for code updates in wireless sensor networks. Proceedings of the 27th IEEE Conference on Computer Communications (INFOCOM '08), 2008, Phoenix, Aariz, USA 1517-1525.
Katti S, Rahul H, Hu W, Katabi D, Medard M, Crowcroft J: XORs in the air: practical wireless network coding. IEEE/ACM Transactions on Networking 2008, 16(3):497-510.
Rayanchu S, Sen S, Wu J, Baneriee S, Senqupta S: Loss-aware network coding for unicast wireless sessions: design, implementation, and performance evaluation. Proceedings of the ACM International Conference on Measurement and Modeling of Computer Systems (SIGMETRICS '08), 2008, Annapolis, Md, USA 85-96.
Kuo F-C, Tan K, Li XY, Zhang J, Fu X: XOR rescue: exploiting network coding in lossy wireless networks. Proceedings of the 6th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON '09), June 2009, Rome, Italy 1-9.
Banerjee S, Khuller S: A clustering scheme for hierarchical control in wireless networks. Proceedings of the 20th IEEE Annual Joint Conference of the Computer and Communications Societies (INFOCOM '01), 2001 1028-1037.
Iwanicki K, Van Steen M: Multi-hop cluster hierarchy maintenance in wireless sensor networks: a case for gossip-based protocols. In Proceedings of the 6th European Conference on Wireless Sensor Networks, February 2009, Cork, Ireland. Springer; 102-117.
Hartl G, Li B: Loss inference in wireless sensor networks based on data aggregation. Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks (IPSN '04), April 2004 396-404.
Chachulski S, Jennings M, Katti S, Katabi D: Trading structure for randomness in wireless opportunistic routing. Proceedings of the ACM Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications (SIGCOMM '07), 2007, Kyoto, Japan 169-180.
Acknowledgment
This paper is supported by the National Science Foundation of China under Grant no. 60773036.
Author information
Authors and Affiliations
Corresponding author
Appendices
A. Proof of Lemma 1
According to [8], we can obtain that the total number of transmissions without coding to successfully deliver sufficient large  packets to
packets to  receivers is
receivers is  , where each receiver keeps in active mode during data transmission process.
, where each receiver keeps in active mode during data transmission process.
However, in the data dissemination process, receiver sensor  may be in sleep mode and can not successfully receive a packet. Therefore, the probability that sensor
may be in sleep mode and can not successfully receive a packet. Therefore, the probability that sensor  can successfully receive the packet at any time slot is
can successfully receive the packet at any time slot is  . In other words, the probability that sensor
. In other words, the probability that sensor  will lose the packet is
will lose the packet is  . Thus, considering sleep scheduling, the total number of transmissions required without coding is
. Thus, considering sleep scheduling, the total number of transmissions required without coding is


where  and
and  ,
,  .
.
B. Proof of Lemma 2
From [8], we know that the total number of transmissions with XORs coding to successfully deliver sufficient large  packets to
packets to  receivers is
receivers is  , where each receiver keeps in active mode during the data transmission process.
, where each receiver keeps in active mode during the data transmission process.
As in Appendix , the probability that sensor  can not successfully receive the packet with sleep scheduling is changed into
can not successfully receive the packet with sleep scheduling is changed into  . Thus, the total number of transmissions required with XORs coding to transmit sufficient large
. Thus, the total number of transmissions required with XORs coding to transmit sufficient large  packets to
packets to  receivers is
receivers is


C. Proof of Corollary 1
With two receivers, from Lemma 1, the total number of transmissions required for  packets without coding is
packets without coding is  , and from Lemma 2, the total number of transmissions with XORs coding is
, and from Lemma 2, the total number of transmissions with XORs coding is  , where
, where  .
.
Without loss of generality, suppose that  and
and  ,
,  . We have
. We have


Define a function  with
with  being the variable. We can easily prove that
being the variable. We can easily prove that  is an increasing function. Thus, when
is an increasing function. Thus, when  is 1, the value of function
is 1, the value of function  is maximum. That is when
is maximum. That is when  , the network coding gain
, the network coding gain  is maximum, which proves our Corollary 1.
is maximum, which proves our Corollary 1.
D. Proof of Lemma 3
From the analysis in the previous section, we can see that the total number of active time slots consumed for data dissemination with XORs coding is


where  is the probability that sensor
is the probability that sensor  is in sleep mode at each time slot.
is in sleep mode at each time slot.
However, if there is no sleep scheduling at sensors, that is  , the total number of transmissions for disseminating sufficient large
, the total number of transmissions for disseminating sufficient large  packets to
packets to  receivers with XORs coding is
receivers with XORs coding is


Since no sensors are in sleep mode, the total number of active time slots consumed for disseminating packets with XORs coding is


From the above formulation, we know that only if  , sleep scheduling has contribution to save energy consumed by idle listening, otherwise, the retransmission due to sleep scheduling in sensors imposes more energy consumption. The above
, sleep scheduling has contribution to save energy consumed by idle listening, otherwise, the retransmission due to sleep scheduling in sensors imposes more energy consumption. The above  changes into
changes into


That is


where  .
.
Thus, if (D.8) can be satisfied, the current sleep scheduling must have contribution to save energy compared with no sleep scheduling.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, X., Wang, J. & Xu, Y. Data Dissemination in Wireless Sensor Networks with Network Coding. J Wireless Com Network 2010, 465915 (2010). https://doi.org/10.1155/2010/465915
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/465915

 , if
, if 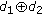 is sent, all four receivers can obtain a "wanted" packet by
is sent, all four receivers can obtain a "wanted" packet by 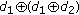 or
or 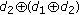 . Eventually, it will take 8 time slots to finish the data dissemination process as shown in Figure
. Eventually, it will take 8 time slots to finish the data dissemination process as shown in Figure 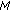 native packets are sent followed by the recovering process [
native packets are sent followed by the recovering process [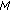 native packets are received by all sensors in the cluster, the cluster head proceeds to transmit the following batch of packets. The data dissemination is accomplished when all batches of packets are obtained by all sensor nodes in the network. In Figure
native packets are received by all sensors in the cluster, the cluster head proceeds to transmit the following batch of packets. The data dissemination is accomplished when all batches of packets are obtained by all sensor nodes in the network. In Figure 
 is true, there must be exactly one true assignment for
is true, there must be exactly one true assignment for  . Without loss of generality, we assume that
. Without loss of generality, we assume that  is true while
is true while 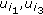 are both false. According to the construction of the instance, only
are both false. According to the construction of the instance, only 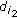 is participated in encoding while neither
is participated in encoding while neither  nor
nor 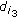 is participated in encoding. In other words, only one lost packet of
is participated in encoding. In other words, only one lost packet of 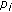 is participated in encoding and
is participated in encoding and 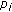 has all other packets involved in encoding, thus,
has all other packets involved in encoding, thus, 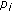 can decode out one "wanted" native packet
can decode out one "wanted" native packet 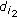 . Therefore, if there is a clause which is true in the MAXIMUM ONE-IN-THREE SAT problem, there must be a receiver which can obtain a "wanted" native packet. Then, we have
. Therefore, if there is a clause which is true in the MAXIMUM ONE-IN-THREE SAT problem, there must be a receiver which can obtain a "wanted" native packet. Then, we have 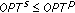 .
.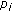 can decode a new native packet
can decode a new native packet 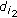 from the encoded one. According to the decoding strategy, the other two "wanted" packets
from the encoded one. According to the decoding strategy, the other two "wanted" packets  must not be encoded into the new one, that is,
must not be encoded into the new one, that is, 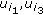 both have false assignment while
both have false assignment while 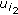 is true. In this assignment,
is true. In this assignment, 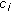 also has a true value. So, we have
also has a true value. So, we have 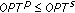 .
.
 , batch size
, batch size 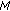 , sleep probability and packet loss probability on the network coding gain under different dissemination schemes within one cluster.
, sleep probability and packet loss probability on the network coding gain under different dissemination schemes within one cluster. on the delay and the total number of transmissions required in a multihop cluster hierarchy.
on the delay and the total number of transmissions required in a multihop cluster hierarchy.


 With
With 

 With
With 


 on the Delay and the Total Number of Transmissions Required
on the Delay and the Total Number of Transmissions Required
 . Hierarchy with 5 layersHierarchy with 6 layers
. Hierarchy with 5 layersHierarchy with 6 layers
 . Hierarchy with 5 layersHierarchy with 6 layers
. Hierarchy with 5 layersHierarchy with 6 layers