- Research Article
- Open access
- Published:
The Waterfilling Game-Theoretical Framework for Distributed Wireless Network Information Flow
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 482975 (2010)
Abstract
We present a general game-theoretical framework for power allocation in the downlink of distributed wireless small-cell networks, where multiple access points (APs) or small base stations send independent coded network information to multiple mobile terminals (MTs) through orthogonal channels. In such a game-theoretical study, a central question is whether a Nash equilibrium (NE) exists, and if so, whether the network operates efficiently at the NE. For independent continuous fading channels, we prove that the probability of a unique NE existing in the game is equal to 1. Furthermore, we show that this power allocation problem can be studied as a potential game, and hence efficiently solved. In order to reach the NE, we propose a distributed waterfilling-based algorithm requiring very limited feedback. The convergence behavior of the proposed algorithm is discussed. Finally, numerical results are provided to investigate the price of anarchy or inefficiency of the NE.
1. Introduction
Recently, there has been an increasing interest for small-cell networks. In fact, they have been recognized as an effective and low-cost architecture to provide wireless data rate access to Internet users [1, 2]. These networks consist of numerous and densely deployed APs, known as outdoor femto cells or small-cells, connected to an existing backbone network with heterogeneous links, for example, fibers, ADSLs, and power lines. The general idea is to provide signal coverage and high data rates in dense environments, that is, areas with high user concentrations, by installing low-cost wireless access nodes and exploiting the existing heterogeneous wired infrastructures without a new high-cost cabling. In reality, the femto nodes may belong to different service providers eventually organized in coalitions to maximize their own revenues. In such a context, there is a critical trade-off between cooperation and competition among different providers who may share information and resources to maximize their own revenues. In order to enable both cooperation among providers and network scalability, the femto nodes need self-organizing mechanisms to perform communications and network control functions. Thus, distributed algorithms accounting for the revenues of different providers play a key role in this context.
In contrast to the legacy cell networks, in a small-cell network a user may be served by more than one femto node. This feature is strategic to cope with the heterogeneity of the core network. In fact, if a user were only connected to a single out-door femto-cell, it would suffer from low throughput from time to time due to the limited-backhaul capacity, despite the presence of a high-speed wireless link. As a result, users would access simultaneously to different femto-cells in order to aggregate the sum capacity of the backhaul links.
In this paper, we describe a small-cell network with  MTs served simultaneously by
MTs served simultaneously by  femto nodes over
femto nodes over  orthogonal channels, for example, FDMA, TDMA, and OFDM. For such a system, and we study the power allocation problem under the constraint of maximum transmit power at each femto node (The issue of load balancing [3] in the wired network, and how the different packets are split with respect to the backhaul capacity from a main decentralized scheduler, although important, is not investigated in this paper. We assume that perfect load balancing holds). This system is substantially different from the ones typically analyzed in literature. In fact, it does not reduce to a classical downlink of a cellular network modeled as a broadcast channel since there are several APs transmitting information simultaneously to the same MT. Nor does it reduce to
orthogonal channels, for example, FDMA, TDMA, and OFDM. For such a system, and we study the power allocation problem under the constraint of maximum transmit power at each femto node (The issue of load balancing [3] in the wired network, and how the different packets are split with respect to the backhaul capacity from a main decentralized scheduler, although important, is not investigated in this paper. We assume that perfect load balancing holds). This system is substantially different from the ones typically analyzed in literature. In fact, it does not reduce to a classical downlink of a cellular network modeled as a broadcast channel since there are several APs transmitting information simultaneously to the same MT. Nor does it reduce to  independent multiple access channels when considering each mobile as a receiver because of the power constraints at the APs. Finally, the considered system does not reduce to a multicellular or an adhoc network modeled as an interference channel since all the signals received at each MT carry useful information to be decoded. In this paper we assume that each signal of interest is decoded considering the remaining signals as interference. This scheme is susceptible to improvement by joint decoding of all the received signals. However, this decoding approach exceeds the scope of this paper.
independent multiple access channels when considering each mobile as a receiver because of the power constraints at the APs. Finally, the considered system does not reduce to a multicellular or an adhoc network modeled as an interference channel since all the signals received at each MT carry useful information to be decoded. In this paper we assume that each signal of interest is decoded considering the remaining signals as interference. This scheme is susceptible to improvement by joint decoding of all the received signals. However, this decoding approach exceeds the scope of this paper.
In traditional wireless cellular networks, the power allocation is often implemented with centralized algorithms aiming at maximizing the sum of the Shannon transmission rate [4]. The maximization problem is solved by waterfilling algorithms [5–8] extended to multiuser contexts. The optimization is in general nonconvex but algorithms that reach local maximum are available [9–11]. Such a centralized power control scheme usually requires a unique shared resource allocation controller and complete channel state information (CSI) with consequent feedback and overhead. It is worth noting that this overload scales exponentially with the number of transmitters and receivers. Thus, such a fully centralized approach is not suitable for small-cell networks without centralized devices and with multiple service providers interested in their own revenues. Additionally, it is not scalable in dense networks.
Game theory [12] provides a possible analytical framework to develop decentralized and/or distributed algorithms for resource allocation in the context of interacting entities having eventually conflicting interests. Recently, noncooperative game theory and its analytical methodologies have been widely applied in wireless systems to solve communication control problems [13]. Distributed power allocation algorithms based on noncooperative games have been proposed for uplink single cell systems, that is, multiple access channels, and downlink multicellular networks or ad hoc networks, that is, interference channels. In [14], general results on potential games are provided and specialized to an uplink single-cell system with multiple access channel based on code division multiple access (CDMA). In [15], a digital subscriber line (DSL) is modeled as a multiple access system based on an OFDM scheme and an iterative waterfilling algorithm is proposed along the lines of the results in [16]. The classical uplink single-cell scenario is relaxed in [17] to include a jammer in the system and an iterative waterfilling algorithm is proposed.
In [16], power allocation on the interference channel is modeled as a noncooperative game, and the conditions for the existence and uniqueness of Nash equilibrium (NE) are established for a two-player version of the game. Similar conditions for the existence and uniqueness have been extended to the multiuser case in [18], where the authors focus on the practical design of distributed algorithms to compute the NE and propose an asynchronous iterative waterfilling algorithm for an interference channel. In [9], the so-called symmetric waterfilling game was studied. The authors assume that for a set of subchannels and receivers the channel gains from all transmitters are the same. The game is shown to have an infinite number of equilibria. The framework of the interference channel has been relaxed in [19] to include cognitive radio systems with transmitters and receivers equipped with multiple antennas, that is, multiple input multiple output (MIMO) systems. A distributive algorithm for the design of the beamformers at each secondary transmitter based on a noncooperative game is developped. Uniqueness and global stability of the Nash equilibrium are studied. Finally, it is worth to note that the DSL power allocation game in [15] is similar to our game from the mathematical point of view. However, it can be shown that with DSL crosstalk link channel coefficients the game in [15] is not a potential game. Therefore, in general, all the nice properties from potential games do not necessarily hold in their case.
In this paper, we adopt game-theoretical methodologies for power allocation problem in the downlink of small-cell networks (Note that a similar power allocation game can be considered for the uplink where MTs are the players taking decisions. However, it is impractical for MTs to have complete uplink CSI. Then, realistic models should take into account the assumption of knowledge reduction at the transmitters. The interested readers are referred to [20] for the framework of Bayesian games). We model femto cells of different operators as players who adaptively and rationally choose their transmission strategies, that is, their transmit power levels, with the aim of maximizing their own transmission sum-rates under maximum power constraints. We first consider the case where each femto cell decides its own power allocation based on the assumption of complete CSI. Later we remove this assumption, and we show that the same equilibrium can still be reached. In such a context it is important to characterize the NE set, for example, the existence and uniqueness of NE. This aspect plays a key role for the application of a distributed game-theoretical-based algorithm. In fact, the existence and uniqueness of an NE guarantees a predictable power allocation and the behavior of a self-organizing network. An answer to this relevant issue depends strongly on the channel fading statistics and the number of players of the investigated channel setting, as is apparent from the comparison of the results in [9–11]. We show that, for a quasi-static fading channel (a fading channel is quasi-static if it is constant during the transmission of a codeword but it may change from a codeword to the following one) with continuous probability density functions of the channel power attenuations, an NE exists and is unique with unit probability. Additionally, we point out that the considered game is a potential game and a simple decentralized algorithm based on the best-response algorithm can be readily proposed. However, a straightforward decentralized algorithm based on complete CSI would not be scalable since the required overhead would scale exponentially with the number of transmitters and receivers. Then, we propose a distributed iterative algorithm which requires the transmission of the total received power at each MT at each iteration step. With this distributed algorithm, the overhead scales only linearly with the number of receivers. The convergence rate of the proposed algorithm is analyzed. The price of anarchy is also investigated by numerical analysis.
The paper is organized as follows. In Section 2, we introduce the system model and formulate the problem. In Section 3, we study the existence and uniqueness of NE and characterize the NE set. In Section 4, we show that the game at hand is a potential game. Based on the property of potential games and observations on the required information, we propose a distributed algorithm converging to the NE. We investigate the convergence issue. Numerical analysis of the price of anarchy and the convergence rate are provided in Section 5. Section 6 concludes the paper by summarizing the main results and insights on the system behaviour acquired in this work.
2. System Model and Problem Statement
2.1. MultiSource MultiDestination System Model
We consider a wireless system in downlink with  noncooperative APs simultaneously sending information to
noncooperative APs simultaneously sending information to  MTs over
MTs over  orthogonal channels, for example, different time slots, frequency bands, or groups of subcarriers in time division multiple access (TDMA), frequency division multiple access (FDMA), or OFDM systems, respectively, as shown in Figure 2. Each channel is preassigned to a different MT by a scheduler and each MT receives signals only on the assigned channel. Without loss of generality, throughout this paper we assign channel
orthogonal channels, for example, different time slots, frequency bands, or groups of subcarriers in time division multiple access (TDMA), frequency division multiple access (FDMA), or OFDM systems, respectively, as shown in Figure 2. Each channel is preassigned to a different MT by a scheduler and each MT receives signals only on the assigned channel. Without loss of generality, throughout this paper we assign channel  to MT
to MT  , for
, for  . This implies that both the MT set and the channel set share the same index in our model. Note that the system model at hand does not reduce to a classical multiple access channel, a broadcast channel, or an interference channel [6].
. This implies that both the MT set and the channel set share the same index in our model. Note that the system model at hand does not reduce to a classical multiple access channel, a broadcast channel, or an interference channel [6].
We assume that the channels are block fading (in different scientific communities these channels are also referred to as quasi-static fading or delay constrained channels), that is, the fading coefficients are constant during the transmission of a codeword or block. Within a given transmission block, let  be the channel gain matrix whose
be the channel gain matrix whose  entry is
entry is  , the channel gain of the link from AP
, the channel gain of the link from AP  to MT
to MT  on the preassigned channel
on the preassigned channel  . The matrix
. The matrix  is random with independent entries. We further assume that the distribution function of each positive entry
is random with independent entries. We further assume that the distribution function of each positive entry  is a continuous function.
is a continuous function.
By assuming that the MTs use low-complexity single-user decoders [6], the signal-to-interference-plus-noise-ratio (SINR) of the signal from AP  received at MT
received at MT  is given by
is given by

where  is the power transmitted from AP
is the power transmitted from AP  on subchannel
on subchannel  , and
, and  is the variance of the white Gaussian noise. For AP
is the variance of the white Gaussian noise. For AP  , write the maximum achievable sum-rate as [6]
, write the maximum achievable sum-rate as [6]

and the power constraint as

where  is maximum transmit power of AP
is maximum transmit power of AP  and
and  for all
for all  .
.
2.2. Power Allocation as a NonCooperative Game
Here, we introduce the power allocation problem as a noncooperative strategic game. Because of the competitive nature of the APs, belonging in general to different service providers, AP  aims to maximize its own transmission rate
aims to maximize its own transmission rate  (2) by choosing its transmit power vector
(2) by choosing its transmit power vector  , subject to its power constraint (3). Denote by vector
, subject to its power constraint (3). Denote by vector  the outcome of the game in terms of transmit power levels of all
the outcome of the game in terms of transmit power levels of all  APs on the
APs on the  channels. We can completely describe this noncooperative power allocation game as
channels. We can completely describe this noncooperative power allocation game as

where the elements of the game are
-
(i)
Player set:
 ;
; -
(ii)
Strategy set:
 , where the strategy set of player
, where the strategy set of player  is
is (5)
(5) -
(iii)
Utility or payoff function set:
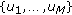 , with
, with (6)
(6)where
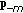 denotes the power vector of length
denotes the power vector of length  consisting of elements of
consisting of elements of  other than the
other than the 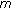 th element, that is,
th element, that is, (7)
(7)
In such a noncooperative game setting, each player  acts selfishly, aiming to maximize its own payoff, given other players' strategies and regardless of the impact of its strategy may have on other players and thus on the overall performance. The process of such selfish behaviors usually results in Nash equilibrium, a common solution concept for noncooperative games [21].
acts selfishly, aiming to maximize its own payoff, given other players' strategies and regardless of the impact of its strategy may have on other players and thus on the overall performance. The process of such selfish behaviors usually results in Nash equilibrium, a common solution concept for noncooperative games [21].
Definition 1.
A power strategy profile  is a Nash equilibrium If, for every
is a Nash equilibrium If, for every  ,
,

for all  .
.
From the previous definition, it is clear that an NE simply represents a particular "steady" state of a system, in the sense that, once reached, no player has any motivation to unilaterally deviate from it. The powers allocated in our system correspond to an NE.
3. Characterization of Nash Equilibrium Set
In many cases, an NE results from learning and evolution processes of all the game participants. Therefore, it is fundamental to predict and characterize the set of such points from the system design perspective of wireless networks. In the rest of the paper, we focus on characterizing the set of NEs. The following questions are addressed one by one.
-
(i)
Does an NE exist in our game?
-
(ii)
Is the NE unique or there exist multiple NE points?
-
(iii)
How to reach an NE if it exists?
-
(iv)
How does the system perform at NE?
Throughout this section we investigate the existence and uniqueness of a Nash equilibrium.
It is known that in general an NE point does not necessarily exist. In the following theorem we establish the existence of a Nash equilibrium in our game.
Theorem 1.
A Nash equilibrium exists in game  .
.
Proof.
Since  is convex, closed, and bounded for each
is convex, closed, and bounded for each  ;
;  is continuous in both
is continuous in both  and
and  ; and
; and  is concave in
is concave in  for any set
for any set  , at least one Nash equilibrium point exists for
, at least one Nash equilibrium point exists for  [12, 22].
[12, 22].
Once existence is established, it is natural to consider the characterization of the equilibrium set. The uniqueness of an equilibrium is a rare but desirable property, if we wish to predict the network behavior. In fact, many game problems have more than one NE [12]. As an example of games with infinite NEs, we could consider a special case of our game  , namely, the symmetric waterfilling game [9] where the channel coefficients are assumed to be symmetric. Then, in general, our game
, namely, the symmetric waterfilling game [9] where the channel coefficients are assumed to be symmetric. Then, in general, our game  does not have a unique NE. But with the assumption of independent and identically distributed (i.i.d.) continuous entries in
does not have a unique NE. But with the assumption of independent and identically distributed (i.i.d.) continuous entries in  , we will show that the probability of having a unique NE is equal to
, we will show that the probability of having a unique NE is equal to  .
.
For any player  , given all other players' strategy profile
, given all other players' strategy profile  , the best-response power strategy
, the best-response power strategy  can be found by solving the following maximization problem:
can be found by solving the following maximization problem:

which is a convex optimization problem, since the objective function  is concave in
is concave in  and the constraint set is convex. Therefore, the Karush-Kuhn-Tucker (KKT) conditions for optimization are sufficient and necessary for the optimality [5]. The KKT conditions are derived from the Lagrangian for each player
and the constraint set is convex. Therefore, the Karush-Kuhn-Tucker (KKT) conditions for optimization are sufficient and necessary for the optimality [5]. The KKT conditions are derived from the Lagrangian for each player  ,
,

and are given by



where  for all
for all  and for all
and for all  are dual variables associated with the power constraint and transmit power positivity, respectively. The solution to (11)–(13) is known as waterfilling [6]:
are dual variables associated with the power constraint and transmit power positivity, respectively. The solution to (11)–(13) is known as waterfilling [6]:

where  and
and  satisfies
satisfies

In order to analyze the equilibrium set, we establish necessary and sufficient conditions for a point being an NE in the game 
Theorem 2.
A power strategy profile  is a Nash equilibrium of the game
is a Nash equilibrium of the game  if and only if each player's power
if and only if each player's power  is the single-player waterfilling result
is the single-player waterfilling result  while treating other players' signals as noise. The corresponding necessary and sufficient conditions are:
while treating other players' signals as noise. The corresponding necessary and sufficient conditions are:



The proof can be found in Appendix A.
From (16), it is easy to verify that necessarily  , since
, since  and
and  for all
for all  and for all
and for all  . Also, from (17), we have
. Also, from (17), we have

This equation implies that, at the NE, all APs transmit at their maximum power by conveniently distributing the power over all the orthogonal channels.
However, it is still difficult to find an analytical solution from (16)–(18), since the system consisting of (14) and (15) is nonlinear. To simplify this problem, we could consider linear equations instead of nonlinear ones. The following lemma provides a key step in this direction.
Lemma 1.
For any realization of channel matrix  , there exist unique values of the Lagrange dual variables
, there exist unique values of the Lagrange dual variables  and
and  for any Nash equilibrium of the game
for any Nash equilibrium of the game  . Furthermore, there is a unique vector
. Furthermore, there is a unique vector  such that any vector
such that any vector  corresponding to a Nash equilibrium satisfies
corresponding to a Nash equilibrium satisfies

The proof can be found in Appendix B.
Now, let  be the following
be the following  matrix:
matrix:

where  is the
is the  th column of
th column of  ,
,  is the
is the  identity matrix, and
identity matrix, and  is the zero vector of length
is the zero vector of length  . Let
. Let  be the following vector of length
be the following vector of length  :
:

Then, (19) and (20) can be written in the form of linear matrix equation

Define the following sets:

and denote by  and
and  their cardinalities. From (18), if an index
their cardinalities. From (18), if an index  we must have
we must have  . Without loss of generality, we assume that
. Without loss of generality, we assume that  for
for  . Let
. Let  be the
be the  matrix formed from the first
matrix formed from the first  rows and first
rows and first  columns of
columns of  ,
,  is formed from the first
is formed from the first  elements of
elements of  , and
, and  is formed from the first
is formed from the first  elements of
elements of  . Then, any NE solution must satisfy
. Then, any NE solution must satisfy

Let  be the
be the  matrix formed from the columns of
matrix formed from the columns of  that correspond to the elements of
that correspond to the elements of  . Similarly, let
. Similarly, let  be the vector of length
be the vector of length  with entries
with entries  such that
such that  (same order as they were in
(same order as they were in  ). Then, any NE solution satisfies
). Then, any NE solution satisfies

Lemma 2.
For any realization of a random  channel gain matrix
channel gain matrix  with i.i.d. continuous entries, if
with i.i.d. continuous entries, if  , the probability that
, the probability that  is equal to
is equal to  .
.
Lemma 3.a
( ) If
) If  and
and  , the probability that
, the probability that  is equal to
is equal to  .
.
( ) If
) If  , the probability that
, the probability that  is equal to
is equal to  .
.
The proofs of Lemmas 2 and 3 can be found in Appendices C and D, respectively.
Based on Lemmas 1, 2, and 3, we derive the following theorem.
Theorem 3.
For any realization of a random  channel gain matrix
channel gain matrix  with statistically independent continuous entries, the probability that a unique Nash equilibrium exists in the game
with statistically independent continuous entries, the probability that a unique Nash equilibrium exists in the game  is equal to
is equal to  .
.
The proof can be found in Appendix E.
Thus, from Theorems 1 and 3, we have established the existence and uniqueness of NE in our game  .
.
4. Distributed Power Allocation and Its Convergence to the Nash Equilibrium
An equilibrium has practical interests only if it is reachable from nonequilibria states. In fact, there is no reason to expect a system to operate initially at equilibrium. The convergence of an algorithm to an equilibrium is in general a very hard problem usually related to the specific algorithm and requiring the analysis of synchronous or asynchronous update mechanisms (for power allocation algorithms in interference channels see [18, 23]).
4.1. Potential Game Approach
Fortunately, our game  can be studied as a potential game (The notation of potential games was firstly used for games in strategic form by Rosenthal (1973) [24], and later generalized and summarized by Monderer (1996) [25]). Potential games are known to have appealing properties for the convergence of the best-response or greedy algorithms to the equilibrium. All the potential games admit a potential function. This potential function is a unique global function that all the players optimize when they optimize their own utility functions. Thus, the set of pure Nash equilibria can be found by simply locating the local optima of the potential function. Such games have received increasing attention recently in wireless networks [14, 26, 27], since the existence of potential function enables the design of fully distributed algorithms for resource allocation problems. In fact, there are various notions of potential games such as exact potential, weighted potential, ordinal potential, generalized ordinal potential, pseudo potential, and so forth. These potential games could possess slightly different properties for the existence and convergence of NE. Here, we consider only the exact potential games, since they are closely related to our game. Exact potential games are defined in the following statement.
can be studied as a potential game (The notation of potential games was firstly used for games in strategic form by Rosenthal (1973) [24], and later generalized and summarized by Monderer (1996) [25]). Potential games are known to have appealing properties for the convergence of the best-response or greedy algorithms to the equilibrium. All the potential games admit a potential function. This potential function is a unique global function that all the players optimize when they optimize their own utility functions. Thus, the set of pure Nash equilibria can be found by simply locating the local optima of the potential function. Such games have received increasing attention recently in wireless networks [14, 26, 27], since the existence of potential function enables the design of fully distributed algorithms for resource allocation problems. In fact, there are various notions of potential games such as exact potential, weighted potential, ordinal potential, generalized ordinal potential, pseudo potential, and so forth. These potential games could possess slightly different properties for the existence and convergence of NE. Here, we consider only the exact potential games, since they are closely related to our game. Exact potential games are defined in the following statement.
Definition 2.
A strategic game  is an exact potential game if there exists a function
is an exact potential game if there exists a function  satisfying
satisfying

for all  . The function
. The function  is referred to as exact potential of the game.
is referred to as exact potential of the game.
Equation (27) implies that the NE of the original game  must coincide with the NE of the potential game, which is defined as a new game with
must coincide with the NE of the potential game, which is defined as a new game with  as an identical utility function for all the players. Therefore, we can transform the noncooperative strategic game
as an identical utility function for all the players. Therefore, we can transform the noncooperative strategic game  into a potential game, if we can find a potential function that quantifies the variation in terms of utility due to unilateral perturbation of each player's strategy, as indicated in (27).
into a potential game, if we can find a potential function that quantifies the variation in terms of utility due to unilateral perturbation of each player's strategy, as indicated in (27).
Taking inspiration from the result derived in the single channel case [14], we have the following lemma.
Lemma 4.
The game  is an exact potential game with the following potential function:
is an exact potential game with the following potential function:

Proof.
From (28) and (6), we observe that the first derivatives of  and
and  are equal, that is,
are equal, that is,

which implies that the property of exact potential (28) is satisfied. This completes the proof.
We denote by  the term
the term  which stands for the aggregate interference plus noise of user
which stands for the aggregate interference plus noise of user  on subchannel
on subchannel  . In order to find user
. In order to find user  's single-user best-response in the potential game, one needs to solve the following maximization problem:
's single-user best-response in the potential game, one needs to solve the following maximization problem:

Note that the problem (30) can be solved as a convex optimization, when the private channel gain  and the aggregate interference plus noise
and the aggregate interference plus noise  are both known to player
are both known to player  . It is easy to verify that this single-user best-response is the same waterfilling solution expressed in (14), due to the property of potential function.
. It is easy to verify that this single-user best-response is the same waterfilling solution expressed in (14), due to the property of potential function.
4.2. Distributed Algorithm and Convergence Property
Note that if each AP has complete CSI, that is, knowledge of the channel gain matrix  , defined as in Section 2, the uniqueness of the NE guaranties that each AP can determine independently the power allocation at the NE in a decentralized manner. In order to acquire information about the whole matrix
, defined as in Section 2, the uniqueness of the NE guaranties that each AP can determine independently the power allocation at the NE in a decentralized manner. In order to acquire information about the whole matrix  at each AP, a feedback channel is usually needed to transmit the channel estimations from MTs to APs. With this information, each AP can solve locally the system of equations (16)–(18) or perform locally a best-response algorithm based on the repeated maximization of problem (30) by starting from a random point
at each AP, a feedback channel is usually needed to transmit the channel estimations from MTs to APs. With this information, each AP can solve locally the system of equations (16)–(18) or perform locally a best-response algorithm based on the repeated maximization of problem (30) by starting from a random point  However, the structure of problem (30) suggests an alternative distributed approach to reduce eventually the signalling on the feedback channel. In fact, the repeated optimization of problem (30) can be performed in a distributed way by feeding back at each AP
However, the structure of problem (30) suggests an alternative distributed approach to reduce eventually the signalling on the feedback channel. In fact, the repeated optimization of problem (30) can be performed in a distributed way by feeding back at each AP  only the private channel gain
only the private channel gain  and the aggregate interference plus noise
and the aggregate interference plus noise  . Nevertheless, note that such a distributed implementation of the algorithm would lead to a transition phase where the APs are not transmitting at an equilibrium point. In our numerical results, we ignore the cost of feedback, and we focus on analyzing the theoretical upper-bound.
. Nevertheless, note that such a distributed implementation of the algorithm would lead to a transition phase where the APs are not transmitting at an equilibrium point. In our numerical results, we ignore the cost of feedback, and we focus on analyzing the theoretical upper-bound.
The above discussion yields a simple algorithm based on the iterative waterfilling [28] detailed in the following.
In this algorithm, we assume that the same game could be myopically played repeatedly: in each round, every myopic player (a myopic player has no memory of past game-rounds) chooses its best-response according to the single-player waterfilling that depends on the current state of the game. The following theorem shows the convergence and optimality of the algorithm.
Theorem 4.
The DPIWF algorithm converges to a unique Nash equilibrium of the noncooperative game  .
.
The proof can be found in Appendix F.
A more general discussion about the convergence and stability properties of potential games can be found in [25, 29]. In [25], it shows that every bounded potential game (a game is called a bounded game if the payoff functions are bounded) has the approximate finite improvement property (AFIP), that is, for every  , every
, every  -improvement path is finite. Then, it is obvious that every such finite improvement path of the exact potential games terminates in an
-improvement path is finite. Then, it is obvious that every such finite improvement path of the exact potential games terminates in an  -equilibrium point (an
-equilibrium point (an  -equilibrium is a strategy profile that approximately satisfies the condition of Nash equilibrium). In other words, the sequential best-response (players move in turn and always choose a best-response) converges to the
-equilibrium is a strategy profile that approximately satisfies the condition of Nash equilibrium). In other words, the sequential best-response (players move in turn and always choose a best-response) converges to the  -equilibrium independent of the initial point. Note that this is a very flexible condition for the convergence, since order of playing can be deterministic or random and need not to be synchronized. It is one of the most interesting properties of the potential games, especially in order to distributively find the equilibrium in self-organizing systems. In [29], it shows that potential games are characterized by strong stability properties (Lyapunov stable, see its definition in Theorem
-equilibrium independent of the initial point. Note that this is a very flexible condition for the convergence, since order of playing can be deterministic or random and need not to be synchronized. It is one of the most interesting properties of the potential games, especially in order to distributively find the equilibrium in self-organizing systems. In [29], it shows that potential games are characterized by strong stability properties (Lyapunov stable, see its definition in Theorem  of [29]). Also note that if the game has a unique NE, then it is globally stable.
of [29]). Also note that if the game has a unique NE, then it is globally stable.
In the simultaneous best-response algorithm all the players choose their best-responses simultaneously at each iteration. It is not difficult to verify that, in the general case, it does not necessarily converge, due to the "ping-pong" effect generated by myopic players. However, [30] has shown that for infinite pseudopotential games, a general class of games including also exact potential games, with convex strategy space and single-valued best-response (games with strictly multiconcave potential, concave in each players' unilateral deviation, have single-valued best-response), the sequence of simultaneous best-responses, reminiscent of fictitious play, also converges to the equilibrium.
It is interesting to note that for many practical systems with finite transmit power states, similar results still hold for the convergence of the sequential best-response. The only difference is that, in the finite case, the existence of exact potential function implies the finite improvement property (FIP), and therefore, the sequential best-response converges to the exact NE instead of an  -equilibrium.
-equilibrium.
Although the final convergence of the DPIWF algorithm is proved, one may wonder whether the optimum of the potential function (28) coincides with the optimum social welfare, that is, the optimal total information rate transmitted in the network. We discuss the price of anarchy in the following section.
5. Numerical Evaluation
In this part, numerical results are provided to validate our theoretical claims and assess the price of anarchy, that is, the performance loss in terms of the transmit sum-rate of all APs in the network due to a noncooperative game compared to the maximum social welfare. We denote this transmit sum-rate in the network as the actual total network rate, and defined it as

We consider frequency-selective fading channels with channel matrix  of size
of size  , where
, where  is the total number of transmitters (players) and
is the total number of transmitters (players) and  is the total number of receivers. We assume that the Rayleigh fading channel gain
is the total number of receivers. We assume that the Rayleigh fading channel gain  are i.i.d. among players and channels. The maximum power constraint for each player
are i.i.d. among players and channels. The maximum power constraint for each player  is assumed to be identical and normalized to
is assumed to be identical and normalized to  .
.
In Figure 3, we show the convergence behaviors of potential function and the actual total network rate, shortly referred to as "actual rate", by using the proposed DPIWF algorithm for a random channel realization. We set the number of transmitters to  and the number of receivers to
and the number of receivers to  . As expected, in both Figures 3(a) and 3(b) the potential function converges rapidly (at the 4th iteration). In Figure 3(a), the actual rate converges slightly slower (at the 6th iteration) and maintains a monotonically increasing slope. However, in Figure 3(b), the actual rate finally converges, but unfortunately it does not increase monotonically and it converges only at the 34th iteration with a convergence rate much slower than the potential function. Note that we use this example to show that a "defective" convergence may happen during the iteration steps.
. As expected, in both Figures 3(a) and 3(b) the potential function converges rapidly (at the 4th iteration). In Figure 3(a), the actual rate converges slightly slower (at the 6th iteration) and maintains a monotonically increasing slope. However, in Figure 3(b), the actual rate finally converges, but unfortunately it does not increase monotonically and it converges only at the 34th iteration with a convergence rate much slower than the potential function. Note that we use this example to show that a "defective" convergence may happen during the iteration steps.
In order to measure the performance efficiency of distributed networks operating at the unique NE, we provide here the optimal centralized approach as a target upper-bound for the total network rate. We ignore the performance loss caused by the necessary uplink and downlink signalling transmission. The total network rate maximization problem can be formulated as

The optimization problem (32) is difficult to solve since the objective function is nonconvex in  . However, a relaxation of this optimization problem [11] can be considered as a geometric programming problem [31]. As well known, a geometric programming can be transformed into a convex optimization problem and then solved in an efficient way. A low-complexity algorithm was proposed in [11] to solve the dual problem by updating dual variables through a gradient descent. Note that the algorithm always converges, but may converges to a local maximum point in a few cases. We use this algorithm in our simulations.
. However, a relaxation of this optimization problem [11] can be considered as a geometric programming problem [31]. As well known, a geometric programming can be transformed into a convex optimization problem and then solved in an efficient way. A low-complexity algorithm was proposed in [11] to solve the dual problem by updating dual variables through a gradient descent. Note that the algorithm always converges, but may converges to a local maximum point in a few cases. We use this algorithm in our simulations.
In the following part, we address two main practical questions through numerical results.
-
(1)
How does the network performance behave in average at the unique NE in comparison to the global optimal solution or global welfare? More precisely, we are interested in comparing the average total network rate instead of the instantaneous total network rate. We denote by
 the average total network rate for a
the average total network rate for a  transmitters and
transmitters and  receivers system, that is,
receivers system, that is,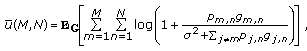 (33)
(33) -
(2)
What about the convergence behavior for the actual total network rate when using DPIWF algorithm? Does it converge as rapidly as in Figure 3(a) for the most of the cases?
Let us consider the first question. In Figure 4, we compare the average total network rate of both decentralized and centralized networks for two different channel noise levels  and
and  , respectively. The plots are obtained through Monte-Carlo simulations over
, respectively. The plots are obtained through Monte-Carlo simulations over  realizations for the channel gain matrix
realizations for the channel gain matrix  . Figures 4(a) and 4(b) show the total network rate as a function of the number of transmitters
. Figures 4(a) and 4(b) show the total network rate as a function of the number of transmitters  for different number of receivers
for different number of receivers  More specifically,
More specifically,  We note that in both Figures 4(a) and 4(b), the centralized optimal approach always outperforms the decentralized noncooperative algorithm. Additionally, for a fixed number of transmitters
We note that in both Figures 4(a) and 4(b), the centralized optimal approach always outperforms the decentralized noncooperative algorithm. Additionally, for a fixed number of transmitters  , when we increase the number of receivers
, when we increase the number of receivers  , the performance loss of decentralized systems compared to the centralized social welfare becomes greater and greater. This phenomenon can be intuitively understood as follows: when there is a great number of selfish players, the hostile competition turns the multiuser communication system into an interference-limited environment, where interference significantly degrade the performance efficiency.
, the performance loss of decentralized systems compared to the centralized social welfare becomes greater and greater. This phenomenon can be intuitively understood as follows: when there is a great number of selfish players, the hostile competition turns the multiuser communication system into an interference-limited environment, where interference significantly degrade the performance efficiency.
In Figure 4, we also note that for a fixed  the average performance of centralized systems is an increasing function of
the average performance of centralized systems is an increasing function of  , and the average performance of decentralized systems corresponding to NE reaches a maximum and then decreases flatting out. For the typical values of
, and the average performance of decentralized systems corresponding to NE reaches a maximum and then decreases flatting out. For the typical values of  , that is,
, that is,  , in Figure 4(a), when
, in Figure 4(a), when  the average performance of decentralized systems are maximized at
the average performance of decentralized systems are maximized at  , respectively; in Figure 4(b), when
, respectively; in Figure 4(b), when  the average performance of decentralized systems are maximized at
the average performance of decentralized systems are maximized at  , respectively. This comparison simply shows that different noise variance (in general channel condition) have a different impact on the decentralized system performance. This observation is fundamental for improving the spectral efficiency of a distributed multiuser small cell networks: For a given area, that is, a given number of receivers
, respectively. This comparison simply shows that different noise variance (in general channel condition) have a different impact on the decentralized system performance. This observation is fundamental for improving the spectral efficiency of a distributed multiuser small cell networks: For a given area, that is, a given number of receivers and given channel conditions, there exists an optimal number of access points, denoted as
and given channel conditions, there exists an optimal number of access points, denoted as to be installed in the network. Roughly speaking, when
to be installed in the network. Roughly speaking, when  , the system is saturated due to the increasing competition for the shared limited resources; when
, the system is saturated due to the increasing competition for the shared limited resources; when  , the system operates in a unsaturated state, since system resources are not fully exploited.
, the system operates in a unsaturated state, since system resources are not fully exploited.
Let us now consider the second question. In Figure 5, we show the probability of convergence to the NE within  iterations for
iterations for  and
and  , respectively. To be more precise, we say that the algorithm converges at the fifth iteration if the total network rate exceeds
, respectively. To be more precise, we say that the algorithm converges at the fifth iteration if the total network rate exceeds  of the rate at the NE. We find that the probability of convergence is satisfactory. It is greater than
of the rate at the NE. We find that the probability of convergence is satisfactory. It is greater than  in all cases and tends to
in all cases and tends to  when
when  and
and  . Another interesting observation is that the minimal convergence probability always occurs when
. Another interesting observation is that the minimal convergence probability always occurs when  , regardless of the noise value
, regardless of the noise value  .
.
6. Conclusions and Future Works
In this paper, we study the power allocation problem in the wireless small-cell networks as a strategic noncooperative game. Each transmitter (AP) is modeled as a player in the game who decides, in a distributed way, how to allocate its total power through several independent fading channels. We studied the existence and uniqueness of NE. Under the condition of independent continuous fading channels, we showed that the probability of having a unique equilibrium is equal to  . The game at hand is shown to be a potential game. A distributed algorithm requiring very limited feedback has been proposed based on the potential game analysis. The convergence and stability issues have been addressed. Numerical studies have shown that the DPIWF algorithm can converge rapidly within
. The game at hand is shown to be a potential game. A distributed algorithm requiring very limited feedback has been proposed based on the potential game analysis. The convergence and stability issues have been addressed. Numerical studies have shown that the DPIWF algorithm can converge rapidly within  iterations with very high probability.
iterations with very high probability.
Algorithm 1: DPIWF algorithm.
initialize  ,
, 
repeat

for  to
to  do
do
for  to
to  do
do

end for

end for
until convergence
References
Debbah M: Mobile flexible networks: the challenges ahead. Proceedings of International Conference on Advanced Technologies for Communications (ATC '08), October 2008, Hanoi, Vietnam 3-7. invited paper
Kandula S, Katabi D, Sinha S, Berger A: Dynamic load balancing without packet reordering. ACM Journal of Computer and Communication Review 2007, 37(2):51-62. 10.1145/1232919.1232925
Shannon CE: A mathematical theory of communication. Bell System Technical Journal 1948, 27: 379-423, 623–656.
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, UK; 2004.
Cover TM, Thomas JA: Elements of Information Theory. John Wiley & Sons, New York, NY, USA; 1991.
Goldsmith AJ, Varaiya PP: Capacity of fading channels with channel side information. IEEE Transactions on Information Theory 1997, 43(6):1986-1992. 10.1109/18.641562
Tse D, Viswanath P: Fundamentals of Wireless Communication. Cambridge University Press, Cambridge, UK; 2005.
Altman E, Avrachenkov K, Garnaev A: Closed form solutions for symmetric water filling games. Proceedings of the 27th IEEE Communications Society Conference on Computer Communications (INFOCOM '08), April 2008, Phoenix, Ariz, USA 673-681.
Song KB, Chung ST, Ginis G, Cioffi JM: Dynamic spectrum management for next-generation DSL systems. IEEE Communications Magazine 2002, 40(10):101-109. 10.1109/MCOM.2002.1039864
Papandriopoulos J, Evans JS: Low-complexity distributed algorithms for spectrum balancing in multi-user DSL networks. Proceedings of the IEEE International Conference on Communications (ICC '06), July 2006 3270-3275.
Fudenberg D, Tirole J: Game Theory. MIT Press, Cambridge, Mass, USA; 1991.
Lasaulce S, Debbah M, Altman E: Methodologies for analyzing equilibria in wireless games: a look at pure, mixed, and correlated equilibria. IEEE Signal Processing Magazine 2009, 26(5):41-52.
Scutari G, Barbarossa S, Palomar DP: Potential games: a framework for vector power control problems with coupled constraints. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), May 2006, Toulouse, France 241-244.
Luo Z-Q, Pang J-S: Analysis of iterative waterfilling algorithm for multiuser power control in digital subscriber lines. EURASIP Journal on Applied Signal Processing 2006, 2006:-10.
Yu W, Ginis G, Cioffi JM: Distributed multiuser power control for digital subscriber lines. IEEE Journal on Selected Areas in Communications 2002, 20(5):1105-1115. 10.1109/JSAC.2002.1007390
Gohary RH, Huang Y, Luo Z-Q, Pang J-S: A generalized iterative water-filling algorithm for distributed power control in the presence of a Jammer. IEEE Transactions on Signal Processing 2009, 57(7):2660-2674.
Scutari G, Palomar DP, Barbarossa S: Asynchronous iIterative water-filling for Gaussian frequency-selective interference channels. IEEE Transactions on Information Theory 2008, 54(7):2868-2878.
Scutari G, Palomar DP: MIMO cognitive radio: a game theoretical approach. IEEE Transactions on Signal Processing 2010, 58(2):761-780.
He G, Debbah M, Altman E: A Bayesian game-theoretic approach for distributed resource allocation in fading multiple access channels. EURASIP Journal on Wireless Communications and Networking 2010, 2010:-10.
John N: Equilibrium points in N-person games. Proceedings of the National Academy of Sciences 1950, 36(1):48-49. 10.1073/pnas.36.1.48
Rosen JB: Existence and uniqueness of equilibrium points for concave N-person games. Econometrica 1965, 33: 520-534. 10.2307/1911749
Scutari G, Palomar DP, Barbarossa S: Simultaneous iterative water-filling for Gaussian frequency-selective interference channels. Proceedings of IEEE International Symposium on Information Theory (ISIT '06), July 2006 600-604.
Rosenthal RW: A class of games possessing pure-strategy Nash equilibria. International Journal of Game Theory 1973, 2(1):65-67. 10.1007/BF01737559
Monderer D, Shapley LS: Potential games. Games and Economic Behavior 1996, 14(1):124-143. 10.1006/game.1996.0044
Neel JO, Reed JH, Gilles RP: Convergence of cognitive radio networks. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC '04), March 2004, Atlanta, Ga, USA 4: 2250-2255.
Heikkinen T: A potential game approach to distributed power control and scheduling. Computer Networks 2006, 50(13):2295-2311. 10.1016/j.comnet.2005.09.010
Yu W: Competition and cooperation in multi-user communication environements, Ph.D. thesis. Stanford University; 2002. http://www.comm.utoronto.ca/~weiyu/thesis_2.pdf
Neel J: Analysis and design of cognitive radio networks and distributed radio resource management algorithms, PhD dissertation. September 2006. http://scholar.lib.vt.edu/theses/available/etd-12082006-141855/
Dubey P, Haimanko O, Zapechelnyuk A: Strategic complements and substitutes, and potential games. Games and Economic Behavior 2006, 54(1):77-94. 10.1016/j.geb.2004.10.007
Chiang M: Geometric programming for communication systems. Foundations and Trends in Communications and Information Theory 2005, 2(1-2):1-153. 10.1561/0100000005
Meyer CD: Matrix Analysis and Applied Linear Algebra. SIAM, Philadelphia, Pa, USA; 2000.
Acknowledgment
This paper was supported by the French research agency ANR by the Project ANR-09-VERS0: ECOSCELLS.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendices
A. Proof of Theorem 2
Proof.
We prove the necessary and sufficient parts separately.
-
(1)
Proof of necessary condition (the only if part). From the definition of NE (Definition 1), if a power set
 is an NE, it must satisfy all the best-response conditions in (8) simultaneously. Suppose a situation that all the players' power except player
is an NE, it must satisfy all the best-response conditions in (8) simultaneously. Suppose a situation that all the players' power except player 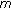 's power reaches the NE point:
's power reaches the NE point: 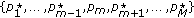 . In this case when all other players' powers are fixed, as shown in (9), the best-response of player
. In this case when all other players' powers are fixed, as shown in (9), the best-response of player  is to set its power according to (14)
is to set its power according to (14) This is exactly given by the single-player waterfilling treating all other players' signals as noise.
This is exactly given by the single-player waterfilling treating all other players' signals as noise. -
(2)
Proof of sufficient condition (the if part). From convex optimization theory [5], we know that the KKT conditions of the convex optimization problem are necessary and sufficient conditions for optimality. Therefore, we can say that a power strategy
 satisfies the best-response condition if and only if it satisfies the single-player KKT conditions (11)–(13). Then collectively, we say a set
satisfies the best-response condition if and only if it satisfies the single-player KKT conditions (11)–(13). Then collectively, we say a set 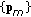 satisfies all the best-response conditions simultaneously if and only if it satisfies (16)–(18). From Definition 1, if a set
satisfies all the best-response conditions simultaneously if and only if it satisfies (16)–(18). From Definition 1, if a set 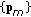 satisfies all the best-response conditions, it must be an NE.
satisfies all the best-response conditions, it must be an NE.
This completes the proof.
B. Proof of Lemma 1
Proof.
Consider an NE  Theorem 2 yields the following equation:
Theorem 2 yields the following equation:

where

Now, let us assume that there exist two different Nash equilibria, for example,  Then, the following equation must also hold:
Then, the following equation must also hold:

Equation (B.3) implies that

From the previous expressions, it is easy to see that (B.3) holds if and only if we have  and
and  These conditions are equivalent to the following:
These conditions are equivalent to the following:

First, from (B.5), we observe that the value of  with
with  is fixed for any NE point. Second, for a specific positive power coefficient, for example,
is fixed for any NE point. Second, for a specific positive power coefficient, for example,  , we must have
, we must have  due to (13). Therefore, from (25) we must also have
due to (13). Therefore, from (25) we must also have  . This implies
. This implies  because of (11). Finally, since
because of (11). Finally, since  is fixed for any NE point, we obtain
is fixed for any NE point, we obtain  for all
for all  The same proof holds for any other index
The same proof holds for any other index  .
.
C. Proof of Lemma 2
Proof.
When  , from (11) we have
, from (11) we have

where  . From Lemma 1, we know that all the Nash equilibria must satisfy (C.1), with the same
. From Lemma 1, we know that all the Nash equilibria must satisfy (C.1), with the same  and
and  . In (C.1), the number of independent linear equations is
. In (C.1), the number of independent linear equations is  , while the number of unknown parameters is
, while the number of unknown parameters is  since the remaining
since the remaining  are known to be
are known to be  It is well known that the set of solutions to a system of linear equations is empty, if the number of independent equations is larger than the number of variables [32]. Since each random entry
It is well known that the set of solutions to a system of linear equations is empty, if the number of independent equations is larger than the number of variables [32]. Since each random entry  is independently distributed with continuous distribution function, it is obvious that, with probability
is independently distributed with continuous distribution function, it is obvious that, with probability  , the equations of the system (C.1) are independent from each other. Therefore, we must have
, the equations of the system (C.1) are independent from each other. Therefore, we must have  .
.
D. Proof of Lemma 3
Proof.
We only give the proof for the case as  The case as
The case as  can be proved in a similar way. Matrix
can be proved in a similar way. Matrix  can be transformed into a
can be transformed into a  block matrices, by applying some elementary column and row operations, as follows:
block matrices, by applying some elementary column and row operations, as follows:

where  ,
,  .
.  is a
is a  matrix, where each column contains one or two random variables, and each row contains at least one random variable. Again we can transform
matrix, where each column contains one or two random variables, and each row contains at least one random variable. Again we can transform  in row echelon form, denoted as
in row echelon form, denoted as  . Note that the rank of
. Note that the rank of  is
is  with probability 1, since each leading coefficient of a row is a random variable or the linear combination of two i.i.d. random variables. So, with probability 0, any leading coefficient takes the value of 0. Therefore, we have
with probability 1, since each leading coefficient of a row is a random variable or the linear combination of two i.i.d. random variables. So, with probability 0, any leading coefficient takes the value of 0. Therefore, we have  with probability
with probability  .
.
E. Proof of Theorem 3
Proof.
If  , we have from Lemma 2 that, with probability 1,
, we have from Lemma 2 that, with probability 1,  . Any NE must satisfy (26); assume that two different power strategies
. Any NE must satisfy (26); assume that two different power strategies  and
and  are both solutions to (26). Then
are both solutions to (26). Then  . Since the rank of
. Since the rank of  is equal to the number of its columns, the rank-nullity theorem [32] implies
is equal to the number of its columns, the rank-nullity theorem [32] implies  Then, if the NE exists it is unique.
Then, if the NE exists it is unique.
If  , we have from Lemma 3 that, with probability
, we have from Lemma 3 that, with probability  , there is at most one solution to (25). Since any NE must satisfy (25) and we know that there is at least one NE solution, we conclude that NE is unique.
, there is at most one solution to (25). Since any NE must satisfy (25) and we know that there is at least one NE solution, we conclude that NE is unique.
F. Proof of Theorem 4
Proof.
We prove this theorem in two steps.
-
(1)
Algorithm convergence. It is easy to see that the potential function
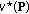 is nondecreasing within each round of the single-player waterfilling. Moreover, since each player's transmit power is limited by a maximum but finite power constraint, there must exist an upper-bound for the potential function
is nondecreasing within each round of the single-player waterfilling. Moreover, since each player's transmit power is limited by a maximum but finite power constraint, there must exist an upper-bound for the potential function 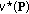 . This confirms the convergence.
. This confirms the convergence. -
(2)
Converge to NE. From the discussions above, we directly have that the KKT condition of the potential game coincide with the KKT condition of the original OFDM game
 , due to the property of potential function (27). By using the sufficient part of Theorem 2, we know that if each player's power allocation
, due to the property of potential function (27). By using the sufficient part of Theorem 2, we know that if each player's power allocation 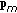 is given by the single-player waterfilling while treating other players's signals as noise, the set
is given by the single-player waterfilling while treating other players's signals as noise, the set  must be an NE of the original game
must be an NE of the original game  . Therefore, we can conclude that if the algorithm DPIWF converges (through the process of iterating single-player waterfilling), it converges to an NE point.
. Therefore, we can conclude that if the algorithm DPIWF converges (through the process of iterating single-player waterfilling), it converges to an NE point.
This completes the proof.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
He, G., Cottatellucci, L. & Debbah, M. The Waterfilling Game-Theoretical Framework for Distributed Wireless Network Information Flow. J Wireless Com Network 2010, 482975 (2010). https://doi.org/10.1155/2010/482975
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/482975


 ;
; , where the strategy set of player
, where the strategy set of player  is
is
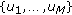 , with
, with
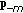 denotes the power vector of length
denotes the power vector of length  consisting of elements of
consisting of elements of  other than the
other than the 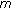 th element, that is,
th element, that is,

 the average total network rate for a
the average total network rate for a  transmitters and
transmitters and  receivers system, that is,
receivers system, that is,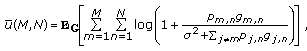




 iterations.
iterations.


 is an NE, it must satisfy all the best-response conditions in (8) simultaneously. Suppose a situation that all the players' power except player
is an NE, it must satisfy all the best-response conditions in (8) simultaneously. Suppose a situation that all the players' power except player 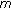 's power reaches the NE point:
's power reaches the NE point: 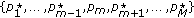 . In this case when all other players' powers are fixed, as shown in (9), the best-response of player
. In this case when all other players' powers are fixed, as shown in (9), the best-response of player  is to set its power according to (14)
is to set its power according to (14) This is exactly given by the single-player waterfilling treating all other players' signals as noise.
This is exactly given by the single-player waterfilling treating all other players' signals as noise. satisfies the best-response condition if and only if it satisfies the single-player KKT conditions (11)–(13). Then collectively, we say a set
satisfies the best-response condition if and only if it satisfies the single-player KKT conditions (11)–(13). Then collectively, we say a set 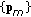 satisfies all the best-response conditions simultaneously if and only if it satisfies (16)–(18). From Definition 1, if a set
satisfies all the best-response conditions simultaneously if and only if it satisfies (16)–(18). From Definition 1, if a set 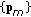 satisfies all the best-response conditions, it must be an NE.
satisfies all the best-response conditions, it must be an NE.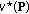 is nondecreasing within each round of the single-player waterfilling. Moreover, since each player's transmit power is limited by a maximum but finite power constraint, there must exist an upper-bound for the potential function
is nondecreasing within each round of the single-player waterfilling. Moreover, since each player's transmit power is limited by a maximum but finite power constraint, there must exist an upper-bound for the potential function 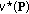 . This confirms the convergence.
. This confirms the convergence. , due to the property of potential function (27). By using the sufficient part of Theorem 2, we know that if each player's power allocation
, due to the property of potential function (27). By using the sufficient part of Theorem 2, we know that if each player's power allocation 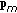 is given by the single-player waterfilling while treating other players's signals as noise, the set
is given by the single-player waterfilling while treating other players's signals as noise, the set  must be an NE of the original game
must be an NE of the original game  . Therefore, we can conclude that if the algorithm DPIWF converges (through the process of iterating single-player waterfilling), it converges to an NE point.
. Therefore, we can conclude that if the algorithm DPIWF converges (through the process of iterating single-player waterfilling), it converges to an NE point.