- Research Article
- Open access
- Published:
Group-Orthogonal Code-Division Multiplex: A Physical-Layer Enhancement for IEEE 802.11n Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 483758 (2010)
Abstract
The new standard for wireless local area networks (WLANs), named IEEE 802.11n, has been recently released. This new norm builds upon and remains compatible with the previous WLANs standards IEEE 802.11a/g while it is able to achieve transmission rates of up to 600 Mbps. These increased data rates are mainly a consequence of two important new features: (1) multiple antenna technology at transmission and reception, and (2) optional doubling of the system bandwidth thanks to the availability of an additional 20 MHz band. This paper proposes the use of Group-Orthogonal Code Division Multiplex (GO-CDM) as a means to improve the performance of the 802.11n standard by further exploiting the inherent frequency diversity. It is explained why GO-CDM synergistically matches with the two aforementioned new features and the performance gains it can offer under different configurations is illustrated. Furthermore, the effects that group-orthogonal has on key implementation issues such as channel estimation, carrier frequency offset, and peak-to-average power ratio (PAPR) are also considered.
1. Introduction
The last decade has seen an explosive growth in the deployment of wireless local area networks (WLANs) making the concept of nomadic computing a reality. Nowadays, most of these networks are based on one of the flavours of the IEEE 802.11 family of standards. The original standard, usually referred to as 802.11 legacy, was introduced with limited success in 1997. Operating at 2.4 GHz, it was based on direct sequence spread spectrum modulation (DSSS) and supported a maximum data rate of 2 Mbps. Wide WLAN deployment was achieved by the enhanced versions, IEEE 802.11a and IEEE 802.11b, released in 1999. The 11b version uses a refined form of DSSS, based on complementary code keying (CCK), allowing data rates up to 11 Mbps to be realised. In contrast, the 11a version operates at 5 GHz and it is based on orthogonal frequency division multiplexing (OFDM) leading to data rates up to 54 Mbps. More recently, in 2003, another OFDM-based version operating at 2.4 GHz, namely, IEEE 802.11g, has been introduced supporting the same data rates as 11a. The newer OFDM-based versions remain backward compatible with DSSS-based systems by switching to CCK when connecting to 802.11b equipment. A comprehensive treatment of WLANs standards can be found in [1].
Very recently, the standardization of what should be the next generation of WiFi systems, named IEEE 802.11n, has been completed by the IEEE 802.11 High Throughput Task Group committee [2]. The new standard supports much higher transmission rates thanks to the use of multiple antenna technology and other enhancements such as the possibility of operating on a 40 MHz bandwidth (employing more subcarriers), transmission modes using a reduced guard interval and frame aggregation to minimize the overhead introduced by packet preambles. In its fastest mode, 802.11n is expected to reach a transmission rate of 600 Mbps. Despite all the introduced enhancements, it is mandatory for the new standard to remain compatible with multicarrier legacy systems (802.11a/b/g) and therefore, 802.11n-compliant devices should have means to fall back to older 802.11 specifications when necessary. The standard incorporates three mechanisms to exploit the available spatial diversity in different MIMO configurations, namely, space-time block coding (STBC) [3], spatial division multiplexing (SDM) [4], and cyclic delay diversity (CDD) [5]. By appropriately combining these three techniques, different operating points in the bit rate versus reliability plane can be attained making 802.11n-compliant systems extremely flexible and adaptable to the environment and quality of service (QoS) requirements.
The new 802.11n standard, like its predecessors 802.11a and 802.11g, deals with the severe frequency selectivity of the indoor radio channel using OFDM. This is a block transmission scheme where the incoming user symbols are grouped, serial-to-parallel (S/P) converted, and modulated onto different subcarriers. Choosing the subcarriers to be orthogonal, and assuming perfect synchronisation, allows the block of symbols to be transmitted in parallel with minimal bandwidth usage and without interference. The S/P conversion allows the transmission rate to be reduced to a fraction of the original user rate combating in this way the frequency selectivity of the channel.
A significant improvement over conventional OFDM was the introduction of multicarrier code division multiplex (MC-CDM) by Kaiser in [6]. In MC-CDM, rather than transmitting a single symbol on each subcarrier as in conventional OFDM, symbols are code-division multiplexed by means of orthogonal spreading codes and simultaneously transmitted onto the available subcarriers. Since each symbol travels on more than one subcarrier, thus providing frequency diversity, MC-CDM offers improved resilience against subcarrier fading. This technique resembles very much the principle behind multicarrier code-division multiple access (MC-CDMA) [7] where each user is assigned a specific spreading code to share a group of subcarriers with other users. It should be noted that MC-CDMA and MC-CDM differ in the use made of the subcarriers: while in MC-CDMA subcarriers are employed to multiplex different users, in MC-CDM subcarriers are used to multiplex symbols from a given user. In MC-CDM, user multiplexing is typically implemented by means of time division multiple access (TDMA) or orthogonal frequency division multiple access (OFDMA). Group-orthogonal MC-CDMA (GO-MC-CDMA) [8] has recently been introduced as a particular flavour of MC-CDMA whereby users are split in groups and each group exclusively uses a (small) subset of all the available subcarriers. The subcarriers forming a group are chosen to be as separate as possible in the available bandwidth in order to maximise the frequency diversity gain [8]. A GO-MC-CDMA setup can be seen as many independent MC-CDMA systems of lower dimension operating in parallel. This reduced dimension allows the use of optimum receivers for each group based on maximum likelihood detection at a reasonable computational cost. Group-orthogonality has also been proposed for the (uncoded) MC-CDM systems in [9] where results are given for group dimensioning and spreading code selection. The idea is to split suitably interleaved symbols from a given user into orthogonal groups, and then, apply a spreading matrix on each group with the objective of further exploiting the channel frequency diversity. By keeping the group size relatively small, optimum detection can be implemented to fully use the available diversity.
The goal of this paper is to present an overview on the application of a particular flavour of MC-CDM, namely, group-orthogonal CDM (GO-CDM), within the context of IEEE 802.11n. This technique has been shown to be useful in those cases where the transmitter does not have a priori information about the state of the channel, hence this paper focuses on this scenario. It is shown how GO-CDM is able to exploit the extra diversity offered by the additional transmit antennas and larger bandwidth to improve the error performance while keeping the transmission and reception architectures computationally feasible. The rest of the paper is structured as follows. In Section 2, a concise description of the basic architecture of IEEE 802.11n physical layer is presented, particular attention is paid to the different multiple transmit antenna configurations the standard allows. Section 3 explains in detail the concept of GO-CDM and why it is a desirable extension to IEEE 802.11n. A receiver architecture for the enhanced system is proposed in Section 5. Numerical results are presented in Section 6 showing the gains achieved through GO-CDM while demonstrating its robustness against key implementation issues such as channel/offset estimation errors and peak-to-average power ratio (PAPR) performance. Finally, Section 7 concludes the paper by summarizing the main results.
This introduction ends with a notational remark. Vectors and matrices are denoted by lower- and uppercase bold letters, respectively. The  -dimensional identity matrix and the
-dimensional identity matrix and the  zero matrix (or vector) are represented by
zero matrix (or vector) are represented by  and
and  , respectively. The symbol
, respectively. The symbol  serves to denote a diagonal matrix with
serves to denote a diagonal matrix with  at its main diagonal and the operator
at its main diagonal and the operator  defines the Kronecker product of two matrices. Finally, superscript
defines the Kronecker product of two matrices. Finally, superscript  is used to denote the transpose of a vector (or matrix).
is used to denote the transpose of a vector (or matrix).
2. IEEE 802.11n General Transmitter
Figure 1 shows a block diagram of the definition of an IEEE 802.11n transmitter with the potential GO-CDM extension represented using dashed-line boxes. As seen in this figure, the transmission process begins by feeding the  scrambled information bits forming a packet into a 1/2-rate convolutional encoder that, after puncturing, achieves overall rates of 1/2, 2/3, 3/4, or 5/6 (optionally, the same rates can be attained by using a low density parity check (LDPC) encoder at different coding rates). The resulting coded bits are divided into
scrambled information bits forming a packet into a 1/2-rate convolutional encoder that, after puncturing, achieves overall rates of 1/2, 2/3, 3/4, or 5/6 (optionally, the same rates can be attained by using a low density parity check (LDPC) encoder at different coding rates). The resulting coded bits are divided into  spatial streams (support for
spatial streams (support for  is compulsory, whereas
is compulsory, whereas  remains optional), which will then be sent through different transmit antennas. Note that the IEEE 802.11n transmission modes used to fix the operating data rate, usually referred to as the modulation-coding set (MCS), are determined by the puncturing rate, the modulation alphabet, and, unlike previous standards, by the number of spatial streams. The bits on each spatial stream are interleaved and mapped to symbols from one of the allowed
remains optional), which will then be sent through different transmit antennas. Note that the IEEE 802.11n transmission modes used to fix the operating data rate, usually referred to as the modulation-coding set (MCS), are determined by the puncturing rate, the modulation alphabet, and, unlike previous standards, by the number of spatial streams. The bits on each spatial stream are interleaved and mapped to symbols from one of the allowed  -ary constellations (BPSK, QPSK, 16-QAM, or 64-QAM). Skipping for the moment the proposed GO-CDM steps represented by the dashed boxes in Figure 1 (see Section 3), the symbols on each stream, after serial-to-parallel conversion, are optionally supplied to an STBC encoder following the Alamouti coding rule [3]. An important point to mention here is that STBC takes place on a per subcarrier basis and between two successive OFDM symbols. Note that in this case, the multiple antennas are used to enhance performance, that is, lower the error rate, without increasing the throughput. The next step in the current IEEE 802.11n specification is the antenna mapping. This stage has a double function: first, it takes care of assigning the incoming flows (either original spatial streams or each output branch of the STBC) to transmit antennas; second, if there are more antennas than strictly necessary to support the number of spatial streams (with or without STBC), the antenna mapping stage distributes the incoming streams among all the available transmit antennas by means of an orthogonal spreading code (Walsh-Hadamard or Fourier) in order to fully exploit the available diversity. After antenna mapping, an optional cyclic delay (CD) can be added in order to implement cyclic delay diversity. At this point, symbols are modulated onto orthogonal subcarriers typically using an
-ary constellations (BPSK, QPSK, 16-QAM, or 64-QAM). Skipping for the moment the proposed GO-CDM steps represented by the dashed boxes in Figure 1 (see Section 3), the symbols on each stream, after serial-to-parallel conversion, are optionally supplied to an STBC encoder following the Alamouti coding rule [3]. An important point to mention here is that STBC takes place on a per subcarrier basis and between two successive OFDM symbols. Note that in this case, the multiple antennas are used to enhance performance, that is, lower the error rate, without increasing the throughput. The next step in the current IEEE 802.11n specification is the antenna mapping. This stage has a double function: first, it takes care of assigning the incoming flows (either original spatial streams or each output branch of the STBC) to transmit antennas; second, if there are more antennas than strictly necessary to support the number of spatial streams (with or without STBC), the antenna mapping stage distributes the incoming streams among all the available transmit antennas by means of an orthogonal spreading code (Walsh-Hadamard or Fourier) in order to fully exploit the available diversity. After antenna mapping, an optional cyclic delay (CD) can be added in order to implement cyclic delay diversity. At this point, symbols are modulated onto orthogonal subcarriers typically using an  -point inverse fast Fourier transform (IFFT). The number of subcarriers is set to
-point inverse fast Fourier transform (IFFT). The number of subcarriers is set to  when employing a single frequency band of 20 MHz or to
when employing a single frequency band of 20 MHz or to  if the second band is also available. Not all subcarriers are devoted to carry data, some of them are left unused as guard bands and some others are employed to carry pilots. These pilots are then used at reception for functions such as channel estimation or subcarrier synchronisation. This reduces the number of data subcarriers to
if the second band is also available. Not all subcarriers are devoted to carry data, some of them are left unused as guard bands and some others are employed to carry pilots. These pilots are then used at reception for functions such as channel estimation or subcarrier synchronisation. This reduces the number of data subcarriers to  (20 MHz) or
(20 MHz) or  (
( MHz). As a final step in the baseband processing, a guard interval (GI) is appended to each OFDM symbol in order to minimise interference among successive OFDM symbols. Finalising the transmission process, the baseband signals are upconverted to either 2.4 or 5 GHz and sent out through the available
MHz). As a final step in the baseband processing, a guard interval (GI) is appended to each OFDM symbol in order to minimise interference among successive OFDM symbols. Finalising the transmission process, the baseband signals are upconverted to either 2.4 or 5 GHz and sent out through the available  transmit antennas. It is worth noting the flexibility provided by this standard to exploit the spatial dimension by means of SDM, STBC, and/or CDD and their combinations depending on the number of spatial streams to be transmitted and the number of available antennas. The rest of the paper assumes that just one of the spatial mechanisms (either SDM, STBC or CDD) is in use at a given time, that is,
transmit antennas. It is worth noting the flexibility provided by this standard to exploit the spatial dimension by means of SDM, STBC, and/or CDD and their combinations depending on the number of spatial streams to be transmitted and the number of available antennas. The rest of the paper assumes that just one of the spatial mechanisms (either SDM, STBC or CDD) is in use at a given time, that is,  for CDD and STBC and
for CDD and STBC and  for SDM. Nevertheless, it is important to mention that the combination of either SDM or STBC with CDD does not imply significant changes in the system architecture as the CDD effects can be transparently embedded in the channel model. In contrast, the combination of SDM and STBC requires more sophisticated processing at reception (see [10]), and for simplicity of exhibition, this case will not be treated here.
for SDM. Nevertheless, it is important to mention that the combination of either SDM or STBC with CDD does not imply significant changes in the system architecture as the CDD effects can be transparently embedded in the channel model. In contrast, the combination of SDM and STBC requires more sophisticated processing at reception (see [10]), and for simplicity of exhibition, this case will not be treated here.
3. GO-CDM Enhancement
The dashed boxes in Figure 1 detail the steps required to implement the GO-CDM extension. These processing stages take place on a per-stream basis just after the modulation mapping stage and comprise the following steps for an arbitrary spatial stream  (with
(with  ).
).
-
(1)
Segmentation of the incoming symbol stream (including pilot symbols) into blocks of length
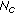 , and serial to parallel conversion (S/P) resulting in
, and serial to parallel conversion (S/P) resulting in 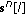 , with
, with 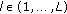 denoting the OFDM-symbol index and
denoting the OFDM-symbol index and 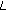 representing the number of OFDM-symbols per stream in a packet.
representing the number of OFDM-symbols per stream in a packet. -
(2)
Arrangement of the symbols in each block into groups
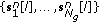 , where
, where 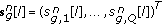 represents an individual group.
represents an individual group. -
(3)
Group spreading by linear combining,
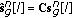 , where
, where 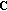 is a
is a 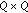 orthonormal matrix, typically chosen to be a rotated and scaled Walsh-Hadamard matrix [9].
orthonormal matrix, typically chosen to be a rotated and scaled Walsh-Hadamard matrix [9]. -
(4)
Frequency interleaver
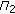 , operating across the different OFDM-symbols composing the packet, designed to ensure that modulated symbols from different OFDM-symbols in each group have experienced uncorrelated noise samples upon deinterleaving at the receiver end.
, operating across the different OFDM-symbols composing the packet, designed to ensure that modulated symbols from different OFDM-symbols in each group have experienced uncorrelated noise samples upon deinterleaving at the receiver end.Notice that the frequency interleaver
 implicitly performs the group subcarrier allocation taking care that subcarriers forming a group are frequentially well separated in order to maximise the frequency diversity gain. It is easy to show that, generally, this is achieved by choosing group subcarriers to be equispaced across the available bandwidth [8]. An special case to be taken into account is when CDD is employed, in which case a certain number of adjacent subcarriers are totally uncorrelated and therefore groups might be formed by combining both adjacent and well-separated subcarriers.
implicitly performs the group subcarrier allocation taking care that subcarriers forming a group are frequentially well separated in order to maximise the frequency diversity gain. It is easy to show that, generally, this is achieved by choosing group subcarriers to be equispaced across the available bandwidth [8]. An special case to be taken into account is when CDD is employed, in which case a certain number of adjacent subcarriers are totally uncorrelated and therefore groups might be formed by combining both adjacent and well-separated subcarriers.
Despite the proven benefits of CDM in uncoded scenarios [6], the benefits of CDM-OFDM are rather limited when measuring the coded performance in typical operating scenarios conforming to IEEE 802.11a specifications. This is due to the large subcarrier correlation found in many wireless environments, which severely limits the achievable frequency diversity gain [11]. However, GO-CDM becomes attractive in IEEE 802.11n when multiple transmit and receive antennae are employed and/or the expanded bandwidth (e.g., 40 MHz) is operational. Under these circumstances, the subcarrier correlation within a group can be greatly reduced by picking up the subcarriers forming a group taking into account the spatial dimension and/or the available wider bandwidth. Numerical results presented in Section 6 show that, when using an adequate receiver, GO-CDM becomes again an attractive add-on, leading to significant performance gains.
4. Channel Model
The channel linking an arbitrary pair of Tx and Rx antennas is assumed to be time varying and frequency selective with an scenario-dependent power delay profile  , common to all Tx-Rx pairs, given by
, common to all Tx-Rx pairs, given by

where  denotes the number of independent paths of the channel and
denotes the number of independent paths of the channel and  and
and  denote the power and delay of the
denote the power and delay of the  th path. The power delay profile is assumed to be normalized to unity (i.e.,
th path. The power delay profile is assumed to be normalized to unity (i.e.,  ). A particular realization of the channel impulse response between Tx-antenna
). A particular realization of the channel impulse response between Tx-antenna  and Rx-antenna
and Rx-antenna  at time instant
at time instant  has the form
has the form

where it holds that  . The corresponding frequency response is then given by
. The corresponding frequency response is then given by

which, when evaluated over the  operating subcarrier frequencies, yields the vector
operating subcarrier frequencies, yields the vector  where
where  . Given the group-based operation of the whole system, it is also useful to define the channel frequency response for the
. Given the group-based operation of the whole system, it is also useful to define the channel frequency response for the  th group as
th group as  . Provided that group subcarriers are chosen equispaced across the available bandwidth in order to maximise frequency diversity [8, 9], all groups will have statistically identical behaviour. Without loss of generality, and since groups are orthogonal to each other, subsequent modeling and analysis can solely focus on a single group. Moreover, assuming the channel to be static over the duration of a packet encompassing several OFDM symbols, the time index
. Provided that group subcarriers are chosen equispaced across the available bandwidth in order to maximise frequency diversity [8, 9], all groups will have statistically identical behaviour. Without loss of generality, and since groups are orthogonal to each other, subsequent modeling and analysis can solely focus on a single group. Moreover, assuming the channel to be static over the duration of a packet encompassing several OFDM symbols, the time index  can be dropped from this point onwards.
can be dropped from this point onwards.
5. Receiver for GO-CDM-Enhanced IEEE 802.11n
The proposed receiver structure is shown in Figure 2. The reception procedure invariably begins by demodulating the incoming signal to baseband frequency and, after discarding the guard interval, performing an FFT to recover the frequency domain information. Perfect synchronisation and a guard interval longer than the maximum channel delay are assumed. Both assumptions allow the derivation of a simple reception equation.
5.1. Reception Equation
The reception equation for the baseband samples of an arbitrary group depends on the spatial processing technique in use, therefore, each case is treated separately.
5.1.1. SDM
In a pure SDM system it holds that  and the reception equation for the
and the reception equation for the  th OFDM symbol can be written as
th OFDM symbol can be written as

where  contains the channel response for all Tx-Rx pairs over all frequencies forming a group and it is given by
contains the channel response for all Tx-Rx pairs over all frequencies forming a group and it is given by

 is the vector of transmitted symbols with
is the vector of transmitted symbols with  representing the
representing the  symbol vector transmitted on the
symbol vector transmitted on the  th antenna, and
th antenna, and  denotes the receiver noise.
denotes the receiver noise.
5.1.2. STBC
Focusing on the particular case of the Alamouti code (e.g.,  ), the optimal combining rule as given by Alamouti decoding (STBC preprocessing in Figure 2) can be merged with the channel matrix allowing the reception equation to be expressed as
), the optimal combining rule as given by Alamouti decoding (STBC preprocessing in Figure 2) can be merged with the channel matrix allowing the reception equation to be expressed as

where the channel-STBC combining matrix is defined as

with  , where
, where  represents the Alamouti combining step [12]. The transmitted symbol vector in this case is given by
represents the Alamouti combining step [12]. The transmitted symbol vector in this case is given by  . Finally,
. Finally,  is the AWGN component. Note in (6) that the index
is the AWGN component. Note in (6) that the index  is used to represent individual STBC blocks, each related to two consecutive OFDM sampling instants (e.g.,
is used to represent individual STBC blocks, each related to two consecutive OFDM sampling instants (e.g.,  ). It is easy to check that the matrix affecting symbol group
). It is easy to check that the matrix affecting symbol group  in (6), that is,
in (6), that is,  , has a 2-block diagonal structure thanks to the Alamouti code orthogonality. This implies that the symbols transmitted over the two time instants (
, has a 2-block diagonal structure thanks to the Alamouti code orthogonality. This implies that the symbols transmitted over the two time instants ( and
and  ) can be independently detected without any performance degradation.
) can be independently detected without any performance degradation.
5.1.3. CDD
When using CDD, the same information is transmitted, cyclically shifted, throughout the  transmit antennas. It is easy to show that, with a proper choice of the cyclic delays
transmit antennas. It is easy to show that, with a proper choice of the cyclic delays  [13], this amounts to transmit the same information from a single virtual antenna over the composite channel reaching receive antenna
[13], this amounts to transmit the same information from a single virtual antenna over the composite channel reaching receive antenna  given by
given by

In this case the reception equation takes the form of

where

 and
and  represents the additive noise component. Notice that, due to the CDD component, this is equivalent to transmit the information stream over a channel derived from a delay profile
represents the additive noise component. Notice that, due to the CDD component, this is equivalent to transmit the information stream over a channel derived from a delay profile  with increased frequency selectivity.
with increased frequency selectivity.
It is important to mention that the data symbols to be transmitted  , are suitably scaled to have power
, are suitably scaled to have power  , allowing the operating signal to noise ratio to be written as
, allowing the operating signal to noise ratio to be written as  .
.
5.2. Iterative Detection and Decoding
Despite different spatial processing techniques lead to different reception equations, it is obvious that all of them can be casted in a general equation of the form (to simplify notation, the time index ( for SDM/CDD and
for SDM/CDD and  for STBC) is omitted from this point onwards as OFDM symbols/STBC blocks are independent from one another)
for STBC) is omitted from this point onwards as OFDM symbols/STBC blocks are independent from one another)

where  represents the system matrix that gathers the channel, spatial processing, and frequency spreading effects,
represents the system matrix that gathers the channel, spatial processing, and frequency spreading effects,  is the vector of transmitted symbols over the group frequencies either from different antennas (SDM/CDD) or over different time instants (STBC), and
is the vector of transmitted symbols over the group frequencies either from different antennas (SDM/CDD) or over different time instants (STBC), and  represents the additive noise vector whose entries are zero-mean, uncorrelated and have variance
represents the additive noise vector whose entries are zero-mean, uncorrelated and have variance  (for STBC, the Alamouti decoding step is also included in the system matrix.). Given the general reception equation of (11), symbol estimates can be obtained using group-by-group maximum likelihood (ML) detection, a process that can be mathematically expressed as [8]
(for STBC, the Alamouti decoding step is also included in the system matrix.). Given the general reception equation of (11), symbol estimates can be obtained using group-by-group maximum likelihood (ML) detection, a process that can be mathematically expressed as [8]

A naive implementation of the ML detector would be computationally very demanding as its complexity grows exponentially with  ,
,  and
and  , therefore, alternatives should be sought. The list sphere detector (LSD) [14, 15] is an efficient method to conduct an exhaustive search among a set of candidates (i.e., ML detection) producing not only the most likely estimate but also a list with the closest candidates, which can then be used to form likelihood ratios (LLRs) for each bit (i.e., soft information). Moreover, this detector not only produces soft information but it can also incorporate any available a priori information (also in the form of LLRs) into the detection process. This feature, in combination with a soft-input soft-output channel decoder, allows the implementation of iterative reception schemes. Three factors play a role in limiting the computational complexity of this detector: first, a subset of candidates (the most likely ones), rather than an exhaustive list, is used when computing the LLRs [14], second, the detection is conducted on a per-group basis whose size, as shown in [9], can be kept relatively small (
, therefore, alternatives should be sought. The list sphere detector (LSD) [14, 15] is an efficient method to conduct an exhaustive search among a set of candidates (i.e., ML detection) producing not only the most likely estimate but also a list with the closest candidates, which can then be used to form likelihood ratios (LLRs) for each bit (i.e., soft information). Moreover, this detector not only produces soft information but it can also incorporate any available a priori information (also in the form of LLRs) into the detection process. This feature, in combination with a soft-input soft-output channel decoder, allows the implementation of iterative reception schemes. Three factors play a role in limiting the computational complexity of this detector: first, a subset of candidates (the most likely ones), rather than an exhaustive list, is used when computing the LLRs [14], second, the detection is conducted on a per-group basis whose size, as shown in [9], can be kept relatively small ( ) and last, group independence facilitates the parallelisation of the detection process.
) and last, group independence facilitates the parallelisation of the detection process.
For completeness, the derivation of the LLRs is now presented. To this end the transformation  is defined as the modulation mapping to arrive to symbol vector
is defined as the modulation mapping to arrive to symbol vector  from the corresponding group bits
from the corresponding group bits  (to simplify notation, the group index is skipped when referring to the bits) where
(to simplify notation, the group index is skipped when referring to the bits) where

Making use of the Max-log approximation, the LLR for a given bit,  , can be approximated by [14]
, can be approximated by [14]

where the symbols  and
and  represent the sets of
represent the sets of  bit vectors whose
bit vectors whose  th position is a "+1'' or "
th position is a "+1'' or " '', respectively. The
'', respectively. The  vector
vector  contains the a priori LLR for each bit in
contains the a priori LLR for each bit in  except for the
except for the  th bit. All a priori LLRs are assumed to be zero for the first iteration. Moderate values of
th bit. All a priori LLRs are assumed to be zero for the first iteration. Moderate values of  and/or
and/or  make the sets
make the sets  and
and  extremely large, making the search in (14) computationally unfeasible. To address this issue, LSD limits the search to the sets
extremely large, making the search in (14) computationally unfeasible. To address this issue, LSD limits the search to the sets  and
and  where
where  is the set containing the bit vectors corresponding to the
is the set containing the bit vectors corresponding to the  group candidates closer, in an Euclidean sense, to the received group vector, that is,
group candidates closer, in an Euclidean sense, to the received group vector, that is,  where
where  with
with  being the
being the  group candidates for which
group candidates for which  is smallest.
is smallest.
Notice in Figure 2 that each group detector, apart from the received samples  , gets as input the a priori LLRs for the bits in the group (
, gets as input the a priori LLRs for the bits in the group ( ), which will obviously be zero for the first iteration. In posterior iterations, the a priori LLRs can be incorporated into the information provided by the LSD to yield the a posteriori LLRs for each group (
), which will obviously be zero for the first iteration. In posterior iterations, the a priori LLRs can be incorporated into the information provided by the LSD to yield the a posteriori LLRs for each group ( ). The LLR De-grouping block takes care of gathering the LLRs produced by the detector for the different OFDM symbols composing the packet and structure them in the form of spatial streams
). The LLR De-grouping block takes care of gathering the LLRs produced by the detector for the different OFDM symbols composing the packet and structure them in the form of spatial streams  . As typically done in iterative schemes, only new (e.g., extrinsic) information is interchanged among the different subsystems. To this end, by subtracting the interleaved extrinsic information generated by the maximum a posteriori (MAP) decoder
. As typically done in iterative schemes, only new (e.g., extrinsic) information is interchanged among the different subsystems. To this end, by subtracting the interleaved extrinsic information generated by the maximum a posteriori (MAP) decoder  properly structured in streams
properly structured in streams  , the extrinsic information of the detection process is formed
, the extrinsic information of the detection process is formed  . Deinterleaving and spatial deparsing of
. Deinterleaving and spatial deparsing of  results in the a priori information for the MAP decoder, labeled in Figure 2 as
results in the a priori information for the MAP decoder, labeled in Figure 2 as  . The receiver deinterleaving (
. The receiver deinterleaving ( )/interleaving(
)/interleaving( ) processes include both the IEEE 802.11n (de)interleaver and the one proposed in the GO-CDM extension. The MAP decoder returns the LLRs of the information bits to be sliced in order to form the final bit estimates and also produces LLRs for the coded bits
) processes include both the IEEE 802.11n (de)interleaver and the one proposed in the GO-CDM extension. The MAP decoder returns the LLRs of the information bits to be sliced in order to form the final bit estimates and also produces LLRs for the coded bits  , which can then be fed back for the next iteration.
, which can then be fed back for the next iteration.
Obviously, the overall complexity of the reception process depends on the number of iterations conducted. A simplified noniterative receiver can be obtained by discarding the soft information (e.g., list of candidates) and relying only on the ML estimates provided by the LSD. After symbol slicing and proper restructuring, these can be supplied to a conventional hard decision Viterbi decoder.
6. Numerical Results
Simulation results are now presented for three different IEEE 802.11n configurations all making use of MIMO processing. Without loss of generality antenna elements at Tx/Rx are assumed to be sufficiently spaced apart so as to make the spatial correlation negligible. Channel Model E-NLOS [16] has been used in all simulations. This channel profile corresponds to a large office environment and it is made of 38 independent paths distributed among 4 clusters, characterized by an  delay spread of 100 ns. Quasi-static fading has been assumed, that is, each packet sees an independent channel realisation that remains fixed for the whole packet. Initially, perfect channel estimation and no carrier frequency offset are assumed while later the effects of these implementation inaccuracies are taken into account.
delay spread of 100 ns. Quasi-static fading has been assumed, that is, each packet sees an independent channel realisation that remains fixed for the whole packet. Initially, perfect channel estimation and no carrier frequency offset are assumed while later the effects of these implementation inaccuracies are taken into account.
Results are presented for three different detection strategies, namely, Viterbi with hard decisions, noniterative MAP (i.e., soft Viterbi), and MAP with two additional iterations. The LSD detector was upper-limited to  candidates when generating the soft information (notice that for some of the studied configurations this bound was sufficient to take into account all candidates in the search space). For the sake of clarity, when GO-CDM is active, the number of subcarriers per group has been fixed to
candidates when generating the soft information (notice that for some of the studied configurations this bound was sufficient to take into account all candidates in the search space). For the sake of clarity, when GO-CDM is active, the number of subcarriers per group has been fixed to  , which provides a good compromise between performance enhancement and detection complexity [9].
, which provides a good compromise between performance enhancement and detection complexity [9].
Configuration 1 uses the single 20 MHz band, transmitter and receiver have  and
and  antennas, respectively, which are used to transmit a single spatial stream
antennas, respectively, which are used to transmit a single spatial stream  . The multiple transmit antennas are configured to operate using solely CDD, that is, the single stream is transmitted from the four antennas with different cyclic delays. Modulation has been set to 16-QAM, which jointly with the number of streams and coding rate, and according to the IEEE 802.1n specification in [17], corresponds to the modulation coding set MCS = 3 and it is able to support a data rate of
. The multiple transmit antennas are configured to operate using solely CDD, that is, the single stream is transmitted from the four antennas with different cyclic delays. Modulation has been set to 16-QAM, which jointly with the number of streams and coding rate, and according to the IEEE 802.1n specification in [17], corresponds to the modulation coding set MCS = 3 and it is able to support a data rate of  Mbps. Packet error rates are shown in Figure 3 for systems with and without GO-CDM component when using the three different detection strategies. It can be seen that the configuration with GO-CDM clearly outperforms the conventional system when both employ iterative detection. In particular, gains between 1 and more than 2 dB are observed across the range of PER values of practical interest. Note that in the standard configuration, the iterative detection hardly provides any PER reduction over soft Viterbi decoding. Also noticeable is the fact that when using GO-CDM, iterations are required to overcome the increase of interference, which causes performance to worsen in comparison with the non GO-CDM system using the noniterative MAP decoder. When hard Viterbi decoding is in use, differences become even more apparent in favour of the GO-CDM enhanced system.
Mbps. Packet error rates are shown in Figure 3 for systems with and without GO-CDM component when using the three different detection strategies. It can be seen that the configuration with GO-CDM clearly outperforms the conventional system when both employ iterative detection. In particular, gains between 1 and more than 2 dB are observed across the range of PER values of practical interest. Note that in the standard configuration, the iterative detection hardly provides any PER reduction over soft Viterbi decoding. Also noticeable is the fact that when using GO-CDM, iterations are required to overcome the increase of interference, which causes performance to worsen in comparison with the non GO-CDM system using the noniterative MAP decoder. When hard Viterbi decoding is in use, differences become even more apparent in favour of the GO-CDM enhanced system.
Configuration 2 has the same spatial and bandwidth parameters as the first one ( MHz,
MHz,  ,
,  ,
,  ) but the transmit antennas are configured to operate in a different manner: the information stream is STBC encoded with each output branch configured to employ CDD, that is, each output STBC branch is sent, cyclically shifted, from two different antennas. In this case, the modulation is set to QPSK resulting in MCS = 1 with transmission rate of
) but the transmit antennas are configured to operate in a different manner: the information stream is STBC encoded with each output branch configured to employ CDD, that is, each output STBC branch is sent, cyclically shifted, from two different antennas. In this case, the modulation is set to QPSK resulting in MCS = 1 with transmission rate of  Mbps. As seen in Figure 4, the same comments as for Configuration 1 apply here with gains up to 2 dB for usual PER targets when using GO-CDM. The only remarkable difference is that now, even the nonrecursive MAP decoder performs better when GO-CDM is active.
Mbps. As seen in Figure 4, the same comments as for Configuration 1 apply here with gains up to 2 dB for usual PER targets when using GO-CDM. The only remarkable difference is that now, even the nonrecursive MAP decoder performs better when GO-CDM is active.
Finally, Configuration 3 is defined as a pure SDM system with three transmit and receive antennas ( ) used to send three spatial streams (
) used to send three spatial streams ( ) over the extended bandwidth of
) over the extended bandwidth of  MHz. These settings correspond to the (optional) mode MCS = 16 and attain a transmission rate of
MHz. These settings correspond to the (optional) mode MCS = 16 and attain a transmission rate of  Mbps. In order to show a different performance measure, Figure 5 depicts the physical-layer throughputs for the conventional and the GO-enhanced systems (physical-layer throughput is defined as
Mbps. In order to show a different performance measure, Figure 5 depicts the physical-layer throughputs for the conventional and the GO-enhanced systems (physical-layer throughput is defined as  .). As with PER figures, it can again be seen that GO-CDM provides a significant enhancement in terms of throughput. For example, when employing iterative soft detection at
.). As with PER figures, it can again be seen that GO-CDM provides a significant enhancement in terms of throughput. For example, when employing iterative soft detection at  dB, the GO-CDM enhanced architecture attains a transmission rate of 17.6 Mbps whereas the conventional system barely surpassed a rate of 10 Mbps. The benefit of GO-CDM is even more pronounced when employing hard Viterbi detection.
dB, the GO-CDM enhanced architecture attains a transmission rate of 17.6 Mbps whereas the conventional system barely surpassed a rate of 10 Mbps. The benefit of GO-CDM is even more pronounced when employing hard Viterbi detection.
In any multicarrier system, there are implementation issues that should be taken into account when evaluating their performance. Three important effects that must be considered are channel estimation imperfections, channel frequency offset (CFO) due to synchronisation mismatch between transmitter and receiver, and peak to average power ratio (PAPR).
It can be shown that with an adequate processing of the pilots (see [18]), channel estimation errors can be accurately accounted for by adding to the true channel coefficients independent zero-mean Gaussian noise samples with variance  , where
, where  is the OFDM symbol period,
is the OFDM symbol period,  is the largest delay of the channel profile, and
is the largest delay of the channel profile, and  is the AWGN noise power. Note that the effect of channel estimation errors (CEE) diminishes with increasing SNR. Figure 6 depicts the results of Configuration 1 with (dashed lines) and without (solid lines) CEE. Logically, when channel estimation imperfections are present, the PER worsens. Nevertheless, notice that these curves show a trend to converge to the corresponding CEE-free curve as
is the AWGN noise power. Note that the effect of channel estimation errors (CEE) diminishes with increasing SNR. Figure 6 depicts the results of Configuration 1 with (dashed lines) and without (solid lines) CEE. Logically, when channel estimation imperfections are present, the PER worsens. Nevertheless, notice that these curves show a trend to converge to the corresponding CEE-free curve as  grows. Noticeably, and for the case of iterative soft detection, the PER reduction due to the GO-CDM enhancement becomes even clearer when CEE is present as reflected by the larger gap between the curves corresponding to
grows. Noticeably, and for the case of iterative soft detection, the PER reduction due to the GO-CDM enhancement becomes even clearer when CEE is present as reflected by the larger gap between the curves corresponding to  and
and  . This effect can be explained by the fact that a large error in the estimation of a subcarrier, which will most likely lead to an unrecoverable symbol detection error, is smeared among the rest of subcarriers in the group by the action of the GO-CDM and later corrected by the turbo processing scheme.
. This effect can be explained by the fact that a large error in the estimation of a subcarrier, which will most likely lead to an unrecoverable symbol detection error, is smeared among the rest of subcarriers in the group by the action of the GO-CDM and later corrected by the turbo processing scheme.
Another important implementation issue to consider is channel frequency offset (CFO), which leads to intercarrier interference (ICI). As stated in [19, page 128], the presence of ICI leads to a degradation in the SNR level, which for an arbitrary subcarrier  is given by
is given by

with  denoting the carrier frequency offset. Figure 7 compares the PER performance of the conventional and GO-CDM-enhanced systems for a fixed SNR of
denoting the carrier frequency offset. Figure 7 compares the PER performance of the conventional and GO-CDM-enhanced systems for a fixed SNR of  dB over a range of values of
dB over a range of values of  . These results indicate that GO-CDM keeps reporting significant benefits even in the presence of CFO.
. These results indicate that GO-CDM keeps reporting significant benefits even in the presence of CFO.
Finally, the effect of GO-CDM on the peak-to-average power ratio (PAPR) has been assessed. Using the common definition of PAPR [20]

where  represents the post-IFFT signal at transmission and
represents the post-IFFT signal at transmission and  is the duration of the data load in an OFDM symbol (e.g., no GI considered), a significant PAPR performance measure is given by the complementary cumulative distribution function (CCDF) of the PAPR of a data block. The CCDF represents the probability that a data block of an arbitrary OFDM symbol exceeds a given threshold (
is the duration of the data load in an OFDM symbol (e.g., no GI considered), a significant PAPR performance measure is given by the complementary cumulative distribution function (CCDF) of the PAPR of a data block. The CCDF represents the probability that a data block of an arbitrary OFDM symbol exceeds a given threshold ( ). As an example, Figure 8 shows the CCDF for the system defined by Configuration 1 with and without GO-CDM. For completeness, this figure also shows PAPR results for a system based on Configuration 1 but operating on a 40 MHz bandwidth (128 subcarriers). It can be concluded from this figure that GO-CDM does not increase PAPR and, in fact, it leads to a consistent (yet marginal) reduction. Measures on the other configurations produced similar results.
). As an example, Figure 8 shows the CCDF for the system defined by Configuration 1 with and without GO-CDM. For completeness, this figure also shows PAPR results for a system based on Configuration 1 but operating on a 40 MHz bandwidth (128 subcarriers). It can be concluded from this figure that GO-CDM does not increase PAPR and, in fact, it leads to a consistent (yet marginal) reduction. Measures on the other configurations produced similar results.
It is fair to recognize that GO-CDM is not effective in all situations. When there are many (uncorrelated) antennas at the receiver, the large amount of spatial diversity available renders the extra frequency diversity provided by GO-CDM marginal. Also, when the channel is markedly frequency nonselective, GO-CDM does not provide significant gains, in very much the same way that MIMO gains are greatly diminished when the antenna elements exhibit large correlations. The point to be noted with this work is that GO-CDM is an attractive option in many configurations, specially on those where the number of receive antennas is roughly the same as the number of transmitted spatial streams. Moreover, GO-CDM, by properly adjusting the spreading factor  , can act as a performance/complexity knob.
, can act as a performance/complexity knob.
7. Conclusions
In this paper, the use of GO-CDM in IEEE 802.11n networks as a means to improve performance has been proposed. It has been shown that this technique can exploit the availability of multiple transmit antennas (and its various MIMO processing mechanisms) and larger spectrum bandwidth, not available in previous WLANs standards. A soft iterative receiver, based on the LSD algorithm, has been proposed. This detector has been shown to be able to exploit the additional frequency diversity provided by GO-CDM yet remaining computationally feasible. Numerical results for different configurations, with parameters derived from the new standard, show that GO-CDM is able to offer significant performance gains over the conventional IEEE 802.11n specification. Implementation issues like channel estimation errors, carrier frequency offset and peak to average power ratio have been shown to further reinforce the potential of GO-CDM.
Finally, it is important to stress that the techniques presented in this paper could also be applied to other multicarrier-based systems such as 3GPP-LTE, WiMax, or the proposal developed within the European project WINNER. In this latter system, where bandwidths in the order of 100 MHz are being considered, GO-CDM would allow large frequency diversity gains to be realised boosting in this way its performance.
References
Bing B: Emerging Technologies for Wireless LANs: Theory, Design and Deployment. Cambridge University Press, Cambridge, UK; 2007.
IEEE draft standard for information technology-telecommunications and information exchange between systemslocal and metropolitan area networks-specific equirements-part 11: Wireless LAN medium access control (MAC) and physical layer (PHY) specifications amendment : Enhancements for higher throughput IEEE Approved Draft Std P802.11n/D11.0, June, 2009
Alamouti SM: A simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998, 16(8):1451-1458. 10.1109/49.730453
Foschini GJ: Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas. Bell Labs Technical Journal 1996, 1(2):41-59.
Wittneben S: A new bandwidth efficient transmit antenna modulation diversity scheme for linear digital modulation. Proceedings of the IEEE International Conference on Communications, May 1993, Geneva, Switzerland 1630-1634.
Kaiser S: OFDM code-division multiplexing in fading channels. IEEE Transactions on Communications 2002, 50(8):1266-1273. 10.1109/TCOMM.2002.801460
Yee N, Linnartz J-P, Fettweis G: Multi-carrier CDMA in indoor wireless radio networks. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '93), September 1993,, Yokohama, Japan 109-113.
Cai X, Zhou S, Giannakis GB: Group-Orthogonal Multicarrier CDMA. IEEE Transactions on Communications 2004, 52(1):90-99. 10.1109/TCOMM.2003.822174
Riera-Palou F, Femenias G, Ramis J: On the design of uplink and downlink group-orthogonal multicarrier wireless systems. IEEE Transactions on Communications 2008, 56(10):1656-1665.
Riera-Palou F, Femenias G: Improved linear group detection for combined spatial multiplexing/STBC systems. IEEE Transactions on Communications 2009, 57(11):3252-3257.
Femenias G, Riera-Palou F: Enhancing IEEE 802.11n WLANs using group-orthogonal code-division multiplex. Proceedings of the IFIP International Federation for Information Processing, September 2007, Prague, Czech Republic 245: 184-195.
Riera-Palou F, Femenias G: Improving STBC performance in IEEE 802.11n using group-orthogonal frequency diversity. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '08), April 2008, Las Vegas, Nev, USA 193-198.
Bauch G, Malik JS: Cyclic delay diversity with bit-interleaved coded modulation in orthogonal frequency division multiple access. IEEE Transactions on Wireless Communications 2006, 5(8):2092-2100.
Hochwald BM, ten Brink S: Achieving near-capacity on a multiple-antenna channel. IEEE Transactions on Communications 2003, 51(3):389-399. 10.1109/TCOMM.2003.809789
Hassibi B, Vikalo H: On the sphere-decoding algorithm I. Expected complexity. IEEE Transactions on Signal Processing 2005, 53(8):2806-2818.
Erceg V: Indoor MIMO WLAN Channel Models. doc.: IEEE 802.11-03/871r0. Draft proposal, November 2003
Mujtaba SA: TGn sync proposal technical specification. doc.: IEEE 802.11-04/0889r7. Draft proposal, July 2005
Li Y: Simplified channel estimation for OFDM systems with multiple transmit antennas. IEEE Transactions on Wireless Communications 2002, 1(1):67-75. 10.1109/7693.975446
Fazel K, Kaiser S: Multi-Carrier and Spread Spectrum Systems. John Wiley & Sons, New York, NY, USA; 2005.
Han SH, Lee JH: An overview of peak-to-average power ratio reduction techniques for multicarrier transmission. IEEE Wireless Communications 2005, 12(2):56-65. 10.1109/MWC.2005.1421929
Acknowledgments
This paper has been supported in part by MEC and FEDER under Project COSMOS (TEC2008-02422), Govern de les Illes Balears under Grant PCTIB-2005GC1-09, and a Ramon y Cajal fellowship (partially funded by the European Social Fund), Spain.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Riera-Palou, F., Femenias, G. Group-Orthogonal Code-Division Multiplex: A Physical-Layer Enhancement for IEEE 802.11n Networks. J Wireless Com Network 2010, 483758 (2010). https://doi.org/10.1155/2010/483758
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/483758

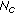 , and serial to parallel conversion (S/P) resulting in
, and serial to parallel conversion (S/P) resulting in 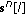 , with
, with 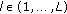 denoting the OFDM-symbol index and
denoting the OFDM-symbol index and 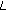 representing the number of OFDM-symbols per stream in a packet.
representing the number of OFDM-symbols per stream in a packet.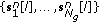 , where
, where 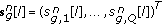 represents an individual group.
represents an individual group.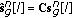 , where
, where 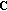 is a
is a 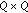 orthonormal matrix, typically chosen to be a rotated and scaled Walsh-Hadamard matrix [
orthonormal matrix, typically chosen to be a rotated and scaled Walsh-Hadamard matrix [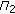 , operating across the different OFDM-symbols composing the packet, designed to ensure that modulated symbols from different OFDM-symbols in each group have experienced uncorrelated noise samples upon deinterleaving at the receiver end.
, operating across the different OFDM-symbols composing the packet, designed to ensure that modulated symbols from different OFDM-symbols in each group have experienced uncorrelated noise samples upon deinterleaving at the receiver end. implicitly performs the group subcarrier allocation taking care that subcarriers forming a group are frequentially well separated in order to maximise the frequency diversity gain. It is easy to show that, generally, this is achieved by choosing group subcarriers to be equispaced across the available bandwidth [
implicitly performs the group subcarrier allocation taking care that subcarriers forming a group are frequentially well separated in order to maximise the frequency diversity gain. It is easy to show that, generally, this is achieved by choosing group subcarriers to be equispaced across the available bandwidth [

 ), 16-QAM modulation. PER performance with (solid markers) and without (hollow markers) GO-CDM.
), 16-QAM modulation. PER performance with (solid markers) and without (hollow markers) GO-CDM.
 ), QPSK modulation. PER performance with (solid markers) and without (hollow markers) GO-CDM.
), QPSK modulation. PER performance with (solid markers) and without (hollow markers) GO-CDM.
 ), BPSK modulation. Throughput with (solid markers) and without (hollow markers) GO-CDM.
), BPSK modulation. Throughput with (solid markers) and without (hollow markers) GO-CDM.

