- Research Article
- Open access
- Published:
On the Effect of Self-Interference Cancelation in MultiHop Wireless Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 513952 (2010)
Abstract
In a wireless network, the problem of self-interference arises when a node transmits and receives simultaneously in the same frequency band. So far only two extreme approaches to circumvent this problem were thoroughly investigated in the literature. The first one prevents any node to transmit and receive simultaneously which may lead to a too conservative design. The second one assumes perfect self-interference cancelation which can be too optimistic since it ignores all possible technological limitations. To fill this gap, we provide a method based on complementary geometric programming for evaluating the gains achievable at the network layer when the network nodes employ self-interference cancelation techniques with different degrees of accuracy. The gains are evaluated in terms of average sum rate and average network congestion by using a network utility maximization framework. The method provides insights into the behavior of different network topologies when self-interference cancellation is employed in nodes. In addition, it can be used to assess the required degrees of accuracy of the self-interference in order to achieve substantial benefits. Thus, from a network design perspective, the proposed method is very beneficial. Numerical results suggest that the benefits from self-interference cancelation are more pronounced in tandem wireless network setups in which the network nodes are located in a linear grid.
1. Introduction
The self-interference problem arises in wireless networks when a node transmits and receives simultaneously in the same frequency band. The main reason for this problem is the huge imbalance between the transmitted signal power and the received signal power of nodes. Typically, the transmitted signal strength is few order of magnitude larger than the received signal strength. Thus, when a node transmits and receives simultaneously in the same channel, the useful signal at the receiver of the incoming link is overwhelmed by the transmitted signal of the node itself. As a result, the signal-to-interference-and-noise-ratio (SINR) values at the incoming link of a node that simultaneously transmits in the same channel is very small. Therefore, the self-interference problem plays a central role in link scheduling and rate/power control in wireless networks.
Information theoretic aspects of this problem can be traced back to the classic work of Shannon on "Two-way communication channels" [1]. Although the capacity region of the two-way channel is not known for the general case [2], it is completely characterized for certain particular cases, for example, for the Gaussian two-way channel it is shown that the channel can be decomposed into two independent Gaussian channels [2, Section  ]. In [2] authors discuss a technique for achieving the capacity of the Gaussian two-way channel: each transmitter uses a Gaussian codebook and each receiver decodes its own signal after subtracting the unwanted signal (i.e., the self-interfering signal) from the received waveform. Such techniques allow the possibility of perfect self-interference cancelation.
]. In [2] authors discuss a technique for achieving the capacity of the Gaussian two-way channel: each transmitter uses a Gaussian codebook and each receiver decodes its own signal after subtracting the unwanted signal (i.e., the self-interfering signal) from the received waveform. Such techniques allow the possibility of perfect self-interference cancelation.
However, in practice there are numerous technological limitations [3–6] which can severely limit the accuracy of the self-interference cancelation. Thus, it is common in practice to separate transmissions and receptions in time domain, that is, TDD (time division duplex) or in frequency domain, that is, FDD (frequency division duplex) [7] in order to facilitate the implementation challenges. It is worth of noting that, in terms of capacity analysis, there is no difference between resource partitioning across time or frequency [7, Section  ]. In general, any of the aforementioned orthogonal resource partitioning schemes are suboptimal as compared to the case of perfect self-interference cancellation. For example, only half of the sum capacity in a Gaussian symmetric two-way channel can be achieved [2] by using either TDD or FDD when the system is operating in the bandwidth-limited regime [7, page 203] (In practice, the high data rate wireless communication systems operate in the bandwidth-limited regime.). In the context of time-slotted wireless network that operate in a shared medium, one approach of dealing with the self-interference consists of adding supplementary combinatorial constraints which prevent any node in the network to transmit and receive simultaneously [8–15]. This is sometime called node-exclusive interference model. Various methods for performing the self-interference cancelation at the nodes' receivers are discussed in [16–20]. The bottom line is that there is always a tradeoff between transceiver complexity and the accuracy of the self-interference cancelation. The proposals [18–20] provide cost-effective mechanisms for an up to 55 dB reduction in the self-interference and also provide insightful comments on the performance of self-interference cancellation based on a simple two-node network. Resent work [21] further discusses techniques which envisage the self-interference cancellation in practice. Thus, as the spectrum is getting extremely scarce, it is important to understand in general the potential gains in the network performance provided by the self-interference cancellation.
]. In general, any of the aforementioned orthogonal resource partitioning schemes are suboptimal as compared to the case of perfect self-interference cancellation. For example, only half of the sum capacity in a Gaussian symmetric two-way channel can be achieved [2] by using either TDD or FDD when the system is operating in the bandwidth-limited regime [7, page 203] (In practice, the high data rate wireless communication systems operate in the bandwidth-limited regime.). In the context of time-slotted wireless network that operate in a shared medium, one approach of dealing with the self-interference consists of adding supplementary combinatorial constraints which prevent any node in the network to transmit and receive simultaneously [8–15]. This is sometime called node-exclusive interference model. Various methods for performing the self-interference cancelation at the nodes' receivers are discussed in [16–20]. The bottom line is that there is always a tradeoff between transceiver complexity and the accuracy of the self-interference cancelation. The proposals [18–20] provide cost-effective mechanisms for an up to 55 dB reduction in the self-interference and also provide insightful comments on the performance of self-interference cancellation based on a simple two-node network. Resent work [21] further discusses techniques which envisage the self-interference cancellation in practice. Thus, as the spectrum is getting extremely scarce, it is important to understand in general the potential gains in the network performance provided by the self-interference cancellation.
The main contribution of this paper is to provide a method to evaluate the potential gains achievable at the network layer when the network nodes employ self-interference cancelation techniques with different degrees of accuracy. We do not consider any specific self-interference cancelation mechanism, which is extraneous to our main objective. Instead, the imperfect self-interference cancelation is modeled as a variable power gain from the transmitter to the receiver at all nodes. Nevertheless, this simple model gives insight into the behavior of different network topologies when self-interference cancellation is employed in network nodes. The proposed method also can be used to find the required level of accuracy for the self-interference cancelation such that certain gains are achieved at the network layer. In general, the proposed system model can handle any network topology. In addition, it provides a simple way to evaluate the impact of scaling the distance between network nodes on the accuracy level of the self-interference cancellation. Thus, from a network design perspective, the proposed method can be very useful.
The network layer gains are evaluated in terms of average sum rate and average network congestion by using a network utility maximization (NUM) framework. As shown in [22, Section III.A], the NUM-optimal cross-layer control policy can be decomposed into three subproblems: (1) flow control, (2) next-hop routing and in-node scheduling, and (3) resource allocation (RA). The first two are convex optimization problems and they can be solved relatively easily. For solving the RA subproblem we propose an algorithm based on our previous work [23, 24].
The rest of the paper is organized as follows. The network model and the NUM problem formulation are presented in Section 2. The resource allocation algorithm used for solving the RA subproblem is presented in Section 3. The impact of scaling the distance between network nodes on the accuracy level of the self-interference cancellation is discussed in Section 4. The numerical results are presented in Section 5 and Section 6 concludes our paper.
2. System Model
2.1. Network Model
The wireless network consists of a collection of nodes which can send, receive and relay data across wireless links. The set of all nodes is denoted by  and we label the nodes with the integer values
and we label the nodes with the integer values  . A wireless link is represented as an ordered pair
. A wireless link is represented as an ordered pair  of distinct nodes. The set of links is denoted by
of distinct nodes. The set of links is denoted by  and we label the links with the integer values
and we label the links with the integer values  . We define
. We define  as the transmitter node of link
as the transmitter node of link  , and
, and  as the receiver node of link
as the receiver node of link  . The existence of a link
. The existence of a link  implies that a direct transmission is possible from node
implies that a direct transmission is possible from node  to node
to node  . Furthermore, we define
. Furthermore, we define  as the set of links that are outgoing from node
as the set of links that are outgoing from node  , and
, and  as the set of links that are incoming to node
as the set of links that are incoming to node  .
.
The network is assumed to operate in slotted time with slots normalized to integer values  . All wireless links are sharing a single channel and the interference between distinct nodes is solely controlled via power control. In every time slot, a network controller decides the power and rates allocated to each link. We denote by
. All wireless links are sharing a single channel and the interference between distinct nodes is solely controlled via power control. In every time slot, a network controller decides the power and rates allocated to each link. We denote by  the power allocated to each link
the power allocated to each link  during time slot
during time slot  . The power allocation is subject to a maximum power constraint
. The power allocation is subject to a maximum power constraint  for each node
for each node  , where
, where  denotes the maximum node transmission power. Let
denotes the maximum node transmission power. Let  denote the power gain from the transmitter of link
denote the power gain from the transmitter of link  to the receiver of link
to the receiver of link  during time slot
during time slot  . We assume a block fading Rayleigh channel model, where the channel coefficients are constant during each time slot and change independently from slot-to-slot. Specifically, the power gains
. We assume a block fading Rayleigh channel model, where the channel coefficients are constant during each time slot and change independently from slot-to-slot. Specifically, the power gains  , between distinct nodes are given by
, between distinct nodes are given by

where  is the distance from the transmitter of link
is the distance from the transmitter of link  to the receiver of link
to the receiver of link  ,
,  is the far-field reference distance beyond which this model is applicable (i.e.,
is the far-field reference distance beyond which this model is applicable (i.e.,  ) [25],
) [25],  is the path loss exponent, and
is the path loss exponent, and  are exponentially distributed random variables with unit mean, independent over the time slots and channels between distinct pairs of nodes (Due to the channel reciprocity the forward channel and the reverse channel between distinct nodes have identical gains.). The first term of (1) represents the path loss factor and the second term models the Rayleigh small-scale fading. For any pair of distinct links
are exponentially distributed random variables with unit mean, independent over the time slots and channels between distinct pairs of nodes (Due to the channel reciprocity the forward channel and the reverse channel between distinct nodes have identical gains.). The first term of (1) represents the path loss factor and the second term models the Rayleigh small-scale fading. For any pair of distinct links  , we denote the interference coefficient from link
, we denote the interference coefficient from link  to link
to link  by
by  .
.
Note that when  and
and  , the term
, the term  represents the power gain within the same node from its transmitter to its receiver, and is referred to as the self-interference gain (see Figure 1). Let us denote the set of all link pairs
represents the power gain within the same node from its transmitter to its receiver, and is referred to as the self-interference gain (see Figure 1). Let us denote the set of all link pairs  for which the transmitter of link
for which the transmitter of link  and the receiver of link
and the receiver of link  coincide as
coincide as  . We parameterize the self-interference by a scalar
. We parameterize the self-interference by a scalar  . That is for all link pairs
. That is for all link pairs  , we set
, we set  to model the residual self-interference gains after a certain self-interference cancelation technique was employed at the network's nodes. A value
to model the residual self-interference gains after a certain self-interference cancelation technique was employed at the network's nodes. A value  means that no self-interference cancelation technique is used whilst
means that no self-interference cancelation technique is used whilst  correspond to a perfect self-interference cancelation. We refer to the scalar
correspond to a perfect self-interference cancelation. We refer to the scalar  as the self-interference coefficient. For all link pairs
as the self-interference coefficient. For all link pairs  , the term
, the term  represents the power of the interference signal at the receiver node of link
represents the power of the interference signal at the receiver node of link  when one unit of power is allocated to the transmitter node of link
when one unit of power is allocated to the transmitter node of link  . That is for all link pairs
. That is for all link pairs  , we set
, we set  .
.
It is worthwhile to notice that the interference model described previously can be easily extended to accommodate different multiple access techniques by reinterpreting appropriately the interference coefficients. For example, in the case of wireless CDMA networks the interference coefficient  would model the residual interference at the output of despreading filter of node
would model the residual interference at the output of despreading filter of node  [7]. Similarly, in the case wireless SDMA networks where nodes are equipped with multiple antennas,
[7]. Similarly, in the case wireless SDMA networks where nodes are equipped with multiple antennas,  represents the equivalent interference coefficient measured at the output of antenna combiner of node
represents the equivalent interference coefficient measured at the output of antenna combiner of node  [7]. Extensions to a multichannel scenario (e.g., FDMA or FDMA-SDMA networks) is also possible by introducing multiple links between nodes, one link for each available spectral channel, and by setting
[7]. Extensions to a multichannel scenario (e.g., FDMA or FDMA-SDMA networks) is also possible by introducing multiple links between nodes, one link for each available spectral channel, and by setting  if links
if links  and
and  corresponds to orthogonal channels. However, these implementation-related aspects are beyond the main scope of this paper.
corresponds to orthogonal channels. However, these implementation-related aspects are beyond the main scope of this paper.
In this paper we restrict ourselves to the case where all receivers perform single-user detection (i.e., they decode each of their intended signals by treating all other interfering signals as noise) and assume that the achievable rate of link  during time slot
during time slot  is given by
is given by

where  represents the power of the thermal noise at the receiver.
represents the power of the thermal noise at the receiver.
For all  we define the signal-to-noise-ratio (SNR) of link
we define the signal-to-noise-ratio (SNR) of link  as
as  . It represents the average SNR at
. It represents the average SNR at  when
when  allocates all its transmission power to link
allocates all its transmission power to link  and all the other nodes are silent. Finally, we denote with
and all the other nodes are silent. Finally, we denote with  the overall power allocation matrix, that is,
the overall power allocation matrix, that is,  .
.
2.2. NUM Problem Formulation
Exogenous data arrive at the source nodes and they are delivered to the destination nodes over several, possibly multihop, paths. We identify the data by their destinations, that is, all data with the same destination are considered as a single commodity, regardless of its source. We label the commodities with integers  (
( ) and the destination node of commodity
) and the destination node of commodity  is denoted by
is denoted by  . For every node, we define
. For every node, we define  as the set of commodities which can arrive exogenously at node
as the set of commodities which can arrive exogenously at node  .
.
We consider a network utility maximization (NUM) framework similar to the ones considered in [22, Section III.A] and [26, Section 5.1]. Specifically, exogenously arriving data is not directly admitted to the network layer. Instead, the exogenous data is first placed in the transport layer storage reservoirs. At each source node, a set of flow controllers decides the amount of each commodity data admitted every time slot in the network. Let  denote the amount of data of commodity
denote the amount of data of commodity  admitted in the network at node
admitted in the network at node  during time slot
during time slot  . At the network layer, each node maintains a set of
. At the network layer, each node maintains a set of  internal queues for storing the current backlog (or unfinished work) of each commodity. Let
internal queues for storing the current backlog (or unfinished work) of each commodity. Let  denote the current backlog of commodity
denote the current backlog of commodity  data stored at node
data stored at node  . We formally let
. We formally let  , that is, it is assumed that data which is successfully delivered to its destination exits the network layer. Let
, that is, it is assumed that data which is successfully delivered to its destination exits the network layer. Let  be the average rate with which the data of commodity
be the average rate with which the data of commodity  is sent from node
is sent from node  to
to  over the used paths, that is,
over the used paths, that is,  . Associated with each node-commodity pair
. Associated with each node-commodity pair  we define a concave and nondecreasing utility function
we define a concave and nondecreasing utility function , representing the "reward" received by sending data of commodity
, representing the "reward" received by sending data of commodity  from node
from node  to node
to node  at an average rate of
at an average rate of  [bits/slot]. The NUM problem under stability constraints can be formulated as
[bits/slot]. The NUM problem under stability constraints can be formulated as

where the optimization variables are  and
and  represents the network layer capacity region [26, Definition 3.7].
represents the network layer capacity region [26, Definition 3.7].
A dynamic cross-layer control algorithm which achieves data rates  arbitrarily close to the optimal operating point has been introduced in [22, Section III.A]. Particularized to our network model, every time slot
arbitrarily close to the optimal operating point has been introduced in [22, Section III.A]. Particularized to our network model, every time slot  , the algorithm performs the following.
, the algorithm performs the following.
Algorithm 1 (Dynamic Cross-Layer Control Algorithm [22]).
-
(1)
Flow Control: for each node
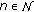 ,
, 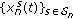 is obtained as the set of rates
is obtained as the set of rates 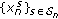 which solves the following problem:
which solves the following problem: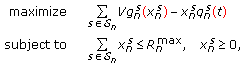 (4)
(4)where
 and
and 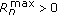 are the algorithm's parameters as described in [22].
are the algorithm's parameters as described in [22]. -
(2)
Next-hop Routing and In-node Scheduling: for each link
 , let
, let  . If
. If  , the commodity that maximizes the differential backlog is selected for potential routing over link
, the commodity that maximizes the differential backlog is selected for potential routing over link  .
. -
(3)
Resource Allocation: the power allocation
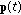 is given by
is given by  whose entries
whose entries 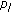 solve the problem
solve the problem (5)
(5)
and the rate allocation is given by (2).
3. Resource Allocation Subproblem
In this section we focus on resource allocation (RA) subproblem (5). Note that, due to interference, the achievable rates on different links are interdependent, that is, the achievable rate of a particular link depends on the powers allocated to all other links. In general, this coupling makes the RA subproblem (5) extremely difficult to solve since the problem is not amendable to a convex formulation [27]. In [28] it was shown that, problem (5) is NP-hard. Even though global optimization techniques (e.g., exhaustive search-based solution methods, branch and bound method) can be adapted to find the optimal solution of problem (5), the complexity of these approaches grows exponentially with the size of the network. Thus, even for a moderate size network with few nodes and links, finding the optimal solution becomes quickly impractical.
In our previous work [23, 24] we provided a efficient local solution method to RA subproblem (5) in the case of self-interference coefficient  . In the sequel, we adapt these approaches in order to handle the RA with any arbitrary self-interference coefficient
. In the sequel, we adapt these approaches in order to handle the RA with any arbitrary self-interference coefficient  in the range
in the range  .
.
For the sake of notational simplicity, let us drop the time index  and to denote the SINR of link
and to denote the SINR of link  by
by  , that is,
, that is,

As a result, the objective function of problem (5) can be expressed as  . By noticing that the objective function of problem (5) increases with respect to each
. By noticing that the objective function of problem (5) increases with respect to each  and
and  is an increasing function, problem (5) can be reformulated equivalently as
is an increasing function, problem (5) can be reformulated equivalently as

where the variables now are  . The key idea of the solution methods proposed in [23, 24] is to apply signomial programming to problem (7). A signomial program is an iterative algorithm in which the original problem is approximated by a geometric program in each iteration and iterations continue until a stopping criterion is satisfied [29]. Note that the solution obtained by using signomial programming is local [29].
. The key idea of the solution methods proposed in [23, 24] is to apply signomial programming to problem (7). A signomial program is an iterative algorithm in which the original problem is approximated by a geometric program in each iteration and iterations continue until a stopping criterion is satisfied [29]. Note that the solution obtained by using signomial programming is local [29].
Particularized to our RA problem, in each iteration the objective function of problem (7) is replaced from its best local monomial approximation at a feasible SINR point  . Note that the best local monomial approximation of the objective function of problem (7) at
. Note that the best local monomial approximation of the objective function of problem (7) at  is given by [23]
is given by [23]

Note that  is a multiplicative constant which does not affect the problem solution. Thus, the signomial program to find a locally optimal solution for problem (7) can be summarized as follows.
is a multiplicative constant which does not affect the problem solution. Thus, the signomial program to find a locally optimal solution for problem (7) can be summarized as follows.
Algorithm 2 (RA via signomial programming ( )).
)).
-
(1)
Given tolerance
 , a feasible power allocation
, a feasible power allocation 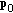 ; The initial SINR guess
; The initial SINR guess 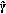 is given by (6).
is given by (6). -
(2)
Solve the following geometric program (GP):
 (9)
(9)with the positive variables
 . Denote the solution by
. Denote the solution by 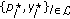 .
. -
(3)
If
 set
set 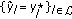 and go to Step (2); otherwise stop.
and go to Step (2); otherwise stop.
Note that the first set of inequality constraints of problem (9), that is,  ,
,  are called trust region constraints [29]. These trust region constraints confine the domain of variables
are called trust region constraints [29]. These trust region constraints confine the domain of variables  to a region around
to a region around  where the monomial approximation given in (8) is sufficiently accurate. The parameter
where the monomial approximation given in (8) is sufficiently accurate. The parameter  controls the desired approximation accuracy. In most practical cases, a fixed value
controls the desired approximation accuracy. In most practical cases, a fixed value  offers a good speed/accuracy tradeoff [29].
offers a good speed/accuracy tradeoff [29].
Algorithm 2 can be used as such for solving the RA subproblem in a particular class of wireless networks, where there is no self-interference problem (i.e., for which  ). In such networks, the set of nodes can be divided into two distinct subsets, the set of transmitting nodes and the set of receiving nodes. A simple uniform power allocation can be used to initialize Algorithm 2.
). In such networks, the set of nodes can be divided into two distinct subsets, the set of transmitting nodes and the set of receiving nodes. A simple uniform power allocation can be used to initialize Algorithm 2.
In the general case where  the RA algorithm must also cope with the self-interference problem. The difficulty comes from the fact that the self-interference gains
the RA algorithm must also cope with the self-interference problem. The difficulty comes from the fact that the self-interference gains  can be few order of magnitude larger than the power gains between distinct network nodes
can be few order of magnitude larger than the power gains between distinct network nodes  (when no self-interference cancelation technique is employed). Thus, the SINR values at the incoming links of a node that simultaneously transmits in the same channel are very small and the convergence of Algorithm 2 becomes very slow if it starts with an initial SINR guess
(when no self-interference cancelation technique is employed). Thus, the SINR values at the incoming links of a node that simultaneously transmits in the same channel are very small and the convergence of Algorithm 2 becomes very slow if it starts with an initial SINR guess  containing entries with nearly zero values.
containing entries with nearly zero values.
A standard way to deal with the self-interference problem consists of adding a supplementary combinatorial constraint in the RA subproblem which does not allow any node in the network to transmit and receive simultaneously [8, 9, 12]. We will refer to a power allocation which satisfies this constraint as admissible. Note that this approach would require solving a power optimization problem for each possible subsets of links that can be simultaneously activated. As the complexity of this approach grows exponentially with the number of nodes, this solution become quickly impractical. Furthermore, when self-interference cancelation techniques are employed at network's nodes, the solution of RA subproblem (5) is not necessary admissible. To avoid such enormous complexity we proposed an iterative method, which runs Algorithm 2 for incrementally increasing values of the self-interference coefficient. It alternates between two steps: increasing the value of a virtual self-interference coefficient  (note that this increasing is done using a dummy variable and should not be confused with the exact value of the self-interference coefficient
(note that this increasing is done using a dummy variable and should not be confused with the exact value of the self-interference coefficient  ) and running Algorithm 2 for updated values of self-interference gains (the last point found is used as the initial point for Algorithm 2 in the next iteration). The algorithm repeats these steps until a stopping criterion is satisfied.
) and running Algorithm 2 for updated values of self-interference gains (the last point found is used as the initial point for Algorithm 2 in the next iteration). The algorithm repeats these steps until a stopping criterion is satisfied.
Algorithm 3 (Successive approximation algorithm for RA in the presence of self-interferers).
-
(1)
Given an initial value for the self-interference coefficient
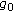 ,
, 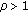 , and an initial (feasible) power allocation
, and an initial (feasible) power allocation 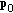 ; Let
; Let  and
and  .
. -
(2)
Set
 for all
for all 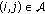 .
. -
(3)
Update the SINR guess
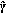 by using (6) and perform Steps (2) and (3) of Algorithm 2.
by using (6) and perform Steps (2) and (3) of Algorithm 2. -
(4)
If
 such that
such that  , then set
, then set 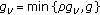 and go to Step (5), otherwise stop.
and go to Step (5), otherwise stop. -
(5)
If
 , go to Step (2), otherwise stop.
, go to Step (2), otherwise stop.
The initial self-interference gain  is chosen in the same range of values as the power gains between distinct nodes. Specifically, in our simulations we select
is chosen in the same range of values as the power gains between distinct nodes. Specifically, in our simulations we select  . For any feasible power allocations
. For any feasible power allocations  , the initial SINR guess
, the initial SINR guess  is given by (6) where all self-interference gains, that is,
is given by (6) where all self-interference gains, that is,  , are replaced by a virtual self-interference coefficient
, are replaced by a virtual self-interference coefficient  which is gradually increased in each iteration. Note that Algorithm 3 terminates either when the power allocation obtained at Step (2) is admissible or when the virtual self-interference gain
which is gradually increased in each iteration. Note that Algorithm 3 terminates either when the power allocation obtained at Step (2) is admissible or when the virtual self-interference gain  reaches the true value of the interference coefficient
reaches the true value of the interference coefficient  . Terminating Algorithm 3 if the solution is admissible is intuitively obvious for the following reason. The data associated with problem (9) become independent of self-interference gains and therefore further increase in
. Terminating Algorithm 3 if the solution is admissible is intuitively obvious for the following reason. The data associated with problem (9) become independent of self-interference gains and therefore further increase in  after having an admissible solution has no effect on the results.
after having an admissible solution has no effect on the results.
A simple extension on the method can be used to dramatically decrease the complexity per GP in (9). Here, we eliminate the power variables  and the associated SINR variables
and the associated SINR variables  from problem (9) when they have relatively very small contributions to the overall objective value of (9). Specifically, the exponent term
from problem (9) when they have relatively very small contributions to the overall objective value of (9). Specifically, the exponent term  in the objective of (9) is evaluated for all
in the objective of (9) is evaluated for all  and if
and if  then
then  's and the associated
's and the associated  's are eliminated in successive GPs.
's are eliminated in successive GPs.
4. Scaling of Distance and Maximum Node Transmission Power
Let us consider a network that is obtained from another one by scaling the distance between distinct nodes and the maximum node transmission power such that all link SNRs (see Section 2.1 for the definition of the link SNR) are conserved. We show that, in order to preserve the achievable rate region, the accuracy level of the self-interference cancelation techniques must also be scaled appropriately.
We start by defining two matrices which will be useful in the sequel. Let  denote the node distance matrix defined as
denote the node distance matrix defined as  . We denote by
. We denote by  the power gain matrix during time slot
the power gain matrix during time slot  defined as
defined as  . The achievable rate region (recall from Section 2.1 that all receivers perform single-user detection) for a given
. The achievable rate region (recall from Section 2.1 that all receivers perform single-user detection) for a given  and a maximum node transmission power
and a maximum node transmission power  can be expressed as
can be expressed as

From (10), it follows that if the power gain matrix  is scaled by a factor of
is scaled by a factor of  and the maximum node transmission power
and the maximum node transmission power  is scaled by a factor of
is scaled by a factor of  , then the achievable rate region is unchanged, that is,
, then the achievable rate region is unchanged, that is,

Let  . According to the exponential path loss model given in (1), the scaling of
. According to the exponential path loss model given in (1), the scaling of  by a factor of
by a factor of  (or
(or  ) is equivalent to the scaling of node distance matrix
) is equivalent to the scaling of node distance matrix  by a factor of
by a factor of  and the scaling of self-interference gains
and the scaling of self-interference gains  by a factor of
by a factor of  . Therefore, with a slight abuse of notation, we will rewrite (11) as
. Therefore, with a slight abuse of notation, we will rewrite (11) as

To interpret the relation in (12), we consider a network characterized by  ,
,  , and
, and  . If we construct another network by scaling
. If we construct another network by scaling  by a factor of
by a factor of  and by scaling
and by scaling  by a factor of
by a factor of  , then to preserve the achievable rate region, the accuracy level of the self-interference cancelation should be improved to
, then to preserve the achievable rate region, the accuracy level of the self-interference cancelation should be improved to  . This is intuitively obvious since, the larger the distance between network nodes, the larger the power levels required to preserve the link SINRs, and therefore, the higher the accuracy level required by the self-interference cancelation techniques to remove the increased transmit power at nodes. Based on (12) we can establish similar equivalences in terms of network layer performance metrics as well. Roughly speaking, relation (12) suggests that in networks where the nodes are located far apart (e.g., cellular type of wireless networks), the accuracy of self-interference cancellation is more stringent as compared to that in networks where the nodes are located in close vicinity (e.g., a wireless network setup in an office room).
. This is intuitively obvious since, the larger the distance between network nodes, the larger the power levels required to preserve the link SINRs, and therefore, the higher the accuracy level required by the self-interference cancelation techniques to remove the increased transmit power at nodes. Based on (12) we can establish similar equivalences in terms of network layer performance metrics as well. Roughly speaking, relation (12) suggests that in networks where the nodes are located far apart (e.g., cellular type of wireless networks), the accuracy of self-interference cancellation is more stringent as compared to that in networks where the nodes are located in close vicinity (e.g., a wireless network setup in an office room).
5. Numerical Results
In this section, we make use of the RA algorithm presented in Section 3 to investigate quantitatively the gains achievable at the network layer due to the self-interference cancelation performed at the network nodes. Specifically, we consider the following two performance metrics: (1) the average sum rate and (2) the average network congestion
and (2) the average network congestion , and we study their dependence on the self-interference coefficient
, and we study their dependence on the self-interference coefficient  . By changing
. By changing  in the interval
in the interval  , the results are able to capture effect of the self-interference cancelation performed with different levels of accuracy.
, the results are able to capture effect of the self-interference cancelation performed with different levels of accuracy.
We assume that the average rates  corresponding to all node-commodity pairs
corresponding to all node-commodity pairs  ,
,  are subject to proportional fairness, therefore we select the utility functions
are subject to proportional fairness, therefore we select the utility functions  . In every time slot
. In every time slot  , the rate allocation at Step (3) of the Dynamic Cross-Layer Control Algorithm (i.e., Algorithm 1, Section 2.2) is obtained by using the RA Algorithm 3 (Section 3). To model an orthogonal resource sharing scheme, we also consider a more restrictive RA policy, where only one link can be activated during each time slot. This policy is called baseline single link activation (BLSLA). The optimal RA based on BLSLA policy can be easily found (Note that in all considered setups Algorithm 3 is simply initialized at a point close to the BLSLA solution.) and it consists of activating during each time slot only the link which achieves the maximum weighted rate. In all simulations we assumed
, the rate allocation at Step (3) of the Dynamic Cross-Layer Control Algorithm (i.e., Algorithm 1, Section 2.2) is obtained by using the RA Algorithm 3 (Section 3). To model an orthogonal resource sharing scheme, we also consider a more restrictive RA policy, where only one link can be activated during each time slot. This policy is called baseline single link activation (BLSLA). The optimal RA based on BLSLA policy can be easily found (Note that in all considered setups Algorithm 3 is simply initialized at a point close to the BLSLA solution.) and it consists of activating during each time slot only the link which achieves the maximum weighted rate. In all simulations we assumed  and
and  m for the exponential path loss model (1) and distance between adjacent nodes are
m for the exponential path loss model (1) and distance between adjacent nodes are  m. The SNR operating point is defined as
m. The SNR operating point is defined as  , and it represents the average SNR of the links between adjacent nodes.
, and it represents the average SNR of the links between adjacent nodes.
Inspired by the Gaussian two-way channel [2], we first consider a simple two-node wireless network as shown in Figure 2. There are two commodities, the first one arrives at node 1, and is intended for node 2; the second commodity arrives at node 2, and is intended for node 1. As explained in [2], a Gaussian two-way channel is equivalent with two independent Gaussian channels where perfect self-interference cancelation is realized (i.e.,  ). As a result, the sum capacity of the symmetric Gaussian two-way channel becomes twice the capacity of either of the equivalent Gaussian channels. The considered two-node network allows us to illustrate a similar behavior in terms of the network layer average sum rate.
). As a result, the sum capacity of the symmetric Gaussian two-way channel becomes twice the capacity of either of the equivalent Gaussian channels. The considered two-node network allows us to illustrate a similar behavior in terms of the network layer average sum rate.
Figure 3 shows the dependence of the average sum rate (Figure 3(a)) and of the average network congestion (Figure 3(b)) on the self-interference coefficient  . We consider three link SNR values,
. We consider three link SNR values,  , and 30 [dB] which correspond to low, medium, and high data rate systems respectively. The results show that the average sum rate with perfect self-interference cancelation (i.e.,
, and 30 [dB] which correspond to low, medium, and high data rate systems respectively. The results show that the average sum rate with perfect self-interference cancelation (i.e.,  ) is increased by a factor of 2 and the average network congestion reduced significantly, as compared to no self-interference cancelation (i.e.,
) is increased by a factor of 2 and the average network congestion reduced significantly, as compared to no self-interference cancelation (i.e.,  ). The results also reveal that even with an imperfect self-interference cancelation technique we can achieve the performance limits guaranteed by perfect self-interference cancelation. For example, a decrease of the self-interference coefficient up to a value
). The results also reveal that even with an imperfect self-interference cancelation technique we can achieve the performance limits guaranteed by perfect self-interference cancelation. For example, a decrease of the self-interference coefficient up to a value  is enough to double the average sum rate for link SNR = 5 dB.
is enough to double the average sum rate for link SNR = 5 dB.
Let us now consider a tandem wireless network as shown in Figure 4. There are two commodities, the first one arrives at node 1, and is intended for node 4; the second commodity arrives at node 4, and is intended for node 1. Thus we have  , and
, and  for all
for all  .
.
Figure 5 shows the dependence of the average sum rate (Figure 5(a)) and of the average network congestion (Figure 5(b)) on the self-interference coefficient  for SNR values 5, 16, and 30 dB. We first focus to the case of low SNR value, that is, SNR = 5 dB. The results show that by decreasing the self-interference coefficient from
for SNR values 5, 16, and 30 dB. We first focus to the case of low SNR value, that is, SNR = 5 dB. The results show that by decreasing the self-interference coefficient from  to
to  the average sum rate is increased by a factor of around 1.82 and the average network congestion reduced significantly.
the average sum rate is increased by a factor of around 1.82 and the average network congestion reduced significantly.
Let us next consider a fully connected multihop, multi-commodity wireless network as shown in Figure 6. There are  nodes and
nodes and  commodities. The commodities arrive exogenously at different nodes in the network as shown in Figure 6, where different commodities are represented by different colors. Thus we have
commodities. The commodities arrive exogenously at different nodes in the network as shown in Figure 6, where different commodities are represented by different colors. Thus we have  ,
,  ,
,  ,
,  ,
,  , and
, and  for all
for all  . The nodes are located in a rectangular grid such that the horizontal and vertical distances between adjacent nodes are
. The nodes are located in a rectangular grid such that the horizontal and vertical distances between adjacent nodes are  m.
m.
Figure 7 shows the dependence of the average sum rate (Figure 7(a)) and of the average network congestion (Figure 7(b)) on the self-interference coefficient  for SNR values 5, 16, and 30 dB. Let us first consider the case of low SNR value, that is, SNR = 5 dB. The results show that by decreasing the self-interference coefficient from
for SNR values 5, 16, and 30 dB. Let us first consider the case of low SNR value, that is, SNR = 5 dB. The results show that by decreasing the self-interference coefficient from  to
to  the average sum rate is increased by a factor of about 1.22 and the average network congestion is reduced. The network performance remains the same as in the case of perfect self-interference cancelation for all values of
the average sum rate is increased by a factor of about 1.22 and the average network congestion is reduced. The network performance remains the same as in the case of perfect self-interference cancelation for all values of  . In this region the network performance is limited by the interference between distinct nodes, and no further improvement is possible by only increasing the accuracy of the self-interference cancelation. On the other hand, no gain in the network performance is achieved by using an imperfect self-interference cancelation technique which leads to
. In this region the network performance is limited by the interference between distinct nodes, and no further improvement is possible by only increasing the accuracy of the self-interference cancelation. On the other hand, no gain in the network performance is achieved by using an imperfect self-interference cancelation technique which leads to  . In this region the RA solution provided by Algorithm 3 is always admissible (i.e., no node transmits and receives simultaneously).
. In this region the RA solution provided by Algorithm 3 is always admissible (i.e., no node transmits and receives simultaneously).
In each network setup (Figures 2, 4, and 7) a similar behavior of the results holds for medium and high SNR values as well (i.e., SNR = 16 and 30 dB). Moreover, as we change SNR from low values to high values, the accuracy level required by the self-interference cancelation becomes more stringent. For example, in the case of fully connected multihop, multi-commodity wireless network in Figure 6, if SNR operating point is changed from 5 to 30 dB, then the accuracy level required by the self-interference cancelation should be improved from  to
to  to start gaining in network layer performances. This is intuitively expected since, the larger the SNR operating point, the larger the power levels of the nodes, and therefore, the higher the accuracy level required by the self-interference cancelation techniques to remove the increased transmit power at nodes.
to start gaining in network layer performances. This is intuitively expected since, the larger the SNR operating point, the larger the power levels of the nodes, and therefore, the higher the accuracy level required by the self-interference cancelation techniques to remove the increased transmit power at nodes.
Note that the relative gains due to self-interference cancellation in the considered fully connected multihop network is smaller as compared to the relative gains experienced in the tandem wireless network (Figure 4). This behavior is intuitively explained by looking in to the network topology. When the self-interference is significantly canceled, the resultant interference at the receiver node of any link in the case of the tandem multihop wireless network (Figure 4) is smaller on average to that of the multihop wireless network (Figure 6) (Note that any receiver node of the fully connected multihop network has many adjacent interfering nodes.). Thus, with zero self-interference, links in tandem network can operate at larger rates and therefore larger relative gains.
Finally, we show by an example, how to apply the rate-equivalence (12) to find the required value of self-interference coefficient  in order to preserve network layer performances if the distance between nodes are scaled. Let us construct a new network by scaling the distances between the nodes of the original network (see Figure 6) by a factor of
in order to preserve network layer performances if the distance between nodes are scaled. Let us construct a new network by scaling the distances between the nodes of the original network (see Figure 6) by a factor of  and the maximum node transmission power
and the maximum node transmission power  by a factor of
by a factor of  (note that
(note that  ). We refer to this new network as the scaled network. To illustrate the idea let us consider the case SNR = 5 dB in Figure 7 and focus to the point
). We refer to this new network as the scaled network. To illustrate the idea let us consider the case SNR = 5 dB in Figure 7 and focus to the point  for which the average sum rate is 3.5 [bits/slot]. The value of
for which the average sum rate is 3.5 [bits/slot]. The value of  at this point can be considered as the minimum required accuracy level of the self-interference cancelation to achieve an average sum rate of 3.5 bits/slot in the original network. Now we ask what is the required self-interference coefficient
at this point can be considered as the minimum required accuracy level of the self-interference cancelation to achieve an average sum rate of 3.5 bits/slot in the original network. Now we ask what is the required self-interference coefficient  that would result in the same average sum rate value (i.e., 3.5 bits/slot) in the scaled network. From (12) it follows that the required accuracy level of self-interference cancelation should be improved at least to a level of
that would result in the same average sum rate value (i.e., 3.5 bits/slot) in the scaled network. From (12) it follows that the required accuracy level of self-interference cancelation should be improved at least to a level of  .
.
6. Conclusions
We provided a method to evaluate the gains achievable at the network layer when the network nodes employ self-interference cancelation techniques with different degree of accuracy. By using a NUM framework, the gains were evaluated in terms of average sum rate and average network congestion.
Numerical results have shown that the self-interference cancelation requires a certain level of accuracy to obtain quantifiable gains at the network layer. The gains saturate after a certain cancelation accuracy. The level of accuracy required by the self-interference cancelation techniques depends on many factors such as distances between the network nodes and the operating power levels of the network nodes. For the considered network setups, the numerical results showed that a self-interference reduction in the range 20–60 dB leads to significant gains at the network layer. We emphasize that this level of accuracy is practically achievable, for example, the recent proposals [18–21] provide cost-effective mechanisms for an up to 55 dB reduction in the self-interference coefficient. Numerical results further shows that the topology of the network has a substantial influence on the performance gains. For example, in the case of tandem multihop wireless networks the benefits due to self-interference cancellation are more pronounced as compared to that of a multihop network in which the nodes are located in a square grid.
References
Shannon CE: Two-way communication channels. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, June-July 1961, Berkeley, Canada. Volume 1. Edited by: Neyman J. University of California Press; 611-644.
Cover TM, Thomas JA: Elements of Information Theory. 2nd edition. Wiley, New York, NY, USA; 2006.
Pan K, Wu H, Shang R, Lai F, Lin Y: Communications over two-way waveform channels in wireless networks. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering, May 1999, Alberta, Canada. Volume 1. Shaw Conference Center; 45-50.
Raghavan A, Gebara E, Tentzeris EM, Laskar J: Analysis and design of an interference canceller for collocated radios. IEEE Transactions on Microwave Theory and Techniques 2005, 53(11):3498-3508.
Nikolaou S, Bairavasubramanian R, Lugo C Jr., Carrasquillo I, Thompson DC, Ponchak GE, Papapolymerou J, Tentzeris MM: Pattern and frequency reconfigurable annular slot antenna using pin diodes. IEEE Transactions on Antennas and Propagation 2006, 54(2):439-448. 10.1109/TAP.2005.863398
Eliezer OE, Staszewski RB, Bashir I, Bhatara S, Balsara PT: A phase domain approach for mitigation of self-interference in wireless transceivers. IEEE Journal of Solid-State Circuits 2009, 44(5):1436-1453.
Tse D, Viswanath P: Fundamentals of Wireless Communication. Cambridge University Press, Cambridge, UK; 2005.
Hajek B, Sasaki G: Link scheduling in polynomial time. IEEE Transactions on Information Theory 1988, 34(5):910-917. 10.1109/18.21215
Borbash SA, Ephremides A: The feasibility of matchings in a wireless network. IEEE Transactions on Information Theory 2006, 52(6):2749-2755.
ElBatt T, Ephremides A: Joint scheduling and power control for wireless ad hoc networks. IEEE Transactions on Wireless Communications 2004, 3(1):74-85. 10.1109/TWC.2003.819032
Wu X, Srikant R: Regulated maximal matching: a distributed scheduling algorithm for multi-hop wireless networks with node-exclusive spectrum sharing. Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference (CDC-ECC '05), December 2005, Seville, Spain 2005: 5342-5347.
Borbash SA, Ephremides A: Wireless link scheduling with power control and SINR constraints. IEEE Transactions on Information Theory 2006, 52(11):5106-5111.
Lin X, Shroff NB, Srikant R: A tutorial on cross-layer optimization in wireless networks. IEEE Journal on Selected Areas in Communications 2006, 24(8):1452-1463.
Bui L, Eryilmaz A, Srikant R, Wu X: Asynchronous congestion control in multi-hop wireless networks with maximal matching-based scheduling. IEEE/ACM Transactions on Networking 2008, 16(4):826-839.
Kim T-S, Yang Y, Hou JC, Krishnamurthy SV: Joint resource allocation and admission control in wireless mesh networks. Proceedings of the 7th International Symposium on Modeling and Optimization in Mobile, Ad Hoc and Wireless Networks (WiOpt '09), June 2009, Seoul, Korea
Suzuki H, Itoh K, Ebin Y, Sato M: A booster configuration with adaptive reduction oftransmitter-receiver antenna coupling for pager systems. Proceedings of the 50th IEEE Vehicular Technology Conference (VTC '99), September 1999, Amsterdam, The Netherlands 3: 1516-1520.
Halperin D, Anderson T, Wetherall D: Taking the sting out of carrier sense: interference cancellation for wireless LANs. Proceedings of the 14th Annual International Conference on Mobile Computing and Networking (MobiCom '08), September 2008, San Francisco, Calif, USA 339-350.
Radunović B, Gunawardena D, Proutiere A, Singh N, Balan V, Key P: Efficiency and fairness in distributed wireless networks through self-interference cancellation and scheduling. Tech. Rep. MSR-TR-2009-27,Microsoft Research, March 2009.http://research.microsoft.com/apps/pubs/default.aspx?id=79933
Radunović B, Gunawardena D, Key P, et al.: Rethinking indoor wireless: low power, low frequency, full-duplex. Tech. Rep. MSR-TR-2009-148, Microsoft Research, July 2009.http://research.microsoft.com/apps/pubs/default.aspx?id=104950
Radunović B, Gunawardena D, Key P, Proutiere A, Singh N, Balan V, Dejean G: Rethinking indoor wireless mesh design: low power, low frequency, full-duplex. Proceedings of the 5th IEEE Workshop on Wireless Mesh Networks (WiMesh '10), June 2010 25-30.
Choi JI, Jain M, Srinivasan K, Levis P, Katti S: Achieving single channel, full duplex wireless communication. Proceedings of the ACM International Conference on Mobile Computing and Networking, September 2010, Chicago, Ill, USA 1-12.
Neely MJ, Modiano E, Li C-P: Fairness and optimal stochastic control for heterogeneous networks. IEEE/ACM Transactions on Networking 2008, 16(2):396-409.
Codreanu M, Weeraddana C, Latva-Aho M: Cross-layer utility maximization subject to stability constraints for multi-channel wireless networks. Proceedings of the 43rd Asilomar Conference on Signals, Systems and Computers, November 2009, Pacific Grove, Calif, USA 776-780.
Weeraddana C, Codreanu M, Latva-aho M, Ephremides A: Resource allocation for cross-layer utility maximization in multi-hop wireless networks in the presence of self interference. Proceedings of the 8th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt '10), May-June 2010, Avignon, France 70-75.
Kumar A, Manjunath D, Kuri J: Wireless Networking. Elsevier, Burlington, Mass, USA; 2008.
Georgiadis L, Neely MJ, Tassiulas L: Resource allocation and cross-layer control in wireless networks. Foundations and Trends in Networking 2006, 1(1):1-144. 10.1561/1700000002
Luo Z-Q, Yu W: An introduction to convex optimization for communications and signal processing. IEEE Journal on Selected Areas in Communications 2006, 24(8):1426-1438.
Luo Z-Q, Zhang S: Dynamic spectrum management: complexity and duality. IEEE Journal on Selected Topics in Signal Processing 2008, 2(1):57-73.
Boyd S, Kim S-J, Vandenberghe L, Hassibi A: A tutorial on geometric programming. Optimization and Engineering 2007, 8(1):67-127. 10.1007/s11081-007-9001-7
Acknowledgments
This research was supported by the Finnish Funding Agency for Technology and Innovation (Tekes), Academy of Finland, Nokia, Nokia Siemens Networks, Elektrobit, Graduate School in Electronics, Telecommunications and Automation (GETA) Foundations, and US Army Research Office Grant W911NF-08-1-0238.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Weeraddana, P.C., Codreanu, M., Latva-aho, M. et al. On the Effect of Self-Interference Cancelation in MultiHop Wireless Networks. J Wireless Com Network 2010, 513952 (2010). https://doi.org/10.1155/2010/513952
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/513952

 .
. ,
, 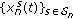 is obtained as the set of rates
is obtained as the set of rates 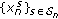 which solves the following problem:
which solves the following problem: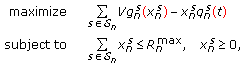
 and
and 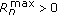 are the algorithm's parameters as described in [
are the algorithm's parameters as described in [ , let
, let  . If
. If  , the commodity that maximizes the differential backlog is selected for potential routing over link
, the commodity that maximizes the differential backlog is selected for potential routing over link  .
.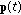 is given by
is given by  whose entries
whose entries 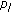 solve the problem
solve the problem
 , a feasible power allocation
, a feasible power allocation 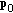 ; The initial SINR guess
; The initial SINR guess 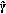 is given by (6).
is given by (6).
 . Denote the solution by
. Denote the solution by 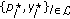 .
. set
set 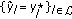 and go to Step (2); otherwise stop.
and go to Step (2); otherwise stop.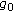 ,
, 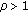 , and an initial (feasible) power allocation
, and an initial (feasible) power allocation 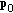 ; Let
; Let  and
and  .
. for all
for all 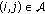 .
.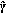 by using (6) and perform Steps (2) and (3) of Algorithm 2.
by using (6) and perform Steps (2) and (3) of Algorithm 2. such that
such that  , then set
, then set 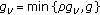 and go to Step (5), otherwise stop.
and go to Step (5), otherwise stop. , go to Step (2), otherwise stop.
, go to Step (2), otherwise stop.
 nodes,
nodes,  links, and
links, and  commodities. Different commodities are represented by different color.
commodities. Different commodities are represented by different color.
 (a) and of the average network congestion
(a) and of the average network congestion  (b) on the self-interference coefficient
(b) on the self-interference coefficient  .
.
 nodes and
nodes and  commodities. Different commodities are represented by different color.
commodities. Different commodities are represented by different color.
 (a) and of the average network congestion
(a) and of the average network congestion  (b) on the self-interference coefficient
(b) on the self-interference coefficient  .
.
 nodes and
nodes and  commodities. Different commodities are represented by different color.
commodities. Different commodities are represented by different color.
 (a) and of the average network congestion
(a) and of the average network congestion  (b) on the self-interference coefficient
(b) on the self-interference coefficient  .
.