- Research Article
- Open access
- Published:
A Low-Complexity Transmission and Scheduling Scheme for WiMAX Systems with Base Station Cooperation
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 527591 (2010)
Abstract
This paper considers base station cooperation as an interference management technique for the downlink of a WiMAX network (IEEE 802.16 standard) with frequency reuse factor of 1. A low-complexity cooperative transmission and scheduling scheme is proposed that requires limited feedback from the users and limited information exchange between the base stations. The proposed scheme requires minor modifications to the legacy IEEE 802.16e systems. The performance of the proposed scheme is compared with noncooperative schemes with similar complexity through computer simulations. Results demonstrate that base station cooperation provides an attractive solution for mitigating the cochannel interference and increases the system spectral efficiency compared to traditional cellular architectures based on frequency reuse.
1. Introduction
Multiple-input and multiple-output (MIMO) and orthogonal frequency division multiple access (OFDMA) techniques have become essential components of contemporary wireless communication systems such as WiMAX (IEEE 802.16e standard [1]). Channel state information (CSI) at the transmitter is important in OFDMA systems in order to exploit the frequency and multiuser diversities to increase the system spectral efficiency. However, due to the multiple carrier nature of OFDMA systems, the necessary feedback from users to base stations increases significantly. MIMO systems require even more CSI feedback for achieving full spectral efficiency. Hence, a MIMO-OFDMA network with full CSI knowledge at the base stations is not practical to implement in real-world systems and thus, effective suboptimum methods of data transmission and scheduling based on limited CSI are being researched.
Random beamforming at the downlink [2] is an attractive solution for spectrally efficient MIMO transmission requiring limited channel knowledge at the transmitter. Using pseudorandom unitary transmit beamforming vectors, it is possible to achieve remarkable performance gains with the help of opportunistic scheduling and multiuser diversity. This is illustrated in [3] for single cell OFDMA systems. In [4], layered random beamforming method for MIMO-OFDMA systems is considered, where users can be multiplexed on different spatial layers.
An important performance degrading factor in multicellular networks is the cochannel interference (CCI), which can decrease the system spectral efficiency significantly, especially for the users at cell edges. In traditional cellular systems, to cope with this problem, frequency reuse scheme with a frequency reuse factor other than 1 is used. Hence, neighboring cells use nonoverlapping frequency bands to avoid interference, which results in a loss in spectral efficiency. In [5], different frequency reuse patterns are compared in terms of throughput and outage probability for a WiMAX network. A noncooperative solution offered to mitigate CCI is to use fractional frequency reuse [6, 7]. In this method, the cell is partitioned into two regions. At the inner region where the CCI level is low, subchannels are used systemwide by all base stations, while in the outer region, where the CCI level is high, subchannels are orthogonally shared among base stations. In [8], this partitioning is done adaptively based on signal power feedback from users to base stations for a WiMAX network.
Base station (BS) cooperation is another attractive technique to mitigate CCI for systems with frequency reuse factor of 1, where the whole spectrum allocated to the system is used in every cell/sector. Since BSs are already connected to each other with high-speed links in current networks, it is viable for BSs to share information over the backhaul to jointly schedule users and cooperatively transmit data. In [9], a cooperative scheme is proposed, where BSs sometimes act as a relay to achieve frequency reuse factor of 1. In [10–14], BSs act as distributive antenna systems to make collaborative MIMO transmissions using linear precoding techniques. In [15], two different transmission schemes are considered. For inner cell users BSs make noncooperative transmission, while for cell edge users BSs perform cooperative beamforming to mitigate CCI. However, all aforementioned works on BS cooperation assume full CSI at BSs, which becomes impractical for OFDMA systems due to their multiple carrier nature. Furthermore, in these proposed schemes multiuser MIMO concepts are utilized which results in each BS transmitting information to several users (some located in other cells) simultaneously over the same system resource to take advantage of spatial diversity. However, this approach violates the OFDMA structure adopted in current WiMAX systems.
In this paper, we propose a cooperative transmission scheme for the downlink of a WiMAX network which requires limited feedback from the users. Our aim is to keep the complexity of the scheme low while requiring minor modifications to the legacy IEEE 802.16e systems. The main idea is to have an adaptive transmission scheme where BSs can choose to transmit to users individually or collaboratively based on the feedback about CCI levels observed by the users. Through computer simulations, we study the performance gains from BS cooperation by comparing the performance of the proposed scheme to other noncooperative solutions in the literature with similar system architecture.
The rest of the paper is organized as follows. In Section 2, we introduce the multicellular downlink transmission model considered. Section 3 presents the proposed cooperative transmission and scheduling scheme. Numerical results are summarized in Section 4. Finally, Section 5 offers some concluding remarks.
The notation used in the paper is as follows. Boldface lower case letters are for vectors and boldface upper case letters are for matrices.  denotes identity matrix of size
denotes identity matrix of size  . We use
. We use  and
and  to denote the Hermitian transpose and matrix inverse operators, respectively.
to denote the Hermitian transpose and matrix inverse operators, respectively.  denotes the
denotes the  th column of matrix
th column of matrix  .
.
2. System Model
We consider the downlink of a multicellular MIMO-OFDMA system utilizing a frequency reuse factor of 1 with a total of  users, each with
users, each with  receive antennas, and
receive antennas, and  base stations, each with
base stations, each with  transmit antennas. The OFDMA system has a total of
transmit antennas. The OFDMA system has a total of  subcarriers where
subcarriers where  of them are used for data transmission. These subcarriers are grouped into
of them are used for data transmission. These subcarriers are grouped into  subchannels as in [1]. To reduce the feedback load and scheduling complexity, users are scheduled on a subchannel basis. Since only one user is scheduled on each subchannel by a single BS, the orthogonal structure of OFDMA within a cell is preserved. Furthermore, it is assumed that there is no intercarrier interference (ICI) due to mobility and thus orthogonality of the subcarriers is preserved. With these assumptions, the problem of maximizing the system spectral efficiency is simplified to using opportunistic scheduling on each subchannel, that is, choosing the user with the highest achievable data rate on that subchannel.
subchannels as in [1]. To reduce the feedback load and scheduling complexity, users are scheduled on a subchannel basis. Since only one user is scheduled on each subchannel by a single BS, the orthogonal structure of OFDMA within a cell is preserved. Furthermore, it is assumed that there is no intercarrier interference (ICI) due to mobility and thus orthogonality of the subcarriers is preserved. With these assumptions, the problem of maximizing the system spectral efficiency is simplified to using opportunistic scheduling on each subchannel, that is, choosing the user with the highest achievable data rate on that subchannel.
Let  be the index of the user scheduled by BS
be the index of the user scheduled by BS  on subcarrier
on subcarrier  . For simplicity, it is assumed that each scheduled user has
. For simplicity, it is assumed that each scheduled user has  independent data streams to be transmitted over a subcarrier. The elements of the
independent data streams to be transmitted over a subcarrier. The elements of the  data vector to be transmitted over subcarrier
data vector to be transmitted over subcarrier  ,
,  , are modeled as independent and identically distributed (i.i.d.) circularly symmetric complex Gaussian (c.s.c.g.) random variables with zero mean and variance 1. The signal vector sent from BS
, are modeled as independent and identically distributed (i.i.d.) circularly symmetric complex Gaussian (c.s.c.g.) random variables with zero mean and variance 1. The signal vector sent from BS  to scheduled user
to scheduled user  on subcarrier
on subcarrier  is given as
is given as  , where
, where  is the
is the  unitary beamforming matrix at BS
unitary beamforming matrix at BS  for subcarrier
for subcarrier  and
and  is the
is the  diagonal power allocation matrix with
diagonal power allocation matrix with  th diagonal entry as
th diagonal entry as  , indicating the power allocated to substream
, indicating the power allocated to substream  of the user served by BS
of the user served by BS  on subcarrier
on subcarrier  . The total data transmission power of the system becomes
. The total data transmission power of the system becomes  .
.
After FFT operation and cyclic prefix removal, the received signal by user  on subcarrier
on subcarrier  is given by
is given by

where the elements of the  channel matrix between user
channel matrix between user  and BS
and BS  ,
,  , and the noise vector,
, and the noise vector,  , are modeled as i.i.d. zero mean c.s.c.g. random variables. The variance of the elements of the channel matrix is given as
, are modeled as i.i.d. zero mean c.s.c.g. random variables. The variance of the elements of the channel matrix is given as  , where
, where  is the distance between BS
is the distance between BS  and user
and user  ,
,  is the path loss exponent, and
is the path loss exponent, and  is a zero mean Gaussian random variable with variance
is a zero mean Gaussian random variable with variance  , modeling the lognormal shadowing. The elements of the noise vector have unit variance.
, modeling the lognormal shadowing. The elements of the noise vector have unit variance.
To keep the receiver structure simple, it is assumed that users do not cooperate with each other and do not use complex signal processing methods to mitigate the CCI and interstream interference and treat these two sources of interference as additional Gaussian noise. Users postprocess the received vector  with a
with a  receive beamforming matrix,
receive beamforming matrix,  , to form
, to form  of size
of size  . Each element of the data vector is then detected individually using the corresponding element of
. Each element of the data vector is then detected individually using the corresponding element of  . The signal model for user
. The signal model for user  on subcarrier
on subcarrier  is depicted in Figure 1.
is depicted in Figure 1.
Under these assumptions, the achievable system spectral efficiency (sum rate) is calculated as

bits/s/Hz, where  denotes the signal to interference plus noise ratio (SINR) of user
denotes the signal to interference plus noise ratio (SINR) of user  for subcarrier
for subcarrier  and data stream
and data stream  . Note that if user
. Note that if user  is not scheduled on subcarrier
is not scheduled on subcarrier  , then
, then  for all
for all  .
.
Our design objective is to determine (a) the transmit beamforming matrix used by BS  on subcarrier
on subcarrier  ,
,  ; (b) the user scheduled by BS
; (b) the user scheduled by BS  on subcarrier
on subcarrier  ,
,  ; (c) the power allocation strategy, that is, the power allocated to BS
; (c) the power allocation strategy, that is, the power allocated to BS  on subcarrier
on subcarrier  and data stream
and data stream  ,
,  , which depends on the scheduled user,
, which depends on the scheduled user,  ; (d) the receive beamformer matrix used by user
; (d) the receive beamformer matrix used by user  on subcarrier
on subcarrier  ,
,  ; such that the system spectral efficiency
; such that the system spectral efficiency  is maximized under the total transmit power constraint
is maximized under the total transmit power constraint  . As mentioned above, under the assumptions and the system structure described above, the system spectral efficiency is maximized when on each subchannel the corresponding user with the maximum achievable data rate is scheduled. Furthermore, to reduce the feedback load, we assume that BSs have limited CSI knowledge. Therefore, the choice of transmit beamformer matrices, power allocation and scheduling (i.e., the selection of the user to be served in each subchannel) strategies should be based on very limited knowledge about the channel conditions and easily be performed cooperatively.
. As mentioned above, under the assumptions and the system structure described above, the system spectral efficiency is maximized when on each subchannel the corresponding user with the maximum achievable data rate is scheduled. Furthermore, to reduce the feedback load, we assume that BSs have limited CSI knowledge. Therefore, the choice of transmit beamformer matrices, power allocation and scheduling (i.e., the selection of the user to be served in each subchannel) strategies should be based on very limited knowledge about the channel conditions and easily be performed cooperatively.
3. Proposed Cooperative Transmission and Scheduling Algorithm
For systems with limited CSI knowledge at the transmitter, random beamformer matrices provide an attractive solution to increase system spectral efficiency by taking advantage of opportunistic scheduling and multiuser diversity. Therefore, we assume that BSs utilize random unitary beamformer matrices for each subcarrier. These beamforming matrices are produced pseudorandomly at the BSs with no channel knowledge, using predefined seeds.
Assuming that users can perfectly estimate their instantaneous channel gains from all BSs, if the users also know the transmit beamforming matrices and the power allocation strategy used by BSs, then it is well known that the optimum receive beamforming matrix maximizing the achievable data rate on a given subcarrier is the minimum mean square error (MMSE) beamformer matrix given by

where


 is the set of indices of the BSs serving user
is the set of indices of the BSs serving user  on subcarrier
on subcarrier  . It should be noted that, in this formulation the first term in the inverse operator is the noise covariance matrix, the second term is the desired signal covariance matrix and the last term is the summation of CCI covariance matrices originating from interfering BSs not serving user
. It should be noted that, in this formulation the first term in the inverse operator is the noise covariance matrix, the second term is the desired signal covariance matrix and the last term is the summation of CCI covariance matrices originating from interfering BSs not serving user  on subcarrier
on subcarrier  .
.
Since the transmit beamformer matrices at each BS are generated pseudorandomly with predetermined seeds, it is reasonable to assume that users are informed about the seeds used by the BSs and thus they know the transmit beamformer matrices used by each BS on a given subcarrier perfectly. However, for the users to calculate the MMSE beamformers perfectly, the users should also be able to predetermine the power allocation strategy to be used by BSs, prior to scheduling of the users.
In order to keep the feedback load low, users are envisioned to feed back a single channel information metric for each subchannel. Due to the limited knowledge BSs receive from their users about the instantaneous channel conditions, it is not possible to perform optimal power allocation over subcarriers in a given subchannel and over data substreams transmitted over each subcarrier. Furthermore, it is unreasonable to assume that users know the scheduling and power allocation strategy used in the neighboring cells, therefore power allocation over subchannels is also not feasible. As a result, we will assume that the total transmit power is divided uniformly over all data subcarriers and all data substreams transmitted over each subcarrier, that is,  for all
for all  and
and  . The power allocation problem is now simplified to sharing of the power allocated to each subcarrier between the BSs. It should be noted that this results in a nonuniform transmit power distribution over BSs. However, this is a known problem for MIMO broadcast channels designed to optimize the system spectral efficiency under total transmit power constraints, rather than per BS antenna power constraints [16].
. The power allocation problem is now simplified to sharing of the power allocated to each subcarrier between the BSs. It should be noted that this results in a nonuniform transmit power distribution over BSs. However, this is a known problem for MIMO broadcast channels designed to optimize the system spectral efficiency under total transmit power constraints, rather than per BS antenna power constraints [16].
Since BSs are already connected to each other over a high-speed and more reliable wired backbone, we assume that they can share information about the system and perform joint transmission and scheduling. However, in order to keep the backbone traffic low, we will assume that the BSs will only consider two transmission strategies for the user to be scheduled on each subchannel.
-
(1)
Individual Transmission Strategy (TS 1). On the subchannel considered, each BS transmits to a user in its own cell. As a result, on the subchannel considered, users are served simultaneously, and thus each user observes CCI from other cells.
-
(2)
Joint Transmission Strategy (TS 2). On the subchannel considered, a user is jointly served by all BSs. In this case, only one user is scheduled on a given subchannel, and it does not observe any CCI from other users in the system on this subchannel.
For TS 1, since users do not know which user will be scheduled in other cells, for users to predetermine the power allocation between BSs, the allocation strategy needs to be BS specific and independent of the scheduled users in other cells. Therefore, it is reasonable to assume uniform power allocation over BSs, that is,  for all
for all  , where
, where  .
.
For TS 2, the optimum joint power allocation and subcarrier scheduling scheme, maximizing the system spectral efficiency is identified by solving the following optimization problem:

where  is the set of indices of the subcarriers on which user
is the set of indices of the subcarriers on which user  is scheduled. However, this is a complex optimization problem that cannot be solved distributively with limited CSI at BSs, that is, with feedback of just the achievable data rates of the users on each subchannel. Therefore, we will resort to a heuristic power allocation technique for this transmission strategy. With the assumption that both BSs and users can determine the distances between themselves, they can predict the path loss. Ignoring lognormal shadowing and small scale fading effects, a simple power allocation method based solely on path loss can be utilized. The proposed power allocation for user
is scheduled. However, this is a complex optimization problem that cannot be solved distributively with limited CSI at BSs, that is, with feedback of just the achievable data rates of the users on each subchannel. Therefore, we will resort to a heuristic power allocation technique for this transmission strategy. With the assumption that both BSs and users can determine the distances between themselves, they can predict the path loss. Ignoring lognormal shadowing and small scale fading effects, a simple power allocation method based solely on path loss can be utilized. The proposed power allocation for user  under TS 2 is
under TS 2 is

Note that this power allocation is user specific, since it depends on the location of the user with respect to all BSs and can easily be solved with the well-known waterfilling method. It does not optimize the achievable data rate, but it is easy to implement without requiring additional feedback. Since there is no CCI in this transmission strategy on the subchannel considered, BSs share the power such that closer BS transmits with higher power under TS 2.
In order to calculate the achievable data rates on each subchannel, users must firstly calculate their achievable SINRs. However, since power allocation strategies and the source of interference observed are different under two transmission strategies, SINR expressions for the two transmission strategies are different. It should be noted that these are the maximum achievable SINRs when optimum MMSE receiver beamformers in (3) are used. For TS 1, the SINR for OFDM symbol  is calculated as
is calculated as

where

 , and
, and  is the index of the BS in user
is the index of the BS in user  's cell.
's cell.
For TS 2, the SINR for OFDM symbol  is calculated as
is calculated as

where  .
.
After the SINR calculation, user  calculates its achievable data rate on subchannel
calculates its achievable data rate on subchannel  for OFDM symbol
for OFDM symbol  under each TS
under each TS  as
as

where  and
and  is the set of indices of the subcarriers within subchannel
is the set of indices of the subcarriers within subchannel  . Each user feeds back these two data rates,
. Each user feeds back these two data rates,  and
and  , only to the BS in its own cell. Then BS
, only to the BS in its own cell. Then BS  computes the maximum of data rates fed back by its users for subchannel
computes the maximum of data rates fed back by its users for subchannel  under each transmission strategy as
under each transmission strategy as

where  is the set of indices of users in the cell served by BS
is the set of indices of users in the cell served by BS  . BSs exchange this information with each other over the backhaul. Lastly, they calculate the maximum achievable sum rate on subchannel
. BSs exchange this information with each other over the backhaul. Lastly, they calculate the maximum achievable sum rate on subchannel  as
as

where


Note that the data rate in (14) corresponds to the sum of data rates of the scheduled users in different cells where individual transmission strategy is used. The data rate in (15) corresponds to the data rate of the user served jointly by all BSs with joint transmission strategy. Hence, the algorithm chooses individual transmission strategy if there is no gain from cooperation. Finally, BSs jointly decide on the transmission strategy to use on subchannel  and the corresponding user(s) to schedule on the subchannel. Hence, by using opportunistic scheduling on each subchannel
and the corresponding user(s) to schedule on the subchannel. Hence, by using opportunistic scheduling on each subchannel  , the system sum rate
, the system sum rate  is maximized since
is maximized since

The scheduling described above is based on maximizing the sum rate of the users. It is well known that maximum sum rate (MSR) scheduling results in an unfair rate allocation [2]. If fairness between the users is desired, one can implement proportionally fair scheduling (PFS) by modifying the algorithm such that, the data rate to be fed back by the users for subchannel  ,
,  , is the instantaneous achievable data rate on that subchannel weighted by the inverse of the time averaged data rate achieved so far:
, is the instantaneous achievable data rate on that subchannel weighted by the inverse of the time averaged data rate achieved so far:

where time averaged data rate  of user
of user  is calculated with the exponential low pass filter [2]
is calculated with the exponential low pass filter [2]

where  is the window length,
is the window length,  is the set of subchannels where user
is the set of subchannels where user  is scheduled, and
is scheduled, and  is the achieved rate of user
is the achieved rate of user  on subchannel
on subchannel  with the chosen transmission strategy,
with the chosen transmission strategy,  .
.
It should be emphasized that in the proposed algorithm, power allocation and scheduling are performed together. If individual transmission is chosen on a subchannel, then uniform power distribution allocation is used regardless of the scheduled user. However, for the case of joint transmission, power allocation strategy on that subchannel depends on the location of the user with respect to all BSs. As a summary, a flowchart of the algorithm is given in Figure 2, illustrating the information exchange between the BSs over the backhaul, and the users and the BSs on the uplink.
4. Numerical Results
To investigate the gains from cooperation, we compared the performance of the proposed scheme to noncooperative schemes with similar computational complexity and feedback load using computer simulations. We model a multicellular MIMO-OFDMA system, where CCI is assumed to be limited to the area of intersection of 120-degree sectors of three neighboring cells, as illustrated in Figure 3. In this case, we can focus on cooperation of BSs in these three cells.
The parameters used in the simulations are summarized in Table 1. In each subchannel equal number of subcarriers is assumed. ITU Pedestrian-B channel model with user velocity  km/hr and partial usage of subchannels (PUSC) subchannelization described in [1] are used. Note that the average received signal to noise ratio (SNR) of a user depends on many factors including the total transmission power, noise level, distance between the user and the BSs, number of subchannels allocated to the user, and so forth. In order to provide a meaningful comparison of total transmit power, we define the metric, worst case received SNR per data stream, which is computed as
km/hr and partial usage of subchannels (PUSC) subchannelization described in [1] are used. Note that the average received signal to noise ratio (SNR) of a user depends on many factors including the total transmission power, noise level, distance between the user and the BSs, number of subchannels allocated to the user, and so forth. In order to provide a meaningful comparison of total transmit power, we define the metric, worst case received SNR per data stream, which is computed as  , where
, where  is the transmit power per BS per data subcarrier per data substream under TS 1 and
is the transmit power per BS per data subcarrier per data substream under TS 1 and  is the cell radius. Note that
is the cell radius. Note that  is independent of the small scale fading, shadowing and CCI effects. Therefore, it does not indicate the actual SNR of the worst user. As
is independent of the small scale fading, shadowing and CCI effects. Therefore, it does not indicate the actual SNR of the worst user. As  increases, transmission power and consequently CCI levels relative to noise also increase. The average data rates are computed for 100 random user location scenarios, where users are uniformly distributed in the hexagonal area of interest (shaded in Figure 3) and for each scenario, user rates are averaged over 100 different channel realizations and random beamformer matrices. The time averaged user rates are computed over 100 OFDM symbols.
increases, transmission power and consequently CCI levels relative to noise also increase. The average data rates are computed for 100 random user location scenarios, where users are uniformly distributed in the hexagonal area of interest (shaded in Figure 3) and for each scenario, user rates are averaged over 100 different channel realizations and random beamformer matrices. The time averaged user rates are computed over 100 OFDM symbols.
Different transmission schemes (TSC) that are compared in this section are summarized below.
-
(1)
Conventional Frequency Reuse (Fr) Scheme: This is a noncooperative scheme, where subchannels are shared orthogonally between the three sectors in a predetermined manner. Since only one BS transmits in a given subchannel,
 , for all subcarriers used by the BS to have the total transmit power over the system bandwidth to be equal to
, for all subcarriers used by the BS to have the total transmit power over the system bandwidth to be equal to  .
. -
(2)
Fractional Frequency Reuse (FFr) Scheme: This is a noncooperative scheme, where subchannels are divided into two categories with equal number of subchannels. The subchannels in the first category are shared orthogonally between the three sectors in a predetermined manner. The subchannels in the second category can be used in all three sectors in a noncooperative manner, that is, each BS schedules a user in its cell on the subchannels in the second category resulting in CCI observed by the users scheduled on other sectors. For orthogonal subchannels in FFr scheme,
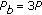 , whereas
, whereas  for the subchannels in the second category.
for the subchannels in the second category. -
(3)
Noncooperative (Noncoop) Scheme: This scheme corresponds to a system where only TS 1 is used on all subchannels.
-
(4)
Cooperative (Coop) Scheme: This is the proposed scheme described in Section 3.
Assuming that each data rate is quantized into  bits and observing the fact that the rate computations, the feedback from the users and the information exchange between BSs must occur at every scheduling slot,which is equal to 2 OFDM symbol durations for PUSC permutation, the comparison of the considered transmission schemes in terms of feedback and backhaul loads and computational complexity is presented in Table 2. The second column of the table represents the total number of bits to be fed back by a user per OFDM symbol (Feedback). Note that in all transmission schemes except the proposed cooperative algorithm, each user feeds back one data rate per subchannel allocated to users' own BS, whereas in the proposed algorithm (Coop) each user feeds back two data rates (one for each TS) per subchannel per scheduling slot. As a result, the feedback load of the proposed algorithm is
bits and observing the fact that the rate computations, the feedback from the users and the information exchange between BSs must occur at every scheduling slot,which is equal to 2 OFDM symbol durations for PUSC permutation, the comparison of the considered transmission schemes in terms of feedback and backhaul loads and computational complexity is presented in Table 2. The second column of the table represents the total number of bits to be fed back by a user per OFDM symbol (Feedback). Note that in all transmission schemes except the proposed cooperative algorithm, each user feeds back one data rate per subchannel allocated to users' own BS, whereas in the proposed algorithm (Coop) each user feeds back two data rates (one for each TS) per subchannel per scheduling slot. As a result, the feedback load of the proposed algorithm is  bits/OFDM symbol. For the noncooperative scheme the feedback load is halved since only one transmission strategy is considered for each subchannel. For fractional frequency reuse scheme the feedback load is
bits/OFDM symbol. For the noncooperative scheme the feedback load is halved since only one transmission strategy is considered for each subchannel. For fractional frequency reuse scheme the feedback load is  , that is, one third of the load for the proposed algorithm. Finally, for the traditional frequency reuse scheme since only one third of the subchannels is allocated to each sector, the feedback load is the lowest,
, that is, one third of the load for the proposed algorithm. Finally, for the traditional frequency reuse scheme since only one third of the subchannels is allocated to each sector, the feedback load is the lowest,  . It should be noted that for the cooperative schemes proposed in the literature that are based on full CSI at the BSs, the feedback load is given as
. It should be noted that for the cooperative schemes proposed in the literature that are based on full CSI at the BSs, the feedback load is given as  bits per OFDM symbol since users need to feedback one complex-valued number per subcarrier per channel between a transmit and a receive antenna. The feedback load of the proposed cooperative scheme is a factor of
bits per OFDM symbol since users need to feedback one complex-valued number per subcarrier per channel between a transmit and a receive antenna. The feedback load of the proposed cooperative scheme is a factor of  smaller than the load for cooperative schemes with full CSI.
smaller than the load for cooperative schemes with full CSI.
In Table 2, the third column corresponds to the backhaul traffic load (Backhaul), that is, the number of bits that a BS has to exchange with other BSs per OFDM symbol. Since only the proposed algorithm requires information exchange between BSs, the only nonzero entry of this column is for the proposed scheme which is equal to  . The last column of Table 2 is the computational complexity per OFDM symbol (Comp). Since SINR computation is the most computationally expensive step for the users, involving a matrix inversion, to give an idea about computational complexity of different schemes we approximated the computational complexity as the number of SINR computations that a user need to perform per subcarrier allocated to user's BS per OFDM symbol. For the proposed algorithm, computational complexity is 2 SINR computations (one for each TS) per subcarrier per scheduling slot, that is,
. The last column of Table 2 is the computational complexity per OFDM symbol (Comp). Since SINR computation is the most computationally expensive step for the users, involving a matrix inversion, to give an idea about computational complexity of different schemes we approximated the computational complexity as the number of SINR computations that a user need to perform per subcarrier allocated to user's BS per OFDM symbol. For the proposed algorithm, computational complexity is 2 SINR computations (one for each TS) per subcarrier per scheduling slot, that is,  . This value is halved for the noncooperative scheme since users compute one SINR per subcarrier per scheduling slot. For the fractional frequency reuse scheme, the complexity becomes
. This value is halved for the noncooperative scheme since users compute one SINR per subcarrier per scheduling slot. For the fractional frequency reuse scheme, the complexity becomes  SINR computations per OFDM symbol since only two thirds of the subcarriers can be used in each sector simultaneously. Like the feedback load, the computational complexity is lowest for the traditional frequency reuse scheme, where only one SINR value is computed by each user for
SINR computations per OFDM symbol since only two thirds of the subcarriers can be used in each sector simultaneously. Like the feedback load, the computational complexity is lowest for the traditional frequency reuse scheme, where only one SINR value is computed by each user for  subcarriers per scheduling slot.
subcarriers per scheduling slot.
In Figure 4, the relative cooperation gain of the proposed algorithm over the noncooperative scheme is plotted against varying  and
and  under MSR scheduling. We define the relative gain as Relative gain =
under MSR scheduling. We define the relative gain as Relative gain =  , where
, where  and
and  are the sum rates of the proposed and noncooperative schemes, respectively. It should be noted that, since cooperative scheme involves noncooperative scheme, it should always have a better performance as long as there is a gain from cooperation. We observed that, this gain diminishes at low transmit SNR where CCI level is low and when number of users are large, in which case each BS can find a user with a good instantaneous channel in its own cell.
are the sum rates of the proposed and noncooperative schemes, respectively. It should be noted that, since cooperative scheme involves noncooperative scheme, it should always have a better performance as long as there is a gain from cooperation. We observed that, this gain diminishes at low transmit SNR where CCI level is low and when number of users are large, in which case each BS can find a user with a good instantaneous channel in its own cell.
In Figure 5, we analyze the relative gains in the sum rates of the proposed and the fractional frequency reuse schemes over the conventional frequency reuse scheme under MSR scheduling. The relative gain of a scheme over the conventional frequency reuse scheme in this case is defined as Relative gain =  , where
, where  is the sum rate of the considered scheme (Coop or FFr). It is observed that the proposed algorithm can provide up to
is the sum rate of the considered scheme (Coop or FFr). It is observed that the proposed algorithm can provide up to  gain over the conventional frequency reuse scheme at low SNR and large number of users. Furthermore, relative gains of the cooperative scheme is remarkably higher than those for the fractional frequency reuse scheme. This is due to the fact that the proposed algorithm can provide significant spatial diversity gains due to BS cooperation and there is no penalty on the spectral efficiency since all subchannels are used in all sectors.
gain over the conventional frequency reuse scheme at low SNR and large number of users. Furthermore, relative gains of the cooperative scheme is remarkably higher than those for the fractional frequency reuse scheme. This is due to the fact that the proposed algorithm can provide significant spatial diversity gains due to BS cooperation and there is no penalty on the spectral efficiency since all subchannels are used in all sectors.
In Figure 6, we compare the sum rates of different schemes under PFS when the total number of users equals to  . It is observed that the proposed algorithm provides the best sum rate when the transmit power is high, that is, in the region where CCI is dominant over noise. It is also observed that the sum rate for the Noncoop scheme could not be improved by increasing the transmit power, due to CCI observed by users at cell edges. It is observed that for low transmit SNR, FFr and Noncoop schemes obtain higher data rates than the proposed algorithm, since Coop scheme is targeting fairness over the three sectors considered, whereas other noncooperative schemes target fairness only within a sector when scheduling the users.
. It is observed that the proposed algorithm provides the best sum rate when the transmit power is high, that is, in the region where CCI is dominant over noise. It is also observed that the sum rate for the Noncoop scheme could not be improved by increasing the transmit power, due to CCI observed by users at cell edges. It is observed that for low transmit SNR, FFr and Noncoop schemes obtain higher data rates than the proposed algorithm, since Coop scheme is targeting fairness over the three sectors considered, whereas other noncooperative schemes target fairness only within a sector when scheduling the users.
However, in Figure 7, the complementary cumulative distribution function (cCDF) of the minimum user data rate for different user location scenarios is plotted for PFS with  and low transmit SNR. It is observed that the minimum data rates provided by the cooperative algorithm is significantly better than those for the FFr and the Noncoop schemes. Furthermore, the minimum user data rate, which might be considered as a lower bound on achievable user data rate, cannot be improved by increasing the transmit power in the Noncoop scheme. Thus, the proposed cooperative scheme is better at guaranteeing the minimum data rate requirements of the users and maintaining systemwide fairness.
and low transmit SNR. It is observed that the minimum data rates provided by the cooperative algorithm is significantly better than those for the FFr and the Noncoop schemes. Furthermore, the minimum user data rate, which might be considered as a lower bound on achievable user data rate, cannot be improved by increasing the transmit power in the Noncoop scheme. Thus, the proposed cooperative scheme is better at guaranteeing the minimum data rate requirements of the users and maintaining systemwide fairness.
Lastly, the performance of the proposed cooperative scheme is compared with four different power allocation strategies for TS 2:
-
(1)
PA 1: the proposed power allocation.
-
(2)
PA 2: a uniform power allocation between BSs.
-
(3)
PA 3: an adaptive power allocation, where on each subchannel, the power allocation among PA 1 and PA 2 that results in the highest data rate for joint transmission is used.
-
(4)
PA 4: a nearly optimum power allocation, where the available power on each subchannel (
 ) is distributed optimally between the subcarriers and substreams of the given subchannel using waterfilling. Note that, this method requires singular value decomposition of channel matrix, and hence full CSI knowledge of all users at all BSs. This can be accomplished by either the feedback of perfect channel knowledge by all users to all BSs or by the feedback of all channel gains to user's own BS over the uplink which should then be shared between BSs over the backhaul.
) is distributed optimally between the subcarriers and substreams of the given subchannel using waterfilling. Note that, this method requires singular value decomposition of channel matrix, and hence full CSI knowledge of all users at all BSs. This can be accomplished by either the feedback of perfect channel knowledge by all users to all BSs or by the feedback of all channel gains to user's own BS over the uplink which should then be shared between BSs over the backhaul.
In Figure 8, the sum rates are plotted for  and varying
and varying  , under PFS for different power allocation strategies. At high transmit SNRs, the proposed power control method, PA 1, can increase the performance by approximately 2 bits/s/Hz. However, at small transmit SNRs it has a slightly worse performance. This can be expected, since there is no guarantee that the proposed power allocation PA 1 is optimum for all users. However, generally PA 1 still seems to have a better performance and can be used instead of the uniform power allocation, PA 2. The adaptive power allocation method PA 3 considered has a slightly better performance than the proposed power allocation strategy. This adaptive power control may be considered as a modification for the proposed algorithm, albeit with an increase in the feedback load. For each subchannel, users should calculate two data rates for TS 2 with both power allocations, PA 1 and PA 2, and can feed back an extra indication bit showing whichever power allocation strategy has the best performance. As expected, the nearly optimum power allocation, PA 4, has a better performance but at the same time increases feedback and backhaul loads significantly.
, under PFS for different power allocation strategies. At high transmit SNRs, the proposed power control method, PA 1, can increase the performance by approximately 2 bits/s/Hz. However, at small transmit SNRs it has a slightly worse performance. This can be expected, since there is no guarantee that the proposed power allocation PA 1 is optimum for all users. However, generally PA 1 still seems to have a better performance and can be used instead of the uniform power allocation, PA 2. The adaptive power allocation method PA 3 considered has a slightly better performance than the proposed power allocation strategy. This adaptive power control may be considered as a modification for the proposed algorithm, albeit with an increase in the feedback load. For each subchannel, users should calculate two data rates for TS 2 with both power allocations, PA 1 and PA 2, and can feed back an extra indication bit showing whichever power allocation strategy has the best performance. As expected, the nearly optimum power allocation, PA 4, has a better performance but at the same time increases feedback and backhaul loads significantly.
5. Conclusion
In this paper, we proposed a cooperative data transmission and scheduling scheme, requiring limited CSI feedback and limited information exchange between the base stations. Numerical results demonstrate that the proposed scheme offers a promising solution to mitigate the CCI and improve the spectral efficiency of WiMAX systems without requiring major modifications to the legacy IEEE 802.16e systems. It outperforms other noncooperative schemes, when CCI is the performance limiting factor, by providing significant spatial diversity gains and utilizing adaptive and systemwide usage of subchannels to exploit multiuser diversity. Finally, it can provide the cell edge users with a better spectral efficiency, maintaining systemwide fairness more effectively than the noncooperative schemes considered.
We are currently investigating methods that can further reduce the feedback load, without significantly reducing the cooperation gains. We are also looking into the effects of ICI on the gains from cooperation. The numerical results presented in this paper are for low-mobility scenarios. Our preliminary results indicate that under high-mobility scenarios envisioned for WiMAX, such as for a car with 120 km/hr speed on a highway or for a high-speed train with speeds over 300 km/hr, the effects of ICI can become very significant. We are looking into improving the proposed algorithm to better mitigate ICI effects due to high-mobility.
References
Local and Metropolitan Area Networks Part 16: Air Interface for Fixed and Mobile Broadband Wireless Access Systems. IEEE 802.16e-2005 Std
Viswanath P, Tse DNC, Laroia R: Opportunistic beamforming using dumb antennas. IEEE Transactions on Information Theory 2002, 48(6):1277-1294. 10.1109/TIT.2002.1003822
Han C, Doufexi A, Armour S, McGeehan J, Sun Y: Random beamforming OFDMA for future generation cellular communication systems. Proceedings of the IEEE 66th Vehicular Technology Conference (VTC '07), October 2007, Baltimore, Md, USA 516-520.
Han C, Doufexi A, Armour S, McGeehan J, Sun Y: Layered random beamforming OFDMA with fair scheduling algorithms. Proceedings of the IEEE 67th Vehicular Technology Conference-Spring (VTC' 08), May 2008, Singapore 1097-1101.
Maqbool M, Coupechoux M, Godlewski P: Comparison of various frequency reuse patterns for WiMAX networks with adaptive beamforming. Proceedings of the IEEE Vehicular Technology Conference (VTC '08), 2008 2582-2586.
Chou K, Chen Y, Cheng P, Fu I: Adaptive frequency reuse for interference management in IEEE 802.16m system. contribution to IEEE 802.16 Working Group on Broadband Wireless Access Standards—Task Group m, 2008
Ksairi N, Bianchi P, Ciblat P, Hachem W: Resource allocation for downlink cellular OFDMA systems—part I: optimal allocation. IEEE Transactions on Signal Processing 2010, 58(2):720-734.
Sarperi L, Hunukumbure M, Vadgama S: Simulation study of fractional frequency reuse in WiMAX networks. Fujitsu Scientific and Technical Journal 2008, 44(3):318-324.
Pischella M, Belfiore J-C: Achieving a frequency reuse factor of 1 in OFDMA cellular networks with cooperative communications. Proceedings of the IEEE 67th Vehicular Technology Conference-Spring (VTC '08), May 2008, Singapore 653-657.
Molisch AF, Orlik PV, Tao Z, et al.: Base station cooperation. contribution to IEEE 802.16 Working Group on Broadband Wireless Access Standards—Task Group m, 2008
Wu K, Li D, Yang H, Zhu X: Downlink multi-BS MIMO PHY amendments—closed-loop macro diversity and collaborative precoding. contribution to IEEE 802.16 Working Group on Broadband Wireless Access Standards—Task Group m, 2009
Song Y, Cai L, Wu K, Yang H: Collaborative MIMO based on multiple base station coordination. contribution to IEEE 802.16 Working Group on Broadband Wireless Access Standards—Task Group m, 2007
Huh H, Papadopoulos HC, Caire G: Multiuser MISO transmitter optimization for intercell interference mitigation. IEEE Transactions on Signal Processing 2010, 58(8):4272-4285.
Dahrouj H, Yu W: Coordinated beamforming for the multi-cell multi-antenna wireless system. Proceedings of the 42nd Annual Conference on Information Sciences and Systems (CISS '08), March 2008, Princeton, NJ, USA 429-434.
Zhang J, Andrews JG: Adaptive spatial intercell interference cancellation in multicellular wireless networks. IEEE Journal on Selected Areas in Communications. Submitted for publication, http://arxiv.org/abs/0909.2894 IEEE Journal on Selected Areas in Communications. Submitted for publication,
Yu W, Lan T: Transmitter optimization for the multi-antenna downlink with per-antenna power constraints. IEEE Transactions on Signal Processing 2007, 55(6 I):2646-2660.
Local and Metropolitan Area Networks Part 16: Air Interface for Fixed and Mobile Broadband Wireless Access Systems—Advanced Air Interface—P802.16m Evaluation Methodology Document. IEEE 802.16m-2008 Std
Acknowledgments
This work is supported in part by the Scientific and Technological Research Council of Turkey (TUBITAK) Career Program under Grant EEEAG-107E199 and the European Commission 7th Framework Programme WiMAGIC project, Contract no. 215167.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tokel, T.B., Aktas, D. A Low-Complexity Transmission and Scheduling Scheme for WiMAX Systems with Base Station Cooperation. J Wireless Com Network 2010, 527591 (2010). https://doi.org/10.1155/2010/527591
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/527591

 on subcarrier
on subcarrier  .
.

 , for all subcarriers used by the BS to have the total transmit power over the system bandwidth to be equal to
, for all subcarriers used by the BS to have the total transmit power over the system bandwidth to be equal to  .
.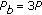 , whereas
, whereas  for the subchannels in the second category.
for the subchannels in the second category.


 .
.
 .
. ) is distributed optimally between the subcarriers and substreams of the given subchannel using waterfilling. Note that, this method requires singular value decomposition of channel matrix, and hence full CSI knowledge of all users at all BSs. This can be accomplished by either the feedback of perfect channel knowledge by all users to all BSs or by the feedback of all channel gains to user's own BS over the uplink which should then be shared between BSs over the backhaul.
) is distributed optimally between the subcarriers and substreams of the given subchannel using waterfilling. Note that, this method requires singular value decomposition of channel matrix, and hence full CSI knowledge of all users at all BSs. This can be accomplished by either the feedback of perfect channel knowledge by all users to all BSs or by the feedback of all channel gains to user's own BS over the uplink which should then be shared between BSs over the backhaul.
 .
.