- Research Article
- Open access
- Published:
SPM: Source Privacy for Mobile Ad Hoc Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 534712 (2009)
Abstract
Source privacy plays a key role in communication infrastructure protection. It is a critical security requirement for many mission critical communications. This is especially true for mobile ad hoc networks (MANETs) due to node mobility and lack of physical protection. Existing cryptosystem-based techniques and broadcasting-based techniques cannot be easily adapted to MANET because of their extensive cryptographic computation and/or large communication overhead. In this paper, we first propose a novel unconditionally secure source anonymous message authentication scheme (SAMAS). This scheme enables message sender to transmit messages without relying on any trusted third parties. While providing source privacy, the proposed scheme can also provide message content authenticity. We then propose a novel communication protocol for MANET that can ensure communication privacy for both message sender and message recipient. This protocol can also protect end-to-end routing privacy. Our security analysis demonstrates that the proposed protocol is secure against various attacks. The theoretical analysis and simulation show that the proposed scheme is efficient and can provide high message delivery ratio. The proposed protocol can be used for critical infrastructure protection and secure file sharing in mobile ad hoc networks where dynamic groups can be formed.
1. Introduction
The decentralized nature of mobile ad hoc networks (MANETs) makes rapid deployment of independent mobile users practical. MANETs are suitable for many applications, such as establishing survivable, dynamic communication for emergency/rescue operations, disaster relief efforts, and military networks. MANETs consist of autonomous collection of mobile users that communicate over bandwidth constrained wireless links. All these issues make security, jamming protection, and even node capture significant concerns. Without privacy protection, adversaries can easily learn the identities of the communication parties and the relevant information that two users are communicating. For example, the adversaries can track your on-line orders, the web sites that you access, the doctors that you visit and many more. Adversaries can also easily overhear all the messages, passively eavesdrop on communications and perform traffic analysis, routing monitoring, and denial-of-service (DoS) attacks.
For a tactical military communication networks, communication privacy is becoming an essential security requirement. As an example, an abrupt change in traffic pattern or volume may indicate some forthcoming activities. The exposure of such information could be extremely dangerous in that adversaries can easily identify critical network nodes and then launch direct DoS attacks on them. Communication privacy is also an indispensable security requirement for applications such as e-voting, e-cash and so on.
In the past two decades, originated largely from Chaum's mixnet [1] and DC-net [2], a number of privacy-preserving communication protocols have been proposed, including for example, onion routing [3],  -anonymous message transmission [4], Web MIXes [5], Mixminion [6], Mixing email [7], Mixmaster Protocol [8], Crowds [9], and Buses seat allocation [10], to name a few. The mixnet family protocols use a set of "mix" servers that mix the received packets to make the communication parties (including the sender and the recipient) ambiguous. They rely on the statistical properties of background traffic that is also referred to as cover traffic to achieve the desired source privacy. The DC-net family protocols [2, 4, 11, 12] on the other hand, utilize secure multiparty computation techniques. They provide provable source privacy without relying on trusted third parties. However, to broadcast a message, each party of the group that the message sender hides, called the ambiguity set (AS), needs to choose a random position. Even if all parties are honest, there are no effective noninteractive means that can enable players to select distinct message positions. This means that multiple parties may transmit messages in the same slot. This is called the transmission collision problem. There is no existing practical solution to solve this problem [12].
-anonymous message transmission [4], Web MIXes [5], Mixminion [6], Mixing email [7], Mixmaster Protocol [8], Crowds [9], and Buses seat allocation [10], to name a few. The mixnet family protocols use a set of "mix" servers that mix the received packets to make the communication parties (including the sender and the recipient) ambiguous. They rely on the statistical properties of background traffic that is also referred to as cover traffic to achieve the desired source privacy. The DC-net family protocols [2, 4, 11, 12] on the other hand, utilize secure multiparty computation techniques. They provide provable source privacy without relying on trusted third parties. However, to broadcast a message, each party of the group that the message sender hides, called the ambiguity set (AS), needs to choose a random position. Even if all parties are honest, there are no effective noninteractive means that can enable players to select distinct message positions. This means that multiple parties may transmit messages in the same slot. This is called the transmission collision problem. There is no existing practical solution to solve this problem [12].
As the computing, communicating, and cryptographic techniques progress rapidly, increasing emphasis has been placed on developing new efficient and secure anonymous communication schemes and network protocols without relying on trusted third parties and free of collision.
In this paper, we first propose a novel unconditionally secure source anonymous message authentication scheme (SAMAS). While providing source privacy, the proposed scheme can also provide message content authenticity without relying on any trusted third parties. We then propose a novel communication protocol for MANET that can ensure communication privacy for both communication parties and their end-to-end communications. The proposed network protocol can be used for critical information distribution, infrastructure protection, and secure file sharing. Our security analysis demonstrates that the proposed protocol is secure against various attacks. The theoretical analysis and simulation results show that the proposed scheme is efficient and can ensure high message delivery ratio.
The rest of this paper is organized as follows. In Section 2, the terminology, assumptions, and previous related works are briefly reviewed. The proposed unconditionally secure source anonymous message authentication scheme (SAMAS) and security analysis are described in Section 3. In Section 4, we propose an anonymous communication protocol in detail along with security analysis and simulation results in Section 5. Finally, Section 6 concludes this paper.
2. Terminology and Preliminary
In this section, we will briefly describe the terminology that will be used in this paper. Then we will introduce some cryptographic tools that will be used in this paper. Finally, we will present a brief overview of the related works in this area.
2.1. Terminology
Privacy is sometimes referred to as anonymity. Communication anonymity in information management has been discussed in a number of previous works [1, 2, 9, 13–15]. It generally refers to the state of being not identifiable within a set of subjects. This set is called the ambiguity se t (AS). Three types of anonymity were defined [13]: sender anonymity, recipient anonymity, and relationship anonymity. Sender anonymity means that a particular message is not linkable to any sender and no message if linkable to a particular sender. Recipient anonymity similarly means that a message cannot be linked to any recipient and that no message is linkable to a recipient. Relationship anonymity means that the sender and the recipient are unlinkable. In other words, sender and recipient cannot be identified as communicating with each other, though it may be clear they are participating in some communications. Relationship anonymity is a weaker property than that of sender anonymity and recipient anonymity. The above anonymities are also referred to as the full anonymities, since they guarantee that an adversary cannot infer anything about the sender, the recipient, or the communication relationship from a transmitted message.
We will start with the definition of unconditionally secure source anonymous message authentication scheme (SAMAS).
Definition 1 (SAMAS).
An SAMAS consists of the following two algorithms:
-
(i)
generate
 : Given a message
: Given a message 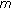 and the public keys
and the public keys 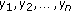 ??of the ambiguity set(AS)
??of the ambiguity set(AS) , the actual message sender
, the actual message sender 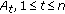 , produces an anonymous message
, produces an anonymous message  using her own private key
using her own private key 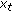 ;
; -
(ii)
verify
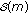 : Given a message
: Given a message  and an anonymous message
and an anonymous message 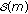 , which includes the public keys of all members in the AS, a verifier can determine whether
, which includes the public keys of all members in the AS, a verifier can determine whether 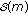 is generated by a member in the AS.
is generated by a member in the AS.
The security requirements for SAMAS include
-
(i)
Sender ambiguity: The probability that a verifier successfully determines the real sender of the anonymous message is exactly
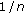 , where
, where  is the total number of AS;
is the total number of AS; -
(ii)
Unforgeability: An anonymous message scheme is unforgeable if no adversary, given the public keys of all members of the AS and the anonymous messages
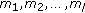 adaptively chosen by the adversary, can produce in polynomial time a new valid anonymous message with nonnegligible probability.
adaptively chosen by the adversary, can produce in polynomial time a new valid anonymous message with nonnegligible probability.
In this paper, the user ID and user public key will be used interchangeably without making any distinguish.
2.2. Modified ElGamal Signature Scheme (MES)
Definition 2 (MES).
The modified ElGamal signature scheme [16] consists of the following three algorithms:
-
(i)
Key generation algorithm: Let
 be a large prime,
be a large prime, 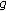 be a generator of
be a generator of  Both
Both 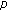 and
and 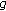 are made public. For a random private key
are made public. For a random private key 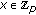 , the public key
, the public key 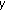 is computed from
is computed from 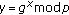 ;
; -
(ii)
Signature algorithm: The MES can also have many variants [17, 18]. For the purpose of efficiency, we will describe the variant, called optimal scheme. To sign a message
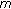 , one chooses a random
, one chooses a random 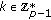 , then computes the exponentiation
, then computes the exponentiation 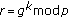 ??and solves
??and solves  from
from

where  is a one-way hash function. The signature of message
is a one-way hash function. The signature of message  is defined as the pair
is defined as the pair  ;
;
-
(iii)
Verification algorithm: The verifier checks the signature equation
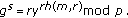 If the equality holds true, then the verifier
If the equality holds true, then the verifier  the signature and
the signature and  otherwise.
otherwise.
2.3. Previous Work
The existing anonymous communication protocols are largely stemmed from either mixnet [1] or DC-net [2]. A mixnet provides anonymity via packet reshuffling through (at least one trusted) "mix". In a mixnet, a sender encrypts an outgoing message and the ID of the recipient using the public key of the mix. The mix accumulates a batch of encrypted messages, decrypts and reorders these messages, and forwards them to the recipients. An eavesdropper cannot link a decrypted output message with any particular (encrypted) input message. The mixnet thus protects the secrecy of users' communication relationships. Recently, Möler presented a secure public-key encryption algorithm for mixnet [19]. This algorithm has been adopted by Mixminion [6]. However, since mixnet-like protocols rely on the statistical properties of background traffic, they cannot provide provable anonymity.
DC-net [2, 15] is an anonymous multiparty computation amongst a set of participants, some pairs of which share secret keys. DC-net provides perfect (information theoretic) sender anonymity without requiring trusted servers. In a DC-net, users send encrypted broadcasts to the entire group, thus achieving receiver anonymity. However, all members of the group are made aware of when a message is sent, so DC-net does not have the same level of sender-receiver anonymity. Also, in DC-net, only one user can send at a time, so it takes additional bandwidth to handle collisions and contention. Lastly, a DC-net participant fixes its anonymity versus bandwidth trade off when joining the system, and there are no provisions to rescale that trade off when others join the system.
Crowds [9] extends the idea of anonymizer and is designed for anonymous web browsing. However, Crowds only provides sender anonymity. It does not hide the receivers and the packet content from the nodes en route. Hordes [20] builds on the Crowds. It uses multicast services and provides only sender anonymity.
Recently, message sender anonymity based on ring signatures was introduced [21]. This approach can enable message sender to generate source anonymous message signature with content authenticity assurance, while hiding the real identity of the message sender. The major idea is that the message sender (say Alice) randomly selects  of ring members as the AS on her own without awareness of these members. To generate a ring signature, for each member in the ring other than the actual sender (Alice), Alice randomly selects an input and computes the one-way output using message signature forgery. For the trapdoor one-way function corresponding to the actual sender Alice, she needs to solve the "message" that can "glue" the ring together, and then signs this "message" using her knowledge of the trap-door information. The original scheme has very limited flexibility and the complexity of the scheme is quite high. Moreover, the original paper only focuses on the cryptographic algorithm, the relevant network issues were totally left unaddressed.
of ring members as the AS on her own without awareness of these members. To generate a ring signature, for each member in the ring other than the actual sender (Alice), Alice randomly selects an input and computes the one-way output using message signature forgery. For the trapdoor one-way function corresponding to the actual sender Alice, she needs to solve the "message" that can "glue" the ring together, and then signs this "message" using her knowledge of the trap-door information. The original scheme has very limited flexibility and the complexity of the scheme is quite high. Moreover, the original paper only focuses on the cryptographic algorithm, the relevant network issues were totally left unaddressed.
In this paper, we first propose an unconditionally secure and efficient source anonymous message authentication scheme based on the modified ElGamal signature scheme. This is because the original ElGamal signature scheme is existentially forgeable with a generic message attack [22, 23]. While the modified ElGamal signature (MES) scheme is secure against no-message attack and adaptive chosen-message attack in the random oracle model [24].
2.4. Threat Model and Assumptions
We assume the participating MANET nodes voluntarily cooperate with each other to provide the service. All nodes are potential message originators of anonymous communications. The adversaries can collaborate to passively monitor and eavesdrop every MANET traffic. In addition, they may compromise any node in the target network to become an internal adversary, which could be the internal perpetrators. In this paper, we assume that passive adversaries can only compromise a fraction of the nodes. We also assume that the adversaries are computationally bounded so that inverting and reading of encrypted messages are infeasible. Otherwise, it is believed that there is no workable cryptographic solution.
An agent of the adversary at a compromised node observes and collects all the information in the message, and thus reports the immediate predecessor and successor node for each message traversing the compromised node. Assume also that the adversary collects this information from all the compromised nodes, and uses it to derive the identity of the sender of a message. The sender has no information about the number or identity of nodes being compromised. The adversary collects all the information from the agents on the compromised nodes, and attempts to derive the true identity of the sender.
3. Unconditionally Secure Source Anonymous Message Authentication Scheme (SAMAS)
In this section, we propose an unconditionally secure and efficient source anonymous message authentication scheme (SAMAS). The main idea is that for each message  to be released, the message sender, or the sending node, generates a source anonymous message authentication for the message
to be released, the message sender, or the sending node, generates a source anonymous message authentication for the message  . The generation is based on the MES scheme. Unlike ring signatures, which requires to compute a forgery signature for each member in the AS separately, our scheme only requires three steps to generate the entire SAMAS, and link all nonsenders and the message sender to the SAMAS alike. In addition, our design enables the SAMAS to be verified through a single equation without individually verifying the signatures.
. The generation is based on the MES scheme. Unlike ring signatures, which requires to compute a forgery signature for each member in the AS separately, our scheme only requires three steps to generate the entire SAMAS, and link all nonsenders and the message sender to the SAMAS alike. In addition, our design enables the SAMAS to be verified through a single equation without individually verifying the signatures.
3.1. The Proposed SAMAS Scheme
Suppose that the message sender (say Alice) wishes to transmit a message  anonymously from her network node to any other node. The AS includes
anonymously from her network node to any other node. The AS includes  members,
members,  for example,
for example,  where the actual message sender Alice is
where the actual message sender Alice is  , for some value
, for some value  .
.
Let  be a large prime number and
be a large prime number and  be a primitive element of
be a primitive element of  . Then
. Then  is also a generator of
is also a generator of  . That is
. That is  . Both
. Both  and
and  are made public and shared by all members in
are made public and shared by all members in  . Each
. Each  has a public key
has a public key  , where
, where  is a randomly selected private key from
is a randomly selected private key from  . In this paper, we will not distinguish between the node
. In this paper, we will not distinguish between the node  and its public key
and its public key  . Therefore, we also have
. Therefore, we also have  .
.
Suppose  is a message to be transmitted. The private key of the message sender Alice is
is a message to be transmitted. The private key of the message sender Alice is  . To generate an efficient SAMAS for message
. To generate an efficient SAMAS for message  , Alice performs the following three steps:
, Alice performs the following three steps:
-
(1)
Select a random and pairwise different
 for each
for each 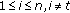 and compute
and compute 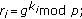
-
(2)
Choose a random
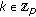 and compute
and compute 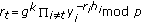 such that
such that 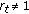 and
and  for any
for any  where
where 
-
(3)
Compute
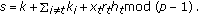
The SAMAS of the message  is defined as
is defined as

where  and
and 
3.2. Verification of SAMAS
A verifier can verify an alleged SAMAS  for message
for message  by verifying whether the following equation
by verifying whether the following equation

holds. If (3) holds true, the verifier  the SAMAS as valid for message
the SAMAS as valid for message  . Otherwise the verifier
. Otherwise the verifier  the SAMAS.
the SAMAS.
In fact, if the SAMAS has been correctly generated, then we have

Therefore, the verifier should always  the SAMAS if it is correctly generated without being modified.
the SAMAS if it is correctly generated without being modified.
Remark 1.
As a trade-off between computation and transmission, the SAMAS can also be defined as  . In case
. In case  is also clear, it can be eliminated from the SAMAS.
is also clear, it can be eliminated from the SAMAS.
3.3. Security Analysis
In this subsection, we will prove that the proposed SAMAS scheme is unconditionally anonymous and provably unforgeable against adaptive chosen-message attack.
3.3.1. Anonymity
In order to prove that the proposed SAMAS is unconditionally anonymous, we have to prove that (i) for anybody other than the members of  the probability to successfully identify the real sender is
the probability to successfully identify the real sender is  , and (ii) anybody from
, and (ii) anybody from  can generate SAMAS.
can generate SAMAS.
Theorem 1.
The proposed source anonymous message authentication scheme (SAMAS) can provide unconditional message sender anonymity.
Proof.
The identity of the message sender is unconditionally protected with the proposed SAMAC scheme. This is because that regardless of the sender's identity, there are exactly  different options to generate the SAMAC, and all of them can be chosen by the SAMAC generation procedure and by any of the members in the AS with equal probability without depending on any complexity-theoretic assumptions. The proof for the second part, that anybody from
different options to generate the SAMAC, and all of them can be chosen by the SAMAC generation procedure and by any of the members in the AS with equal probability without depending on any complexity-theoretic assumptions. The proof for the second part, that anybody from  can generate the SAMAC is straightforward. This finishes the proof of this theorem.
can generate the SAMAC is straightforward. This finishes the proof of this theorem.
3.3.2. Unforgeability
The design of the proposed SAMAS relies on the ElGamal signature scheme. Signature schemes can achieve different levels of security. Security against existential forgery under adaptive-chosen message attack is the maximum level of security.
In this section, we will prove that the proposed SAMAS is secure against existential forgery under adaptive-chosen message attacks in the random oracle model [25]. The security of our result is based on the well-known discrete logarithms problem (DLP), which assumes that the computation of discrete logarithm in  for large
for large  is computationally infeasible. In other words, no efficient algorithms are known for non-quantum computers.
is computationally infeasible. In other words, no efficient algorithms are known for non-quantum computers.
We will introduce two lemmas first. Lemma 2, or the Splitting Lemma, is a well-known probabilistic lemma from reference [24]. The basic idea of the Splitting Lemma is that when a subset  is "large" in a product space
is "large" in a product space  , it will have many "large" sections. Lemma 3 is a slight modification of the Forking Lemma presented in [24]. The proof of this theorem is mainly probability theory related. We will skip the proof of these two lemmas here.
, it will have many "large" sections. Lemma 3 is a slight modification of the Forking Lemma presented in [24]. The proof of this theorem is mainly probability theory related. We will skip the proof of these two lemmas here.
Lemma 2 (The Splitting Lemma).
Let  such that
such that  . For any
. For any  , define
, define  , and
, and  then the following statements hold
then the following statements hold
-
(1)

-
(2)
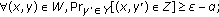
-
(3)
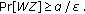
Lemma 3 (The Forking Lemma).
Let  be a Probabilistic Polynomial Time (PPT) Turing machine. Given only the public data as input, if
be a Probabilistic Polynomial Time (PPT) Turing machine. Given only the public data as input, if  can find, with nonnegligible probability, a valid SAMAS
can find, with nonnegligible probability, a valid SAMAS  within a bounded polynomial time
within a bounded polynomial time  , then with nonnegligible probability, a replay of this machine which has control over
, then with nonnegligible probability, a replay of this machine which has control over  and a different oracle, outputs another valid SAMAS
and a different oracle, outputs another valid SAMAS  , such that
, such that  , for all
, for all  for some fixed
for some fixed  .
.
Theorem 4.
The proposed SAMAS is secure against adaptive chosen-message attack in the random oracle model.
Proof.
(Sketch) If an adversary can forgery a valid SAMAS with nonnegligible probability, then according to the Forking Lemma, the adversary can get two valid SAMACs

such that for  , and
, and  . That is
. That is


Divide equations (6) and (7), we obtain

Equivalently, we have

Therefore, we can compute the discrete logarithm of  in base
in base  with nonnegligible probability, which contradicts to the assumption that it is computationally infeasible to compute the discrete logarithm of
with nonnegligible probability, which contradicts to the assumption that it is computationally infeasible to compute the discrete logarithm of  in base
in base  . Therefore, it is computationally infeasible for any adversary to forge a valid SAMAC.
. Therefore, it is computationally infeasible for any adversary to forge a valid SAMAC.
4. The Proposed Privacy-Preserving Communication Protocol
4.1. Network Model
Keeping confidential who sends which messages, in a world where any physical transmission can be monitored and traced to its origin, seems impossible. To solve this problem, in this paper, we consider networks with multiple MANETs. That is, the participating nodes are divided into a set of small subgroups. We classify the network nodes into two categories, normal nodes and super nodes. A normal node is a network node that may not be able to communicate direct with the nodes in other MANETs. A super node can be a normal node that can also provide message forward services to other MANET nodes. It can also be a special node dedicated to providing message forward services to other MANET nodes. For energy optimization, the normal nodes can take turn to be the super nodes.
Prior to network deployment, there should be an administrator. The administrator is responsible for selection of security parameters and a group-wise master key  . The group master key should be well safeguarded from unauthorized access and never be disclosed to the ordinary group members. The administrator then chooses a collision-resistant cryptographic hash function
. The group master key should be well safeguarded from unauthorized access and never be disclosed to the ordinary group members. The administrator then chooses a collision-resistant cryptographic hash function  , mapping arbitrary inputs to fixed-length outputs on
, mapping arbitrary inputs to fixed-length outputs on  , for example, SHA-1 [26].
, for example, SHA-1 [26].
The administrator assigns each super node a sufficiently large set of collision-free pseudonyms that can be used to substitute the real IDs in communications to defend against passive attacks. If a super node uses one pseudonym continuously for some time, it will not help to defend against possible attacks since the pseudonym can be analyzed in the same way as its real ID. To solve this problem, each node should use dynamic pseudonyms instead. This requires each super node to sign up with the administrator, who will assign each super node a list of random and collision-resistant pseudonyms:

In addition, each super node will also be assigned a corresponding secret set: 
4.2. Anonymous Local MANET Communication
To realize anonymous network layer communications, obviously there should be no explicit information (such as the message sender and recipient addresses) in the message content. All of the information related to addresses, including the destination MANET where the recipient resides, should be embedded into the anonymizing message payload (Figure 1).
Prior to network deployment, the administrator needs to select a set of security parameters for the entire system, including a large prime  and a generator
and a generator  of
of  The network nodes
The network nodes  and the corresponding public keys
and the corresponding public keys  of the
of the  participating network nodes, where
participating network nodes, where  is a randomly selected private key of node
is a randomly selected private key of node  , and
, and  is computed from
is computed from  .
.
A normal node only communicates to other nodes in the same MANET. The communication between two normal nodes in different MANETs has to be forwarded through the supper nodes in the respected local MANETs. Each message contains a nonce ( ), a message flag (
), a message flag ( ), a recipient flag
), a recipient flag  and a secret key. The nonce is a random number that is used only once to prevent message replay attack. The recipient flag enables the recipient to know whether he is the targeted receiver or a forwarding node. The secret key is used to encrypt the message payload through symmetric encryption algorithm.
and a secret key. The nonce is a random number that is used only once to prevent message replay attack. The recipient flag enables the recipient to know whether he is the targeted receiver or a forwarding node. The secret key is used to encrypt the message payload through symmetric encryption algorithm.
More specifically, for a node  to transmit a message
to transmit a message  anonymously to a node
anonymously to a node  in the same MANET, through the nodes
in the same MANET, through the nodes  where
where  , node
, node  generates a new message
generates a new message  defined in (11),
defined in (11),

where for  is a nonce,
is a nonce,  is a message flag,
is a message flag,  is a recipient flag,
is a recipient flag,  is the secret key used for one time message encryption, and
is the secret key used for one time message encryption, and  stands for message concatenation.
stands for message concatenation.
When the node  receives the message packet, the node decrypts the first block of the received message using its private key corresponding to
receives the message packet, the node decrypts the first block of the received message using its private key corresponding to  After that, the node will get the recipient flag and message flag with the instruction for the subsequent actions.
After that, the node will get the recipient flag and message flag with the instruction for the subsequent actions.
When a message reaches the targeted recipient, to ensure traffic balance, the node will generate a dummy message to its subsequent nodes. Only the super nodes can terminate or initiate a dummy message. In this way, the amount of traffic flow that a node creates as the initiator is concealed in the traffic that it forwards since the overall traffic that it receives is the same as the traffic that it forwards. In addition, the message is encrypted with the private key that only the recipient can recover. While the intermediate nodes can only view the instruction of the message allowed. The sender's message is indistinguishable by other nodes. The sender and the recipient are thus hidden amongst the other nodes. It is infeasible for the adversary to correlate messages using traffic analysis and timing analysis due to message encryption. Therefore, perfect obscure of its own messages can be assured. Detailed security analysis will be presented later.
Remark 2.
When the message is delivered to the recipient's local MANET, if the super node is close enough to the recipient node, then the super node can simply broadcast the message. In this case, the message format in (11) can be adjusted accordingly.
4.3. Dynamic Local MANET Formation
Due to node mobility in the MANET, the local MANET will dynamically change over time. This makes reforming of the local MANET an essential part of our proposed scheme. The dynamic updating of the MANET can be characterized through mobility of each individual node, that can leave and join a local MANET.
4.3.1. Process for a Node to Join a Local MANET
When a node, say node  wishes to join a local MANET, it needs to send a request message to the local super node in the form of:
wishes to join a local MANET, it needs to send a request message to the local super node in the form of:

where  is the public key of node
is the public key of node  and
and  is a timestamp. After receiving this request message, the super node has to determine the relative location of this node according to the direction and strength of the request signal provided by nodes that also received this message. The super node will determine where the node should be located in the local MANET logically. Then the super node will broadcast a message in the following format to inform the local MANET that node
is a timestamp. After receiving this request message, the super node has to determine the relative location of this node according to the direction and strength of the request signal provided by nodes that also received this message. The super node will determine where the node should be located in the local MANET logically. Then the super node will broadcast a message in the following format to inform the local MANET that node  will be joining the local MANET in between node
will be joining the local MANET in between node  and node
and node  :
:

where  is a timestamp.
is a timestamp.
4.3.2. Process for a Node to Leave a Local MANET
A node can leave a local MANET either positively or passively. For positive leaving, the node, say node  , is aware that it is leaving the local MANET. It will send a request message to the local super node in the format of:
, is aware that it is leaving the local MANET. It will send a request message to the local super node in the format of:

where  is the public key of node
is the public key of node  , and
, and  is a timestamp. For passive leaving, the node will just leave the local MANET without informing anyone. The super node will discover a node's leaving through message transmission failure and Hello message detection.
is a timestamp. For passive leaving, the node will just leave the local MANET without informing anyone. The super node will discover a node's leaving through message transmission failure and Hello message detection.
When a super node is aware of a node's leaving through either of the two manners, it will inform all of the local MANET members through broadcasting a message:

which means a node with public key  has left the local MANET, and it should be removed from the local MANET.
has left the local MANET, and it should be removed from the local MANET.
4.4. Anonymous Communications between Two Arbitrary Super Nodes
In the previous subsections, we present the mechanism that allows two arbitrary nodes to communicate anonymously within the same MANET. This includes communications between two super nodes in the same MANET. For any two arbitrary super nodes in different MANETs to communicate anonymously, we will first introduce the concept of anonymous authentication or secret handshake by Balfanz et al. [27]. Anonymous authentication allows two nodes in the same group to authenticate each other secretly in the sense that each party reveals its group membership to the other party only if the other party is also a group member. Nonmembers are not able to recognize group members.
The scheme consists of a set of super nodes and an administrator who creates groups and enrolls super nodes in groups. For this purpose, the administrator will assign each super node  a set of pseudonyms
a set of pseudonyms  , where
, where  is a large security parameter. In addition, the administrator also calculates a corresponding secret set
is a large security parameter. In addition, the administrator also calculates a corresponding secret set for super node
for super node  , where
, where  is the group's secret and
is the group's secret and  is a hash function. The pseudonyms will be dynamically selected and used to substitute the real IDs for each communication. This means that two super nodes
is a hash function. The pseudonyms will be dynamically selected and used to substitute the real IDs for each communication. This means that two super nodes  and
and  can know each other's group membership only if they belong to the same group.
can know each other's group membership only if they belong to the same group.
When the super node  wants to authenticate to the super node
wants to authenticate to the super node  , the following secret handshake can be conducted:
, the following secret handshake can be conducted:
-
(1)
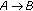 : Super node
: Super node 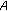 randomly selects an unused pseudonym
randomly selects an unused pseudonym 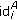 and a random nonce
and a random nonce 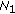 , then sends
, then sends  to super node
to super node 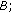
-
(2)
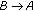 : Super node
: Super node 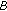 randomly selects an unused pseudonym
randomly selects an unused pseudonym 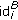 and a random nonce
and a random nonce 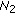 , then sends
, then sends  to super node
to super node  , where
, where 
-
(3)
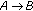 : Super node
: Super node 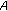 sends
sends 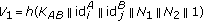 to super node
to super node 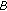 , where
, where  .
.
Since  ,
,  can verify
can verify  by checking whether
by checking whether  If the verification succeeds, then
If the verification succeeds, then  knows that
knows that  is an authentic group peer. Similarly,
is an authentic group peer. Similarly,  can verify
can verify  by checking whether
by checking whether  If the verification succeeds, then
If the verification succeeds, then  knows that
knows that  is also an authentic group peer. However, in this authentication process, neither super node
is also an authentic group peer. However, in this authentication process, neither super node  , nor super node
, nor super node  can get the real identity of the other node. In other words, the real identities of super node
can get the real identity of the other node. In other words, the real identities of super node  and super node
and super node  remain anonymous after the authentication process.
remain anonymous after the authentication process.
4.5. Anonymous Communication between Two Arbitrary Normal Nodes
As mentioned before, there should be no explicit exposure about the addresses of the message sender and recipient. To transmit a message, the sender first randomly selects a local super node and transmits the message to the super node according to the mechanism described before. On receiving the message, the local super node first determines the destination MANET ID by checking the message recipient flag  , either
, either  or
or  . If it is
. If it is  , then the recipient and the super node are in the same MANET. The message can be forwarded in the recipient node using the previously described mechanism. If
, then the recipient and the super node are in the same MANET. The message can be forwarded in the recipient node using the previously described mechanism. If  is
is  , then the recipient is in a different MANET, The super node forwards the message to a super node in the destination MANET as described in the previous subsection. Finally, when the super node in the recipient's local MANET receives the message, the communication again becomes local MANET communications. The message can now be transmitted in the same way that the sender and the recipient are in the same MANET.
, then the recipient is in a different MANET, The super node forwards the message to a super node in the destination MANET as described in the previous subsection. Finally, when the super node in the recipient's local MANET receives the message, the communication again becomes local MANET communications. The message can now be transmitted in the same way that the sender and the recipient are in the same MANET.
While providing message recipient anonymity, the message can also be encrypted so that only the message recipient can decrypt the message. The proposed anonymous communication is quite general and can be used in a variety of situations for communication anonymity in MANET, including anonymous file sharing.
4.6. Security Analysis
In this subsection, we will analyze anonymity, impersonation attack, and replay attack of the proposed anonymous communication protocol.
4.6.1. Anonymity
We will first prove that the proposed communication protocol can provide both message sender and recipient anonymity in the local MANET communications.
Theorem 5.
It is computationally infeasible for an adversary to identify the message sender and recipient in the local MANET. Therefore, the proposed anonymous communication protocol provides both sender and recipient anonymity in the local MANET.
Proof.
(Sketch) First, since the number of message packages that each node receives from its immediate predecessor is the same as the number of packets that it forwards to its immediate successor, so the adversaries cannot determine the message source based on the traffic volume or the number of message packets. Second, since the message packages are encrypted using either the public keys or the shared secret keys of the intermediate nodes. No adversary is able to distinguish the real meaningful message from the dummy message in the transmission in any of the network nodes due to the traffic balance property and message content encryption. Therefore, the adversary cannot distinguish the initiator traffic from the indirection traffic and learn whether the node is a recipient, a receiver, or simply a node that provides message forward service. Consequently, both the message sender and recipient information is anonymous for the adversary attack.
For any two normal nodes in different MANETs to communicate anonymously, the communication can be broken into three segments: the communication between the sender and a local super node in the message sender's local MANET, the communication between two super nodes in the corresponding MANETs, and the communication between the recipient super node and the recipient. Theorem 5 has assured the communication anonymity between a super node and a normal node in the local MANETs. Therefore, we only need to ensure anonymity between two super nodes in different MANETs in order to achieve full anonymity between the sender and recipient.
We already described before that each super node is being assigned a large set of pseudonyms. A dynamically selected pseudonym will be used for each communication. The pseudonyms do not carry the user information implicitly. Therefore, the adversary cannot get any information of the super nodes from the network. This result can be summarized into the following theorem.
Theorem 6.
The proposed communication protocol can provide both message sender and recipient anonymity between any two super nodes.
Corollary 7.
The proposed anonymous communication protocol can provide full anonymity for any sender and recipient in the MANETs.
4.6.2. Impersonation Attacks
For an adversary elected to perform impersonation attack to a normal node, he needs to be able to conduct forgery attack. We already proved in Theorem 4 that this is infeasible. Therefore, we only need to consider whether it is feasible for an adversary to forge a super node.
For an adversary to impersonate as a super node, he needs to be able to authenticate himself with a super node  . This requires the adversary
. This requires the adversary  to compute
to compute  , where
, where  is the identity of the adversary and
is the identity of the adversary and  is the
is the  th pseudonym of the super node
th pseudonym of the super node  . However, since the adversary does not know the master secret
. However, since the adversary does not know the master secret  , he is unable to compute
, he is unable to compute  and impersonate as a super node. Therefore, we have the following theorem.
and impersonate as a super node. Therefore, we have the following theorem.
Theorem 8.
It is computationally infeasible for a PPT adversary  to impersonate as a super node.
to impersonate as a super node.
Like all other network communication protocols, in our proposed protocol, an adversary may choose to drop some of the messages. However, if the immediate predecessor and the successor nodes are honest and willing to cooperate, then the messages being dropped, and the substitution of the valid messages with the dummy messages can be effectively tracked using the provided message flags.
An adversary that is elected as a super node may refuse to forward messages across the MANETs and thus block the anonymous communications between the sender and the receiver. This attack can be hard to detect if the sender does not have the capability to monitor all network traffic. However, the sender can randomly select the super nodes for each data transmission. If the nonce is properly generated, when a packet is lost, the recipient should be able to know.
4.6.3. Message Replay Attacks
The message replay attack occurs when an adversary can intercept the communication packet, correlate the message to the corresponding sender and recipient, and retransmit it. We have the following theorem.
Theorem 9.
It is computationally infeasible for an adversary to successfully modify/reply an (honest) node's message.
Proof.
According to (11), each message package in communication has a unique one-time session ID (nonce) to protect the message package from being modified or replayed. In addition, these fields are encrypted using the intermediate receiver nodes' public key so that only the designated receiver nodes can decrypt the message. In this way, each packet transmitted across different MANETs bears different and uncorrelated IDs and content for PPT adversaries. Therefore, it is computationally infeasible for the adversary to modify or replay any messages in the MANET. This includes the case that even if the same message is being transmitted multiple times, the adversary still cannot link them together without knowing all the private keys of the intermediate nodes.
5. Performance Analysis and Simulation Results
In this section, we will provide simulation results of our proposed protocol on energy consumption, communication delay, and message delivery ratio. For energy consumption, we provide simulations for both the normal nodes and the super nodes. For wireless communications, due to collision and packet drop, it is very challenging to assure high messages delivered ratio. However, our simulation results demonstrate that the proposed protocol can achieve high message delivery ratio (Figure 2).
Our simulation was performed using ns-2 on Linux system. In the simulation, the target area is a square field of size  meters. There are 64 rings located in this area. The number of the nodes on each ring, that is, the ring length, is set to be from 7 to 16 in our simulation. The message generation interval is set to be four different values: 60 seconds, 90 seconds, 120 seconds, and 150 seconds in our simulation for comparison. The messages transmitted in the network are 512 bytes long.
meters. There are 64 rings located in this area. The number of the nodes on each ring, that is, the ring length, is set to be from 7 to 16 in our simulation. The message generation interval is set to be four different values: 60 seconds, 90 seconds, 120 seconds, and 150 seconds in our simulation for comparison. The messages transmitted in the network are 512 bytes long.
6. Conclusion
In this paper, we first propose a novel and efficient source anonymous message authentication scheme (SAMAS) that can be applied to any messages. While ensuring message sender privacy, SAMAS can also provide message content authenticity. To provide provable communication privacy without suffering from transmission collusion problem, we then propose a novel privacy-preserving communication protocol for MANETs that can provide both message sender and recipient privacy protection. Security analysis shows that the proposed protocol is secure against various attacks. Our performance analysis and simulation results both demonstrate that the proposed protocol is efficient and practical. It can be applied for secure routing protection and file sharing.
References
Chaum D: Untraceable electronic mail, return addresses, and digital pseudonyms. Communications of the ACM 1981, 24: 84-88. 10.1145/358549.358563
Chaum D: The dining cryptographers problemml: unconditional sender and recipient untraceability. Journal of Cryptology 1988, 1(1):65-75.
Reed M, Syverson P, Goldschlag D: Anonymous connections and onion routing. IEEE Journal on Selected Areas in Communications 1998, 16(4):482-494. 10.1109/49.668972
von Ahn L, Bortz A, Hopper N:
 -anonymous message transmission. Proceedings of the 10th ACM Conference on Computer and Communications Security (CCS '03), October 2003, Washingtion, DC, USA 122-130.
-anonymous message transmission. Proceedings of the 10th ACM Conference on Computer and Communications Security (CCS '03), October 2003, Washingtion, DC, USA 122-130.Berthold O, Federrath H, Köpsell S: Web MIXes: a system for anonymous and unobservable internet access. Proceedings of the Workshop on Design Issues in Anonymity and Unobservability, 2001, Lecture Notes in Computer Science 2248: 115-129.
Danezis G, Dingledine R, Mathewson N: Mixminion: design of a type III anonymous remailer protocol. Proceedings of the IEEE Computer Society Symposium on Research in Security and Privacy, May 2003, Oakland, Calif, USA 2-15.
Gülcü C, Tsudik G: Mixing email with babel. Proceedings of the Symposium on Network and Distributed System Security, February 1996, San Diego, Calif, USA
Möller U, Cottrell L, Palfrader P, Sassaman L: Mixmaster protocol. Version 2, July 2003
Reiter M, Rubin A: Crowds: anonymity for web transaction. ACM Transactions on Information and System Security 1998, 1(1):66-92. 10.1145/290163.290168
Beimel A, Dolev S: Buses for anonymous message delivery. Journal of Cryptology 2003, 16(1):25-39. 10.1007/s00145-002-0128-6
Goel S, Robson M, Polte M, Sirer E: Herbivore: a scalable and efficient protocol for anonymous communication. Tech. Rep. 2003-1890, Cornell University, Ithaca, NY, USA; 2003.
Golle P, Juels A: Dining cryptographers revisited. Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques (Eurocrypt '04), May 2004, Interlaken, Switzerland, Lecture Notes in Computer Science 456-473.
Pfitzmann A, Hansen M: Anonymity, unlinkability, unobservability, pseudonymity, and identity management a proposal for terminology. February 2008, http://dud.inf.tu-dresden.de/literatur/Anon_Terminology_v0.31.pdf
Pfitzmann A, Waidner M: Networks without user observability-design options. Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques (Eurocrypt '85), April 1985, Linz, Austria, Lecture Notes in Computer Science 219: 245-253.
Waidner M: Unconditional sender and recipient untraceability in spite of active attacks. Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques (Eurocrypt '89), April 1989, Houthalen, Belgium, Lecture Notes in Computer Science 434: 302-319.
Pointcheval D, Stern J: Security arguments for digital signatures and blind signatures. Journal of Cryptology 2000, 13(3):361-396. 10.1007/s001450010003
Harn L, Xu Y: Design of generalised ElGamal type digital signature schemes based on discrete logarithm. Electronics Letters 1994, 30(24):2025-2026. 10.1049/el:19941398
Nyberg K, Rueppel RA: Message recovery for signature schemes based on the discrete logarithm problem. Proceedings of the International Conference on the Theory and Application of Cryptographic Techniques (Eurocrypt '95), May 1995, Saint-Malo, France, Lecture Notes in Computer Science 950: 182-193.
Möller B: Provably secure public-key encryption for length-preserving chaumian mixes. Proceedings of the Cryptographer's Track at the RSA Conference (CT-RSA '03), April 2003, San Francisco, Calif, USA, Lecture Notes in Computer Science 2612: 244-262.
Shields C, Levine BN: A protocol for anonymous communication over the Internet. In Proceedings of the 7th ACM Conference on Computer and Communication Security, November 2000, Athens, Greece. Edited by: Gritzalis D. ACM Press;
Rivest R, Shamir A, Tauman Y: How to leak a secret. In Proceedings of the 7th International Conference on the Theory and Application of Cryptology and Information Security (ASIACRYPT '01), December 2001, Gold Coast, Australia, Lecture Notes in Computer Science. Volume 2248. Springer;
ElGamal TA: A public-key cryptosystem and a signature scheme based on discrete logarithms. IEEE Transactions on Information Theory 1985, 31(4):469-472. 10.1109/TIT.1985.1057074
Goldwasser S, Micali S, Rivest R: A digital signature scheme secure against adaptive chosen-message attacks. SIAM Journal on Computing 1988, 17: 281-308. 10.1137/0217017
Pointcheval D, Stern J: Security proofs for signature schemes. Proceedings of the International Conference on the Theory and Application of Cryptographic Techniques (EUROCRYPT '96), May 1996, Saragossa, Spain, Lecture Notes in Computer Science 1070: 387-398.
Bellare M, Rogaway P: Random oracles are practical: a paradigm for designing efficient protocols. Proceedings of the 1st ACM Conference on Computer and Communications Security (CCS '93), November 1993, Fairfax, Va, USA 62-73.
F. P. 180-1 : Secure hash standard. April 1995, http://www.itl.nist.gov/fipspubs/fips180-1.htm
Balfanz D, Durfee G, Shankar N, Smetters D, Staddon J, Wong HC: Secure handshakes from pairing-based key agreements. Proceedings of the IEEE Symposium on Security & Privacy, May 2003, Oakland, Calif, USA
Acknowledgments
This research is supported in part by NSF grants CNS 0845812, CNS 0848569, CNS 0716039 and CNS 0746811.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ren, J., Li, Y. & Li, T. SPM: Source Privacy for Mobile Ad Hoc Networks. J Wireless Com Network 2010, 534712 (2009). https://doi.org/10.1155/2010/534712
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/534712
 : Given a message
: Given a message 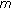 and the public keys
and the public keys 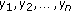 ??of the ambiguity set(AS)
??of the ambiguity set(AS) , the actual message sender
, the actual message sender 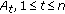 , produces an anonymous message
, produces an anonymous message  using her own private key
using her own private key 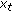 ;
;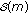 : Given a message
: Given a message  and an anonymous message
and an anonymous message 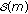 , which includes the public keys of all members in the AS, a verifier can determine whether
, which includes the public keys of all members in the AS, a verifier can determine whether 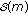 is generated by a member in the AS.
is generated by a member in the AS.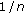 , where
, where  is the total number of AS;
is the total number of AS;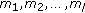 adaptively chosen by the adversary, can produce in polynomial time a new valid anonymous message with nonnegligible probability.
adaptively chosen by the adversary, can produce in polynomial time a new valid anonymous message with nonnegligible probability. be a large prime,
be a large prime, 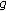 be a generator of
be a generator of  Both
Both 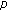 and
and 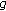 are made public. For a random private key
are made public. For a random private key 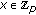 , the public key
, the public key 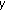 is computed from
is computed from 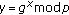 ;
;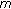 , one chooses a random
, one chooses a random 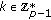 , then computes the exponentiation
, then computes the exponentiation 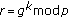 ??and solves
??and solves  from
from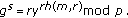 If the equality holds true, then the verifier
If the equality holds true, then the verifier  the signature and
the signature and  otherwise.
otherwise. for each
for each 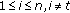 and compute
and compute 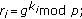
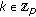 and compute
and compute 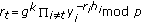 such that
such that 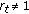 and
and  for any
for any  where
where 
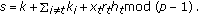

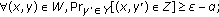
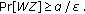

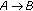 : Super node
: Super node 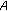 randomly selects an unused pseudonym
randomly selects an unused pseudonym 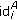 and a random nonce
and a random nonce 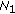 , then sends
, then sends  to super node
to super node 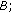
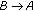 : Super node
: Super node 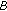 randomly selects an unused pseudonym
randomly selects an unused pseudonym 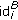 and a random nonce
and a random nonce 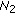 , then sends
, then sends  to super node
to super node  , where
, where 
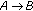 : Super node
: Super node 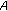 sends
sends 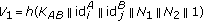 to super node
to super node 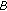 , where
, where  .
.
 -anonymous message transmission. Proceedings of the 10th ACM Conference on Computer and Communications Security (CCS '03), October 2003, Washingtion, DC, USA 122-130.
-anonymous message transmission. Proceedings of the 10th ACM Conference on Computer and Communications Security (CCS '03), October 2003, Washingtion, DC, USA 122-130.