- Research Article
- Open access
- Published:
Efficient Transmission Schemes for Multiuser MIMO Downlink with Linear Receivers and Partial Channel State Information
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 572675 (2010)
Abstract
Downlink of a multiuser MIMO system is considered, in which the base station (BS) and the user terminals are both equipped with multiple antennas. Efficient transmission schemes based on zero-forcing (ZF) linear receiver processing, eigenmode transmission, and partial channel state information (CSI) at the BS transmitter are proposed. The proposed schemes utilize a handshaking procedure between the BS and the users to select (schedule) a subset of users and determine the precoding matrix at the BS. The advantage of the proposed limited feedback schemes lies in enabling relatively low-complexity user scheduling algorithms and high sum-rate throughput, even for a small pool of users. For large user pools and when the number of antennas at each user terminal is at least equal to the number of antennas at the BS, we show that the proposed scheme is asymptotically optimum.
1. Introduction
Increasing demand for broadband wireless services calls for much higher throughputs in future wireless communication systems. It has been shown that with the use of multiple antennas at the transmitter (Tx) and the receiver (Rx), the capacity of a point-to-point communication link increases linearly with min where
where  is the number of Tx antennas and
is the number of Tx antennas and  is the number of Rx antennas [1, 2]. Recently, there has been a great interest in multiuser multiple-input multiple-output (MU-MIMO) systems and transmission strategies that would enable similar capacity gains in multiuser environment [3–5]. In a multiuser downlink with the base station (BS) equipped with multiple antennas, multiple users can be served simultaneously. In fact, it has been shown that to obtain the MU-MIMO downlink sum capacity, transmitting to several users simultaneously must be considered [6]. Since the number of users in the system is usually greater than the maximum number that can be served simultaneously through spatial multiplexing, user selection is required. User selection (or scheduling) favours users, which experience better propagation condition while being sufficiently separated in space. Such user scheduling leads to multiuser diversity gain [7, 8], which increases with increasing number of users awaiting transmission.
is the number of Rx antennas [1, 2]. Recently, there has been a great interest in multiuser multiple-input multiple-output (MU-MIMO) systems and transmission strategies that would enable similar capacity gains in multiuser environment [3–5]. In a multiuser downlink with the base station (BS) equipped with multiple antennas, multiple users can be served simultaneously. In fact, it has been shown that to obtain the MU-MIMO downlink sum capacity, transmitting to several users simultaneously must be considered [6]. Since the number of users in the system is usually greater than the maximum number that can be served simultaneously through spatial multiplexing, user selection is required. User selection (or scheduling) favours users, which experience better propagation condition while being sufficiently separated in space. Such user scheduling leads to multiuser diversity gain [7, 8], which increases with increasing number of users awaiting transmission.
It has been shown that the capacity of the MU-MIMO downlink can be achieved by dirty paper coding (DPC) [6], which is a transmitter multiuser encoding strategy based on interference presubtraction. DPC requires nonlinear search for optimal precoding matrices as well as noncausal channel coding for these users, which is practically impossible in real-time systems. Therefore, suboptimum transmission strategies such as different forms of beamforming have been considered in the literature. In MU-MIMO beamforming, linear or nonlinear transmitter precoding algorithms together with user scheduling are designed to maximize the system's sum rate or some other related objective function (e.g., sum rate under fairness constraint). Unfortunately, most beamforming algorithms considered assume availability of perfect channel state information at the transmitter, which presents a big challenge to their practical implementation (references [9, 10] and references therein contain an overview of the subject).
To overcome this challenge, suboptimal MU-MIMO downlink transmission based on partial channel state information (CSI) has been studied in the literature. Some of the proposed approaches can be applied to systems with only single antenna user terminals [11–16], while some accommodate multiple antenna user terminals [17–23]. When multiple antenna user terminals are considered, often it is assumed that all user terminals have the same number of antennas. This might not be true in practice. However, schemes which rely on this assumption may use antenna selection to meet the requirement. Most of the existing MU-MIMO downlink schemes using partial CSI fall under three main categories.
-
(1)
Transmission schemes based on availability of quantized channel state information at the BS: the quantized CSI is used to utilize a variant of beamforming at the BS. See [12] and references therein for further details.
-
(2)
User scheduling and precoder selection from a codebook of vectors/matrices known a priori to both the BS and the users based on partial CSI: the scheme proposed in [17] called transmit beam matching (TBM) is one example, which extends the per-user unitary rate control (PU
 RC) [12, 24] approach to multiple antenna users. PU
RC) [12, 24] approach to multiple antenna users. PU RC is Samsung Electronic's proposal to the 3rd Generation Partnership Project (3GPP). The proposed approach is characterized by the relatively low complexity structure of PU
RC is Samsung Electronic's proposal to the 3rd Generation Partnership Project (3GPP). The proposed approach is characterized by the relatively low complexity structure of PU RC, and it uses channel matrix pseudoinverse operation in order to minimize interstream interference at each user's terminal. However, when users have fewer antennas than the base station, the pseudoinverse operation can not completely eliminate interstream interference, which leads to some performance degradation. A similar approach called random precoding has been introduced in [19].
RC, and it uses channel matrix pseudoinverse operation in order to minimize interstream interference at each user's terminal. However, when users have fewer antennas than the base station, the pseudoinverse operation can not completely eliminate interstream interference, which leads to some performance degradation. A similar approach called random precoding has been introduced in [19]. -
(3)
Eigenmode transmission with limited feedback: One example is [20], which employs singular value decomposition (SVD) of user channel matrices and data transmission on the eigenmode with the largest gain. Another example is [25], in which the authors propose a combination of zero-forcing beamforming (ZF-BF) with eigenmode transmission.
All schemes mentioned above use precoding at the BS. In addition to precoding at the BS, multiple antenna users can use their antennas to process their received signal vector using relatively low-complexity linear schemes such as zero-forcing (ZF) and minimum mean squared error (MMSE) processing and send back some sort of channel quality indicator (CQI), for example, SINR or rate, to the BS. One example is [21], in which a MIMO downlink scheme with opportunistic feedback is proposed. In this scheme users use ZF linear processors and send back the quality indicator for each spatial channel to the base station according to an opportunistic feedback protocol. The main contribution of [21] lies in its feedback protocol and not the transmission scheme itself.
In this paper, we present a transmission scheme for MU-MIMO downlink using eigenmode transmission, and ZF linear processing, which only requires partial CSI and falls under the third category mentioned above. We assume that all users have the same number of Rx antennas. With this assumption and the number of Rx antennas of each user terminal being less or greater than the number of transmit antennas, two transmission strategies are proposed. For systems where the number of Rx antennas is greater than or equal to the number of Tx antennas, one user is selected to receive data through eigenmode transmission and its right eigenvector matrix is used for precoding, while other selected users use ZF linear processing. When the number of Rx antennas of each user terminal is less than the number of Tx antennas at the base station, partial CSI at the base station is used to design a precoding matrix such that the number of interfering streams at the selected user terminals (after Rx preprocessing) is reduced to the number of Rx antennas, and ZF receiver processing can be efficiently applied. Analytical expressions and approximations are derived for the sum rate of the proposed scheme and also for time division multiplexing (TDM) with eigenmode transmission.
For the case of  (
( denotes the number of Rx antennas at each user terminal;
denotes the number of Rx antennas at each user terminal;  denotes the number of Tx antennas at the BS), our work is distinct from [20] in the following aspects. (
denotes the number of Tx antennas at the BS), our work is distinct from [20] in the following aspects. ( ) In our proposed scheme the users do not need to send back their channel singular vectors as required in the scheme of [20]; only one user is asked to send back its right singular vector matrix. (
) In our proposed scheme the users do not need to send back their channel singular vectors as required in the scheme of [20]; only one user is asked to send back its right singular vector matrix. ( ) The scheme presented here results in zero interuser and interstream interferences, whereas the scheme of [20] does not. (
) The scheme presented here results in zero interuser and interstream interferences, whereas the scheme of [20] does not. ( ) In our scheme user selection criterion is straightforward and there is no need for a greedy search algorithm to select users as required by the scheme introduced in [20]. Compared to [25], what distinguishes our work is the use of ZF receiver processing and the lower complexity of our user scheduling and eigenmode assignment to selected users compared to the high complexity of exhaustive search to find the threshold value (denoted by
) In our scheme user selection criterion is straightforward and there is no need for a greedy search algorithm to select users as required by the scheme introduced in [20]. Compared to [25], what distinguishes our work is the use of ZF receiver processing and the lower complexity of our user scheduling and eigenmode assignment to selected users compared to the high complexity of exhaustive search to find the threshold value (denoted by  in [25]). Parts of this work have been presented in [26, 27]. Nevertheless, this paper generalizes our proposed scheme to any number (greater than one) of Tx (at the BS) and Rx (at each user terminal) antennas and provides further analysis on the proposed scheme's sum rate.
in [25]). Parts of this work have been presented in [26, 27]. Nevertheless, this paper generalizes our proposed scheme to any number (greater than one) of Tx (at the BS) and Rx (at each user terminal) antennas and provides further analysis on the proposed scheme's sum rate.
The paper is organized as follows. In Section 2, the system model for multiuser MIMO downlink is described. Two well-known transmission schemes based on limited feedback are briefly outlined in Sections 3 and 4. Section 5 describes the proposed transmission techniques along with asymptotic analysis for the case of  . Numerical results are provided in Section 6, and Section 7 concludes the paper.
. Numerical results are provided in Section 6, and Section 7 concludes the paper.
Throughout this paper, upper case and lower case bold characters denote matrices and vectors, respectively.  denotes the conjugate transpose of the matrix argument.
denotes the conjugate transpose of the matrix argument.  is the expectation operation.
is the expectation operation.  denotes the trace of the matrix argument.
denotes the trace of the matrix argument.
2. System Model
Figure 1 shows the block diagram of a MU-MIMO downlink. Consider a Gaussian MIMO broadcast channel where the base station is equipped with  antennas, and there are
antennas, and there are  homogeneous users each equipped with
homogeneous users each equipped with  antennas. A quasistatic Rayleigh flat fading model is assumed for the channel where the channel gains do not change within a frame and change independently from frame to frame following complex Gaussian distribution. The
antennas. A quasistatic Rayleigh flat fading model is assumed for the channel where the channel gains do not change within a frame and change independently from frame to frame following complex Gaussian distribution. The  th user receives the following signal vector:
th user receives the following signal vector:

where  is the downlink channel gain matrix between the base station and the
is the downlink channel gain matrix between the base station and the  th user, and
th user, and  is the noise vector. Both
is the noise vector. Both  s and
s and  s are assumed to have independently and identically distributed (i.i.d.) zero mean unit variance complex Gaussian elements,
s are assumed to have independently and identically distributed (i.i.d.) zero mean unit variance complex Gaussian elements,  . The vector
. The vector  is the transmitted signal vector such that
is the transmitted signal vector such that  . Hence, the average signal-to-noise ratio (SNR) equals
. Hence, the average signal-to-noise ratio (SNR) equals  , which also defines the average power constraint of the base station. The data symbol vector
, which also defines the average power constraint of the base station. The data symbol vector  is a size
is a size  vector. When precoding is used, the precoding matrix is denoted by
vector. When precoding is used, the precoding matrix is denoted by  where
where  , and in case of spatial multiplexing
, and in case of spatial multiplexing  . Let the total (sum) rate delivered by the base station to the users during one time slot be
. Let the total (sum) rate delivered by the base station to the users during one time slot be  . Then the expected throughput of the system is obtained by taking ensemble average of
. Then the expected throughput of the system is obtained by taking ensemble average of  over
over  s, that is,
s, that is,  . Throughout the paper, the terms system throughput and sum rate are used interchangeably.
. Throughout the paper, the terms system throughput and sum rate are used interchangeably.
3. Eigenmode Transmission
Consider the singular value decomposition (SVD) of the  th user's channel gain matrix
th user's channel gain matrix

where  and
and  are
are  left singular vector and
left singular vector and  right singular vector unitary matrices, respectively. The matrix
right singular vector unitary matrices, respectively. The matrix  is an
is an  diagonal matrix with nonnegative numbers (singular values) on its diagonal. Consider data transmission to only one user at any given time. When the transmitter has the knowledge of
diagonal matrix with nonnegative numbers (singular values) on its diagonal. Consider data transmission to only one user at any given time. When the transmitter has the knowledge of  , it precodes the transmitted signal by
, it precodes the transmitted signal by  , while the
, while the  th receiver uses
th receiver uses  as its receive processing matrix. Therefore, the channel is diagonalized into parallel interference-free channels, also called eigenchannels [28], where the gain of each channel equals its corresponding singular value. In this case, the rate delivered to user
as its receive processing matrix. Therefore, the channel is diagonalized into parallel interference-free channels, also called eigenchannels [28], where the gain of each channel equals its corresponding singular value. In this case, the rate delivered to user  (in bits/s/Hz) is obtained as
(in bits/s/Hz) is obtained as

where  is the
is the  th eigenvalue of
th eigenvalue of  while
while  is the
is the  th singular value of
th singular value of  .
.  denotes the power given to the
denotes the power given to the  th data stream and
th data stream and  . The optimum power distribution over the spatial channels is obtained through water-filling [28]. For the case of equal power allocation we have
. The optimum power distribution over the spatial channels is obtained through water-filling [28]. For the case of equal power allocation we have  . This transmission scheme has been considered within the context of time-division multiplexing (TDM) where the users send back their achievable rate,
. This transmission scheme has been considered within the context of time-division multiplexing (TDM) where the users send back their achievable rate,  , to the base station and the base station selects the user with the largest achievable transmission rate in each time slot. Compared to multiuser MIMO schemes in which multiple users are served simultaneously, this scheme is very suboptimal as it does not take full advantage of multiuser diversity, which implies that some of the eigenmodes of the selected user's channel matrix might be very weak.
, to the base station and the base station selects the user with the largest achievable transmission rate in each time slot. Compared to multiuser MIMO schemes in which multiple users are served simultaneously, this scheme is very suboptimal as it does not take full advantage of multiuser diversity, which implies that some of the eigenmodes of the selected user's channel matrix might be very weak.
4. Zero-Forcing Receiver Processing and Scheduling based on Partial Side Information
In case of  , with spatial multiplexing at the base station when an independent data stream is transmitted from each Tx antenna and ZF receiver processing is used at each user terminal, the scheduled users can detect their data without interstream interference.
, with spatial multiplexing at the base station when an independent data stream is transmitted from each Tx antenna and ZF receiver processing is used at each user terminal, the scheduled users can detect their data without interstream interference.
ZF receiver processing at the  th user is applied by multiplying the received signal by
th user is applied by multiplying the received signal by

The postprocessing SNR of the  th data stream at user
th data stream at user  is then given as [29]
is then given as [29]

where  and
and  denotes the
denotes the  th diagonal term of the matrix
th diagonal term of the matrix  . Once the base station is informed of postprocessing SNR of a specific data stream by all users, it will assign that data stream to the user with the highest postprocessing SNR. Therefore, the sum rate (in bits/s/Hz) will be given by
. Once the base station is informed of postprocessing SNR of a specific data stream by all users, it will assign that data stream to the user with the highest postprocessing SNR. Therefore, the sum rate (in bits/s/Hz) will be given by

where  . While this scheme is asymptotically optimal [30], that is,
. While this scheme is asymptotically optimal [30], that is,

where  is the sum rate of the DPC scheme, for a small pool of users it achieves a relatively poor sum rate.
is the sum rate of the DPC scheme, for a small pool of users it achieves a relatively poor sum rate.
5. The proposed Transmission Scheme: Eigenmode Transmission with Zero-Forcing Receiver Processing
In the next subsections our proposed transmission scheme is presented for two scenarios. In the first scenario, each user terminal has the number of antennas at least equal to that of the base station ( ), and in the second scenario the base station has more antennas than each user terminal (
), and in the second scenario the base station has more antennas than each user terminal ( ).
).
5.1. Case  : Precoding with Right Singular Vector Matrix
: Precoding with Right Singular Vector Matrix
The proposed scheme is presented in an algorithmic form as follows.
-
(1)
All the users perform SVD of their own channel and report back a single rate value evaluated according to
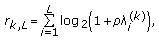 (8)
(8)where
 . The parameter
. The parameter 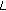 is evaluated beforehand based on the system parameters and will be discussed in the next subsection.
is evaluated beforehand based on the system parameters and will be discussed in the next subsection. 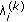 s are the ordered eigenvalues of the matrix
s are the ordered eigenvalues of the matrix  which is a complex Wishart matrix [31].
which is a complex Wishart matrix [31]. 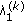 is the largest eigenvalue.
is the largest eigenvalue. -
(2)
The base station scheduler selects the user with the largest
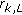 (user
(user 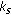 ) and asks that user to send its
) and asks that user to send its 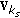 matrix to the BS. The matrix
matrix to the BS. The matrix  is obtained through the SVD of the selected users' channel matrix. The matrix
is obtained through the SVD of the selected users' channel matrix. The matrix 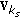 is then used as the precoding matrix,
is then used as the precoding matrix,  . User
. User  will receive its data through the first
will receive its data through the first 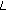
 data streams (encompassing data symbols
data streams (encompassing data symbols  ), using
), using 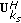 as its receiver processing matrix (eigenmode transmission).
as its receiver processing matrix (eigenmode transmission). -
(3)
User
 (
( ) will estimate its equivalent channel, which at this stage is
) will estimate its equivalent channel, which at this stage is  . Then all users (except user
. Then all users (except user  ) will apply ZF linear processing using the estimated equivalent channel and send back the postprocessing SNR of data streams
) will apply ZF linear processing using the estimated equivalent channel and send back the postprocessing SNR of data streams  to
to  to the base station.
to the base station. -
(4)
For each of the remaining
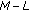 data streams, the base station selects the user with the highest postprocessing SNR.
data streams, the base station selects the user with the highest postprocessing SNR.
5.1.1. Finding the Optimum Number of Eigenmodes ( )
)
Since the precoding matrix,  , in this case is a unitary matrix, the statistics of the equivalent channel
, in this case is a unitary matrix, the statistics of the equivalent channel  do not change. Assuming that the first
do not change. Assuming that the first  data symbols have been assigned to user
data symbols have been assigned to user  and the remaining
and the remaining  to users with ZF receivers, which have the highest postprocessing SNR, the average sum rate is obtained by taking the ensemble average of the rate contribution from eigenmode transmission on the first
to users with ZF receivers, which have the highest postprocessing SNR, the average sum rate is obtained by taking the ensemble average of the rate contribution from eigenmode transmission on the first  eigenmodes,
eigenmodes,  , and the rate contribution from the remaining
, and the rate contribution from the remaining  data streams using linear ZF receiver processing,
data streams using linear ZF receiver processing,  , over a large number of channel realizations:
, over a large number of channel realizations:

where  , and
, and  denotes the
denotes the  th diagonal term of its matrix argument. The user
th diagonal term of its matrix argument. The user  is the user which has the largest postprocessing SNR for the
is the user which has the largest postprocessing SNR for the  th data stream among
th data stream among  users (user
users (user  has been subtracted out from the set
has been subtracted out from the set  ), that is,
), that is,

The probability density function (pdf) of  for a square system
for a square system  is obtained using order statistics and is given by [29]
is obtained using order statistics and is given by [29]

which is independent of data stream's index,  . For a nonsquare system (
. For a nonsquare system ( ), the exponential functions in (11) are replaced with chi-square distribution functions with
), the exponential functions in (11) are replaced with chi-square distribution functions with  degrees of freedom [29]. Using (11), the expected throughput contribution from ZF Rx processing is obtained as
degrees of freedom [29]. Using (11), the expected throughput contribution from ZF Rx processing is obtained as

which for the case of  is further simplified to [29]
is further simplified to [29]

where  is the exponential integral function [32]. To obtain the expected throughput of the eigenmode transmission, the pdf of ordered eigenvalues of
is the exponential integral function [32]. To obtain the expected throughput of the eigenmode transmission, the pdf of ordered eigenvalues of  is required. The joint pdf of the ordered eigenvalues is given by [33]
is required. The joint pdf of the ordered eigenvalues is given by [33]

where  is the product of
is the product of  Gamma functions.
Gamma functions.
For  , a closed form analytical expression for the average throughput contribution from eigenmode transmission,
, a closed form analytical expression for the average throughput contribution from eigenmode transmission,  , is very complicated to evaluate. However, a close approximation for
, is very complicated to evaluate. However, a close approximation for  can be obtained using the following proposition.
can be obtained using the following proposition.
Proposition 1 :.
For a Gaussian MIMO broadcast channel with  transmit antennas and
transmit antennas and  users each equipped with
users each equipped with  receive antennas, a close approximation to the average sum rate of eigenmode transmission on the first
receive antennas, a close approximation to the average sum rate of eigenmode transmission on the first  eigenmodes is
eigenmodes is

where

and  is the achievable rate on the
is the achievable rate on the  th eigenmode.
th eigenmode.
Proof.
See the appendix.
In summary, to find the optimum  , one has to find the smallest eigenvalue,
, one has to find the smallest eigenvalue,  , for which
, for which  . Then the optimum value for
. Then the optimum value for  is
is  . To obtain
. To obtain  , the marginal pdf, CDF, and joint pdfs of
, the marginal pdf, CDF, and joint pdfs of  are required, which can be obtained using (14).
are required, which can be obtained using (14).  is then approximated using (15). Based on (12) and (15), the optimum
is then approximated using (15). Based on (12) and (15), the optimum  value depends on
value depends on  ,
,  ,
,  and
and  . For a system with specific number of Tx and Rx antennas,
. For a system with specific number of Tx and Rx antennas,  can be evaluated for different values of
can be evaluated for different values of  and
and  beforehand and stored in a lookup table to be used later.
beforehand and stored in a lookup table to be used later.
5.1.2. Scaling Law of Sum Rate of the Proposed Scheme
In this subsection, the asymptotic behaviour of the average sum rate of the proposed scheme described in 5.1 is investigated for systems with a large number of users. First we start with the following lemma,
Lemma 1.
For fixed  ,
,  , and
, and  one has,
one has,

where  is the natural logarithm.
is the natural logarithm.
Proof.
An upper bound for  is
is

Using the definition of the trace of a matrix,

which is a chi-square random variable with  degrees of freedom. Since
degrees of freedom. Since  , according to [30, 34] we have
, according to [30, 34] we have

and that completes the proof.
As the sum capacity (achievable with DPC) for  data streams asymptotically increases with
data streams asymptotically increases with  [35],
[35],  , in general is not asymptotically optimum. However, for the case of
, in general is not asymptotically optimum. However, for the case of  we present the following theorem.
we present the following theorem.
Theorem 1.
The proposed scheme with  is asymptotically optimal
is asymptotically optimal

Proof.
For  we have
we have

When  is very large, referring to Lemma 1, and according to [36]
is very large, referring to Lemma 1, and according to [36]

where  . Also [30]
. Also [30]

Considering (23) and (24),

and since DPC has the optimum scaling sum rate, the ratio in the above equation can not be greater than one.
The above lemma and theorem make one expect that as the number of users increases, the optimum  value will decrease to one, which is confirmed by simulations in Section 6.
value will decrease to one, which is confirmed by simulations in Section 6.
5.2. Case  : Null Space Precoding with Singular Vector Selection
: Null Space Precoding with Singular Vector Selection
In this section, the general algorithm proposed for this case is presented, before a novel scheme for the specific case of  Tx and
Tx and  Rx antennas is discussed.
Rx antennas is discussed.
Assume the precoding matrix to consist of  vectors each selected from the right singular vector matrix of a selected user (there is a possibility that one user contributes more than one vector) given in general form by
vectors each selected from the right singular vector matrix of a selected user (there is a possibility that one user contributes more than one vector) given in general form by

where  and
and  . The signal vector at the
. The signal vector at the  th user,
th user,  , after eigenmode Rx pre-processing (multiplying the received signal vector by
, after eigenmode Rx pre-processing (multiplying the received signal vector by  ) is
) is

Considering the fact that the last  columns of
columns of  are all zero columns, and also for
are all zero columns, and also for  ,
,  , it can be shown that when
, it can be shown that when  contains
contains  rightmost vectors of
rightmost vectors of  , then the nonzero terms of
, then the nonzero terms of  form the following submatrix:
form the following submatrix:

where  is an
is an  matrix,
matrix,  is an
is an  square diagonal matrix with
square diagonal matrix with  singular values on its diagonal,
singular values on its diagonal,  contains only the first
contains only the first  columns of
columns of  , and
, and  contains
contains  vectors that belong to
vectors that belong to  s where
s where  and
and  . In this case, (27) can be rewritten as
. In this case, (27) can be rewritten as

where  is a size
is a size  vector and is obtained by eliminating
vector and is obtained by eliminating  terms from
terms from  . Then user
. Then user  uses
uses  as its receiver processing matrix to detect
as its receiver processing matrix to detect  out of the total
out of the total  transmitted data streams.
transmitted data streams.
For the  th receiver to be able to detect its data using ZF receiver processing, the number of interfering data streams (after Rx pre-processing) must not be greater than
th receiver to be able to detect its data using ZF receiver processing, the number of interfering data streams (after Rx pre-processing) must not be greater than  . In other words, the matrix
. In other words, the matrix  must have
must have  zero columns. This further implies that the precoding matrix needs to contain
zero columns. This further implies that the precoding matrix needs to contain  basis vectors of the null space (space spanned by the rightmost
basis vectors of the null space (space spanned by the rightmost  vectors of
vectors of  ) of each selected user's channel matrix. Therefore,
) of each selected user's channel matrix. Therefore,  users can be served simultaneously (
users can be served simultaneously ( denotes floor of its argument). Therefore, to be able to take greater advantage of multiuser diversity,
denotes floor of its argument). Therefore, to be able to take greater advantage of multiuser diversity,  should be as close as possible to
should be as close as possible to  with the best case being
with the best case being  . When
. When  this scheme becomes identical to TDM.
this scheme becomes identical to TDM.
Since the postprocessing SNR of each data stream in this case depends on the precoding matrix and each selected user's  and
and  matrices, finding users with channel conditions that maximize the sum rate based on partial CSI turns out to be not straightforward. Nevertheless, a heuristic approach would be to adopt a two-stage user selection, where in the first stage a set of users is selected based on a channel quality indicator (CQI), for example, the largest singular value. In the next stage, the selected users send back their full CSI to the BS, and the BS broadcasts their CSI to all users. Then, knowing the CSI of the selected users, each user (outside of the set of selected users) substitutes itself sequentially for each of the selected users and evaluates the resulting sum rate for each substitution. If a user finds that by substituting itself for one of the selected users, the sum rate increases, it will inform the BS of it. The BS will update the user set according to the suggestion of the user which has reported the maximum increase in the sum rate. Our results show that the sum rate obtained by adopting this scheme and user selection based on the largest eigenvalue achieve a higher sum rate compared to TDM, while the gap between the sum rate of this scheme and the optimum DPC increases as the number of antennas increases. In the following subsection we present an efficient transmission scheme for the special case of
matrices, finding users with channel conditions that maximize the sum rate based on partial CSI turns out to be not straightforward. Nevertheless, a heuristic approach would be to adopt a two-stage user selection, where in the first stage a set of users is selected based on a channel quality indicator (CQI), for example, the largest singular value. In the next stage, the selected users send back their full CSI to the BS, and the BS broadcasts their CSI to all users. Then, knowing the CSI of the selected users, each user (outside of the set of selected users) substitutes itself sequentially for each of the selected users and evaluates the resulting sum rate for each substitution. If a user finds that by substituting itself for one of the selected users, the sum rate increases, it will inform the BS of it. The BS will update the user set according to the suggestion of the user which has reported the maximum increase in the sum rate. Our results show that the sum rate obtained by adopting this scheme and user selection based on the largest eigenvalue achieve a higher sum rate compared to TDM, while the gap between the sum rate of this scheme and the optimum DPC increases as the number of antennas increases. In the following subsection we present an efficient transmission scheme for the special case of  and
and  .
.
The Case of  and
and 
Considering the general idea discussed for null space precoding based on eigenvector selection, in this case we consider two possibilities for the precoding matrix. One possibility is to construct  using three vectors each taken from right singular vector matrix of a distinct user's channel matrix. Therefore, three users can be served and each user sees only one interfering data stream. However, in order to find the best set of users which maximizes the sum rate, either the base station requires full channel state information of all users which results in a considerably increased complexity compared to limited feedback schemes, or an approach similar to the one discussed in the previous section can be applied. The second option is to construct
using three vectors each taken from right singular vector matrix of a distinct user's channel matrix. Therefore, three users can be served and each user sees only one interfering data stream. However, in order to find the best set of users which maximizes the sum rate, either the base station requires full channel state information of all users which results in a considerably increased complexity compared to limited feedback schemes, or an approach similar to the one discussed in the previous section can be applied. The second option is to construct  using right singular vectors of two selected user channel matrices. Assume that users
using right singular vectors of two selected user channel matrices. Assume that users  and
and  where
where  are the indexes of users that will be ultimately scheduled by the proposed algorithm. In the proposed scheme which is based on a heuristic approach the precoding matrix is assumed to be
are the indexes of users that will be ultimately scheduled by the proposed algorithm. In the proposed scheme which is based on a heuristic approach the precoding matrix is assumed to be

The reasoning behind this choice of precoding matrix will be clarified once the algorithm is presented. Here are the steps of the proposed algorithm.
-
(1)
Each user performs the SVD of its channel matrix and sends back
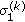 to the base station.
to the base station. -
(2)
The base station selects the user with the largest
 , user
, user  , and asks that user for
, and asks that user for 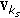 matrix. To detect its data, user
matrix. To detect its data, user  uses
uses  as its receiver processing matrix,
as its receiver processing matrix, (31)
(31)where
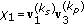 ,
, 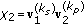 ,
, 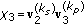 , and
, and  . As seen in (31), the interference caused by the first data stream to the second and third data streams after Rx processing at user
. As seen in (31), the interference caused by the first data stream to the second and third data streams after Rx processing at user 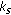 has been canceled. Therefore, a ZF linear receiver can be used and for the second data stream we have [29]
has been canceled. Therefore, a ZF linear receiver can be used and for the second data stream we have [29] (32)
(32)where
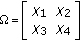 . Thus, the achievable rate for this user will be
. Thus, the achievable rate for this user will be  .
. -
(3)
The base station broadcasts
 and
and 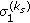 to all users.
to all users. -
(4)
For now, let us assume that user
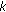 is the second selected user. Then the precoding matrix will be
is the second selected user. Then the precoding matrix will be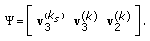 (33)
(33)User
 once selected uses
once selected uses 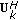 as its receiver processing matrix which will result in
as its receiver processing matrix which will result in (34)
(34)where
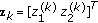 ,
, 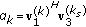 , and
, and  . It is evident that the interfering effect of
. It is evident that the interfering effect of  on the other data streams is canceled, and the first data stream can be detected using a matched filter, which results in
on the other data streams is canceled, and the first data stream can be detected using a matched filter, which results in 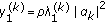 as postprocessing SNR for the first data stream (
as postprocessing SNR for the first data stream (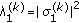 ).
).To detect the third data stream, the effect of the first detected data stream is subtracted out, that is,
 (
( denotes the first detected data symbol). Canceling the effect of the the first data stream is possible due to the knowledge of
denotes the first detected data symbol). Canceling the effect of the the first data stream is possible due to the knowledge of 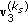 at user
at user  which enables it to evaluate
which enables it to evaluate 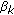 . The SNR for the third data stream,
. The SNR for the third data stream,  , after interference cancelation and matched filtering, is obtained as
, after interference cancelation and matched filtering, is obtained as 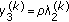 (ignoring error propagation).
(ignoring error propagation).Considering (32) and the third step of the algorithm, user
 has all the required information to evaluate the rate of user
has all the required information to evaluate the rate of user 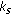 as well as its own rate. Therefore, it will send back a sum rate value,
as well as its own rate. Therefore, it will send back a sum rate value, 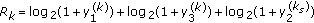 , that is achieved by scheduling data transmission to itself and user
, that is achieved by scheduling data transmission to itself and user  .
. -
(5)
The base station selects the second user, user
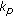 , which has the largest
, which has the largest 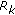 and asks that user to send back
and asks that user to send back  and
and  vectors.
vectors.At this stage data transmission to the selected users begins. User
 will receive its data from the first and third Tx antennas, and user
will receive its data from the first and third Tx antennas, and user  will receive its data from the second Tx antenna.
will receive its data from the second Tx antenna.
6. Numerical Results
In this section, the expected throughputs of the proposed schemes are compared to limited feedback MIMO-downlink techniques using transmit beam matching (TBM) [17], which is a modified version of PU RC for multiple antenna users, zero-forcing beamforming (ZF-BF) using channel vector quantization (CVQ) [18, 37, 38], spatial multiplexing with zero-forcing receiver processing, and TDM with eigenmode transmission for different numbers of antennas, users, and SNR values. The throughput of the DPC scheme is also given as an upper bound on the sum rate. The sum rate curves for DPC have been obtained using the iterative water-filling algorithm introduced in [39]. In the following, we consider two case examples, in which
RC for multiple antenna users, zero-forcing beamforming (ZF-BF) using channel vector quantization (CVQ) [18, 37, 38], spatial multiplexing with zero-forcing receiver processing, and TDM with eigenmode transmission for different numbers of antennas, users, and SNR values. The throughput of the DPC scheme is also given as an upper bound on the sum rate. The sum rate curves for DPC have been obtained using the iterative water-filling algorithm introduced in [39]. In the following, we consider two case examples, in which  , and one example for the case
, and one example for the case  .
.
The Case of  and
and 
In this case, we find the optimum choice for  in terms of maximizing the average sum rate. Using (14) it can easily be shown that the distributions of the ordered eigenvalues,
in terms of maximizing the average sum rate. Using (14) it can easily be shown that the distributions of the ordered eigenvalues,  and
and  , are
, are

respectively. The cumulative distribution functions (CDF) of the eigenvalues are then as followss

To schedule users in this case we consider three possibilities.
-
(i)
The proposed scheme with
 .
.The average rate for this scheme is obtained as:
 (37)
(37) -
(ii)
Selecting user
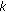 which has the largest
which has the largest 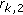 (8) and only serving that user in each time slot (TDM with eigenmode transmission).
(8) and only serving that user in each time slot (TDM with eigenmode transmission).According to Proposition 1, the average sum rate for this scheme can be approximated by
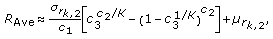 (38)
(38)where
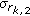 and
and  are obtained using (16).
are obtained using (16). -
(iii)
ZF receiver Rx processing with partial CSI.
The average sum rate for this scheme is obtained as
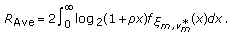 (39)
(39)
According to Figure 2, the proposed scheme with  achieves a considerably higher sum rate compared to ZF linear processing and TDM. Furthermore, Figure 2 compares the average sum rate of the proposed scheme with that of TBM. For the TBM scheme, a codebook size of
achieves a considerably higher sum rate compared to ZF linear processing and TDM. Furthermore, Figure 2 compares the average sum rate of the proposed scheme with that of TBM. For the TBM scheme, a codebook size of  has been considered, where each codebook consists of a
has been considered, where each codebook consists of a  unitary matrix and it is assumed that each user sends back to the base station
unitary matrix and it is assumed that each user sends back to the base station  SNR values, corresponding to all vectors of all unitary matrices in the codebook. As the figure shows, even for a very small user pool, for example,
SNR values, corresponding to all vectors of all unitary matrices in the codebook. As the figure shows, even for a very small user pool, for example,  users, the proposed scheme has a great sum rate advantage over the sum rate of other limited feedback schemes, which are plotted. Sum rate curves obtained using the analytical expressions of (37), (38), and (39) are in good agreement with the simulation results.
users, the proposed scheme has a great sum rate advantage over the sum rate of other limited feedback schemes, which are plotted. Sum rate curves obtained using the analytical expressions of (37), (38), and (39) are in good agreement with the simulation results.
The case of  and
and 
We consider four possibilities for this case.
-
(i)
The proposed scheme with
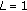 .
.The average sum rate for this scheme is obtained as
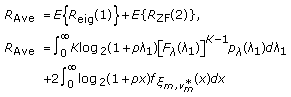 (40)
(40)with the pdf and CDF of
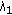 given as follows
given as follows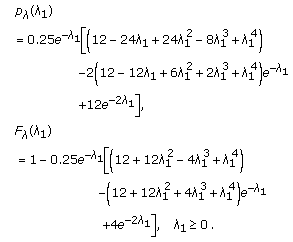 (41)
(41) -
(ii)
The proposed scheme with

In this case the average sum rate is obtained as
 (42)
(42)where
 and
and 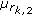 are obtained using (16), and marginal and joint eigenvalue distributions are given by
are obtained using (16), and marginal and joint eigenvalue distributions are given by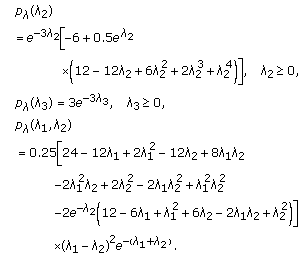 (43)
(43) -
(iii)
Selecting user
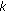 which achieves the largest rate and only serving that user in each time slot (TDM with eigenvalue distribution). The average sum rate in this case is approximated by (15) with
which achieves the largest rate and only serving that user in each time slot (TDM with eigenvalue distribution). The average sum rate in this case is approximated by (15) with  and using [40] where more simplified expressions (for case
and using [40] where more simplified expressions (for case  ) have been given for
) have been given for  and
and 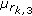 .
. -
(iv)
ZF receiver processing scheme using partial side information.
The average sum rate for this scheme is obtained as
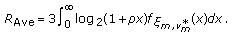 (44)
(44)
The average sum rates of the four cases considered above are compared in Figure 3. As seen in the figure, the proposed scheme with  achieves a higher average sum rate compared to the case of
achieves a higher average sum rate compared to the case of  while there are up to
while there are up to  users in the system. When there are more users in the system, the proposed scheme with
users in the system. When there are more users in the system, the proposed scheme with  achieves a higher sum rate. The intersection of the average sum rate curves for
achieves a higher sum rate. The intersection of the average sum rate curves for  and
and  can be explained by considering the fact that for a small pool of users it is less likely that a subset of users with high ZF postprocessing SNR (good channel conditions) exist in the system, and therefore transmitting on the first two noninterfering eigenmodes to one user leads to a higher sum rate. For larger user pools and in agreement with Theorem 1 due to multiuser diversity it is more likely that a user subset can be found such that it achieves higher sum rate than eigenmode transmission on the first two eigenmodes to one user. According to Figure 3, the proposed scheme achieves a considerably higher sum rate compared to ZF receiver processing. For transmit beam matching (TBM), a codebook size of
can be explained by considering the fact that for a small pool of users it is less likely that a subset of users with high ZF postprocessing SNR (good channel conditions) exist in the system, and therefore transmitting on the first two noninterfering eigenmodes to one user leads to a higher sum rate. For larger user pools and in agreement with Theorem 1 due to multiuser diversity it is more likely that a user subset can be found such that it achieves higher sum rate than eigenmode transmission on the first two eigenmodes to one user. According to Figure 3, the proposed scheme achieves a considerably higher sum rate compared to ZF receiver processing. For transmit beam matching (TBM), a codebook size of  has been considered, where each codebook consists of a
has been considered, where each codebook consists of a  unitary matrix and it is assumed that each user sends back
unitary matrix and it is assumed that each user sends back  SNR values to the base station. Sum rate curves obtained using the analytical expressions given above are in good agreement with the simulation results.
SNR values to the base station. Sum rate curves obtained using the analytical expressions given above are in good agreement with the simulation results.
In Table 1, the optimum  values for
values for  to
to  antennas have been given for systems with equal numbers of Tx and Rx antennas along with the percentage sum rate increase achieved by using the proposed scheme over the transmission schemes using ZF receiver processing and TDM, when there are
antennas have been given for systems with equal numbers of Tx and Rx antennas along with the percentage sum rate increase achieved by using the proposed scheme over the transmission schemes using ZF receiver processing and TDM, when there are  users available in the system and at
users available in the system and at  dB SNR. The gain of the proposed scheme over ZF receiver processing and TDM with eigenmode transmission schemes (TDM in brief) have been normalized to the sum rate of these schemes, respectively (i.e.,
dB SNR. The gain of the proposed scheme over ZF receiver processing and TDM with eigenmode transmission schemes (TDM in brief) have been normalized to the sum rate of these schemes, respectively (i.e.,  for the case of ZF Rx processing). As seen in Table 1, the proposed scheme provides a significant sum rate increase over ZF receiver processing and TDM for different numbers of antennas. For example for the case of
for the case of ZF Rx processing). As seen in Table 1, the proposed scheme provides a significant sum rate increase over ZF receiver processing and TDM for different numbers of antennas. For example for the case of  Tx and
Tx and  Rx antennas, the proposed scheme exceeds the sum rate of that achieved by ZF receiver processing scheme by about
Rx antennas, the proposed scheme exceeds the sum rate of that achieved by ZF receiver processing scheme by about  .
.
 values and the percentage increase of the proposed scheme's sum rate over ZF and TDM schemes for different numbers of antennas.
values and the percentage increase of the proposed scheme's sum rate over ZF and TDM schemes for different numbers of antennas.The Case of  and
and 
This case example was explained in detail in Section 5.2. Figure 4 shows the average sum rate advantage of the proposed scheme over two well-known limited feedback schemes. As seen in the figure, the proposed scheme achieves a higher sum rate compared to TBM and zero-forcing beamforming (ZF-BF) with channel vector quantization (CVQ). The proposed scheme has over  bit/s/Hz advantage over TBM and ZF-BF with CVQ for even small user pools (
bit/s/Hz advantage over TBM and ZF-BF with CVQ for even small user pools ( ).
).
6.1. Comparison of Feedback Requirement for Different Schemes
In limited feedback schemes, there is usually a tradeoff between the sum rate and feedback load. An example of this tradeoff is seen in the PU RC scheme where there are two feedback modes. In one mode which achieves higher average sum rate, the SINRs of all codewords are sent back to the base station, and in the other mode only the largest SINR and the index of its corresponding codeword are sent back to the base station. In ZF-BF with CVQ each user sends back the index of a selected quantization vector along with its corresponding SINR lower bound [18, 37]. In the transmission scheme based on spatial multiplexing at the base station with linear receiver processing at each user terminal, each user sends back
RC scheme where there are two feedback modes. In one mode which achieves higher average sum rate, the SINRs of all codewords are sent back to the base station, and in the other mode only the largest SINR and the index of its corresponding codeword are sent back to the base station. In ZF-BF with CVQ each user sends back the index of a selected quantization vector along with its corresponding SINR lower bound [18, 37]. In the transmission scheme based on spatial multiplexing at the base station with linear receiver processing at each user terminal, each user sends back  SNR values to the base station. In TDM with eigenmode transmission, each user sends back only one real value (a rate value), before the user with the highest reported rate is asked to send back its right singular matrix, which for a system with
SNR values to the base station. In TDM with eigenmode transmission, each user sends back only one real value (a rate value), before the user with the highest reported rate is asked to send back its right singular matrix, which for a system with  has
has  real terms.
real terms.
In our proposed scheme and for the case of  , users send back information in three stages. At the first stage all users send back a single rate value, in the second stage one user sends back an
, users send back information in three stages. At the first stage all users send back a single rate value, in the second stage one user sends back an  matrix of complex values, and in the third stage all users except one send back
matrix of complex values, and in the third stage all users except one send back  SNR values. This amount of feedback is larger than the amount required in TDM with eigenmode transmission, yet it is comparable to PU
SNR values. This amount of feedback is larger than the amount required in TDM with eigenmode transmission, yet it is comparable to PU RC and spatial multiplexing at the base station with ZF receiver processing schemes at user terminals described in Section 4.
RC and spatial multiplexing at the base station with ZF receiver processing schemes at user terminals described in Section 4.
For the proposed scheme in case of  and
and  , each user needs to feedback only one real value to the base station in the first stage. In the second stage, one user needs to send back a
, each user needs to feedback only one real value to the base station in the first stage. In the second stage, one user needs to send back a  matrix, and in the third stage all users except one need to send back one rate value. Finally, the second selected user sends back two vectors to the base station. This amount of feedback is larger than the amount required in TDM with eigenmode transmission. Yet, it is less than ZF-BF with CVQ [37], since except for the two users, all other users send back only two real values in two stages.
matrix, and in the third stage all users except one need to send back one rate value. Finally, the second selected user sends back two vectors to the base station. This amount of feedback is larger than the amount required in TDM with eigenmode transmission. Yet, it is less than ZF-BF with CVQ [37], since except for the two users, all other users send back only two real values in two stages.
7. Conclusion
We have proposed limited-feedback MIMO downlink transmission schemes for a system in which the base station and each user terminal are equipped with  and
and  antennas, respectively. For the case of
antennas, respectively. For the case of  , one user receives data through eigenmode transmission on its
, one user receives data through eigenmode transmission on its  strongest eigenmodes (
strongest eigenmodes ( is a predetermined value, which maximizes the average sum rate) while each of the remaining
is a predetermined value, which maximizes the average sum rate) while each of the remaining  data streams is assigned to a user with the highest ZF receiver postprocessing SNR. We have shown that in this case the average sum rate of the proposed scheme scales with
data streams is assigned to a user with the highest ZF receiver postprocessing SNR. We have shown that in this case the average sum rate of the proposed scheme scales with  (
( is the number of users in the system), which is asymptotically optimal. In case of
is the number of users in the system), which is asymptotically optimal. In case of  , the precoding matrix consists of right singular vectors of at least two and at most
, the precoding matrix consists of right singular vectors of at least two and at most  users such that the number of interfering streams at each selected user terminal is reduced to the number of its receive antennas, and hence, the interstream interference can be effectively removed using ZF receiver processing. The results show that the proposed schemes lead to a higher average sum rate compared to a number of well-known limited feedback schemes, especially for a small pool of users.
users such that the number of interfering streams at each selected user terminal is reduced to the number of its receive antennas, and hence, the interstream interference can be effectively removed using ZF receiver processing. The results show that the proposed schemes lead to a higher average sum rate compared to a number of well-known limited feedback schemes, especially for a small pool of users.
References
Foschini GJ, Gans MJ: On limits of wireless communications in a fading environment when using multiple antennas. Wireless Personal Communications 1998, 6(3):311-335. 10.1023/A:1008889222784
Telatar E: Capacity of multi-antenna Gaussian channels. European Transactions on Telecommunications 1999, 10(6):585-595. 10.1002/ett.4460100604
Caire G, Shamai S: On the achievable throughput of a multiantenna Gaussian broadcast channel. IEEE Transactions on Information Theory 2003, 49(7):1691-1706. 10.1109/TIT.2003.813523
Vishwanath S, Jindal N, Goldsmith A: Duality, achievable rates, and sum-rate capacity of Gaussian MIMO broadcast channels. IEEE Transactions on Information Theory 2003, 49(10):2658-2668. 10.1109/TIT.2003.817421
Yu W, Cioffi JM: Sum capacity of Gaussian vector broadcast channels. IEEE Transactions on Information Theory 2004, 50(9):1875-1892. 10.1109/TIT.2004.833336
Weingarten H, Steinberg Y, Shamai S: The capacity region of the Gaussian MIMO broadcast channel. Proceedings of the IEEE International Symposium on Information Theory (ISIT '04), June-July 2004, Chicago, USA 174.
Viswanath P, Tse DNC, Laroia R: Opportunistic beamforming using dumb antennas. IEEE Transactions on Information Theory 2002, 48(6):1277-1294. 10.1109/TIT.2002.1003822
Sharif M, Hassibi B: A comparison of time-sharing, DPC, and beamforming for MIMO broadcast channels with many users. IEEE Transactions on Communications 2007, 55(1):11-15.
Spencer QH, Peel CB, Swindlehurst AL, Haardt M: An introduction to the multi-user MIMO downlink. IEEE Communications Magazine 2004, 42(10):60-67. 10.1109/MCOM.2004.1341262
Gesbert D, Kountouris M, Heath RW Jr., Chae C-B, Sälzer T: Shifting the MIMO Paradigm. IEEE Signal Processing Magazine 2007, 24(5):36-46.
Yoo T, Jindal N, Goldsmith A: Multi-antenna downlink channels with limited feedback and user selection. IEEE Journal on Selected Areas in Communications 2007, 25(7):1478-1491.
Huang K, Andrews JG, Heath RW Jr.: Performance of orthogonal beamforming for SDMA with limited feedback. IEEE Transactions on Vehicular Technology 2009, 58(1):152-164.
Zhang W, Letaief KB: MIMO broadcast scheduling with limited feedback. IEEE Journal on Selected Areas in Communications 2007, 25(7):1457-1467.
Choi W, Forenza A, Andrews JG, Heath RW Jr.: Opportunistic space-division multiple access with beam selection. IEEE Transactions on Communications 2007, 55(12):2371-2380.
Trivellato M, Boccardi F, Tosato F: A random precoding technique for the downlink of multiuser MIMO systems. Proceedings of the IEEE Vehicular Technology Conference (VTC '07), April 2007, Dublin, Ireland 2089-2093.
Kountouris M, de Francisco R, Gesbert D, Slock D, Salzer T: A random precoding technique for the downlink of multiuser MIMO systems. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '07), April 2007, Honolulu, USA 109-112.
Tae HK, Heath RW Jr., Choi S: Multiuser MIMO downlink with limited feedback using transmit-beam matching. Proceedings of the IEEE International Conference on Communications (ICC'08), May 2008, Beijing, China 3506-3510.
Dietl G, Bauch G: Linear precoding in the downlink of limited feedback multiuser MIMO systems. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007, Washington, USA 4359-4364.
Bala E, Cimini LJ Jr.: A random precoding technique for the downlink of multiuser MIMO systems. Proceedings of the IEEE Conference on Information Sciences and Systems (CISS '06), March 2006, Princeton, USA 750-754.
Boccardi F, Huang H, Trivellato M: Multiuser eigenmode transmission for MIMO broadcast channels with limited feedback. Proceedings of the IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '07), June 2007, Helsinki, Finland 1-5.
Tang T, Heath RW Jr., Cho S, Yun S: Opportunistic feedback for multiuser MIMO systems with linear receivers. IEEE Transactions on Communications 2007, 55(5):1020-1032.
Wang C, Murch RD: MU-MIMO decomposition transmission with limited feedback. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '07), March 2007, Hong Kong, China 1109-1114.
Maddah-Ali MA, Sadrabadi MA, Khandani AK: Broadcast in MIMO systems based on a generalized QR decomposition: signaling and performance analysis. IEEE Transactions on Information Theory 2008, 54(3):1124-1138.
Samsung Electronics : Downlink MIMO for EUTRA. 3GPP TSG RAN WG1 R1-060335, Febuary 2006
Bayesteh A, Khandani AK: On the user selection for MIMO broadcast channels. IEEE Transactions on Information Theory 2008, 54(3):1086-1107.
Eslami M, Krzymień WA: Scheduling for MIMO broadcast channels with linear receivers and partial channel state information. Proceedings of the IEEE Vehicular Technology Conference (VTC '08), May 2008, Singapore 2467-2471.
Eslami M, Krzymień WA: Downlink limited feedback transmission schemes for asymmetric MIMO channels. Proceedings of the IEEE Vehicular Technology Conference (VTC '08), September 2008, Calgary, Canada
Tse D, Viswanath P: Fundamentals of Wireless Communications. Cambridge University Press, New York, USA; 2005.
Chen C-J, Wang L-C: Performance analysis of scheduling in multiuser MIMO systems with zero-forcing receivers. IEEE Journal on Selected Areas in Communications 2007, 25(7):1435-1445.
Airy M, Heath RW Jr., Shakkottai S: Multi-user diversity for the multiple antenna broadcast channel with linear receivers: asymptotic analysis. Proceedings of the IEEE Conference on Signals, Systems and Computers, 2004, Pacific Grove, USA 1: 886-890.
Tulino AM, Verdu S: Random Matrix Theory and Wireless Communications. Now Publishers, Hanover, USA;
Abramowitz M, Stegun IA: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover, New York, USA; 1972.
Edelman A: Eigenvalues and condition numbers of random matrices, Ph.D. dissertation. MIT, Cambridge, USA; 1989.
Sharif M, Hassibi B: On the capacity of MIMO broadcast channels with partial side information. IEEE Transactions on Information Theory 2005, 51(2):506-522. 10.1109/TIT.2004.840897
Sharif M, Hassibi B: A comparison of time-sharing, DPC, and beamforming for MIMO broadcast channels with many users. IEEE Transactions on Communications 2007, 55(1):11-15.
Jindal N, Goldsmith A: Dirty-paper coding versus TDMA for MIMO broadcast channels. IEEE Transactions on Information Theory 2005, 51(5):1783-1794. 10.1109/TIT.2005.846425
Jindal N: MIMO broadcast channels with finite-rate feedback. IEEE Transactions on Information Theory 2006, 52(11):5045-5060.
Philips : Comparison between MU-MIMO codebook-based channel reporting techniques for LTE downlink. 3GPP TSG RAN WG1, October 2006
Jindal N, Rhee W, Vishwanath S, Jafar SA, Goldsmith A: Sum power iterative water-filling for multi-antenna Gaussian broadcast channels. IEEE Transactions on Information Theory 2005, 51(4):1570-1580. 10.1109/TIT.2005.844082
Smith PJ, Shafi M: On a Gaussian approximation to the capacity of wireless MIMO systems. Proceedings of the International Conference on Communications (ICC '02), May 2002, New York, USA 406-410.
Chen C-C, Tyler CW: Accurate approximation to the extreme order statistics of Gaussian samples. Communications in Statistics Part B 1999, 28(1):177-188.
Shore H: Enhancement for two commonly-used approximations for the inverse cumulative function of the normal distribution. Communications in Statistics Part B 1997, 26(3):1041-1047.
Acknowledgments
Funding for this work has been provided by TRLabs, Huawei Technologies, the Rohit Sharma Professorship, and the Natural Sciences and Engineering Research Council (NSERC) of Canada.
Author information
Authors and Affiliations
Corresponding author
Appendix
Let  where
where  . Then, as in [40], the pdf of
. Then, as in [40], the pdf of  can be approximated by a Gaussian distribution. However, the parameters of the distribution are different from those given in [40] as in this case only the first
can be approximated by a Gaussian distribution. However, the parameters of the distribution are different from those given in [40] as in this case only the first  largest eigenvalues are considered. To obtain the mean value for this Gaussian approximation, the marginal pdfs of the first
largest eigenvalues are considered. To obtain the mean value for this Gaussian approximation, the marginal pdfs of the first  eigenvalues are required, which can be obtained from (14). The mean value is then obtained as
eigenvalues are required, which can be obtained from (14). The mean value is then obtained as


The variance of  is obtained by evaluating
is obtained by evaluating

 denotes the covariance of
denotes the covariance of  . Equation (A.2) is further simplified to
. Equation (A.2) is further simplified to
 , which is done by integrating (14) over all
, which is done by integrating (14) over all  eigenvalues, except the
eigenvalues, except the  th and the
th and the  th ones. In case of
th ones. In case of  , a further simplified expression for
, a further simplified expression for  is given in [40].By approximating the pdf of
is given in [40].By approximating the pdf of  as Gaussian,
as Gaussian,  ,
,  will be the mean value of maximum of
will be the mean value of maximum of  Gaussian distributed terms, which itself is approximated by [41]
Gaussian distributed terms, which itself is approximated by [41]
 is the standard normal CDF.
is the standard normal CDF.  is well approximated by [42]
is well approximated by [42]
 and
and  . Substituting (A.5) into (A.4) completes the proof.
. Substituting (A.5) into (A.4) completes the proof.



Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Eslami, M., Krzymień, W.A. Efficient Transmission Schemes for Multiuser MIMO Downlink with Linear Receivers and Partial Channel State Information. J Wireless Com Network 2010, 572675 (2010). https://doi.org/10.1155/2010/572675
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/572675
 RC) [
RC) [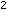 RC is Samsung Electronic's proposal to the 3rd Generation Partnership Project (3GPP). The proposed approach is characterized by the relatively low complexity structure of PU
RC is Samsung Electronic's proposal to the 3rd Generation Partnership Project (3GPP). The proposed approach is characterized by the relatively low complexity structure of PU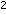 RC, and it uses channel matrix pseudoinverse operation in order to minimize interstream interference at each user's terminal. However, when users have fewer antennas than the base station, the pseudoinverse operation can not completely eliminate interstream interference, which leads to some performance degradation. A similar approach called random precoding has been introduced in [
RC, and it uses channel matrix pseudoinverse operation in order to minimize interstream interference at each user's terminal. However, when users have fewer antennas than the base station, the pseudoinverse operation can not completely eliminate interstream interference, which leads to some performance degradation. A similar approach called random precoding has been introduced in [
 : Precoding with Right Singular Vector Matrix
: Precoding with Right Singular Vector Matrix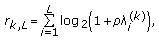
 . The parameter
. The parameter 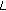 is evaluated beforehand based on the system parameters and will be discussed in the next subsection.
is evaluated beforehand based on the system parameters and will be discussed in the next subsection. 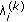 s are the ordered eigenvalues of the matrix
s are the ordered eigenvalues of the matrix  which is a complex Wishart matrix [
which is a complex Wishart matrix [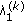 is the largest eigenvalue.
is the largest eigenvalue.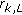 (user
(user 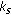 ) and asks that user to send its
) and asks that user to send its 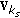 matrix to the BS. The matrix
matrix to the BS. The matrix  is obtained through the SVD of the selected users' channel matrix. The matrix
is obtained through the SVD of the selected users' channel matrix. The matrix 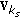 is then used as the precoding matrix,
is then used as the precoding matrix,  . User
. User  will receive its data through the first
will receive its data through the first 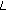
 data streams (encompassing data symbols
data streams (encompassing data symbols  ), using
), using 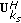 as its receiver processing matrix (eigenmode transmission).
as its receiver processing matrix (eigenmode transmission). (
( ) will estimate its equivalent channel, which at this stage is
) will estimate its equivalent channel, which at this stage is  . Then all users (except user
. Then all users (except user  ) will apply ZF linear processing using the estimated equivalent channel and send back the postprocessing SNR of data streams
) will apply ZF linear processing using the estimated equivalent channel and send back the postprocessing SNR of data streams  to
to  to the base station.
to the base station.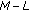 data streams, the base station selects the user with the highest postprocessing SNR.
data streams, the base station selects the user with the highest postprocessing SNR. )
) : Null Space Precoding with Singular Vector Selection
: Null Space Precoding with Singular Vector Selection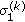 to the base station.
to the base station. , user
, user  , and asks that user for
, and asks that user for 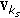 matrix. To detect its data, user
matrix. To detect its data, user  uses
uses  as its receiver processing matrix,
as its receiver processing matrix,
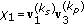 ,
, 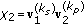 ,
, 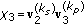 , and
, and  . As seen in (31), the interference caused by the first data stream to the second and third data streams after Rx processing at user
. As seen in (31), the interference caused by the first data stream to the second and third data streams after Rx processing at user 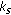 has been canceled. Therefore, a ZF linear receiver can be used and for the second data stream we have [
has been canceled. Therefore, a ZF linear receiver can be used and for the second data stream we have [
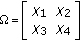 . Thus, the achievable rate for this user will be
. Thus, the achievable rate for this user will be  .
. and
and 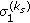 to all users.
to all users.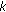 is the second selected user. Then the precoding matrix will be
is the second selected user. Then the precoding matrix will be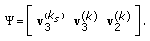
 once selected uses
once selected uses 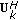 as its receiver processing matrix which will result in
as its receiver processing matrix which will result in
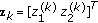 ,
, 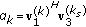 , and
, and  . It is evident that the interfering effect of
. It is evident that the interfering effect of  on the other data streams is canceled, and the first data stream can be detected using a matched filter, which results in
on the other data streams is canceled, and the first data stream can be detected using a matched filter, which results in 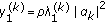 as postprocessing SNR for the first data stream (
as postprocessing SNR for the first data stream (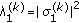 ).
). (
( denotes the first detected data symbol). Canceling the effect of the the first data stream is possible due to the knowledge of
denotes the first detected data symbol). Canceling the effect of the the first data stream is possible due to the knowledge of 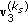 at user
at user  which enables it to evaluate
which enables it to evaluate 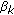 . The SNR for the third data stream,
. The SNR for the third data stream,  , after interference cancelation and matched filtering, is obtained as
, after interference cancelation and matched filtering, is obtained as 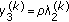 (ignoring error propagation).
(ignoring error propagation). has all the required information to evaluate the rate of user
has all the required information to evaluate the rate of user 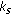 as well as its own rate. Therefore, it will send back a sum rate value,
as well as its own rate. Therefore, it will send back a sum rate value, 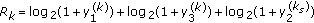 , that is achieved by scheduling data transmission to itself and user
, that is achieved by scheduling data transmission to itself and user  .
.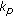 , which has the largest
, which has the largest 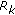 and asks that user to send back
and asks that user to send back  and
and  vectors.
vectors. will receive its data from the first and third Tx antennas, and user
will receive its data from the first and third Tx antennas, and user  will receive its data from the second Tx antenna.
will receive its data from the second Tx antenna. .
.
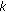 which has the largest
which has the largest 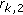 (8) and only serving that user in each time slot (TDM with eigenmode transmission).
(8) and only serving that user in each time slot (TDM with eigenmode transmission).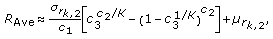
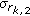 and
and  are obtained using (16).
are obtained using (16).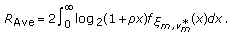

 Tx and
Tx and  Rx antennas at
Rx antennas at  dB SNR.
dB SNR. .
.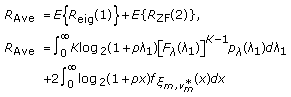
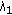 given as follows
given as follows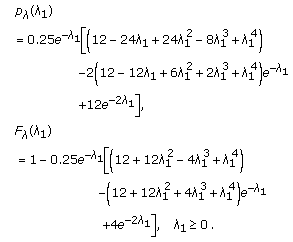


 and
and 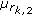 are obtained using (16), and marginal and joint eigenvalue distributions are given by
are obtained using (16), and marginal and joint eigenvalue distributions are given by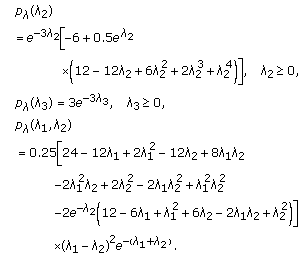
 which achieves the largest rate and only serving that user in each time slot (TDM with eigenvalue distribution). The average sum rate in this case is approximated by (15) with
which achieves the largest rate and only serving that user in each time slot (TDM with eigenvalue distribution). The average sum rate in this case is approximated by (15) with  and using [
and using [ ) have been given for
) have been given for  and
and 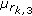 .
.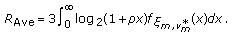

 and
and  compared to a number of multiuser MIMO techniques for
compared to a number of multiuser MIMO techniques for  Tx and
Tx and  Rx antennas at
Rx antennas at  dB SNR.
dB SNR.
 RC), ZFBF with CVQ, and TDM with eigenmmode transmission for
RC), ZFBF with CVQ, and TDM with eigenmmode transmission for  Tx and
Tx and  Rx antennas at
Rx antennas at  dB SNR.
dB SNR.