- Research Article
- Open access
- Published:
Karhunen-Loève-Based Reduced-Complexity Representation of the Mixed-Density Messages in SPA on Factor Graph and Its Impact on BER
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 574607 (2011)
Abstract
The sum product algorithm on factor graphs (FG/SPA) is a widely used tool to solve various problems in a wide area of fields. A representation of generally-shaped continuously valued messages in the FG/SPA is commonly solved by a proper parameterization of the messages. Obtaining such a proper parameterization is, however, a crucial problem in general. The paper introduces a systematic procedure for obtaining a scalar message representation with well-defined fidelity criterion in a general FG/SPA. The procedure utilizes a stochastic nature of the messages as they evolve during the FG/SPA processing. A Karhunen-Loève Transform (KLT) is used to find a generic canonical message representation which exploits the message stochastic behavior with mean square error (MSE) fidelity criterion. We demonstrate the procedure on a range of scenarios including mixture-messages (a digital modulation in phase parametric channel). The proposed systematic procedure achieves equal results as the Fourier parameterization developed especially for this particular class of scenarios.
1. Introduction
A factor graph (FG) based technique provides a unifying strategy to a vast variety of the problems in communications, signal processing and general inference algorithms [1, 2]. FG-based algorithms (e.g., sum-product algorithm (SPA) typically in Bayesian based decision and estimation problems) operate with messages representing the stochastic description of the variable at a given node. A direct exact canonical form of SPA operates with probability density function (PDF) or probability mass function (PMF) for continuous or discrete variables respectively. The messages for finite cardinality discrete variables (most notably for binary variables) can be easily parameterized by a number of numerically convenient representations (e.g., log-likelihood ratio, etc.) [1, 2] which allow an easy implementation.
Practical communication and signal processing scenarios, however, frequently lead to an FG representation containing a mixture of continuous and discrete parameters, for example the discrete data and continuous-valued channel state parameters (e.g., phase). The FG-based SPA algorithm solving this mixture variable problem inevitably involves messages with a complicated general-shaped mixture PDFs. This is a direct consequence of the marginalization operation of the factor node (FN) with both PDF and PMF inputs. A strict pristine implementation of the FG/SPA would require passing messages in the form of complicated PDF. It would make the practical implementation infeasible. A number of solutions for this situation appeared (see a detailed discussion later). All of them are based on a message PDF approximation done by a proper parameterization of a small set of canonical messages. Then, instead of the PDF itself, the set of parameters is used to represent the message.
The problem of finding a suitable set of canonical messages with a proper parameterization is, however, a crucial one. All previous attempts in the literature have chosen the canonical basis in an ad hoc manner or by inferring a function shape for a particular scenario context. A wrong choice easily leads to a large number of the parameters needed to represent the message with a given fidelity or to a high computational load when processing FN update equations. An obvious goal is to have a canonical representation with the smallest possible number of parameters and an easy enough FN update evaluation for the given approximation fidelity.
This paper introduces a systematic procedure for obtaining such a set of canonical messages with well-defined fidelity criterion. We base our method on a stochastic nature of the messages as they evolve during FG/SPA processing. A Karhunen-Loève transform (KLT) is used to exploit the message stochastic behavior with well-defined fidelity (mean square error (MSE)) criterion.
2. Background, Related Work and Contributions
This section summarizes the background and the related work available in the current literature. We have structured the related work according to various aspects of the FG-based processing and the message representation.
2.1. General FG-Based Processing
The FG/SPA is unambiguously given by the FG structure, update rules and scheduling algorithm [1, 2]. To enable the processing, it is necessary to store the messages in iterations between updates. The implementation of the FG/SPA gives exact results for an arbitrary cycle-free FG with exact evaluation of the update rules, exact message representation and with an arbitrary scheduling algorithm, which considers all messages in the FG. When all of these assumptions are fulfilled, the FG/SPA provides an elegant optimal evaluation algorithm. As an example, the forward/backward Bahl-Cocke-Jelinek-Raviv algorithm [1] might be mentioned.
The FG/SPA, however, often works well also in cases when the mentioned conditions are violated. First of all, the FG might contain loops. In such a case, the FG/SPA works only approximately. Many of iterative algorithms such as iterative decoding are solvable utilizing the looped FG/SPA. Several works focused on the convergence criteria for the looped FG/SPA [3, 4]. The role of the scheduling algorithm becomes important for the looped FG/SPA. A number of results was proposed in [5].
In a contrast with these principal difficulties, the representation of the messages (and corresponding update rules) forms an implementation-related problem.
2.2. FG Processing with Mixed Continuous and Discrete Variables
The most straightforward representation is a discretization (sampling) of the continuous message. The message is represented by a piecewise-constant function. An exact (we mean exact with respect to the definition of the SPA) evaluation of the update rules is approximated by the numerical integration with the rectangular rule [6–8]. The discretization of the continuously valued message is straightforward but highly inefficient in terms of the number of coefficients required to obtain a given fidelity goal. This representation was adopted as a reference model in this paper (Section 3.4).
The continuously valued message in FG/SPA stands for a PDF up to a scale factor. Thus the message can be easily described by its moments. The main interest is focused on the Gaussian message, which is fully described by its mean and variance. The Gaussian representation is extremely suitable for all linear models (only superposition and scaling factor nodes are allowed). The update rules are then closed-form operations on the Gaussian messages. See [8] for details.
Nevertheless, the use of the Gaussian representation might bring good results also in nonlinear models (e.g., joint phase estimation and data detection [9]). A mixture Gaussian message (the message given by superposition of several Gaussian kernels) might be also used as a message representation. A common problem of the Gaussian mixtures is the increasing number of mixtures in the update rules. A mixture number reducing approach based on the approximation of the resulting PDF was considered, for example, in [10, 11].
Some authors consider alternative methods of the message representation such as a representation by a single point, function value and a gradient at a point [6, 7] or a list of samples [6, 8, 12].
2.3. Canonical Representation of Mixture Densities
A unified design framework based on the canonical distribution was proposed in [13]. This design consists of a set of kernel functions and related parameters describing the message. The sets of the parameter are passed through the FG/SPA instead of the continuous messages. Following this framework, the iterative decoding algorithms based on Fourier and Tikhonov parameterization were proposed in [14]. The parameterizations are suited for the channels affected with strong phase noise. The Fourier and Tikhonov parameterizations are, however, chosen only by inferring the suitable shape from the given particular application scenario. No systematic general procedure is developed.
2.4. Goals of this Paper and Contributions
This paper provides the following results and contributions.
-
(1)
We develop a systematic procedure for finding canonical message kernels.
-
(2)
The procedure is based on the stochastic nature of the messages as they evolve in iterations of FG/SPA with random system excitations.
-
(3)
We use KLT-based procedure which provides an easy connection between message description complexity and the fidelity criterion.
-
(4)
The resulting orthonormality of the kernels allows relatively simple update rule implementation.
-
(5)
We demonstrate the procedure on number of example applications.
3. KLT Message Representation
3.1. Core Principle
This section summarizes the core principle in a "barebones" manner. The details follow in the sections below.
Let us assume an FG model with mixture PDF messages and an FN update algorithm (e.g., SPA). We assume the FG containing cycles with an iterative update evaluation (e.g., by a flooding algorithm). A particular shape of the message describing a given variable  depends on (1) random observation inputs of the FG
depends on (1) random observation inputs of the FG  (the received signal) and (2) an iteration number
(the received signal) and (2) an iteration number  of the network for other given parameters (SNR, preamble, etc.). Let us denote the true message evaluated in the FG/SPA without any implementation issues by
of the network for other given parameters (SNR, preamble, etc.). Let us denote the true message evaluated in the FG/SPA without any implementation issues by  . It is a randomly parameterized function (by
. It is a randomly parameterized function (by  ) in
) in  variable. As such, it can be approximated by a linear superposition of kernels (basis functions)
variable. As such, it can be approximated by a linear superposition of kernels (basis functions) 

Expansion coefficients  are random. The message
are random. The message  is then fully represented by the vector
is then fully represented by the vector  .
.
A particular form of this expansion should provide an efficient (minimal dimensionality) representation of the message with well-defined fidelity criterion. The KLT can serve for this efficient representation. It provides orthonormal kernels based on the second-order message statistics. The resulting coefficients are uncorrelated. The second-order moments of the coefficients are also directly related to the residual MSE of the approximation.
The second-order statistics (the correlation function) of the true messages can be easily numerically approximated (by simulation) by an empirical correlation function. A reduced complexity approximation of the message  is obtained by truncating the dimensionality of the original vector
is obtained by truncating the dimensionality of the original vector  . Due to the orthonormality of the basis, the residual MSE will be purely additive as a function of the truncation length. Significantly contributing kernels are easily identified by the second moment of the corresponding coefficient. This gives an easy and direct relation between the description complexity and the approximation fidelity.
. Due to the orthonormality of the basis, the residual MSE will be purely additive as a function of the truncation length. Significantly contributing kernels are easily identified by the second moment of the corresponding coefficient. This gives an easy and direct relation between the description complexity and the approximation fidelity.
3.2. KLT Message Representation Details
The analysis is built on the stochastic properties of the message  . We assume the message to be a real valued function of argument
. We assume the message to be a real valued function of argument  , where
, where  is an interval. Furthermore, we assume the existence of the integral (3) and the message being from
is an interval. Furthermore, we assume the existence of the integral (3) and the message being from  space. The autocorrelation function of the message is given by
space. The autocorrelation function of the message is given by

where  and
and  stands for the expectation over the set of iterations (we can consider an arbitrary subset of all iterations) and the observation vector.
stands for the expectation over the set of iterations (we can consider an arbitrary subset of all iterations) and the observation vector.
Once the autocorrelation function is given, the solution of the characteristic equation

provides the eigenfunctions as a canonical basis of the message. We index the sorted eigenvalues such as for all  :
:  and the eigenfunction is indexed
and the eigenfunction is indexed  if and only if the pair
if and only if the pair  forms eigenpair, that is, it solves (3).
forms eigenpair, that is, it solves (3).
Using the orthonormal property of the KLT-basis system, we obtain the expansion coefficients as

These coefficients jointly with the set of eigenfunctions describe the message by (1).
The complexity is reduced by omitting several components. We neglect the components with index  , where
, where  stands for the number of used components (dimensionality of the message). Then we can easily control the MSE of the approximated message
stands for the number of used components (dimensionality of the message). Then we can easily control the MSE of the approximated message  by the term
by the term  .
.
Note that, as a result of the KLT-approximation, the message might become negative at some points, that is, there may exist such a number  that
that  . It violates assumptions of the almost all FN update algorithms and it must be rectified by a proper translation.
. It violates assumptions of the almost all FN update algorithms and it must be rectified by a proper translation.
3.3. Empirical Correlation Function Measurement
The evaluation of the autocorrelation function  is the key issue of the evaluation of the kernel basis functions. A direct calculation using (2) is sometimes difficult to be done, especially for complex models. If the continuous message is approximated by a piecewise constant function (see Section 3.4 for details), the autocorrelation matrix might be empirically estimated by
is the key issue of the evaluation of the kernel basis functions. A direct calculation using (2) is sometimes difficult to be done, especially for complex models. If the continuous message is approximated by a piecewise constant function (see Section 3.4 for details), the autocorrelation matrix might be empirically estimated by

where  stands for number of iterations,
stands for number of iterations,  stands for number of realizations and
stands for number of realizations and  is a discrete vector resulting from the discretization of the message
is a discrete vector resulting from the discretization of the message  . A discrete form of the characteristic equation (3) is given by
. A discrete form of the characteristic equation (3) is given by  , where
, where  denotes again the eigenvalues as in (3) and
denotes again the eigenvalues as in (3) and  is the eigenvector, which is assumed to be the discretized eigenfunction
is the eigenvector, which is assumed to be the discretized eigenfunction  . The evaluation of the expansion coefficients (4) might be done by
. The evaluation of the expansion coefficients (4) might be done by

Finally, the message is represented by

Of course, the correlation evaluation requires small discretization steps. But since this operation is done only off-line during the system design phase, its complexity is not an issue at all.
3.4. Reference Message Representation Models
Our goal is to compare the capabilities of the message types (KLT against others) to represent the reference message as exactly as possible. We assume that we use a reference model without any implementation issues affecting the message representation and the update rules. Thus we are not interested in the update rules for particular representations. This is an important difference in contrast to other works (e.g., [6, 14]), where the authors try to obtain the message representation jointly with the update rules.
For our analysis, we need only an unambiguous relation between the reference (possibly highly complex) message and its approximation. In each iteration, the relation is used for the evaluation of the approximated message which is then inserted into the run of the reference model instead of the original reference message during the analysis. The results of this analysis might be interpreted as the ideal behavior of the particular message representation with an exact implementation of the update rules.
All considered representations in this section are only based on a deterministic description. Thus we might lighten the notation a little bit. The reference message is denoted by  . We suppose the following representations.
. We suppose the following representations.
3.4.1. Sample Representation
The discretization of the continuous message is a straightforward method of the practically feasible representation as it was discussed in Section 2.2 or [6, 12]. An arbitrary precision might be achieved using this representation (of course at the expense of the high complexity). Nevertheless, the representation offers a direct way to the empirical evaluation of the autocorrelation function (see Section 3.3). Thus it is a suitable option for our reference model.
The reference message  is represented by the vector
is represented by the vector  , where
, where  . And the approximated continuous message is then composed as a piecewise function from the samples
. And the approximated continuous message is then composed as a piecewise function from the samples

where  ,
,  for
for  , and
, and  otherwise.
otherwise.
The sample representation is considered in two cases. The first one is the reference model, where we select as many samples as the approximation of the message can be neglected. We also use the representation by samples to be compared with the proposed KLT-message for a given dimensionality.
3.4.2. Fourier Representation
The well known Fourier decomposition enables to parameterize the message by the Fourier's series as

where  and
and 

 . Dimensionality is given by
. Dimensionality is given by  . In [14], the authors have derived update rules for the Fourier coefficients in a special case of random-walk phase model.
. In [14], the authors have derived update rules for the Fourier coefficients in a special case of random-walk phase model.
3.4.3. Dirac-Delta Representation
The message is represented by a single number situated in the maximum of the message. In [7, 8] the authors present the gradient method to obtain  , which is the main part of their work. Nevertheless, from our point of view, the message might be easily obtained from the reference message. Therefore it is selected to be compared with the proposed representation. The message is given by
, which is the main part of their work. Nevertheless, from our point of view, the message might be easily obtained from the reference message. Therefore it is selected to be compared with the proposed representation. The message is given by

3.4.4. Gaussian Representation
Gaussian representation is widely used in literature as a message representation (e.g., [10]). We consider the simplest possible scalar real-valued Gaussian message given by the pair  with the interpretation
with the interpretation

where  and
and  .
.
4. Application Examples and Discussion of Results
The properties of the proposed method are demonstrated using different models. First, the models are introduced, then the FG of the models including the reference case is discussed. Finally, the numerical results obtained from the models are figured and discussed.
4.1. System Model
We assume several models situated in the signal space (Figure 1) and an MSK model situated into the phase space (see Figure 2).
4.1.1. Signal Space Models
We assume a binary i.i.d. data vector  of length
of length  as an input. The coded symbols are given by
as an input. The coded symbols are given by  . The modulated signal vector is given by
. The modulated signal vector is given by  , where
, where  is a signal space mapper. The channel is selected to be the AWGN channel with phase shift modeled by the random walk (RW) phase model. The phase as the function of time samples is described by
is a signal space mapper. The channel is selected to be the AWGN channel with phase shift modeled by the random walk (RW) phase model. The phase as the function of time samples is described by  , where
, where  is a zero mean real Gaussian random value (RV) with variance
is a zero mean real Gaussian random value (RV) with variance  . Thus the received signal is
. Thus the received signal is  , where
, where  stands for the vector of complex zero mean Gaussian RV with variance
stands for the vector of complex zero mean Gaussian RV with variance  . The model is depicted in Figure 1.
. The model is depicted in Figure 1.
4.1.2. Phase Space Model
We again assume the vector  as an input into the minimum-shift keying (MSK) modulator. The modulator is modeled by the canonical form, that is, by the continuous phase encoder (CPE) and nonlinear memoryless modulator (NMM) as shown in [15]. The modulator is implemented in the discrete time with two samples per symbol. The phase of the MSK signal is given by
as an input into the minimum-shift keying (MSK) modulator. The modulator is modeled by the canonical form, that is, by the continuous phase encoder (CPE) and nonlinear memoryless modulator (NMM) as shown in [15]. The modulator is implemented in the discrete time with two samples per symbol. The phase of the MSK signal is given by  , where
, where  is the
is the  -th sample of the phase function,
-th sample of the phase function,  is the
is the  -th state of the CPE and the sampled modulated signal is given by
-th state of the CPE and the sampled modulated signal is given by  . The communication channel is selected to be the AWGN channel with constant phase shift, that is,
. The communication channel is selected to be the AWGN channel with constant phase shift, that is,  , where
, where  stands for the received vector,
stands for the received vector,  is the constant phase shift of the channel and
is the constant phase shift of the channel and  is the AWGN vector. The nonlinear limiter phase discriminator (LPD) captures the phase of the vector
is the AWGN vector. The nonlinear limiter phase discriminator (LPD) captures the phase of the vector  , that is,
, that is,  . The whole system is shown in Figure 2.
. The whole system is shown in Figure 2.
4.2. Factor Graph of the System at Hand
The FG/SPA is used as a joint synchronizer-decoder (see Figure 3) for all mentioned models. Note that the FG for the considered models might be found in the literature (phase space model in [9] and signal space models in [6, 14]).
Prior the description itself, we found a notation to enable a common description of the models. We define
-
(i)
 ,
, 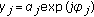 and
and  , where
, where 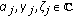 for the signal space models with the RW phase model,
for the signal space models with the RW phase model, -
(ii)
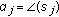 ,
,  and
and  , where
, where  for the phase space model with the constant phase model.
for the phase space model with the constant phase model.
One can see, that  for both models. The FG is depicted in Figure 3. We shortly describe the presented factor nodes and message types presented in the FG.
for both models. The FG is depicted in Figure 3. We shortly describe the presented factor nodes and message types presented in the FG.
4.2.1. Factor Nodes
We denote  and then we use
and then we use  as the phase distribution of the RV given by
as the phase distribution of the RV given by  , where
, where  stands for the zero mean complex Gaussian RV with variance
stands for the zero mean complex Gaussian RV with variance  ;
;  and
and  .
.
-
(i)
Factor Nodes in the Signal Space Models
Phase Shift (PS):

AWGN (W):

-
(ii)
Factor Nodes in the Phase Space Model
Phase Shift (PS):

AWGN (W):

-
(iii)
Factor Nodes Common for Both Signal and Phase Space
Random Walk (RW):

Other Factor Nodes
Other factor nodes such as the coder, CPE, and signal space mappers FN are situated in the discrete part of the model and their description is obvious from the definition of the related components (see, e.g., [1] for an example of such a description).
4.2.2. Message Types Presented in the FG/SPA
The FG contains both discrete and continuous messages. The discrete messages are presented in the coder. There is no need for the investigation of their representation, because they are exactly represented by PMF.Several parameterizable continuous messages might be exactly represented using a straightforward parameterization (e.g., Gaussian message). These messages are presented in the AWGN channel model. The rest of the messages are mixed continuous and discrete messages. These mixture messages are continuously valued messages without an obvious way of their representation. The messages are situated in the phase model.
4.3. The FG/SPA Reference Model
The empirical stochastic analysis requires a sample of the message realizations. Thus we ideally need a perfect implementation of the FG/SPA for each model. We call this perfect or better said almost perfect FG/SPA implementation as the reference model. Note that even if the implementation of the FG/SPA is perfect, the convergence of the FG/SPA is still not secured in the looped cases. We call the perfect implementation such a model that does
not suffer from the implementation-related issues such as an update rules design and a messages representation. The flood schedule message passing algorithm is assumed. The reference model might suffer (and our models do) from the numerical complexity and it is therefore unsuitable for a direct implementation.
Prior we classify the messages appearing in the reference FG/SPA model (Figure 3) and their update rules, we found the following notation. We denote  the message from
the message from  variable node to
variable node to  factor node and the opposite message is denoted by
factor node and the opposite message is denoted by  and
and  the factor node RW, which lies between
the factor node RW, which lies between  -th and
-th and  -th section according to Figure 4. Analogously,
-th section according to Figure 4. Analogously,  stands for the FN between
stands for the FN between  -th and
-th and  -th section.
-th section.
.
4.3.1. Discrete Type Messages
They are situated in the discrete part of the FG/SPA. As we have already said, their representation by PMF and the exact evaluation of the update rules according to the definition [1] are straightforward.
4.3.2. Unimportant Messages
The messages from PS factor node to the observation ( ,
,  ,
,  , and
, and  ) lead to the open branch and neither an update nor a representation of them is required, because these messages cannot affect the estimation of the target parameters (data, phase).
) lead to the open branch and neither an update nor a representation of them is required, because these messages cannot affect the estimation of the target parameters (data, phase).
4.3.3. Parameterizable Continuous Messages
The messages  and
and  are representable by a number
are representable by a number  meaning
meaning  ,
,  and
and  are representable by the pair
are representable by the pair  meaning
meaning  ,
,  , respectively. One can easily find the slightly modified update rules derived from the standard update rules. Examples of those may be seen in [12].
, respectively. One can easily find the slightly modified update rules derived from the standard update rules. Examples of those may be seen in [12].
4.3.4. Mixture Messages
The representation of the remaining messages, that is,  ,
,  ,
,  ,
,  ,
,  , and
, and  , is not obvious. These messages are thus discretized and the marginalization is performed using numerical integration with the rectangle rule [8, 12] in the update rules. The number of samples is chosen sufficiently large so that the impact of the approximation can be neglected. The mentioned mixture messages are real valued one-dimensional functions for all considered models.
, is not obvious. These messages are thus discretized and the marginalization is performed using numerical integration with the rectangle rule [8, 12] in the update rules. The number of samples is chosen sufficiently large so that the impact of the approximation can be neglected. The mentioned mixture messages are real valued one-dimensional functions for all considered models.
4.4. Scenarios
We specify four scenarios for the analysis purpose. All of the scenarios might be seen as a special case of the system model described in the Section 4.1. All scenarios use the FG/SPA containing the loops, except the first one.
4.4.1. Uncoded QPSK Modulation
The QPSK modulation is situated in the AWGN channel with RW-model of the phase shift. The length of the frame is  data symbols, the length of the preamble is 4 symbols and the preamble is situated at the beginning of the frame. The variance of the phase noise equals
data symbols, the length of the preamble is 4 symbols and the preamble is situated at the beginning of the frame. The variance of the phase noise equals  . This scenario is cycle-free and thus only inaccuracies caused by the imperfect implementation are presented. The information needed to resolve the phase ambiguity is contained in the preamble and, by a proper selection of the analyzed message, we can maximize the approximation impact to the key metrics such as BER or MSE of the phase estimation. We thus select the message
. This scenario is cycle-free and thus only inaccuracies caused by the imperfect implementation are presented. The information needed to resolve the phase ambiguity is contained in the preamble and, by a proper selection of the analyzed message, we can maximize the approximation impact to the key metrics such as BER or MSE of the phase estimation. We thus select the message  to be analyzed.
to be analyzed.
4.4.2. Coded 8PSK Modulation
In addition to the previous scenario, the  convolutional coder
convolutional coder  is presented. The length of the frame is
is presented. The length of the frame is  data symbols, the length of the preamble is 2 symbols. The same message is selected to be analyzed
data symbols, the length of the preamble is 2 symbols. The same message is selected to be analyzed  .
.
4.4.3. MSK Modulation with Constant-Phase Model of the Phase Shift
The length of the frame is  data symbols. The analyzed message is
data symbols. The analyzed message is  . These messages are nearly equal for all possible PS factor nodes (e.g., [12]).
. These messages are nearly equal for all possible PS factor nodes (e.g., [12]).
4.4.4. Bit-Interleaved Coded Modulation
The model employs a bit-interleaved coded modulation (BICM) with  convolutional code and QPSK signal-space mapper. The phase is modeled by the RW model with
convolutional code and QPSK signal-space mapper. The phase is modeled by the RW model with  . The length of the frame is
. The length of the frame is  data symbols and 150 of those are pilot symbols. This model slightly changes our concept. Instead of the investigation of the single message, we analyze all
data symbols and 150 of those are pilot symbols. This model slightly changes our concept. Instead of the investigation of the single message, we analyze all  and
and  messages jointly. It means that all of the analyzed messages are approximated in the simulations and the stochastic analysis is performed over all investigated messages.
messages jointly. It means that all of the analyzed messages are approximated in the simulations and the stochastic analysis is performed over all investigated messages.
4.5. Eigensystem Analysis
The first objective is to investigate the eigensystem of the mixture messages. We demonstrate the analysis by numerical evaluation of the eigenvalues and eigenvectors for various scenarios mentioned before.
The main result of the eigensystem analysis consists in the observed fact, that the KLT of the messages in all considered models leads to the eigenfunctions very similar to the harmonic functions independently of the parameters of the simulation as one can see in Figure 5. It is also independent of the other parts of the scenario such as coder or mapper (see Figure 7).
The dimensionality of the message is upper bounded by number of samples in the reference message in our approach. The eigenvalues resulting from the analysis offer important information for the approximation purposes as it was discussed in Section 3.2. The eigenvalues resulting from the characteristic equation are shown in Figure 6 for the MSK modulation. The eigenvalues of the other models look very similar. The floor is caused by the finite floating precision. As one can see, the higher SNR, the slower is the descent of the eigenvalues with the dimension index. The curves in the plots point out to the fact that the eigenvalues are descending in pairs that is,  .
.
4.6. Relation of the MSE of the Approximated Message with the Target Criteria Metrics
The KLT-approximated message provides the best approximation in the MSE sense. The minimization of the MSE of the approximated message, however, does not guarantee the minimization of the target criteria metrics such as MSE for the phase estimation or BER for data decoding. We have therefore performed several numerical simulations to inspect the behavior of the KLT-approximated message. We also consider the message types mentioned in the Section 3.4 into our simulation.
Few notes are addressed before going over the results. The MSE of the phase estimation is computed as an average over all MSE of the phase estimates in the model. The measurement of the MSE is limited by the granularity of the reference model. The simulations of the stochastic analysis are numerically intensive. We are limited by the computing resources. The simulations of the BER might suffer from this, especially for small error rates. The threshold of the detectable error rate is about  for the uncoded QPSK model and
for the uncoded QPSK model and  for the BICM model.
for the BICM model.
4.6.1. Simulation Results for the Uncoded QPSK Modulation
We start with the results in cycle-free FG (see Figures 8 and 9). One can see several interesting points. First of all, the Fourier representation gives absolutely equal results as the KLT representation for both MSE and BER target metrics. Due to the shapes of the eigenfunctions, this result is not very surprising. One can see that  evaluated according to (1) and (9) is equal when the set of basis functions
evaluated according to (1) and (9) is equal when the set of basis functions  in (1) is given exactly by the harmonic functions. However, it has a significant consequence. The harmonic function-based linear basis optimizes the MSE at least in the models considered in this analysis.
in (1) is given exactly by the harmonic functions. However, it has a significant consequence. The harmonic function-based linear basis optimizes the MSE at least in the models considered in this analysis.
Another interesting point might be seen in Figure 9. Adding the sixth component to KLT (and also Fourier) canonical representation, the performance is slightly worse than the five-component approximated message. It means that the proportional relationship between MSE of the approximated message and BER does not work, at least in this given case.
The representation by samples does not seem to work well. It is probably caused by relatively high SNR. A few samples hardly cover the narrow shape of the message. The limitation of the Gaussian message is given by its incapability to describe the phase in vicinity of 0 and  . Relatively good result is achieved using the Dirac-Delta message.
. Relatively good result is achieved using the Dirac-Delta message.
4.6.2. Simulation Results for the BICM
The last measurement was performed with the BICM model for SNR=8 dB. As it was mentioned, the randomness of the message is given not only by the iteration and the observation vector, but also by the position in the FG (of course only the messages  and
and  ).
).
The results of the analysis are shown in Figures 11 and 10. The first point is that the KLT message representation does not give the same results as the Fourier representation. The KLT-approximated message seems to converge a little bit faster than the Fourier representation up to approx. 45th iteration, where the KLT-approximated message achieves the error floor. There are two possible reasons for the error floor appearance (see Figure 11). First, the eigenvectors which constitute the basis system are not evaluated with a sufficient precision. Second, the evaluated KLT basis is the best linear approximation in average through all iterations and this basis is not capable to describe the messages appearing in the higher iterations sufficiently. If we focus on the issue discussed in the last model, where the 5-component message outperforms the 6-component one, we might observe this artifact again. A similar point might be seen in Figure 10 for both KLT and Fourier representations, where the 3-component messages outperform the 4-component messages. We can remind the point discussed in the eigenvalues section about the pairs of the eigenvalues. It seems (roughly said) the eigenfunctions work in pair so that adding only one of the pair might have a slightly negative impact for the target metrics.
Furthermore, we can observe a good behavior of the Dirac-Delta message in the BER measurement case. The MSE of the phase estimation, however, does not give such good results for the Dirac-Delta representation.
5. Conclusions
We have proposed a methodical way for the canonical message representation based on the KLT. The method itself is not restricted for a particular scenario. It is sufficient to have a stochastic description of the message or at least a satisfactory number of message realizations. The method, as it is presented, is restricted to real-valued one-dimensional messages in the FG/SPA.
We presented several example implementations of the method for several particular scenarios. The investigated message describes the phase shift of the communication channel for all models. The results of the simulations show that the KLT analysis of the message leads to the harmonic functions (or functions very similar) for all considered models and parameters. One might offer a conclusion that the KLT-basis is given only by the variable described by the analyzed message (the phase shift in our case).
The next point is also a consequence of the phenomenon that the KLT analysis of the message leads to the harmonic functions. The harmonic functions based linear basis optimizes the MSE of the approximated messages for the considered models.
We also evaluated some crucial performance metrics (BER and MSE of the phase estimation) for differently corrupted messages. The corruption consists in the incompleteness of the message (number of canonical basis). We compared the KLT-approximated message with several message types presented in the literature. We compare only the message representations. The update rules are performed "ideally" by the numerical integration in the simulations. The Fourier representation presented in [14] seems to be the best complexity/fidelity trade-off for the considered models. The KLT-approximation gives the same results as the Fourier representation in the model, where a relatively good stochastic description is available. In the second model, the Fourier representation slightly outperforms the KLT representation, but it can be caused by insufficient stochastic analysis of the message. An interesting complexity/fidelity trade-off offers the Dirac-Delta representation for the BER evaluation. The results of the Gaussian representation are limited by its incapability to describe the phase in vicinity of 0 and  .
.
Finally, we have found a case, where an increase in the approximation dimensionality affects negatively the performance in both Fourier and KLT message representations. It shows that the relation of both BER and MSE of the phase estimation and MSE of the approximated message is not generally proportional as one might expect.
References
Kschischang FR, Frey BJ, Loeliger HA: Factor graphs and the sum-product algorithm. IEEE Transactions on Information Theory 2001, 47(2):498-519. 10.1109/18.910572
Loeliger HA: An introduction to factor graphs. IEEE Signal Processing Magazine 2004, 21(1):28-41. 10.1109/MSP.2004.1267047
Mooij JM, Kappen HJ: Sufficient conditions for convergence of the sum-product algorithm. IEEE Transactions on Information Theory 2007, 53(12):4422-4437.
Yedidia JS, Freeman WT, Weiss Y: Constructing free-energy approximations and generalized belief propagation algorithms. IEEE Transactions on Information Theory 2005, 51(7):2282-2312. 10.1109/TIT.2005.850085
Elidan G, McGraw I, Koller D: Residual belief propagation: informed scheduling for asynchronous message passing. Proceedings of the 22nd Conference on Uncertainty in AI (UAI '06), July 2006, Boston, Mass, USA
Dauwels J, Loeliger HA: Phase estimation by message passing. Proceedings of the IEEE International Conference on Communications, June 2004 523-527.
Andrea Loeliger H: Some remarks on factor graphs. Proceedings of the 3rd International Symposium on Turbo Codes and Related Topics, 2003 111-115.
Loeliger HA, Dauwels J, Hu J, Korl S, Ping L, Kschischang FR: The factor graph approach to model-based signal processing. Proceedings of the IEEE 2007, 95(6):1295-1322.
Sykora J, Prochazka P: Error rate performance of the factor graph phase space CPM iterative decoder with modulo mean canonical messages. COST 2100 MCM, June 2008, Trondheim, Norway 1-7.
Simoens F, Moeneclaey M: Code-aided estimation and detection on time-varying correlated mimo channels: a factor graph approach. EURASIP Journal on Applied Signal Processing 2006, 2006:-11.
Kurkoski B, Dauwels J: Message-passing decoding of lattices using Gaussian mixtures. Proceedings of the IEEE International Symposium on Information Theory (ISIT '08), July 2008 2489-2493.
Dauwels JHG: On graphical models for communications and machine learning: algorithms, bounds, and analog implementation, Ph.D. dissertation. Swiss Federal Institute of Technology, Zürich, Switzerland; May 2006.
Worthen AP, Stark WE: Unified design of iterative receivers using factor graphs. IEEE Transactions on Information Theory 2001, 47(2):843-849. 10.1109/18.910595
Colavolpe G, Barbieri A, Caire G: Algorithms for iterative decoding in the presence of strong phase noise. IEEE Journal on Selected Areas in Communications 2005, 23(9):1748-1757.
Rimoldi BE: A decomposition approach to CPM. IEEE Transactions on Information Theory 1988, 34(2):260-270. 10.1109/18.2634
Acknowledgments
This work was supported by the European Science Foudation through COST Action 2100, FP7-ICT SAPHYRE project, the Grant Agency of the Czech Republic, Grant 102/09/1624, and the Ministry of Education, Youth and Sports of the Czech Republic, prog. MSM6840770014, Grant OC188 and by the Grant Agency of the Czech Technical University in Prague, Grant no. SGS10/287/OHK3/3T/13.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Prochazka, P., Sykora, J. Karhunen-Loève-Based Reduced-Complexity Representation of the Mixed-Density Messages in SPA on Factor Graph and Its Impact on BER. J Wireless Com Network 2010, 574607 (2011). https://doi.org/10.1155/2010/574607
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/574607



 ,
, 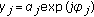 and
and  , where
, where 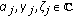 for the signal space models with the RW phase model,
for the signal space models with the RW phase model,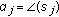 ,
,  and
and  , where
, where  for the phase space model with the constant phase model.
for the phase space model with the constant phase model.






