- Research Article
- Open access
- Published:
Oblique Projection Polarization Filtering-Based Interference Suppressions for Radar Sensor Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 605103 (2010)
Abstract
The interferences coming from the radar members degrade the detection and recognition performance of the radar sensor networks (RSNs) if the waveforms of the radar members are nonorthogonal. In this paper, we analyze the interferences by exploring the polarization information of the electromagnetic (EM) waves. Then, we propose the oblique projection polarization filtering- (OPPF-) based scheme to suppress the interferences while keeping the amplitude and phase of its own return in RSNs, even if the polarized states of the radar members are not orthogonal. We consider the cooperative RSNs environment where the polarization information of each radar member is known to all. The proposed method uses all radar members' polarization information to establish the corresponding filtering operator. The Doppler-shift and its uncertainty are independent of the polarization information, which contributes that the interferences can be suppressed without the utilization of the spatial, the temporal, the frequency, the time-delay and the Doppler-shift information. Theoretical analysis and the mathematical deduction show that the proposed scheme is a valid and simple implementation. Simulation results also demonstrate that this method can obtain a good filtering performance when dealing with the problem of interference suppressions for RSNs.
1. Introduction
Due to the complex and time-varying environments, also with respect to the manmade or natural interferences, the detection and recognition performance of the single radar system is limited by several issues. Since the techniques on electromagnetic countermeasure (ECM) and counter-counter measures (CCM) are developing more and more sophisticated, we can foresee that it is considerably difficult to fulfil the goal of giving the most accurate interpretation about what the target is at any given point in time for any detection and recognition system. It is also known to all that the slow fluctuations of the target radar cross section (RCS), which result in the radar target fades, are a main factor of degrading the detection and recognition performance of the radar systems [1].
The single radar systems encountering those problems mentioned above boost the radar researchers and engineers to exploit the new and effective schemes, therein, the radar sensor networks (RSNs) appear [2–10]. The RSNs are promised to operate with multiple goals managed by an intelligent platform network that can manage the dynamics of each radar member to meet the common goals of the platform, rather than each radar to operate as an independent system. This is the so-called cooperative radar networks with communication function [6]. While the performance of RSNs degrades because the radar members are likely to interfere with each other if their waveforms are not orthogonally designed, or their polarized states of the waveforms are not properly allocated [7]. In order to eliminate these interferences, much attention has been paid to the waveform design for RSNs [4–7, 9, 10]. The utilization of the polarization information for RSNs attracts relatively little attention than the waveform design, while our work tries to exploit the polarization information of the electromagnetic (EM) waves for RSNs, and we expect to seek an effective and easy implementation for RSNs to mitigate the interferences based on the use of the polarization information.
For the single radar systems, the polarization filtering (PF) technique is an effective method of interference suppressions, and the PF attracts much attention in recent decades [11–18]. While the conventional polarization filtering (CPF) [11–13] suffers distortions on both amplitude and phase of the target signal when establishing the orthogonal complementary vector of the interference polarization to cancel the interference, because of the neglect of the target polarization. The distortions on target is called the polarization loss introduced by the PF [14], and the polarization loss is determined by the distance when representing the polarization of the target and the interference in the form of the Poincare-Sphere. If and only if the distance between them is 180°, that is, their polarizations are orthogonal, no polarization loss is introduced. The polarization loss limits the filtering performance of the PF. To avoid the distortions on target, the null-phase-shift polarization filtering (NPSPF) was proposed in [15]. Although the NPSPF can solve the problem of distortions, it would suppress both the interference and the target when they hold the same polarized angle, and the CPF also encounters this problem when the target and the interference are both vertical polarization. These issues limit the application scopes of the PF. Meanwhile, little attention has been paid to the applications of the PF for RSNs.
In this paper, we propose a novel polarization filtering-based approach for RSNs, the suggested scheme suppresses the interferences from the radar members by using the oblique projection polarization filtering (OPPF) [16–20], and the OPPF is the extension to the CPF and the NPSPF. The proposed OPPF can separate the signals effectively if the polarization information of them is different, and the polarized states are not needed to be orthogonal due to the merits of the oblique projections [20]. The detailed implementation of the OPPF is to construct the polarization subspaces of the target and the interference, respectively, then the filtering operator is established according to the oblique projection operator. After passing through the OPPF, the interferences (other radar members' returned signals) are effectively cancelled while keeping the desired return with the same amplitude/phase and the polarization before the operation by the OPPF, even if their waveforms and polarized states are not orthogonal. The proposed scheme can effectively separate the desired returned signal and the interferences without additional transformation and compensation processing. With the desired return not suffering distortions after separation, the scheme is still valid when the desired return and the interferences hold the same polarized angle but with different phase difference in polarized angle.
Since the polarization filtering is independent of the frequency, the spatial, and the temporal domains, the proposed design is expected to exploit more resources which can achieve better suppression performance of the clutter and the interferences for RSNs. The Doppler-shift and its uncertainty are also independent of polarization, and this shows the implementation of the suggested scheme is simpler than the waveform-design-based systems.
We consider that all radar members' polarization information are shared among each radar member, that is, in a cooperative way. The proposed method utilizes all of the radar members' polarization information to establish the corresponding filtering operator for each radar member. Theoretical analysis and the mathematical deduction show that the proposed scheme is a valid and simple implementation. Simulation results also demonstrate that this method can obtain a good filtering performance when dealing with the problem of interference suppressions for RSNs.
The remainder of this paper is organized as follows. System model and fundamentals of the oblique projections are introduced in Section 2. The OPPF-based interference suppressions for the cooperative scenario is discussed in Section 3. Detailed analysis and the simulation results are done and illustrated in Section 4. Finally, Section 5 concludes this paper.
Typographic Conventions
A scalar is represented by any symbol in an italic font, for example,  . Vectors are column vectors and are represented by a boldface symbol, such as
. Vectors are column vectors and are represented by a boldface symbol, such as  . Matrices are represented by symbols in a bold font and are usually uppercase, such as
. Matrices are represented by symbols in a bold font and are usually uppercase, such as  . The subspace spanned by the columns of a matrix is represented with angle brackets around the symbol for the matrix, for example,
. The subspace spanned by the columns of a matrix is represented with angle brackets around the symbol for the matrix, for example,  . We use the symbol
. We use the symbol  to denote the orthogonal complement of
to denote the orthogonal complement of  . The symbol
. The symbol  denotes the complex Euclidean space of dimension
denotes the complex Euclidean space of dimension  . We use
. We use  to represent an
to represent an  -by-
-by- array matrix defined in the complex Euclidean space of dimension
array matrix defined in the complex Euclidean space of dimension  .
.  is the unit matrix.
is the unit matrix.  is the operation of calculating the expectation.
is the operation of calculating the expectation.
A superscript  is used to indicate the transpose of a matrix or vector, such as
is used to indicate the transpose of a matrix or vector, such as  , and
, and  denotes the Hermitian transpose, for example,
denotes the Hermitian transpose, for example,  .
.  is the dot product of two vectors,
is the dot product of two vectors,  is the symbol of pseudoinverse of a matrix, such as
is the symbol of pseudoinverse of a matrix, such as  , and
, and  denotes the conjugate operating.
denotes the conjugate operating.  is the imaginary part unit, and
is the imaginary part unit, and  is the conjugate of a complex number.
is the conjugate of a complex number.
2. System Model and Oblique Projections
2.1. System Model
We assume that the RSN consists of  radar members and is organized together in a self-organizing fashion. Figure 1 shows the block diagram of the discussed RSN. For the
radar members and is organized together in a self-organizing fashion. Figure 1 shows the block diagram of the discussed RSN. For the  th radar member, the received signal contains its own return (red color) and returned signals of other radar members (dashed lines). In our discussed RSN, each radar member is equipped with an orthogonal dual polarized antenna (ODPA) which can radiate and receive any polarization pattern.
th radar member, the received signal contains its own return (red color) and returned signals of other radar members (dashed lines). In our discussed RSN, each radar member is equipped with an orthogonal dual polarized antenna (ODPA) which can radiate and receive any polarization pattern.
Since the polarization information is taken into our consideration, we should represent the transmitted and the received signals in the form of the polarization representation. When representing the completely polarized EM waves using the  vector in a right-handed
vector in a right-handed  coordinate system with the
coordinate system with the  coordinate representing the direction of propagation and the orthogonal basis defined by a pair of
coordinate representing the direction of propagation and the orthogonal basis defined by a pair of  and
and  representing the horizontal (
representing the horizontal ( ) and the vertical (
) and the vertical ( ) components, ignoring the absolute phase of the horizontal component, the transmitted modulated waveform
) components, ignoring the absolute phase of the horizontal component, the transmitted modulated waveform  of the
of the  th radar member can be modelled as
th radar member can be modelled as

where  is the constant amplitude pulse envelope;
is the constant amplitude pulse envelope;  is a normalization factor to let
is a normalization factor to let  , wherein,
, wherein,  is the energy of the waveform and
is the energy of the waveform and  is the time duration for the radar pulses and each oscillator;
is the time duration for the radar pulses and each oscillator;  is the center frequency;
is the center frequency;  and
and  are its polarization parameters with
are its polarization parameters with  denoting the polarized angle, and
denoting the polarized angle, and  the phase difference in polarized angle. The polarized angle and the phase difference in polarized angle determine the polarized states of the signal as follows.
the phase difference in polarized angle. The polarized angle and the phase difference in polarized angle determine the polarized states of the signal as follows.
-
(1)
If
 , the polarization is linear.
, the polarization is linear. -
(2)
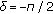 ,
,  indicates the right-handed circular polarization, and
indicates the right-handed circular polarization, and  ,
, 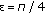 shows the left-handed circular polarization.
shows the left-handed circular polarization. -
(3)
If
 and
and  , then the polarization is left-handed elliptic. When
, then the polarization is left-handed elliptic. When  and
and 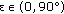 , the polarization is right-handed elliptic.
, the polarization is right-handed elliptic.
The polarized state is determined by the amplitude and phase relationship between the two components received by the ODPA. Taking the polarization of the  th radar member as an instance, the polarized angle and the phase difference in polarized angle are calculated as
th radar member as an instance, the polarized angle and the phase difference in polarized angle are calculated as


respectively, where  indicates the argument of the vector
indicates the argument of the vector  . After being radiated by the ODPA, the EM waves may produce the so-called cross-polarization (XP) component whose polarization is orthogonal to the original transmitted polarization, and this is known as the effect of depolarization [21, 22]. The degree of the depolarization is described by the cross-polarization discrimination (XPD) which indicates the ratio of the original transmitted polarization component power and the cross-polarization component power at the same location point. The depolarization effect can be eliminated by introducing the depolarization compensation technology [23].
. After being radiated by the ODPA, the EM waves may produce the so-called cross-polarization (XP) component whose polarization is orthogonal to the original transmitted polarization, and this is known as the effect of depolarization [21, 22]. The degree of the depolarization is described by the cross-polarization discrimination (XPD) which indicates the ratio of the original transmitted polarization component power and the cross-polarization component power at the same location point. The depolarization effect can be eliminated by introducing the depolarization compensation technology [23].
There are also many methods for estimation of the polarized states (see [15, 24]). In a communication realization, the polarized states can be estimated in the frequency domain if each user holds different frequency bands [15]. If they overlap in the frequency domain, then we can estimate their polarized states in the Fractional Fourier domain, because the modulation rate or the starting frequency of each member may be different. By using the Fractional Fourier Transformation (FrFT), their polarized states can be estimated effectively. We assume that the polarized state is already known at the receiver in this paper.
As depicted in Figure 1, a point moving target at an instant range is taken into our consideration. The two-way time delay of the  th radar member is denoted as
th radar member is denoted as  . Due to the movement of the target, the Doppler-shift denoting as
. Due to the movement of the target, the Doppler-shift denoting as  is introduced. Hence, the back-scattered radiation of the
is introduced. Hence, the back-scattered radiation of the  th radar member from the target is written as
th radar member from the target is written as

where  is the amplitude of the return of the
is the amplitude of the return of the  th radar member;
th radar member;  and
and  are the polarization information of its own return. If the target is a fluctuating one, the most popular and reasonable model for
are the polarization information of its own return. If the target is a fluctuating one, the most popular and reasonable model for  is the "Swerling 2" model. Therefore,
is the "Swerling 2" model. Therefore,  follows the Rayleigh distribution [1].
follows the Rayleigh distribution [1].
The polarized state suffers changes during the propagation [21, 22], for example, the reflections and the shadowing effect can destroy the polarization. Hence, the estimation of the polarized states (or polarization measurement) is essential for the PF. When the polarized states suffers changes, the depolarization compensation technology is valid to compensate the changes [23].
Since all of the radar members are transmitting signals, the received signal for all the radar members are mixed signals containing its own desired back-scattered signal and scattered signals generated by others. Then, the signal received by the ODPA of the  th radar member can be modelled as
th radar member can be modelled as

where  is the amplitude of the returned signal from the
is the amplitude of the returned signal from the  th radar member;
th radar member;  is the additive white Gaussian noise (AWGN) with mean value zero and variance
is the additive white Gaussian noise (AWGN) with mean value zero and variance  .
.
In order to suppress those components coming from other radar members, several work based on the waveform design of the signal has been proposed [4–7, 9, 10]. The propagation processing also destroys the orthogonality of the waveforms. Due to the movement of the target, the relative speed rate of the target to each radar member is different, and the Doppler-shift and its uncertainty are essential to the waveform-design-based systems. In this paper, we make use of the polarization information to suppress those interferences. It is obvious that the polarization is independent of the frequency, and the Doppler-shift and its uncertainty.
2.2. Oblique Projections
Herein, we consider two full column rank matrices  and
and  , and suppose
, and suppose  . The columns of
. The columns of  and
and  are nonoverlapped indicating that the intersection of the range subspaces
are nonoverlapped indicating that the intersection of the range subspaces  and
and  , respectively, spanned by
, respectively, spanned by  and
and  only contains vector
only contains vector  . It is obvious that the condition of nonoverlapped implies that the vector spaces are linear independent. If their intersection of the range subspaces only contains vector
. It is obvious that the condition of nonoverlapped implies that the vector spaces are linear independent. If their intersection of the range subspaces only contains vector  , then they are called as disjointed vector spaces. Two vectors are disjointed does not imply that they are orthogonal with each other. It is easy to find that the composite matrix
, then they are called as disjointed vector spaces. Two vectors are disjointed does not imply that they are orthogonal with each other. It is easy to find that the composite matrix  is also a full column rank matrix with rank
is also a full column rank matrix with rank  .
.
The oblique projection operator along the subspace  onto the subspace
onto the subspace  is defined as [20]
is defined as [20]

The properties of the oblique projection operator are as follows [20]:

It can be found that the range space of the oblique projection operator  is
is  , and
, and  is a subset of its null subspace.
is a subset of its null subspace.
As an extension to the orthogonal projection, oblique projection does not need the condition that the two subspaces are orthogonal. If they are orthogonal, the projection operator becomes the orthogonal projection operator.
3. OPPF in the Cooperative Scenario
According to the polarization information and equations (1) and (4), equation (5) can be rearranged in the matrix form and written as

We consider that all radar members share their polarization information. For convenience, we assume that there are two radar members in the RSN, that is,  . It is proved that the OPPF can solve the problem of interference suppressions when there are more than two radar members [18]. We propose the polarization vector transformation (PVT) to fulfil the multiinterference suppressions based on the merits of the oblique projections.
. It is proved that the OPPF can solve the problem of interference suppressions when there are more than two radar members [18]. We propose the polarization vector transformation (PVT) to fulfil the multiinterference suppressions based on the merits of the oblique projections.
The polarization can be defined as a domain or a subspace, and the polarized waves can be considered as belonging to its corresponding polarization subspace, or different polarized states are corresponding to different components of the polarization subspaces. It is obvious that two arbitrary different polarized states satisfy the requirement of disjointed. Signals with different polarized states can be represented by different components in the polarization subspaces. According to the fundamental theory of the oblique projection, the target signal (the desired return) polarization subspace  and the interference (return from the second radar member) polarization subspace
and the interference (return from the second radar member) polarization subspace  are defined as
are defined as

Obviously,  and
and  are column vectors and are both full column rank (rank is 1). If the polarized states of the target and the interference are different, then the subspaces
are column vectors and are both full column rank (rank is 1). If the polarized states of the target and the interference are different, then the subspaces  and
and  are disjointed, where the composite matrix
are disjointed, where the composite matrix  is a full column rank matrix.
is a full column rank matrix.
Furthermore, we define

For two radar members, the signal received by the 1st radar member is described as

where  and
and  are
are

With (6), the oblique projection operator corresponding to the polarization subspaces of the target and the interference can be constructed to extract the target signal. The expression of formula (6) is expanded as [20]

where  is the orthogonal projection operator onto the orthogonal complementary subspace of
is the orthogonal projection operator onto the orthogonal complementary subspace of  , which can be calculate as
, which can be calculate as

where  is the orthogonal projection operator onto the interference polarization subspace
is the orthogonal projection operator onto the interference polarization subspace  .
.
From (7), the output signal  of the received signal passing through the oblique projection operator
of the received signal passing through the oblique projection operator  , can be obtained as
, can be obtained as

where  is the result after
is the result after  passing through
passing through  .
.
Formula (15) demonstrates that the interference is suppressed totally, and the output is the original target signal plus the additive Gaussian noise, with the amplitude and phase of the target signal remaining the same after projection processing. As long as the polarized states of the target signal and the interference are different, that is, the polarized angles and the phase difference in polarized angle are not equal simultaneously, then the oblique projection operator can suppress the interference totally and keep the amplitude and phase information of the target. The proposed scheme does not require the information of the frequency, the time-scale, and the Doppler-shift and its uncertainty. If the target signal and the interference are overlapped in the frequency domain, the interference can also be suppressed by using the oblique projection operator.
The output of the oblique projection operator is a two-dimension signal that contains the horizontal component and the vertical component, which keeps the entire information of the original signal including the polarization information. Therefore, posterior polarization processing is still available after adopting the proposed filtering algorithm, for example, another polarization filtering can be implemented. In order to obtain the one-dimension signal, we project the results obtained from the oblique projection orthogonally onto the subspace of  , where
, where  is described as
is described as

The orthogonal projection can be written as

And  can be defined as the OPPF operator
can be defined as the OPPF operator 

where

The OPPF operator contains the polarization information of the target and the interference. If the polarized states of both the target signal and the interference are known, the OPPF operator can be constructed according to the formulaes (18)-(19) to extract the target signal.
Along the same analysis flow, it can be found out that the oblique projection operator  along subspace
along subspace  onto subspace
onto subspace  can also extract the components of
can also extract the components of  . Hence, in the cooperative RSN, each radar can obtain its own target signal while suppressing other radar members' interfering signals, since
. Hence, in the cooperative RSN, each radar can obtain its own target signal while suppressing other radar members' interfering signals, since  and
and  .
.
Consider that there are more than two radar members in the RSN, that is,  . For simplicity of analysis, we assume there are three radar members, while it can be extended to more radar members in a straightforward way.
. For simplicity of analysis, we assume there are three radar members, while it can be extended to more radar members in a straightforward way.
Let

Therefore, the received signal of the 1st radar member can be written as

It is easy to find that the linear model for oblique projections is not a full column rank matrix, the model is a matrix belonging to  , that is,
, that is,  . In order to construct a model that satisfies the full-rank property, we utilize the polarization vector transformation (PVT) to transform the target signal into a vertically polarized waves.
. In order to construct a model that satisfies the full-rank property, we utilize the polarization vector transformation (PVT) to transform the target signal into a vertically polarized waves.
The transformation matrix is defined as [15]

where

Let  , and
, and  , that is,
, that is,  denotes the vertical polarization. It is easy to obtain that
denotes the vertical polarization. It is easy to obtain that  . Then after the transformation, the returned signal of the 1st user is a vertically polarized waves.
. Then after the transformation, the returned signal of the 1st user is a vertically polarized waves.
After the transformation by  , (21) is obtained as
, (21) is obtained as

We focus on the polarization changes of other two radar members. It can be achieved that

where  ,
,  ,
,  , and
, and  (
( ) are the parameters after transformation by
) are the parameters after transformation by  .
.
Then the horizontal component of the transformed signal, that is, the first array of the matrix, can be obtained as,

Ignoring the absolute phase of interferences, (26) is achieved as

where  , and
, and  are both real numbers. Particularly,
are both real numbers. Particularly,  and
and  can be chosen as the modulus of the complex number
can be chosen as the modulus of the complex number  and
and  , or can be also just selected the real part of
, or can be also just selected the real part of  and
and  .
.
We can add the  as the third component of the signal
as the third component of the signal

Therefore, the system model can be constructed as,

If the target signal and the two interferences hold the different polarized states, it can be verified that the matrix  is a full-rank one, that is,
is a full-rank one, that is,  . According to (6) and (13), the OPPF can be established, and the oblique projection operator can be written as
. According to (6) and (13), the OPPF can be established, and the oblique projection operator can be written as

where

After the projection process, the other two radar members' returned signals are suppressed. We select only the first two array components of the projection results since the third array is a virtual component.
For more than three radar members, we can select  and
and  as different parameters. Take four radar members as an instance, for the
as different parameters. Take four radar members as an instance, for the  st user, it should add at least two virtual components to its true received signals. The first virtual component can be selected according to the analysis mentioned above, and the second component can be selected according to the following principle: transform the second radar member's polarization to vertical polarization, then repeat the same process.
st user, it should add at least two virtual components to its true received signals. The first virtual component can be selected according to the analysis mentioned above, and the second component can be selected according to the following principle: transform the second radar member's polarization to vertical polarization, then repeat the same process.
Figure 2 shows the block diagram of the radar member's receiver in the RSN. The signal received by the  radar member's ODPA is fed to the Transformer
radar member's ODPA is fed to the Transformer  and the Combination Device, and the parameters of
and the Combination Device, and the parameters of  are selected from the Set of Polarized States (SPS) which contain all radar members' polarized states. Each radar member is equipped with the Estimator of Polarized State (EPS). After transformation by
are selected from the Set of Polarized States (SPS) which contain all radar members' polarized states. Each radar member is equipped with the Estimator of Polarized State (EPS). After transformation by  , the results are fed to the Combination Device, and the Combination Device combines the true signals and the virtual signals as a new signal. Finally, the new signal is fed to the OPPF, and the OPPF suppresses other radar members' signals.
, the results are fed to the Combination Device, and the Combination Device combines the true signals and the virtual signals as a new signal. Finally, the new signal is fed to the OPPF, and the OPPF suppresses other radar members' signals.
4. Detailed Analysis and Simulation Results
In order to fully understand the performance of the proposed OPPF, the detailed analysis and the simulation results are presented in this section.
If the polarized states are not exactly estimated, that is, some estimation errors are introduced, we also consider the case of two-radar-member in the RSN for simplifying the complexity of analysis. For the 1st user, if  cannot be estimated exactly,
cannot be estimated exactly,  will suffer distortions after passing through the OPPF, since the oblique projection cannot be established correctly. And if the estimation of
will suffer distortions after passing through the OPPF, since the oblique projection cannot be established correctly. And if the estimation of  is not the exact value, the component of
is not the exact value, the component of  cannot be suppressed totally.
cannot be suppressed totally.
Considering that there is estimation error on  while other parameters are exactly estimated, the filtering operator
while other parameters are exactly estimated, the filtering operator  which is established by the incorrect parameter is different from the filtering operator
which is established by the incorrect parameter is different from the filtering operator  obtained from the exact parameters. Suppose that the output of the received signal after passing through
obtained from the exact parameters. Suppose that the output of the received signal after passing through  is
is  and the output of the received signal after passing through
and the output of the received signal after passing through  is
is  , then
, then  is obtained as
is obtained as

The absolute error between the desired output  and the actual output
and the actual output  can be obtained as
can be obtained as

And the relative error is given by

For simplicity of analysis, let the polarized angle of target signal be  , and assume the estimation of polarized angle be
, and assume the estimation of polarized angle be  . Then, the absolute error and relative error are
. Then, the absolute error and relative error are

Figure 3 illustrates the relationship between the relative error and the estimation error on  (the exact value of
(the exact value of  is 90°). As can be seen from the figure, when the estimation
is 90°). As can be seen from the figure, when the estimation  is fixed, the relative error has the relationship with
is fixed, the relative error has the relationship with  : the smaller the angle is, the less the errors will be introduced, which can be easily demonstrated from the PF theory. We can also prove that the larger the polarization difference, the better the performance. For example, when
: the smaller the angle is, the less the errors will be introduced, which can be easily demonstrated from the PF theory. We can also prove that the larger the polarization difference, the better the performance. For example, when  is 89.5° and
is 89.5° and  is 60°, the relative error is 1.8
is 60°, the relative error is 1.8 ; when
; when  is 20°, the relative error is 0.4
is 20°, the relative error is 0.4 . If the relative error must be controlled below 10
. If the relative error must be controlled below 10 , the estimation error on
, the estimation error on  cannot be more than 1°.
cannot be more than 1°.
When there is estimation error on  , the interference cannot be totally suppressed for the
, the interference cannot be totally suppressed for the  st radar member. The performance degradation brought by the estimation error is analyzed by the relationship between the error deviation
st radar member. The performance degradation brought by the estimation error is analyzed by the relationship between the error deviation  on
on  and the gain of signal-to-interference ratio
and the gain of signal-to-interference ratio  .
.
The signal-to-interference ratio of the received signal  is
is

Since there is estimation error on  , the OPPF operator is not an accurate one. if the parameters in formula (18) are denoted by
, the OPPF operator is not an accurate one. if the parameters in formula (18) are denoted by  ,
,  , and
, and  , the signal-to-interference ratio after OPPF is given by
, the signal-to-interference ratio after OPPF is given by

The gain of signal-to-interference ratio is

By (38), the gain of signal-to-interference ratio has a relationship with the difference between  and the error deviation
and the error deviation  . The larger the
. The larger the  is, the larger the
is, the larger the  can be obtained. In order to get good
can be obtained. In order to get good  performance, a moderately large difference between the polarized angles of each radar member should be designed.
performance, a moderately large difference between the polarized angles of each radar member should be designed.
Fig. 4 describes the relationship between  ,
,  and
and  . When
. When  is 0.1° and
is 0.1° and  is 60°, he gain of signal-to-interference ratio which can be obtained is about 54dB, and if
is 60°, he gain of signal-to-interference ratio which can be obtained is about 54dB, and if  is 30°, the gain of signal-to-interference ratio is 50 dB. When
is 30°, the gain of signal-to-interference ratio is 50 dB. When  is 1° and
is 1° and  are 60° and 45°, the gains of signal-to-interference ratio are 34 dB and 32 dB, respectively. This indicates that the gain of signal-to-interference ratio is sensitive to
are 60° and 45°, the gains of signal-to-interference ratio are 34 dB and 32 dB, respectively. This indicates that the gain of signal-to-interference ratio is sensitive to  .
.
To show the performance when the RSN adopts the proposed OPPF intuitively, we verify its performance by using  simulations.
simulations.
Figure 5 shows the filtering performance comparison between the proposed OPPF and the NPSPF. The sampling rate of this simulation is 1 GHz. The target signal is a linear frequency modulation (LFM) type with the amplitude 1.5 A, the initial normalized frequency 0.001, and the final normalized frequency 0.15. The interferences are two LFM signals with amplitudes 3 A and 2 , the initial normalized frequency 0.1 and 0.13, and the final normalized frequency 0.2 and 0.3, respectively. we let both the target and the interferences be the vertical polarization. The signal-to-noise ratio (SNR) is 10 dB. The yellow dashed line is the received signal. The filtering result of the OPPF is illustrated in the form of the red line. It can be clearly seen that the interferences are suppressed effectively, and the original LFM type target signal appears after the operation of the OPPF. The blue line is the filtering result of the NPSPF, since both the target and the interferences are vertically polarized, they are cancelled simultaneously by the NPSPF. This simulation result shows that the application scope of the proposed OPPF is wider than the NPSPF when introducing the PF into RSNs for interference suppressions.
, the initial normalized frequency 0.1 and 0.13, and the final normalized frequency 0.2 and 0.3, respectively. we let both the target and the interferences be the vertical polarization. The signal-to-noise ratio (SNR) is 10 dB. The yellow dashed line is the received signal. The filtering result of the OPPF is illustrated in the form of the red line. It can be clearly seen that the interferences are suppressed effectively, and the original LFM type target signal appears after the operation of the OPPF. The blue line is the filtering result of the NPSPF, since both the target and the interferences are vertically polarized, they are cancelled simultaneously by the NPSPF. This simulation result shows that the application scope of the proposed OPPF is wider than the NPSPF when introducing the PF into RSNs for interference suppressions.
In Figure 6, we simulate an environment where there is a continuous-time type interference. The radar member radiates the pulses with LFM pattern modulation. Figure 6(a) is the expected returned signal for the radar member without AWGN. The SIR in this simulation is −12 dB, and the SNR is 12 dB. The polarized states of the target and the interference are defined as follows: the target signal is a linear polarization with the polarized angle 60°, and the interference is a right-handed circular polarization. Figure 6(b) shows the received signal for the radar member, and we can find out that the returned pulses are embedded in the interference and cannot be detected directly from the received signal. The filtering result of the OPPF is illustrated in the Figure 6(c), and the two pulses can be easily detected after the operation by the OPPF. This shows the application of the OPPF is valid for RSNs.
In order to fully validate the effectiveness of the OPPF for RSNs, we consider there are three radar members in the RSN. The expected returned signal is shown in Figure 7(a). The interferences coming from other two radar members are simulated as follows: the first interference is one radar member's scattered signals, and the second interference is the transmitted signal of the other radar member and this transmitted signal is modulated with the Gaussian envelope. Figure 7(b) is the received signal of the radar member. After filtering by the OPPF, the returned signal for the radar member is shown in Figure 7(c).
In Figure 8, there are two radar members in the RSN, and the received signal for the desired radar member is shown in Figure 8(b). It can be seen that the returned signals of the two radar members overlap in the pulse-width distance. After the processing by the OPPF, the returned signals for the desired radar member is shown in Figure 8(c).
These simulation results show that once the polarization of each radar member is different from each other, the proposed OPPF are valid when dealing with the problem of interference suppressions for RSNs. Moreover, after the operation of the OPPF, the diversity combination can also be available, besides the spatial and the time diversity, the polarization diversity can also be exploited in the OPPF-based RSNs.
5. Conclusion
In the RSNs, the radar members interfere with each other if their waveforms are nonorthogonal and this introduces degradation to the detection and estimation performance of the RSNs. In this paper, we introduce the polarization information rather than the waveform design for RSNs, and discuss the feasibility when using the proposed oblique projection polarization filtering (OPPF)-based scheme to suppress the interferences in a cooperative RSN where all the polarization information of the radar member are shared. The analysis shows that the Doppler-shift and its uncertainty are independent of the polarization information, which contributes that the interferences can be suppressed without the utilization of the spatial, the temporal, the frequency, the time-delay, and the Doppler-shift information. Theoretical analysis and the mathematical deduction show that the proposed scheme is a valid and simple implementation to the interference suppressions problems for RSNs. Simulation results also illustrates a good filtering performance when adopting the proposed OPPF for the cooperative RSN.
References
Skolnik M: Introduction to Radar Systems. 3rd edition. McGraw Hill, New York, NY, USA; 2001.
Łubczonek J, Stateczny A: Aspects of spatial planning of radar sensor network for inland waterways surveillance. Proceedings of the 6th European Radar Conference (EuRAD '09), 2009 501-504.
Liang Q: Collaborative signal processing using radar sensor networks. Proceedings of the IEEE Military Communications Conference (MILCOM '06), 2006 1-6.
Xu L, Liang Q: Radar sensor network using a new triphase coded waveform: theory and application. Proceedings of the IEEE International Conference on Communications (ICC '09), 2009 1-5.
Liang Q: Radar sensor networks for automatic target recognition with delay-doppler uncertainty. Proceedings of the IEEE Military Communications Conference (MILCOM '07), 2007 1-7.
Liang J, Liang Q, Zhou Z: Radar sensor network design and optimization for blind speed alleviation. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '07), 2007 2645-2649.
Liang Q: Waveform design and diversity in radar sensor networks: theoretical analysis and application to automatic target recognition. Proceedings of the 3rd Annual IEEE Communications Society on Sensor and Ad Hoc Communications and Networks (Secon '06), 2006 2: 684-689.
Pescosolido L, Barbarossa S, Scutari G: Radar sensor networks with distributed detection capabilities. Proceedings of the IEEE Radar Conference (RADAR '08), 2008 1-6.
Liang J, Liang Q: Orthogonal waveform design and performance analysis in radar sensor networks. Proceedings of the IEEE Military Communications Conference (MILCOM '06), 2006 1-6.
Ly HD, Liang Q: Spatial-temporal-frequency diversity in radar sensor networks. Proceedings of the IEEE Military Communications Conference (MILCOM '07), 2007 1-7.
Poelman AJ: Virtual polarisation adaptation-a method of increasing the detection capability of a radar system through polarisation-vector processing. IEE Proceedings. Part F 1981, 128(5):261-270.
Gherardelli M, Giuli D, Fossi M: Suboptimum adaptive polarisation cancellers for dual-polarisation radars. IEE Proceedings, Part F 1988, 135(1):60-72.
Poelman AJ: Virtual polarization adaption—a method of increasing detection capability of a radar system through polarization-vector processing. IEE Proceedings, Part F 1981, 128(5):261-270.
Mao X, Liu Y: Validity of polarization filtering technique. Journal of Harbin Institute of Technology 2002, 34(4):577-580.
Mao X-P, Liu Y-T: Null phase-shift polarization filtering for high-frequency radar. IEEE Transactions on Aerospace and Electronic Systems 2007, 43(4):1397-1408.
Cao B, Liu A-J, Mao X-P, Zhang Q-Y: An oblique projection polarization filter. Proceeding of the International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM '08), 2008 1893-1896.
Cao B, Zhang Q, et al.: Blind adaptive polarization filtering based on oblique projection. Proceedings of the IEEE International Conference on Communications (ICC '10), 2010
Wang J, Zhang Q-Y, Cao B: Multi-notch polarization filtering based on oblique projection. Proceedings of the Global Mobile Congress (GMC '09), 2009 1-5.
Zhang Q, Cao B, Wang J, Zhang N: Polarization filtering technique based on oblique projections. Science in China, Series F 2010, 2010(53):1056-1066.
Behrens RT, Scharf LL: Signal processing applications of oblique projection operators. IEEE Transactions on Signal Processing 1994, 42(6):1413-1424. 10.1109/78.286957
Huang J, Wang Y: Application of Weibull distribution in prediction for the rain induced depolarization of millimeter waves. Acta Electronica Sinica 1993, 21(12):93-96.
Yang R, Huang J, Lv X: Identification for the rain induced depolarization discrimination in millimeter wave propagation. Journal of Xidian University (Natural Science) 2000, 27(4):487-490.
Zheng L, Liu G: Adaptive compensation techniques for rain depolarization at millimeter wavelength. Journal of Xidian University (Natural Science) 1989, 16(2):185-196.
Roueff A, Chanussot J, Mars JI: Estimation of polarization parameters using time-frequency representations and its application to waves separation. Signal Processing 2006, 86(12):3714-3731. 10.1016/j.sigpro.2006.03.019
Acknowledgment
This work has been supported by the National Natural Sciences Foundation of China (NSFC) under the Grant No. 60432040 No. 60702034 and the National Basic Research Program of China under Grant No. 2007CB310606.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cao, B., Zhang, QY., Jin, L. et al. Oblique Projection Polarization Filtering-Based Interference Suppressions for Radar Sensor Networks. J Wireless Com Network 2010, 605103 (2010). https://doi.org/10.1155/2010/605103
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/605103

 , the polarization is linear.
, the polarization is linear.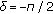 ,
,  indicates the right-handed circular polarization, and
indicates the right-handed circular polarization, and  ,
, 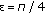 shows the left-handed circular polarization.
shows the left-handed circular polarization. and
and  , then the polarization is left-handed elliptic. When
, then the polarization is left-handed elliptic. When  and
and 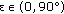 , the polarization is right-handed elliptic.
, the polarization is right-handed elliptic.

 ,
,  and the relative error.
and the relative error.
 ,
,  and
and  .
.


