- Research Article
- Open access
- Published:
Lower Bounds on the Maximum Energy Benefit of Network Coding for Wireless Multiple Unicast
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 605421 (2010)
Abstract
We consider the energy savings that can be obtained by employing network coding instead of plain routing in wireless multiple unicast problems. We establish lower bounds on the benefit of network coding, defined as the maximum of the ratio of the minimum energy required by routing and network coding solutions, where the maximum is over all configurations. It is shown that if coding and routing solutions are using the same transmission range, the benefit in d-dimensional networks is at least  . Moreover, it is shown that if the transmission range can be optimized for routing and coding individually, the benefit in 2-dimensional networks is at least 3. Our results imply that codes following a decode-and-recombine strategy are not always optimal regarding energy efficiency.
. Moreover, it is shown that if the transmission range can be optimized for routing and coding individually, the benefit in 2-dimensional networks is at least 3. Our results imply that codes following a decode-and-recombine strategy are not always optimal regarding energy efficiency.
1. Introduction
Emerging applications in wireless networks, like environment monitoring in rural areas by ad hoc networks, require more and more resources. One of the most important limitations is formed by battery life. Since battery technology is not keeping up with the increasing demand from resource-consuming applications, it is imperative that more efficient use is made of the available energy. There has been significant recent attention to the problem of minimizing energy consumption in networks. Some of the topics considered are minimum cost routing [1–3], power control algorithms [4–6], and cross-layer protocol design for energy minimization [7]. In this work, we are interested in the use of network coding [8–14] for reducing the energy consumption in wireless networks. We compare the reduction with traditional routing solutions. The contributions of this work are lower bounds on the energy reduction that can be achieved by using network coding for multiple unicast problems in wireless networks.
In recent years, there has been significant interest in network coding with the aim of reducing energy consumption in networks. More generally, network coding with a cost criterion has been considered. Much progress has been made in understanding the case of multicast traffic. In fact, it has been shown by Lun et al. that a minimum-cost network coding solution can be found in a distributed fashion in polynomial time [15]. The fact that the complexity of finding this solution is polynomial in time is surprising, since the corresponding routing problem is a Steiner tree problem that is known to be NP-complete [16].
Besides constructing minimum-cost coding solutions, it is also of interest to know what the benefits of network coding are compared to routing. In this work we, are interested in the energy benefit of network coding, which is the ratio of the minimum energy solution in a routing solution compared to the minimum energy network coding solution, maximized over all configurations. It has been shown by Goel and Khanna [17] that the energy benefit of network coding for multicast problems in wireless networks is upper bounded by a constant. The problem of reducing energy consumption for many-to-many broadcast traffic in wireless networks has been studied by Fragouli et al. in [18] and Widmer and Le Boudec in [19], providing lower bounds on the energy benefit of network coding for specific topologies. More importantly, algorithms have been presented in [18, 19] that allow to exploit these benefits in practical scenarios, that is, in a distributed fashion.
The above demonstrates that for multicast traffic and for many-to-many broadcast traffic, there is some understanding of the energy benefits of network coding and how to exploit them. In order to reduce energy consumption in practical networks, however, it is important to consider also multiple unicast traffic. Indeed, in practice a large part of the data will be generated by unicast sessions. For the case of multiple unicast traffic, contrary to multicast and broadcast, not much is known. This paper deals with the energy benefits of network coding for wireless multiple unicast. Remember from the above that for multicast, the problem of minimum-cost routing is hard, whereas minimum-cost network coding is easy. In stark contrast, the problem of minimum-cost multiple unicast routing is easy. One constructs the minimum-cost solution, that is, the shortest path, for each session individually. The minimum-cost multiple unicast network coding problem, however, seems hard and in general very little is known.
Network coding for the multiple unicast problem was first studied by Wu et al. in [20], in which it was shown that in the information exchange problem on the line network, the energy saving achieved by network coding is a factor two. The network codes that we construct in this work are in a sense a generalization of the results on one-dimensional networks [20], to higher-dimensional networks. The networks considered in this work are lattices. More specifically, the hexagonal lattice and the rectangular lattice. Effros et al. [21] and Kim et al. [22] have considered energy-efficient network codes on the hexagonal lattice. We improve the lower bounds on the energy savings of network on the hexagonal lattice given in [21]. More precisely, we improve the previously known bound of  and obtain a new bound of
and obtain a new bound of  .
.
Kramer and Savari have developed techniques that can be used to upper bound the achievable throughputs in a multiple unicast problem [23]. No methods are known, however, to lower bound the cost of network coding solutions for a configuration. A lower bound to the ratio of the minimum energy consumption of routing and coding solutions for a given multiple unicast configuration was provided by Keshavarz-Haddad and Riedi in [24]. For the type of configurations used in this paper, however, the results from [24] give the trivial lower bound of one. We will see, however, that network coding has large energy savings for these configurations.
An important class of network codes operates according to a principle that we will refer to in the remainder as decode-and-recombine. These codes satisfy the constraint that each symbol in each linear combination that is transmitted is explicitly known by the node transmitting that linear combination. Note, that this is a restriction from the general linear coding strategy, in which linear combinations of coded messages can be retransmitted. The motivation behind using decode-and-recombine codes is that it prevents information from spreading too much in the network, away from the path between source and destination, a heuristic introduced by Katti et al. [25]. The use of a decode-and-recombine strategy results in reduced complexity. However, an important question that has to be addressed is whether the use of decode-and-recombine codes leads to a higher energy consumption than is strictly necessary. We answer this question affirmatively. An upper bound of three on the energy benefit of decode-and-recombine codes has been given by Liu et al. [26]. One of the contributions of this work is to show that larger energy benefits can be obtained by considering also other types of codes.
This paper is organized as follows. In Section 2 we specify our model and problem statement more precisely. Our main results are presented in Section 3. Constructions of configurations that allow a large energy benefit for network coding and proofs of our results are given in Sections 4 and 5. In Section 6, finally, we discuss our work.
2. Model and Problem Statement
Let  be the nodes of a
be the nodes of a  -dimensional wireless network. We consider a wireless network model with broadcast, where all nodes within range
-dimensional wireless network. We consider a wireless network model with broadcast, where all nodes within range  of a transmitting node can receive, and nodes outside this range cannot. More precisely, given a transmission range
of a transmitting node can receive, and nodes outside this range cannot. More precisely, given a transmission range  , a node
, a node  is broadcasting to all nodes in the set
is broadcasting to all nodes in the set

where  denotes the Euclidean norm of
denotes the Euclidean norm of  . The energy required to transmit one unit of information to all other nodes within range
. The energy required to transmit one unit of information to all other nodes within range  equals
equals  , where
, where  is the path loss exponent and
is the path loss exponent and  is some constant. In analyzing the energy consumption of nodes, we will consider only the energy consumed by transmitting. Receiver energy consumption as well as energy consumed by processing are assumed to be negligible compared to transmitter energy consumption. In particular, note that little additional processing is required for network coding, compared to the processing that is performed in a traditional wireless protocol stack.
is some constant. In analyzing the energy consumption of nodes, we will consider only the energy consumed by transmitting. Receiver energy consumption as well as energy consumed by processing are assumed to be negligible compared to transmitter energy consumption. In particular, note that little additional processing is required for network coding, compared to the processing that is performed in a traditional wireless protocol stack.
The traffic pattern that we consider is multiple unicast. All symbols are from the field  , that is, they are bits and addition corresponds to the xor operation. The source of each unicast session has a sequence of source symbols that need to be delivered to the corresponding destination. Let
, that is, they are bits and addition corresponds to the xor operation. The source of each unicast session has a sequence of source symbols that need to be delivered to the corresponding destination. Let  be the set of unicast sessions. We call
be the set of unicast sessions. We call  a wireless multiple unicast configuration.
a wireless multiple unicast configuration.
We will compare energy consumption of routing and network coding. Our goal is to establish lower bounds on the maximum of the ratio of the minimum energy required by routing and network coding solutions, where the maximum is over all configurations. We will refer to this ratio as the energy benefit of network coding. Let  and
and  be the minimum energy required for network coding and routing solutions, respectively, for a configuration
be the minimum energy required for network coding and routing solutions, respectively, for a configuration  . The energy consumption of a coding or routing scheme is defined as the time-average of the total energy spent by all nodes in the network to deliver one symbol for each unicast session. In analyzing coding schemes, we will ignore the energy consumption in an initial startup phase and consider only steady-state behavior.
. The energy consumption of a coding or routing scheme is defined as the time-average of the total energy spent by all nodes in the network to deliver one symbol for each unicast session. In analyzing coding schemes, we will ignore the energy consumption in an initial startup phase and consider only steady-state behavior.
Note that since energy consumption per transmission equals  , the transmission range
, the transmission range  is an important factor in the energy consumption. Therefore, it is of particular interest to optimize the transmission range such that energy consumption is minimized. In this work, we consider two different quantities: (
is an important factor in the energy consumption. Therefore, it is of particular interest to optimize the transmission range such that energy consumption is minimized. In this work, we consider two different quantities: ( )
)  , denoting the energy benefit that can be obtained if the transmission range is given and fixed and (
, denoting the energy benefit that can be obtained if the transmission range is given and fixed and ( )
)  , denoting the energy benefit that can be obtained if one is allowed to optimize the transmission range. Note that the transmission range can be individually optimized for the routing and network coding scenarios. More precisely, the goal of this work is to establish lower bounds on
, denoting the energy benefit that can be obtained if one is allowed to optimize the transmission range. Note that the transmission range can be individually optimized for the routing and network coding scenarios. More precisely, the goal of this work is to establish lower bounds on

where the maximization is over all node locations  , multiple unicast sessions
, multiple unicast sessions  , and transmission ranges
, and transmission ranges  , with the transmission range equal for the routing and network coding solutions, and
, with the transmission range equal for the routing and network coding solutions, and

where the maximization is over all node locations  and multiple unicast sessions
and multiple unicast sessions  , with the transmission range being optimized individually for the routing and network coding solutions. If no confusion can arise, we will omit dependency on
, with the transmission range being optimized individually for the routing and network coding solutions. If no confusion can arise, we will omit dependency on  in the notation for
in the notation for  and
and  .
.
Since in  ,
,  is equal for
is equal for  and
and  , the energy per transmission is equal in
, the energy per transmission is equal in  and
and  and the benefit is equal to the ratio of the number of transmissions required in routing and network coding solutions.
and the benefit is equal to the ratio of the number of transmissions required in routing and network coding solutions.
Since we are interested in energy consumption only, we can assume that all transmissions are scheduled sequentially and/or that there is no interference. All coding and routing schemes that we consider proceed in time slots or rounds. In each time slot, all nodes are allowed to transmit one or more messages. We assume that the length of the time slot is large enough to accommodate sequential transmission of all messages in that round. Coding operations will be based on messages received in previous time slots only. Finally, we assume that all nodes have complete knowledge of the network topology and the network code that is being used.
To conclude this section, we introduce here some of the notation that will be used in the remainder of the paper. The symbol transmitted by a node  in time slot
in time slot  is denoted by
is denoted by  . If
. If  transmits more than one symbol in time slot
transmits more than one symbol in time slot  , these will be distinguished by a superscript, giving, for instance,
, these will be distinguished by a superscript, giving, for instance,  and
and  . Nodes are represented by vectors. Given vectors
. Nodes are represented by vectors. Given vectors  and
and  , let
, let  ,
,  , and
, and  .
.
Unicast sessions are denoted by  , with
, with  being an integer and
being an integer and  a vector. We will see in Sections 4 and 5 that
a vector. We will see in Sections 4 and 5 that  defines the location of the source and
defines the location of the source and  the relative location of the destination, that is, the direction of the session. In some cases
the relative location of the destination, that is, the direction of the session. In some cases  will be denoted as
will be denoted as  or similar forms. The
or similar forms. The  th source symbol of a session
th source symbol of a session  is denoted by
is denoted by  . The source and destination of session
. The source and destination of session  are denoted by
are denoted by  and
and  , respectively.
, respectively.
3. Results
We provide lower bounds on  and
and  .
.
Theorem 1.
The ratio of the minimum energy consumption of routing solutions and the minimum energy consumption of network coding solutions, maximized over all node locations, multiple unicast sessions, and transmission ranges, with the transmission range equal for the routing and network coding solutions, is at least  , that is,
, that is,

The result states that  is at least
is at least  ,
,  , and
, and  for
for  -,
-,  - and
- and  -dimensional networks, respectively. The result that
-dimensional networks, respectively. The result that  is at least
is at least  in one-dimensional networks also follows from the results in [20]. The lower bound
in one-dimensional networks also follows from the results in [20]. The lower bound  for
for  -dimensional networks exceeds the previously known bound of
-dimensional networks exceeds the previously known bound of  [21]. This new lower bound is of particular interest, since it exceeds the upper bound of
[21]. This new lower bound is of particular interest, since it exceeds the upper bound of  for decode-and-recombine type network codes [26]. Indeed, the code that we construct does not follow a decode-and-recombine strategy. This shows that energy can be saved by considering strategies other than decode-and-recombine. No lower bounds for three-dimensional networks have been previously established.
for decode-and-recombine type network codes [26]. Indeed, the code that we construct does not follow a decode-and-recombine strategy. This shows that energy can be saved by considering strategies other than decode-and-recombine. No lower bounds for three-dimensional networks have been previously established.
Before proving Theorem 1 in Section 5, we provide some intuition. The configuration used to proof Theorem 1 has nodes placed at a  -dimensional rectangular lattice, connectivity
-dimensional rectangular lattice, connectivity  and is parameterized by an integer
and is parameterized by an integer  controlling the size of the network. The network is given in Figure 1 for
controlling the size of the network. The network is given in Figure 1 for  and
and  . For
. For  , the result of Theorem 1 is obtained as follows. First consider the case of routing. Note, that the minimum-energy solution is to route all packets along the shortest path between source and destination. Therefore, all nodes in the interior of the network will need to transmit four times. Now, for the case of network coding, we will show in Section 5 that it is possible to construct a network code in which each node in the interior of the network is transmitting only once in each time slot. Therefore, by considering large
, the result of Theorem 1 is obtained as follows. First consider the case of routing. Note, that the minimum-energy solution is to route all packets along the shortest path between source and destination. Therefore, all nodes in the interior of the network will need to transmit four times. Now, for the case of network coding, we will show in Section 5 that it is possible to construct a network code in which each node in the interior of the network is transmitting only once in each time slot. Therefore, by considering large  and neglecting the energy consumption at the borders of the network, the obtained energy benefit is
and neglecting the energy consumption at the borders of the network, the obtained energy benefit is  .
.
In Section 5 we will consider the general case of arbitrary  . Again, the network coding solution will be such that each of the
. Again, the network coding solution will be such that each of the  nodes in the interior of the network is transmitting only once in each time slot. In analyzing the routing solution, some care needs to the taken. Since
nodes in the interior of the network is transmitting only once in each time slot. In analyzing the routing solution, some care needs to the taken. Since  , the number of hops that need to be taken on the shortest path between source and destination equals
, the number of hops that need to be taken on the shortest path between source and destination equals  . By noting that the number of sessions is roughly equal to the number of nodes at the border of the network, that is,
. By noting that the number of sessions is roughly equal to the number of nodes at the border of the network, that is,  , and ignoring all transmission from nodes at the border of the network, we establish
, and ignoring all transmission from nodes at the border of the network, we establish

Details of the configuration and a proof of Theorem 1 are given in Section 5.
The configuration and network code construction used for Theorem 1 are not useful for obtaining bounds on  . Since
. Since  , the cost per transmission in the network coding scheme is
, the cost per transmission in the network coding scheme is  . One can verify, however, that the optimal transmission range under routing is
. One can verify, however, that the optimal transmission range under routing is  . This requires
. This requires  hops per session, with the cost per transmission being equal to
hops per session, with the cost per transmission being equal to  . Using the network code described above and the optimal routing solution at
. Using the network code described above and the optimal routing solution at  gives
gives

which is at most  , since
, since  . Note that it was already shown in [20] that
. Note that it was already shown in [20] that  and in [21] that
and in [21] that  .
.
By considering a different configuration, we show that  .
.
Theorem 2.
For  -dimensional wireless networks, the ratio of the minimum energy consumption of routing solutions and the minimum energy consumption of network coding solutions, maximized over all node locations and multiple unicast sessions, with the transmission range optimized individually for the routing and network coding solutions, is at least
-dimensional wireless networks, the ratio of the minimum energy consumption of routing solutions and the minimum energy consumption of network coding solutions, maximized over all node locations and multiple unicast sessions, with the transmission range optimized individually for the routing and network coding solutions, is at least  , that is,
, that is, 
Here we provide an intuitive explanation of this result; details of the configuration and a proof of Theorem 2 are provided in Section 4. The result is established using a multiple unicast configuration on a subset of the  -dimensional hexagonal lattice as depicted in Figure 2. The minimum cost routing solution on this network follows shortest paths for all sessions and will require all nodes in the interior of the network to transmit three times in order to deliver one symbol for each session. In Section 4, we construct a network code in which each node in the interior is only transmitting once per delivered symbol. By making the size of the network large, the influence of the borders becomes negligible. Hence, the energy benefit is
-dimensional hexagonal lattice as depicted in Figure 2. The minimum cost routing solution on this network follows shortest paths for all sessions and will require all nodes in the interior of the network to transmit three times in order to deliver one symbol for each session. In Section 4, we construct a network code in which each node in the interior is only transmitting once per delivered symbol. By making the size of the network large, the influence of the borders becomes negligible. Hence, the energy benefit is  .
.
Besides providing new lower bounds on the energy benefit of network, the network codes that are constructed in this paper are of interest by themselves. They might lead to insight in how to operate in networks with another structure. Finally, even though the case  is not of any practical relevance, the bounds as well as the code constructions might lead to a better insight for lower-dimensional networks.
is not of any practical relevance, the bounds as well as the code constructions might lead to a better insight for lower-dimensional networks.
4. An Efficient Code on the Hexagonal Lattice
In this section, we present a multiple unicast configuration in which the nodes form a subset of the hexagonal lattice. It will be shown that the energy benefit on this configuration is  , proving Theorem 2. Since the code construction used here is less involved then the construction used to prove Theorem 1, we start with the proof of Theorem 2. This section is organized as follows. In Section 4.1 we present the configuration in more detail after which we give the construction of the network code in Section 4.2. Section 4.3 is used to prove that the code is valid. Finally, in Section 4.4 we analyze the energy consumption of the network code and prove Theorem 2.
, proving Theorem 2. Since the code construction used here is less involved then the construction used to prove Theorem 1, we start with the proof of Theorem 2. This section is organized as follows. In Section 4.1 we present the configuration in more detail after which we give the construction of the network code in Section 4.2. Section 4.3 is used to prove that the code is valid. Finally, in Section 4.4 we analyze the energy consumption of the network code and prove Theorem 2.
4.1. Configuration
The size of the configuration is parameterized by a positive integer  . The nodes
. The nodes  form a subset of the hexagonal lattice. We index nodes with a tuple
form a subset of the hexagonal lattice. We index nodes with a tuple  .
.  is given by
is given by

The location of node  in
in  is given by
is given by  , where
, where

Let  denote the interior of the network, that is,
denote the interior of the network, that is,

The transmission range that we are interested in is  . This leads to connectivity between the six nearest neighbours. Hence, the neighbours of a node
. This leads to connectivity between the six nearest neighbours. Hence, the neighbours of a node  are
are

The nodes  and the connectivity are depicted in Figure 3.
and the connectivity are depicted in Figure 3.
There are  unicast sessions, denoted by
unicast sessions, denoted by  ,
,  , and
, and  ,
,  . Sources and destinations of the sessions are positioned as follows:
. Sources and destinations of the sessions are positioned as follows:

as depicted in Figure 4. Remember from Section 2, that session  has the sequence of source symbols
has the sequence of source symbols  to be transferred.
to be transferred.
The unicast sessions on the network from Figure 3.
4.2. Network Code
The network code is such that in each time slot a new source symbol from each session is transmitted. Also, one symbol of each session is decoded by its destination in each time slot. After successfully decoding a symbol, it is retransmitted by the destination in the next time slot. Nodes at the border will, therefore, transmit twice in each time slot. Nodes in the interior of the network transmit only once. The symbol that they transmit is a linear combination of one symbol from each of the sessions for which the shortest path between source and destination includes that node.
The operation of the network code is demonstrated in Figure 5 in which the transmissions of all nodes in the first four time slots are depicted. Different transmissions by the same node are separated by a comma. Note, moreover, that there is a startup phase, time slots  to
to  , in which not all destinations are able to decode a symbol. From time slot
, in which not all destinations are able to decode a symbol. From time slot  onwards, all destinations decode one symbol in every time slot. In analyzing the energy consumption of the coding scheme, we will ignore the startup phase.
onwards, all destinations decode one symbol in every time slot. In analyzing the energy consumption of the coding scheme, we will ignore the startup phase.
Example operation of the network code of Section 4, with  . The transmissions of all nodes in the time slots
. The transmissions of all nodes in the time slots  are depicted. Different transmissions by the same node are separated by a comma. Note, that the symbol transmitted at
are depicted. Different transmissions by the same node are separated by a comma. Note, that the symbol transmitted at  by the node with dotted border can be obtained by summing all transmissions from nodes with a dashed border in earlier time slots. All nodes in the interior of the network perform this simple coding operation.
by the node with dotted border can be obtained by summing all transmissions from nodes with a dashed border in earlier time slots. All nodes in the interior of the network perform this simple coding operation.



The symbol transmitted at  by the node with the dotted border can be obtained by summing all transmissions from nodes with a dashed border in earlier time slots. Indeed
by the node with the dotted border can be obtained by summing all transmissions from nodes with a dashed border in earlier time slots. Indeed

This coding operation (i.e., in time slot  , a node transmits the sum of what was transmitted by its top-left neighbour in time slot
, a node transmits the sum of what was transmitted by its top-left neighbour in time slot  , by its top right-neighbour in time slot
, by its top right-neighbour in time slot  , and so forth, as visualized in Figure 5) is performed by all nodes that are in the interior of the network. The idea behind the coding operation is to cancel, by means of the XOR operation, all symbols that should not be retransmitted. In (12), for instance, we have
, and so forth, as visualized in Figure 5) is performed by all nodes that are in the interior of the network. The idea behind the coding operation is to cancel, by means of the XOR operation, all symbols that should not be retransmitted. In (12), for instance, we have  . The exact operation of the network code is made more precise in the remainder of this subsection. The coding operation for interior nodes is given in exact form in (17).
. The exact operation of the network code is made more precise in the remainder of this subsection. The coding operation for interior nodes is given in exact form in (17).
Nodes at the border of the network operate as follows. Let  . In time slot
. In time slot  node
node  transmits two symbols
transmits two symbols  and
and  , where
, where
 Left border:
Left border:

Since  is the source of session
is the source of session  it has source symbol
it has source symbol  , available. Also,
, available. Also,  is the destination for session
is the destination for session  . It remains to be shown that symbol
. It remains to be shown that symbol  can be decoded by
can be decoded by  using the information obtained from its neighbours up to time slot
using the information obtained from its neighbours up to time slot  . For notational convenience, let
. For notational convenience, let
 Left border:
Left border:

In a similar fashion, we have the following transmissions at the right and bottom borders of the network.
 Right border:
Right border:

 Bottom border:
Bottom border:

where  ,
,  , and
, and  . Moreover,
. Moreover,  and
and  are not symbols that are transmitted, but only notational shortcuts.
are not symbols that are transmitted, but only notational shortcuts.
Nodes in the interior of the network transmit once in each time slot. Let  . The coding operation it performs is given by
. The coding operation it performs is given by


4.3. Validity of the Network Code
We need to show that destinations can decode in time in order to retransmit the required symbols according to (13), (15), and (16). In order to do so we first analyze how data propagates through the network. If we look at the nodes in the network that transmit linear combinations that contain a certain source symbol, we see that symbols propagate exactly along the shortest paths between source and destination. This is made more precise in the following two lemmas.
Lemma 1.
Let  . Assume that the only nonzero source symbol transmitted in the network is
. Assume that the only nonzero source symbol transmitted in the network is  by node
by node  in time slot
in time slot  . Then, for all
. Then, for all  and
and 

Proof.
We use induction over time. The base case is time slot  , for which it is readily verified that the statement is true. Now, for the induction step, suppose that the lemma holds for all
, for which it is readily verified that the statement is true. Now, for the induction step, suppose that the lemma holds for all  smaller than
smaller than  . This implies that for all
. This implies that for all  and
and  ,
,

Hence,

which by the induction hypothesis is equal to  if
if  and
and  and zero otherwise.
and zero otherwise.
Lemma 2.
Let  .
.

Proof.
From Lemma 1, the time-invariance of the system, and the symmetry of the coding operation (17) of the internal nodes.
We are now ready to prove that the destinations can correctly decode source symbols. We present the decoding procedure for nodes on the right border of the network. The decoding procedures at the other borders can be obtained by exploiting the symmetry of the system.
Lemma 3.
Consider  , with
, with  ,
,  , that is, the destination of session
, that is, the destination of session  . It can decode symbol
. It can decode symbol  at the end of time slot
at the end of time slot  as
as

Proof.
From Lemma 2, (15), it follows that (22) equals

4.4. Energy Consumption
The energy consumption of the network coding scheme presented above is given in the following lemma.
Lemma 4.
 .
.
Proof.
From (13)–(17), we have that each of the  nodes at the border that are source or destination are transmitting twice in each time slot. Each of the
nodes at the border that are source or destination are transmitting twice in each time slot. Each of the  internal nodes is transmitting once in each time slot. Since
internal nodes is transmitting once in each time slot. Since  , the energy consumption per transmission is
, the energy consumption per transmission is  . This gives
. This gives

Next, we give the minimum energy required by a routing solution.
Lemma 5.
 .
.
Proof.
Since we consider routing, we need to take the shortest path for each session. Since the energy consumption per hop equals  , the energy consumption under routing is minimized for
, the energy consumption under routing is minimized for  . Now, we see that the number of transmissions required to deliver a symbol for the sessions
. Now, we see that the number of transmissions required to deliver a symbol for the sessions  equals
equals  . Adding the transmissions for sessions of type
. Adding the transmissions for sessions of type  and
and  gives
gives

Using the above two lemmas, we are able to prove Theorem 2.
Proof of Theorem 2.
Remember that  is defined as the maximum of
is defined as the maximum of  over
over  and
and  . Hence,
. Hence,  for any specific
for any specific  and
and  will provide a lower bound to
will provide a lower bound to  . In addition, any upper bound to
. In addition, any upper bound to  will result in a lower bound to
will result in a lower bound to  . Hence, from Lemmas 4 and 5, we have
. Hence, from Lemmas 4 and 5, we have

5. An Efficient Code on the 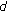 -Dimensional Rectangular Lattice
-Dimensional Rectangular Lattice
In this section, we present a multiple unicast configuration in which the nodes are placed at integer coordinates in a  -dimensional space, that is, at the rectangular lattice.
-dimensional space, that is, at the rectangular lattice.
5.1. Configuration
The size of the configuration is parameterized by a positive integer  . We have
. We have

The interior of the network is given by

We will make use of

which corresponds to those nodes that are part of exactly one face of the network.
The transmission range that will be used is  . This transmission range induces a neighbourhood consisting of all neighbours within distance
. This transmission range induces a neighbourhood consisting of all neighbours within distance  . The coding operation of our network code is based on only part of the neighbourhood, that is, it uses
. The coding operation of our network code is based on only part of the neighbourhood, that is, it uses

Note, that for  ,
,  corresponds to the complete neighbourhood of
corresponds to the complete neighbourhood of  . We will be using
. We will be using  , that is,
, that is,  denotes the Manhattan distance from
denotes the Manhattan distance from  to
to  . The network and its connectivity are depicted for
. The network and its connectivity are depicted for  in Figure 6.
in Figure 6.
A source is located at each  . Therefore, there are
. Therefore, there are  sessions. If
sessions. If  , we denote the session corresponding to this source by
, we denote the session corresponding to this source by  . Recall from Section 2 that
. Recall from Section 2 that  denotes the
denotes the  dimensional vector obtained by removing the
dimensional vector obtained by removing the  th element from
th element from  . If
. If  , we denote the session by
, we denote the session by  . The destination of each session is located at the other side of the network, that is, we have
. The destination of each session is located at the other side of the network, that is, we have  and
and  . The positions of sources and destinations are depicted for
. The positions of sources and destinations are depicted for  in Figure 7. It can be seen that
in Figure 7. It can be seen that  and
and  form oppositely directed sessions.
form oppositely directed sessions.
The unicast sessions on the network from Figure 6.
5.2. Network Code
We introduce sets  ,
,  , which are defined recursively as follows:
, which are defined recursively as follows:

where  denotes symmetric difference and
denotes symmetric difference and  . Note that irrespective of
. Note that irrespective of  we have
we have  . As an example for
. As an example for  we have
we have  ,
,  and
and  .
.
The scheme is very similar in flavour to the scheme presented in Section 4; its operation is demonstrated in Figure 8 in which, for  and
and  , the transmissions of all nodes in the first four time slots are depicted. The operation of the scheme is such that in time slot
, the transmissions of all nodes in the first four time slots are depicted. The operation of the scheme is such that in time slot  sources transmit the
sources transmit the  th source symbol and destinations decode the
th source symbol and destinations decode the  th source symbol. Besides transmitting a new source symbol in each time slot, sources/destinations will also retransmit the symbol that has been decoded in that time slot, that is, they transmit two different symbols in each time slot. In the figure, different transmissions by the same node are separated by a comma. Nodes in the interior of the network transmit only once. The symbol that they transmit is a linear combination of one symbol from each of the sessions for which the shortest path between source and destination includes that node. The symbol transmitted at
th source symbol. Besides transmitting a new source symbol in each time slot, sources/destinations will also retransmit the symbol that has been decoded in that time slot, that is, they transmit two different symbols in each time slot. In the figure, different transmissions by the same node are separated by a comma. Nodes in the interior of the network transmit only once. The symbol that they transmit is a linear combination of one symbol from each of the sessions for which the shortest path between source and destination includes that node. The symbol transmitted at  by the node with the dotted border can be obtained by summing all transmissions from nodes with a dashed border in earlier time slots. This coding operation is performed by all nodes that are in the interior of the network. The exact operation of the network code is made more precise in the remainder of this subsection. The coding operation for interior nodes is given in exact form in (34).
by the node with the dotted border can be obtained by summing all transmissions from nodes with a dashed border in earlier time slots. This coding operation is performed by all nodes that are in the interior of the network. The exact operation of the network code is made more precise in the remainder of this subsection. The coding operation for interior nodes is given in exact form in (34).
Example operation of the network code of Section 5, with  . The transmissions of all nodes in the time slots
. The transmissions of all nodes in the time slots  are depicted. Different transmissions by the same node are separated by a comma. Note, that the symbol transmitted at
are depicted. Different transmissions by the same node are separated by a comma. Note, that the symbol transmitted at  by the node with dotted border can be obtained by summing all transmissions from nodes with a dashed border in earlier time slots. All nodes in the interior of the network perform this simple coding operation.
by the node with dotted border can be obtained by summing all transmissions from nodes with a dashed border in earlier time slots. All nodes in the interior of the network perform this simple coding operation.



Let node  . Remember that
. Remember that  implies that there exists a unique
implies that there exists a unique  such that
such that  . Node
. Node  transmits
transmits

For notational convenience, let

The coding operation performed by an internal node is as follows:

5.3. Validity of the Network Code
The following result follows directly from the definition of the sets  , but is stated here as a lemma because of its importance in the remainder of the paper.
, but is stated here as a lemma because of its importance in the remainder of the paper.
Lemma 6.
Let  be a sequence of symbols from
be a sequence of symbols from  and let
and let  . We have
. We have

Lemma 7.
Consider node  . Assume that the only nonzero source symbol transmitted in the network is
. Assume that the only nonzero source symbol transmitted in the network is  by node
by node  in time slot
in time slot  . Then
. Then

for all  and
and  .
.
Proof.
We use induction over  . At time
. At time  the lemma holds, giving us our base case. Now suppose that the lemma holds for all time slots smaller than
the lemma holds, giving us our base case. Now suppose that the lemma holds for all time slots smaller than  . If
. If  , the lemma follows directly from (32)–(33). In the remainder we consider
, the lemma follows directly from (32)–(33). In the remainder we consider  . From the induction hypothesis, it follows that for any
. From the induction hypothesis, it follows that for any 

If  , it follows from (32) and the induction hypothesis that
, it follows from (32) and the induction hypothesis that

Now, at  the coding operation performed by
the coding operation performed by  can be decomposed as
can be decomposed as

where

In the remainder, we show that

which proves the lemma, since by the induction hypothesis  if
if  and zero otherwise.
and zero otherwise.
For  we, have
we, have

where the second equality follows from Lemma 6, the third equality follows from (37)-(38), and the last equality holds because we work over  .
.
For  , we have
, we have

Lemma 8.
Let 

Proof.
By linearity, time-invariance and symmetry of (34) together with Lemma 7.
We are now ready to prove that the destinations can correctly decode source symbols. We present the decoding procedure for nodes on the right border of the network, that is, for nodes of type  . The decoding procedures at the other borders can be obtained by exploiting the symmetry of the system.
. The decoding procedures at the other borders can be obtained by exploiting the symmetry of the system.
Lemma 9.
Consider node  . At the end of time slot
. At the end of time slot  , it can decode symbol
, it can decode symbol  as
as

Proof.
First note that all terms in (45) correspond to symbols that have been received by  before or in time slot
before or in time slot  .
.
Now, from Lemma 8, we have

where  holds, because for
holds, because for  , Lemma 6 gives
, Lemma 6 gives

and

From (32) it follows that

and

The proof of the lemma follows by adding the final expressions from (46), (49) and (50) observing that the outcome is  .
.
5.4. Energy Consumption
The energy consumption of the network coding scheme presented above provides an upper bound to  .
.
Lemma 10.
 .
.
Proof.
All transmissions are over distance  and cost
and cost  . The nodes in
. The nodes in  are transmitting twice. On each of the
are transmitting twice. On each of the  sides of the network, there are
sides of the network, there are  nodes from
nodes from  ; hence
; hence  . This gives
. This gives  transmissions. In addition, there are
transmissions. In addition, there are  nodes in the interior, that are all transmitting once.
nodes in the interior, that are all transmitting once.
Next, we give the minimum energy required by a routing solution.
Lemma 11.
 .
.
Proof.
Since the transmission range is equal to  , a routing solution requires
, a routing solution requires  transmissions per session. Moreover, there are
transmissions per session. Moreover, there are  sessions.
sessions.
Using the above two lemmas, we are able to prove Theorem 1.
Proof of Theorem 1.
Lemmas 10 and 11 give

6. Discussion
We have given several constructions of energy-efficient network codes. These constructions serve to show that compared to plain routing, network coding has the potential of reducing energy consumption in wireless networks. Since we have provided only codes that are based on a centralized design, it remains to be shown in future work if and how this potential can be exploited using practical codes. Moreover, it would also be of interest to consider the energy-benefit in topologies in which the nodes are not positioned at a lattice, for instance, random networks.
In this work we have provided lower bounds on the energy benefit of network coding for wireless multiple unicast. Another open problem is to find upper bounds on the benefit.
References
Chen S, Nahrstedt K: An overview of quality of service routing for next-generation high-speed networks: problems and solutions. IEEE Network 1998, 12(6):64-79. 10.1109/65.752646
Tassiulas L, Chang J: Energy conserving routing in wireless ad hoc networks. Proceedings of the 5th Annual ACM/IEEE International Conference on Mobile Computing and Network (MobiCom '98), August 1998, Dallas, Tex, USA
Rodoplu V, Meng TH: Minimum energy mobile wireless networks. IEEE Journal on Selected Areas in Communications 1999, 17(8):1333-1344. 10.1109/49.779917
Ramanathan R, Rosales-Hain R: Topology control of multihop wireless networks using transmit power adjustment. Proceedings of the IEEE 19th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '00), March 2000 404-413.
Jones CE, Sivalingam KM, Agrawal P, Chen JC: A survey of energy efficient network protocols for wireless networks. Wireless Networks 2001, 7(4):343-358. 10.1023/A:1016627727877
Saraydar CU, Mandayam NB, Goodman DJ: Efficient power control via pricing in wireless data networks. IEEE Transactions on Communications 2002, 50(2):291-303. 10.1109/26.983324
Goldsmith AJ, Wicker SB: Design challenges for energy-constrained ad hoc wireless networks. IEEE Wireless Communications 2002, 9(4):8-27. 10.1109/MWC.2002.1028874
Ahlswede R, Cai N, Li S-YR, Yeung RW: Network information flow. IEEE Transactions on Information Theory 2000, 46(4):1204-1216. 10.1109/18.850663
Li S-YR, Yeung RW, Cai N: Linear network coding. IEEE Transactions on Information Theory 2003, 49(2):371-381.
Koetter R, Médard M: An algebraic approach to network coding. IEEE/ACM Transactions on Networking 2003, 11(5):782-795. 10.1109/TNET.2003.818197
Ho T, Médard M, Koetter R, Karger DR, Effros M, Shi J, Leong B: A random linear network coding approach to multicast. IEEE Transactions on Information Theory 2006, 52(10):4413-4430.
Yeung RW, Cai N: Network coding theory. Foundations and Trends in Communications and Information Theory 2006, 2(4):241-381.
Fragouli C, Soljanin E: Network coding fundamentals. Foundations and Trends in Networking 2007, 2(1):1-133. 10.1561/1700000004
Fragouli C, Soljanin E: Network coding applications. Foundations and Trends in Networking 2007, 2(2):135-269. 10.1561/1300000013
Lun DS, Ratnakar N, Médard M, Koetter R, Karger DR, Ho T, Ahmed E, Zhao F: Minimum-cost multicast over coded packet networks. IEEE Transactions on Information Theory 2006, 52(6):2608-2623.
Winter P: Steiner problem in networks: a survey. Networks 1987, 17(2):129-167. 10.1002/net.3230170203
Goel A, Khanna S: On the network coding advantage for wireless multicast in Euclidean space. Proceedings of the International Conference on Information Processing in Sensor Networks (IPSN '08), April 2008 64-69.
Fragouli C, Widmer J, Le Boudec J-Y: Efficient broadcasting using network coding. IEEE/ACM Transactions on Networking 2008, 16(2):450-463.
Widmer J, Le Boudec J-Y: Network coding for efficient communication in extreme networks. In Applications, Technologies, Architectures, and Protocols for Computer Communication. ACM Press, New York, NY, USA; 2005:284-291.
Wu Y, Chou PA, Kung S-Y: Information exchange in wireless networks with network coding and physical-layer broadcast. Proceedings of the 39th Annual Conference on Information Sciences and Systems (CISS '05), 2005
Effros M, Ho T, Kim S: A tiling approach to network code design for wireless networks. In Proceedings of the IEEE Information Theory Workshop (ITW '06), March 2006, punta del Este, Uruguay. IEEE; 62-66.
Kim S, Effros M, Ho T: On low-power multiple unicast network coding over a wireless triangular grid. Proceedings of the 45th Annual Allerton Conference on Communication, Control and Computing, 2007
Kramer G, Savari SA: Edge-cut bounds on network coding rates. Journal of Network and Systems Management 2006, 14(1):49-66. 10.1007/s10922-005-9019-0
Keshavarz-Haddad A, Riedi R: Bounds on the benefit of network coding: throughput and energy saving in wireless networks. Proceedings of the 27th IEEE Communications Society Conference on Computer Communications (INFOCOM '08), April 2008 376-384.
Katti S, Rahul H, Hu W, Katabi D, Médard M, Crowcroft J: XORs in the air: practical wireless network coding. Proceedings of the Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications (ACM SIGCOMM '06) 243-254.
Liu J, Goeckelt D, Towsley D: Bounds on the gain of network coding and broadcasting in wireless networks. Proceedings of the 26th IEEE International Conference on Computer Communications (INFOCOM '07), May 2007 6-12.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Goseling, J., Matsumoto, R., Uyematsu, T. et al. Lower Bounds on the Maximum Energy Benefit of Network Coding for Wireless Multiple Unicast. J Wireless Com Network 2010, 605421 (2010). https://doi.org/10.1155/2010/605421
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/605421

 , with
, with  depicted here, is achievable. Nodes are located at integer coordinates in a
depicted here, is achievable. Nodes are located at integer coordinates in a  -dimensional space, with connectivity given by
-dimensional space, with connectivity given by  , as depicted in (a). Unicast sessions are placed according to (b).
, as depicted in (a). Unicast sessions are placed according to (b).
 is achievable. Nodes are a subset of the hexagonal lattice, with connectivity as depicted in (a). Unicast sessions are placed according to (b).
is achievable. Nodes are a subset of the hexagonal lattice, with connectivity as depicted in (a). Unicast sessions are placed according to (b).
 . The size of the network is controlled by
. The size of the network is controlled by  , with
, with  in this figure.
in this figure.

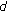 -Dimensional Rectangular Lattice
-Dimensional Rectangular Lattice
 -dimensional rectangular lattice,
-dimensional rectangular lattice,  depicted in the figure, with the connectivity induced by a transmission range
depicted in the figure, with the connectivity induced by a transmission range  . The size of the network is controlled by
. The size of the network is controlled by  , with
, with  in this figure.
in this figure.
