- Research Article
- Open access
- Published:
Fully Decentralized and Collaborative Multilateration Primitives for Uniquely Localizing WSNs
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 605658 (2009)
Abstract
We provide primitives for uniquely localizing WSN nodes. The goal is to maximize the number of uniquely localized nodes assuming a fully decentralized model of computation. Each node constructs a cluster of its own and applies unique localization primitives on it. These primitives are based on constructing a special order for multilaterating the nodes within the cluster. The proposed primitives are fully collaborative and thus the number of iterations required to compute the localization is fewer than that of the conventional iterative multilateration approaches. This further limits the messaging requirements. With relatively small clusters and iteration counts, we can localize almost all the uniquely localizable nodes.
1. Introduction
Many applications and systems from areas such as environment and habitat monitoring, weather forecast, and health applications require use of many sensor nodes organized as a network collectively gathering useful data; see [1] for a survey. In such applications it is usually necessary to know the actual locations of the sensors. Sensor network localization is the problem of assigning geographic coordinates to each sensor node in a given network. Although Global Positioning System (GPS) can determine the geographic coordinates of an object, a GPS device has to have at least four lines of sight communication lines between different satellites in order to locate itself. Thus, in cluttered space or indoor environments GPS may be ineffective. Additional disadvantages including the power consumption, cost, and size limitations allow only a small portion of nodes in a large scale sensor network having GPS capabilities. It is important to design methods that achieve localization with limited use of such systems. A common paradigm introduced to overcome this difficulty is the iterative multilateration where only a small portion of the nodes are assumed to be anchor nodes with a priori location information. Every node uses its ranging sensors to measure distances to the neighbors and shares the measurement and location information if available. Multilateration techniques are then employed in an iterative manner to collectively estimate node locations from such information [2]. Assuming no measurement errors, "unique'' localization of a sensor node is achieved via trilateration from three anchor positions if distance to those anchors is known. Although this is a sufficient condition for uniqueness, it is rarely necessary in wireless sensor networks settings. A finite number of possible locations for a set of neighbor nodes for which range information is available may also provide unique location for a sensor node. In this paper we propose primitives for unique localization of nodes in a sensor network. Assuming measurements with no noise, the goal is to maximize the number of uniquely localized nodes employing iterative multilateration. The proposed primitives are fully decentralized, fully collaborative. The suggested collaboration model gives rise to a high rate of unique localization. Moreover, this is achieved with reasonably low energy requirements for message exchanges as the average number of iterations per node is low.
2. Related Work
We can classify the previous work based on where the computation takes place and the type of localization solution produced. Centralized methods assume the availability of global information about the network at a central computer where the computation takes place [3–5]. Whereas in decentralized methods each node usually processes some local information gathered via a limited number of message exchanges [6, 7]. A second distinction between different methods is the localization output produced. In unique localization a single position is assigned to each node in the network [8]. Even though the topology of the underlying graph may not give rise to a unique localization, it may still be possible to assign a finite set of positions for each node, called finite localization [4]. There has been recent interest and theoretical results on uniquely localizing networks. However, the suggested methods usually rely on centralized models [4]. To overcome this difficulty, cluster-based approaches or collaborative multilateration have been suggested. Moore et al. propose the idea of localizing clusters where each cluster is constructed using two-hop ranging information [7]. Only trilateration is employed as the localization primitive which results in fewer nodes being uniquely localized as compared to the primitives we propose. Savvides et al. propose  -hop collaborative multilateration. The nodes organize into collaborative subtrees, then using simple geometric relationships each node constructs a position estimate and finally the estimate is refined using a least-squares method. The collaboration is on sharing distance and position information within
-hop collaborative multilateration. The nodes organize into collaborative subtrees, then using simple geometric relationships each node constructs a position estimate and finally the estimate is refined using a least-squares method. The collaboration is on sharing distance and position information within  -hops but each node is still responsible for locating itself. With our model of full collaboration, not only does a node receive information to compute its position but it may also receive information regarding its own location from neighboring nodes as well.
-hops but each node is still responsible for locating itself. With our model of full collaboration, not only does a node receive information to compute its position but it may also receive information regarding its own location from neighboring nodes as well.
3. Unique Localization Primitives
Our unique network localization method relies on two low level primitives: Reliable internode distance measurement and internode communication mechanisms. Several techniques such as TDoA, RSSI, ToA may be used to obtain distance between two sensor nodes [9, 10]. The gathered distance information is assumed to be error-free. We also assume that the communication between sensor nodes is through broadcasting and that the broadcasted data is received by all neighboring nodes within the sensing range of the broadcaster.
The main unit of localization is a cluster. Each node  in the sensor network
in the sensor network  goes through an initial setup phase constructing
goes through an initial setup phase constructing  , the
, the  -radius cluster centered at
-radius cluster centered at  . Let
. Let  denote the immediate neighborhood of node
denote the immediate neighborhood of node  . We assume that
. We assume that  has already gathered
has already gathered  , distance to
, distance to  . With this information every
. With this information every  creates its own cluster
creates its own cluster  , where
, where  is at the center; there is an edge
is at the center; there is an edge  with weight
with weight  for every
for every  . At the second round of information exchange, every node shares its cluster with all the nodes in its neighborhood. As a result each node
. At the second round of information exchange, every node shares its cluster with all the nodes in its neighborhood. As a result each node  can construct
can construct  , and so on. After the final iteration of broadcasting/gathering of packets, the cluster
, and so on. After the final iteration of broadcasting/gathering of packets, the cluster  is constructed with the collected data. With this construction,
is constructed with the collected data. With this construction,  is a star graph centered around
is a star graph centered around  , and
, and  is a wheel graph centered at
is a wheel graph centered at  , together with the edges connecting to the wheel. We note that with this model a pair of clusters may share many nodes. Although this may seem like a waste, we show that these overlaps give rise to efficient collaboration in terms of unique localization. The collaboration is modelled via the iterative localization. At each iteration, each node constructs a new set of uniquely localized nodes in its cluster
, together with the edges connecting to the wheel. We note that with this model a pair of clusters may share many nodes. Although this may seem like a waste, we show that these overlaps give rise to efficient collaboration in terms of unique localization. The collaboration is modelled via the iterative localization. At each iteration, each node constructs a new set of uniquely localized nodes in its cluster  using our proposed primitives, broadcasts this set to the neighbors, gathers analogous information, and iterates the same process.
using our proposed primitives, broadcasts this set to the neighbors, gathers analogous information, and iterates the same process.
3.1. Bilaterations and Unique Localization
The network localization problem can be converted into that of graph realization problem. Let  be the graph corresponding to a physical sensor network
be the graph corresponding to a physical sensor network  . Each vertex
. Each vertex  corresponds to a specific physical sensor node
corresponds to a specific physical sensor node  in
in  . Vertices
. Vertices  are the nodes with known positions, called anchors. There exists an edge
are the nodes with known positions, called anchors. There exists an edge  if nodes
if nodes  and
and  are within sensing range or both
are within sensing range or both  . Each edge
. Each edge  , where
, where  and
and  is associated with a real number which represents the Euclidean distance between the two nodes
is associated with a real number which represents the Euclidean distance between the two nodes  ,
,  . Formally, the graph realization problem is assigning coordinates to the vertices so that the Euclidean distance between any two adjacent vertices is equal to the real number associated with that edge [11, 12]. The graph realization problem has intrinsic connections with the graph rigidity theory. If we think of a graph in terms of bars and joints, a rigid graph means "not deformable'' or "not flexible'' [12]. Formally, the rigidity of a graph can be characterized by Laman's condition: A graph with
. Formally, the graph realization problem is assigning coordinates to the vertices so that the Euclidean distance between any two adjacent vertices is equal to the real number associated with that edge [11, 12]. The graph realization problem has intrinsic connections with the graph rigidity theory. If we think of a graph in terms of bars and joints, a rigid graph means "not deformable'' or "not flexible'' [12]. Formally, the rigidity of a graph can be characterized by Laman's condition: A graph with  vertices and
vertices and  edges is rigid if no subgraph with
edges is rigid if no subgraph with  vertices contains more than
vertices contains more than  edges [13]. Obviously if the graph is not rigid, infinite number of realizations are possible through continuous deformations. However, even when the graph is rigid there may be ambiguities that give rise to more than one possible realization. In order to formalize these ambiguities, the term globally rigid is introduced [14]. A graph is globally rigid if and only if it is 3-connected and redundantly rigid. Global rigidity is a necessary and sufficient condition for unique realizations. We note that the discussions of rigidity and global rigidity apply to "generic'' frameworks, that is, those with algebraically independent vertex coordinates over the rationals [8, 14]. As almost all point sets are generic and the generic global rigidity can be described solely in terms of combinatorial properties of the graph itself, in what follows the term globally rigid assumes the genericity of the frameworks.
edges [13]. Obviously if the graph is not rigid, infinite number of realizations are possible through continuous deformations. However, even when the graph is rigid there may be ambiguities that give rise to more than one possible realization. In order to formalize these ambiguities, the term globally rigid is introduced [14]. A graph is globally rigid if and only if it is 3-connected and redundantly rigid. Global rigidity is a necessary and sufficient condition for unique realizations. We note that the discussions of rigidity and global rigidity apply to "generic'' frameworks, that is, those with algebraically independent vertex coordinates over the rationals [8, 14]. As almost all point sets are generic and the generic global rigidity can be described solely in terms of combinatorial properties of the graph itself, in what follows the term globally rigid assumes the genericity of the frameworks.
It is NP-Hard to find a realization of  even if
even if  is globally rigid [15, 16]. However, there exists an exceptional graph class called trilateration graphs that is uniquely localizable in polynomial time. A graph is a trilateration graph if it has a trilateration ordering
is globally rigid [15, 16]. However, there exists an exceptional graph class called trilateration graphs that is uniquely localizable in polynomial time. A graph is a trilateration graph if it has a trilateration ordering  , where
, where  ,
,  ,
,  form a
form a  and each
and each  has at least three neighbors that come before
has at least three neighbors that come before  in
in  . Although easily localizable, trilateration is a strong requirement for unique localization.
. Although easily localizable, trilateration is a strong requirement for unique localization.  , for instance, contains a wheel graph centered at
, for instance, contains a wheel graph centered at  . A wheel graph is uniquely localizable although it is not a trilateration graph. If the graph is not 3-connected, there exists a pair of vertices whose removal disconnects the graph. The graph can be flipped through the line passing through the disconnecting pair. Although flipping introduces nonunique realizations, the fact that finite possibilities arise as a result is the main motivation behind bilateration graphs. A graph is a bilateration graph if it has a bilateration ordering
. A wheel graph is uniquely localizable although it is not a trilateration graph. If the graph is not 3-connected, there exists a pair of vertices whose removal disconnects the graph. The graph can be flipped through the line passing through the disconnecting pair. Although flipping introduces nonunique realizations, the fact that finite possibilities arise as a result is the main motivation behind bilateration graphs. A graph is a bilateration graph if it has a bilateration ordering  , where
, where  ,
,  ,
,  form a
form a  and each
and each  has at least two neighbors that come before
has at least two neighbors that come before  in
in  . For the localization application, fixing the initial
. For the localization application, fixing the initial  allows one to neglect the global rotations and translations. Our main focus is on localizing bilateration graphs that arise within the defined cluster
allows one to neglect the global rotations and translations. Our main focus is on localizing bilateration graphs that arise within the defined cluster  . For
. For  the constructed model is no different than the usual trilateration primitive. We provide useful remarks regarding bilateration graphs and the clusters, more specifically for small values of
the constructed model is no different than the usual trilateration primitive. We provide useful remarks regarding bilateration graphs and the clusters, more specifically for small values of  , since for the sensor network settings those are of special interest.
, since for the sensor network settings those are of special interest.
Remark 3.1 (For  ).
).
If  is globally rigid, then it is a bilateration graph. However, even if
is globally rigid, then it is a bilateration graph. However, even if  is globally rigid, not every ordering is a bilateration ordering. For instance,
is globally rigid, not every ordering is a bilateration ordering. For instance,  in Figure 1 is globally rigid. Starting an ordering with any one of the four triangles formed between
in Figure 1 is globally rigid. Starting an ordering with any one of the four triangles formed between  ,
,  ,
,  ,
,  bilateration does not contain
bilateration does not contain  completely. However, starting an ordering with any other triangle in the cluster provides a complete bilateration of
completely. However, starting an ordering with any other triangle in the cluster provides a complete bilateration of  .
.
Remark 3.2 (For  ).
).
There exist globally rigid clusters which are not bilateration graphs.  in Figure 1 is globally rigid and therefore uniquely localizable, but it is not a bilateration graph.
in Figure 1 is globally rigid and therefore uniquely localizable, but it is not a bilateration graph.
3.2. Unique Localization within Iterative Collaboration
The goal is to finitely localize as many nodes as possible and share the resulting unique node positions with the neighbors. The main localization method is iterative. Each node  executes the localization method on its own cluster. If
executes the localization method on its own cluster. If  creates the unique positions of some new nodes within
creates the unique positions of some new nodes within  , then it shares this information with the neighbors, some of which may have overlapping clusters with
, then it shares this information with the neighbors, some of which may have overlapping clusters with  . Those neighbors may benefit this exchange if the shared nodes are part of a globally rigid component within their clusters. This procedure continues iteratively until no node creates any new unique positions and gathers any new information from the neighbors. The main localization procedure is shown in Algorithm 1 which is repeated at every iteration.
. Those neighbors may benefit this exchange if the shared nodes are part of a globally rigid component within their clusters. This procedure continues iteratively until no node creates any new unique positions and gathers any new information from the neighbors. The main localization procedure is shown in Algorithm 1 which is repeated at every iteration.
Algorithm 1: Iterated at  each time new anchors in
each time new anchors in  are received from
are received from  .
.
-
(1)
procedure UniqueLocalization(
 )
) -
(2)
Let
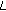 indicate the set of finitely localized nodes
indicate the set of finitely localized nodes -
(3)
for all
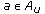 do
do -
(4)
Update(
 ,
,  )
) -
(5)
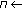 FindBilaterationOrder
FindBilaterationOrder -
(6)
for all
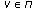 do
do -
(7)
Multilaterate(
 ,
,  ),
), -
(8)
where
 are neighbors of
are neighbors of  that are to
that are to
the left of it in 
-
(9)
Broadcast new anchors in
 to
to 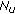
At the beginning of each iteration node,  gathers a recently discovered set of anchors,
gathers a recently discovered set of anchors,  , by listening to the broadcasts made by nodes in
, by listening to the broadcasts made by nodes in  . We note that we use anchor as a more general term in the sense that every node that is uniquely localized throughout the localization process is called an anchor. If a newly discovered anchor node
. We note that we use anchor as a more general term in the sense that every node that is uniquely localized throughout the localization process is called an anchor. If a newly discovered anchor node  is not finitely localized,
is not finitely localized,  and its position are appended to
and its position are appended to  , the set of finitely localized nodes and their positions. Otherwise all positions other than the real one are removed. Next, a bilateration order
, the set of finitely localized nodes and their positions. Otherwise all positions other than the real one are removed. Next, a bilateration order  of the nodes in
of the nodes in  is found. As stated in Remark 3.1, not every ordering covers
is found. As stated in Remark 3.1, not every ordering covers  completely. To find a bilateration order
completely. To find a bilateration order  in general, we select a seed set as the first level in the ordering. We continue a breadth-first traversal to construct new levels of nodes while making sure every node in a level has at least two neighbors in the preceding levels. As iterations of the localization procedure increase, the set of finitely localized nodes grows, therefore it constitutes a good candidate for the seed set. However, for the initial iterations we try every possible triple as a candidate for the seeds and take the maximum size set. Following the order in
in general, we select a seed set as the first level in the ordering. We continue a breadth-first traversal to construct new levels of nodes while making sure every node in a level has at least two neighbors in the preceding levels. As iterations of the localization procedure increase, the set of finitely localized nodes grows, therefore it constitutes a good candidate for the seed set. However, for the initial iterations we try every possible triple as a candidate for the seeds and take the maximum size set. Following the order in  , multilaterations are done to compute position possibilities for each node. The traversal is done in a breadth-first manner rather than a depth-first manner so as to decrease the number of position possibilities as early as possible during this process. The rest of the localization procedure where each node in
, multilaterations are done to compute position possibilities for each node. The traversal is done in a breadth-first manner rather than a depth-first manner so as to decrease the number of position possibilities as early as possible during this process. The rest of the localization procedure where each node in  is multilaterated in order is the same as the centralized localization method of [4]. Going through
is multilaterated in order is the same as the centralized localization method of [4]. Going through  , finite positions are created for each
, finite positions are created for each  using two consistent positions
using two consistent positions  ,
,  of immediate ancestors
of immediate ancestors  ,
,  . This is via bilateration, computing the intersection points of two circles centered at
. This is via bilateration, computing the intersection points of two circles centered at  ,
,  with appropriate radii. Each generated position has a localization history in the form of an ancestors list which stores the consistent positions of
with appropriate radii. Each generated position has a localization history in the form of an ancestors list which stores the consistent positions of  , and the ancestors of those positions, check the consistency of a pair of points, then involves comparing their ancestries. If a node exists in the ancestries of both, but with different positions, then they are not consistent. Finally positions of the rest of the immediate ancestors of
, and the ancestors of those positions, check the consistency of a pair of points, then involves comparing their ancestries. If a node exists in the ancestries of both, but with different positions, then they are not consistent. Finally positions of the rest of the immediate ancestors of  in
in  are checked for consistency with the new positions of
are checked for consistency with the new positions of  . Throughout bilateration and update bilateration, every position that has been found inconsistent is removed immediately and thus further localizations do not take into account any unnecessary data. We note that all removals in the unique localization are recursive in the sense that the removal of a point
. Throughout bilateration and update bilateration, every position that has been found inconsistent is removed immediately and thus further localizations do not take into account any unnecessary data. We note that all removals in the unique localization are recursive in the sense that the removal of a point  causes the removal of positions containing
causes the removal of positions containing  in their ancestries as well.
in their ancestries as well.
3.3. Analysis
Let  denote the average degree of a node in
denote the average degree of a node in  . The size of a packet broadcasted by a node in the
. The size of a packet broadcasted by a node in the  th iteration of the initial setup is
th iteration of the initial setup is  . The total size of all packets broadcasted throughout the network in this phase is
. The total size of all packets broadcasted throughout the network in this phase is  , where
, where  is the number of nodes in the network. During the unique localization within iterations, each recently discovered anchor is broadcasted at most once. The number of nodes in a cluster
is the number of nodes in the network. During the unique localization within iterations, each recently discovered anchor is broadcasted at most once. The number of nodes in a cluster  is bounded by
is bounded by  . Therefore, the total size of all packets broadcasted throughout the network is the same as the first phase,
. Therefore, the total size of all packets broadcasted throughout the network is the same as the first phase,  which is the total size overall. Assuming
which is the total size overall. Assuming  ,
,  are constants, the total packet size is linear in terms of the size of the network. In terms of running time, a single execution of the localization takes
are constants, the total packet size is linear in terms of the size of the network. In terms of running time, a single execution of the localization takes  time in the worst case. Although exponential on the size of a cluster, assuming the cluster sizes are constant, each iteration requires constant time. Same argument holds for the memory requirements of a sensor node. For practical considerations, the value of
time in the worst case. Although exponential on the size of a cluster, assuming the cluster sizes are constant, each iteration requires constant time. Same argument holds for the memory requirements of a sensor node. For practical considerations, the value of  is of crucial importance in determining the efficiency in terms of the messaging overhead, time and space requirements. For most of the experiments the maximum number of position possibilities for the whole cluster rarely exceeds
is of crucial importance in determining the efficiency in terms of the messaging overhead, time and space requirements. For most of the experiments the maximum number of position possibilities for the whole cluster rarely exceeds  for all practical values of
for all practical values of  .
.
Assuming the iterative model of collaboration, the value of  is also important for determining the unique localizability as the next lemma shows.
is also important for determining the unique localizability as the next lemma shows.
Lemma 3.3 (For  ).
).
Within the defined model of collaboration between clusters, there exists a class of graphs that have  uniquely localizable nodes for
uniquely localizable nodes for  , whereas
, whereas  uniquely localizable nodes for
uniquely localizable nodes for  .
.
Proof.
The flower graph of Figure 2 is such a class. The middle part called the sepal is a circulant graph of vertices  . Within the sepal, each
. Within the sepal, each  has edges to
has edges to  ,
,  ,
,  ,
,  . Thus the sepal is the circulant graph of
. Thus the sepal is the circulant graph of  vertices,
vertices,  , which is globally rigid. Corresponding to each
, which is globally rigid. Corresponding to each  there is a petal
there is a petal which is a wheel centered at
which is a wheel centered at  .
.  itself is globally rigid and shares exactly two vertices with the two neighboring petals
itself is globally rigid and shares exactly two vertices with the two neighboring petals  and
and  . Vertices
. Vertices  ,
,  are shared with the petal of
are shared with the petal of  , and
, and  ,
,  are shared with that of
are shared with that of  . We set
. We set  . The cluster
. The cluster  includes the sepal in its entirety and is globally rigid. If three anchors belong to the same petal, the center of the petal can collapse its petal, and therefore the sepal completely, which further enables the unique localization of every petal in the graph and the whole network is uniquely localized. However,
includes the sepal in its entirety and is globally rigid. If three anchors belong to the same petal, the center of the petal can collapse its petal, and therefore the sepal completely, which further enables the unique localization of every petal in the graph and the whole network is uniquely localized. However,  is not globally rigid. Unless each petal contains at least three anchors, that is, it is independently localizable, unique localization is not possible.
is not globally rigid. Unless each petal contains at least three anchors, that is, it is independently localizable, unique localization is not possible.
We can assign equal sizes to the petals, such that each petal consists of almost  nodes. An immediate consequence then is that, assuming a random assignment of anchors, the probability of localizing
nodes. An immediate consequence then is that, assuming a random assignment of anchors, the probability of localizing  nodes under the
nodes under the  cluster model is the same as that of localizing the complete network under the
cluster model is the same as that of localizing the complete network under the  cluster model. This is true since in
cluster model. This is true since in  a petal is uniquely localizable either in its entirety or none at all. Moreover, a uniquely localizable petal in
a petal is uniquely localizable either in its entirety or none at all. Moreover, a uniquely localizable petal in  gives rise to uniquely localizable network in
gives rise to uniquely localizable network in  . It implies that, deploying the same number of anchors, with
. It implies that, deploying the same number of anchors, with  , we can localize the complete network, whereas only ten percent of the network is localizable for
, we can localize the complete network, whereas only ten percent of the network is localizable for  . We note that in practical deployment scenarios the likelihood of flower-like configurations is higher for small values of
. We note that in practical deployment scenarios the likelihood of flower-like configurations is higher for small values of  . Therefore, the contrast between the uniquely localizable node ratios for
. Therefore, the contrast between the uniquely localizable node ratios for  is quite remarkable and is verified with the experiments of the following section.
is quite remarkable and is verified with the experiments of the following section.
4. Experiments and Discussion of Results
The implementation is coded in C++ using LEDA library [17]. The implementations are available at http://hacivat.khas.edu.tr/~cesim/uniloc.rar. Experiments are performed on a computer with the configuration of AMD X2 3800+ of CPU and 3 GB of RAM. Because we propose a distributed algorithm, a discrete event simulation system has been designed. We start by generating a random network with parameters  and
and  . Firstly,
. Firstly,  random points in the plane are generated using the random number generation of LEDA [17]. All nodes are assumed to have equal sensing range which is increased iteratively until average degree equals
random points in the plane are generated using the random number generation of LEDA [17]. All nodes are assumed to have equal sensing range which is increased iteratively until average degree equals  . All experiments are reproducible in any platform. Network size is fixed at
. All experiments are reproducible in any platform. Network size is fixed at  and four randomly chosen
and four randomly chosen  s are declared as anchors. The experiments are run for
s are declared as anchors. The experiments are run for  ,
,  values, where
values, where  varies from
varies from  to
to  , and
, and  varies from
varies from  to
to  . Every unique configuration is repeated 10 times. The recorded results are divided into two when appropriate. First phase results are those arising from the cluster construction and the second phase results correspond to those of the actual unique localization.
. Every unique configuration is repeated 10 times. The recorded results are divided into two when appropriate. First phase results are those arising from the cluster construction and the second phase results correspond to those of the actual unique localization.
We select performance measures in order to analyze and construe localization, messaging performances, and running time and space requirements. LNR (Localized Node Ratio) is the number of uniquely localized nodes divided by  . BC (average Broadcast Count per node) is total number of broadcasted messages divided by
. BC (average Broadcast Count per node) is total number of broadcasted messages divided by  . The size of each broadcasted packet differs especially in the second phase. Thus BC alone does not fully represent bandwidth usage per node. BA (average Broadcast Amount per node) is the total size of all broadcasted packets divided by
. The size of each broadcasted packet differs especially in the second phase. Thus BC alone does not fully represent bandwidth usage per node. BA (average Broadcast Amount per node) is the total size of all broadcasted packets divided by  . AT (Average Time per node) is the average time spent for computations required by the localization algorithm on a physical sensor node. MP (Maximum possibilities per node) is defined as
. AT (Average Time per node) is the average time spent for computations required by the localization algorithm on a physical sensor node. MP (Maximum possibilities per node) is defined as  (
( ). In our implementation we bound
). In our implementation we bound  to be at most 1024. Finally, TP (average Total Possibilities per cluster) is
to be at most 1024. Finally, TP (average Total Possibilities per cluster) is  , which is a measure of the average space requirements of a sensor node. Figure 3 is a visual illustration of our unique localization method. All the uniquely localizable nodes (almost
, which is a measure of the average space requirements of a sensor node. Figure 3 is a visual illustration of our unique localization method. All the uniquely localizable nodes (almost  of the whole network) are uniquely localized with
of the whole network) are uniquely localized with  , whereas
, whereas  of the network is uniquely localizable for
of the network is uniquely localizable for  (anchors),
(anchors),  for
for  , and
, and  for
for  . We note that in the simplest case, for
. We note that in the simplest case, for  , our method is analogous to iterative trilateration [7].
, our method is analogous to iterative trilateration [7].
Figure 4(a) shows the growth of LNR with respect to  and
and  . As
. As  increases, LNR grows as expected. There exist partial graphs, such as the one in Figure 2, that are localizable only for a specific
increases, LNR grows as expected. There exist partial graphs, such as the one in Figure 2, that are localizable only for a specific  . Howeve, since the occurrence probability of such graphs is inversely proportional to
. Howeve, since the occurrence probability of such graphs is inversely proportional to  , for
, for  when
when  , LNR does not grow drastically. The change in BC values with respect to
, LNR does not grow drastically. The change in BC values with respect to  ,
,  is plotted in Figure 4(b). Since the number of broadcasts in the Initial Setup phase is constant, the irregularity of the plot is caused by the broadcasts in the Iterative Localization phase. Number of broadcasts in this phase depends on how many new anchors are localized at each iteration. The BC values are maximum for
is plotted in Figure 4(b). Since the number of broadcasts in the Initial Setup phase is constant, the irregularity of the plot is caused by the broadcasts in the Iterative Localization phase. Number of broadcasts in this phase depends on how many new anchors are localized at each iteration. The BC values are maximum for  . For sparse networks when
. For sparse networks when  , the messaging overhead is low since not that many nodes are localized to be broadcasted in the first place. In contrast, when
, the messaging overhead is low since not that many nodes are localized to be broadcasted in the first place. In contrast, when  each localization iteration uniquely localizes many nodes at once therefore requires few broadcasts. However, as can be verified in Figure 5(a), the BA values indicating the broadcast size per node grow proportionally in terms of
each localization iteration uniquely localizes many nodes at once therefore requires few broadcasts. However, as can be verified in Figure 5(a), the BA values indicating the broadcast size per node grow proportionally in terms of  and
and  . Figure 5(b) shows the MP values. The peak values are reached at
. Figure 5(b) shows the MP values. The peak values are reached at  for almost all
for almost all  values, since low connectivity does not enable too many bilaterations, therefore possible locations, whereas high connectivity leads to unique localization too quickly.
values, since low connectivity does not enable too many bilaterations, therefore possible locations, whereas high connectivity leads to unique localization too quickly.
Similar reasoning could apply to TP except that cluster size plays an important role as well in this case; see Figure 6(a). The average cluster size is  , therefore for large values of
, therefore for large values of  (
( ), TP is constant or grows slightly even though MP decreases. High connectivity leads to ease of unique localization but also gives rise to large clusters, which seem to cancel out each others' effects in terms of space requirements of a sensor node. It is interesting to analyze the time spent for localization computations at each node, since it depends on both MP and TP. As can be seen in Figure 6(b), the growth seems to be similar to that of MP for
), TP is constant or grows slightly even though MP decreases. High connectivity leads to ease of unique localization but also gives rise to large clusters, which seem to cancel out each others' effects in terms of space requirements of a sensor node. It is interesting to analyze the time spent for localization computations at each node, since it depends on both MP and TP. As can be seen in Figure 6(b), the growth seems to be similar to that of MP for  . However, the large cluster sizes reflected in TP seem to overcome the advantages created by low MP for larger connectivities and the running time required for localization increases.
. However, the large cluster sizes reflected in TP seem to overcome the advantages created by low MP for larger connectivities and the running time required for localization increases.
5. Conclusion
We provided primitives for uniquely localizing nodes in a given sensor network. Assuming measurements with no noise, the suggested fully decentralized and fully collaborative computational model gives rise to a high rate of unique localization. Moreover, this goal is achieved with reasonably low energy requirements for message exchanges as the average number of iterations per node is low. An important direction for future work is to generalize the unique localization framework to handle error in measurements. It would also be useful to conduct experiments to analyze the efficiency of the model when the network is employed in various regions with randomly placed obstacles.
References
Akyildiz IF, Su W, Sankarasubramaniam Y, Cayirci E: A survey on sensor networks. IEEE Communications Magazine 2002, 40(8):102-114. 10.1109/MCOM.2002.1024422
Krishnamachari B: Networking Wireless Sensors. Cambridge University Press, New York, NY, USA; 2006.
Efrat A, Erten C, Forrester D, Kobourov SG: A force-directed approaches to sensor localization. Proceedings of the 8th Workshop on Algorithm Engineering and Experiments (ALENEX '06), January 2006, Miami, Fla, USA 108-118.
Goldenberg DK, Bihler P, Cao M, Fang J: Localization in sparse networks using sweeps. Proceedings of the 15th International Conference on Mobile Computing and Networking (MOBICOM '06), September 2006, Los Angeles, Calif, USA 110-121.
Hu L, Evans D: Localization for mobile sensor networks. Proceedings of the 10th International Conference on Mobile Computing and Networking (MOBICOM '04), September-October 2004, Philadelphia, Pa, USA 45-57.
Basu A, Gao J, Mitchell JSB, Sabhnani G: Distributed localization using noisy distance and angle information. Proceedings of the 7th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '06), May 2006, Florence, Italy 262-273.
Moore D, Leonard J, Rus D, Teller S: Robust distributed network localization with noisy range measurements. Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems (SenSys '04), November 2004, Baltimore, Md, USA 50-61.
Aspnes J, Eren T, Goldenberg D, et al.: A theory of network localization. IEEE Transactions on Mobile Computing 2006, 5(12):1663-1678.
Hightower J, Borriello G: Location systems for ubiquitous computing. Computer 2001, 34(8):57-66. 10.1109/2.940014
Mao G, Fidan B, Anderson BDO: Wireless sensor network localization techniques. Computer Networks 2007, 51(10):2529-2553. 10.1016/j.comnet.2006.11.018
Aspnes J, Goldenberg D, Yang Y: On the computational complexity of sensor network localization. Proceedings of the 1st International Workshop on Algorithmic Aspects of Wireless Sensor Networks, July 2004, Turku, Finland 3121: 32-44.
Hendrickson B: Conditions for unique graph realizations. SIAM Journal on Computing 1992, 21(1):65-84. 10.1137/0221008
Laman G: On graphs and rigidity of plane skeletal structures. Journal of Engineering Mathematics 1970, 4(4):331-340. 10.1007/BF01534980
Connelly R: Generic global rigidity. Discrete and Computanional Geometry 2005, 33(4):549-563. 10.1007/s00454-004-1124-4
Berg AR, Jordán T: A proof of Connelly's conjecture on 3-connected circuits of the rigidity matroid. Journal of Combinatorial Theory Series B 2003, 88(1):77-97. 10.1016/S0095-8956(02)00037-0
Jackson B, Jordán T: Connected rigidity matroids and unique realizations of graphs. Journal of Combinatorial Theory Series B 2005, 94(1):1-29. 10.1016/j.jctb.2004.11.002
Mehlhorn K, Naeher S: LEDA: a platform for combinatorial and geometric computing. Communications of the ACM 1999, 38(1):96-102.
Acknowledgment
This work was partially supported by The Scientific and Technological Research Council of Turkey (TUBITAK) Grant no. 106E071.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cakiroglu, A., Erten, C. Fully Decentralized and Collaborative Multilateration Primitives for Uniquely Localizing WSNs. J Wireless Com Network 2010, 605658 (2009). https://doi.org/10.1155/2010/605658
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/605658

 . (b) No order exists for
. (b) No order exists for  .
. )
) indicate the set of finitely localized nodes
indicate the set of finitely localized nodes do
do ,
,  )
) FindBilaterationOrder
FindBilaterationOrder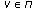 do
do ,
,  ),
), are neighbors of
are neighbors of  that are to
that are to to
to 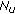

 , uniquely localizable for
, uniquely localizable for  .
.
 and
and  . Squares are localized for
. Squares are localized for  (anchors), purple circles for
(anchors), purple circles for  , dashes for
, dashes for  , diamonds for
, diamonds for  , and gray circles are unlocalizable.
, and gray circles are unlocalizable.

