- Research Article
- Open access
- Published:
An Optimal Adaptive Network Coding Scheme for Minimizing Decoding Delay in Broadcast Erasure Channels
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 618016 (2010)
Abstract
We are concerned with designing feedback-based adaptive network coding schemes with the aim of minimizing decoding delay in each transmission in packet-based erasure networks. We study systems where each packet brings new information to the destination regardless of its order and require the packets to be instantaneously decodable. We first formulate the decoding delay minimization problem as an integer linear program and then propose efficient algorithms for finding its optimal solution(s). We show that our problem formulation is applicable to memoryless erasures as well as Gilbert-Elliott erasures with memory. We then propose a number of heuristic algorithms with worst case linear execution complexity that can be used when an optimal solution cannot be found in a reasonable time. We verify the delay and speed performance of our techniques through numerical analysis. This analysis reveals that by taking channel memory into account in network coding decisions, one can considerably reduce decoding delays.
1. Introduction
In this paper, we are concerned with designing feedback-based adaptive network coding schemes that can deliver high throughputs and low decoding delays in packet erasure networks. We first present some background on existing work and emphasize that the notion of delay and the choice of a suitable network coding strategy are highly entangled with the underlying application.
1.1. Motivation and Background
Consider a broadcast packet-based transmission from one source to many destinations where erasures can occur in the links between the source and destinations. Two main throughput optimal schemes to deal with such erasures are fountain codes [1] and random linear network codes (RLNC) [2]. In the latter scheme, for example, the source transmits random linear mixtures of all the packets to be delivered. It is well-known that if the random coefficients are chosen from a finite field with a sufficiently large size, each coded packet will almost surely become linearly independent of all previously received coded packets and hence, innovative for every destination [2]. The scheme is therefore almost surely throughput optimal. Another benefit of fountain codes and RLNC is that they do not require feedback about erasures in individual links in order to operate.
However in these schemes, throughput optimality comes at the cost of large decoding delays, as the receiver needs, in general, to collect all coded packets in a block before being able to decode. Despite this drawback, there are applications which are insensitive to such delays. Consider, for example, a simple software update (file download). The update only starts to work when the whole file is downloaded. In this case, the main desired properties are throughput optimality and the mean completion time and there is often little or no incentive to aim for partial "premature" decoding. The completion time performance of RLNC for rateless file download applications has been considered in [3]. In [3], the mean completion time of RLNC is shown to be much shorter than scheduling. Reference [4] considers time division duplex systems with large round-trip link latencies and proposes solutions for the number of coded packet transmissions before waiting for acknowledgement on the received number of degrees of freedom.
There are applications where partial decoding can crucially influence the end user's experience. Consider, for example, broadcasting a continuous stream of video or audio in live or playback modes. Even though fountain codes and RLNC are throughput optimal, having to wait for the entire coded block to arrive can result in unacceptable delays in the application layer. But, we also note that partial decoding of packets out of their natural temporal order does not necessarily translate into low delivery delays desired by the application layer. The authors in [5, 6] have proposed feedback-based throughput-optimal schemes to deal with the transmitter queue size, as well as decoding and delivery delays at the destinations. When the traffic load approaches system capacity, their methods are shown to behave "gracefully" and meet the delay performance benchmark of single-receiver automatic repeat request (ARQ) schemes.
There is yet another set of applications for which partial decoding is beneficial and can result in lower delays irrespective of the order in which packets are being decoded. Consider, for example, a wireless sensor network in which there is a fusion/command center together with numerous sensors/agents scattered in a region. Each sensor/agent has to execute or process one or more complex commands. Each command and its associated data is dispatched from the center in a packet. For coordination purposes, each agent needs to know its own and other agents' commands. Therefore, commands are broadcast to everyone in the network. In this application, in-order processing/execution of commands may not be a real issue. However, fast command execution may be crucial and therefore, it is imperative that innovative packets arrive and get decoded at the destinations as quickly as possible regardless of their order. As another example, consider emergency operations in a large geographical region where emergency-related updates of the map of the area need to be dispatched to all emergency crew members. In such situations too, updates of different parts of the map can be decoded in any order and still be useful for handling the emergency.
Finally, some applications may be designed in such a way that they are insensitive to in-order delivery. This can be particularly useful where the transport medium is unreliable. In such a case, it may be natural to use multiple-description source coding techniques [7], in which every decoded packet brings new information to the destination, irrespective of its order. In light of the emergency applications described above, one can perform multiple-description coding for map updates, so that updates of different subregions can be divided into multiple packets and each packet can provide an improved view of one region in a truly order-insensitive fashion.
1.2. Contributions
In this paper, we are inspired by the last set of order-insensitive packet delivery applications and hence, focus on designing network coding schemes that, with the help of feedback, can deliver innovative packets in any order to the destination and also guarantee fast decoding of such packets. As a first step towards such goal, we limit ourselves to broadcast erasure channels, but emphasize that the ideas can be extended to other more complicated scenarios. We also consider the class of instantaneously decodable network coding schemes, in which each coded transmission contains at most one new source packet that a receiver has not decoded yet. The rationale is that in an order-insensitive application, any innovative packet that cannot be decoded immediately incurs a unit of delay. Obviously, one other source of delay is when a coded packet does not contain any new information for a receiver and hence, is not innovative. A similar definition of the decoding delay was first considered in [8], where the authors presented a number of heuristic algorithms to reduce order-insensitive decoding delay. In this context, our main contributions are the following.
-
(i)
In Section 1.1, we have motivated the problem in light of possible applications in sensor and ad hoc networks. To the best of our knowledge, such application-dependent classification of network coding delays did not previously exist in the literature.
-
(ii)
In Section 3.1, we present a systematic framework for the minimization of decoding delay in each transmission subject to the instantaneous decodability constraint. We show that this problem can be cast into a special integer linear programming (ILP) framework, where instantaneously decodable packet transmission corresponds to a set packing problem [9] on an appropriately defined set structure.
-
(iii)
In Section 3.2, we provide a customized and efficient method for finding the optimal solution to the set packing problem (which is in general NP-hard). Our numerical results in Section 6 show that for reasonably sized number of receivers, the optimum solution(s) can be found in a time that is linearly proportional to the total number of packets.
-
(iv)
In Section 4, we discuss decoding delay minimization for an important class of erasure channels with memory, which can occur in wireless communication systems due to deep fades and shadowing [10]. We show that the general set packing framework in Section 3 can be easily modified to account for the erasure memory. Our results in Section 6 reveal that by adapting network coding decisions based on channel erasure conditions, significant improvements in delay are possible compared to when decisions are taken irrespective of channel states.
-
(v)
In Section 5, we provide a number of heuristic variations of the optimal search for finding (possibly suboptimal) solutions faster, if needed. Our results in Section 6 show that such heuristics work very well and often provide solutions that are very close to the search algorithm. Moreover, they improve on the proposed random opportunistic method in [8].
2. Network Model
Consider a single source that wants to broadcast some data to  receivers, denoted by
receivers, denoted by  for
for  . The data to be broadcast is divided into
. The data to be broadcast is divided into  packets, denoted by
packets, denoted by  for
for  . Time is slotted and the source can transmit one (possibly coded) packet per slot.
. Time is slotted and the source can transmit one (possibly coded) packet per slot.
A packet erasure link  connects the source to each individual receiver
connects the source to each individual receiver  . Erasures in different links can be independent or correlated with each other. Different erasures in a single link can be independent (memoryless) or correlated with each other (with memory) over time.
. Erasures in different links can be independent or correlated with each other. Different erasures in a single link can be independent (memoryless) or correlated with each other (with memory) over time.
For memoryless erasures, an erasure in link  can occur with a probability of
can occur with a probability of  in each packet transmission round independent of previous erasures.
in each packet transmission round independent of previous erasures.
For correlated erasures, we consider the well-known Gilbert-Elliott channel (GEC) [11], which is a Markov model with a good and a bad state. If the channel is in the good state, packets can be successfully received, while in the bad state packets are lost (e.g., due to deep fades or shadowing in the channel). The probability of moving from the good state  to the bad state
to the bad state  in link
in link  is
is  and the probability of moving from the bad state
and the probability of moving from the bad state  to the good state
to the good state  is
is  , where
, where  is the time slot index. Steady-state probabilities are given by
is the time slot index. Steady-state probabilities are given by  and
and  . Following [12], we define the memory content of the GEC in link
. Following [12], we define the memory content of the GEC in link  as
as  , which signifies the persistence of the channel in remaining in the same state. A small
, which signifies the persistence of the channel in remaining in the same state. A small  means a channel with little memory and a large
means a channel with little memory and a large  means a channel with large memory.
means a channel with large memory.
Before transmission of the next packet, the source collects error-free and delay-free 1-bit feedback from each destination indicating if the packet was successfully received or not. A successful reception generates an acknowledgement (ACK) and an erasure generates a negative acknowledgement (NAK). This feedback is used for optimizing network coding decisions at the source for the next packet transmission round, as described in future sections.
In this work, we consider linear network coding [2] in which coded packets are formed by taking linear combinations of the original source packets. Packets are vectors of fixed size over a finite field  . The coefficient vector used for linear network coding is sent in the packet header so that each destination can at some point recover the original packets. Since in this paper we are only dealing with instantaneously decodable packet transmission, it suffices to consider linear network coding over
. The coefficient vector used for linear network coding is sent in the packet header so that each destination can at some point recover the original packets. Since in this paper we are only dealing with instantaneously decodable packet transmission, it suffices to consider linear network coding over  . That is, coded packets are formed using binary XOR of the original source packets. Thus, network coding is performed in a similar manner as in [13].
. That is, coded packets are formed using binary XOR of the original source packets. Thus, network coding is performed in a similar manner as in [13].
Definition 1.
A transmitted packet is instantaneously decodable for receiver  if it is a linear combination of source packets containing at most one source packet that
if it is a linear combination of source packets containing at most one source packet that  has not decoded yet. A scheme is called instantaneously decodable if all transmissions have this property for all receivers.
has not decoded yet. A scheme is called instantaneously decodable if all transmissions have this property for all receivers.
Definition 2.
At the end of transmission round  in an instantaneously decodable scheme, the knowledge of receiver
in an instantaneously decodable scheme, the knowledge of receiver  is the set consisting of all packets that the receiver has decoded so far. The receiver can therefore, compute any linear combination of the packets that it has decoded for decoding future packets.
is the set consisting of all packets that the receiver has decoded so far. The receiver can therefore, compute any linear combination of the packets that it has decoded for decoding future packets.
Definition 3.
In an instantaneously decodable scheme, a coded packet is called non-innovative for receiver  if it only contains source packets that the receiver has decoded so far. Otherwise, the packet is innovative.
if it only contains source packets that the receiver has decoded so far. Otherwise, the packet is innovative.
Definition 4.
A scheme is called rate or throughput optimal if all transmissions are innovative for the entire set of receivers.
Definition 5.
In time slot  , receiver
, receiver  experiences one unit of delay if it successfully receives a packet that is either non-innovative or not instantaneously decodable. If we impose instantaneous decodability on the scheme, a delay can only occur if the received packet is not innovative.
experiences one unit of delay if it successfully receives a packet that is either non-innovative or not instantaneously decodable. If we impose instantaneous decodability on the scheme, a delay can only occur if the received packet is not innovative.
Note that in the last definition, we do not count channel inflicted delays due to erasures. The delay only counts "algorithmic" overhead delays when we are not able to provide innovative and instantaneously decodable packets to a receiver.
As an example, if the knowledge of  is
is  , receiving
, receiving  will cause
will cause  to experience one unit of delay, whereas
to experience one unit of delay, whereas  is innovative and instantaneously decodable, hence does not incur any delay.
is innovative and instantaneously decodable, hence does not incur any delay.
We note that a packet that is not transmitted yet or transmitted but not received by any receiver can be transmitted in an uncoded manner at any transmission slot without incurring any algorithmic delay. In fact, this is how the transmission starts: by sending  uncoded, for example.
uncoded, for example.
A zero-delay scheme would require all packets to be both innovative and instantaneously decodable to all receivers. Thus zero-delay implies rate optimality, but not vice versa. As the authors show in [8, Theorem 1] for the case of  and
and  receivers, there exists an offline algorithm that is both rate optimal and delay-free. For
receivers, there exists an offline algorithm that is both rate optimal and delay-free. For  the authors prove that a zero-delay algorithm does not exist. By offline we mean that the algorithm needs to know future realizations of erasures in broadcast links. In contrast, an online algorithm decides on what to send in the next time slot based on the information received in the past and in the current slot. In this paper, we focus on designing online algorithms.
the authors prove that a zero-delay algorithm does not exist. By offline we mean that the algorithm needs to know future realizations of erasures in broadcast links. In contrast, an online algorithm decides on what to send in the next time slot based on the information received in the past and in the current slot. In this paper, we focus on designing online algorithms.
3. Optimization Framework
3.1. Problem Formulation Based on Integer Linear Programming
Instantaneous decodability can be naturally cast into the framework of integer optimization. To this end, let us fix the packet transmission round to  and consider the knowledge of all receivers, which is also available at the source because of the feedback. The state of the entire system at time index
and consider the knowledge of all receivers, which is also available at the source because of the feedback. The state of the entire system at time index  (in terms of packets that are still needed by the receivers) can be described by an
(in terms of packets that are still needed by the receivers) can be described by an  binary receiver-packet incidence matrix
binary receiver-packet incidence matrix  with elements
with elements

Columns of matrix  are denoted by
are denoted by  to
to  . We assume that packets received by all receivers are removed from the receiver-packet incidence matrix. Hence,
. We assume that packets received by all receivers are removed from the receiver-packet incidence matrix. Hence,  does not contain any all-zero columns.
does not contain any all-zero columns.
Example 1.
Consider  receivers and
receivers and  packets. Before the transmission begins, the receiver-packet incidence matrix
packets. Before the transmission begins, the receiver-packet incidence matrix  is an all-one
is an all-one  matrix. If we send packet
matrix. If we send packet  in the first transmission round
in the first transmission round  and assuming that only receiver
and assuming that only receiver  successfully receives it,
successfully receives it,  will become
will become

If we send packet  in the next transmission round
in the next transmission round  and assuming that only receiver
and assuming that only receiver  successfully receives it,
successfully receives it,  will then be
will then be

The condition of instantaneous decodability means that at any transmission round we cannot choose more than one packet which is still unknown to a receiver  . In the example above, at
. In the example above, at  , we cannot send
, we cannot send  because it contains more than one packet unknown to
because it contains more than one packet unknown to  .
.
Let  represent a binary decision vector of length
represent a binary decision vector of length  that determines which packets are being coded together. The transmitted packet consists of the binary XOR of the source packets for which
that determines which packets are being coded together. The transmitted packet consists of the binary XOR of the source packets for which  . More formally, we can define the instantaneous decodability constraint for all receivers as
. More formally, we can define the instantaneous decodability constraint for all receivers as  , where
, where  represents an all-one vector of length
represents an all-one vector of length  and the inequality is examined on an element-by-element basis (Note that although
and the inequality is examined on an element-by-element basis (Note that although  is a binary or Boolean vector,
is a binary or Boolean vector,  is calculated in real domain. Hence,
is calculated in real domain. Hence,  is in fact a pseudo-Boolean constraint.). This condition ensures that a transmitted coded packet contains at most one unknown source packet for each receiver. A vector
is in fact a pseudo-Boolean constraint.). This condition ensures that a transmitted coded packet contains at most one unknown source packet for each receiver. A vector  is called infeasible if it does not satisfy the instantaneous decodability condition. In other words,
is called infeasible if it does not satisfy the instantaneous decodability condition. In other words,  is called infeasible if and only if there exists at least one
is called infeasible if and only if there exists at least one  for which
for which  in
in  . A vector
. A vector  is called a solution if and only if it satisfies
is called a solution if and only if it satisfies  . In the rest of this paper, "
. In the rest of this paper, " " and "
" and " is a solution" are used interchangeably.
is a solution" are used interchangeably.
Now consider sets  , where
, where  is the nonempty set of receivers that still need source packet
is the nonempty set of receivers that still need source packet  . Note that these sets can be easily determined by looking at the columns of matrix
. Note that these sets can be easily determined by looking at the columns of matrix  . The "importance" of packet
. The "importance" of packet  can be, for example, taken to be the size of set
can be, for example, taken to be the size of set  , which is the number of receivers that still need
, which is the number of receivers that still need  .
.
We now formally describe the optimization procedure that should be performed at the transmitter. Maximizing the number of receivers for which a transmission is innovative, subject to the constraint of instantaneous decodability, can be posed as the following (binary-valued) integer linear program (ILP):

where  . This is a standard problem in combinatorial optimization, usually called set packing [9]. Here the universe is the set of all receivers and we need to find disjoint (due to instantaneous decodability condition) subsets
. This is a standard problem in combinatorial optimization, usually called set packing [9]. Here the universe is the set of all receivers and we need to find disjoint (due to instantaneous decodability condition) subsets  with the largest total size. In the (most desirable) case when equality holds in
with the largest total size. In the (most desirable) case when equality holds in  for every receiver, we also speak of a set partition. This is equivalent to a zero-delay transmission.
for every receiver, we also speak of a set partition. This is equivalent to a zero-delay transmission.
In Section 4, we will consider other measures of packet importance and discuss the role of  in tailoring the optimization problem according to the application requirements or channel conditions, such as memory in erasure links.
in tailoring the optimization problem according to the application requirements or channel conditions, such as memory in erasure links.
We assume that elements of  , which signify packet importance, are all positive. If one has already found a solution such as
, which signify packet importance, are all positive. If one has already found a solution such as  with
with  , then changing this solution into
, then changing this solution into  by changing
by changing  into
into  can only result in a
can only result in a  strictly smaller than
strictly smaller than  . We say that given solution
. We say that given solution  ,
,  is clearly suboptimal and hence, can be discarded in an algorithm that searches for the optimal solution(s).
is clearly suboptimal and hence, can be discarded in an algorithm that searches for the optimal solution(s).
3.2. Efficient Search Methods for Finding the Optimal Solution of (4)
It is well known that the set packing problem is NP-hard [9]. Here, we present an efficient ILP solver designed to take advantage of the specific problem structure. Later, we will see that for many practical situations of interest, our method performs well empirically. Based on this framework, we will also present some heuristics in Section 5 to deal with more complicated and time-consuming problem instances.
We begin presenting our method by first defining constrained and unconstrained variables.
Definition 6.
Two binary-valued variables are said to be constrained if they cannot be simultaneously  in a solution. Or formally,
in a solution. Or formally,  and
and  are constrained if for any
are constrained if for any  satisfying
satisfying  ,
,  (Again, note that the addition of variables takes place in real domain.). We also say that
(Again, note that the addition of variables takes place in real domain.). We also say that  is constrained to
is constrained to  and vice versa. It can be proven that
and vice versa. It can be proven that  and
and  are constrained if and only if there exits at least one row index
are constrained if and only if there exits at least one row index  in
in  for which
for which  .
.
Definition 7.
The set of all variables constrained to  is called the constrained set of
is called the constrained set of  and is denoted by
and is denoted by  . That is,
. That is,

If  and
and  are not constrained to each other (
are not constrained to each other ( and
and  ), then columns
), then columns  and
and  in
in  cannot have nonzero elements in the same row position. That is, for each row index
cannot have nonzero elements in the same row position. That is, for each row index  ,
,  and
and  .
.
Definition 8.
A variable  is said to be unconstrained if
is said to be unconstrained if  . The set of all unconstrained variables is denoted by
. The set of all unconstrained variables is denoted by  and is referred to as the unconstrained set.
and is referred to as the unconstrained set.
If  is an unconstrained variable, then for each row index
is an unconstrained variable, then for each row index  ,
,  for all
for all  (otherwise,
(otherwise,  and
and  would become constrained).
would become constrained).
Example 2.
Consider the following receiver-packet incidence matrix 

One can easily verify the relations defined above. For example, variables  and
and  are constrained because for
are constrained because for  ,
,  . Variables
. Variables  and
and  are not constrained to each other because columns
are not constrained to each other because columns  and
and  do not have a nonzero element in the same row position. Variable
do not have a nonzero element in the same row position. Variable  is unconstrained because no other column has a nonzero element in rows 6 or 7. In summary,
is unconstrained because no other column has a nonzero element in rows 6 or 7. In summary,  ,
,  ,
,  ,
,  and
and  .
.
To design an efficient search algorithm, one needs to efficiently prune the parameter space and reduce the problem size. We make the following observations for pruning of the parameter space.
-
(1)
Unconstrained variables must be set to 1. In other words, setting those variables to 0 does not contribute to the optimal solution (note that the elements in
 are positive). In the above example,
are positive). In the above example, 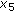 and
and 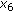 must be set to 1 because no other variable is constrained to them (we will make this statement formal in the optimality proof of the algorithm in the appendix).
must be set to 1 because no other variable is constrained to them (we will make this statement formal in the optimality proof of the algorithm in the appendix). -
(2)
If a constrained variable is set to 1 all members of its constrained set must be set to 0. In the above example, setting
 forces
forces  and
and 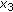 to zero.
to zero. -
(3)
At a given step, the parameter space can be pruned most by resolving the variable with the largest constrained set.
Application of the third observation, in a search algorithm results in greedy pruning of the parameter space. We note that greedy pruning is only optimal for a given step of the algorithm and is not guaranteed to result in the optimal reduction of the overall complexity of the search.
We now make a final remark before presenting the search algorithm. In particular, we have observed that finding constrained sets for each variable in each step of the algorithm can be somewhat time consuming. A very effective alternative is to first sort matrix  , column-wise, in descending order of the number of
, column-wise, in descending order of the number of  's in each column. Setting the "most important" head variable
's in each column. Setting the "most important" head variable  (with the highest
(with the highest  ) to
) to  is likely to result in the largest constrained set (because it potentially overlaps with many other variables) and hence, many variables will be resolved in the next recursion. We will refer to the approach based on finding the largest constrained set as the greedy pruning strategy and to the alterative approach as the sorted pruning search strategy.
is likely to result in the largest constrained set (because it potentially overlaps with many other variables) and hence, many variables will be resolved in the next recursion. We will refer to the approach based on finding the largest constrained set as the greedy pruning strategy and to the alterative approach as the sorted pruning search strategy.
The greedy pruning search strategy is shown in Figure 1, which with appropriate modifications can also represent the sorted pruning variation.Let  denote the problem of size
denote the problem of size  whose input is an
whose input is an  receiver-packet incidence matrix
receiver-packet incidence matrix  and whose output is a set of solutions of the form
and whose output is a set of solutions of the form  of length
of length  which satisfy the instantaneous decodability condition
which satisfy the instantaneous decodability condition  . The algorithms can be described as shown in Algorithm 1.
. The algorithms can be described as shown in Algorithm 1.
Algorithm 1: Recursive search for the optimal solution(s) of (4).
( ) Start with the original problem of size
) Start with the original problem of size .
.
( ) if sorted pruning strategy is desired then
) if sorted pruning strategy is desired then
( ) Rearrange the variables in
) Rearrange the variables in in descending order of packet importance (number of
in descending order of packet importance (number of 's in each column).
's in each column).
( ) end if
) end if
-
(5)
Solve
 :
:
-
(6)
if
 then
then
-
(7)
Return
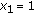 (since the variable is not constrained).
(since the variable is not constrained).
-
(8)
else
-
(9)
if greedy pruning strategy is desired then
-
(10)
Determine the constrained set for all variables
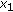 to
to
 .
.
-
(11)
Denote the index of the variable with the largest constrained set by
 and the cardinality of its constrained
and the cardinality of its constrained
set by
 .
.
-
(12)
else
(13) Determine the constrained set for the head variable with cardinality
with cardinality and also the set of unconstrained
and also the set of unconstrained
variables (Note that we have overused index 1 to refer to the head variable in the reordered matrix at each
recursion.). Set .
.
-
(14)
end if
(15) Denote the cardinality of the unconstrained set by
by .
.
(16) Set all the unconstrained variables to 1.
(17) Set and the variables in its corresponding constrained set
and the variables in its corresponding constrained set to 0.
to 0.
(18) Reduce the problem by removing resolved variables. Reduce accordingly.
accordingly.
(19) Solve (Note that
(Note that unconstrained variables are set to one,
unconstrained variables are set to one, and
and variables constrained by
variables constrained by
are set to zero, hence a total of variables are resolved.).
variables are resolved.).
(20) Combine the solution with previously resolved variables. Save solution.
(21) Set .
.
(22) Reduce the problem by removing resolved variables. Reduce accordingly.
accordingly.
(23) Solve (Note that
(Note that unconstrained variables are set to one and
unconstrained variables are set to one and , hence a total of
, hence a total of variables
variables
are resolved.).
(24) Combine the solution with previously resolved variables. Return solution(s).
(25) end if
In the appendix, we prove by structural induction that Algorithm 1 is guaranteed to return all optimal solutions of (4). However, we note that not every solution returned by Algorithm 1 is optimal. The nonoptimal solutions can be easily discarded by testing against the objective function (4) at the end of the algorithm. We also note that in Algorithm 1, we can simply remove those packets received by every receiver from the problem. If there are  such variables, we can start step
such variables, we can start step  above from
above from  instead of
instead of  . The Matlab code for both the greedy and sorted pruning algorithms can be found at http://users.rsise.anu.edu.au/~parastoo/netcod/.
. The Matlab code for both the greedy and sorted pruning algorithms can be found at http://users.rsise.anu.edu.au/~parastoo/netcod/.
We conclude this section by a brief note on the computational complexity of Algorithm 1. Let us denote the number of recursions required to solve the problem of size  by
by  . According to Algorithm 1, this problem is always broken into two smaller problems of size
. According to Algorithm 1, this problem is always broken into two smaller problems of size  and
and  . Therefore, one can find the number of recursions required to solve
. Therefore, one can find the number of recursions required to solve  by recursively computing
by recursively computing  . The recursion stops when one reaches a problem of size 1 (only one packet to transmit) where
. The recursion stops when one reaches a problem of size 1 (only one packet to transmit) where  .
.
4. Adaptive Network Coding in the Presence of Erasure Memory
Here, we present a generalization of the set packing approach for coded transmission in erasure channels with memory. The idea is that the importance of a packet  is no longer determined by how many receivers need
is no longer determined by how many receivers need  , but by the probability that
, but by the probability that  will be successfully decoded by the receivers that need it. In computing this probability, one can use the fact that successive channel erasures in a link are usually correlated with each other and hence, their history can be used to make predictions about whether a receiver is going to experience erasure or not in the next time slot. To present the idea, we focus on the GEC model for representing channel erasures. More general memory models for erasure can also be incorporated into our framework.
will be successfully decoded by the receivers that need it. In computing this probability, one can use the fact that successive channel erasures in a link are usually correlated with each other and hence, their history can be used to make predictions about whether a receiver is going to experience erasure or not in the next time slot. To present the idea, we focus on the GEC model for representing channel erasures. More general memory models for erasure can also be incorporated into our framework.
We define the reward  of sending a packet to receiver
of sending a packet to receiver  as the probability of successful reception by
as the probability of successful reception by  in the next time slot:
in the next time slot:  , where
, where  is the state of
is the state of  in the previous transmission round (Statements like "state of
in the previous transmission round (Statements like "state of  " should be interpreted as the state of the physical link
" should be interpreted as the state of the physical link  connecting the source to
connecting the source to  .). The total reward or importance of sending packet
.). The total reward or importance of sending packet  is then
is then

The above weight vector gives higher priority to a packet  for which there is a higher chance of successful reception, because the receivers that need
for which there is a higher chance of successful reception, because the receivers that need  are more likely to be in good state in the next time slot. With this newly defined weight vector, one can try to solve the optimization problem given in (4) under the same instantaneous decodability condition.
are more likely to be in good state in the next time slot. With this newly defined weight vector, one can try to solve the optimization problem given in (4) under the same instantaneous decodability condition.
Remark 1.
We conclude this section by emphasizing that the optimization framework in (4) is very flexible in accommodating other possibilities for the weight vector  , which can be appropriately determined based on the application. For example, instead of allocating the same weight to a packet needed by a subset of receivers, one can allocate different weights to the same packet (looking column-wise at
, which can be appropriately determined based on the application. For example, instead of allocating the same weight to a packet needed by a subset of receivers, one can allocate different weights to the same packet (looking column-wise at  ) depending on the priorities or demands of each user. In the map update example described in the Introduction, different emergency units can adaptively flag to the base station different parts of the map as more or less important depending on their distance from a certain disaster zone. The task of the base station is then to send a packet combination that satisfies the largest total priority. One can also combine user-dependent packet weights with the channel state prediction outcomes in a GEC. One possibility is to multiply the probabilities
) depending on the priorities or demands of each user. In the map update example described in the Introduction, different emergency units can adaptively flag to the base station different parts of the map as more or less important depending on their distance from a certain disaster zone. The task of the base station is then to send a packet combination that satisfies the largest total priority. One can also combine user-dependent packet weights with the channel state prediction outcomes in a GEC. One possibility is to multiply the probabilities  by the receiver priority. It could then turn out that although a receiver is more likely to be in erasure in the next transmission round, it may be served because of a high priority request.
by the receiver priority. It could then turn out that although a receiver is more likely to be in erasure in the next transmission round, it may be served because of a high priority request.
5. Heuristic Search Algorithms
In Section 3.2, we proposed efficient search algorithms for finding the optimal solution(s) of (4). However, there may be situations where one would like to obtain a (possibly suboptimal) solution much more quickly. This may be the case, for example, when the total number of packets to be transmitted is very large. Therefore, designing efficient heuristic algorithms to complement the optimal search is important. In this section, we propose a number of such heuristics.
5.1. Heuristic 1—Weight Sorted Heuristic Algorithm
The idea behind this recursive algorithm is very simple. As in Algorithm 1, we start with the original problem of size  . We then rearrange the columns of the matrix
. We then rearrange the columns of the matrix  in descending order of
in descending order of  (starting from the packet with the highest weight). Note that this is different from the sorted pruning version of the Algorithm 1, in which the columns of
(starting from the packet with the highest weight). Note that this is different from the sorted pruning version of the Algorithm 1, in which the columns of  were sorted in descending order of
were sorted in descending order of  to potentially result in large constrained sets. We then set the head variable
to potentially result in large constrained sets. We then set the head variable  and find its corresponding constrained set
and find its corresponding constrained set  to resolve
to resolve  variables that are to be set to zero. We then solve the smaller problem of size
variables that are to be set to zero. We then solve the smaller problem of size  and continue until the problem cannot be further reduced. One main difference between Heuristic 1 and Algorithm 1 is that at each recursion, the head variable is only set to one; the other possibility of
and continue until the problem cannot be further reduced. One main difference between Heuristic 1 and Algorithm 1 is that at each recursion, the head variable is only set to one; the other possibility of  is not pursued at all. In a sense, this heuristic algorithm finds greedy solutions to the problem at each recursion by serving the highest priority packet. In this heuristic algorithm, all
is not pursued at all. In a sense, this heuristic algorithm finds greedy solutions to the problem at each recursion by serving the highest priority packet. In this heuristic algorithm, all  unconstrained variables are naturally set to 1 in the course of the algorithm. The computational complexity of this method is at worst proportional to
unconstrained variables are naturally set to 1 in the course of the algorithm. The computational complexity of this method is at worst proportional to  , which can happen when there is no constraint between packets.
, which can happen when there is no constraint between packets.
5.2. Heuristic 2—Search Algorithm 1 with Maximum Recursions/Elapsed Time
It is possible to terminate the recursive search Algorithm 1 prematurely once it reaches a maximum number of allowed recursions/elapsed time. If the algorithm reaches this value and the search is not complete, it performs a termination procedure whereby it heuristically resolves the remaining unresolved packets in the current incomplete solution. That is, it performs Heuristic 1 on a smaller problem, which is yet to be solved. It then returns the best solution that has been found so far. We note that due the extra termination procedure, the actual number of recursions/elapsed time can be (slightly) higher than the preset value.
Two comments are in order here. Firstly, Algorithm 1 is designed to sort the matrix  based on the number of receivers that need a packet. It only reverts to sorting the unresolved variables based on the vector
based on the number of receivers that need a packet. It only reverts to sorting the unresolved variables based on the vector  in the termination process. Secondly, if the maximum number of recursions is set to one, Algorithm 1 just performs the termination process and becomes identical to Heuristic 1.
in the termination process. Secondly, if the maximum number of recursions is set to one, Algorithm 1 just performs the termination process and becomes identical to Heuristic 1.
5.3. Heuristic 3—Dynamic Number of Recursions
This heuristic is based on Heuristic 2, where we dynamically increase the number of allowed recursions as needed. At each transmission round, we start with only one allowed recursion (effectively run Heuristic 1). If the throughput (Let  denote the index of receivers that still need at least one packet and
denote the index of receivers that still need at least one packet and  denote such receivers. The achieved throughput at time slot
denote such receivers. The achieved throughput at time slot  is defined as
is defined as  , where
, where  is the found solution and
is the found solution and  is an appropriate function of receivers' needs. For memoryless erasures
is an appropriate function of receivers' needs. For memoryless erasures  and for GEC's
and for GEC's  (refer to Section 4 and (7)).) is higher than a desired value, there is no need to proceed any further. Otherwise, we can gradually increase the number of recursions by an appropriate step size. This heuristic stops when it either reaches the maximum allowed recursions or when increasing the number of recursions does not result in a noticeable improvement in the throughput.
(refer to Section 4 and (7)).) is higher than a desired value, there is no need to proceed any further. Otherwise, we can gradually increase the number of recursions by an appropriate step size. This heuristic stops when it either reaches the maximum allowed recursions or when increasing the number of recursions does not result in a noticeable improvement in the throughput.
6. Numerical Results and Secondary Coding Considerations
We start this section by presenting end-to-end decoding delay results for memoryless erasure channels. We then specialize to erasure channels with memory. The end-to-end problem is the complete transmission of  packets. End-to-end decoding delay of a receiver is the sum of decoding delays for the receiver in each transmission step. In the following, when we say "the delay performance of method X", we are referring to the delay performance of the end-to-end transmission, where method X is applied at each step.
packets. End-to-end decoding delay of a receiver is the sum of decoding delays for the receiver in each transmission step. In the following, when we say "the delay performance of method X", we are referring to the delay performance of the end-to-end transmission, where method X is applied at each step.
In the course of presenting the results and based on the observed trends, we will discuss some secondary coding techniques and post processing considerations that can improve the decoding delay. Throughout the analysis of this section, we assume independent erasures in different links with identical probabilities. Hence, we can drop subscript  when referring to link erasure probabilities.
when referring to link erasure probabilities.
Figure 2 shows the median of decoding delay for the transmission of  packets to
packets to  to
to  receivers. Channel erasures are memoryless and occur with a high probability of
receivers. Channel erasures are memoryless and occur with a high probability of  independently in every link. The median of delay is computed across all receivers and is, in fact, also the median across many stochastic runs of the algorithms. The first curve from below shows the delay obtained from Algorithm 1 (Throughout the numerical evaluations, we used the sorted pruning version of Algorithm 1.). The middle curve is the delay obtained by performing Heuristic 1. The top curve shows a reproduction of delay results reported in [8] which are based on a random opportunistic instantaneous network coding strategy. In this case, the transmitter first selects a packet needed by at least one receiver at random. Then, it goes over other packets in some order and adds a packet to the current choice only if their addition still results in instantaneous decodability. In comparison, Heuristic 1 performs noticeably better than that in [8] and more importantly, is not much far away from the results of Algorithm 1. This is specially important since for some number of receivers, Heuristic 1 can run considerably faster than Algorithm 1, which will be shown in the coming figures shortly.
independently in every link. The median of delay is computed across all receivers and is, in fact, also the median across many stochastic runs of the algorithms. The first curve from below shows the delay obtained from Algorithm 1 (Throughout the numerical evaluations, we used the sorted pruning version of Algorithm 1.). The middle curve is the delay obtained by performing Heuristic 1. The top curve shows a reproduction of delay results reported in [8] which are based on a random opportunistic instantaneous network coding strategy. In this case, the transmitter first selects a packet needed by at least one receiver at random. Then, it goes over other packets in some order and adds a packet to the current choice only if their addition still results in instantaneous decodability. In comparison, Heuristic 1 performs noticeably better than that in [8] and more importantly, is not much far away from the results of Algorithm 1. This is specially important since for some number of receivers, Heuristic 1 can run considerably faster than Algorithm 1, which will be shown in the coming figures shortly.
Median of decoding delay for the transmission of  packets to
packets to  to
to  receivers. Channel erasures are memoryless and occur with a high probability of
receivers. Channel erasures are memoryless and occur with a high probability of  independently in every link. Algorithm 1, Heuristic 1 and random Heuristic [8] are compared with each other.
independently in every link. Algorithm 1, Heuristic 1 and random Heuristic [8] are compared with each other.
Figure 3 compares the mean delay performance of different heuristics presented in Section 5 with that of Algorithm 1. Similar to the previous figure, mean delay is computed across all receivers. The delay performance of Heuristic 2, Heuristic 3, and Algorithm 1 are close, whereas Heuristic 1 results in the largest delay. A careful reader may notice that the end-to-end performance of Heuristic 2 is at times better than Algorithm 1. While the difference is practically insignificant, this deserves some explanation. The end-to-end transmission problem involves making packet transmission decisions at each step. While all algorithms start with the same packet incidence matrix (all-ones), due to packet erasures and as they make decisions about transmission of packets at each step, they take diverging paths in the solution space. As a result, they end up with different packet incidence matrices to solve over time. Hence, it is conceivable for an algorithm to make suboptimal decisions at one or more steps and yet end up with a better end-to-end delay than Algorithm 1 that strictly makes optimal decisions at every step. Intuition suggests that an algorithm such as Heuristic 1 that consistently makes suboptimal decisions is unlikely to outperform Algorithm 1 end-to-end, which is confirmed by the numerical results. However, an algorithm such as Heuristic 2 which almost always makes optimal decisions with only infrequent exceptions, may outperform Algorithm 1. According to Figure 3, these perturbations in end-to-end performance are practically insignificant and the intuitive choice of the optimal or a largely optimal algorithm at each step will result in the best end-to-end performance.
We note that the delays presented here (and also in the following figures) are, in fact, excess median or mean delays beyond the minimum required number of transmissions, which is  . For example, a mean delay of 10 slots for
. For example, a mean delay of 10 slots for  packets signifies on average
packets signifies on average  overhead, which is the price for guaranteeing instantaneous decodability. In other words, one measure of throughput is
overhead, which is the price for guaranteeing instantaneous decodability. In other words, one measure of throughput is  , where
, where  is the mean delay across all receivers. An example is shown in Figure 3. For up to around
is the mean delay across all receivers. An example is shown in Figure 3. For up to around  receivers in the system, Algorithm 1, Heuristics 2, and 3 ensure an average throughput loss of
receivers in the system, Algorithm 1, Heuristics 2, and 3 ensure an average throughput loss of  .
.
It is quite possible that Algorithm 1 returns multiple network coding solutions all of which have the same objective value  . A natural question that arises is whether systematic selection of a solution with a particular property is better than others in the presence of erasures in the channel. Our experiments verify that indeed some secondary post processing on the solutions can improve the end-to-end delay. In particular, we compare two post processing techniques:
. A natural question that arises is whether systematic selection of a solution with a particular property is better than others in the presence of erasures in the channel. Our experiments verify that indeed some secondary post processing on the solutions can improve the end-to-end delay. In particular, we compare two post processing techniques:  selecting a solution which involves minimum amount of coding (lowest number of 1's in the solution vector
selecting a solution which involves minimum amount of coding (lowest number of 1's in the solution vector  ) and
) and  selecting a solution with maximum amount of coding (highest number of 1's in the solution vector
selecting a solution with maximum amount of coding (highest number of 1's in the solution vector  ). Figure 4 shows the effects of such processing on the overall decoding delays. It is clear that maximum coding is not a reasonable choice and results in worse delays compared with minimum coding. We attempt to explain this behavior by means of an example and intuitive reasoning. Let us assume that there are
). Figure 4 shows the effects of such processing on the overall decoding delays. It is clear that maximum coding is not a reasonable choice and results in worse delays compared with minimum coding. We attempt to explain this behavior by means of an example and intuitive reasoning. Let us assume that there are  packets to be transmitted to
packets to be transmitted to  receivers and at the beginning of the third transmission round, matrix
receivers and at the beginning of the third transmission round, matrix  is given as follows
is given as follows

It is clear that there are two optimal solutions: we can either send packets  or packet
or packet  by itself, where the former involves coding and latter is uncoded. Now let us assume that we select the maximum coding strategy and send
by itself, where the former involves coding and latter is uncoded. Now let us assume that we select the maximum coding strategy and send  . If in the third transmission round only
. If in the third transmission round only  successfully receives,
successfully receives,  will become
will become

and clearly the optimal solution is sending packet  . If in the fourth transmission round only
. If in the fourth transmission round only  successfully receives,
successfully receives,  will become
will become

where it is evident that in the fifth transmission round, we cannot find a packet which is innovative and instantaneously decodable for all the three receivers. On the other hand, one can verify that if we adopt a minimum coding strategy and send packet  in the third transmission round, we can always find innovative and instantaneously decodable packets for all three receivers in the future regardless of erasures in the channel. In summary, solutions with less coding tend to cause less constrains on the problem in the future.
in the third transmission round, we can always find innovative and instantaneously decodable packets for all three receivers in the future regardless of erasures in the channel. In summary, solutions with less coding tend to cause less constrains on the problem in the future.
It is noted in Figure 4 that the first solution returned by Algorithm 1 performs almost the same as the minimum coding solution. The reason for this is that Algorithm 1 first ranks the packets based on the number of receivers that need them. Therefore, the first solution picked by the algorithm is likely to contain packets with largest constrained sets and hence, many resolved packets are set to zero, which often translates into small amount of coding. Throughout this section, unless otherwise stated, we have shown the delay results based on the first returned solution of Algorithm 1.
It is interesting to analyze the actual number of recursions that the search in Algorithm 1 takes to find the optimum solution. This is shown in Figure 5 for  packets along with the number of recursions required in Heuristics 1, 2, and 3. Algorithm 1 shows three modes of behavior: low, medium, and high number of recursions. When the number of receivers is larger than
packets along with the number of recursions required in Heuristics 1, 2, and 3. Algorithm 1 shows three modes of behavior: low, medium, and high number of recursions. When the number of receivers is larger than  , Algorithm 1 finds the optimal solution very quickly and the number of recursions is very close to the number of packets
, Algorithm 1 finds the optimal solution very quickly and the number of recursions is very close to the number of packets  . However, when the number of receivers is lower, the constraints that each receiver imposes on the network coding decisions cannot limit the search space enough and hence, a large number of combinations have to be tested. Obviously, Heuristic 1 has the lowest number of recursions. Compared to Heuristic 2 with 100 fixed recursions, dynamic Heuristic 3 can almost halve the number of recursions with negligible effect on delay performance (see Figure 3). By referring to Figure 3, we conclude that for the system under consideration, the excessive number of recursions in Algorithm 1 is not warranted as it does not result in any noticeable delay improvement compared to Heuristics 2 or 3.
. However, when the number of receivers is lower, the constraints that each receiver imposes on the network coding decisions cannot limit the search space enough and hence, a large number of combinations have to be tested. Obviously, Heuristic 1 has the lowest number of recursions. Compared to Heuristic 2 with 100 fixed recursions, dynamic Heuristic 3 can almost halve the number of recursions with negligible effect on delay performance (see Figure 3). By referring to Figure 3, we conclude that for the system under consideration, the excessive number of recursions in Algorithm 1 is not warranted as it does not result in any noticeable delay improvement compared to Heuristics 2 or 3.
Average number of recursions in Algorithm 1 and Heuristics 1–3. The maximum number of recursions for both Heuristic 2 and 3 is set to 100. By referring to Figure 3, we observe that for small number of receivers, Heuristics 2-3 can provide same decoding delays at a fraction of computational complexity.
Figure 6 shows the effect of increasing the number of packets on the computational complexity of Algorithm 1 in terms of number of recursions to complete the search.Three different numbers of receivers  ,
,  , and
, and  are considered. The complexity remains linear with the number of packets for well-sized receiver populations (30 and 40 receivers). This is in agreement with observations in Figure 5. When the number of receivers is not so large (see the blue curve in Figure 6 for
are considered. The complexity remains linear with the number of packets for well-sized receiver populations (30 and 40 receivers). This is in agreement with observations in Figure 5. When the number of receivers is not so large (see the blue curve in Figure 6 for  ), we see a sudden growth in complexity, in terms of number of recursions, when
), we see a sudden growth in complexity, in terms of number of recursions, when  packets. In such situations, truncating the number of recursion to be linear with the number of packets (Heuristic 2) is a good alternative.
packets. In such situations, truncating the number of recursion to be linear with the number of packets (Heuristic 2) is a good alternative.
Figure 7 shows the impact of the number of packets and also erasure probability on the decoding delay. The normalized mean delay versus number of packets  is plotted for three different erasure probabilities
is plotted for three different erasure probabilities  ,
,  , and
, and  , which are still high erasure probabilities. The number of receivers is fixed to
, which are still high erasure probabilities. The number of receivers is fixed to  . The delay performance of Heuristics 1 and 3 are shown. A few observations are made. Firstly, as expected, the delay (both absolute and normalized measures) decreases as the erasure probability decreases. Secondly, the difference in the delay performance between Heuristics 1 and 3 decreases as the erasure probability decreases. This trend has also been observed for other number of receivers. Moreover, the difference between heuristics and Algorithm 1 decreases with erasure probability, which is not shown here for clarity of figure. Finally, the normalized delay decreases as the number of packets increases. We noted, however, that the absolute delay may increase or decrease depending on the number of receivers in the system. We attribute possible decrease in the normalized delay to the fact that when there are more packets to transmit, the transmitter has more options to choose from and hence, encounters delays less often in a normalized sense.
. The delay performance of Heuristics 1 and 3 are shown. A few observations are made. Firstly, as expected, the delay (both absolute and normalized measures) decreases as the erasure probability decreases. Secondly, the difference in the delay performance between Heuristics 1 and 3 decreases as the erasure probability decreases. This trend has also been observed for other number of receivers. Moreover, the difference between heuristics and Algorithm 1 decreases with erasure probability, which is not shown here for clarity of figure. Finally, the normalized delay decreases as the number of packets increases. We noted, however, that the absolute delay may increase or decrease depending on the number of receivers in the system. We attribute possible decrease in the normalized delay to the fact that when there are more packets to transmit, the transmitter has more options to choose from and hence, encounters delays less often in a normalized sense.
The effect of number of packets and erasure probabilities on the normalized delay. The maximum number of recursions for Heuristic 3 is set to 100. As the erasure probability decreases, the delay decreases as expected. The normalized delay decreases with  for this particular
for this particular  (this is not always the case).
(this is not always the case).
An important question that may arise in practical situations is how to choose the "block size" or the number of packets that are taken into account for making network coding decisions. If one has a total of  packets to transmit, does it make sense to divide them into subblocks of smaller sizes or does it make sense to treat them as one single block of packets? The short answer is to include all "order-insensitive" packets in making transmission decisions and only break the packets into subblocks when the assumption of order insensitivity between subblocks breaks down. In the extreme case, an infinite number of order-insensitive packets provides an infinite pool of packets to choose from that can satisfy the demands of all receivers and are instantaneously decodable. Figure 8 shows the end-to-end delay when the number of packets in a block is finite and
packets to transmit, does it make sense to divide them into subblocks of smaller sizes or does it make sense to treat them as one single block of packets? The short answer is to include all "order-insensitive" packets in making transmission decisions and only break the packets into subblocks when the assumption of order insensitivity between subblocks breaks down. In the extreme case, an infinite number of order-insensitive packets provides an infinite pool of packets to choose from that can satisfy the demands of all receivers and are instantaneously decodable. Figure 8 shows the end-to-end delay when the number of packets in a block is finite and  packets is chosen as the reference for comparison. We can see that although the delay of transmitting
packets is chosen as the reference for comparison. We can see that although the delay of transmitting  packets,
packets,  , can be larger than that of transmitting
, can be larger than that of transmitting  packets
packets  , the delay does not increase by a factor of
, the delay does not increase by a factor of  . That is
. That is  and one does not benefit from breaking
and one does not benefit from breaking  packets into
packets into  subblocks of size
subblocks of size  packets each. By treating
packets each. By treating  subblocks of size
subblocks of size  as one block of size
as one block of size  , we add more degrees of freedom in making decisions.
, we add more degrees of freedom in making decisions.
The effect of block size on the mean delay. If the delay of transmitting  packets in Heuristic 1,
packets in Heuristic 1,  , is taken as the reference, we can see that the delay of including
, is taken as the reference, we can see that the delay of including  packets in transmission is less than
packets in transmission is less than  . The same observation applies to the delay of Algorithm 1. In general, it is recommended to include all "order-insensitive" packets in making transmission decisions and only break the packets into subblocks when the assumption of order insensitivity between subblocks breaks down.
. The same observation applies to the delay of Algorithm 1. In general, it is recommended to include all "order-insensitive" packets in making transmission decisions and only break the packets into subblocks when the assumption of order insensitivity between subblocks breaks down.
Now we turn our attention to the delay performance of our algorithms in channels with memory. Figure 9 shows the mean delay of different algorithms for  packets and
packets and  receivers. The GEC parameters for all links are identical with
receivers. The GEC parameters for all links are identical with  . The horizontal axis shows the memory content
. The horizontal axis shows the memory content  .The first curve from above shows the performance of Algorithm 1 when the transmitter does not take channel conditions into account in making coding decisions. In other words,
.The first curve from above shows the performance of Algorithm 1 when the transmitter does not take channel conditions into account in making coding decisions. In other words,  is used in Algorithm 1 as if the channel states were memoryless. For relatively large memory contents, this method results in the largest mean delay. The next curve shows the delay performance of Heuristic 1. The next two curves, which are almost indistinguishable, show the performance of Algorithm 1 which takes channel states into account (using (7)) and Heuristic 2 with 100 recursions. The last curve shows the best delay that can be achieved by occasionally violating the instantaneous decodability rule for one receiver in favor of the other two receivers that are predicted to be in good state in the next transmission round. More details can be found in [14].
is used in Algorithm 1 as if the channel states were memoryless. For relatively large memory contents, this method results in the largest mean delay. The next curve shows the delay performance of Heuristic 1. The next two curves, which are almost indistinguishable, show the performance of Algorithm 1 which takes channel states into account (using (7)) and Heuristic 2 with 100 recursions. The last curve shows the best delay that can be achieved by occasionally violating the instantaneous decodability rule for one receiver in favor of the other two receivers that are predicted to be in good state in the next transmission round. More details can be found in [14].
Figure 10 shows the delay performance of Algorithm 1 using packet weights according to (7) for  to
to  receivers. Both the mean delay and mean delay plus one standard deviation of delay (across 1000 stochastic runs of the transmission) are shown. As expected, the delay increases as the number of receivers increases. Comparing the delay's standard deviation with its mean, we observe that when the number of receivers is 3–5, the delay is relatively more variant than when the number of receivers is 10–15. For example, for
receivers. Both the mean delay and mean delay plus one standard deviation of delay (across 1000 stochastic runs of the transmission) are shown. As expected, the delay increases as the number of receivers increases. Comparing the delay's standard deviation with its mean, we observe that when the number of receivers is 3–5, the delay is relatively more variant than when the number of receivers is 10–15. For example, for  and
and  , the ratio of standard deviation to mean delay is around
, the ratio of standard deviation to mean delay is around  , whereas for
, whereas for  and
and  this ratio reduce to only
this ratio reduce to only  . One should keep these variations in mind when designing the transmission system.
. One should keep these variations in mind when designing the transmission system.
Delay performance of Algorithm 1 with weights defined using (7) for different number of receivers. As expected, the delay increases with the number of receivers. Both the mean delay (solid curves) and mean delay plus one standard deviation of delay (dashed-dotted curves) across 1000 stochastic runs of the transmission are shown.
We conclude this section with a brief look at the effect of post processing on the delay performance in channels with memory. Figure 11 shows different delays for  receivers and
receivers and  packets. The figure confirms our earlier finding that selecting the maximum amount of coding among the optimal solutions provided by Algorithm 1 can result in larger end-to-end delays. We also note that serving the maximum number of receivers can have an adverse effect on the delay in GEC's. To explain this, consider an example where there are
packets. The figure confirms our earlier finding that selecting the maximum amount of coding among the optimal solutions provided by Algorithm 1 can result in larger end-to-end delays. We also note that serving the maximum number of receivers can have an adverse effect on the delay in GEC's. To explain this, consider an example where there are  left packets to be transmitted to
left packets to be transmitted to  receivers. Packet 1 is needed by
receivers. Packet 1 is needed by  to
to  and packet 2 is needed by
and packet 2 is needed by  and
and  . Since both packets are needed by
. Since both packets are needed by  , we can either send packet 1 or 2, but not both. Now assume that
, we can either send packet 1 or 2, but not both. Now assume that  to
to  are all predicted to be in good state with probability
are all predicted to be in good state with probability  and
and  is predicted to be in good state with probability
is predicted to be in good state with probability  , so that
, so that  according to (7). Therefore, transmission of either packet seems to be equally optimal. However, one can easily verify that the probability of at least one receiver among
according to (7). Therefore, transmission of either packet seems to be equally optimal. However, one can easily verify that the probability of at least one receiver among  to
to  receiving packet 1 is only
receiving packet 1 is only  , whereas the probability of either
, whereas the probability of either  or
or  receiving packet 2 is
receiving packet 2 is  . Therefore, it makes sense to satisfy only two receivers, one of which has a high priority due its good channel conditions.
. Therefore, it makes sense to satisfy only two receivers, one of which has a high priority due its good channel conditions.
7. Conclusions
In this paper, we provided an online optimal network coding scheme with feedback to minimize decoding delay in each transmission round in erasure broadcast channels. Efficient search algorithms for the optimal network coding solution, as well as heuristic methods were presented and their delay and computational performance were tested in several system scenarios. We found that adopting an optimized approach using as much information about the channel as possible, such as memory, leads to a significantly better decoding delay. An interesting problem for future research is to relax the instantaneous decodability condition to  -step decodability and investigate the delay-throughput tradeoff.
-step decodability and investigate the delay-throughput tradeoff.
References
Shokrollahi A: Raptor codes. IEEE Transactions on Information Theory 2006, 52(6):2551-2567.
Ho T, Medard M, Koetter R, et al.: A random linear network coding approach to multicast. IEEE Transactions on Information Theory 2006, 52(10):4413-4430.
Eryilmaz A, Ozdaglar A, Medard M: On delay performance gains from network coding. Proceedings of the IEEE Annual Conference on Information Sciences and Systems (CISS '06), March 2006, Princeton, NJ, USA 864-870.
Lucani DE, Stojanovic M, Medard M: Random linear network coding for time division duplexing: when to stop talking and start listening. Proceedings of the IEEE Conference on Computer Communications (INFOCOM '09), April 2009 1800-1808.
Sundararajan J-K, Shah D, Medard M: Feedback-based online network coding. Submitted to IEEE Transactions on Information Theory, http://arxiv.org/pdf/0904.1730v1 Submitted to IEEE Transactions on Information Theory,
Sundararajan J-K, Sadeghi P, Medard M: A feedback-based adaptive broadcast coding scheme for reducing in-order delivery delay. Proceedings of the Workshop on Network Coding, Theory, and Applications (NetCod '09), June 2009, Lausanne, Switzerland
Goyal VK: Multiple description coding: compression meets the network. IEEE Signal Processing Magazine 2001, 18(5):74-93. 10.1109/79.952806
Keller L, Drinea E, Fragouli C: Online broadcasting with network coding. Proceedings of the 4th Workshop on Network Coding, Theory, and Applications (NetCod '08), January 2008, Hong kong
Bertsimas D, Weissmantel R: Optimization Over Integers. Dynamic Ideas, Belmont, Mass, USA; 2005.
Rappaport TS: Wireless Communications, Principles and Practice. 2nd edition. Prentice Hall, Upper Saddle River, NJ, USA; 2002.
Sadeghi P, Kennedy RA, Rapajic PB, Shams R: Finite-state Markov modeling of fading channels: a survey of principles and applications. IEEE Signal Processing Magazine 2008, 25(5):57-80.
Mushkin M, Bar-David I: Capacity and coding for the Gilbert-Elliot channels. IEEE Transactions on Information Theory 1989, 35(6):1277-1290.
Katti S, Rahul H, Hu W, Katabi D, Medard M, Crowcroft J: XORs in the air: practical wireless network coding. In Proceedings of the ACM Computer Communication Review (SIGCOMM '06), October 2006. Volume 36. ACM Press; 243-254.
Sadeghi P, Traskov D, Koetter R: Adaptive network coding for broadcast channels. Proceedings of the Workshop on Network Coding, Theory, and Applications (NetCod '09), June 2009, Lausanne, Switzerland 80-85.
Acknowledgments
The authors wish to thank anonymous reviewers for their valuable comments which helped to improve the presentation of this paper. In the early stages of this work, the authors benefited from fruitful discussions with Ralf Koetter. This paper is dedicated to his memory. Preliminary results of this paper were presented in the 2009 Workshop on Network Coding, Theory and Applications (NetCod 2009), Lausanne, Switzerland. The work of P. Sadeghi was supported under ARC Discovery Projects funding scheme (Project no. DP0984950). The work of D. Traskov was supported by the European Commission in the framework of the FP7 Network of Excellence in Wireless COMmunications NEWCOM++ (Contract no. 216715).
Author information
Authors and Affiliations
Corresponding author
Appendix
Here we prove by structural induction that (a) every result returned by Algorithm 1 is a solution of (4) and (b) the set of solutions returned by the algorithm contains all the optimal solutions. We note that the algorithm is designed to discard infeasible vectors and those solutions that are clearly suboptimal at each recursion to improve performance. The latter is based on positiveness of the elements of  as explained below.The algorithm generates a binary tree. Each node represents a problem of size
as explained below.The algorithm generates a binary tree. Each node represents a problem of size  and
and  , and branches into two subproblems of size
, and branches into two subproblems of size  and
and  . The former subproblem is a result of setting
. The former subproblem is a result of setting  and the latter a result of setting
and the latter a result of setting  . A leaf is reached when we need to solve
. A leaf is reached when we need to solve  . Without loss of generality let us assume that the variable to be examined is the first variable (
. Without loss of generality let us assume that the variable to be examined is the first variable ( ) which is followed by
) which is followed by  variables (
variables ( to
to  ) that are constrained to
) that are constrained to  ,
,  variables (
variables ( to
to  ) that are constrained but not to
) that are constrained but not to  , and finally
, and finally  unconstrained variables
unconstrained variables  to
to  . This can be easily accomplished by rearranging the columns of
. This can be easily accomplished by rearranging the columns of  .For
.For  , it is clear that the only optimal solution to
, it is clear that the only optimal solution to  is
is  which is returned by the algorithm. Hence, the minimal structure of the algorithm returns the optimal solution and our claim is true for
which is returned by the algorithm. Hence, the minimal structure of the algorithm returns the optimal solution and our claim is true for  . The induction hypothesis is that the two subproblems
. The induction hypothesis is that the two subproblems  and
and  have only discarded infeasible vectors and some suboptimal solutions. We need to prove that the same statement applies to the parent problem
have only discarded infeasible vectors and some suboptimal solutions. We need to prove that the same statement applies to the parent problem  .We first look at the left branch where
.We first look at the left branch where  . According to the construction of the algorithm, any solution such as
. According to the construction of the algorithm, any solution such as  of length
of length  provided by the left branch
provided by the left branch  is appended by the parent problem
is appended by the parent problem  to form
to form

 is set to one, variables constrained to
is set to one, variables constrained to  are set to zero and all unconstrained variables are set to one. We first prove that
are set to zero and all unconstrained variables are set to one. We first prove that  is indeed a solution and then show that changing any element of
is indeed a solution and then show that changing any element of  results in either an infeasible or a clearly suboptimal
results in either an infeasible or a clearly suboptimal  . We use Definitions 6–8.(i)For
. We use Definitions 6–8.(i)For
 as a weighted sum of columns of
as a weighted sum of columns of  . That is,
. That is,  , where
, where  is a submatrix of
is a submatrix of  of size
of size  , which is input to
, which is input to  , and according to the induction hypothesis
, and according to the induction hypothesis  . But since no variable in
. But since no variable in  is constrained to
is constrained to  , no column in
, no column in  and
and  can have ones in the same row position. Therefore,
can have ones in the same row position. Therefore,  .(ii)Since
.(ii)Since  to
to  are unconstrained, no column
are unconstrained, no column  to
to  can have ones in the same row position. Hence,
can have ones in the same row position. Hence,  .(iii)Using similar arguments, we can assert that no column in
.(iii)Using similar arguments, we can assert that no column in  or
or  can have ones in the same row positions as
can have ones in the same row positions as  to
to  do. Therefore,
do. Therefore,  and
and  is a solution.(iv)We now argue that variables
is a solution.(iv)We now argue that variables  to
to  cannot be anything other than zero. This directly follows from the fact that
cannot be anything other than zero. This directly follows from the fact that  is constrained with
is constrained with  for
for  and hence, in any given solution they cannot be simultaneously one.(v)Since we have already found a solution
and hence, in any given solution they cannot be simultaneously one.(v)Since we have already found a solution  where the first and last
where the first and last  variables are one, we know that any other solution such as
variables are one, we know that any other solution such as  with one or more zeros in these positions becomes suboptimal and can be discarded. That is,
with one or more zeros in these positions becomes suboptimal and can be discarded. That is,  due to positiveness of elements of
due to positiveness of elements of  .(vi)Finally, according to induction hypothesis, we know that
.(vi)Finally, according to induction hypothesis, we know that  cannot be changed into anything other than what
cannot be changed into anything other than what  provides without making it either infeasible or suboptimal. In summary, for each solution
provides without making it either infeasible or suboptimal. In summary, for each solution  provided by the left branch
provided by the left branch  , the constructed vector
, the constructed vector
 . According to the construction of the algorithm, a given solution such as
. According to the construction of the algorithm, a given solution such as  of length
of length  provided by the right branch
provided by the right branch  is appended by the parent problem
is appended by the parent problem  to form
to form
 this is indeed a solution. We then show that changing any element of
this is indeed a solution. We then show that changing any element of  can only result in an infeasible vector, a clearly suboptimal solution, or a duplicate solution already provided by the left branch and hence, can be discarded. We use Definitions 6–8.(i)We write
can only result in an infeasible vector, a clearly suboptimal solution, or a duplicate solution already provided by the left branch and hence, can be discarded. We use Definitions 6–8.(i)We write  as
as  , where
, where  is a submatrix of
is a submatrix of  of size
of size  , which is input to
, which is input to  , and according to the induction hypothesis
, and according to the induction hypothesis  . Similar to the arguments for the left branch, we can assert that no column
. Similar to the arguments for the left branch, we can assert that no column  to
to  corresponding to unconstrained variables can have ones in the same row position. Hence,
corresponding to unconstrained variables can have ones in the same row position. Hence,  . Furthermore, that no column in
. Furthermore, that no column in  can have ones in the same row positions as
can have ones in the same row positions as  to
to  . Therefore,
. Therefore,  and
and  is a solution.(ii)Since we have already found a solution
is a solution.(ii)Since we have already found a solution  where the last
where the last  variables are one, we know that any other solution such as
variables are one, we know that any other solution such as  with one or more zeros in these positions becomes suboptimal and can be discarded.(iii)Finally, we show that any vector of the form
with one or more zeros in these positions becomes suboptimal and can be discarded.(iii)Finally, we show that any vector of the form
 . If
. If  for any
for any  , then we have already shown in the analysis of the left branch that
, then we have already shown in the analysis of the left branch that
 and
and  are constrained to each other. If none of
are constrained to each other. If none of  to
to  are one, then
are one, then  will be of the form
will be of the form
 . But,
. But,  has to be a solution of
has to be a solution of  . Hence, considering vectors of the form
. Hence, considering vectors of the form
 provided by the right branch
provided by the right branch  , the constructed vector
, the constructed vector









Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sadeghi, P., Shams, R. & Traskov, D. An Optimal Adaptive Network Coding Scheme for Minimizing Decoding Delay in Broadcast Erasure Channels. J Wireless Com Network 2010, 618016 (2010). https://doi.org/10.1155/2010/618016
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/618016
 are positive). In the above example,
are positive). In the above example, 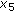 and
and 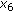 must be set to 1 because no other variable is constrained to them (we will make this statement formal in the optimality proof of the algorithm in the appendix).
must be set to 1 because no other variable is constrained to them (we will make this statement formal in the optimality proof of the algorithm in the appendix). forces
forces  and
and 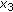 to zero.
to zero. :
:
 then
then
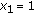 (since the variable is not constrained).
(since the variable is not constrained).
 to
to
 .
.
 and the cardinality of its constrained
and the cardinality of its constrained

 and
and  within itself.
within itself.

 packets to
packets to  to
to  receivers. Algorithm 1 is compared with Heuristics 1–3. Both Heuristics 2 and 3 perform very closely to Algorithm 1. The maximum number of recursions for both Heuristic 2 and 3 is set to 100.
receivers. Algorithm 1 is compared with Heuristics 1–3. Both Heuristics 2 and 3 perform very closely to Algorithm 1. The maximum number of recursions for both Heuristic 2 and 3 is set to 100.






