- Research Article
- Open access
- Published:
Throughput-Efficient Dynamic Coalition Formation in Distributed Cognitive Radio Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 653913 (2010)
Abstract
We formulate the problem of distributed throughput-efficient sensing in cognitive radio (CR) networks as a dynamic coalition formation game based on a Markovian model. The proposed coalition formation enables the CRs to increase their achievable throughput, under the detection probability constraint, while also taking into account the overhead in sensing reports combining. The dynamic model of coalition formation is used to express and model the behavior of the coalition forming CRs over time. In the proposed game, CRs form coalitions either to increase their individual gains (selfish coalition formation) or to maximize the overall gains of the group (altruistic coalition formation). We show that the proposed coalition formation solutions yield significant gains in terms of reduced average false alarm probability and increased average throughput per CR as compared to the non-cooperative solutions. Given a target detection probability for a coalition, we adopt a weighted target detection probability for individual CRs in a coalition. We find that the weighted target detection probability for individual CRs results in increased average throughput per CR as compared to when each CR is assigned the same target detection probability in a coalition.
1. Introduction
Access to radio spectrum has traditionally been regulated by government agencies. This approach to radio spectrum management has been mostly successful in interference avoidance, but at the expense of efficiency in overall spectrum utilization. Cognitive radio networks are envisioned to utilize the radio spectrum more efficiently through opportunistic access to licensed frequency spectrum. A CR utilizes spectrum opportunistically by monitoring the licensed frequency spectrum to reliably detect the licensed (primary) user signals and operating whenever the primary user is absent. The detection of primary user signals is called spectrum sensing. As with any detection problem, the two types of errors associated with spectrum sensing are false alarms and missed detections. The lower the missed detection probability, the better the primary user is protected. However, to increase the achievable throughput of the CRs, the false alarm probability must also be low. Thus, there exists an inherent tradeoff between protection of primary users and achievable throughput for the cognitive radio network [1, 2].
Cooperation in sensing can reduce the false alarm probability of the cooperating CRs [3, 4]. In cooperative spectrum sensing, each CR performs spectrum sensing and sends its sensing report to a data collector known as the fusion center. To reduce signaling cost, the report may be binary (hard decision), consisting of zeros (primary user not present) and ones (primary user present). Hard decisions may be combined at the fusion center using, for example, "OR", "AND", and "MAJORITY" rules [1, 2]. However, in distributed CR networks, individual CRs need to interact with each other without a centralized fusion center.
This paper formulates the problem of distributed throughput-efficient sensing in cognitive radio networks as a dynamic coalition formation game based on a Markovian model. Our model is dynamic in the sense that distributed CRs reach self-organizing stable coalition structures (where no two coalitions have an incentive to merge) through a time-evolving sequence of steps. We model coalition structures as a sequence of random variables describing the state of the CR network, and the transition mechanism between coalition structures is modeled as a Markov chain [5–7]. The dynamics of the coalition formation enable us to analyze (1) How are the coalitions formed? and (2) How do CRs arrive at equilibrium? We choose a coalition formation framework as it provides tools for the radios to decide which coalitions to form to achieve their goals more efficiently via cooperation [8–10]. In coalition formation, a coalition is a set of distinct, autonomous agents or players which may cooperate in order to increase their individual gains, which we call as selfish cooperation. Or they may cooperate to maximize the overall gains of the group, which we call altruistic cooperation [11, 12]. A key question this paper tries to address is how to coordinate distributed cognitive radios to perform cooperative sensing to minimize their false alarm probabilities and therefore increase their achievable throughput, under a probability of detection constraint. Our model also takes into account the overhead in combining sensing reports.
Two different game theoretic analyses of distributed cooperative spectrum sensing are presented in [13, 14]. In [14], an evolutionary game theoretic framework is used to analyze the interactions among distributed selfish CRs in cooperative sensing. It is assumed in [14] that the selfish CRs overhear the detection results from the other CRs and can free ride by refusing to take part in spectrum sensing. Hence [14] models the spectrum sensing problem as a noncooperative game. Distributed coalition formation for cooperative spectrum sensing CRs is the topic of [13]. Using a merge-and-split based coalition formation game model, the authors in [13] analyze the average missed detection probability per CR. However, unlike [13], we propose a value function that encourages collaborating CRs to minimize their false alarm probabilities for a given target primary user detection probability ( ). This is an important requirement for coexistence with primary users; otherwise, CRs will not be allowed to operate in the primary user band [15]. Moreover, in contrast with [13], the coalition formation model proposed in this paper also takes into account the overhead in combining sensing reports within a coalition. In [5], a dynamic coalition formation game based on a Markovian model is used to analyze the selfish interactions among distributed nodes for spectrum sharing in an interference channel. Unlike [5], we analyze the interactions among CRs for the problem of distributed throughput-efficient sensing in CR networks. Moreover, selfish coalition formation proposed in [5] for distributed networks may lead to a suboptimal equilibrium where nodes, through their interactions, reach an undesirable coalition structure from a network point of view. Hence, we extend the dynamic model of coalition formation proposed in [5] to determine whether and how the coalitional behavior of CRs will change if coalition formation is "not entirely selfish".
). This is an important requirement for coexistence with primary users; otherwise, CRs will not be allowed to operate in the primary user band [15]. Moreover, in contrast with [13], the coalition formation model proposed in this paper also takes into account the overhead in combining sensing reports within a coalition. In [5], a dynamic coalition formation game based on a Markovian model is used to analyze the selfish interactions among distributed nodes for spectrum sharing in an interference channel. Unlike [5], we analyze the interactions among CRs for the problem of distributed throughput-efficient sensing in CR networks. Moreover, selfish coalition formation proposed in [5] for distributed networks may lead to a suboptimal equilibrium where nodes, through their interactions, reach an undesirable coalition structure from a network point of view. Hence, we extend the dynamic model of coalition formation proposed in [5] to determine whether and how the coalitional behavior of CRs will change if coalition formation is "not entirely selfish".
In this paper, using a coalition game-theoretic framework we devise distributed cooperative strategies for CRs that are either selfish or altruistic. We propose a coalition formation model for these CRs to utilize primary user spectrum efficiently, under the constraint of a target probability of detection. We take into account the cost of distributed cooperative sensing in terms of overhead in combining sensing reports within a coalition. We analyze the impact of this cost on the distributed cooperative strategies of CRs. Given a target detection probability for a coalition, we also adopt a weighted target detection probability for individual CRs in a coalition and analyze its impact on the average throughput per CR. We model the stable network structure that emerged as a result of the dynamic coalition formation as the absorbing state of a Markov chain. Using absorbing Markov chain theory, we analyze the mean  and the variance
and the variance  of the time for the game to reach the stable coalition structures. We propose a technique to reduce the time taken by the CRs to form a stable coalition. Using simulations we assess the performance of the proposed altruistic and selfish coalition formation solutions in terms of gains in increased average throughput per CR. We compare these results to the throughput achieved by a noncooperative strategy and by the grand coalition (when all the CRs cooperate). We also determine average maximum coalition sizes for both altruistic and selfish coalition formation solutions. Finally, we evaluate the impact of the distance between the primary user transmitter and the distributed CR network on cooperative strategies of the distributed CRs.
of the time for the game to reach the stable coalition structures. We propose a technique to reduce the time taken by the CRs to form a stable coalition. Using simulations we assess the performance of the proposed altruistic and selfish coalition formation solutions in terms of gains in increased average throughput per CR. We compare these results to the throughput achieved by a noncooperative strategy and by the grand coalition (when all the CRs cooperate). We also determine average maximum coalition sizes for both altruistic and selfish coalition formation solutions. Finally, we evaluate the impact of the distance between the primary user transmitter and the distributed CR network on cooperative strategies of the distributed CRs.
The rest of the paper is organized as follows. Section 2 presents the system setup, while Section 3 introduces the proposed coalition formation game for distributed spectrum sensing. Section 4 introduces the dynamic coalition formation model for the proposed game. Section 5 presents simulation results and an analysis of the proposed dynamic coalition formation model, and Section 6 concludes the paper.
2. System Setup
The system setup used in this paper includes a primary user transmitter and a distributed CR network of  active CRs (transmitter/receiver pairs). The CRs are uniformly and independently distributed in a circle with radius
active CRs (transmitter/receiver pairs). The CRs are uniformly and independently distributed in a circle with radius  and centered at the coordinates
and centered at the coordinates  . The PU (primary user transmitter) is at coordinates
. The PU (primary user transmitter) is at coordinates  as shown in Figure 1. This corresponds to, for example, using only downlink frequencies for CR access. The primary user and CRs are both assumed to use a time-slotted system with perfect time synchronization, and one transmission by primary user corresponds to one time slot, as in [16, 17]. In this approach, the primary user is either present for the whole time slot, or absent for the whole time slot. The CRs use the beginning of each slot for sensing. We assume that
as shown in Figure 1. This corresponds to, for example, using only downlink frequencies for CR access. The primary user and CRs are both assumed to use a time-slotted system with perfect time synchronization, and one transmission by primary user corresponds to one time slot, as in [16, 17]. In this approach, the primary user is either present for the whole time slot, or absent for the whole time slot. The CRs use the beginning of each slot for sensing. We assume that  cognitive radios employ energy detection to make primary user detection observations in the frequency band they are monitoring. The probability of primary user present is denoted by
cognitive radios employ energy detection to make primary user detection observations in the frequency band they are monitoring. The probability of primary user present is denoted by  . In order to detect the primary user, each CR can either sense the spectrum on its own (noncooperative strategy) or it can perform cooperative sensing by forming coalitions with other CRs (cooperative strategy).
. In order to detect the primary user, each CR can either sense the spectrum on its own (noncooperative strategy) or it can perform cooperative sensing by forming coalitions with other CRs (cooperative strategy).
Let us represent the received signal-to-noise ratio (SNR) from the primary user to the  th CR by
th CR by

where  represents noise power and
represents noise power and  is the signal power received by CR
is the signal power received by CR  .
.  is the primary user's signal power,
is the primary user's signal power,  is the distance between the primary user and the
is the distance between the primary user and the  th CR,
th CR,  is the path-loss exponent and
is the path-loss exponent and  is a scalar. In our system setup we assume a complex-valued PSK primary user signal and circular symmetric complex Gaussian (CSCG) noise. For the CSCG noise case the probability of false alarm of CR
is a scalar. In our system setup we assume a complex-valued PSK primary user signal and circular symmetric complex Gaussian (CSCG) noise. For the CSCG noise case the probability of false alarm of CR  for a chosen detection threshold
for a chosen detection threshold  is given by [4, 18]
is given by [4, 18]

where Q( ) is the tail probability for the standard normal distribution and
) is the tail probability for the standard normal distribution and  represents the time-bandwidth product, given as
represents the time-bandwidth product, given as  , where
, where  is the sensing duration and
is the sensing duration and  is the measurement bandwidth. For a chosen threshold
is the measurement bandwidth. For a chosen threshold  , the probability of detection of CR
, the probability of detection of CR  is approximated by [4, 18]
is approximated by [4, 18]

To protect the primary user against harmful interference from the CRs, the detection probability is fixed at a desired target value,  . In practice,
. In practice,  is required to be close to 1 [2]. The probability of false alarm of each CR
is required to be close to 1 [2]. The probability of false alarm of each CR  for the targeted
for the targeted  can be rewritten as
can be rewritten as

It may be seen from (4) that a high detection probability requirement may lead to a high false alarm probability for an individual CR if its  is low, thus reducing the achievable throughput of that CR. In this case, the individual CRs may interact to form coalitions to help decrease the false alarm probability. Within a coalition, sensing decisions by individual CRs are transmitted over the narrowband common control channel to a CR selected as a coalition head. Although the optimal decision fusion rule is the Chair-Varshney rule [19], for simplicity of implementation we assume that an OR fusion rule is used by the coalition head to combine the individual CR sensing decisions within a coalition. The OR rule is a simple decision rule explained as follows: if one out of
is low, thus reducing the achievable throughput of that CR. In this case, the individual CRs may interact to form coalitions to help decrease the false alarm probability. Within a coalition, sensing decisions by individual CRs are transmitted over the narrowband common control channel to a CR selected as a coalition head. Although the optimal decision fusion rule is the Chair-Varshney rule [19], for simplicity of implementation we assume that an OR fusion rule is used by the coalition head to combine the individual CR sensing decisions within a coalition. The OR rule is a simple decision rule explained as follows: if one out of  CRs in a coalition detects the primary user, the final decision for the coalition declares a primary user is present, where
CRs in a coalition detects the primary user, the final decision for the coalition declares a primary user is present, where  represents the number of CRs in a coalition
represents the number of CRs in a coalition  . CRs in any coalition
. CRs in any coalition  decide to transmit or not, based on the final combined sensing decision of the coalition head. Therefore, the probabilities of detection and false alarm of a coalition head are also the probabilities of detection and false alarm of each CR
decide to transmit or not, based on the final combined sensing decision of the coalition head. Therefore, the probabilities of detection and false alarm of a coalition head are also the probabilities of detection and false alarm of each CR  that is the member of
that is the member of  .
.
Assuming that all decisions are conditionally independent (this means that the sensing measurements performed by CRs are independent, but that for each CR the same hypotheses  ,
,  not present and
not present and  present, apply) then using the OR rule, the detection probability of the coalition
present, apply) then using the OR rule, the detection probability of the coalition  is given as
is given as

For a given  , the individual CR's target probability of detection in a coalition using OR fusion rule is written as (assuming same target probability of detection for every CR, as in [4, 14])
, the individual CR's target probability of detection in a coalition using OR fusion rule is written as (assuming same target probability of detection for every CR, as in [4, 14])

The probability of false alarm of each CR  for the
for the  can be written as
can be written as

However, it may happen that some of the CRs have better received SNR from the PU than the others. To gain from this SNR diversity, we adopt a weighted target probability of detection for any CR  . The weighted target probability of detection modifies
. The weighted target probability of detection modifies  in (6) and takes a sensing CR's received SNR
in (6) and takes a sensing CR's received SNR  into consideration. We propose to use weighted target probability of detection for CR
into consideration. We propose to use weighted target probability of detection for CR  given by
given by

While we make no claims as to the optimality of the selected weighting method, these probabilities preserve the relationship in (5) and assign a higher expectation on detection accuracy to the CRs that experience higher SNR. We justify the use of  as follows. For a given SNR
as follows. For a given SNR  and
and  , false alarm probability of CR
, false alarm probability of CR  is a function of the target detection probability for that CR (see (7) and Figure 2). It can be seen from Figure 2 that the impact of target detection probability on the false alarm probability of individual CRs varies for the different values of
is a function of the target detection probability for that CR (see (7) and Figure 2). It can be seen from Figure 2 that the impact of target detection probability on the false alarm probability of individual CRs varies for the different values of  . If a CR has high
. If a CR has high  , for instance
, for instance  , then the target detection probability has little impact on its false alarm probability. However, if a CR has low
, then the target detection probability has little impact on its false alarm probability. However, if a CR has low  , for instance
, for instance  , then the target detection probability has strong impact on its false alarm probability.
, then the target detection probability has strong impact on its false alarm probability.
In this approach, the CR with high  is assigned relatively high target detection probability. However, due to high
is assigned relatively high target detection probability. However, due to high  , the assignment of high target detection probability has little impact on the false alarm probability of that CR. The CR with low
, the assignment of high target detection probability has little impact on the false alarm probability of that CR. The CR with low  is assigned relatively low target detection probability which results in low false alarm probability for that CR (see Figure 2), as compared to when each CR is assigned the same target detection probability in a coalition.
is assigned relatively low target detection probability which results in low false alarm probability for that CR (see Figure 2), as compared to when each CR is assigned the same target detection probability in a coalition.
The probability of false alarm of each CR  for the
for the  is written as
is written as

Using the OR rule, the false alarm probability  of the coalition
of the coalition  is given as
is given as

It may be seen from (7) and (9) that, for a given  and
and  , the CRs with low values of
, the CRs with low values of  have incentives to form coalitions as it helps to decrease
have incentives to form coalitions as it helps to decrease  (due to the increase in
(due to the increase in  or
or  term which in turn decreases
term which in turn decreases  ). However, for a given
). However, for a given  the coalitional false alarm probability given by (10) is an increasing function of coalition size
the coalitional false alarm probability given by (10) is an increasing function of coalition size  .
.
3. Coalition Game-Theoretic Framework for Distributed Cooperative Sensing
Coalition game theory provides useful tools to decide which group of players will cooperate with each other to efficiently achieve their goals [8, 20]. Therefore, to analyze cooperative interactions among CRs performing distributed spectrum sensing, we model the problem as a coalition game.
3.1. Preliminaries
Let  denote the set of players (CRs) playing the coalition game. A coalition,
denote the set of players (CRs) playing the coalition game. A coalition,  , is a subset of
, is a subset of  ,
,  . An individual non-cooperating player is called a singleton coalition and the set
. An individual non-cooperating player is called a singleton coalition and the set  is called the grand coalition, where all players cooperate. The utility of a coalition in a coalition game is called the coalition value, and is denoted by
is called the grand coalition, where all players cooperate. The utility of a coalition in a coalition game is called the coalition value, and is denoted by  . Coalitions are assumed to be non-overlapping, that is, CRs are members of at most one coalition.
. Coalitions are assumed to be non-overlapping, that is, CRs are members of at most one coalition.
The most common form of a coalition game is the characteristic function form. In the characteristic function form (CFF) of coalition games, utilities achieved by the players in a coalition are unaffected by those outside it.
Definition 1.
A nontransferable utility (NTU) game is a coalition game in CFF, in which the value  of a coalition
of a coalition  cannot be arbitrarily divided among the coalition's players. In such games, each player will have its own value within a coalition
cannot be arbitrarily divided among the coalition's players. In such games, each player will have its own value within a coalition  . The value function
. The value function  represents the value of player
represents the value of player  that belongs to a coalition
that belongs to a coalition  .
.
3.2. Throughput of a CR
For a noncooperative CR network with periodic spectrum sensing, each slot consists of sensing duration  and data transmission duration
and data transmission duration  . To focus on the coalition formation model for the sensing-throughput tradeoff problem in distributed CR networks; we assume that the entire primary user band is divided into
. To focus on the coalition formation model for the sensing-throughput tradeoff problem in distributed CR networks; we assume that the entire primary user band is divided into  subbands and, when the primary user is absent each CR operates exclusively in one of the
subbands and, when the primary user is absent each CR operates exclusively in one of the  subbands. (We do not analyze scheduling policies in this work and assume a very simple and predetermined orthogonal sub-band allocation policy for the CRs when the primary user band is free for access. Our ongoing work, outside the scope of this paper, addresses competition among CRs for subbands that are free.) This assumption is in line with the other models in the literature [14, 21]. For the noncooperative case, the average throughput of the CR
subbands. (We do not analyze scheduling policies in this work and assume a very simple and predetermined orthogonal sub-band allocation policy for the CRs when the primary user band is free for access. Our ongoing work, outside the scope of this paper, addresses competition among CRs for subbands that are free.) This assumption is in line with the other models in the literature [14, 21]. For the noncooperative case, the average throughput of the CR  is approximated by [1, 14]
is approximated by [1, 14]

where  is the probability of primary user absent,
is the probability of primary user absent,  represents the total frame length and
represents the total frame length and  represents the transmission rate of the CR
represents the transmission rate of the CR  to its receiver when the primary user is absent.
to its receiver when the primary user is absent.
In distributed CR networks when CRs decide to perform cooperative sensing by forming coalitions with one another they may incur overhead costs in terms of time delay due to the process of coalition formation and due to combining sensing reports within a formed coalition. Note that the time delay due to the process of coalition formation depends on how frequently the coalition process is initiated which in turn depends on changes in the network configuration (for, e.g., CR mobility, etc.). However, the time delay in data transmissions of a coalition due to the overhead in combining sensing reports is periodic (since this overhead is incurred in every time slot). In this work, we analyze the impact of overhead costs in terms of time spent during combining sensing reports on the throughput of distributed CRs. We ignore the overhead in terms of time delay due to the process of coalition formation. One of the extensions we envision for our current work is the consideration of the effects due to overhead in terms of spending time and resources due to the process of coalition formation and also the effects due to overhead in terms of energy consumed by a coalition head to collect and combine sensing reports.
When the CRs decide to form a coalition then the entire coalition cannot transmit data until sensing reports are collected and the final combined sensing decision is transmitted to all the coalition members (see Figure 3). One simple method of sensing reports collection by the coalition head can be stated as follows. The coalition head grants a contention free channel to individual cognitive radios by polling them (using their identity numbers) for transmitting their local decisions. The coalition head may employ a round-robin scheduler [22, 23], and on being polled, a CR transmits its local decision to the coalition head. In this sensing reports collection method there is cost in terms of time delay in data transmissions of a coalition due to the overhead in combining sensing reports. This cost generally increases with the number of coalition forming CRs as more decisions need to be reported to the coalition head. The average throughput of the CR  considering the cost in terms of overhead in sensing reports combining within a coalition is approximated as
considering the cost in terms of overhead in sensing reports combining within a coalition is approximated as

where  is the time spent on reporting a sensing decision to the coalition head.
is the time spent on reporting a sensing decision to the coalition head.
For a target detection probability,  , the CRs may form coalitions to reduce their false alarm probability and therefore increase their average throughput given by (12). The coalition forming CRs may also increase their average throughput by reducing their sensing time
, the CRs may form coalitions to reduce their false alarm probability and therefore increase their average throughput given by (12). The coalition forming CRs may also increase their average throughput by reducing their sensing time  via joint coalitional sensing. However, we note that for the distributed spectrum sensing problem when the coalition forming CRs are allowed to vary sensing time
via joint coalitional sensing. However, we note that for the distributed spectrum sensing problem when the coalition forming CRs are allowed to vary sensing time  , it generates significant uncertainties in the coalition values. For instance, if two or more CRs reduce their sensing time
, it generates significant uncertainties in the coalition values. For instance, if two or more CRs reduce their sensing time  (or in other words increase their data transmission time) via forming the coalition
(or in other words increase their data transmission time) via forming the coalition  then it may happen that the CRs in
then it may happen that the CRs in  start transmitting data while some CRs outside
start transmitting data while some CRs outside  may still be sensing. This may lead to a change in the coalition value (in terms of false alarm probabilities) of the CRs outside the coalition
may still be sensing. This may lead to a change in the coalition value (in terms of false alarm probabilities) of the CRs outside the coalition  . To avoid this uncertainty in the coalition value due to CR transmissions, we fix the sensing duration
. To avoid this uncertainty in the coalition value due to CR transmissions, we fix the sensing duration  for each individual CR.
for each individual CR.
3.3. Coalition Value with Nontransferable Utility
For a target detection probability,  , and the fixed sensing duration
, and the fixed sensing duration  , the coalition value
, the coalition value  must characterize the incentives to form coalitions in terms of the decreased false alarm probability
must characterize the incentives to form coalitions in terms of the decreased false alarm probability  of the coalition. Moreover, the coalition value must also take into account the cost in terms of delay in data transmissions of a coalition due to the overhead in combining sensing reports. A suitable coalition value that satisfies the above requirements is given by
of the coalition. Moreover, the coalition value must also take into account the cost in terms of delay in data transmissions of a coalition due to the overhead in combining sensing reports. A suitable coalition value that satisfies the above requirements is given by

where  denotes the average throughput for CR
denotes the average throughput for CR  given by (12), for
given by (12), for  . In the proposed coalition formation game, each CR has it is own value within a coalition and its nontransferable due to the following reasons.
. In the proposed coalition formation game, each CR has it is own value within a coalition and its nontransferable due to the following reasons.
Indivisible False Alarm Probability
The probability of false alarm  of each CR
of each CR  , where
, where  , is also given by the probability of false alarm of the coalition
, is also given by the probability of false alarm of the coalition  , that is,
, that is,  (as explained in Section 2) and it cannot be divided among the radios.
(as explained in Section 2) and it cannot be divided among the radios.
Indivisible Cost
Each CR incurs the same cost in terms of overhead in combining sensing reports, that is,  , and this cost cannot be divided among the CRs.
, and this cost cannot be divided among the CRs.
Indivisible Bandwidth
Finally, each CR operates exclusively in one of the  subbands. Therefore, they cannot arbitrarily divide the spectrum among themselves.
subbands. Therefore, they cannot arbitrarily divide the spectrum among themselves.
Therefore, each CR will have its own value within the coalition  and hence, the proposed game is an NTU game.
and hence, the proposed game is an NTU game.
When two or more CRs form a coalition  , then any CR within
, then any CR within  is selected as a coalition head to combine the individual CR sensing decisions within the coalition. The decisions to form coalitions by the CRs are based on consensus, that is, a coalition is formed only if it is acceptable to everyone involved. We also assume that CRs are myopic, that is, CRs care only about their current payoffs.
is selected as a coalition head to combine the individual CR sensing decisions within the coalition. The decisions to form coalitions by the CRs are based on consensus, that is, a coalition is formed only if it is acceptable to everyone involved. We also assume that CRs are myopic, that is, CRs care only about their current payoffs.
3.4. Selfish Coalition Formation
Definition 2.
Internal stability means that no CR has an incentive to leave its coalition to become a singleton (individual noncooperative CR), that is,  , for all
, for all  .
.
We assume that CRs are individually rational, that is, CRs seek to maximize their payoffs, conditional on feasibility. Therefore, for selfish coalition formation, the merge of two coalitions only occurs when all CRs in the new coalition  are at least as well off through the merge as they were before it. Mathematically speaking, coalitions
are at least as well off through the merge as they were before it. Mathematically speaking, coalitions  and
and  will merge to form
will merge to form  only: if for all
only: if for all  , where
, where  and
and  ,
,  and also
and also  . Due to this coalition formation condition, whenever CRs agree to form
. Due to this coalition formation condition, whenever CRs agree to form  the new coalition is internally stable, that is, no CR has an incentive to become a singleton (an individual noncooperative CR).
the new coalition is internally stable, that is, no CR has an incentive to become a singleton (an individual noncooperative CR).
3.5. Altruistic Coalition Formation
The model of selfish coalition formation discussed above is in line with much of the coalition formation literature, which assumes that users form coalitions to maximize their individual payoffs. However, it is equally interesting to investigate the question of whether and how the achievable throughput of CRs will change if CRs are assumed to be "not entirely selfish". Intuitively, we want to model the case when two or more CRs propose to form a new coalition  by taking into account one another's welfare. Before studying altruistic coalition formation, we first define the concept of altruistic contribution of a coalition as follows [11].
by taking into account one another's welfare. Before studying altruistic coalition formation, we first define the concept of altruistic contribution of a coalition as follows [11].
Definition 3.
Let  and
and  be two disjoint coalitions. The altruistic contribution of
be two disjoint coalitions. The altruistic contribution of  to
to  , where
, where  , is
, is  ; the altruistic contribution of
; the altruistic contribution of  to
to  is
is  ; and the sum of altruistic contributions of
; and the sum of altruistic contributions of  and
and  is
is  .
.
In simple words, the altruistic contribution of coalition  to
to  represents the change in the value of the CRs in
represents the change in the value of the CRs in  , when the CRs in
, when the CRs in  are added to the coalition
are added to the coalition  . It can be easily seen that if any proposed coalition
. It can be easily seen that if any proposed coalition  has
has  , then the merger of
, then the merger of  and
and  to form
to form  would do more good than harm to the overall value of the coalition
would do more good than harm to the overall value of the coalition  . Formally, we assume that to maximize the achievable throughput of the proposed coalition
. Formally, we assume that to maximize the achievable throughput of the proposed coalition  , an altruistic coalition decides to form the coalition
, an altruistic coalition decides to form the coalition  whenever
whenever

4. A Markovian Model of Coalition Formation Game
To model all  CR coalitions, we define coalition structures as follows.
CR coalitions, we define coalition structures as follows.
Definition 4.
A coalition structure is a partition of  into exhaustive and disjoint subsets, where each subset is a coalition. The set of all possible coalition structures is denoted as
into exhaustive and disjoint subsets, where each subset is a coalition. The set of all possible coalition structures is denoted as  .
.
In this section, we introduce a dynamic model of coalition formation for distributed cooperative spectrum sensing in CR networks where multiple distributed CRs coexist and opportunistically access the spectrum. In the proposed dynamic coalition formation game the CRs follow a time evolving sequence of steps to reach self-organizing stable spectrum sensing coalition structures. Coalition structures in the dynamic coalition formation game are modeled as a sequence of random variables describing the state of the system, with the mechanism of transitions between coalition structures represented by a Markov chain. To incorporate slow changes in the network configuration (for, e.g., due to CR mobility), the initial round of coalition formation game restarts some time  after reaching equilibrium. This time
after reaching equilibrium. This time  may be assigned according to variations in the network configuration. We assume that during one round of coalition formation the received primary user's SNR, that is,
may be assigned according to variations in the network configuration. We assume that during one round of coalition formation the received primary user's SNR, that is,  , and the transmission rate
, and the transmission rate  of each CR
of each CR  does not change. At the very beginning of each round of the coalition formation game, the distributed CR network is composed of all singleton coalitions, that is, noncooperative CRs.
does not change. At the very beginning of each round of the coalition formation game, the distributed CR network is composed of all singleton coalitions, that is, noncooperative CRs.
4.1. A Coalition Formation Game Model
The coalition formation game involves five steps. The five steps of the proposed model are summarized as follows:
Node Discovery
Discover the CRs within the network.
Initialization
Each individual CR computes its received SNR  from the PU.
from the PU.
Coalition Formation Proposal
-
(a)
At each time slot, each coalition, with probability
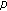 , proposes a new coalition structure. In this process, one of the CRs in the coalition acts on its behalf. (In the case of singleton coalitions, each singleton coalition, i.e., each CR, individually proposes a new coalition structure with some probability
, proposes a new coalition structure. In this process, one of the CRs in the coalition acts on its behalf. (In the case of singleton coalitions, each singleton coalition, i.e., each CR, individually proposes a new coalition structure with some probability 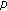 ; when two or more CRs form a coalition
; when two or more CRs form a coalition 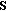 , then any CR within
, then any CR within 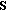 is selected as a coalition head to propose a new coalition structure with some probability
is selected as a coalition head to propose a new coalition structure with some probability  on behalf of that coalition.) (b) The evolution from one coalition structure to the next can only occur through the merging of two existing coalitions. For instance, any coalition head of any existing coalition
on behalf of that coalition.) (b) The evolution from one coalition structure to the next can only occur through the merging of two existing coalitions. For instance, any coalition head of any existing coalition  may propose to merge with another coalition
may propose to merge with another coalition 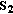 , forming
, forming 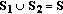 .
.
Coalition Formation Decision
-
(a)
When the CRs are assumed to be selfish then they form a coalition if for all
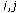 , where
, where  and
and 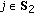 ,
,  and also
and also  . (b) When the CRs are assumed to be altruistic then they form a coalition if
. (b) When the CRs are assumed to be altruistic then they form a coalition if 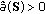 . (see Sections 3.4 and 3.5 for the details).
. (see Sections 3.4 and 3.5 for the details).
Steps (3) and (4) of the coalition formation are repeated until all the coalitions have made their coalition formation decisions, resulting in a final stable coalition structure  .
.
Coalitional Spectrum Sensing
Each CR within a coalition computes its local sensing decision and transmits it to the coalition head over the common control channel. The coalition head combines the local sensing decisions (including its own sensing decision) using an OR decision fusion rule.
The proposed distributed coalition formation can be performed by coalition formation message exchanges between CRs over a common control channel. In practice, if all CRs use the same control channel to report sensing decisions to their respective coalition heads then the reporting time may increase. To decrease the reporting time coalitions may use different control channels. However, since the number of available channels in general is limited and the number of coalitions may be large, control channels must be spatially reused. For simplicity, we have assumed different reporting channels for each coalition.
4.2. Dynamics of Coalition Formation: Game Model
The dynamic coalition process can be modeled using a Markov chain, with each state representing a different coalition structure. A finite set  of all possible coalition structures for
of all possible coalition structures for  CRs forms the state space of the coalition formation game. Our work in [5] provides further detail on this modeling, including examples of the Markov chain structure for
CRs forms the state space of the coalition formation game. Our work in [5] provides further detail on this modeling, including examples of the Markov chain structure for  , and
, and  transmitter/receiver pairs.
transmitter/receiver pairs.
4.2.1. Selfish Coalition Formation
Any coalition may propose a coalition structure change to another coalition in the current state  , and if all the CRs in the proposed coalition are at least as well as before the merge, the game moves to
, and if all the CRs in the proposed coalition are at least as well as before the merge, the game moves to  . When each of
. When each of  prevailing coalitions with some probability
prevailing coalitions with some probability  proposes a new coalition structure then the transition probabilities for the
proposes a new coalition structure then the transition probabilities for the  CR selfish coalition game with coalition structures as state space
CR selfish coalition game with coalition structures as state space  are given as
are given as

where  is an indicator function equal to 1 if condition
is an indicator function equal to 1 if condition  is satisfied, and zero otherwise,
is satisfied, and zero otherwise,  and
and  are the values of the two coalitions participating in the coalition formation to form the proposed coalition
are the values of the two coalitions participating in the coalition formation to form the proposed coalition  ,
,  is the value of the proposed coalition
is the value of the proposed coalition  , and
, and  represents the set of all new possible coalition structure states to which coalitions can transit from
represents the set of all new possible coalition structure states to which coalitions can transit from  . The set
. The set  is given as
is given as  . Given
. Given  coalitions in the present state
coalitions in the present state  , it is possible to transition from
, it is possible to transition from  to one of the
to one of the  possible states, where
possible states, where  can be calculated as
can be calculated as

For instance, if the number of coalitions  , then it is possible to move from the state
, then it is possible to move from the state  to one of
to one of  different states (besides itself), provided that the coalition formation condition is satisfied. As explained previously, two coalitions can merge only if all CRs within the proposed coalition
different states (besides itself), provided that the coalition formation condition is satisfied. As explained previously, two coalitions can merge only if all CRs within the proposed coalition  are at least as well off as before the merge. The indicator function
are at least as well off as before the merge. The indicator function  in (15) represents the possible agreement or disagreement among the CRs participating in the coalition game to form the proposed coalition
in (15) represents the possible agreement or disagreement among the CRs participating in the coalition game to form the proposed coalition  . As the transition probability at any present state
. As the transition probability at any present state  does not depend upon the prior states of the coalition structures, the Markov property holds.
does not depend upon the prior states of the coalition structures, the Markov property holds.
4.2.2. Altruistic Coalition Formation
For the altruistic-cooperation case, the indicator function (coalition formation decision) in (15) is changed from  to
to  . It simply means that each CR now decides to merge if the merger of two coalitions would do more good than harm to the overall value of the merged coalition
. It simply means that each CR now decides to merge if the merger of two coalitions would do more good than harm to the overall value of the merged coalition  .
.
Using simulation results in Section 5.3 we will compare the performance of the coalition formation based on altruistic decision with the selfish decision in terms of average throughput per CR, for different network sizes.
Using standard theory of absorbing Markov chains one can calculate how long will it take for the process to reach stable coalition structures, that is, one can calculate the mean time  and its variance
and its variance  for the dynamic coalition game starting from the initial state of all singleton coalitions to reach stable coalition structures (where no two coalitions have an incentive to merge) [5].
for the dynamic coalition game starting from the initial state of all singleton coalitions to reach stable coalition structures (where no two coalitions have an incentive to merge) [5].
In Section 5.3, we analyze the mean  and the variance
and the variance  of the time for the proposed coalition formation to reach the stable coalitions.
of the time for the proposed coalition formation to reach the stable coalitions.
5. Dynamic Game Analysis and Simulation Results
To perform the coalition formation, CRs need to exchange their received primary user's signal-to-noise ratio (SNR). The amount of information exchange necessary to reach stable coalition structures can be measured by the total number of coalition formation proposals sent by the  CRs during the coalition formation process. For instance if
CRs during the coalition formation process. For instance if  number of coalition formation proposals are sent during the entire coalition formation process and each proposal requires the exchange of
number of coalition formation proposals are sent during the entire coalition formation process and each proposal requires the exchange of  messages for coalition heads to take a coalition formation decision then to reach equilibrium
messages for coalition heads to take a coalition formation decision then to reach equilibrium  messages need to be exchanged among the CRs. When we are not taking into account the loss of coalition formation proposals due to collisions among distributed uncoordinated CRs then in the worst case, that is, where almost all proposals are rejected, the number of proposals is only
messages need to be exchanged among the CRs. When we are not taking into account the loss of coalition formation proposals due to collisions among distributed uncoordinated CRs then in the worst case, that is, where almost all proposals are rejected, the number of proposals is only  , where
, where  . Thus for the worst case, coalition formation proposals can be said to be order of
. Thus for the worst case, coalition formation proposals can be said to be order of  . In the best case, that is, where all proposals are accepted and the coalition formation leads to the formation of the grand coalition, the number of coalition formation proposals necessary is only
. In the best case, that is, where all proposals are accepted and the coalition formation leads to the formation of the grand coalition, the number of coalition formation proposals necessary is only  . Thus for the best case, coalition formation proposals can be said to be order of
. Thus for the best case, coalition formation proposals can be said to be order of  . In practical scenarios the complexity is between these two extremes.
. In practical scenarios the complexity is between these two extremes.
This reduction in the information exchange is due to the reason that when coalitions are formed then instead of all the CRs only the coalition heads exchange proposals on behalf of their respective coalition members.
5.1. Stable Coalition Structures
As CRs form self-organizing spectrum sensing coalition structures, we analyze under what conditions the coalition formation process will reach a stable coalition structure (where no two coalitions have an incentive to merge anymore).
Selfish Coalition Formation
For the proposed selfish coalition formation, a coalition structure state  is an equilibrium state if it satisfies the following condition
is an equilibrium state if it satisfies the following condition

or for some 
 .
.
The above stated condition ensures that no two coalitions in the prevailing coalition structure  have an incentive to merge anymore.
have an incentive to merge anymore.
The following simple fact proves that the selfish coalition formation process converges to an equilibrium state: In the proposed selfish coalition formation, if a certain coalition structure is not an equilibrium state, there must exist at least two coalitions that can decide to merge to improve their value functions. As long as such two coalitions exist, the coalition structure changes to another coalition structure, until an equilibrium state is reached.
Altruistic Coalition Formation
For the proposed altruistic coalition formation, a coalition structure  is an equilibrium state if it satisfies the following condition
is an equilibrium state if it satisfies the following condition

Following the same reasoning as we did for the selfish coalition formation process, it is easy to see that the altruistic coalition formation process converges to an equilibrium.
5.2. Coalition Sizes
The study of coalition formation in wireless networks has previously focused on cohesive games [24], that is, games where the value of the grand coalition formed by the set of all users  is at least as large as the sum of the values of any partition of
is at least as large as the sum of the values of any partition of  . The authors in [24], also assume that there is no cost to the coalition formation process. In such coalition games, coalition structure generation is trivial because the wireless nodes always benefit by forming the grand coalition.
. The authors in [24], also assume that there is no cost to the coalition formation process. In such coalition games, coalition structure generation is trivial because the wireless nodes always benefit by forming the grand coalition.
However, many coalition game models of wireless node cooperation are not cohesive (see, e.g., [25]). In such network scenarios, the network welfare maximizing coalition structure varies.
For the proposed selfish coalition formation where CRs seek to maximize their payoffs, conditional on feasibility, it is interesting to note that the higher the  (the signal power received by CR
(the signal power received by CR  ), the lower the
), the lower the  given by (7). CRs with high values of
given by (7). CRs with high values of  may have either less or no incentive to cooperate with CRs with low values of
may have either less or no incentive to cooperate with CRs with low values of  (or with high
(or with high  ). Hence, cooperation among all CRs is desirable only when all CRs experience similar
). Hence, cooperation among all CRs is desirable only when all CRs experience similar  . Therefore, in the proposed coalition formation, the grand coalition of all the CRs may not always form.
. Therefore, in the proposed coalition formation, the grand coalition of all the CRs may not always form.
For the proposed altruistic coalition formation where CRs seek to merge if the merger of two coalitions would do more good than harm to the overall value of the merged coalition, it is interesting to note that the CRs with high  values may form coalitions with the CRs having low
values may form coalitions with the CRs having low  values as long as the overall value of the newly formed coalition
values as long as the overall value of the newly formed coalition  is increased.
is increased.
Using simulation results in Section 5.3 we will present average maximum number of CRs per formed coalition for both selfish and altruistic coalition formation.
5.3. Simulation Results
Using simulation our aim is to compare the performance (for, e.g., in terms of average throughput per CR) of the coalition structure that emerges as the outcome of the proposed coalition formation solutions to a noncooperative solution and to the grand coalition.
For simulation illustrations, the following distributed CR network is set up:  CRs are uniformly and independently distributed in a circle with radius
CRs are uniformly and independently distributed in a circle with radius  m and centered at the coordinates
m and centered at the coordinates  . The PU transmitter is at coordinates
. The PU transmitter is at coordinates  as shown in Figure 1. The sensing time
as shown in Figure 1. The sensing time  ms, the time-bandwidth product is set as
ms, the time-bandwidth product is set as  , and the frame duration is set to be
, and the frame duration is set to be  ms. We set the path loss exponent
ms. We set the path loss exponent  . The PU power
. The PU power  , scalar
, scalar  and noise power
and noise power  are set at a value such that
are set at a value such that  (PU's SNR at CR
(PU's SNR at CR  ) at the coordinates
) at the coordinates  is −15 dB. The probability of primary user present is assumed to be
is −15 dB. The probability of primary user present is assumed to be  . To keep our simulation analysis simple, we assume that all the CRs have the same transmission rate, that is,
. To keep our simulation analysis simple, we assume that all the CRs have the same transmission rate, that is,  bits/sec/Hz in (12), where
bits/sec/Hz in (12), where  is signal-to-noise ratio from a CR to its receiver. Simulations were performed by "dropping" the CRs randomly around the coordinates
is signal-to-noise ratio from a CR to its receiver. Simulations were performed by "dropping" the CRs randomly around the coordinates  . For the target detection probability
. For the target detection probability  and
and  , in Figures 4(a) and 4(b), we show the average (averaged over the simulation runs) throughput per CR for different network sizes, when all CRs sense independently (noncooperative strategy), and when CRs can form coalitions (selfish and altruistic). It can be seen from Figures 4(a) and 4(b) that the proposed coalition formation (both selfish and altruistic) yields an improvement in the average throughput as compared to the noncooperative solution. However, the selfish coalition formation solution leads to a loss in average throughput as compared to the altruistic coalition formation solution. In Figure 5, we compare the performance of altruistic and selfish coalition formation solutions with the noncooperative solution in terms of average false alarm probability per CR for different network sizes. It can be seen that the altruistic coalition formation solution significantly reduces the average false alarm per CR, as compared to both selfish coalition formation and noncooperative solutions. It can also be seen from Figures 4 and 5 that the weighted target detection probability for individual CRs in a coalition results in better average throughput and reduced average false alarm per CR as compared to when each CR is assigned the same target detection probability.
, in Figures 4(a) and 4(b), we show the average (averaged over the simulation runs) throughput per CR for different network sizes, when all CRs sense independently (noncooperative strategy), and when CRs can form coalitions (selfish and altruistic). It can be seen from Figures 4(a) and 4(b) that the proposed coalition formation (both selfish and altruistic) yields an improvement in the average throughput as compared to the noncooperative solution. However, the selfish coalition formation solution leads to a loss in average throughput as compared to the altruistic coalition formation solution. In Figure 5, we compare the performance of altruistic and selfish coalition formation solutions with the noncooperative solution in terms of average false alarm probability per CR for different network sizes. It can be seen that the altruistic coalition formation solution significantly reduces the average false alarm per CR, as compared to both selfish coalition formation and noncooperative solutions. It can also be seen from Figures 4 and 5 that the weighted target detection probability for individual CRs in a coalition results in better average throughput and reduced average false alarm per CR as compared to when each CR is assigned the same target detection probability.
Average throughput per CR for different network sizes and for different scenarios. (a) Average throughput (bits/sec/Hz) per CR,  ,
,  m and
m and  in (12) is set to 0.001ms (the time spent for reporting a sensing decision to the coalition head). Given a target detection probability for a coalition, "same
in (12) is set to 0.001ms (the time spent for reporting a sensing decision to the coalition head). Given a target detection probability for a coalition, "same  " means that each CR is required to satisfy the same target probability of detection (see (7)), whereas "weighted
" means that each CR is required to satisfy the same target probability of detection (see (7)), whereas "weighted  " means that each CR is required to satisfy an SNR-dependent target detection probability (see (9)). (b) Average throughput per CR,
" means that each CR is required to satisfy an SNR-dependent target detection probability (see (9)). (b) Average throughput per CR,  ,
,  m and
m and  in (12) is set to 0.001 ms.
in (12) is set to 0.001 ms.
When the overhead cost, that is, the cost in terms of collecting and combining sensing reports at the coalition head is not taken into account then the altruistic coalition formation solution yields the same results as if all the CRs perform cooperative sensing, that is, form the grand coalition, see Figure 6. This is because, for no overhead cost, with increasing the number of cooperating CRs, a target detection probability may be achieved by having low detection probability at the individual CRs. The low detection probability at the individual CRs is translated to a low false alarm probability and therefore increase in throughput. However, in practice the reporting of the local CR sensing decisions to the report combining entity (coalition head, fusion center, etc.) incurs overhead in the sense that the entire reporting group cannot transmit until all the sensing reports are collected and combined by that entity. In the literature (also in IEEE 802.22), polling of CRs by the report combining entity is suggested for the collection of sensing reports [3, 23, 26]. This method has communication overhead that increases linearly with the number of cooperating CRs. When the overhead cost of collecting and combining sensing reports is taken into account (e.g.,  in (12) is set to 1 ms) then it can be seen in Figure 6 that the performance of the grand coalition degrades significantly as the number of CR increases, as compared to the altruistic coalition formation solution. In Figure 7(a), we compare the performance of altruistic and selfish coalition formation solutions in terms of average throughput per CR for a network size of 20 CRs. In this figure, we show that for small
in (12) is set to 1 ms) then it can be seen in Figure 6 that the performance of the grand coalition degrades significantly as the number of CR increases, as compared to the altruistic coalition formation solution. In Figure 7(a), we compare the performance of altruistic and selfish coalition formation solutions in terms of average throughput per CR for a network size of 20 CRs. In this figure, we show that for small  , the altruistic coalition formation (same
, the altruistic coalition formation (same  ) solution yields significant average throughput gains when compared with the selfish coalition formation solution (same
) solution yields significant average throughput gains when compared with the selfish coalition formation solution (same  ). However, when
). However, when  is large then the selfish coalition formation solution (same
is large then the selfish coalition formation solution (same  ) either outperforms or at least matches altruistic solution (same
) either outperforms or at least matches altruistic solution (same  ) with respect to average throughput per CR. This is because the average coalition size for the altruistic coalition formation solution (same
) with respect to average throughput per CR. This is because the average coalition size for the altruistic coalition formation solution (same  ) is large as compared to the selfish coalition formation solution (same
) is large as compared to the selfish coalition formation solution (same  ), see Figure 7(b), and for large values of
), see Figure 7(b), and for large values of  , the sensing reporting overhead becomes significant. Due to this reason, the large coalitions can be more costly as compared to the small ones.
, the sensing reporting overhead becomes significant. Due to this reason, the large coalitions can be more costly as compared to the small ones.
Average throughput per CR for different network sizes and for different scenarios. (a) Average maximum coalition size for selfish and altruistic coalition formation solutions, when the values of  (the time spent for reporting a sensing decision to the coalition head) are varied between 0.001 ms to 0.017 s,
(the time spent for reporting a sensing decision to the coalition head) are varied between 0.001 ms to 0.017 s,  and
and  m. (b) Average throughput per CR for selfish and altruistic coalition formation solutions, when the values of
m. (b) Average throughput per CR for selfish and altruistic coalition formation solutions, when the values of  (the time spent for reporting a sensing decision to the coalition head) are varied between 0.001 ms to 0.017s,
(the time spent for reporting a sensing decision to the coalition head) are varied between 0.001 ms to 0.017s,  and
and  m.
m.
To illustrate the above situation, we can construct an example, for  CRs, where the altruistic coalition formation solution (same
CRs, where the altruistic coalition formation solution (same  ) outperforms selfish solution (same
) outperforms selfish solution (same  ) when
) when  is small. However, for the same scenario, when
is small. However, for the same scenario, when  is set to be large then selfish coalition solution (same
is set to be large then selfish coalition solution (same  ) may outperform altruistic solution (same
) may outperform altruistic solution (same  ).
).
Example 1.
Let  ,
,  and
and  be the received primary user's SNRs at
be the received primary user's SNRs at  CRs. In this three-CR game, when
CRs. In this three-CR game, when  ms and assuming
ms and assuming  bits/sec/Hz then calculating coalition values using (13) and rules explained in Sections 3 and 4 we obtain
bits/sec/Hz then calculating coalition values using (13) and rules explained in Sections 3 and 4 we obtain  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . It may be seen that the altruistic coalition solution (same
. It may be seen that the altruistic coalition solution (same  ) for this scenario results in the formation of grand coalition
) for this scenario results in the formation of grand coalition  of all CRs. However, the selfish coalition solution (same
of all CRs. However, the selfish coalition solution (same  ) results in the formation of either
) results in the formation of either  or
or  . Since,
. Since,  is greater than
is greater than  and
and  , therefore, the altruistic solution (same
, therefore, the altruistic solution (same  ) outperforms the selfish solution (same
) outperforms the selfish solution (same  ) for this scenario. However, when
) for this scenario. However, when  ms then we obtain
ms then we obtain  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  . It may be seen that the selfish coalition solution (same
. It may be seen that the selfish coalition solution (same  ) for this scenario results in the formation of
) for this scenario results in the formation of  . However, the altruistic coalition solution (same
. However, the altruistic coalition solution (same  ) results in the formation of either
) results in the formation of either  or
or  . Since,
. Since,  is greater than
is greater than  , therefore, the selfish solution (same
, therefore, the selfish solution (same  ) either outperforms or at least matches altruistic solution (same
) either outperforms or at least matches altruistic solution (same  ) for this scenario.
) for this scenario.
It can also be seen from Figure 7(a) that for very large values of  , the altruistic solution (same
, the altruistic solution (same  ) matches the selfish solution (same
) matches the selfish solution (same  ) in terms of average throughput per CR. This is because for very large values of
) in terms of average throughput per CR. This is because for very large values of  there are either very little or no gains in terms of average throughput per CR for coalition formation, and network structure is mostly composed of individual noncooperative CRs (see Figure 7(b)).
there are either very little or no gains in terms of average throughput per CR for coalition formation, and network structure is mostly composed of individual noncooperative CRs (see Figure 7(b)).
In Figure 8, we vary the parameter  (distance between the primary user base station and the center of the distributed CR network, see Figure 1), and show average maximum coalition sizes for the selfish and altruistic coalition formation solutions. It can be seen from Figure 8 that for large
(distance between the primary user base station and the center of the distributed CR network, see Figure 1), and show average maximum coalition sizes for the selfish and altruistic coalition formation solutions. It can be seen from Figure 8 that for large  , the network for such scenarios is composed of coalitions of large sizes. In this figure, we also show that for the given simulation scenario the altruistic coalition formation solution results in the formation of the grand coalition of all CRs whenever
, the network for such scenarios is composed of coalitions of large sizes. In this figure, we also show that for the given simulation scenario the altruistic coalition formation solution results in the formation of the grand coalition of all CRs whenever  m. As the value of parameter
m. As the value of parameter  is decreased, the network for such scenarios is composed of independent disjoint coalitions of smaller sizes. It can also be seen from Figure 8 that as the value of the parameter
is decreased, the network for such scenarios is composed of independent disjoint coalitions of smaller sizes. It can also be seen from Figure 8 that as the value of the parameter  is reduced to 500 m then the coalition formation solution results in a network structure mostly composed of individual noncooperative CRs, that is, all singleton coalitions.
is reduced to 500 m then the coalition formation solution results in a network structure mostly composed of individual noncooperative CRs, that is, all singleton coalitions.
Average maximum coalition size for selfish and altruistic coalition formations, when parameter  (distance between the primary base station and the center of the CR network, see Figure 1) is varied between 0 m to 4500 m,
(distance between the primary base station and the center of the CR network, see Figure 1) is varied between 0 m to 4500 m,  msec and
msec and  CRs.
CRs.
The two figures in Figures 9(a) and 9(b) illustrate the mean and variance of the time for the altruistic coalition formation to converge to an absorbing state with different probabilities  of coalition formation proposal. In Figures 9(a) and 9(b), simulation results are generated by dropping
of coalition formation proposal. In Figures 9(a) and 9(b), simulation results are generated by dropping  CRs in a circle with radius
CRs in a circle with radius  m and centered at the coordinates (2000,0) (other simulation parameters, for instance sensing time, slot duration, and so forth, are set to be the same as explained in the beginning of Section 5.3). The stable coalition structure that emerges as the outcome of the coalition formation may be different for the different drops of CRs in the distributed CR network. Therefore, we evaluate the mean and variance of the time to converge to the stable coalition structure (absorbing state) for any single random drop. For the target detection probability
m and centered at the coordinates (2000,0) (other simulation parameters, for instance sensing time, slot duration, and so forth, are set to be the same as explained in the beginning of Section 5.3). The stable coalition structure that emerges as the outcome of the coalition formation may be different for the different drops of CRs in the distributed CR network. Therefore, we evaluate the mean and variance of the time to converge to the stable coalition structure (absorbing state) for any single random drop. For the target detection probability  and
and  ms, when CRs propose altruistic coalitions with some probability
ms, when CRs propose altruistic coalitions with some probability  then the process converges to the grand coalition (absorbing state for a single random drop for the given simulation scenario). The mean and variance of the time to converge to the grand coalition are evaluated for different
then the process converges to the grand coalition (absorbing state for a single random drop for the given simulation scenario). The mean and variance of the time to converge to the grand coalition are evaluated for different  as follows: We repeat the coalition formation for the same drop of CRs with different probability
as follows: We repeat the coalition formation for the same drop of CRs with different probability  of coalition formation proposal. Figure 9(a) shows that for small
of coalition formation proposal. Figure 9(a) shows that for small  ,
,  is high because the mean time between coalition formation messages is too long. If
is high because the mean time between coalition formation messages is too long. If  is too high then the mean time between coalition formation messages is shorter but the number of coalition message collisions is higher, resulting in a longer time between coalition structure changes. This suggests that depending on the number of radios in the game there is an optimum value for
is too high then the mean time between coalition formation messages is shorter but the number of coalition message collisions is higher, resulting in a longer time between coalition structure changes. This suggests that depending on the number of radios in the game there is an optimum value for  . We illustrate this optimum value for
. We illustrate this optimum value for  CRs in Figure 9(a).
CRs in Figure 9(a).
Mean time and its variance for the altruistic coalition formation of  CRs to form the grand coalition (absorbing state for a single random drop for the given simulation scenario) from the transient state of all singleton coalitions for different probabilities
CRs to form the grand coalition (absorbing state for a single random drop for the given simulation scenario) from the transient state of all singleton coalitions for different probabilities  of coalition formation proposal. The dwell time in each state is set to 0.001 ms.
of coalition formation proposal. The dwell time in each state is set to 0.001 ms.
6. Conclusions
We apply a coalitional game-theoretic framework to the study of stable network partitions for the problem of distributed throughput-efficient sensing in cognitive radio (CR) networks. We devise distributed cooperative strategies for cognitive radios that are either selfish or altruistic. We propose a coalition formation model for these CRs to utilize primary user spectrum efficiently, under the constraint of probability of detection. The proposed coalition formation model also takes into account the overhead in sensing reports combining. We demonstrate that when each CR is assigned the same target detection probability in a coalition then for small to moderate values of sensing reporting time, the altruistic solution yields significant gains in terms of average throughput per CR as compared to the selfish and noncooperative solutions. However, for large values of sensing reporting time, the selfish solution either outperforms or at least matches altruistic solution in terms of average throughput per CR. We then adopt a weighted target detection probability for individual CRs in a coalition. We find that the weighted target detection probability for individual CRs results in higher average throughput as compared to when each CR is assigned the same individual target detection probability in a coalition. We also find that when CRs are assigned weighted target detection probabilities in a coalition then the altruistic coalition formation solution significantly increases the average throughput per CR, as compared to noncooperative solution, selfish coalition formation, and the grand coalition of all CRs. Our work employs an absorbing Markov chain model to model the equilibrium state (where no two coalitions have an incentive to merge) of the proposed coalition formation. Using a Markovian model of the coalition game, we analyze the dynamics of the coalition formation game and the stability of different network partitions in a distributed cognitive radio network. We also analyze the mean  and variance
and variance  of the time for the game to reach the stable coalition structures. Finally, we also show the impact of the distance between the primary user transmitter and the distributed CR network on cooperative strategies of the distributed CRs.
of the time for the game to reach the stable coalition structures. Finally, we also show the impact of the distance between the primary user transmitter and the distributed CR network on cooperative strategies of the distributed CRs.
Funding
This work was funded by the Finnish Funding Agency for Technology and Innovation (TEKES) and by Academy of Finland.
References
Liang YC, Zeng Y, Peh ECY, Hoang AT: Sensing-throughput tradeoff for cognitive radio networks. IEEE Transactions on Wireless Communications 2008, 7(4):1326-1337.
Ghasemi A, Sousa ES: Collaborative spectrum sensing for opportunistic access in fading environments. Proceedings of the 1st IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '05), November 2005 131-136.
Mishra SM, Sahai A, Brodersen RW: Cooperative sensing among cognitive radios. Proceedings of IEEE International Conference on Communications (ICC '06), July 2006 1658-1663.
Peh E, Liang YC: Optimization for cooperative sensing in cognitive radio networks. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC '07), March 2007 27-32.
Khan Z, Glisic S, DaSilva L, Lehtomaki J: Modeling the dynamics of coalition formation games for cooperative spectrum sharing in an interference channel. to appear in IEEE Transactions on Computational Intelligence and AI in Games
Arnold T, Schwalbe U: Dynamic coalition formation and the core. Journal of Economic Behavior and Organization 2002, 49(3):363-380. 10.1016/S0167-2681(02)00015-X
Khan Z, Glisic S, DaSilva L, Lehtomäki J: The dynamics of coalition games for cooperation in wireless networks. In Game Theory for Wireless Communications and Networking. Auerbach Publications, CRC Press, Taylor and Francis; 2010.
Myerson RB: Game Theory: Analysis of Conflict. Harvard University Press, Philadelphia, Pa, USA; 1997.
Osbourne MJ: An Introduction to Game Theory. Oxford University Press, Oxford, UK; 2004.
Straffin PD: Game Theory and Strategy. Mathematical Association of America; 2006.
Arney DC, Peterson E: Cooperation in social networks: communication, trust, and selflessness. Proceedings of the Army Science Conference, December 2008 1-8.
Peterson E: Cooperation in subset team games: altruism and selfishness. http://arxiv.org/abs/0907.2376
Saad W, Han Z, Debbah M, Hjørungnes A, Başar T: Coalitional games for distributed collaborative spectrum sensing in cognitive radio networks. Proceedings of the 28th IEEE Conference on Computer Communications (INFOCOM '09), April 2009 2114-2122.
Wang B, Liu KJR, Clancy TC: Evolutionary game framework for behavior dynamics in cooperative spectrum sensing. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '08), December 2008 3123-3127.
Cordeiro S, Sofer E, Chouinard G: Functional requirements for the 802.22 WRAN standard r47. January 2006
Zhao Q, Tong L, Swami A, Chen Y: Decentralized cognitive MAC for opportunistic spectrum access in ad hoc networks: a POMDP framework. IEEE Journal on Selected Areas in Communications 2007, 25(3):589-600.
Fan R, Jiang H: Optimal multi-channel cooperative sensing in cognitive radio networks. IEEE Transactions on Wireless Communications 2010, 9(3):1128-1138.
Poor HV: An Introduction to Signal Detection and Estimation. 2nd edition. Springer, Berlin, Germany; 1994.
Chair Z, Varshney PK: Optimal data fusion in multiple sensor detection systems. IEEE Transactions on Aerospace and Electronic Systems 1986, 22(1):98-101.
Mathur S, Sankaranarayanan L, Mandayam NB: Coalitional games in receiver cooperation for spectrum sharing. Proceedings of the 40th Annual Conference on Information Sciences and Systems (CISS '06), March 2006 949-954.
Unnikrishnan J, Veeravalli VV: Algorithms for dynamic spectrum access with learning for cognitive radio. IEEE Transactions on Signal Processing 2010, 58(2):750-760.
Ghasemi A, Sousa ES: Spectrum sensing in cognitive radio networks: the cooperation-processing tradeoff. Wireless Communications and Mobile Computing 2007, 7(9):1049-1060. 10.1002/wcm.480
Zhang S, Wu T, Lau VKN: A low-overhead energy detection based cooperative sensing protocol for cognitive radio systems. IEEE Transactions on Wireless Communications 2009, 8(11):5575-5581.
Mathur S, Sankar L, Mandayam NB: Coalitions in cooperative wireless networks. IEEE Journal on Selected Areas in Communications 2008, 26(7):1104-1115.
Saad W, Han Z, Debbah M, Hjørungnes A: A distributed merge and split algorithm for fair cooperation in wireless networks. Proceedings if IEEE International Conference on Communications Workshops (ICC '08), May 2008 311-315.
Ghasemi A, Sousa ES: Spectrum sensing in cognitive radio networks: requirements, challenges and design trade-offs. IEEE Communications Magazine 2008, 46(4):32-39.
Acknowledgment
The material in this paper was presented in part at the 5th International Conference on Cognitive Radio Oriented Wireless Networks and Communications (CrownCom), Cannes, France, June, 2010.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Khan, Z., Lehtomäki, J., Codreanu, M. et al. Throughput-Efficient Dynamic Coalition Formation in Distributed Cognitive Radio Networks. J Wireless Com Network 2010, 653913 (2010). https://doi.org/10.1155/2010/653913
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/653913


 .
.

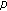 , proposes a new coalition structure. In this process, one of the CRs in the coalition acts on its behalf. (In the case of singleton coalitions, each singleton coalition, i.e., each CR, individually proposes a new coalition structure with some probability
, proposes a new coalition structure. In this process, one of the CRs in the coalition acts on its behalf. (In the case of singleton coalitions, each singleton coalition, i.e., each CR, individually proposes a new coalition structure with some probability  ; when two or more CRs form a coalition
; when two or more CRs form a coalition  , then any CR within
, then any CR within 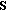 is selected as a coalition head to propose a new coalition structure with some probability
is selected as a coalition head to propose a new coalition structure with some probability  on behalf of that coalition.) (b) The evolution from one coalition structure to the next can only occur through the merging of two existing coalitions. For instance, any coalition head of any existing coalition
on behalf of that coalition.) (b) The evolution from one coalition structure to the next can only occur through the merging of two existing coalitions. For instance, any coalition head of any existing coalition  may propose to merge with another coalition
may propose to merge with another coalition 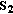 , forming
, forming 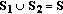 .
.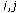 , where
, where  and
and 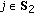 ,
,  and also
and also  . (b) When the CRs are assumed to be altruistic then they form a coalition if
. (b) When the CRs are assumed to be altruistic then they form a coalition if 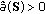 . (see Sections 3.4 and 3.5 for the details).
. (see Sections 3.4 and 3.5 for the details).

 ,
,  in (12) is set to 0. 001 ms and
in (12) is set to 0. 001 ms and  m.
m.


