- Research Article
- Open access
- Published:
Best Signal Quality in Cellular Networks: Asymptotic Properties and Applications to Mobility Management in Small Cell Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 690161 (2010)
Abstract
The quickly increasing data traffic and the user demand for a full coverage of mobile services anywhere and anytime are leading mobile networking into a future of small cell networks. However, due to the high-density and randomness of small cell networks, there are several technical challenges. In this paper, we investigate two critical issues: best signal quality and mobility management. Under the assumptions that base stations are uniformly distributed in a ring-shaped region and that shadowings are lognormal, independent, and identically distributed, we prove that when the number of sites in the ring tends to infinity, then (i) the maximum signal strength received at the center of the ring tends in distribution to a Gumbel distribution when properly renormalized, and (ii) it is asymptotically independent of the interference. Using these properties, we derive the distribution of the best signal quality. Furthermore, an optimized random cell scanning scheme is proposed, based on the evaluation of the optimal number of sites to be scanned for maximizing the user data throughput.
1. Introduction
Mobile cellular networks were initially designed for voice service. Nowadays, broadband multimedia services (e.g., video streaming) and data communications have been introduced into mobile wireless networks. These new applications have led to increasing traffic demand. To enhance network capacity and satisfy user demand of broadband services, it is known that reducing the cell size is one of the most effective approaches [1–4] to improve the spatial reuse of radio resources.
Besides, from the viewpoint of end users, full coverage is particularly desirable. Although today's macro- and micro-cellular systems have provided high service coverage, 100%-coverage is not yet reached because operators often have many constraints when installing large base stations and antennas. This generally results in potential coverage holes and dead zones. A promising architecture to cope with this problem is that of small cell networks [4, 5]. A small cell only needs lightweight antennas. It helps to replace bulky roof top base stations by small boxes set on building facade, on public furniture or indoor. Small cells can even be installed by end users (e.g., femtocells). All these greatly enhance network capacity and facilitate network deployment. Pervasive small cell networks have a great potential. For example, Willcom has deployed small cell systems in Japan [6], and Vodafone has recently launched home 3G femtocell networks in the UK [7].
In principle, high-density and randomness are the two basic characteristics of small cell networks. First, reducing cell size to increase the spatial reuse for supporting dense traffic will induce a large number of cells in the same geographical area. Secondly, end users can set up small cells by their own means [2]. This makes small cell locations and coverage areas more random and unpredictable than traditional mobile cellular networks. The above characteristics have introduced technical challenges that require new studies beyond those for macro- and micro-cellular networks. The main issues concern spectrum sharing and interference mitigation, mobility management, capacity analysis, and network self-organization [3, 4]. Among these, the signal quality, for example, in terms of signal-to-interference-plus-noise ratio (SINR), and mobility management are two critical issues.
In this paper, we first conduct a detailed study on the properties of best signal quality in mobile cellular networks. Here, the best signal quality refers to the maximum SINR received from a number of sites. Connecting the mobile to the best base station is one of the key problems. The best base station here means the base station from which the mobile receives the maximum SINR. As the radio propagation experiences random phenomena such as fading and shadowing, the best signal quality is a random quantity. Investigating its stochastic properties is of primary importance for many studies such as capacity analysis, outage analysis, neighbor cell scanning, and base station association. However, to the best of our knowledge, there is no prior art in this area.
In exploring the properties of best signal quality, we focus on cellular networks in which the propagation attenuation of the radio signal is due to the combination of a distance-dependent path-loss and of lognormal shadowing. Consider a ring  of radii
of radii  and
and  such that
such that  . The randomness of site locations is modeled by a uniform distribution of homogeneous density in
. The randomness of site locations is modeled by a uniform distribution of homogeneous density in  . Using extreme value theory (c.f., [8, 9]), we prove that the maximum signal strength received at the center of
. Using extreme value theory (c.f., [8, 9]), we prove that the maximum signal strength received at the center of  from
from  sites in
sites in  converges in distribution to a Gumbel distribution when properly renormalized and it is asymptotically independent of the total interference, as
converges in distribution to a Gumbel distribution when properly renormalized and it is asymptotically independent of the total interference, as  . The distribution of the best signal quality can thus be derived.
. The distribution of the best signal quality can thus be derived.
The second part of this paper focuses on applying the above results to mobility support in dense small cell networks. Mobility support allows one to maintain service continuity even when users are moving around while keeping efficient use of radio resources. Today's cellular network standards highlight mobile-assisted handover in which the mobile measures the pilot signal quality of neighbor cells and reports the measurement result to the network. If the signal quality from a neighbor cell is better than that of the serving cell by a handover margin, the network will initiate a handover to that cell. The neighbor measurement by mobiles is called neighbor cell scanning. Following mobile cellular technologies, it is known that small cell networking will also use mobile-assisted handover for mobility management.
To conduct cell scanning [10–12], today's cellular networks use a neighbor cell list. This list contains information about the pilot signal of selected handover candidates and is sent to mobiles. The mobiles then only need to measure the pilot signal quality of sites included in the neighbor cell list of its serving cell. It is known that the neighbor cell list has a significant impact on the performance of mobility management, and this has been a concern for many years in practical operations [13, 14] as well as in scientific research [15–18]. Using neighbor cell list is not effective for the scanning in small cell networks due to the aforementioned characteristics of high density and randomness.
The present paper proposes an optimized random cell scanning for small cell networks. This random cell scanning will simplify the network configuration and operation by avoiding maintaining the conventional neighbor cell list while improving user's quality-of-service (QoS). It is also implementable in wideband technologies such as WiMAX and LTE.
In the following, Section 2 describes the system model. Section 3 derives the asymptotic properties and the distribution of the best signal quality. Section 4 presents the optimized random cell scanning and numerical results. Finally, Section 5 contains some concluding remarks.
2. System Model
The underlying network is composed of cells covered by base stations with omnidirectional antennas. Each base station is also called a site. The set of sites is denoted by  . We now construct a model for studying the maximum signal strength, interference, and the best signal quality, after specifying essential parameters of the radio propagation and the spatial distribution of sites in the network.
. We now construct a model for studying the maximum signal strength, interference, and the best signal quality, after specifying essential parameters of the radio propagation and the spatial distribution of sites in the network.
As mentioned in the introduction, the location of a small cell site is often not exactly known even to the operator. The spatial distribution of sites seen by a mobile station will hence be treated as completely random [19] and will be modeled by an homogeneous Poisson point process [20] with intensity  .
.
In the following, it is assumed that the downlink pilot signal is sent at constant power at all sites. Let  be some strictly positive real number. For any mobile user, it is assumed that the distance to his closest site is at least
be some strictly positive real number. For any mobile user, it is assumed that the distance to his closest site is at least  and hence the path loss is in the far field. So, the signal strength of a site
and hence the path loss is in the far field. So, the signal strength of a site  received by a mobile at a position
received by a mobile at a position  is given by
is given by

where  is the location of site
is the location of site  represents the base station's transmission power and the characteristics of propagation,
represents the base station's transmission power and the characteristics of propagation,  is the path loss exponent (here, we consider
is the path loss exponent (here, we consider  ), and the random variables
), and the random variables  , which represent the lognormal shadowing, are defined from
, which represent the lognormal shadowing, are defined from  , an independent and identically distributed (i.i.d.) sequence of Gaussian random variables with zero mean and standard deviation
, an independent and identically distributed (i.i.d.) sequence of Gaussian random variables with zero mean and standard deviation  . Typically,
. Typically,  is approximately 8 dB [21, 22]. Here, we consider that fast fading is averaged out as it varies much faster than the handover decision process.
is approximately 8 dB [21, 22]. Here, we consider that fast fading is averaged out as it varies much faster than the handover decision process.
Cells sharing a common frequency band interfere one another. Each cell is assumed allocated no more than one frequency band. Denote the set of all the cells sharing frequency band  th by
th by  , where
, where  . So
. So  for
for  , and
, and  . The SINR received at
. The SINR received at  from site
from site  is expressible as
is expressible as

where  is the thermal noise average power which is assumed constant. For notational simplicity, let
is the thermal noise average power which is assumed constant. For notational simplicity, let  . Then
. Then  is given by
is given by

In the following, we will use (3) instead of (2).
3. Best Signal Quality
In this section, we derive the distribution of the best signal quality. Given a set of sites  , the best signal quality received from
, the best signal quality received from  at a position
at a position  , denoted by
, denoted by  , is defined as
, is defined as

Let us first consider a single-frequency network (i.e.,  ).
).
Lemma 1.
In the cell set  of single-frequency network, the site which provides a mobile the maximum signal strength will also provide this mobile the best signal quality, namely,
of single-frequency network, the site which provides a mobile the maximum signal strength will also provide this mobile the best signal quality, namely,

where

is the maximum signal strength received at  from the cell set
from the cell set  , and
, and

is the total interference received at  .
.
Proof.
Since  and
and  , (5) follows from the fact that no matter which cell
, (5) follows from the fact that no matter which cell  is considered,
is considered,  is the same and from the fact that
is the same and from the fact that  with
with  constant is an increasing function of
constant is an increasing function of  .
.
Let us now consider the case of multiple-frequency networks. Under the assumption that adjacent-channel interference is negligible compared to cochannel interference, cells of different frequency bands do not interfere one another. Thus, for a given network topology  , the SINRs received from cells of different frequency bands are independent. In the context of a random distribution of sites, the SINRs received from cells of different frequency bands are therefore conditionally independent given
, the SINRs received from cells of different frequency bands are independent. In the context of a random distribution of sites, the SINRs received from cells of different frequency bands are therefore conditionally independent given  . Write cell set
. Write cell set  as
as

with  the subset of
the subset of  allocated to frequency
allocated to frequency  . Let
. Let

be the best signal quality received at  from sites which belong to
from sites which belong to  . The random variables
. The random variables  are conditionally independent given
are conditionally independent given  . As a result,
. As a result,

Remark 1.
For the coming discussions, we define

which is the interference from cells in set  . In the following, for notational simplicity, the location variable
. In the following, for notational simplicity, the location variable  appearing in
appearing in  , and
, and  will be omitted in case of no ambiguity. We will simply write
will be omitted in case of no ambiguity. We will simply write  , and
, and  . Note that
. Note that  since
since  .
.
Following Lemma 1, the distribution of  can be determined by the joint distribution of
can be determined by the joint distribution of  and
and  , which is given below.
, which is given below.
Corollary 1.
The tail distribution of the best signal quality received from cell set  is given by
is given by

where  is the joint probability density of
is the joint probability density of  and
and  .
.
Proof.
By Lemma 1, we have

In view of Corollary 1, we need to study the properties of the maximum signal strength  as well as the joint distribution of
as well as the joint distribution of  and
and  . As described in the introduction, in dense small cell networks, there could be a large number of neighbor cells and a mobile may thus receive from many sites with strong enough signal strength. This justifies the use of extreme value theory within this context.
. As described in the introduction, in dense small cell networks, there could be a large number of neighbor cells and a mobile may thus receive from many sites with strong enough signal strength. This justifies the use of extreme value theory within this context.
For some  and
and  such that
such that  , let
, let  be a ring with inner and outer radii
be a ring with inner and outer radii  and
and  , respectively. In this section, we will establish the following results.
, respectively. In this section, we will establish the following results.
-
(1)
The signal strength
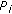 received at the center of
received at the center of  belongs to the maximum domain of attraction (MDA) of the Gumbel distribution (c.f., Theorem 1 in Section 3.1).
belongs to the maximum domain of attraction (MDA) of the Gumbel distribution (c.f., Theorem 1 in Section 3.1). -
(2)
The maximum signal strength and the interference received at the center of
 from
from  sites therein are asymptotically independent as
sites therein are asymptotically independent as 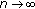 (c.f., Corollary 3 in Section 3.1).
(c.f., Corollary 3 in Section 3.1). -
(3)
The distribution of the best signal quality is derived (c.f., Theorem 2 in Section 3.3).
3.1. Asymptotic Properties
To begin with, some technical details need to be specified. Given a ring  as previously defined, we will study metrics (such as e.g., signal strength, interference, etc.) as seen at the center of
as previously defined, we will study metrics (such as e.g., signal strength, interference, etc.) as seen at the center of  for a set
for a set  of
of  sites located in
sites located in  . We will use the notation
. We will use the notation  , and
, and  instead of
instead of  , and
, and  , respectively, with
, respectively, with

Lemma 2.
Assume that  , that sites are uniformly distributed in
, that sites are uniformly distributed in  , and that the shadowing
, and that the shadowing  follows a lognormal distribution of parameters
follows a lognormal distribution of parameters  . Then the cdf of the signal strength
. Then the cdf of the signal strength  received at the center of
received at the center of  from a site located in
from a site located in  is given by
is given by

where  ,
,  ,
,  ,
,  , and
, and  ,
,  , refers to the cdf of a lognormal distribution of parameters
, refers to the cdf of a lognormal distribution of parameters  , in which
, in which

Proof.
See Appendix .
Under the studied system model,  are independent and identically distributed (i.i.d.), and so the cdf
are independent and identically distributed (i.i.d.), and so the cdf  and probability density function (pdf)
and probability density function (pdf)  of
of  are directly obtained as follows.
are directly obtained as follows.
Corollary 2.
Under the conditions of Lemma 2, the cdf and the pdf of  are given, respectively, by
are given, respectively, by


where  is given by (15), and
is given by (15), and  is the pdf of
is the pdf of  ,
,  .
.
Since  is the maximum of i.i.d. random variables, we can also study its asymptotic properties by extreme value theory. Fisher and Tippett [9, Theorem 3.2.3] proved that under appropriate normalization, if the normalized maximum of i.i.d. random variables tends in distribution to a nondegenerate distribution
is the maximum of i.i.d. random variables, we can also study its asymptotic properties by extreme value theory. Fisher and Tippett [9, Theorem 3.2.3] proved that under appropriate normalization, if the normalized maximum of i.i.d. random variables tends in distribution to a nondegenerate distribution  , then
, then  must have one of the three known forms: Fréchet, Weibull, or Gumbel distribution. In the following, we prove that
must have one of the three known forms: Fréchet, Weibull, or Gumbel distribution. In the following, we prove that  belongs to the MDA of a Gumbel distribution. First of all, we establish the following result that is required to identify the limiting distribution of
belongs to the MDA of a Gumbel distribution. First of all, we establish the following result that is required to identify the limiting distribution of  .
.
Lemma 3.
Under the conditions of Lemma 2, the signal strength received at the center of  from a site located in
from a site located in  has the following tail equivalent distribution:
has the following tail equivalent distribution:


where  , and
, and  .
.
Proof.
See Appendix .
Equation (19b) shows that the tail distribution of the signal strength  is close to that of
is close to that of  , although it decreases more rapidly. The fact that
, although it decreases more rapidly. The fact that  determines the tail behavior of
determines the tail behavior of  is in fact reasonable, since
is in fact reasonable, since  is the distribution of the signal strength received from the closest possible neighboring site (with
is the distribution of the signal strength received from the closest possible neighboring site (with  and
and  ). The main result is given below.
). The main result is given below.
Theorem 1.
Assume that  , that sites are uniformly distributed in
, that sites are uniformly distributed in  , and that shadowings are i.i.d. and follow a lognormal distribution of parameters
, and that shadowings are i.i.d. and follow a lognormal distribution of parameters  with
with  . Then there exists constants
. Then there exists constants  and
and  such that
such that

where  is the standard Gumbel distribution:
is the standard Gumbel distribution:

and  represents the convergence in distribution. A possible choice of
represents the convergence in distribution. A possible choice of  and
and  is
is

with  given by Lemma 3.
given by Lemma 3.
Proof.
See Appendix .
By Theorem 1, the signal strength belongs to the MDA of the Gumbel distribution, denoted by  . From [23, 24], we have the following corollary of Theorem 1.
. From [23, 24], we have the following corollary of Theorem 1.
Corollary 3.
Let  be the variance and
be the variance and  be the mean of signal strength
be the mean of signal strength  . Let
. Let  . Let
. Let  , where
, where  and
and  are given by (22). Under the conditions of Theorem 1,
are given by (22). Under the conditions of Theorem 1,

where  is the Gumbel distribution and
is the Gumbel distribution and  the standard Gaussian distribution, and where the coordinates are independent.
the standard Gaussian distribution, and where the coordinates are independent.
Proof.
Conditions  and
and  provide
provide  . Then the result follows by Theorem 1 and [23, 24].
. Then the result follows by Theorem 1 and [23, 24].
Note that the total interference  can be written as
can be written as  where
where  denotes the complement of
denotes the complement of  in
in  . Under the assumptions that the locations of sites are independent and that shadowings are also independent,
. Under the assumptions that the locations of sites are independent and that shadowings are also independent,  and
and  are independent. The asymptotic independence between
are independent. The asymptotic independence between  and
and  thus induces the asymptotic independence between
thus induces the asymptotic independence between  and
and  . This observation is stated in the following corollary.
. This observation is stated in the following corollary.
Corollary 4.
Under the conditions of Theorem 1,  and
and  are asymptotically independent as
are asymptotically independent as  .
.
This asymptotic independence facilitates a wide range of studies involving the total interference and the maximum signal strength. This result will be used in the coming sub-section to derive the distribution of the best signal quality.
Remark 2.
The asymptotic properties given by Theorem 1 and Corollaries 3 and 4 hold when the number of sites in a bounded area tends to infinity. This corresponds to a network densification process in which more sites are deployed in a given geographical area in order to satisfy the need for capacity, which is precisely the small cell setting.
3.2. Convergence Speed of Asymptotic Limits
Theorem 1 and Corollaries 3 and 4 provide asymptotic properties when  . In practice,
. In practice,  is the number of cells to be scanned, and so it can only take moderate values. Thus, it is important to evaluate the convergence speed of (20) and (23). We will do this based on simulations and will measure the discrepancy using a symmetrized version of the Kullback-Leibler divergence (the so-called Jensen-Shannon divergence (JSdiv)).
is the number of cells to be scanned, and so it can only take moderate values. Thus, it is important to evaluate the convergence speed of (20) and (23). We will do this based on simulations and will measure the discrepancy using a symmetrized version of the Kullback-Leibler divergence (the so-called Jensen-Shannon divergence (JSdiv)).
Let us start with some numerical evaluations of the convergence of  to its limiting distribution. Figure 1(a) shows
to its limiting distribution. Figure 1(a) shows  for different
for different  and compares to empirical simulation results. As expected the analytical distributions obtained by (17) of Corollary 2 match with the empirical distributions for all
and compares to empirical simulation results. As expected the analytical distributions obtained by (17) of Corollary 2 match with the empirical distributions for all  . Figure 1(b) plots the analytical distribution and its limiting distribution, that is, the Gumbel distribution
. Figure 1(b) plots the analytical distribution and its limiting distribution, that is, the Gumbel distribution  . There is a discrepancy in the negative regime (see the circled region in Figure 1(b)). It is worth pointing out that as a maximum of signal strengths,
. There is a discrepancy in the negative regime (see the circled region in Figure 1(b)). It is worth pointing out that as a maximum of signal strengths,  and thus
and thus  since
since  . This means that
. This means that  ,
,  , whereas
, whereas  ,
,  . This explains the gap observed for small
. This explains the gap observed for small  . This dissimilarity should have limited impact as long as we only deal with positive values of
. This dissimilarity should have limited impact as long as we only deal with positive values of  (resp.,
(resp.,  ).
).
We now study the symmetrized divergence between the analytical and limiting distributions of  for some moderate values of
for some moderate values of  and under different
and under different  and
and  . The convergence is best for
. The convergence is best for  around 10 dB and
around 10 dB and  around two to four. For practical systems,
around two to four. For practical systems,  is approx. 8 dB and
is approx. 8 dB and  . We compute the Jensen-Shannon divergence for
. We compute the Jensen-Shannon divergence for  and
and  and plot the results in Figures 2(a) and 2(b), respectively. For these (and other) values (within the range given above) of
and plot the results in Figures 2(a) and 2(b), respectively. For these (and other) values (within the range given above) of  and
and  ,
,  , and
, and  have low divergence.
have low divergence.
Let us now measure the (dis)similarity between the empirical joint distribution,  , and the product of the empirical marginal distributions,
, and the product of the empirical marginal distributions,  . Figure 3 shows an example with
. Figure 3 shows an example with  , and
, and  . We see that these two density functions are very similar. Figure 4 compares these two density functions for different values of
. We see that these two density functions are very similar. Figure 4 compares these two density functions for different values of  and
and  . Within the range defined above, the divergence between the two distributions is again small. Comparing Figure 2 and Figure 4, one can conclude that even if the convergence of
. Within the range defined above, the divergence between the two distributions is again small. Comparing Figure 2 and Figure 4, one can conclude that even if the convergence of  remains slow,
remains slow,  and
and  quickly become uncorrelated. Thus, the independence between
quickly become uncorrelated. Thus, the independence between  and
and  holds for moderate values of
holds for moderate values of  , that is,
, that is,

and so the same conclusion holds for the independence between  and
and  .
.
3.3. Distribution of the Best Signal Quality
From the above results, we have the distribution of  and the asymptotic independence between
and the asymptotic independence between  and
and  . In order to derive the distribution of the best signal quality, we also need the distribution of the total interference.
. In order to derive the distribution of the best signal quality, we also need the distribution of the total interference.
Lemma 4.
Assume that shadowings are i.i.d. and follow a lognormal distribution of parameters  , and that sites are distributed according to a Poisson point process with intensity
, and that sites are distributed according to a Poisson point process with intensity  outside the disk of radius
outside the disk of radius  . Let
. Let  be the interference received at the disk center, and
be the interference received at the disk center, and  be the characteristic function of
be the characteristic function of  . Then:
. Then:
-
(1)
 (25)
(25)where
 , and
, and  is the characteristic function of
is the characteristic function of  ;
; -
(2)
 for all
for all 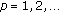 , where
, where 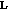 is the space of absolutely integrable functions;
is the space of absolutely integrable functions; -
(3)
If
 is large, then
is large, then  admits the following approximation:
admits the following approximation: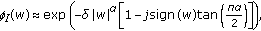 (26)
(26)where
 , with
, with  denoting the gamma function.
denoting the gamma function.
Proof.
See Appendix .
Theorem 2.
Under the assumptions of Lemma 4, let  be the ring of inner and outer radii
be the ring of inner and outer radii  and
and  , respectively. Denote the best signal quality received at the center of
, respectively. Denote the best signal quality received at the center of  from
from  sites in
sites in  by
by  . Assume that
. Assume that  , that
, that  is large, and that
is large, and that  , with high probability, where
, with high probability, where  is some positive integer. Then the tail distribution of
is some positive integer. Then the tail distribution of  can be approximated by
can be approximated by

Proof.
See Appendix .
The approximation proposed in Theorem 2 will be used in Section 4 below. It will be validated by simulation in the context considered there.
4. Random Cell Scanning for Data Services
In this section, the theoretical results developed in Section 3 are applied to random cell scanning.
4.1. Random Cell Scanning
Wideband technologies such as WiMAX, WCDMA, and LTE use a predefined set of codes for the identification of cells at the air interface. For example, 114 pseudonoise sequences are used in WiMAX [25], while 504 physical cell identifiers are used in LTE [26]. When the mobile knows the identification code of a cell, it can synchronize over the air interface and then measure the pilot signal quality of the cell. Therefore, by using a predefined set of codes, these wideband technologies can have more autonomous cell measurement conducted by the mobile. In this paper, this identification code is referred to as cell synchronization identifier (CSID).
In a dense small cell network where a large number of cells are deployed in the same geographical area, the mobile can scan any cell as long as the set of CSIDs used in the network is provided. This capability motivates us to propose random cell scanning which is easy to implement and has only very few operation requirements. The scheme is detailed below.
-
(1)
When a mobile gets admitted to the network, its (first) serving cell provides him/her the whole set of CSIDs used in the network. The mobile then keeps this information in its memory.
-
(2)
To find a handover target, the mobile randomly selects a set of
 CSIDs from its memory and conducts the standardized scanning procedure of the underlying cellular technology, for example, scanning specified in IEEE 802.16 [25], or neighbor measurement procedure specified in 3G [27] and LTE [12].
CSIDs from its memory and conducts the standardized scanning procedure of the underlying cellular technology, for example, scanning specified in IEEE 802.16 [25], or neighbor measurement procedure specified in 3G [27] and LTE [12]. -
(3)
The mobile finally selects the cell with the best received signal quality as the handover target.
In the following, we determine the number of cells to be scanned which maximizes the data throughput.
4.2. Problem Formulation
The optimization problem has to take into account the two contrary effects due to the number of cells to be scanned. On one hand, the larger the set of scanned cells, the better the signal quality of the chosen site, and hence the larger the data throughput obtained by the mobile. On the other hand, scanning can have a linear cost in the number of scanned cells, which is detrimental to the throughput obtained by the mobile.
Let us quantify this using the tools of the previous sections.
Let  be the average cell bandwidth available per mobile and assume that it is a constant. Under the assumption of additive white Gaussian noise, the maximum capacity
be the average cell bandwidth available per mobile and assume that it is a constant. Under the assumption of additive white Gaussian noise, the maximum capacity  that the mobile can have by selecting the best among
that the mobile can have by selecting the best among  randomly scanned cells is
randomly scanned cells is

Hence

where  is the pdf of
is the pdf of  . By an integration by parts of
. By an integration by parts of  and
and  , this becomes
, this becomes

Note that  is the expected throughput from the best cell. Since
is the expected throughput from the best cell. Since  is the maximum signal quality of the
is the maximum signal quality of the  cells,
cells,  increases with
increases with  and so does
and so does  . Hence, the mobile should scan as many cells as possible. However, on the other hand, if scanning many cells, the mobile will consume much time in scanning and thus have less time for data transmission with the serving cell. A typical situation is that where the scanning time increases proportionally with the number of cells scanned and where the data transmission is suspended. This for instance happens if the underlying cellular technology uses a compressed mode scanning, like for example, in IEEE 802.16 [25] and also inter-frequency cell measurements defined by 3GPP [12, 27]. In this mode, scanning intervals, where the mobile temporarily suspends data transmission for scanning neighbor cells, are interleaved with intervals where data transmission with the serving cell is resumed.
. Hence, the mobile should scan as many cells as possible. However, on the other hand, if scanning many cells, the mobile will consume much time in scanning and thus have less time for data transmission with the serving cell. A typical situation is that where the scanning time increases proportionally with the number of cells scanned and where the data transmission is suspended. This for instance happens if the underlying cellular technology uses a compressed mode scanning, like for example, in IEEE 802.16 [25] and also inter-frequency cell measurements defined by 3GPP [12, 27]. In this mode, scanning intervals, where the mobile temporarily suspends data transmission for scanning neighbor cells, are interleaved with intervals where data transmission with the serving cell is resumed.
Another scenario is that of parallel scanning-transmission: here scanning can be performed in parallel to data transmission so that no transmission gap occurs; this is the case in, for example, intrafrequency cell measurements in WCDMA [27] and LTE [12].
Let  be the average time during which the mobile stays in the tagged cell and receives data from it. Let
be the average time during which the mobile stays in the tagged cell and receives data from it. Let  be the time needed to scan one cell (e.g., in WCDMA, the mobile needs
be the time needed to scan one cell (e.g., in WCDMA, the mobile needs  if the cell is in the neighbor cell list and
if the cell is in the neighbor cell list and  if not [28], whereas in WiMAX,
if not [28], whereas in WiMAX,  , i.e., two 5-ms frames). Let
, i.e., two 5-ms frames). Let  be the duration of the suspension of data transmission due to the scanning of the
be the duration of the suspension of data transmission due to the scanning of the  cells:
cells:

Finally, let  be the average throughput received from the serving cell when no scanning at all is performed (this would be the case if the mobile would pick as serving site one of the sites of set
be the average throughput received from the serving cell when no scanning at all is performed (this would be the case if the mobile would pick as serving site one of the sites of set  at random).
at random).
The gain of scanning  cells can be quantified by the following metric, that we will call the acceleration
cells can be quantified by the following metric, that we will call the acceleration

In this definition,  (resp.,
(resp.,  is the expected amount of data transmitted when scanning
is the expected amount of data transmitted when scanning  cells (resp., doing no scanning at all). We aim at finding the value of
cells (resp., doing no scanning at all). We aim at finding the value of  that maximizes the acceleration
that maximizes the acceleration  .
.
It is clear that  when (i)
when (i)  , that is, the mobile stays in and receives data from the tagged cell forever, or (ii)
, that is, the mobile stays in and receives data from the tagged cell forever, or (ii)  , that is, parallel scanning-transmission is enabled. In these cases,
, that is, parallel scanning-transmission is enabled. In these cases,  increases with
increases with  and the mobile "should" scan as many cells as possible. However,
and the mobile "should" scan as many cells as possible. However,  is often concave and the reward of scanning then decreases. To characterize this, we introduce a growth factor
is often concave and the reward of scanning then decreases. To characterize this, we introduce a growth factor defined as follows:
defined as follows:

Special cases as those considered above can be cast within a general framework which consists in finding the value of  that maximizes
that maximizes  under the constraint that
under the constraint that  , where
, where  is a threshold.
is a threshold.
4.3. Numerical Result
In the following, we show how to apply the above results to find the optimal  . We adopt WCDMA as the underlying cellular network technology. 100 omnidirectional small cell base stations are deployed in a square domain of
. We adopt WCDMA as the underlying cellular network technology. 100 omnidirectional small cell base stations are deployed in a square domain of  . The network density is thus equal to
. The network density is thus equal to

It is assumed that any cell synchronization identifier can be found in a radius  . We take
. We take  equal to 2 meters. The propagation path loss is modeled by the picocell path loss model [29]:
equal to 2 meters. The propagation path loss is modeled by the picocell path loss model [29]:

where  is the distance from the base station in meters,
is the distance from the base station in meters,  the number of penetrated floors in the propagation path. For indoor office environments,
the number of penetrated floors in the propagation path. For indoor office environments,  is the default value [22]; however, here, the small cell network is assumed to be deployed in a general domain including outdoor urban areas where there are less penetrated walls and floors. So, we use
is the default value [22]; however, here, the small cell network is assumed to be deployed in a general domain including outdoor urban areas where there are less penetrated walls and floors. So, we use  in our numerical study.
in our numerical study.
It is assumed that the total transmission power including the antenna gain of each small cell base station is  . Shadowing is modeled as a random variable with lognormal distribution with an underlying Gaussian distribution of zero mean and
. Shadowing is modeled as a random variable with lognormal distribution with an underlying Gaussian distribution of zero mean and  standard deviation. The signal strength received at any distance
standard deviation. The signal strength received at any distance  from a base station
from a base station  is expressible as
is expressible as

By (35), we have

The parameters  and
and  appearing in
appearing in  can be identified from (37) after converting the received signal strength from the dBm scale to the linear scale:
can be identified from (37) after converting the received signal strength from the dBm scale to the linear scale:

The received noise power  is given by
is given by

where the effective bandwidth  Hz,
Hz,  is the Boltzmann constant, and
is the Boltzmann constant, and  is the temperature in Kelvin,
is the temperature in Kelvin,  W/Hz and
W/Hz and  is equal to 7 dB.
is equal to 7 dB.
It is assumed that the mobile is capable of scanning eight identified cells within 200 ms [28]. So, the average time needed to scan one cell is given by  .
.
In order to check the accuracy of the approximations used in the analysis, a simulation was built with the above parameter setting. The interference field was generated according to a Poisson point process of intensity  in a region between
in a region between  and
and  . For a number
. For a number  , the maximum of SINR received from
, the maximum of SINR received from  base stations which are randomly selected from the disk
base stations which are randomly selected from the disk  between radii
between radii  and
and  was computed. After that the expectation of the maximal capacity
was computed. After that the expectation of the maximal capacity  received from the
received from the  selected BSs was evaluated.
selected BSs was evaluated.
In Figure 5(a), the expectation of the maximal throughput  for different
for different  is plotted, as obtained through the analytical model and simulation. The agreement between model and simulation is quite evident. As shown in Figure 5(a),
is plotted, as obtained through the analytical model and simulation. The agreement between model and simulation is quite evident. As shown in Figure 5(a),  increases with
increases with  , though the increasing rate slows down as
, though the increasing rate slows down as  increases. Note that in Figure 5(a),
increases. Note that in Figure 5(a),  is plotted after normalization by
is plotted after normalization by  .
.
Figure 5(b) gives an example of acceleration  for
for  second and
second and  . In the plot,
. In the plot,  is normalized by its maximum. Here, an agreement between model and simulation is also obtained. We see that
is normalized by its maximum. Here, an agreement between model and simulation is also obtained. We see that  first increases rapidly with
first increases rapidly with  , attains its maximum at
, attains its maximum at  by simulation and
by simulation and  by model, and then decays.
by model, and then decays.
Next, using the model we compute the optimal number of cells to be scanned and the growth factor  for different
for different  . Note that in (32), the factor
. Note that in (32), the factor  can be rewritten as
can be rewritten as

It is clear that this factor also depends on the ratio  . Figure 5(c) plots the optimal
. Figure 5(c) plots the optimal  for different values of
for different values of  . Larger
. Larger  will drive the optimal
will drive the optimal  towards larger values. Since
towards larger values. Since  can be roughly estimated as the mobile residence time in a cell, which is proportional to the cell diameter divided by the user speed, this can be rephrased by stating that the faster the mobile, the smaller
can be roughly estimated as the mobile residence time in a cell, which is proportional to the cell diameter divided by the user speed, this can be rephrased by stating that the faster the mobile, the smaller  and thus the fewer cells the mobile should scan.
and thus the fewer cells the mobile should scan.
Finally, Figure 5(d) plots the growth factor  with different
with different  . In Figure 5(d), the "limiting case" corresponds to the case when
. In Figure 5(d), the "limiting case" corresponds to the case when  or
or  . We see that
. We see that  is quite stable w.r.t. the variation of
is quite stable w.r.t. the variation of  . Besides,
. Besides,  flattens out at about 30 cells for a wide range of
flattens out at about 30 cells for a wide range of  . Therefore, in practice this value can be taken as a recommended number of cells to be scanned in the system.
. Therefore, in practice this value can be taken as a recommended number of cells to be scanned in the system.
5. Concluding Remarks
In this paper, we firstly develop asymptotic properties of the signal strength in cellular networks. We have shown that the signal strength received at the center of a ring shaped domain  from a base station located in
from a base station located in  belongs to the maximum domain of attraction of a Gumbel distribution. Moreover, the maximum signal strength and the interference received from
belongs to the maximum domain of attraction of a Gumbel distribution. Moreover, the maximum signal strength and the interference received from  cells in
cells in  are asymptotically independent as
are asymptotically independent as  . The above properties are proved under the assumption that sites are uniformly distributed in
. The above properties are proved under the assumption that sites are uniformly distributed in  and that shadowing is lognormal. Secondly, the distribution of the best signal quality is derived. These results are then used to optimize scanning in small cell networks. We determine the number of cells to be scanned for maximizing the mean user throughput within this setting.
and that shadowing is lognormal. Secondly, the distribution of the best signal quality is derived. These results are then used to optimize scanning in small cell networks. We determine the number of cells to be scanned for maximizing the mean user throughput within this setting.
Appendices
A. Proof of Lemma 2
Let  be the distance from a site located at
be the distance from a site located at  to a position
to a position  . Under the assumption that site locations are uniformly distributed in
. Under the assumption that site locations are uniformly distributed in  , the distance
, the distance  from a site located in
from a site located in  , that is,
, that is,  , to the center of
, to the center of  has the following distribution:
has the following distribution:

Let  , for
, for  , its distribution is equal to
, its distribution is equal to

where  ,
,  , and
, and  . The density of
. The density of  is given by
is given by  .
.
Thus, the distribution  of the power
of the power  is equal to
is equal to

Substituting  with lognormal distribution of parameters
with lognormal distribution of parameters  and
and  given above into (A.3), after changing the variable such that
given above into (A.3), after changing the variable such that  , we have
, we have

where the first integral is straightforward. By doing an integration by parts of  and
and  for the second integral, we get
for the second integral, we get

After some elementary simplifications, we can obtain

where  ,
,  ,
,  ,
,  , and
, and  . Let
. Let  , be the lognormal distribution of parameters
, be the lognormal distribution of parameters  ,
,  can be rewritten as (15).
can be rewritten as (15).
B. Proof of Lemma 3
Let  and note that
and note that  , we have from (15)
, we have from (15)

This yields the tail distribution  :
:

For (B.2), we have  . An asymptotic expansion of
. An asymptotic expansion of  for large
for large  [30, 7.1.23] gives us:
[30, 7.1.23] gives us:

in which after a Taylor expansion of the last term on the right-hand side, we can have

This implies that

In the same manner, we have

A substitution of (B.5) and (B.6) into (B.2) results in

Moreover,  yields
yields  . Then, we have the following result for large
. Then, we have the following result for large  :
:

Taking this into account in (B.7), finally we have

C. Proof of Theorem 1
We will use Lemma 3 and the following two lemmas to prove Theorem 1.
Lemma 5 (Embrechts et al. [9]).
Let  be i.i.d. random variables having distribution
be i.i.d. random variables having distribution  , and
, and  . Let
. Let  be an increasing real function, denote
be an increasing real function, denote  , and
, and  . If
. If  with normalizing constant
with normalizing constant  and
and  , then
, then

Lemma 6 (Takahashi [31]).
Let  be a distribution function. Suppose that there exists constants
be a distribution function. Suppose that there exists constants  ,
,  ,
,  , and
, and  such that
such that

For  and
and  , let
, let  . Then,
. Then,  with normalizing constants
with normalizing constants  and
and  , where
, where

Let  be a real function defined on
be a real function defined on  ,
,  is increasing with
is increasing with  . Let
. Let  be the random variable such that
be the random variable such that  . By (19a) of Lemma 3, the tail distribution
. By (19a) of Lemma 3, the tail distribution  is given by
is given by

By (C.4),  satisfies Lemma 6 with constants
satisfies Lemma 6 with constants  ,
,  ,
,  , and
, and  . So,
. So,  with the following normalizing constants:
with the following normalizing constants:

Then, by Lemma 5, we have

By a Taylor expansion of  , we have
, we have

Since  when
when  , we have
, we have

Substituting  and
and  from (C.5) into (C.8), we obtain
from (C.5) into (C.8), we obtain  and
and  for (22). The conditions
for (22). The conditions  ,
,  and
and  provide
provide  . This leads to
. This leads to  , and consequently,
, and consequently,  .
.
D. Proof of Lemma 4
Under the assumptions of the lemma, the interference field can be modeled as a shot noise defined on  excluding the inner disk of radius
excluding the inner disk of radius  . Hence, using Proposition 2.2.4 in [20], the Laplace transform of
. Hence, using Proposition 2.2.4 in [20], the Laplace transform of  is given by
is given by

Noting that

we have from (D.1) that

Using the change of variable  , we obtain
, we obtain

where  . So, substituting this into (D.3), we get the first part of the Lemma 4.
. So, substituting this into (D.3), we get the first part of the Lemma 4.
From (25), for all  , we have
, we have

Since  , we have
, we have

Therefore

where  is some positive constant, and hence the right hand-side of this is an absolutely integrable function. This proves the second assertion of Lemma 4.
is some positive constant, and hence the right hand-side of this is an absolutely integrable function. This proves the second assertion of Lemma 4.
Under the assumption that  ,
,  can be approximated by
can be approximated by

For  , we have
, we have

Since  , we can write
, we can write  . Taking expectations on both sides, we get
. Taking expectations on both sides, we get

Substituting this into (D.8) and noting that

for  lognormally distributed, we obtain (26).
lognormally distributed, we obtain (26).
E. Proof of Theorem 2
Under the assumption that sites are distributed as a homogeneous Poisson point process of intensity  in
in  , the expected number of cells in
, the expected number of cells in  is
is  . We assume that
. We assume that  is much larger than
is much larger than  , which ensures that there are
, which ensures that there are  cells in
cells in  with high probability, so that
with high probability, so that  is well defined.
is well defined.
Under the conditions of Theorem 2,  and
and  are asymptotically independent according to Corollary 4. So, by substituting (24) into (12), we have
are asymptotically independent according to Corollary 4. So, by substituting (24) into (12), we have

where

It is easily seen that  is square-integrable with respect to
is square-integrable with respect to  , and its Fourier transform w.r.t.
, and its Fourier transform w.r.t.  is given by
is given by

which yields:

Besides, according to Lemma 4 we have that  and
and  , where
, where  is the space of square integrable functions. And so, by Theorem 3 in [32, page 509],
is the space of square integrable functions. And so, by Theorem 3 in [32, page 509],  is bounded continuous and square integrable. Hence, by applying the Plancherel-Parseval theorem to the inner integral of (E.1), we have
is bounded continuous and square integrable. Hence, by applying the Plancherel-Parseval theorem to the inner integral of (E.1), we have

where  is the Fourier transform of
is the Fourier transform of  . Take (E.4) into account for (E.5) and (E.1), we have
. Take (E.4) into account for (E.5) and (E.1), we have

where we further have

Note that

And under the assumption that  ,
,  is approximated by (26). Thus, by (26) and (E.4), we have for
is approximated by (26). Thus, by (26) and (E.4), we have for  :
:

By (E.9), we get

Substitute the above into (E.7) and then into (E.6), we have (27).
References
Lee WCY: Smaller cells for greater performance. IEEE Communications Magazine 1991, 29(11):19-23. 10.1109/35.109660
Claussen H, Ho LTW, Samuel LG: Financial analysis of a pico-cellular home network deployment. Proceedings of the IEEE International Conference on Communications, June 2007 5604-5609.
Chandrasekhar V, Andrews JG, Gatherer A: Femtocell networks: a survey. IEEE Communications Magazine 2008, 46(9):59-67.
Saunders S, Carlaw S, Giustina A, Bhat RR, Rao VS, Siegberg R: Femtocells: Opportunities and Challenges for Business and Technology. John Wiley & Sons, New York, NY, USA; 2009.
Urie A: Keynote: the future of mobile networking will be small cells. Proceedings of the IEEE International Workshop on Indoor and Outdoor Femto Cells (IOFC '09), September 2009, Tokyo, Japan
Chika Y: Keynote: true BWA—eXtended Global Platform. Proceedings of the IEEE International Workshop on Indoor and Outdoor Femto Cells (IOFC '09), September 2009, Tokyo, Japan
Judge P: Vodafone Launches Home 3G Femtocell in the UK. eWeekEurope, London, UK; 2009.
Leadbetter MR, Lindgren G, Rootzén H: Extremes and Related Properties of Random Sequences and Processes. Springer, New York, NY, USA; 1983.
Embrechts P, Klüppelberg C, Mikosch T: Modelling Extremal Events for Insurance and Finance. Springer, New York, NY, USA; 1997.
Nawrocki M, Aghvami H, Dohler M: Understanding UMTS Radio Network Modelling, Planning and Automated Optimisation: Theory and Practice. John Wiley & Sons, New York, NY, USA; 2006.
WiMAX Forum : Mobile System Profile. Approved Spec. Release 1.0, Revision 1.4.0, May 2007
3GPP TS 36.331 : Evolved Universal Terrestrial Radio Access (EUTRA) Radio Resource Control (RRC): protocol Specification (Release 8). Tech. spec. v8.8.0, December 2009
NGMN Alliance : Next Generation Mobile Networks Use cases related to self-organising network, Overall description. December 2008., (v2.02):
NGMN Alliance : Next Generation Mobile Networks Recommendation on SON and O&M requirements. Req. Spec. v1.23, December 2008
Magnusson S, Olofsson H: Dynamic neighbor cell list planning in a micro cellular network. Proceedings of the Annual International Conference on Universal Personal Communications Record, October 1997 1: 223-227.
Guerzoni R, Ore I, Valkealahti K, Soldani D: Automatic neighbor cell list optimization for UTRA FDD networks: theoretical approach and experimental validation. Proceedings of the Western Province Motor Club (WPMC '05), 2005, Aalborg, Denmark
Soldani D, Ore I: Self-optimizing neighbor cell list for UTRA FDD networks using detected set reporting. Proceedings of the 65th IEEE Vehicular Technology Conference, 2007 694-698.
Amirijoo M, Frenger P, Gunnarsson F, Kallin H, Moe J, Zetterberg K: Neighbor cell relation list and measured cell identity management in LTE. Proceedings of the IEEE Network Operations and Management Symposium, April 2008 152-159.
Win MZ, Pinto PC, Shepp LA: A mathematical theory of network interference and its applications. Proceedings of the IEEE 2009, 97(2):205-230.
Baccelli F, Błaszczyszyn B: Stochastic geometry and wireless networks volume 1: theory. Foundations and Trends in Networking 2009, 3(3-4):249-449. 10.1561/1300000006
3GPP TR 36.942 : Evolved Universal Terrestrial Radio Access (EUTRA): Radio Frequency (RF) system scenarios (Release 8). May 2009., (v8.2.0):
WiMAX Forum : WiMAX systems evaluation methodology. Spec. v2.1, July 2008
Chow T, Teugels J: The sum and the maximum of i.i.d. random variables. Proceedings of the 2nd Prague Symposium on Asymptotic Statistics, 1978 81-92.
Anderson CW, Turkman KF: The joint limiting distribution of sums and maxima of stationary sequences. Journal of Applied Probability 1991, 28(1):33-44. 10.2307/3214738
IEEE 802.16 : Air Interface for Broadband Wireless Access Systems. IEEE, Standard Std 802.16-2009, May 2009
3GPP TS 36.300 : Evolved Universal Terrestrial Radio Access (EUTRA) and Evolved Universal Terrestrial Radio Access Network (EUTRAN)—Overall description: stage 2 (Release 8). Tech. Spec. v8.11.0, December 2009
3GPP TS 25.331 : Radio Resource Control (RRC): protocol Specification (Release 8). Tech. Spec. v8.6.0, March 2009
3GPP TS 25.133 : Requirements for support of Radio Resource Management FDD (Release 8). Tech. Spec. v8.9.0, Dec. 2009
ETSI TR 101.112 : Selection procedures for the choice of radio transmission technologies of the UMTS. April 1998., (v3.2.0):
Abramowitz M, Stegun IA: Handbook of Mathematical Functions. Dover, New York, NY, USA; 1965.
Takahashi R: Normalizing constants of a distribution which belongs to the domain of attraction of the Gumbel distribution. Statistics and Probability Letters 1987, 5(3):197-200. 10.1016/0167-7152(87)90039-3
Feller W: An Introduction to Probability Theory and Its Applications. Volume 2. 2nd edition. John Wiley & Sons, New York, NY, USA; 1971.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Nguyen, V., Baccelli, F., Thomas, L. et al. Best Signal Quality in Cellular Networks: Asymptotic Properties and Applications to Mobility Management in Small Cell Networks. J Wireless Com Network 2010, 690161 (2010). https://doi.org/10.1155/2010/690161
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/690161
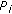 received at the center of
received at the center of  belongs to the maximum domain of attraction (MDA) of the Gumbel distribution (c.f., Theorem 1 in Section 3.1).
belongs to the maximum domain of attraction (MDA) of the Gumbel distribution (c.f., Theorem 1 in Section 3.1). from
from  sites therein are asymptotically independent as
sites therein are asymptotically independent as 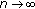 (c.f., Corollary 3 in Section 3.1).
(c.f., Corollary 3 in Section 3.1).
 under different
under different  :
:  . Comparison between analytical and empirical CDFsComparison between analytical and limiting CDFs
. Comparison between analytical and empirical CDFsComparison between analytical and limiting CDFs
 and
and  . Under different
. Under different  :
:  Under different
Under different  :
: 

 and
and  :
:  . Here, norm.
. Here, norm.  refers to
refers to  , while norm.
, while norm.  refers to
refers to  .
.
 and
and  . Under different
. Under different  :
:  Under different
Under different  :
: 

 , and
, and  is the characteristic function of
is the characteristic function of  ;
; for all
for all 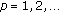 , where
, where  is the space of absolutely integrable functions;
is the space of absolutely integrable functions; is large, then
is large, then  admits the following approximation:
admits the following approximation: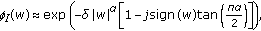
 , with
, with  denoting the gamma function.
denoting the gamma function. CSIDs from its memory and conducts the standardized scanning procedure of the underlying cellular technology, for example, scanning specified in IEEE 802.16 [
CSIDs from its memory and conducts the standardized scanning procedure of the underlying cellular technology, for example, scanning specified in IEEE 802.16 [
 Plot of
Plot of  secondOptimal number of cells to be scannedGrowth factor
secondOptimal number of cells to be scannedGrowth factor  under different
under different 