- Research Article
- Open access
- Published:
Distributed Range-Free Localization Algorithm Based on Self-Organizing Maps
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 692513 (2009)
Abstract
In Mobile Ad Hoc Networks (MANETs), determining the physical location of nodes (localization) is very important for many network services and protocols. This paper proposes a new Distributed Range-Free Localization Algorithm Based on Self-Organizing Maps (SOMs) to deal with this issue. Our proposed algorithm utilizes only connectivity information to determine the location of nodes. By utilizing the intersection areas between radio coverage of neighboring nodes, the algorithm has maximized the correlation between neighboring nodes in distributed implementation of SOM and reduced the SOM learning time. An implementation of the algorithm on Network Simulator 2 (NS-2) was done with the mobility consideration to verify the performance of the proposed algorithm. From our intensive simulations, the results show that the proposed scheme achieves very good accuracy in most cases.
1. Introduction
Recently, mobile ad-hoc network localization has received attention from many researchers [1]. Many algorithms and solutions have been presented so far. These algorithms are ranging from simple to complicated schemes, but they can be categorized as range-based and range-free algorithms. Range-free algorithms utilize only connectivity information and the number of hops between nodes. The others utilize the distance measured between nodes by either using the Time-Of-Arrival (TOA) [2], Time-Differential-Of-Arrival (TDOA) [3], Angle-Of-Arrival (AOA) [4], or Received-Signal-Strength-Indicator (RSSI) [5] technologies. However, they usually need extra hardware to achieve such measurement. When calculating the absolute location, most schemes need at least three anchors (nodes that are equipped with Global Positioning System or know their location in advance).
DV-HOP is a typical range-free algorithm. It was proposed by Niculescu and Nath [6] as an Ad-hoc Positioning System (APS). DV-HOP uses distance-vector forwarding technique to get the minimum hop count from a node to heard anchors. By using corrections calculated by anchors (average hop-distance between anchors), nodes estimate their location by using lateration (triangulation) method. Besides DV-HOP, some other algorithms seem to be more complicated, but have better accuracy. The Multidimensional Scaling Map (MDS-MAP) proposed by Shang et al. [7] is an example. MDS-MAP is originated from a data analytical technique by displaying distance-like data in geometrical visualization. It computes the shortest paths between all pairs of nodes to build a distance matrix and then applies the classical Multidimensional Scaling (MDS) to this matrix to retain the first two largest eigenvalue and eigenvector to a 2D relative map. After that, with three given anchors, it transforms the relative map into an absolute map based on anchors' absolute location. There are some variances of MDS-MAP such as centralized method: MDS-MAP(C), and distributed one: MDS-MAP(P). But, in the distributed method, to get the absolute location, nodes need global information about the subnetwork's map that contains at least three anchors. Tran and Nguyen [8] proposed a new localization scheme based on Support Vector Machine (SVM). The authors have contributed another machine learning method to the localization problem, and proved the upper bound error of this method.
Regarding the localization based on Self-Organizing Maps, some researchers have employed SOM directly or with some modification. The method presented by Giorgetti [9] employed the classical SOM to the localization. This method uses centralized implementation and requires thousands of learning steps in convergence of network topology. The authors also realize that this method is good for small and medium size networks of up to 100 nodes. S. Asakura et al. proposed a distributed localization scheme [10] based on SOM. Hu and Lee [11] also proposed another version of distributed localization based on SOM. In this work, the authors employed a deduced SOM version [12]. But, this method still needs too many iterations (at least 4000) to make the topology to be converged with a relatively low accuracy. In another work [13], the authors use SOM to track a mobile robot with the utilization of surrounding environments from readings of sensor data. In the work presented by Ertin and Priddy [14], another version of SOM was used to implement the localization in wireless sensor networks. This paper extends one of our previous work [15] to improve and adapt it with mobility scenarios. The main contribution of this paper is the utilization of intersection between radio coverage of neighboring nodes in our modified SOM, and the adaptation of the algorithm to the mobility scenarios. It is also noted that our method was verified in both MATLAB and NS-2 environments.
2. Motivation for Distributed SOM-Based Localization
2.1. Self-Organizing Maps
The Self-Organizing Maps (SOMs) were invented by Kohonen [16]. SOM provides a technique for representation of multidimensional data into much lower-dimensional spaces (usually one or two dimensions). It uses a process known as vector quantization. The nature of SOM is a neural network working in unsupervised learning manner. The SOM learning process can be summarized as follows.
-
(1)
Initialization: assign the initial weight,
 , to each neuron in the SOM network.
, to each neuron in the SOM network. -
(2)
Finding the BMU: determine the Best Matching Unit (BMU) or winning neuron
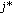 at the iteration
at the iteration  by using Euclidean minimum-distance criterion:
by using Euclidean minimum-distance criterion: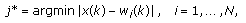 (1)
(1)where
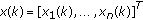 represents the
represents the  input pattern,
input pattern,  is the total number of SOM neurons, and the input pattern has
is the total number of SOM neurons, and the input pattern has  dimensions.
dimensions. -
(3)
Weight adjusting: Adjust the weights of the BMU and its neighbors using the following rule
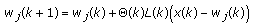 (2)
(2)where
 is the learning rate at time step
is the learning rate at time step 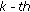 and
and  is the function for topological neighborhood of neuron
is the function for topological neighborhood of neuron  at time step
at time step 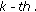
Steps  and
and  are repeated until the convergent criterion is satisfied.
are repeated until the convergent criterion is satisfied.
2.2. Motivation for Distributed SOM-Based Localization
Suppose that we have a mobile ad-hoc network of connected nodes, in which only a small number of nodes know their location in advance (anchor nodes). Now we have to determine the location of the remaining nodes that do not know their location, especially in distributed manner. In our proposed scheme, one can think that a mobile ad-hoc network itself is an SOM network, in which each neuron is a node in that network, and these neurons are connected to their 1-hop neighboring nodes (nodes have direct radio links). The topological position and the weight of each neuron are associated with its estimated location. The learning process takes place locally at each node, where the input pattern is estimated location of the node (this input is dynamically changed over time except that the anchors use their known location). The neighborhood neurons of a node are determined by its 1-hop neighboring nodes. It is obvious that each node becomes the Best-Matching Unit (BMU) at its local region. So when updating weights at the BMU, only its 1-hop neighbors' weights are updated. The BMU node also receives updates from other nodes when it becomes 1-hop neighbor of other nodes. Anchors do not update their known positions during the learning process, so if the network has some nodes know their location in advance (anchors), then each node will utilize the information from these anchors by adjusting its location towards the estimated absolute location based on the information from these heard anchors. At the end of the learning process, the weight at each node (SOM neuron) is its estimated location.
3. Proposed Distributed Localization Algorithm Based on SOM
In this section, we will introduce about our proposed Distributed Range-free Localization Algorithm (LS-SOM). The first two sections describe about initialization and learning stages of the main algorithm. The mobility consideration is presented in the third section.
3.1. Initialization Stage
In the initialization stage, each anchor in the network broadcasts a packet to its neighboring nodes. This packet contains the anchor's location and a hop count initialized to one. When a node receives a packet that contains anchor information, node then decides to discard or forward the packet to its neighboring nodes or not with the following rules.
-
(1)
If the packet is already in the cache, the node then compares the hop count of the packet with that of the cached packet. If the hop count of the arrival packet is less than that of the cached packet, then the cached packet is replaced with a new arrival packet, and forwarded to its neighboring nodes with hop count modified to add one hop. If the hop count of the arrival packet is greater than or equal to that of cached packet, then it is dropped.
-
(2)
If the packet is not in the cache, then it is added to the cache and forwarded to its neighboring nodes with hop count modified to add one hop.
Having information from some anchors, the nodes now initialize their location ready for SOM learning process. In our proposed method, the initial location of a node is calculated based on either randomized value (if node does not receive enough information from three anchors) or a value calculated using a trilateral method. In this initialization stage, nodes also exchange information (using short "HELLO" message broadcast) so that each node has information about its neighboring nodes (1-hop neighbors). Each node also exchanges information about 1-hop neighbors (just the IDs of 1-hop neighbors) with its neighboring nodes, so that all nodes in the network have information about both 1-hop and 2-hop neighboring nodes.
3.2. Learning Stage
Before going into our algorithm details, let us formulate the mathematical notations which will be used in this paper. We represent a wireless ad-hoc network as an undirected connected graph. The vertices are nodes' locations, and edges are the connectivity information (direct connection between neighboring nodes). The target wireless ad-hoc network is formed by  anchors with known locations
anchors with known locations  and N nodes with unknown locations. The unknown nodes have actual locations denoted as
and N nodes with unknown locations. The unknown nodes have actual locations denoted as  and estimated locations denoted as
and estimated locations denoted as  .
.
( ) Estimated location exchange: at this step, each node forwards its estimated location to all of its neighbors, so that it also knows the estimated location of its neighbors as
) Estimated location exchange: at this step, each node forwards its estimated location to all of its neighbors, so that it also knows the estimated location of its neighbors as  with
with  is the number of nodes within its communication range.
is the number of nodes within its communication range.
( ) Local update of relative location: we will now shape the topology at each region formed by the node with location
) Local update of relative location: we will now shape the topology at each region formed by the node with location  together with all of its neighboring nodes. The node with location
together with all of its neighboring nodes. The node with location  plays as the input vector and becomes the winning neuron for that region. Consequently, the neighboring nodes of the node with location
plays as the input vector and becomes the winning neuron for that region. Consequently, the neighboring nodes of the node with location  will receive the updating vector from node with location
will receive the updating vector from node with location  . Suppose that the node with the estimated location
. Suppose that the node with the estimated location  has
has  neighbors. The locations of these neighbors are denoted as
neighbors. The locations of these neighbors are denoted as  . Based on classical SOM, neighboring nodes of the node with location
. Based on classical SOM, neighboring nodes of the node with location  will update their weight with the following formula:
will update their weight with the following formula:

where  is calculated using
is calculated using

in which  is the learning rate exponential decay function at iteration
is the learning rate exponential decay function at iteration  defined in (5).
defined in (5).

where  denotes the
denotes the  time step of the total
time step of the total  learning steps. But, updating by using (3) means that the neighboring nodes will move toward the location determined by
learning steps. But, updating by using (3) means that the neighboring nodes will move toward the location determined by  . This will lead to the problem as showed in Figure 1. From Figure 1, the nodes with location
. This will lead to the problem as showed in Figure 1. From Figure 1, the nodes with location  and
and  are the neighbors of the node with location
are the neighbors of the node with location  , but
, but  is not the neighbor of
is not the neighbor of  . In the worst case, the estimated location of the node with location
. In the worst case, the estimated location of the node with location  falls into the radio range of the node with location
falls into the radio range of the node with location  , then the node with location
, then the node with location  may not escape from that wrong location throughout the learning process (dead location) as illustrated by position
may not escape from that wrong location throughout the learning process (dead location) as illustrated by position  .
.
In this paper, we propose an algorithm to solve this problem as follows. Suppose that at the node with location  , we have to update location for the neighbor node with location
, we have to update location for the neighbor node with location  . First, we find out other
. First, we find out other  neighboring node
neighboring node  of the node with location
of the node with location  that are not the neighbor of the node with location
that are not the neighbor of the node with location  (this is done easily because each node knows its neighbors' neighbors) and find their estimated location falls into radio range of the node with location
(this is done easily because each node knows its neighbors' neighbors) and find their estimated location falls into radio range of the node with location  . Now we calculate the vector that has the direction towards the intersection area as illustrated by the dashed area in Figure 2. As illustrated in Figure 3, this vector is calculated using
. Now we calculate the vector that has the direction towards the intersection area as illustrated by the dashed area in Figure 2. As illustrated in Figure 3, this vector is calculated using

where  denotes the maximum communicable range between node with location
denotes the maximum communicable range between node with location  and node with location
and node with location  . We use vector
. We use vector  as a guidance to update the location of the node with location
as a guidance to update the location of the node with location  by changing (3) to (7),
by changing (3) to (7),

The update by (7) makes each node move toward the intersection area as showed in Figure 2. This update also maximizes the correlation between the neighboring nodes that is the key problem for the speed and accuracy of topological convergence using SOM. In (7),  is a learning bias parameter calculated using
is a learning bias parameter calculated using

with  is a learning threshold. This threshold determines the step to apply this modification. Basically, we can apply this modification after several steps of SOM learning when nodes are in relative order to ensure the convergence of the learning process. At the end of this step, the node with location
is a learning threshold. This threshold determines the step to apply this modification. Basically, we can apply this modification after several steps of SOM learning when nodes are in relative order to ensure the convergence of the learning process. At the end of this step, the node with location  transmits its neighbor location updates based on (7) to all of its neighbors. As a result, it also receives the similar updates from its
transmits its neighbor location updates based on (7) to all of its neighbors. As a result, it also receives the similar updates from its  neighboring nodes as
neighboring nodes as  . Node with location
. Node with location  now calculates its newly estimated location by averaging its current location and the updates from the neighboring nodes using
now calculates its newly estimated location by averaging its current location and the updates from the neighboring nodes using

The learning process is repeated  times.
times.
3.3. Mobility Consideration
In MANETs, nodes may move in arbitrarily manner, so the movement of nodes will affect the performance of the algorithm. To adapt LS-SOM with MANETs, we proposed a repeated learning algorithm as follows.
( ) First Time Initialization. Anchors participate in localization will flood the network just one time, so that nodes can calculate the initial location for fast topology convergence.
) First Time Initialization. Anchors participate in localization will flood the network just one time, so that nodes can calculate the initial location for fast topology convergence.
( ) Repeated Learning. At specified interval, nodes perform neighboring detection by exchanging short "HELLO" messages. Having neighboring information, nodes now proceed with the learning process.
) Repeated Learning. At specified interval, nodes perform neighboring detection by exchanging short "HELLO" messages. Having neighboring information, nodes now proceed with the learning process.
The algorithm is illustrated by the flowchart in Figure 4.
4. Simulation Evaluations
To evaluate the performance of our proposed method, we use the average error ratio in comparison with the radio range of the nodes presented in

4.1. Simulation Parameters
To ease the comparison, we call the method in the existing work [10] as SOM, and our proposed method as LS-SOM. We conducted the simulation for static and mobile scenarios by using MATLAB (we integrated SOM, DV-HOP, and LS-SOM into the program received from [7]) and NS-2, respectively. For static scenarios, each experiment is done on thousands of randomly generated topologies that are deployed by 100 nodes on an area of 10 by 10. For mobile scenarios, we simulated on networks with 25 randomly distributed nodes on an area of 300 by 300 square meters. The propagation model is TwoRayGround and transmission range of each node is 100 meters. The common parameters used in simulation are as follows. Number of SOM learning steps  is 15, and Learning bias threshold
is 15, and Learning bias threshold  is 1.
is 1.
4.2. Static Networks
With static networks, we study how the accuracy is influenced by the connectivity level (the average number of neighboring nodes that a node has direct communication with), and the number of anchor nodes deployed. Figure 5 shows the average error with different connectivity levels. The result indicates that LS-SOM achieves very good accuracy over the SOM, DV-HOP, MDS-MAP(C), and even MDS-MAP(P) from sparse to dense networks. Especially with very sparse networks, LS-SOM still performs better than the others. The performance with the variance of anchors is showed in Figure 6. We find that LS-SOM increases accuracy when the number of anchors increases. When the number of anchors increases, LS-SOM improves accuracy much better than the others. We have tested and realized that on the grid deployment with 50% position error, LS-SOM gets better accuracy than the random deployment. Figure 7 shows the average error through each SOM learning step. LS-SOM needs only 15 to 30 learning steps to achieve a stable result. Comparing to thousands of learning steps in the traditional SOM, LS-SOM decreases network overhead and computational cost. Figure 8(a) shows one of the actual topology that is generated during the simulation. Figures 8(b), 8(c), and 8(d) show the topologies estimated with DV-HOP, SOM and LS-SOM, respectively. In these figures, the rectangles and the circles denote the anchor nodes and the unknown nodes, respectively. From the figures, one can realize that LS-SOM outperforms the topology regeneration. Especially, it is resistant to the perimeter effect.
Figure 9 shows another actual topology in random deployment experiment, and the topology estimation result is reported in Figure 10. The lines in Figure 10 show the differences between the actual location and estimated location of each method used. The shorter the line, the better the accuracy is.
Figure 11 shows the distribution of nodes localized for 1000 randomly generated networks with 100 nodes, number of anchors ranging from 4 to 15, and connectivity is selected randomly from 7 to 15. From Figure 11, 80% of nodes localized with the error around 30% for LS-SOM.
4.3. Mobile Networks
We have implemented LS-SOM in NS-2 environment, in which LS-SOM is designed as an agent installed on each node and runs completely in parallel manner. In our simulation scenarios, 4 anchor nodes are deployed and they are also moving. The movement of nodes is simulated with the RandomWayPoint mobility model. The mobility scenarios are generated with maximum speed of 10 meters per second. Figure 12 shows the performance of LS-SOM by simulation time. From Figure 12, we can see that LS-SOM will give a stable estimation accuracy after the time period for initialization and initial learning. The delay period depends on the network configuration. In our simulation on NS-2, the difficulty is that the transmission delay and packet collision at MAC layer. We just simply solve the packet collision by using randomized packet exchange scheduling. Figure 13 shows the throughput for generated packets by simulation time. We see a burst of traffic at the beginning because of the anchor flooding in the initialization stage. From this observation, we can easily find that the cost for network flooding is very expensive. Figure 14 shows the throughput of dropping packets due to collision. We realize that during the learning process, about 30% of exchanging messages were dropped. Figure 15 shows the distribution of dropping packets at each node. Number of dropped packets of nodes near the center of topology is greater than that of nodes near the perimeters. It is to infer that the number of packet dropped will increase with the connectivity level, and we should consider this problem when designing a practical localization system.
5. Conclusions
We have presented our proposed Distributed Range-free Localization Algorithm Based on Self-Organizing Maps (LS-SOMs) in this paper. By introducing the utilization of intersection areas between radio coverage of neighboring nodes, the algorithm maximizes the correlation between neighboring nodes in distributed SOM implementation. With this correlation maximization, our method increases the quality of the topology estimation and reduces the time of the topological convergence. With our proposed solution for mobility management, LS-SOM is capable of working with networks having high mobility. From intensive simulations, the results show that LS-SOM has achieved good accuracy over the original SOM and other algorithms. LS-SOM has reduced the SOM learning steps to just around 15 to 30 steps. Besides that, LS-SOM is capable of working not only with static networks, but also with mobile networks. Future work will investigate in a more precise distance measurement method to make LS-SOM to be more flexible.
References
Poovendran R, Wang CL, Roy S: Secure Localization and Time Synchronization for Wireless Sensor and Ad Hoc Networks. Springer, Berlin, Germany; 2007.
Wellenhoff BH, Lichtenegger H, Collins J: Global Positioning System: Theory and Practice. 4th edition. Springer, Berlin, Germany; 1997.
Savvides A, Han CC, Strivastava MB: Dynamic finegrained localization in ad-hoc networks of sensors. Proceedings of the 7th Annual International Conference on Mobile Computing and Networking (MobiCom '01), July 2001, Rome, Italy 166-179.
Niculescu D, Nath B: Ad hoc positioning system (APS) using AOA. Proceedings of the 22nd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '03), 2003, San Francisco, Calif, USA 3: 1734-1743.
Patwari N, Hero AO III, Perkins M, Correal NS, O'Dea RJ: Relative location estimation in wireless sensor networks. IEEE Transactions on Signal Processing 2003, 51(8):2137-2148. 10.1109/TSP.2003.814469
Nicolescu D, Nath B: Ad-hoc positioning systems (APS). Proceedings of IEEE Global Telecommunicatins Conference (GLOBECOM '01), 2001, San Antonio, Tex, USA
Shang Y, Ruml W, Zhang Y, Fromherz M: Localization from connectivity in sensor networks. IEEE Transactions on Parallel and Distributed Systems 2004, 15(11):961-974. 10.1109/TPDS.2004.67
Tran DA, Nguyen T: Localization in wireless sensor networks based on support vector machines. IEEE Transactions on Parallel and Distributed Systems 2008, 19(7):981-994.
Giorgetti G, Gupta SKS, Manes G: Wireless localization using self-organizing maps. Proceedings of the 6th International Symposium on Information Processing in Sensor Networks (IPSN '07), April 2007, Cambridge, Mass, USA 293-302.
Asakura S, Umehara D, Kawai M: Distributed location estimation method for mobile terminals based on SOM algorithm. IEICE Transactions on Communications 2002, J85-B(7):1042-1050.
Hu J, Lee G: Distributed localization of wireless sensor networks using self-organizing maps. Proceedings of the IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI '08), 2008, Seoul, South Korea 284-289.
Sum J, Leung CS, Chan LW, Xu L: Yet another algorithm which can generate topograph map. IEEE Transactions on Neural Networks 1997, 8(5):1204-1207. 10.1109/72.623221
Janet JA, Gutierrez R, Chase TA, White MW, Sutton JC III: Autonomous mobile robot global self-localization using Kohonen and region-feature neural networks. Journal of Robotic Systems 1997, 14(4):263-282. 10.1002/(SICI)1097-4563(199704)14:4<263::AID-ROB4>3.0.CO;2-O
Ertin E, Priddy KL: Self-localization of wireless sensor networks using self organizing maps. Intelligent Computing: Theory and Applications III, March 2005, Orlando, Fla, USA, Proceedings of SPIE 5803: 138-145.
Tinh PD, Noguchi T, Kawai M: Localization scheme for large scale wireless sensor networks. Proceedings of the International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP '08), 2008 25-30.
Kohonen T: Self-Organizing Maps. 3rd edition. Springer, Berlin, Germany; 2001.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tinh, P., Kawai, M. Distributed Range-Free Localization Algorithm Based on Self-Organizing Maps. J Wireless Com Network 2010, 692513 (2009). https://doi.org/10.1155/2010/692513
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/692513
 , to each neuron in the SOM network.
, to each neuron in the SOM network.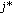 at the iteration
at the iteration  by using Euclidean minimum-distance criterion:
by using Euclidean minimum-distance criterion: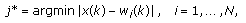
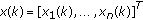 represents the
represents the  input pattern,
input pattern,  is the total number of SOM neurons, and the input pattern has
is the total number of SOM neurons, and the input pattern has  dimensions.
dimensions.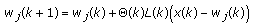
 is the learning rate at time step
is the learning rate at time step 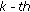 and
and  is the function for topological neighborhood of neuron
is the function for topological neighborhood of neuron  at time step
at time step 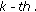

 has wrong estimated location.
has wrong estimated location.

 .
.

 is located at wrong location.
is located at wrong location.





 ,
,  , connectivity = 4. 88): (a) actual topology, (b) DV-HOP (error = 0.50), (c) SOM (error = 0.35), (d) LS-SOM (error = 0.23).
, connectivity = 4. 88): (a) actual topology, (b) DV-HOP (error = 0.50), (c) SOM (error = 0.35), (d) LS-SOM (error = 0.23).


 to 15).
to 15).

 ,
,  , nodes speed = 10 m/s).
, nodes speed = 10 m/s).
 ,
,  , nodes speed = 10 m/s).
, nodes speed = 10 m/s).
 ,
,  , nodes speed=10 m/s).
, nodes speed=10 m/s).