- Research Article
- Open access
- Published:
Characterizing the Path Coverage of Random Wireless Sensor Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 716565 (2010)
Abstract
Wireless sensor networks are widely used in security monitoring applications to sense and report specific activities in a field. In path coverage, for example, the network is in charge of monitoring a path and discovering any intruder trying to cross it. In this paper, we investigate the path coverage properties of a randomly deployed wireless sensor network when the number of sensors and also the length of the path are finite. As a consequence, Boolean model, which has been widely used previously, is not applicable. Using results from geometric probability, we determine the probability of full path coverage, distribution of the number of uncovered gaps over the path, and the probability of having no uncovered gaps larger than a specific size. We also find the cumulative distribution function (cdf) of the covered part of the path. Based on our results on the probability of full path coverage, we derive a tight upper bound for the number of nodes guaranteeing the full path coverage with a desired reliability. Through computer simulations, it is verified that for networks with nonasymptotic size, our analysis is accurate where the Boolean model can be inaccurate.
1. Introduction
Wireless sensor networks (WSNs) have many applications in security monitoring. In such applications, since it is essential to keep track of all activities within the field, network coverage is of great importance and must be considered in the network design stage.
Path coverage is one of the monitoring examples, where WSNs are deployed to sense a specific path and report possible efforts made by intruders to cross it. In a manual network deployment, the desired level of the path coverage can be achieved by proper placement of the sensors over the area. When it is not possible to deploy the network manually, random deployment, for example, dropping sensors from an aircraft, is used. Due to the randomness of the sensors location, network coverage expresses a stochastic behavior and the desired (full) path coverage is not guaranteed. Thus, a detailed analysis of the random network coverage can be ultimately useful in the network design stage to determine the node density for achieving the desired area/path coverage.
Path coverage by a random network (or barrier coverage which is a relaxed version of the path coverage) has been the focus of some previous work [1–6]. In [1], assuming that a random network is deployed over an infinite area with nodes following a Poisson distribution, authors investigate the path coverage of the network. They first study the path coverage over an infinite straight line when the sensor has a random sensing range. Then, they show that in the asymptotic situation, where the sensing range of the sensors tends to 0 and the node density approaches infinity, the results are extendible to finite linear and curvilinear paths. Further, a path coverage analysis is proposed for a high-density Poisson-distributed network in [2] where sensors have a fixed sensing range. The path coverage analysis of [1, 2] is based on the Boolean model of [7], where a Poisson point process is justified.
Kumar et al. study  -barrier coverage provided by a random WSN in [3]. To this end, they develop a theoretical model revealing the behavior of the network coverage over a long narrow belt. It is assumed that the sensors are spread over the belt according to a Poisson distribution. The authors propose an algorithm determining whether an area is
-barrier coverage provided by a random WSN in [3]. To this end, they develop a theoretical model revealing the behavior of the network coverage over a long narrow belt. It is assumed that the sensors are spread over the belt according to a Poisson distribution. The authors propose an algorithm determining whether an area is  -barrier covered or not. Also, they introduce the concepts of weak and strong barrier coverage over the belt and derive the condition on the sensors density guaranteeing the weak barrier coverage.
-barrier covered or not. Also, they introduce the concepts of weak and strong barrier coverage over the belt and derive the condition on the sensors density guaranteeing the weak barrier coverage.
The focus of [4] is on the strong barrier coverage. First, authors present a condition insuring the strong barrier coverage over a strip where the sensors locations follow a Poisson point process. Then, by considering asymptotic situation (on the network size and number of nodes) and using Percolation theory [8], they determine, with a probability approaching 1, whether the network has a strong barrier coverage or not. Then, they use their analysis to devise a distributed algorithm to build strong barrier coverage over the strip.
In this work, unlike most existing studies which focus on asymptotic setups, we study the path coverage of a finite random network (in terms of both network size and the number of nodes). As a result, the Boolean model is not accurate. Alternatively, the methodology of this work is based on some results from geometric probability. Our focus is on the path coverage for a circle, but extension to other path shapes is briefly discussed.
In the ideal case, all sensors are located exactly on the path. This, however, is not a practical assumption for randomly deployed networks. To consider the inaccuracy of the sensors locations, we assume that sensors are inside a ring containing the circular path. As a result, the portion of the path covered by any given sensor is not deterministic. Moreover, other factors may affect the sensing range of a sensor. Thus, our analysis is not based on a fixed sensing range. Indeed, we first develop a random model for the covered segment of the path by each sensor. Then, we study the distribution of the number of uncovered gaps on the path. The full path coverage is a special case where the number of gaps is zero. This is used to determine a tight bound on the number of active sensors assuring the full path coverage with a desired reliability. Also, we find the probability of having all possible gaps smaller than a given size. This probability reflects the reliability of detecting an intruding object with a known size.
In addition to studying the number of gaps, we present a simplified analysis for deriving the cumulative distribution function (cdf) of the covered part of the path. This simplified analysis is based on using the expected value of the covered part of the path by a sensor instead of considering the precise random model. We observe that the simplified analysis can provide a fairly accurate approximation of the path coverage.
Since our analysis studies the effect of the number of nodes on the path coverage of a finite size network, it can readily be used in the design of practical networks. In fact, using our results, one can determine the number of nodes in the network to satisfy a desired level of coverage. An example is provided.
The paper is organized as follows. Section 2 introduces the network model and defines the problem. Our coverage analysis is presented in Section 3. Section 4 includes computer simulations verifying our analysis. Finally, Section 5 concludes the paper.
2. Preliminary
2.1. Network Model
We consider  sensors monitoring a circular path with unit circumference, called
sensors monitoring a circular path with unit circumference, called  . In an ideal case, the sensors are precisely located on the circular path, but this is not usually true for a randomly deployed network. In order to take this fact into account, we assume that sensors are randomly spread over a ring containing
. In an ideal case, the sensors are precisely located on the circular path, but this is not usually true for a randomly deployed network. In order to take this fact into account, we assume that sensors are randomly spread over a ring containing  (See Figure 1). We assume a symmetric distribution for sensors, that is, the sensor density does not depend on the polar angle and is determined only by the distance from the center. It is generally desired to have more sensors in the vicinity of
(See Figure 1). We assume a symmetric distribution for sensors, that is, the sensor density does not depend on the polar angle and is determined only by the distance from the center. It is generally desired to have more sensors in the vicinity of  Thus, distributions with larger values close to
Thus, distributions with larger values close to  are preferred. When no effort is made to put the sensor as close as possible to the path (
are preferred. When no effort is made to put the sensor as close as possible to the path ( sensors are spread totally randomly), the uniform distribution is obtained. Hence, in the sense of placement efforts, uniform distribution reflects the worst case. We consider uniform distribution to verify our analysis by computer simulation in Section 4. Our analysis, however, is presented for any given symmetric distribution. Also, notice that since the number of sensors is finite and known, Poisson distribution, which has been the focus of existing asymptotic analysis, is not applicable.
sensors are spread totally randomly), the uniform distribution is obtained. Hence, in the sense of placement efforts, uniform distribution reflects the worst case. We consider uniform distribution to verify our analysis by computer simulation in Section 4. Our analysis, however, is presented for any given symmetric distribution. Also, notice that since the number of sensors is finite and known, Poisson distribution, which has been the focus of existing asymptotic analysis, is not applicable.
We also assume that sensors sensing range may vary from  to
to  . Obviously, for a fixed sensing range, model
. Obviously, for a fixed sensing range, model  . Without loss of generality, it is assumed that the width of the ring is smaller than or equal to
. Without loss of generality, it is assumed that the width of the ring is smaller than or equal to  and the desired circular path is located at the middle of the ring. Since the sensors farther than
and the desired circular path is located at the middle of the ring. Since the sensors farther than  to the path do not contribute to the path coverage, our assumption on the ring width does not hurt the generality of the analysis.
to the path do not contribute to the path coverage, our assumption on the ring width does not hurt the generality of the analysis.
2.2. Motivation and Problem Definition
Our goal in this work is to investigate the quality of the path coverage by the network. To this end, we study the following features of the path coverage which provide us with a concrete insight to the performance of the network.
-
(i)
Distribution of the number of gaps. Due to the randomness of the network implementation, sensors may not cover the whole path. In this case, one or more gaps appear. Assume that
 represents the number of gaps on
represents the number of gaps on 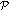 . We are interested to find the probability of having
. We are interested to find the probability of having 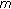 gaps, shown by
gaps, shown by 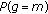 .
. -
(ii)
Full path coverage. It is desired to provide a complete coverage of the path. Since the full path coverage is identical to having no gaps, one can equivalently find
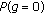 . This can simply be found from the derived distribution of
. This can simply be found from the derived distribution of 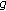 .
. -
(iii)
Reliability of the network in detecting objects. It is important to investigate whether the network is able to detect an object, while the path is not fully covered and there may exist some gaps. Basically, we need to consider the size of the gaps in addition to their number. If one knows the size of the intruders beforehand, it is not necessary to provide the full path coverage. Instead, it is possible to deploy a network such that while the path is not fully covered, the size of the possible gaps is smaller than the intruders. Clearly, implementing a network with possible small gaps requires fewer number of nodes and consequently is less expensive. To this end, we find the probability of having all gaps smaller than a given length
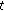 , denoted by
, denoted by 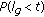 .
. -
(iv)
Distribution of the covered part of the path. The covered part of the path,
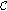 , has a stochastic nature and its distribution provides a general view of the entire path coverage. In fact, the covered part of the network reflects the combined effect of the number of gaps and their sizes. We derive the cdf of
, has a stochastic nature and its distribution provides a general view of the entire path coverage. In fact, the covered part of the network reflects the combined effect of the number of gaps and their sizes. We derive the cdf of 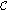 ,
,  .
.
3. Path Coverage Analysis
In this section, we present our analysis of the path coverage. For this purpose, we take advantage of existing results in geometric probability and extend them to our case. After the exact coverage analysis, a less complex approximate analysis is also presented.
An arbitrary point on  is covered if it is within the sensing range of at least one sensor. Here, we assume that the sensing area of sensor
is covered if it is within the sensing range of at least one sensor. Here, we assume that the sensing area of sensor  is a circle denoted by
is a circle denoted by  . The covered part of the path by each
. The covered part of the path by each  is its intersection with
is its intersection with  which is an arc, called
which is an arc, called  . Thus, the total covered part of the path is
. Thus, the total covered part of the path is

Notice that the length of  's depends on the location of the sensor within the ring-shaped network area and its sensing range. Considering an arbitrary point as the origin on
's depends on the location of the sensor within the ring-shaped network area and its sensing range. Considering an arbitrary point as the origin on  and choosing the clockwise direction as the positive direction, each
and choosing the clockwise direction as the positive direction, each  starts from
starts from  and continues (clockwise) until
and continues (clockwise) until  , (Figure 2). In other words,
, (Figure 2). In other words,  determines the most left point of the arc and
determines the most left point of the arc and  specifies the most right point of the arc. There are two noteworthy issues here. First, the size of
specifies the most right point of the arc. There are two noteworthy issues here. First, the size of  's and their positions are random because of the random placement of the sensors over the ring. Second,
's and their positions are random because of the random placement of the sensors over the ring. Second,  is not necessarily connected and there may exist several uncovered gaps on
is not necessarily connected and there may exist several uncovered gaps on  . The number of uncovered gaps on
. The number of uncovered gaps on  and their size can reflect the possible opportunities for intruders to pass
and their size can reflect the possible opportunities for intruders to pass  without being detected by the sensors. If
without being detected by the sensors. If  is fully covered.
is fully covered.
The problem of covering a circle with random arcs has been studied in geometric probability [9–15]. In some cases, it is assumed that the arcs have a fixed length [9, 12, 13, 15] or the analysis is conducted in the asymptotic situation [10, 14]. Asymptotic analysis is suitable for the situation where the sizes of  's are significantly smaller than
's are significantly smaller than  . In the following, we initially use the result of [11] on the coverage of a circle with random arcs of random sizes. This helps us to provide an exact explanation of the path coverage. Then, we use the mean value of
. In the following, we initially use the result of [11] on the coverage of a circle with random arcs of random sizes. This helps us to provide an exact explanation of the path coverage. Then, we use the mean value of  's to provide a simplified approximate analysis based on the fixed-length random arc placement over the circle [12].
's to provide a simplified approximate analysis based on the fixed-length random arc placement over the circle [12].
3.1. Exact Analysis
We apply the following theorem from [11] to find the exact distribution of the number of gaps on  .
.
Theorem 1.
Assume that  arcs are distributed independently with a uniform distribution over a circle of circumference 1. If
arcs are distributed independently with a uniform distribution over a circle of circumference 1. If  shows the cdf of the arc length over
shows the cdf of the arc length over  , the distribution of the number of uncovered gaps on the circle,
, the distribution of the number of uncovered gaps on the circle,  , is
, is

where

Proof.
See [11].
To apply Theorem 1 for finding the number of uncovered gaps on  , we first prove the uniformity of the arc distribution over
, we first prove the uniformity of the arc distribution over  in the following lemma.
in the following lemma.
Lemma 1.
For a symmetric distribution of the sensors over the path, the location of the intersection of the sensors sensing range and  is uniformly distributed over
is uniformly distributed over  .
.
Proof.
We equivalently show that the center points of the arcs are uniformly distributed over the circle. For this purpose, consider a small element with length  on
on  . Then, we build a sector of the ring based on this length element whose left and right sides pass the left and right ends of the length element (Figure 3). The center point of the arcs, resulted from the intersection of the sensing area of the nodes within the sector and
. Then, we build a sector of the ring based on this length element whose left and right sides pass the left and right ends of the length element (Figure 3). The center point of the arcs, resulted from the intersection of the sensing area of the nodes within the sector and  falls within
falls within  . Due to the independence of the sensors distribution from the polar angle, all elements with length
. Due to the independence of the sensors distribution from the polar angle, all elements with length  on the circle have the same chance to include an arc center point. Therefore, the distribution of the arc centers, and consequently arc locations, is uniform on
on the circle have the same chance to include an arc center point. Therefore, the distribution of the arc centers, and consequently arc locations, is uniform on  .
.
Following Lemma 1, in order to find the distribution of the number of gaps on  we need
we need  or in our case
or in our case  the cdf of
the cdf of  's. Notice that
's. Notice that  's are independent and identically distributed (i.i.d) random variables. We find
's are independent and identically distributed (i.i.d) random variables. We find  in the appendix for arbitrary distributions of sensor location and sensing range.
in the appendix for arbitrary distributions of sensor location and sensing range.
As a result of Theorem 1 and Lemma 1, we have the following corollary.
Corollary 1.
The probability of the full path coverage,  , is
, is

Furthermore, one can show that the expected number of gaps on  is [11]
is [11]

where  is the mean of
is the mean of  's.
's.
 can be used to find an upper bound on the number of nodes in the network guaranteeing the full path coverage with a given reliability. This is presented below.
can be used to find an upper bound on the number of nodes in the network guaranteeing the full path coverage with a given reliability. This is presented below.
Corollary 2.
To guarantee a full path coverage with probability  , the following relation holds
, the following relation holds

Proof.
Recall Markov's inequality for a positive random variable 

where  . If we let
. If we let  be the random variable of the number of gaps
be the random variable of the number of gaps  , and put
, and put  , we have
, we have

Combining (5) and (8) results in (6).
Using (6), it is straightforward to find an upper bound on  guaranteeing a desired level of coverage,
guaranteeing a desired level of coverage,  . Later, our simulations show that this bound is in fact very tight.
. Later, our simulations show that this bound is in fact very tight.
Another feature of the path coverage that we like to study is the quality of the coverage in terms of the size of the gaps on  . Assume that we like to guarantee detecting any object bigger than a particular size, say
. Assume that we like to guarantee detecting any object bigger than a particular size, say  . To assure detecting such objects, all of the gaps have to be smaller than
. To assure detecting such objects, all of the gaps have to be smaller than  . Hence, we like to find the probability of having no gaps larger than
. Hence, we like to find the probability of having no gaps larger than  , where
, where  is the length of the largest gap on
is the length of the largest gap on  .
.
Corollary 3.
The probability of having no gaps larger than  is
is

Proof.
Consider a realization of the random placement of arcs on the path. Now, one can consider a scenario where the length of each arc is increased by  . If there exists a gap smaller than
. If there exists a gap smaller than  in the first scenario, this gap will be covered in the second scenario since the arcs are
in the first scenario, this gap will be covered in the second scenario since the arcs are  longer. On the other hand, a gap with any size in the second scenario will be a gap with length more than
longer. On the other hand, a gap with any size in the second scenario will be a gap with length more than  in the first scenario. Notice that the above discussion is valid for any realization of the network. Thus, instead of investigating the probability of having no gaps longer than
in the first scenario. Notice that the above discussion is valid for any realization of the network. Thus, instead of investigating the probability of having no gaps longer than  in the first scenario, we look for the probability of the full coverage in the second scenario. Denoting the length of the arcs in the second scenario by
in the first scenario, we look for the probability of the full coverage in the second scenario. Denoting the length of the arcs in the second scenario by  , one can think of them as being drawn from the distribution
, one can think of them as being drawn from the distribution  or equivalently
or equivalently

This completes the proof.
Using the same approach taken for finding the upper bound on  in (6), one can derive an upper bound on the number of nodes to guarantee having all gaps smaller than
in (6), one can derive an upper bound on the number of nodes to guarantee having all gaps smaller than  .
.
We also like to investigate  that is, the portion of
that is, the portion of  which is covered by the nodes. To find
which is covered by the nodes. To find  , we first reorder the arcs based on their starting points,
, we first reorder the arcs based on their starting points,  's. Thus
's. Thus  . Now, we divide
. Now, we divide  to arcs
to arcs  , where
, where  is an arc starting from
is an arc starting from  and ending at
and ending at  . Finally,
. Finally,  starts from
starts from  and ends at
and ends at  . Since we have
. Since we have  random arcs intersecting with
random arcs intersecting with  , there exist
, there exist  of such spacings on the circle. These
of such spacings on the circle. These  spacings may or may not be covered by the network. Adding the covered parts of the path together, we have
spacings may or may not be covered by the network. Adding the covered parts of the path together, we have

where  . Also,
. Also,  's denotes the length of
's denotes the length of  and
and

Notice that in (12) we assume rotational indices for  's. It means that if
's. It means that if  we replace the index with
we replace the index with  . In (12),
. In (12),  is the length of the connected part of
is the length of the connected part of  starting from
starting from  and continuing clockwise. When
and continuing clockwise. When  , the whole spacing
, the whole spacing  is covered and
is covered and  function should return
function should return  . When
. When  , a portion of
, a portion of  remains uncovered and there exists a gap at the right side of
remains uncovered and there exists a gap at the right side of  . Thus,
. Thus,  function returns
function returns  . It is noteworthy that because of the problem symmetry,
. It is noteworthy that because of the problem symmetry,  's are identically distributed random variables. Thus, we use a single random variable
's are identically distributed random variables. Thus, we use a single random variable  to refer to them.
to refer to them.
The distribution of  can be well approximated by a Gaussian distribution using central limit theorem (CLT) where the mean value of
can be well approximated by a Gaussian distribution using central limit theorem (CLT) where the mean value of  ,
,  , is
, is  . Here,
. Here,  denotes the mean value of
denotes the mean value of  . Also,
. Also,  where
where  and
and  represent the variance of
represent the variance of  and
and  , respectively. In reality, one can safely simplify (12) to
, respectively. In reality, one can safely simplify (12) to

This is because  's are i.i.d. and thus it is very unlikely that, for example,
's are i.i.d. and thus it is very unlikely that, for example,  .
.
3.2. Approximate Analysis
In the following, we present an approximate analysis simplifying our path coverage study. The idea of this approximate analysis is to consider a model where a set of fixed-length arcs are spread randomly over  instead of using the actual random-sized arcs. The length of these fixed arcs is equal to the mean value of the random-sized arcs in the original case. We denote the mean value of these random arcs with
instead of using the actual random-sized arcs. The length of these fixed arcs is equal to the mean value of the random-sized arcs in the original case. We denote the mean value of these random arcs with  . In this case, it can be shown that the number of uncovered gaps on
. In this case, it can be shown that the number of uncovered gaps on  is distributed as follows [12]:
is distributed as follows [12]:

where  . The same technique as before is applicable to find the probability of having no gaps larger than
. The same technique as before is applicable to find the probability of having no gaps larger than  on
on  . For this purpose, we just need to use
. For this purpose, we just need to use  instead of
instead of  in (14). In addition, the distribution of
in (14). In addition, the distribution of  can be derived when the arc size is fixed [12]. In this case, we have
can be derived when the arc size is fixed [12]. In this case, we have

where  is the cdf of
is the cdf of  .
.
One can also calculate the expected value of  . To this aim, we first consider the uncovered part of the path,
. To this aim, we first consider the uncovered part of the path,  , and find its expected value, called
, and find its expected value, called  . Then
. Then  can be found using the fact
can be found using the fact  .
.
An arbitrary point  on
on  remains uncovered when there is no
remains uncovered when there is no  covering it. This is equivalent to having none of
covering it. This is equivalent to having none of  's within an arc with length
's within an arc with length  whose right end point is
whose right end point is  . There are
. There are  sensors in the network, hence, the probability of having
sensors in the network, hence, the probability of having  uncovered,
uncovered,  , is
, is

Consequently,

3.3. Some Remarks
Remark 1.
Our path coverage analysis is applicable to any closed path, for example, ellipse, with finite length when the location of the path segment covered by an arbitrary sensor is uniformly distributed over the path. For this purpose, we just need to have the distribution of the intersection of sensors sensing range and the path. Also, the analysis is applicable to linear path coverage. In fact, the problem of covering a circle with random arcs can be transformed to the problem of covering a piece of line, say the interval  , with random intervals. In this case, sensors are deployed randomly over a strip surrounding the linear path. It is notable that in the linear case, Torus convention [7] is applied. In Torus convention, it is assumed that if a part of the random interval goes out of the line segment, it comes in from the other side of the line piece. However, when the length of the random intervals is small compared to the line piece, one can remove the Torus convention and the analysis remains quite accurate.
, with random intervals. In this case, sensors are deployed randomly over a strip surrounding the linear path. It is notable that in the linear case, Torus convention [7] is applied. In Torus convention, it is assumed that if a part of the random interval goes out of the line segment, it comes in from the other side of the line piece. However, when the length of the random intervals is small compared to the line piece, one can remove the Torus convention and the analysis remains quite accurate.
Remark 2.
In many WSNs, the number of active sensors in the network changes with time. This can be due to, for example, sleep scheduling or death of some nodes. Since our analysis is provided for arbitrary  it can accommodate such situations, simply by replacing
it can accommodate such situations, simply by replacing  with
with  in relevant equations. Consequently, the coverage can be studied as a function of time.
in relevant equations. Consequently, the coverage can be studied as a function of time.
4. Simulation
In this section, we demonstrate the accuracy of our analysis via computer simulations. We have inspected two scenarios for the sensors sensing range. In the first scenario, we assume a network with  sensors all having a fixed sensing range equal to
sensors all having a fixed sensing range equal to  . The sensors are uniformly deployed inside a ring around the circular path, where
. The sensors are uniformly deployed inside a ring around the circular path, where  has unit circumference. In the second scenario, the sensors sensing range is also uniformly distributed between
has unit circumference. In the second scenario, the sensors sensing range is also uniformly distributed between  and
and  . A zero sensing range can represent a dead sensor.
. A zero sensing range can represent a dead sensor.
We evaluate random properties such as the full coverage, number of uncovered gaps, tightness of the bound presented in (6), the intruder detectability, and the portion of the covered path using simulation, and compare the results with our theoretical analysis.
4.1. Uncovered Gaps
Probability density of the number of uncovered gaps on the path,  , was derived in Section 3.1. Figure 4 shows the probability mass function (pmf) of the number of uncovered gaps via simulation for
, was derived in Section 3.1. Figure 4 shows the probability mass function (pmf) of the number of uncovered gaps via simulation for  . Here, we have assumed that the sensing range of all sensor nodes is fixed and is equal to
. Here, we have assumed that the sensing range of all sensor nodes is fixed and is equal to  . The theoretical results using (2) have also been sketched for comparison. It can be concluded that the formulation derived in Section 3.1 quite accurately describes the pmf of the number of uncovered gaps on the path. The third curve in Figure 4 is the result of approximation analysis in Section 3.2. Parameter
. The theoretical results using (2) have also been sketched for comparison. It can be concluded that the formulation derived in Section 3.1 quite accurately describes the pmf of the number of uncovered gaps on the path. The third curve in Figure 4 is the result of approximation analysis in Section 3.2. Parameter  in (14) is set to be the expected value of random variable
in (14) is set to be the expected value of random variable  , derived in the appendix.
, derived in the appendix.
It is clear from Figure 4 that the results from the approximate analysis are fairly close to the exact analysis and the simulations. Due to the complexity of the evaluation of exact analysis, we compare the rest of our simulation results with the approximate analysis presented in Section 3.2 to characterize the coverage properties of the network.
In the case of fixed sensing range, as the width of the ring becomes smaller, the variance of  decreases and the arc lengths become closer to
decreases and the arc lengths become closer to  , making the approximate analysis more accurate. To study the worst case, in our analysis, we assume the ring width
, making the approximate analysis more accurate. To study the worst case, in our analysis, we assume the ring width  is equal to
is equal to  . Notice that any node outside this ring does not contribute to the path coverage. For random sensing range, we choose
. Notice that any node outside this ring does not contribute to the path coverage. For random sensing range, we choose  . Notice that since
. Notice that since  , there will be nodes in the ring that will not contribute to the path coverage.
, there will be nodes in the ring that will not contribute to the path coverage.
Figures 5 and 6 demonstrate the probability of full coverage versus number of sensors deployed in the region. Figure 5 shows the results for the fixed sensing range scenario.  is estimated through simulation for different values of sensing range,
is estimated through simulation for different values of sensing range,  , and is compared with the theoretical results using (14). As seen from the curves, our theoretical formulation can effectively predict probability of full path coverage. Figure 6 represents the results of variable sensing range scenario. The sensing range of sensor nodes is randomly selected from a uniform distribution between
, and is compared with the theoretical results using (14). As seen from the curves, our theoretical formulation can effectively predict probability of full path coverage. Figure 6 represents the results of variable sensing range scenario. The sensing range of sensor nodes is randomly selected from a uniform distribution between  and
and  . We have run the simulation based on three uniform distributions,
. We have run the simulation based on three uniform distributions,  , and compared with the theoretical results. For theoretical calculations, we have computed the average arc length for the case of random sensing range using (A.22) in the appendix, and then substituted the resulting
, and compared with the theoretical results. For theoretical calculations, we have computed the average arc length for the case of random sensing range using (A.22) in the appendix, and then substituted the resulting  into the approximate formula (14). From Figure 6, we can see that the theoretical analysis in Section 3.2 can closely describe the probability of full coverage for random sensing range scenario.
into the approximate formula (14). From Figure 6, we can see that the theoretical analysis in Section 3.2 can closely describe the probability of full coverage for random sensing range scenario.
We have also tested our analysis for full coverage of a straight line segment instead of a circle. Figure 7 depicts the coverage of a straight line segment of length  when sensing range is fixed and is equal to
when sensing range is fixed and is equal to  . The solid line is the result of Poisson assumption in [2] and the dashed line is the result of our formulation. It can be seen that specially for smaller number of sensor nodes, the Boolean model is not well applicable to describe the coverage of small networks.
. The solid line is the result of Poisson assumption in [2] and the dashed line is the result of our formulation. It can be seen that specially for smaller number of sensor nodes, the Boolean model is not well applicable to describe the coverage of small networks.
The expected number of uncovered gaps,  , after deploying
, after deploying  sensors in the ring is given by (5). In Figure 8,
sensors in the ring is given by (5). In Figure 8,  has been calculated versus
has been calculated versus  for three values of fixed sensing range,
for three values of fixed sensing range,  , using simulation as well as the analysis. The expected number of gaps for variable sensing ranges is shown in Figure 9. The sensors sensing range has been taken from the three uniform distributions used previously.
, using simulation as well as the analysis. The expected number of gaps for variable sensing ranges is shown in Figure 9. The sensors sensing range has been taken from the three uniform distributions used previously.
In Section 3.1, we used Markov's inequality to find a relation between the number of nodes and probability of full coverage over the path, presented in (6). The smallest number of nodes that satisfies (6) can efficiently be found by conducting a simple binary search. We denote the value of  found via search by
found via search by  . Table 1 shows the value of
. Table 1 shows the value of  calculated for probability of full coverage being equal to
calculated for probability of full coverage being equal to  . The results found by inequality (6) and simulation are shown for comparison. For probability of full coverage closer to one (the region of interest in practice),
. The results found by inequality (6) and simulation are shown for comparison. For probability of full coverage closer to one (the region of interest in practice),  gets even closer to the value of
gets even closer to the value of  satisfying the desired reliability found via simulation. For example, for probability of full coverage equal to
satisfying the desired reliability found via simulation. For example, for probability of full coverage equal to  , we found
, we found  for various values of
for various values of  It can be inferred that (6) provides a tight upper bound on the number of nodes needed for full path coverage.
It can be inferred that (6) provides a tight upper bound on the number of nodes needed for full path coverage.
 .
.4.2. Detectability of the Object
As discussed in Section 3.1, in real applications of sensor networks, we might not be interested in the full coverage of a path, yet we need to make sure that there are no uncovered gaps on the path, larger than a certain maximum length  . The probability of this kind of coverage,
. The probability of this kind of coverage,  , was given by (9). We use simulation to find
, was given by (9). We use simulation to find  for values of
for values of  equal to
equal to  , when
, when  . Again, comparing simulation results with theoretical ones in Figure 10 verifies our formulation. Our study on the size of the gaps is useful for decreasing the cost of the network implementation. In fact, if we know the size of the intruders, instead of providing a full path coverage, we can design the network with less number of nodes to have all gaps smaller than
. Again, comparing simulation results with theoretical ones in Figure 10 verifies our formulation. Our study on the size of the gaps is useful for decreasing the cost of the network implementation. In fact, if we know the size of the intruders, instead of providing a full path coverage, we can design the network with less number of nodes to have all gaps smaller than  .
.
4.3. Covered Part of the Path
The covered portion of the path,  , is another important metric for path coverage in a WSN. Indeed,
, is another important metric for path coverage in a WSN. Indeed,  is a random variable whose cdf is approximated in Section 3.2. Figure 11 shows the cdf of
is a random variable whose cdf is approximated in Section 3.2. Figure 11 shows the cdf of  , for
, for  and
and  . As it can be seen, our path coverage analysis is more accurate for larger values of
. As it can be seen, our path coverage analysis is more accurate for larger values of  .
.
The formulation for expected covered part,  , is derived in Section 3.2. Figure 12 shows simulation and theoretical results for
, is derived in Section 3.2. Figure 12 shows simulation and theoretical results for  versus
versus  , when
, when  .
.
5. Conclusion
In this paper, we studied the path coverage of a random WSN when neither the area size nor the number of network nodes were infinite. Hence, the widely used Boolean model was no longer valid. Moreover, due to the randomness of the sensors placement over the area, network coverage was nondeterministic. Thus, a probabilistic solution was taken for determining the network coverage features. Our analysis considered the number of gaps, probability of full path coverage, probability of having all uncovered gaps smaller than a specific size, and the cdf of the covered length of the path. All these characteristics were found as a function of the number of sensors  We also proposed a tight upper bound on required
We also proposed a tight upper bound on required  for full coverage. Through computer simulations, we verified the accuracy of our approach. Since our study was performed for finite
for full coverage. Through computer simulations, we verified the accuracy of our approach. Since our study was performed for finite  , using our results on various features of path coverage, one can find the necessary number of sensors for a certain quality of coverage.
, using our results on various features of path coverage, one can find the necessary number of sensors for a certain quality of coverage.
Appendix
In the following, we find the cdf of the intersection between the sensing area of the sensors and  , called
, called  . First, we study the situation where sensors have a fixed sensing range
. First, we study the situation where sensors have a fixed sensing range  and they are uniformly distributed over the ring. Then, we investigate the general case where sensors can have a random sensing range varying from
and they are uniformly distributed over the ring. Then, we investigate the general case where sensors can have a random sensing range varying from  to
to  and have any symmetric distribution over the ring.
and have any symmetric distribution over the ring.
Let us first discuss the case where the sensors have a fixed sensing range. Figure 13 shows the ring-shaped network containing  . As mentioned previously, the circumference of
. As mentioned previously, the circumference of  is 1, hence, the radius of
is 1, hence, the radius of  is
is  . It is also assumed that the ring width is
. It is also assumed that the ring width is  and
and  , where
, where  is the sensing radius of the sensors. Notice that
is the sensing radius of the sensors. Notice that  in Figure 13 shows the distance of a sensor from the center of the ring. Since the sensors are uniformly distributed over the area, it can be easily shown that the cdf of
in Figure 13 shows the distance of a sensor from the center of the ring. Since the sensors are uniformly distributed over the area, it can be easily shown that the cdf of  , is as follows:
, is as follows:

We use  to derive
to derive  .In Figure 13, the intersection of the sensing area of an arbitrary sensor with
.In Figure 13, the intersection of the sensing area of an arbitrary sensor with  is denoted by
is denoted by  . By forming a triangle whose vertices are the center of
. By forming a triangle whose vertices are the center of  , sensor location, and one of the points where the sensing circle of the sensor meets
, sensor location, and one of the points where the sensing circle of the sensor meets  , one can write
, one can write

On the other hand, we have

Replacing  with
with  in (A.2) results in
in (A.2) results in

Solving (A.4), we have

Equivalently,

Now having the cdf of  and using the relation between
and using the relation between  and
and  in (A.5) and (A.6), we will derive
in (A.5) and (A.6), we will derive  . To this end, one can state
. To this end, one can state

Thus,

Replacing  in (A.8) using (A.1), we obtain
in (A.8) using (A.1), we obtain

where

Moreover,  when
when  and
and  when
when  . We use (A.9) for our exact analysis in order to characterize the path coverage features of the network. Notice that when
. We use (A.9) for our exact analysis in order to characterize the path coverage features of the network. Notice that when  is small,
is small,  can be approximated as follows:
can be approximated as follows:

In addition to the cdf of the arc length, we use the mean value of  for our approximate analysis. Recall that for an arbitrary random variable
for our approximate analysis. Recall that for an arbitrary random variable  distributed over
distributed over  ,
,

where  is the mean value of
is the mean value of  and
and  is the cdf of
is the cdf of  . Using (A.12),
. Using (A.12),  can be found as follows:
can be found as follows:

Notice that when  .Now assume that both sensing range and sensor location are random and we like to find
.Now assume that both sensing range and sensor location are random and we like to find  . Sensing range of the sensors,
. Sensing range of the sensors,  , varies over
, varies over  with probability density function (pdf)
with probability density function (pdf)  . Also,
. Also,  such that
such that  , because sensors located farther than
, because sensors located farther than  from the path do not contribute in the path coverage. It is noteworthy that
from the path do not contribute in the path coverage. It is noteworthy that  where
where

This can simply be justified using (A.6).To find  , we partition the problem to two separate cases. In the first case, sensing area of the sensor does not intersect with
, we partition the problem to two separate cases. In the first case, sensing area of the sensor does not intersect with  , that is,
, that is,  . This happens when
. This happens when  or
or  . If
. If  , this never happens and sensing area of the sensor always intersects with
, this never happens and sensing area of the sensor always intersects with  and consequently
and consequently  . If
. If  , we have
, we have

To evaluate two terms in the right side of the above equation, we use the joint distribution of  and
and  . Notice that in the case where sensors sensing range is independent from their location,
. Notice that in the case where sensors sensing range is independent from their location,  , where
, where  is the pdf of
is the pdf of  over
over  . To evaluate
. To evaluate  and
and  , we simply have to integrate from
, we simply have to integrate from  over the area where
over the area where  or
or  . It can be shown that
. It can be shown that

Notice that  states that the pdf of
states that the pdf of  , has a Dirac delta function at
, has a Dirac delta function at  .When sensing area of a sensor intersects with path,
.When sensing area of a sensor intersects with path,  . To find
. To find  in this case, we first find
in this case, we first find  . For this purpose, we apply Jacobian transformation to derive
. For this purpose, we apply Jacobian transformation to derive  , the joint distribution of
, the joint distribution of  and
and  , from
, from  . Using (A.6) and Jacobian transformation, one can show that
. Using (A.6) and Jacobian transformation, one can show that

where

Having  is found by integration over
is found by integration over  . To integrate over
. To integrate over  , the region of integration has to be determined carefully. For any arbitrary value of
, the region of integration has to be determined carefully. For any arbitrary value of  , there exist an infinite number of pairs
, there exist an infinite number of pairs  satisfying (A.6); however, to guarantee an intersection between the sensing range of the sensor and
satisfying (A.6); however, to guarantee an intersection between the sensing range of the sensor and  ,
,  should fall within
should fall within  where
where

In fact,  and
and  are the desired integral bounds. Thus,
are the desired integral bounds. Thus,

Consequently,

The mean value of  , used in our approximate analysis, is also derived as follows:
, used in our approximate analysis, is also derived as follows:

References
Ram SS, Manjunath D, Iyer SK, Yogeshwaran D: On the path coverage properties of random sensor networks. IEEE Transactions on Mobile Computing 2007, 6(5):446-458.
Harada J, Shioda S, Saito H: Path coverage property of randomly deployed sensor networks with finite communication ranges. Proceedings of IEEE International Conference on Communications (ICC '08), May 2008, Beijing, China 2221-2227.
Kumar S, Lai TH, Arora A: Barrier coverage with wireless sensors. Proceedings of the 11th Annual International Conference on Mobile Computing and Networking (MOBICOM '05), August-September 2005, Cologne, Germany 284-298.
Liu B, Dousse O, Wang J, Saipulla A: Strong barrier coverage of wireless sensor networks. Proceedings of the 9th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '08), May 2008, Hong Kong 411-419.
Chen A, Lai TH, Xuan D: Measuring and guaranteeing quality of barrier-coverage in wireless sensor networks. Proceedings of the 9th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '08), May 2008, Hong Kong 421-430.
Chen A, Kumar S, Lai TH: Designing localized algorithms for barrier coverage. Proceedings of the 13th Annual ACM International Conference on Mobile Computing and Networking (MOBICOM '07), September 2007, Montreal, Canada 63-74.
Hall P: Introduction to the Theory of Coverage Process. John Wiley & Sons, New York, NY, USA; 1988.
Stauffer D, Aharony A: Introduction to Percolation Theory. CRC Press, Boca Raton, Fla, USA; 1988.
Dvoretzky A: On covering a circle by randomly placed arcs. Proceedings of the National Academy of Sciences of the United States of America 1956, 42(4):199-203. 10.1073/pnas.42.4.199
Shepp LA: Covering the circle with random ARCS. Israel Journal of Mathematics 1972, 11(3):328-345. 10.1007/BF02789327
Siegel AF, Holst L: Covering the circle with random arcs of random sizes. Journal of Applied Probability 1982, 19(2):373-381. 10.2307/3213488
Huillet T: Random covering of the circle: the size of the connected components. Advances in Applied Probability 2003, 35(3):563-582. 10.1239/aap/1059486818
Yadin M, Zacks S: Random coverage of a circle with application to a shadowing problem. Journal of Applied Probability 1982, 19(3):562-577. 10.2307/3213514
Flatto L: A limit theorem for random coverings of a circle. Israel Journal of Mathematics 1973, 15(2):167-184. 10.1007/BF02764603
Holst L: On convergence of the coverage by random arcs on a circle and the largest spacing. The Annals of Probability 1981, 9(4):648-655. 10.1214/aop/1176994370
Acknowledgment
The authors would like to thank Natural Sciences and Engineering Research Council of Canada (NSERC) and Informatics Circle of Research Excellence (i CORE) for supporting our research.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Noori, M., Movaghati, S. & Ardakani, M. Characterizing the Path Coverage of Random Wireless Sensor Networks. J Wireless Com Network 2010, 716565 (2010). https://doi.org/10.1155/2010/716565
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/716565

 represents the number of gaps on
represents the number of gaps on 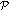 . We are interested to find the probability of having
. We are interested to find the probability of having 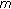 gaps, shown by
gaps, shown by 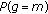 .
.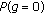 . This can simply be found from the derived distribution of
. This can simply be found from the derived distribution of 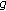 .
.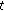 , denoted by
, denoted by 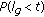 .
.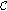 , has a stochastic nature and its distribution provides a general view of the entire path coverage. In fact, the covered part of the network reflects the combined effect of the number of gaps and their sizes. We derive the cdf of
, has a stochastic nature and its distribution provides a general view of the entire path coverage. In fact, the covered part of the network reflects the combined effect of the number of gaps and their sizes. We derive the cdf of 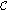 ,
,  .
.
 .
.

 and
and  .
.
 , versus the number of sensor nodes for fixed sensing range.
, versus the number of sensor nodes for fixed sensing range.

 , versus the number of sensor nodes for random sensing range.
, versus the number of sensor nodes for random sensing range.

 when
when  .
.


 when
when  .
.
 .
.
 .
.