- Research Article
- Open access
- Published:
Threshold-Based Relay Selection for Detect-and-Forward Relaying in Cooperative Wireless Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 721492 (2010)
Abstract
This paper studies two-hop cooperative demodulate-and-forward relaying using multiple relays in wireless networks. A threshold based relay selection scheme is considered, in which the reliable relays are determined by comparing source-relay SNR to a threshold, and one of the reliable relays is selected by the destination based on relay-destination SNR. The exact bit error rate of this scheme is derived, and a simple threshold function is proposed. It is shown that the network achieves full diversity order ( ) under the proposed threshold, where
) under the proposed threshold, where  is the number of relays in the network. Unlike some other full diversity achieving protocols in the literature, the requirement that the instantaneous/average SNRs of the source-relay links be known at the destination is eliminated using the appropriate SNR threshold.
is the number of relays in the network. Unlike some other full diversity achieving protocols in the literature, the requirement that the instantaneous/average SNRs of the source-relay links be known at the destination is eliminated using the appropriate SNR threshold.
1. Introduction
1.1. Background
Cooperative relaying can induce spatial diversity in wireless networks without the need for multiple antennas on a single terminal. Various decode-and-forward protocols have been proposed based on selective relaying, distributed space-time coding, and relay selection and have been shown to achieve full diversity [1–5]. Recently, detection aspects of cooperative relaying have been analyzed [5–10]. These works study the detect-and-forward (or demodulate-and-forward) cooperative relaying protocols, in which the relaying does not rely on any error correction or detection codes. Such protocols are particularly attractive for systems that do not use error detection/correction codes due to tight energy constraints. One possible application is sensor networks, which typically function under extremely limited battery-supplied energy. Most coding schemes can consume significant energy, and thus their use reduces sensor and network lifetime if each relay decodes the data. Moreover, the messages transmitted in sensor networks are usually very short while coding is usually efficient only for long messages.
Another relaying scheme that does not rely on any error correction or detection is the amplify-and-forward protocol, in which the relay amplifies and forwards the received waveforms to the destination. The main disadvantage of this scheme is noise amplification, which cannot be avoided due to the physical presence of the thermal noise at the relay receiver. The focus of this paper is on detect-and-forward relaying.
1.2. Related Work
The detect-and-forward protocol has the well-known disadvantage of error propagation. Unlike in ideal decode-and-forward relaying, in detect-and-forward relaying the relays can forward erroneous information, and with a conventional combining scheme such as Maximal Ratio Combining (MRC), these errors propagate to the destination, causing end-to-end (e2e) detection errors. Existing techniques for mitigating error propagation can be classified into two groups. The first of these comprises selective and adaptive relaying techniques, which include link adaptive relaying (LAR) [6] and threshold digital relaying (TDR) [11–13]. Both techniques use link SNRs to evaluate the reliability of the data received by the relay. In TDR a relay forwards the received data only when its received SNR is above a threshold value. In LAR the relay transmits with a fraction  of its maximum transmit power, where
of its maximum transmit power, where  depends on the source-relay and relay-destination SNRs. In [6], a function for calculating
depends on the source-relay and relay-destination SNRs. In [6], a function for calculating  is provided, and the resulting scheme is shown to achieve full diversity if the relays are capable of adjusting their transmit powers continuously. However, the proposed function cannot provide diversity if reduced to two power levels, that is, on/off power adaptation. TDR can also be viewed as on/off power adaptation, and it is shown in [13] that it can achieve full diversity in the single relay case. In [5], a relay selection scheme similar to ours is studied. In this paper an approximate expression for bit error probability is derived as a function of relay threshold assuming that MRC is performed at the destination. It is observed that the performance of threshold based relay selection is sensitive to the value of threshold.
is provided, and the resulting scheme is shown to achieve full diversity if the relays are capable of adjusting their transmit powers continuously. However, the proposed function cannot provide diversity if reduced to two power levels, that is, on/off power adaptation. TDR can also be viewed as on/off power adaptation, and it is shown in [13] that it can achieve full diversity in the single relay case. In [5], a relay selection scheme similar to ours is studied. In this paper an approximate expression for bit error probability is derived as a function of relay threshold assuming that MRC is performed at the destination. It is observed that the performance of threshold based relay selection is sensitive to the value of threshold.
The second approach to mitigate error propagation is to develop better combining schemes for the destination. These schemes take the possibility of error propagation into account and require the relays to send their source-relay link SNRs (average or instantaneous) to the destination. In [8], Wang et al. assume that the destination knows the instantaneous source-relay SNR and derive a linear combining technique, called Cooperative MRC (C-MRC), that approximates the Maximum Likelihood (ML) receiver. This receiver achieves full diversity at the expense of increased signaling to convey the first hop SNR information to the destination. In [7], the authors propose a piecewise linear receiver approximating the ML detector that requires knowledge of the average SNRs of the first hop. Conveying the average link SNRs is less costly than conveying the instantaneous SNR. However, this protocol cannot achieve full diversity for more than one relay. As will be shown in this paper, the protocol we consider requires minimal information on the first hop and still achieves full diversity.
We note that relay selection protocols are much more bandwidth efficient than protocols that require the relays to transmit in multiple orthogonal time slots and also have the potential to achieve full diversity [3, 4]. Recent work in the literature on relay selection covers relay selection for a single hop [10, 14, 15] as well as the selection of relays jointly for multiple hops [16, 17]. Different relay selection criteria have been proposed including those based on instantaneous SNR [3, 18, 19], average SNR [20, 21], and distance [22].
A relay selection protocol related to ours has been proposed in [10]. In this protocol, the relay selection is performed based on the equivalent e2e bit error rate (BER) of each relay channel. This protocol can be viewed as a selection version of C-MRC of [8]. As in C-MRC, it requires the destination to obtain the channel coefficients of the first and second hops or their product in the case of a simpler scheme, to make relay selection. However, in our protocol, the specific source-relay channel information is not required in order to perform relay selection.
1.3. Contributions of the Paper
In this paper, we consider the Threshold based Relay Selection Cooperation (TRSC) protocol, which generalizes threshold digital relaying to multiple relays. The specific contributions of the present paper are as follows.
-
(i)
We derive the e2e BER of the TRSC protocol with
 relays in a closed form given a common threshold value
relays in a closed form given a common threshold value 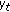 at the relays, assuming that all the relays have identical average source-relay and relay-destination SNRs.
at the relays, assuming that all the relays have identical average source-relay and relay-destination SNRs. -
(ii)
We derive a simple threshold function with which TRSC can achieve full diversity
 in an
in an 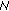 relay network. We show that this function scales as
relay network. We show that this function scales as  .
. -
(iii)
We find the optimal threshold value that minimizes the e2e BER through computer simulation and observe that it shares common properties with the proposed suboptimal threshold function.
-
(iv)
We propose two strategies to apply the TRSC protocol in asymmetric networks, in which relays have different average SNRs. Through numerical examples we analyze the performance of these strategies and show that the TRSC protocol is applicable to asymmetric networks as well.
The rest of this paper is organized as follows. In Section 2, we describe the system model and the TRSC protocol. In Section 3, we derive the e2e BER of the protocol, and in Section 4 we show that the protocol achieves full diversity using a threshold function we propose. We present some numerical results in Section 5 and conclude in Section 6 with a summary of our results.
2. System Model and Protocol
A network as shown in Figure 1 is considered in which a source node  communicates with a destination node
communicates with a destination node  with the assistance of
with the assistance of  relays denoted by
relays denoted by  . All links experience independent Rayleigh fading. For each link we assume quasistatic fading, in which the fading is constant over a two-stage transmission interval but then can change at the next interval. We assume a general modulation scheme for which the bit error probability can be expressed as
. All links experience independent Rayleigh fading. For each link we assume quasistatic fading, in which the fading is constant over a two-stage transmission interval but then can change at the next interval. We assume a general modulation scheme for which the bit error probability can be expressed as  , where
, where  and
and  are positive and where
are positive and where  is the received SNR. Some of our derivations are even more general; they are given in terms of
is the received SNR. Some of our derivations are even more general; they are given in terms of  and
and  and can be evaluated for any modulation scheme.
and can be evaluated for any modulation scheme.
The SNRs of the  , and
, and  links are denoted by
links are denoted by  , and
, and  , respectively. To simplify the analysis, we assume that all the relays have the same average SNRs to the source and to the destination. The variation in SNR is due to the Rayleigh channel gain and the noise and transmit powers do not vary. As
, respectively. To simplify the analysis, we assume that all the relays have the same average SNRs to the source and to the destination. The variation in SNR is due to the Rayleigh channel gain and the noise and transmit powers do not vary. As  and
and  for
for  , the link SNRs are characterized by
, the link SNRs are characterized by  , and
, and  . The Threshold based Relay Selection Cooperation (TRSC) protocol has two phases. In the first phase the source transmits while all the relays and the destination listen. Then each relay
. The Threshold based Relay Selection Cooperation (TRSC) protocol has two phases. In the first phase the source transmits while all the relays and the destination listen. Then each relay  decides independently whether its detection is reliable by comparing its received SNR
decides independently whether its detection is reliable by comparing its received SNR  to a threshold value. Those relays whose received SNRs are larger than the threshold are called reliable relays.
to a threshold value. Those relays whose received SNRs are larger than the threshold are called reliable relays.
One of the reliable relays is selected by the destination for possible retransmission. Each reliable relay informs the destination by sending a short message. The destination can estimate the values of  for all the reliable relays from these messages. The destination replies with another message conveying which relay is selected for retransmission. Let us denote the number of reliable relays by
for all the reliable relays from these messages. The destination replies with another message conveying which relay is selected for retransmission. Let us denote the number of reliable relays by  and reindex the reliable relays to simplify the notation. The destination, then, makes a decision based on the SNRs of the reliable relays and the source to the destination, that is,
and reindex the reliable relays to simplify the notation. The destination, then, makes a decision based on the SNRs of the reliable relays and the source to the destination, that is,  and
and  . Among
. Among  branches
branches  selects the one with the largest SNR. If the branch from the source is selected, the relays do not transmit and the source transmits the next data. Otherwise, the selected reliable relay transmits and
selects the one with the largest SNR. If the branch from the source is selected, the relays do not transmit and the source transmits the next data. Otherwise, the selected reliable relay transmits and  performs detection based on the selected branch only.
performs detection based on the selected branch only.
Alternatively, the relay selection can be performed by all nodes in a distributed manner using a timer at each relay as in [4]. Comparing with relay selection by the destination, this distributed selection scheme does not require the relay to forward the single bit information with regard to the  channel condition, however it requires each relay to obtain the channel gain (i.e.,
channel condition, however it requires each relay to obtain the channel gain (i.e.,  ), which can be assured through feedback from the destination.
), which can be assured through feedback from the destination.
In TRSC the information passed from the relay to the destination regarding the first hop is limited to whether the relay is a reliable relay or not, which can be represented by a single bit. For comparison we study the performance of cooperative relaying schemes in which the destination also knows either the instantaneous  SNRs
SNRs  for all links or their average
for all links or their average  .
.
3. End-to-end BER of the TRSC
In this section, we derive the e2e BER of the system described in Section 2. Since all the relays are assumed to be identical in terms of average SNRs to the relay and the destination, the optimal value of their thresholds must be the same. Hence, we derive the e2e BER of the system for a given common threshold  for all relays. Then the e2e BER is given by
for all relays. Then the e2e BER is given by

where  denotes the probability of an event and
denotes the probability of an event and

as the received SNRs have exponential probability distributions. For  , the destination detects based on the direct link only and, thus,
, the destination detects based on the direct link only and, thus,  . For
. For  , let
, let  denote the event that the destination selects the signal received from the source, and let
denote the event that the destination selects the signal received from the source, and let  denote the event that the destination selects the signal from the
denote the event that the destination selects the signal from the  th reliable relay (
th reliable relay ( ), respectively:
), respectively:

Then, the e2e BER conditioned on the number of reliable relays is equal to

Since all relays are assumed to be identical in their average SNRs to the source and the destination, the terms included in  are the same for all
are the same for all  , and the index
, and the index  can be dropped. When the destination selects the source signal, its bit error rate depends only on the source-destination link. However, if the destination selects reliable relay
can be dropped. When the destination selects the source signal, its bit error rate depends only on the source-destination link. However, if the destination selects reliable relay  , it will have a bit error if either the
, it will have a bit error if either the  link or the
link or the  link has a bit error:
link has a bit error:

The probability of bit error at a reliable relay is given by [11]

Substituting (5) into (4), we obtain the e2e BER conditioned on  as
as

The probability that a particular reliable relay is selected by the destination is equal to

The terms  and
and  are given by
are given by


See Appendix for the derivations of (8)–(10). By substituting (8)–(10) into (7) and then substituting (4), (7) into (1), we obtain an exact expression for the e2e BER of the threshold based relay selection protocol described in Section 2.
4. Diversity Order of TRSC
In this section, we consider a modulation scheme with  , where
, where  is the received SNR. Based on the insight from the e2e BER minimizing threshold derived in [13], for a network with
is the received SNR. Based on the insight from the e2e BER minimizing threshold derived in [13], for a network with  relays we propose to use a threshold function in the form of
relays we propose to use a threshold function in the form of  , where
, where  is a positive constant. Next, we show that TRSC can achieve full diversity with the proposed threshold function.
is a positive constant. Next, we show that TRSC can achieve full diversity with the proposed threshold function.
The e2e BER is given in (1). For the first term we have

Let us denote the asymptotic equivalence of two positive functions  and
and  as
as  . The functions
. The functions  and
and  are called asymptotically equivalent functions if
are called asymptotically equivalent functions if  . If
. If  , we say that
, we say that  is asymptotically less than or equal to
is asymptotically less than or equal to  and denote it as
and denote it as  .
.
With the proposed threshold as  we have
we have

We note that throughout this paper all the logarithms are in the natural base.
Thus,  is of order
is of order

Next, we study how fast the term  (given in (7)) decays with increasing SNR.
(given in (7)) decays with increasing SNR.
Lemma 1 (Asymptotic behavior of  ).
).
With the proposed threshold  , we have
, we have  .
.
See Appendix for the proof.
Combining the result of Lemma 1 with (13), we observe that in (1) the term with index  , that is,
, that is,  decreases as
decreases as  . The order of the sum of these
. The order of the sum of these  terms is determined by the term that has the slowest decay, which is the term with index
terms is determined by the term that has the slowest decay, which is the term with index  . Hence,
. Hence,

We observe that while the  order diversity achieved by conventional diversity combining schemes will decrease as
order diversity achieved by conventional diversity combining schemes will decrease as  , the cooperative diversity achieved by the TRSC protocol has a decay of
, the cooperative diversity achieved by the TRSC protocol has a decay of  . However, at large SNR the
. However, at large SNR the  term becomes insignificant and the diversity order, which is defined in [23], is equal to
term becomes insignificant and the diversity order, which is defined in [23], is equal to

We summarize the results in this section as the following theorem.
Theorem 1.
Assume a general modulation scheme with bit error rate  given receive SNR
given receive SNR  . TRSC can achieve diversity order of
. TRSC can achieve diversity order of  in an
in an  -relay network if the threshold function at each relay is in the form of
-relay network if the threshold function at each relay is in the form of

where  is a positive constant.
is a positive constant.
5. Results
In this section we compare the e2e BER of TRSC to two other Relay Selection Cooperation (RSC) protocols that are described below. We also present simulation results for asymmetric networks in which average SNRs of different relays are not identical.
5.1. Benchmark Protocols
5.1.1. RSC-Inst
In the first protocol, RSC-inst, the relay is selected based on the equivalent instantaneous BER of branches. The equivalent BER of relay  is given by
is given by

and  . The destination selects the branch with the minimum equivalent BER. Note that in this protocol, the specific
. The destination selects the branch with the minimum equivalent BER. Note that in this protocol, the specific  and
and  channel information is required at the destination in order to perform selection. This protocol is very similar to C-MRC with relay selection introduced in [9]. The only difference is that the scheme in [9] combines the direct signal with one of the relay signals, whereas RSC-inst selects either the destination or one of the relays.
channel information is required at the destination in order to perform selection. This protocol is very similar to C-MRC with relay selection introduced in [9]. The only difference is that the scheme in [9] combines the direct signal with one of the relay signals, whereas RSC-inst selects either the destination or one of the relays.
5.1.2. RSC-Avr
The second protocol we compare to is RSC-avr in which the destination has no knowledge of  values and the relay selection is based on
values and the relay selection is based on  , and
, and  values. Then, the equivalent BER of relay
values. Then, the equivalent BER of relay  is given by
is given by

and  . The destination selects the link with the lowest
. The destination selects the link with the lowest  . While RSC-inst is the selection version of the C-MRC of [8], RSC-avg can be viewed as the selection version of the maximum likelihood receiver of [7].
. While RSC-inst is the selection version of the C-MRC of [8], RSC-avg can be viewed as the selection version of the maximum likelihood receiver of [7].
5.2. Numerical Results
For numerical results, we first consider a symmetric network scenario, in which all average link SNRs are the same ( ). Binary phase shift keying (BPSK) modulation is used by all the nodes, that is,
). Binary phase shift keying (BPSK) modulation is used by all the nodes, that is,  . Figures 2 and 3 show the e2e BER of different protocols as a function of
. Figures 2 and 3 show the e2e BER of different protocols as a function of  for
for  and
and  relays, respectively. In each figure, there are two curves for TRSC: optimal TRSC and suboptimal TRSC. The threshold values for optimal TRSC are determined from the numerical minimization of the analytical e2e BER expression obtained in Section 3. For suboptimal TRSC the threshold values are calculated according to the threshold function we propose (given in (16)) with
relays, respectively. In each figure, there are two curves for TRSC: optimal TRSC and suboptimal TRSC. The threshold values for optimal TRSC are determined from the numerical minimization of the analytical e2e BER expression obtained in Section 3. For suboptimal TRSC the threshold values are calculated according to the threshold function we propose (given in (16)) with  , that is,
, that is,  .
.
For  , TRSC and RSC-avr perform similarly, while RSC-inst performs slightly better than these two protocols and all protocols achieve full diversity gain as observed from the slopes of the BER curves. However, as the number of relays is increased to
, TRSC and RSC-avr perform similarly, while RSC-inst performs slightly better than these two protocols and all protocols achieve full diversity gain as observed from the slopes of the BER curves. However, as the number of relays is increased to  , RSC-avr cannot deliver full diversity. In fact, by analyzing RSC-avr for different
, RSC-avr cannot deliver full diversity. In fact, by analyzing RSC-avr for different  values, we observe that the diversity order of RSC-avr is limited to 2. The TRSC with the suboptimal threshold achieves full diversity for both
values, we observe that the diversity order of RSC-avr is limited to 2. The TRSC with the suboptimal threshold achieves full diversity for both  values as evident from the slope of the BER curves, in accordance with our claims in Section 4.
values as evident from the slope of the BER curves, in accordance with our claims in Section 4.
By comparing the TRSC curves with the optimal and the suboptimal threshold we observe that there is approximately 0.5 dB and 2 dB loss in SNR for  and
and  , respectively. We note that the suboptimal threshold we propose achieves full diversity for any positive constant
, respectively. We note that the suboptimal threshold we propose achieves full diversity for any positive constant  . However, this threshold function is not necessarily optimal even if the
. However, this threshold function is not necessarily optimal even if the  value is selected carefully.
value is selected carefully.
In order to examine the behavior of the optimal threshold, in Figure 4, we show the threshold values used by TRSC to minimize e2e BER through numerical optimization. It is seen that the optimal threshold increases with increasing number of relays. As a function of average SNR, the optimal threshold increases logarithmically. We note that the suboptimal threshold we have proposed in this paper also shares these two properties. However, finding optimal thresholds analytically remains a challenging problem for future work.
The motivation of the analysis in this paper was to obtain insight to the threshold selection problem. To simplify the analysis we have assumed that the average source-relay and relay-destination SNRs are common for all relays. In practice, all links are expected to have nonidentical average SNRs and it is desirable to understand the performance of TRSC under different scenarios. For the multiple relay case, finding the optimal threshold for each relay following the same approach as in Section 3 seems intractable. We propose two strategies to determine the threshold values in this case. In the first strategy, which we call TRSC-ind, each relay calculates the optimal threshold (as in TRSC optimal described above) assuming that the remaining  relays have the same
relays have the same  and
and  values as itself. Note that we also assume that each relay knows the number of relays
values as itself. Note that we also assume that each relay knows the number of relays  . Different relays employ TRSC based on their individual threshold values. In the second strategy, which is called TRSC-max, after calculating individual relay thresholds as in TRSC-ind, the largest of
. Different relays employ TRSC based on their individual threshold values. In the second strategy, which is called TRSC-max, after calculating individual relay thresholds as in TRSC-ind, the largest of  thresholds is set as the common threshold of all relays. We assume a separate mechanism to convey the value of the maximum threshold among all relays.
thresholds is set as the common threshold of all relays. We assume a separate mechanism to convey the value of the maximum threshold among all relays.
Next, we present simulation results on the average performance of TRSC over random SNR values. We assume that the relay positions are selected randomly on the line connecting  and
and  . The average SNR values are calculated based on distance assuming a pathloss exponent of
. The average SNR values are calculated based on distance assuming a pathloss exponent of  . The results are averaged over many random relay positions. First, as a reference, in Figure 5 we plot the performance of optimal TRSC for the single relay case. It is seen that the conclusions are similar to those for the symmetric network shown in Figure 2. In Figure 6 we plot the average performance of these two strategies for
. The results are averaged over many random relay positions. First, as a reference, in Figure 5 we plot the performance of optimal TRSC for the single relay case. It is seen that the conclusions are similar to those for the symmetric network shown in Figure 2. In Figure 6 we plot the average performance of these two strategies for  relays. The two strategies perform very closely and the gain over RSC-avr is preserved.
relays. The two strategies perform very closely and the gain over RSC-avr is preserved.
We conclude that TRSC offers a good tradeoff between performance and signaling overhead since it performs comparable to RSC-inst with no instantaneous  SNR knowledge at the destination.
SNR knowledge at the destination.
6. Conclusions and Discussion
In this paper, we have analyzed a threshold based relay selection protocol for two hop, multirelay cooperative communication. This protocol requires minimal information at the destination about the SNRs of the source-relay links. We have proposed a threshold function that increases logarithmically with the link SNRs and linearly with the number of relays. We have shown that, with a threshold of this form, threshold based relay selection protocol achieves full diversity.
We have presented performance results for the threshold based relay selection with the proposed threshold function and optimal threshold values determined through numerical optimization. We have compared the BER of threshold based relay selection to similar protocols found in the literature. Although our mathematical analysis has assumed simplified network scenarios, through simulations we have verified the applicability of threshold based selection relaying for general scenarios.
Appendices
A. Derivation of (8), (9), and (10)
A.1. Derivation of (8)
The probability of  can be expressed as
can be expressed as

Using the binomial expansion for  we obtain
we obtain

Since the probability of being selected by the destinations is the same for all potential relays and independent of index  , we denote it by
, we denote it by  and calculate it as
and calculate it as  . Hence,
. Hence,

A.2. Derivation of (9)
The term  is equal to the following integral:
is equal to the following integral:

Again, using the binomial expansion for  we obtain
we obtain

A.3. Derivation of (10)
Similarly, the error probability given that a particular relay  is selected is equal to
is selected is equal to

B. Proof of Lemma 1
We prove this lemma by analyzing the orders of terms in (7) as  .
.
Part 1.
Let us first analyze the asymptotic behavior of  and
and  . In the absence of errors at the reliable relays the bit error probability at the destination would be equal to the performance of
. In the absence of errors at the reliable relays the bit error probability at the destination would be equal to the performance of  branch selection combining (SC), where one of the branches has average SNR of
branch selection combining (SC), where one of the branches has average SNR of  , and the rest have
, and the rest have  . The probability of bit error of SC can be expressed as
. The probability of bit error of SC can be expressed as

Hence,  and
and  . Since SC is known to achieve diversity order equal to the number of its branches, we conclude that both
. Since SC is known to achieve diversity order equal to the number of its branches, we conclude that both  and
and  decrease at least as fast as
decrease at least as fast as  :
:  and
and  .
.
Part 2.
Now, let us examine the order of the term  if
if  . The analysis closely follows that given in [13] for
. The analysis closely follows that given in [13] for  relay. In [13] for BPSK and any threshold
relay. In [13] for BPSK and any threshold  it is shown that
it is shown that  . In the case of
. In the case of  , this bound can easily be generalized to
, this bound can easily be generalized to

Using the well-known bound  , we obtain
, we obtain

By substituting  , we conclude that
, we conclude that

Thus  .
.
Part 3.
As seen in (8),  depends on
depends on  and
and  only through their ratio. Hence, this quantity is independent of
only through their ratio. Hence, this quantity is independent of  and
and  .
.
Combining Parts 1, 2, and 3, we obtain

Hence,  .
.
References
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Laneman JN, Wornell GW: Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks. IEEE Transactions on Information Theory 2003, 49(10):2415-2425. 10.1109/TIT.2003.817829
Beres E, Adve R: Selection cooperation in multi-source cooperative networks. IEEE Transactions on Wireless Communications 2008, 7(1):118-127.
Bletsas A, Khisti A, Reed DP, Lippman A: A simple cooperative diversity method based on network path selection. IEEE Journal on Selected Areas in Communications 2006, 24(3):659-672.
Michalopoulos DS, Karagiannidis GK: Performance analysis of single relay selection in rayleigh fading. IEEE Transactions on Wireless Communications 2008, 7(10):3718-3724.
Wang T, Giannakis GB, Wang R: Smart regenerative relays for link-adaptive cooperative communications. IEEE Transactions on Communications 2008, 56(11):1950-1960.
Chen D, Laneman JN: Modulation and demodulation for cooperative diversity in wireless systems. IEEE Transactions on Wireless Communications 2006, 5(7):1785-1794.
Wang T, Cano A, Giannakis GB, Laneman JN: High-performance cooperative demodulation with decode-and-forward relays. IEEE Transactions on Communications 2007, 55(7):1427-1438.
Yi Z, Kim IM: Decode-and-forward cooperative networks with relay selection. Proceedings of the IEEE 66th Vehicular Technology Conference (VTC '07), October 2007, Baltimore, Md, USA 1167-1171.
Yi Z, Kim I-M: Diversity order analysis of the decode-and-forward cooperative networks with relay selection. IEEE Transactions on Wireless Communications 2008, 7(5):1792-1799.
Herhold P, Zimmermann E, Fettweis G: A simple cooperative extension to wireless relaying. Proceedings of the International Zurich Seminar on Communications: Access—Transmission -Networking, February 2004, Zurich, Switzerland 36-39.
Onat FA, Adinoyi A, Fan Y, Yanikomeroglu H, Thompson JS, Marsland ID: Threshold selection for SNR-based selective digital relaying in cooperative wireless networks. IEEE Transactions on Wireless Communications 2008, 7(11):4226-4237.
Onat F, Fan Y, Yanikomeroglu H, Thompson J: Asymptotic BER analysis of threshold digital relaying schemes in cooperative wireless systems. IEEE Transactions on Wireless Communications 2008, 7(12):4938-4947.
Lin Z, Erkip E, Stefanov A: Cooperative regions and partner choice in coded cooperative systems. IEEE Transactions on Communications 2006, 54(7):1323-1334.
Ibrahim AS, Sadek AK, Su W, Liu KJR: Cooperative communications with relay-selection: when to cooperate and whom to cooperate with? IEEE Transactions on Wireless Communications 2008, 7(7):2814-2827.
Adam H, Bettstetter C, Senouci SM: Multi-Hop-aware cooperative relaying. Proceedings of the IEEE Vehicular Technology Conference (VTC '09), 2009, Barcelona, Spain
Beres E, Adve R: Cooperation and routing in multi-hop networks. Proceedings of the IEEE International Conference on Communications (ICC '07), June 2007, Glasgow, Scotland 4767-4772.
Bletsas A, Shin H, Win MZ: Cooperative communications with outage-optimal opportunistic relaying. IEEE Transactions on Wireless Communications 2007, 6(9):3450-3460.
Jing Y, Jafarkhani H: Single and multiple relay selection schemes and their diversity orders. Proceedings of the IEEE International Conference on Communications Workshops (ICC '08), May 2008, Beijing, China 349-353.
Luo J, Blum RS, Cimini LJ, Greenstein LJ, Haimovich AM: Link-failure probabilities for practical cooperative Relay networks. Proceedingsof the IEEE 61st Vehicular Technology Conference (VTC '05), June 2005, Stockholm, Sweden 1489-1493.
Onat FA, Avidor D, Mukherjee S: Two-hop relaying in random networks with limited channel state information. Proceedings of the 4th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON '07), June 2007, San Diego, Calif, USA 570-579.
Sadek AK, Han Z, Liu KJR: A distributed relay-assignment algorithm for cooperative communications in wireless networks. Proceedings of the IEEE International Conference on Communications (ICC '06), July 2006, Istanbul, Turkey 1592-1597.
Zheng L, Tse DNC: Diversity and multiplexing: a fundamental tradeoff in multiple-antenna channels. IEEE Transactions on Information Theory 2003, 49(5):1073-1096. 10.1109/TIT.2003.810646
Acknowledgment
This research was supported by the U.S. National Science Foundation under Grant CNS-09-05398.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Atay Onat, F., Fan, Y., Yanikomeroglu, H. et al. Threshold-Based Relay Selection for Detect-and-Forward Relaying in Cooperative Wireless Networks. J Wireless Com Network 2010, 721492 (2010). https://doi.org/10.1155/2010/721492
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/721492
 relays in a closed form given a common threshold value
relays in a closed form given a common threshold value 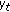 at the relays, assuming that all the relays have identical average source-relay and relay-destination SNRs.
at the relays, assuming that all the relays have identical average source-relay and relay-destination SNRs. in an
in an 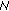 relay network. We show that this function scales as
relay network. We show that this function scales as  .
.

 relay. The BER of direct transmission and the BER in the absence of errors in the
relay. The BER of direct transmission and the BER in the absence of errors in the  links are also shown as reference curves.
links are also shown as reference curves.
 relays. The BER of direct transmission and the BER in the absence of errors in the
relays. The BER of direct transmission and the BER in the absence of errors in the  links are also shown as reference curves.
links are also shown as reference curves.
 of relays.
of relays.

 relay under random topologies.
relay under random topologies.

 relays under random topologies.
relays under random topologies.