- Research Article
- Open access
- Published:
Higher-Order Cyclostationarity Detection for Spectrum Sensing
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 721695 (2010)
Abstract
Recent years have shown a growing interest in the concept of Cognitive Radios (CRs), able to access portions of the electromagnetic spectrum in an opportunistic operating way. Such systems require efficient detectors able to work in low Signal-to-Noise Ratio (SNR) environments, with little or no information about the signals they are trying to detect. Energy detectors are widely used to perform such blind detection tasks, but quickly reach the so-called SNR wall below which detection becomes impossible Tandra (2005). Cyclostationarity detectors are an interesting alternative to energy detectors, as they exploit hidden periodicities present in man-made signals, but absent in noise. Such detectors use quadratic transformations of the signals to extract the hidden sine-waves. While most of the literature focuses on the second-order transformations of the signals, we investigate the potential of higher-order transformations of the signals. Using the theory of Higher-Order Cyclostationarity (HOCS), we derive a fourth-order detector that performs similarly to the second-order ones to detect linearly modulated signals, at SNR around 0 dB, which may be used if the signals of interest do not exhibit second-order cyclostationarity. More generally this paper reviews the relevant aspects of the cyclostationary and HOCS theory, and shows their potential for spectrum sensing.
1. Introduction
Many studies have shown that the static frequency allocation for wireless communication systems is responsible for the inefficient use of the spectrum [1]. This is so because the systems are not continuously transmitting. Cognitive Radios (CRs) networks try to make use of the gaps that can be found in the spectrum at a given time. This opportunistic behavior categorizes CR as secondary users of a given frequency band, by contrast with the systems that were permanently assigned this band (primary users) [2]. For the CR concept to be viable, it is required that it does not interfere with the primary user services. It means that the system must be able to detect primary user signals in low signal-to-noise ratio (SNR) environments fast enough. Efforts are being made to improve the performance of the detectors [3].
A radiometer (also called energy detector) can be used to detect completely unknown signals in a determined frequency band [4]. It is historically the oldest and simplest detector, and it achieves good performance when the SNR is strong enough. Unfortunately, since it is based on an estimation of the in-band noise power spectral density (PSD), it is affected by the noise level uncertainty (due to measurement errors or a changing environment), especially at low SNR [5], where it reaches an absolute performance limit called the SNR wall. Another type of detector is based on the spectral redundancy present in almost every man-made signal. It is called a cyclic feature detector and will be the kind of detector of interest in this paper.
Cyclic feature detectors make use of the cyclostationarity theory, which can be divided in two categories: the second-order cyclostationarity (SOCS) introduced by Gardner in [6–8] and the higher-order cyclostationarity (HOCS) introduced by Gardner and Spooner in [9, 10]. The SOCS uses quadratic nonlinearities to extract sine-waves from a signal, whereas the HOCS is based on  th-order nonlinearities. The idea behind this theory is that man-made signals possess hidden periodicities such as the carrier frequency, the symbol rate or the chip rate, that can be regenerated by a sine-wave extraction operation which produces features at frequencies that depend on these hidden periodicities (hence called cyclic features and cycle frequencies resp.). Since the SOCS is based on quadratic nonlinearities, two frequency parameters are used for the sine-wave extraction function. The result is called the spectral correlation density (SCD), and can be represented in a bifrequency plane. The SCD can be seen as a generalization of the PSD, as it is equal to the PSD when the cycle frequency is equal to zero. Therefore, the SOCS cyclic feature detectors act like energy detectors, but at cycle frequencies different from zero. The advantage of these detectors comes from the absence of features (at least asymptotically) when the input signal is stationary (such as white noise), since no hidden frequencies are present, or when the input signal exhibits cyclostationarity at cycle frequencies different than the one of interest. The HOCS cyclic-feature detectors are based on the same principles, but the equivalent of the SCD is a
th-order nonlinearities. The idea behind this theory is that man-made signals possess hidden periodicities such as the carrier frequency, the symbol rate or the chip rate, that can be regenerated by a sine-wave extraction operation which produces features at frequencies that depend on these hidden periodicities (hence called cyclic features and cycle frequencies resp.). Since the SOCS is based on quadratic nonlinearities, two frequency parameters are used for the sine-wave extraction function. The result is called the spectral correlation density (SCD), and can be represented in a bifrequency plane. The SCD can be seen as a generalization of the PSD, as it is equal to the PSD when the cycle frequency is equal to zero. Therefore, the SOCS cyclic feature detectors act like energy detectors, but at cycle frequencies different from zero. The advantage of these detectors comes from the absence of features (at least asymptotically) when the input signal is stationary (such as white noise), since no hidden frequencies are present, or when the input signal exhibits cyclostationarity at cycle frequencies different than the one of interest. The HOCS cyclic-feature detectors are based on the same principles, but the equivalent of the SCD is a  -dimensional space (
-dimensional space ( ). Like SOCS detectors, HOCS detectors have originally been introduced in the literature to blindly estimate the signal frequency parameters.
). Like SOCS detectors, HOCS detectors have originally been introduced in the literature to blindly estimate the signal frequency parameters.
It has been shown that the second-order cyclostationarity detectors perform better than the energy detectors in low SNR environments [7], and this has recently triggered a lot of research on the use of cyclostationarity detectors for spectrum sensing in the context of cognitive radios [11, 12]. However the second-order detectors suffer from a higher computational complexity that has just become manageable. First field-programmable gate array (FPGA) implementations are presented in [13, 14].
Higher-order detectors are generally even more complex, and since the variance of the features estimators increases when the order rises, most research results concern second-order detectors. We will nevertheless demonstrate that it is possible to derive fourth-order detectors that bear comparable performances to second-order ones to detect linearly modulated baseband signals at SNR around 0 dB. The paper will include a mathematical analysis of the detection algorithm, the effects of each of its parameters and its computational complexity. Performance will be assessed through simulations and compared with the second-order detector.
After introducing the system model in Section 2, we will briefly review the basic notions of cyclostationarity theory in Section 3 in order to understand how second-order detectors work and identify their limitations. Afterwards, we will move on to HOCS theory, and present its most relevant aspects in Section 4, which will be used to characterize the linearly modulated signals in Section 5 and to derive an algorithm that may be used for signal detection of linearly modulated signals in Section 6. We will conclude by a comparison of the new detector performance with second-order detector and energy detector performances in Section 7.
2. System Model
This paper focuses on the detection of linearly modulated signals, like pulse amplitude modulation (PAM) or quadrature amplitude modulation (QAM) signals. The baseband transmitted signal is usually expressed as

where  is the sequence of information symbols transmitted at the rate
is the sequence of information symbols transmitted at the rate  and
and  is the pulse shaping filter (typically a square-root Nyquist filter). After baseband-to-radio frequency (RF) conversion, the RF transmitted signal is given by:
is the pulse shaping filter (typically a square-root Nyquist filter). After baseband-to-radio frequency (RF) conversion, the RF transmitted signal is given by:

where  and
and  is the carrier frequency. In the PAM case, the symbols
is the carrier frequency. In the PAM case, the symbols  are real and only the cosine is modulated. In the QAM case, the symbols
are real and only the cosine is modulated. In the QAM case, the symbols  are complex and both the cosine and sine are modulated. A QAM signal can be seen as two uncorrelated PAM signals modulated in quadrature.
are complex and both the cosine and sine are modulated. A QAM signal can be seen as two uncorrelated PAM signals modulated in quadrature.
For the sake of clarity, we assume that the signal propagates through an ideal channel. Our results can nevertheless be extended to the case of multipath channels, if we consider a new pulse shape that is equal to the convolution of square-root Nyquist filter with the channel impulse response. However, this would make the new pulse random. Simulations have shown that both second-order and fourth-order detectors are affected in the same way by a multipath channel (equivalent degradation of performances). Therefore it does not seem critical to introduce multipath channels in order to compare the two, and it allows us to work with a constant pulse shape. Additive white Gaussian noise (AWGN) of one-sided PSD equal to  corrupts the signal at the receiver. Some amount of noise uncertainty can be added to
corrupts the signal at the receiver. Some amount of noise uncertainty can be added to  . The detection of the signal at the receiver can be either done directly in the RF domain or in the baseband domain after RF-to-baseband conversion.
. The detection of the signal at the receiver can be either done directly in the RF domain or in the baseband domain after RF-to-baseband conversion.
3. Second-Order Cyclostationarity
Two approaches are used to introduce the notion of cyclostationarity [8]. While the first approach introduces the temporal features of cyclostationary signals, the second approach is more intuitive and is based on a graphical representation of spectral redundancy. Both approaches lead to the same conclusion. This section reviews the main results of the second-order cyclostationarity theory, which will be generalized to higher-order cyclostationarity in the next sections.
3.1. Temporal Redundancy
A wide-sense cyclostationary signal  exhibits a periodic autocorrelation function [6, 7]
exhibits a periodic autocorrelation function [6, 7]

where  denotes the statistical expectation operator. Since
denotes the statistical expectation operator. Since  is periodic, it can be decomposed in a Fourier series
is periodic, it can be decomposed in a Fourier series

where the sum is over integer multiples of the fundamental frequencies. The coefficient  is called the cyclic autocorrelation function, and represents the Fourier coefficient of the series given by
is called the cyclic autocorrelation function, and represents the Fourier coefficient of the series given by

When the signal is cyclo-ergodic, the expectation in the definition of the autocorrelation can be replaced by a time average so that

The cyclic autocorrelation is therefore intuitively obtained by extracting the frequency  sine-wave from the time-delay product
sine-wave from the time-delay product  . The SCD
. The SCD  is defined as the Fourier transform of
is defined as the Fourier transform of  over
over  . We notice that the only cyclic frequencies
. We notice that the only cyclic frequencies  for which the SCD will not be null are the ones corresponding to the Fourier coefficients.
for which the SCD will not be null are the ones corresponding to the Fourier coefficients.
3.2. Spectral Redundancy
Let  be the Fourier transform of
be the Fourier transform of  . The SCD measures the degree of spectral redundancy between the frequencies
. The SCD measures the degree of spectral redundancy between the frequencies  and
and  (
( being called the cyclic frequency). It can be mathematically expressed as the correlation between two frequency bins centered on
being called the cyclic frequency). It can be mathematically expressed as the correlation between two frequency bins centered on  and
and  when their width tends toward zero [6, 7]
when their width tends toward zero [6, 7]

where  denotes the short-time Fourier transform of the signal
denotes the short-time Fourier transform of the signal

Since the SCD depends on  and
and  , it can be graphed as a surface over the bifrequency plane
, it can be graphed as a surface over the bifrequency plane  . When
. When  , the SCD reduces to the PSD.
, the SCD reduces to the PSD.
3.3. Baseband and RF Second-Order Features
The performance of the cyclic feature detectors will first depend on the strength of the features they are trying to estimate. The two most common features exploited to detect the linearly modulated signals are linked with the symbol rate and the carrier frequency.
-
(i)
The symbol rate feature is usually exploited after RF-to-baseband conversion at the receiver. As its name suggests it, it originates from the symbol rate at the transmitter. Since this is a discrete signal, its frequency spectrum is periodic, with a period equal to the inverse of the sample rate (which is equal to the symbol rate before RF conversion). If there is some excess bandwidth in the system, or in other words, if the pulse shaping filter
 does not totally cut off the frequency components larger than half the inverse of the symbol rate, some frequencies will be correlated, as shown in Figure 1.
does not totally cut off the frequency components larger than half the inverse of the symbol rate, some frequencies will be correlated, as shown in Figure 1. -
(ii)
The doubled-carrier frequency feature is directly exploited in the RF domain. It is based on the symmetry of the RF spectrum, and it is much stronger than the symbol rate feature (it is as strong as the PSD). Since it depends on the symmetry of the spectrum of the baseband signal, it only exists if the modulation used has no quadrature components. If a real PAM scheme is used, the carrier feature exists, as illustrated in the left part of Figure 2. If a complex QAM scheme is used, the carrier feature vanishes, as illustrated in the right part of Figure 2.
Baseband signal frequency spectrum (top) and SCD at the symbol rate (bottom). The frequency spectrum results from the repetitive discrete signal spectrum and the filter shaping. The SCD is measured by the correlation between two frequency bins centered on  and
and  where
where  is the symbol rate. The symbol rate feature exists for baseband PAM/QAM signals if there is some excess bandwidth in the system.
is the symbol rate. The symbol rate feature exists for baseband PAM/QAM signals if there is some excess bandwidth in the system.
RF signal frequency spectrum (top) and SCD at twice the carrier frequency (bottom). The SCD is measured by the correlation between two frequency bins centered on  and
and  where
where  is the carrier frequency. The doubled-carrier frequency feature exists for RF PAM signals as the baseband frequency spectrum exhibits a correlation between negative and positive frequencies. In the absence of any filtering, this correlation produces a symmetric frequency spectrum (left part). The doubled-carrier frequency feature vanishes for RF QAM signals as the baseband frequency spectrum is uncorrelated (right part).
is the carrier frequency. The doubled-carrier frequency feature exists for RF PAM signals as the baseband frequency spectrum exhibits a correlation between negative and positive frequencies. In the absence of any filtering, this correlation produces a symmetric frequency spectrum (left part). The doubled-carrier frequency feature vanishes for RF QAM signals as the baseband frequency spectrum is uncorrelated (right part).
Since complex modulations are quite common, it would not be possible to implement a cyclic feature detector for CRs based on the doubled-carrier frequency feature. On the other hand, the symbol rate feature solely depends on the pulse shaping filter. Provided that there is some excess bandwidth, the symbol rate feature will exist, whatever the modulation. Unfortunately, that feature is relatively small and depends on the amount of excess bandwidth. We can therefore ask ourselves if it would not be possible to find greater features using a fourth-order detector.
4. Higher-Order Cyclostationarity
The higher-order cyclostationarity (HOCS) theory is a generalization of the second-order cyclostationarity theory, which only deals with second-order moments, to  th-order moments [9, 10]. It makes use of the fraction-of-time (FOT) probability framework (based on time averages of the signals) which is closely related to the theory of high-order statistics (based on statistical expectations of the signals), by ways of statistical moments and cumulants. This section reviews the fundamentals of the HOCS theory and highlights the metrics that can be used for spectrum sensing.
th-order moments [9, 10]. It makes use of the fraction-of-time (FOT) probability framework (based on time averages of the signals) which is closely related to the theory of high-order statistics (based on statistical expectations of the signals), by ways of statistical moments and cumulants. This section reviews the fundamentals of the HOCS theory and highlights the metrics that can be used for spectrum sensing.
4.1. Lag-Product
We must always keep in mind that the goal of the HOCS theory is to extract sine-waves components from a signal, in which they are hidden by random phenomena. To extract, or regenerate, these frequencies, a nonlinear operation must be called upon. The second-order theory uses the time-delay product  which will be transformed in the autocorrelation after averaging. A natural and intuitive generalization of this operation to the
which will be transformed in the autocorrelation after averaging. A natural and intuitive generalization of this operation to the  th-order is called the lag-product and can be expressed as [9]:
th-order is called the lag-product and can be expressed as [9]:


where the vector  is composed of the individual delays
is composed of the individual delays  (
( ). The notation
). The notation  indicates an optional conjugation of the signal
indicates an optional conjugation of the signal  .
.
4.2. Temporal Moment Function and Cyclic Temporal Moment Function
If the signal possesses a  th-order sine-wave of frequency
th-order sine-wave of frequency  , then the averaging of the lag-product, multiplied by a complex exponential of frequency
, then the averaging of the lag-product, multiplied by a complex exponential of frequency  , must be different from zero [9]:
, must be different from zero [9]:

Obviously,  is a generalization of the cyclic autocorrelation function described in (5). It is called the
is a generalization of the cyclic autocorrelation function described in (5). It is called the  th-order cyclic temporal moment function (CTMF). The sum of the CTMF (multiplied by the corresponding complex exponentials) over frequency
th-order cyclic temporal moment function (CTMF). The sum of the CTMF (multiplied by the corresponding complex exponentials) over frequency  is called the temporal moment function (TMF) and is a generalization of the autocorrelation function described in (3):
is called the temporal moment function (TMF) and is a generalization of the autocorrelation function described in (3):

Each term of the sum in (12) is called an impure  th-order sine-wave. This is so because the CTMF may contain products of lower-order sine-waves whose various orders sum to
th-order sine-wave. This is so because the CTMF may contain products of lower-order sine-waves whose various orders sum to  . In order to extract the pure
. In order to extract the pure  th-order sine-wave from the lag-product, it is necessary to subtract the lower-order products. The pure
th-order sine-wave from the lag-product, it is necessary to subtract the lower-order products. The pure  th-order sine-wave counter-part of the CTMF, denoted by
th-order sine-wave counter-part of the CTMF, denoted by  , is called the cyclic temporal cumulant function (CTCF). The pure
, is called the cyclic temporal cumulant function (CTCF). The pure  th-order sine wave counter-part of the TMF, denoted by
th-order sine wave counter-part of the TMF, denoted by  , is called the temporal cumulant function (TCF).
, is called the temporal cumulant function (TCF).
4.3. Temporal Cumulant Function and Cyclic Temporal Cumulant Function
The CTMF and TMF have been computed by using the FOT probability framework. In order to compute the CTCF and TCF, it is interesting to make use of the equivalence between the FOT probability framework and the high-order statistics theory. More specifically, the paper [9] demonstrates that the TMF of a signal can be seen as the  th-order moment of the signal, and that the TCF of a signal can be seen as the
th-order moment of the signal, and that the TCF of a signal can be seen as the  th-order cumulant of the signal (hence their names). By using the conventional relations between the moments and the cumulants found in the high-order statistics theory, the TCF takes therefore the form:
th-order cumulant of the signal (hence their names). By using the conventional relations between the moments and the cumulants found in the high-order statistics theory, the TCF takes therefore the form:

where  denotes the set of partitions of the index set
denotes the set of partitions of the index set  (10),
(10),  is the number of elements in the partition
is the number of elements in the partition  , and
, and  is the TMF of the
is the TMF of the  th-element of order
th-element of order  of the partition
of the partition  .
.
The CTCFs are the Fourier coefficients of the TCF and can be expressed in terms of the CTMFs:

where  denotes the set of vectors of cycle frequencies for the partition
denotes the set of vectors of cycle frequencies for the partition  that sum to
that sum to  (
( ), and
), and  is the CTMF of the
is the CTMF of the  th-element of order
th-element of order  of the partition
of the partition  at the cycle frequency
at the cycle frequency  .
.
The CTCF is periodic in  :
:  (
( is the dimension-
is the dimension- vector composed of ones, meaning that
vector composed of ones, meaning that  is added to all elements of
is added to all elements of  ). Therefore, it is not absolutely integrable in
). Therefore, it is not absolutely integrable in  . To circumvent this problem, one dimension is fixed (e.g.,
. To circumvent this problem, one dimension is fixed (e.g.,  ), and the CTCF becomes:
), and the CTCF becomes:  . This function is called reduced dimension-CTCF (RD-CTCF). It is the key metric of the ensuing algorithms for HOCS detectors. It should be noted that the equivalent exists for the CTMF and is called the RD-CTMF (
. This function is called reduced dimension-CTCF (RD-CTCF). It is the key metric of the ensuing algorithms for HOCS detectors. It should be noted that the equivalent exists for the CTMF and is called the RD-CTMF ( ). However the RD-CTMF is generally not absolutely integrable.
). However the RD-CTMF is generally not absolutely integrable.
4.4. Cyclic Polyspectrum
The need for integrability comes from the desire to compute the Fourier transform of the RD-CTCF, which gives the cyclic polyspectrum (CP). The CP is a generalization of the SCD plane for cyclostationnary signals. However it is not necessary to compute the CP of a signal for sensing applications since detection statistics can be directly derived from a single slice of the RD-CTCF. For this reason, and the computational complexity gain, we will put the spectral parameters aside and devote our attention to the RD-CTCF.
5. Fourth-Order Features of Linearly Modulated Signals
We have previously talked about the second-order cyclic features for communication signals, and we saw that the carrier frequency features tend to vanish from the SCD plane if the modulation is complex. We also asked ourselves if a fourth-order transformation of the signal may suppress the destructive interferences of quadrature components of a signal. We now have to gauge the potential of these fourth-order features. In this section, we compute the RD-CTCF of the baseband and RF linearly modulated signals and identify the interesting features that can be used for signal detection.
5.1. Baseband Signals
The TCF of the baseband signal (1) has been computed in paper [10]. The mathematical derivation results in:

in which  is the
is the  th-order cumulant of the symbol sequence
th-order cumulant of the symbol sequence  :
:

where  is the set of partitions of the set
is the set of partitions of the set  ,
,  is the number of elements in the partition
is the number of elements in the partition  , and
, and  is the order of the
is the order of the  th-element in the partition
th-element in the partition  (
( ).
).  is the
is the  th-order moment of the symbol sequence
th-order moment of the symbol sequence  :
:

The expression of the moment  can be understood this way: given a particular type of modulation, do the symbol variables
can be understood this way: given a particular type of modulation, do the symbol variables  elevated to the power
elevated to the power  (with optional conjugation specified by the operator
(with optional conjugation specified by the operator  ) gives a constant result? The answer to this question is helpful in assessing if a given signal may exhibit
) gives a constant result? The answer to this question is helpful in assessing if a given signal may exhibit  th-order features and what kind of conjugation must be used in the lag-product (10). The appendix illustrates this result for the binary PAM and the quaternary QAM constellations (see also [10, 15]).
th-order features and what kind of conjugation must be used in the lag-product (10). The appendix illustrates this result for the binary PAM and the quaternary QAM constellations (see also [10, 15]).
Computing the Fourier transform of the TCF and canceling  reveals the RD-CTCF in the form of:
reveals the RD-CTCF in the form of:

where the cycle frequencies are integer multiples of the symbol rate ( with
with  integer). The RD-CTCF of the baseband signal is nonzero only for harmonics of the symbol rate. The amplitude of the features tend to zero as the harmonic number
integer). The RD-CTCF of the baseband signal is nonzero only for harmonics of the symbol rate. The amplitude of the features tend to zero as the harmonic number  increases.
increases.
5.2. RF Signals
The RD-CTCF of the RF signal specified by (2) can be inferred from the RD-CTCF of the baseband signal  by noting that the RF signal is obtained by modulating two independent PAM signals in quadrature. We need to calculate the CTCFs of PAM, sine and cosine signals, and to combine them using the following rules:
by noting that the RF signal is obtained by modulating two independent PAM signals in quadrature. We need to calculate the CTCFs of PAM, sine and cosine signals, and to combine them using the following rules:
-
(i)
The cumulant of the sum is equal to the sum of the cumulants if the signals are independent. Therefore, if
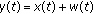 where
where 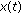 and
and 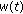 are two independent random signals, we have:
are two independent random signals, we have: (19)
(19)and, after Fourier transform, we obtain:
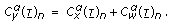 (20)
(20) -
(ii)
The moment of the product is equal to the product of the moments if the signals are independent. Therefore, if
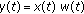 where
where 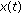 and
and 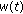 are two independent random signals, we have:
are two independent random signals, we have: (21)
(21)and, after Fourier transform, we obtain:
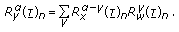 (22)
(22)
Equation (22) means that we have to multiply all CTMFs of  and
and  which sum to
which sum to  . If one of the signals is nonrandom (
. If one of the signals is nonrandom ( in our case), the CTMF of the random signal can be replaced by its CTCF:
in our case), the CTMF of the random signal can be replaced by its CTCF:

The CTCFs of the baseband PAM signals can be computed using (18). The only difference with a QAM signal resides in the cumulant of the symbol sequence  , which must be computed for PAM symbols through (16) and (17) (see the binary PAM case in the appendix).
, which must be computed for PAM symbols through (16) and (17) (see the binary PAM case in the appendix).
The CTMF of the sine and cosine signals can easily be determined from the expression of their lag-products:

where  . The lag-product can be decomposed into a sum of cosine signals at various frequencies using Simpson formulas:
. The lag-product can be decomposed into a sum of cosine signals at various frequencies using Simpson formulas:

for the second order, and:

for the fourth order. It is clear that the CTMF of sine or cosine signals is made of Dirac's deltas at cycle frequencies  ,
,  , and
, and  .
.
Since the real and imaginary parts of  are two statistically independent PAM signals, the CTCF of
are two statistically independent PAM signals, the CTCF of  is the sum of two CTCFs of modulated PAM signals in quadrature. The CTCFs of
is the sum of two CTCFs of modulated PAM signals in quadrature. The CTCFs of  and
and  are equal and denoted by
are equal and denoted by  in our next results. We can finally write:
in our next results. We can finally write:

For  , we observe the destructive interference between the components of
, we observe the destructive interference between the components of  and
and  at twice the carrier frequency, as was introduced in Section 3.
at twice the carrier frequency, as was introduced in Section 3.
For  , we also observe that the components of
, we also observe that the components of  and
and  at twice the carrier frequency cancel out, just as they do for the second order. There only remain the features at zero and four times the carrier frequency:
at twice the carrier frequency cancel out, just as they do for the second order. There only remain the features at zero and four times the carrier frequency:

Since  is a sum of cosines that depend on
is a sum of cosines that depend on  and
and  (the notation
(the notation  indicates an optional sign change according to the expressions (25)-(26)), the features
indicates an optional sign change according to the expressions (25)-(26)), the features  are six times smaller than the features
are six times smaller than the features  (at least when
(at least when  is null) and are therefore less suited for sensing scenarios.
is null) and are therefore less suited for sensing scenarios.
5.3. Baseband and RF Fourth-Order Features
We have to choose between baseband or RF signals and decide on the cycle frequency that will be used by the detector. We have seen that baseband QAM signals have features at the cycle frequencies that are multiples of the symbol rate ( ), whereas RF signals have additional features at cycle frequencies that depend on the carrier frequency (
), whereas RF signals have additional features at cycle frequencies that depend on the carrier frequency ( ,
,  ,
,  ). It has been shown that these additional features are small and that the strongest feature for both baseband and RF signals is obtained when the cycle frequency
). It has been shown that these additional features are small and that the strongest feature for both baseband and RF signals is obtained when the cycle frequency  is equal to zero. Since noise signals do not have any fourth-order feature (the fourth-order cumulant of a Gaussian random variable is equal to zero), even when
is equal to zero. Since noise signals do not have any fourth-order feature (the fourth-order cumulant of a Gaussian random variable is equal to zero), even when  . Note that
. Note that  is a degenerated cycle frequency, which is present even in stationary signals. However, since it gives the strongest 4th-order feature, it is the frequency that will be preferred for our sensing scenario, even if the denomination "cyclic-feature detector" becomes inappropriate in this case.
is a degenerated cycle frequency, which is present even in stationary signals. However, since it gives the strongest 4th-order feature, it is the frequency that will be preferred for our sensing scenario, even if the denomination "cyclic-feature detector" becomes inappropriate in this case.
Simulations made with baseband or RF signals for  have shown that the two detectors exhibit similar performances. From now on, we will focus on the fourth-order feature detection for baseband signals and let aside the fourth-order feature detection for RF signals, as it enables a significant reduction of the received signal sampling frequency. The feature obtained in this situation is illustrated in Figure 3.
have shown that the two detectors exhibit similar performances. From now on, we will focus on the fourth-order feature detection for baseband signals and let aside the fourth-order feature detection for RF signals, as it enables a significant reduction of the received signal sampling frequency. The feature obtained in this situation is illustrated in Figure 3.
Fourth-order RD-CTCF of a 4-QAM baseband signal as a function of the lag parameters  and
and  for the cycle frequency
for the cycle frequency  . The values of
. The values of  and
and  have been fixed to
have been fixed to  and
and  respectively. The system parameters are:
respectively. The system parameters are:  MHz symbol frequency,
MHz symbol frequency,  MHz sample frequency, normalized square-root Nyquist pulse shaping filter of
MHz sample frequency, normalized square-root Nyquist pulse shaping filter of  roll-off factor.
roll-off factor.
6. Fourth-Order Feature Detectors
6.1. RD-CTCF Estimator
In order to estimate the RD-CTCF of the baseband QAM signal, we would have to use (14). Luckily, the signal is complex and the second order features disappear if we do not use any conjugation in the lag product (see the quaternary QAM example in the appendix). Therefore the RD-CTCF is equal to the RD-CTMF:

In practice, the RD-CTCF is estimated based on a size- finite observation window of the received sequence
finite observation window of the received sequence  obtained after sampling the received signal.
obtained after sampling the received signal.

with  and
and  are the elements of the discrete lag-vector
are the elements of the discrete lag-vector  of size
of size  .
.
6.2. Noise Mean and Variance
When there is only noise in the system, the mean of the RD-CTCF is equal to  since the fourth-order cumulant of a Gaussian random variable is null. On the other hand, the variance of the RD-CTCF is a function of the lag-vector given by:
since the fourth-order cumulant of a Gaussian random variable is null. On the other hand, the variance of the RD-CTCF is a function of the lag-vector given by:

in which  is the variance of AWGN noise samples at the input of the RD-CTCF estimator. Simulations illustrated in Figure 4 confirm the result (31). Every discrete lag-vector
is the variance of AWGN noise samples at the input of the RD-CTCF estimator. Simulations illustrated in Figure 4 confirm the result (31). Every discrete lag-vector  for which two or more values
for which two or more values  ,
,  are identical should be avoided, since it increases the noise variance. However, to afford the luxury of choosing lag values that are different from zero, we would have to increase the sampling rate at the receiver, which in turn would increase the noise power. Simulations have shown that it is better to use the lowest sampling rate that still satisfies Shannon's theorem, and set all lag values equal to zero. The RD-CTCF variance also quite naturally decreases as the observation window
are identical should be avoided, since it increases the noise variance. However, to afford the luxury of choosing lag values that are different from zero, we would have to increase the sampling rate at the receiver, which in turn would increase the noise power. Simulations have shown that it is better to use the lowest sampling rate that still satisfies Shannon's theorem, and set all lag values equal to zero. The RD-CTCF variance also quite naturally decreases as the observation window  is increased.
is increased.
6.3. Detector
The detector has to decide between two hypotheses: hypothesis  implying that no signal is present, hypothesis
implying that no signal is present, hypothesis  implying that the linearly modulated signal is present. The absolute value of the feature (here the RD-CTCF) is compared to a threshold
implying that the linearly modulated signal is present. The absolute value of the feature (here the RD-CTCF) is compared to a threshold  to make a decision:
to make a decision:

The threshold is usually fixed to meet a target probability of false alarm (decide  if
if  ). In order to compute the threshold level as a function of the probability of false alarm, we must know the distribution of the RD-CTCF. We already know its mean and variance values and using the central-limit theorem, we assume that the output distribution is Gaussian (see also [16]). As a consequence, the absolute value of the RD-CTCF takes the form of a Rayleigh distribution and the threshold level can be found using:
). In order to compute the threshold level as a function of the probability of false alarm, we must know the distribution of the RD-CTCF. We already know its mean and variance values and using the central-limit theorem, we assume that the output distribution is Gaussian (see also [16]). As a consequence, the absolute value of the RD-CTCF takes the form of a Rayleigh distribution and the threshold level can be found using:

where  is the probability of false alarm.
is the probability of false alarm.
7. Detector Comparison
We will now briefly review the principles of all detectors previously mentioned in this paper, and compare their performance and computational complexity. We assume that second-order and fourth-order detectors work only at a single location of the feature they exploit (the second-order detector works at most favorable frequency, the fourth-order detector works at the most favorable value of the discrete lag-vector  ). Monte-Carlo simulations were used, each of which used 5000 iterations.
). Monte-Carlo simulations were used, each of which used 5000 iterations.
7.1. Energy Detector
This is the most widely used detector in wireless communication systems. It averages the square modulus of the received sequence over time:

Its advantages are its simplicity and its ability to perform blind detection (since it does not require any information about the signal it is trying to detect). Unfortunately, it has been demonstrated that it cannot be used in low-SNR environments due to its sensitivity to noise uncertainty [6].
7.2. Second-Order Detector
This detector computes an estimation of the SCD by averaging, over time and frequency domains, the cyclic periodogram of the signal spectrum  computed for a finite time window at time
computed for a finite time window at time  :
:

where  is the number of time windows and
is the number of time windows and  is the number of frequency bins. It is a much more complex and less efficient detector, which requires some characteristics of the signal in order to work (e.g., the symbol rate must be known in advance). Its advantage resides in the absence of features (at least asymptotically) when the input signal is a white noise, which results in the output mean of the detector always being equal to zero in presence of noise, therefore shielding the detector from noise uncertainty effects. Its computational complexity evolves as
is the number of frequency bins. It is a much more complex and less efficient detector, which requires some characteristics of the signal in order to work (e.g., the symbol rate must be known in advance). Its advantage resides in the absence of features (at least asymptotically) when the input signal is a white noise, which results in the output mean of the detector always being equal to zero in presence of noise, therefore shielding the detector from noise uncertainty effects. Its computational complexity evolves as  if the FFTs used to evaluate the cyclic periodogram [6] have a length of 1024 samples, and the total number of samples is equal to
if the FFTs used to evaluate the cyclic periodogram [6] have a length of 1024 samples, and the total number of samples is equal to  .
.
7.3. Fourth-Order Detector
This detector averages the lag-product of the received sequence over time:

This detector is simpler to implement than the previous one (no Fourier transform of the signal is required since we work in the time domain), which results in a computational complexity evolving as  , the total number of samples. It benefits from the same immunity to noise uncertainty, and is therefore suited for operations at low SNR.
, the total number of samples. It benefits from the same immunity to noise uncertainty, and is therefore suited for operations at low SNR.
7.4. Performance Comparison
We may now take a look at the performance of the different detectors. Figure 5 illustrates the probability of missed detection (decide  if
if  ) curves as a function of the SNR for the three detectors under consideration. The threshold has been set in the three cases to achieve a target probability of false alarm equal to
) curves as a function of the SNR for the three detectors under consideration. The threshold has been set in the three cases to achieve a target probability of false alarm equal to  . These curves have been obtained without adding any noise uncertainty to the signal. In such conditions, the energy detector is the optimal detector for blind detection, and can be considered as a reference. It appears that the second-order detector and the fourth-order detector, have similar performances when the SNR is around zero dB: for the same complexity, (that leads to an observation time ten times longer for the fourth-order detector), both detectors exhibit the same probability of missed detection (roughly 1 percent) at an SNR of −0.8 dB. However, when we consider an SNR of −4 dB, the fourth-order detector requires much more samples, which makes it more complex than the second-order. Besides, the detection-time constraints that are part of the cognitive radios reglementation would not be met if the observation time is too long.
. These curves have been obtained without adding any noise uncertainty to the signal. In such conditions, the energy detector is the optimal detector for blind detection, and can be considered as a reference. It appears that the second-order detector and the fourth-order detector, have similar performances when the SNR is around zero dB: for the same complexity, (that leads to an observation time ten times longer for the fourth-order detector), both detectors exhibit the same probability of missed detection (roughly 1 percent) at an SNR of −0.8 dB. However, when we consider an SNR of −4 dB, the fourth-order detector requires much more samples, which makes it more complex than the second-order. Besides, the detection-time constraints that are part of the cognitive radios reglementation would not be met if the observation time is too long.
Energy, second-order and fourth-order detector probability of missed detection (the solid lines) for a fixed probability of false alarm (the points at  ). The system parameters are: baseband QPSK signal with
). The system parameters are: baseband QPSK signal with  MHz symbol frequency,
MHz symbol frequency,  MHz sample frequency, square-root Nyquist pulse shaping filter of
MHz sample frequency, square-root Nyquist pulse shaping filter of  roll-off factor. No noise uncertainty added. The second-order detector is set to detect the symbol-rate feature (cf = 20 MHz), and the fourth-order detector works with the feature at four-times the carrier frequency, which is equal to zero in the present situation (cf = 0 MHz).Two observation times are considered for the three detectors: 50 and 500
roll-off factor. No noise uncertainty added. The second-order detector is set to detect the symbol-rate feature (cf = 20 MHz), and the fourth-order detector works with the feature at four-times the carrier frequency, which is equal to zero in the present situation (cf = 0 MHz).Two observation times are considered for the three detectors: 50 and 500  s. An observation time of 10 ms has been added for the fourth-order detector
s. An observation time of 10 ms has been added for the fourth-order detector
If we add some amount of noise uncertainty, the energy detector cannot perform reliable detections and must be discarded, whereas the cyclic feature detectors remain unaffected. In order to verify this assumption, we computed the receiver operating characteristics (ROC) curves of the fourth-order detector for two situations, one without any noise uncertainty, and one with  dB of noise uncertainty. The results are illustrated in Figure 6. We observe that the energy detector, which had the best ROC curve in the first case is a lot more affected by the noise uncertainty than the fourth-order detector. ROC curves for the second-order detector can be found in [7], and show the same immunity to noise uncertainty than the fourth-order.
dB of noise uncertainty. The results are illustrated in Figure 6. We observe that the energy detector, which had the best ROC curve in the first case is a lot more affected by the noise uncertainty than the fourth-order detector. ROC curves for the second-order detector can be found in [7], and show the same immunity to noise uncertainty than the fourth-order.
8. Conclusion
This paper has started from the need for robust detectors able to work in low SNR environments. A brief review of the second-order cyclostationarity and second-order cyclic feature detectors has exposed the advantages and drawbacks of such detectors, and explained the intuition that lead to the study of higher-order cyclostationarity (HOCS). The main guideline is to identify features of sufficient strength and to design a detector able to extract it from the signal. The most relevant aspects of HOCS theory have then been analyzed and we have derived a new fourth-order detector that can be used for the detection of linearly modulated signals. Simulation results have shown that fourth-order cyclic feature detectors may be used as a substitute for second-order detectors at SNR around zero dB, which could be needed if the received signals do not exhibit second-order cyclostationarity.
Appendices
A. Cumulants of the Binary PAM
This section computes the second- and fourth-order cumulants of a binary PAM sequence. The symbols take the values  .
.
A.1. Second-Order Cumulant
There are  possible partitions of the set
possible partitions of the set  :
:  and
and  . Since the binary PAM constellation is symmetric, only the first partition has a chance to give a product of moments different from
. Since the binary PAM constellation is symmetric, only the first partition has a chance to give a product of moments different from  . We will limit our investigations to the first partition.
. We will limit our investigations to the first partition.
The partition  gives
gives  for its single element, so that
for its single element, so that  .
.
A.2. Fourth-Order Cumulant
There are  possible partitions of the set
possible partitions of the set  , but only the ones that group
, but only the ones that group  by two or four have a chance to give a product of moments different from
by two or four have a chance to give a product of moments different from  , which reduces the number of interesting partitions to four:
, which reduces the number of interesting partitions to four:  ;
;  ;
;  and
and  .
.
The first partition  gives
gives  for its single element, and the three last partitions
for its single element, and the three last partitions  ;
;  and
and  give
give  for their two elements, so that
for their two elements, so that  .
.
B. Cumulants of the Quaternary QAM
This section computes the second- and fourth-order cumulants of a 4-QAM sequence. The symbols take the values  .
.
B.1. Second-Order Cumulants
There are  possible partitions of the set
possible partitions of the set  :
:  and
and  . Since the 4-QAM constellation is symmetric, only the first partition has a chance to give a product of moments different from
. Since the 4-QAM constellation is symmetric, only the first partition has a chance to give a product of moments different from  . We limit therefore our investigations to the first partition.
. We limit therefore our investigations to the first partition.
Different results are obtained according to the number of conjugations in the lag-product (10):
(i)When no conjugation or two conjugations are used in the lag-product, the partition  gives
gives  for its single element, so that
for its single element, so that  .
.
(ii)When one conjugation is used in the lag-product, the partition  gives
gives  for its single element, so that
for its single element, so that  .
.
B.2. Fourth-Order Cumulant
There are  possible partitions of the set
possible partitions of the set  , but only the ones that group
, but only the ones that group  by two or four have a chance to give a product of moments different from
by two or four have a chance to give a product of moments different from  , which reduces the number of interesting partitions to four:
, which reduces the number of interesting partitions to four:  ;
;  ;
;  and
and  .
.
Different results are obtained according to the number of conjugations in the lag-product (10):
-
(i)
When no conjugation or four conjugations are used in the lag-product, the first partition
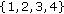 gives
gives 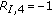 for its single element, and the three last partitions
for its single element, and the three last partitions  ;
;  and
and 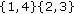 give
give 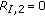 for their two elements, so that
for their two elements, so that 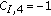 .
. -
(ii)
When two conjugations are used in the lag-product, arbitrary placed for this example on the second and fourth element of the lag-product, the partition
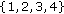 gives
gives  for its single element, the two partitions
for its single element, the two partitions 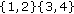 and
and  give
give 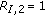 for their two elements, and the partition
for their two elements, and the partition  gives
gives 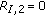 for its two elements, so that
for its two elements, so that 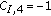 .
. -
(iii)
When one or three conjugations are used in the lag-product, the partition
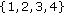 gives
gives 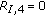 for its single element, and the three last partitions
for its single element, and the three last partitions 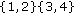 ;
; 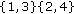 and
and 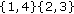 give
give  for at least one of their two elements, so that
for at least one of their two elements, so that  .
.
References
Commission FC: FCC-03-322: Facilitating Opportunities for Flexible, Efficient, and Reliable Spectrum Use Employing Cognitive Radio Technologies. December 2003.
Akyildiz IF, Lee W-Y, Vuran MC, Mohanty S: NeXt generation/dynamic spectrum access/cognitive radio wireless networks: a survey. Computer Networks 2006, 50(13):2127-2159. 10.1016/j.comnet.2006.05.001
Sahai A, Cabric D: Spectrum sensing: fundamental limits and practical challenges. Proceedings of IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '05), November 2005, Baltimore, Md, USA
Urkowitz H: Energy detection of unknown deterministic signals. Proceedings of the IEEE 1967, 55(4):523-531.
Tandra R: Fundamental limits on detection in low SNR, M.S. thesis. , Berkeley, Calif, USA; 2005.
Gardner WA: Signal interception: a unifying theoretical framework for feature detection. IEEE Transactions on Communications 1988, 36(8):897-906. 10.1109/26.3769
Gardner WA, Spooner CM: Signal interception: performance advantages of cyclic-feature detectors. IEEE Transactions on Communications 1992, 40(1):149-159. 10.1109/26.126716
Gardner WA: Statistical Spectral Analysis: A Nonprobabilistic Theory. Prentice-Hall, Englewood Cliffs, NJ, USA; 1987.
Gardner WA, Spooner CM: Cumulant theory of cyclostationary time-series, part I: foundation. IEEE Transactions on Signal Processing 1994, 42(12):3387-3408. 10.1109/78.340775
Spooner CM, Gardner WA: Cumulant theory of cyclostationary time series, part II: development and applications. IEEE Transactions on Signal Processing 1994, 42(12):3409-3429. 10.1109/78.340776
Kim K, Akbar IA, Bae KK, Um J-S, Spooner CM, Reed JH: Cyclostationary approaches to signal detection and classification in cognitive radio. Proceedings of the 2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '07), April 2007, Dublin, Ireland 212-215.
Sutton PD, Nolan KE, Doyle LE: Cyclostationary signatures in practical cognitive radio applications. IEEE Journal on Selected Areas in Communications 2008, 26(1):13-24.
Tkachenko A, Cabric D, Brodersen RW: Cyclostationary feature detector experiments using reconfigurable BEE2. Proceedings of the 2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '07), April 2007, Dublin, Ireland 216-219.
Turunen V, Kosunen M, Huttunen A, Kallioinen S, Ikonen P, Pärssinen A, Ryynänen J: Implementation of cyclostationary feature detector for cognitive radios. Proceedings of the 4th International Conference on Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM '09), June 2009, Hannover, Germany
Dobre OA, Bar-Ness Y, Su W: Higher-order cyclic cumulants for high order modulation classification. Proceedings of IEEE Military Communications Conference (MILCOM '03), October 2003 112-117.
Dandawate AV, Giannakis GB: Statistical tests for presence of cyclostationarity. IEEE Transactions on Signal Processing 1994, 42(9):2355-2369. 10.1109/78.317857
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Renard, J., Verlant-Chenet, J., Dricot, JM. et al. Higher-Order Cyclostationarity Detection for Spectrum Sensing. J Wireless Com Network 2010, 721695 (2010). https://doi.org/10.1155/2010/721695
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/721695
 does not totally cut off the frequency components larger than half the inverse of the symbol rate, some frequencies will be correlated, as shown in Figure
does not totally cut off the frequency components larger than half the inverse of the symbol rate, some frequencies will be correlated, as shown in Figure 

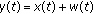 where
where 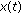 and
and 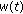 are two independent random signals, we have:
are two independent random signals, we have:
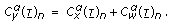
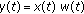 where
where 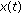 and
and 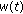 are two independent random signals, we have:
are two independent random signals, we have:
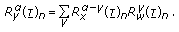


 and
and  for the cycle frequency
for the cycle frequency  . The values of
. The values of  and
and  have been fixed to
have been fixed to  and
and  , respectively. The system parameters are:
, respectively. The system parameters are:  MHz symbol frequency,
MHz symbol frequency,  MHz sample frequency,
MHz sample frequency,  . The number of noise realizations is
. The number of noise realizations is  .
.

 dB uncertainty). The system parameters are:
dB uncertainty). The system parameters are:  MHz symbol frequency,
MHz symbol frequency,  MHz sample frequency, square-root Nyquist pulse shaping filter of
MHz sample frequency, square-root Nyquist pulse shaping filter of  roll-off factor, SNR =
roll-off factor, SNR =  dB.
dB. gives
gives 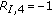 for its single element, and the three last partitions
for its single element, and the three last partitions  ;
;  and
and 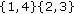 give
give 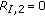 for their two elements, so that
for their two elements, so that 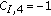 .
.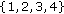 gives
gives  for its single element, the two partitions
for its single element, the two partitions 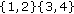 and
and  give
give 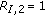 for their two elements, and the partition
for their two elements, and the partition  gives
gives 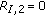 for its two elements, so that
for its two elements, so that 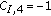 .
.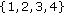 gives
gives 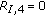 for its single element, and the three last partitions
for its single element, and the three last partitions 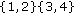 ;
; 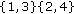 and
and 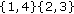 give
give  for at least one of their two elements, so that
for at least one of their two elements, so that  .
.