- Research Article
- Open access
- Published:
Partial Interference and Its Performance Impact on Wireless Multiple Access Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 735083 (2010)
Abstracts
To determine the capacity of wireless multiple access networks, the interference among the wireless links must be accurately modeled. In this paper, we formalize the notion of the partial interference phenomenon observed in many recent wireless measurement studies and establish analytical models with tractable solutions for various types of wireless multiple access networks. In particular, we characterize the stability region of IEEE 802.11 networks under partial interference with two potentially unsaturated links numerically. We also provide a closed-form solution for the stability region of slotted ALOHA networks under partial interference with two potentially unsaturated links and obtain a partial characterization of the boundary of the stability region for the general M-link case. Finally, we derive a closed-form approximated solution for the stability region for general M-link slotted ALOHA system under partial interference effects. Based on our results, we demonstrate that it is important to model the partial interference effects while analyzing wireless multiple access networks. This is because such considerations can result in not only significant quantitative differences in the predicted system capacity but also fundamental qualitative changes in the shape of the stability region of the systems.
1. Introduction
In a wireless network, all stations communicate with each other through wireless links. A fundamental difference between a wireless network and its wired counterpart is that wireless links may interfere with each other, resulting in performance degradation. Therefore in the study of wireless networks, one important performance measure is the capacity of the network when the effects of interlink interference are considered.
In establishing the capacity of a wireless network, we have to predict whether the wireless links interfere with each other. Two most common interference models in the wireless networking literature, namely, for example, protocol model and physical model [1], were proposed to predict whether transmissions in a wireless network are successful. In these interference models, one key assumption is that interference is a binary phenomenon, that is, either the links mutually interfere with each other to result in total loss of throughput of a target link, or there is no link throughput degradation at all. In other words, these models exclude the possibility that interfering links can be active simultaneously and still realize their capacity partially. However, recent empirical studies [2–6] have shown that these binary interference models are not valid in practice. Instead, measurement results have confirmed that there is a nonbinary transitional region [2, 4] (also known as the gray zone in some literature [3]) for the successful packet reception rate (PRR) of a wireless link which changes from zero, that is, 100% lossy, to almost 100%, that is, perfectly reliable, as its signal-to-interference-plus-noise ratio (SINR) increases. These studies have indicated that the range of the transitional regional (in SINR) can exceed 10dB for various types of practical networks including IEEE 802.11a wireless mesh [3, 7] and other low-power multihop sensor networks [2, 4]. More importantly, measurement studies on large-scale wireless mesh testbeds [8, 9] found that a significant number of links in those testbeds were indeed operating at the SINR transitional region, that is, with intermediate level of PRR between zero and 100%. In this paper, we call this phenomenon partial interference. From the physical layer implementation perspective, the partial interference phenomenon can be viewed as a consequence/manifestation of the probabilistic nature of signal decoding in the receiver, its interaction with the well-known capture effect [10, 11], and the specific implementation of the frame reception and capture algorithms in individual chipsets [12].
While the phenomenon of partial interference in wireless networks has been widely observed as mentioned above, its incorporation in the performance modeling of such networks is still in its infancy. Most of the efforts in this direction so far ([2, 7, 12, 13]) have been limited to the characterization of the nonbinary transitional region in the PRR-versus-SINR curve based on measurement data [7, 12, 13] or some analytical means [2, 14]. However, once the PRR-versus-SINR curve is obtained, they only resort to simulations to evaluate the effects of partial interference on the system performance.
While the phenomenon of partial interference in wireless networks has been widely observed as mentioned above, its incorporation in the performance modeling of such networks is still in its infancy. Most of the efforts in this direction so far ([2, 7, 12, 13]) have been limited to the characterization of the nonbinary transitional region in the PRR-versus-SINR curve based on measurement data [7, 12, 13] or some analytical means [2, 14]. However, once the PRR-versus-SINR curve is obtained, they only resort to simulations to evaluate the effects of partial interference on the system performance.
In this paper, our focus is to develop analytical models with tractable solutions for various types of wireless multiple access networks which can accurately capture the performance impact of partial interference. Via analytical and numerical results throughout this paper, we demonstrate that it is important to model the partial interference effects while analyzing wireless multiple access networks. This is because such considerations can result in not only significant quantitative differences in the predicted system capacity but also fundamental qualitative changes in the shape of the stability region of the systems (e.g., from a concave to a convex region).
To quantify the impact of interference on multiple access networks, we propose an analytical framework to characterize partial interference for two representative types of multiple access wireless networks, namely, the IEEE 802.11 Wireless LANs and the classical slotted ALOHA networks. For IEEE 802.11 Wireless LANs, we extend the single-channel Markov model in [15] to take into account the unsaturated traffic conditions, the SINR attained at the receivers, and the modulation scheme employed. These modifications result in a partial interference region, which cannot be captured by the binary interference models used in previous works. We also find out the stability (admissible) region of IEEE 802.11 networks with two interfering, potentially unsaturated links numerically. For slotted ALOHA networks, we extend the model in [16] to derive the exact stability region of slotted ALOHA with two links while considering partial interference. We show that as the link separation increases, the stability region obtained expands gradually under partial interference, as in the case of 802.11.
Despite the simplicity of slotted ALOHA, characterizing its exact stability region with unsaturated links is extremely difficult and has remained to be a key open problem for decades when there are more than two, potentially unsaturated links in the system [16–23]. However, by extending the FRASA (Feedback Retransmission Approximation for Slotted ALOHA) approach [24] to model the partial interference effects, we obtain a closed-form approximation for the exact stability region for any number of links.
In summary, this paper has made the following contributions.
-
(1)
After reviewing related work in Section 2, we formalize the notion of partial interference in Section 3 and then demonstrate its significant performance impact on different types of wireless networks via various examples and their analytical/numerical results throughout the rest of the paper. As an illustration, we show in Section 4 that, by considering partial interference effects while scheduling traffic in a wireless network of regular topology, the gain in network capacity across unit cut can be as high as 67%.
-
(2)
In Section 5, we establish a model to analyze the effects of partial interference on the throughput of IEEE 802.11 networks with unsaturated links. Our approach enables one to compute numerically the stability region of any 2-link 802.11 system under unsaturated traffic conditions.
-
(3)
In Section 6, we investigate the effects of partial interference on the capacity of a slotted ALOHA system with unsaturated links by (i) establishing the exact stability region in closed-form for the 2-link case and (ii) providing a closed-form, partial characterization of the stability region of the general M-link case.
-
(4)
In Section 7, we extend the FRASA approach in [24] to yield a closed-form approximation for the stability region of the general M-link slotted ALOHA system while considering partial interference effects. The capacity region derived by our approximation and the corresponding simulation results are provided for some sample cases. Again, this is to demonstrate the potential qualitative and quantitative differences in the system capacity region when the effect of partial interference is taken into account. We then conclude the paper in Section 8.
2. Related Work
In [1], two interference models, called the protocol model and the physical model, were introduced. The protocol model states that a transmission is successful if the corresponding receiver is located inside the transmission range of the transmitter, and all other active transmitters are located outside the interference range of the receiver. In the physical model, the transmissions from other transmitters are considered as noise, and a transmission is successful if the SINR attained at the receiver exceeds a certain threshold. Based on these models, the capacities of a multihop wireless network under random and optimal node placement were derived.
In [5], the authors measured the interference among links in a single-channel, static 802.11 multihop wireless network. They measured the interference between pairs of links by the link interference ratio and observed that this ratio exhibited a continuum between 0 and 1. In [6], two interfering links were set up in a wireless network with multiple partially overlapped channels to measure TCP and UDP throughputs of an individual link. It was found that the throughputs increased smoothly when the separation between the links increased. The throughputs increased more rapidly as the channel separation between the links increased. Such nonbinary transitional region in the link throughput (or PRR equivalently) as the receiver SINR varies has also been observed by numerous measurement studies including [2–4]. These experimental results all confirmed that the binary assumption in the protocol or physical interference models are not valid in practice.
There has been some analytical work on finding the relationship between the SINR attained at a receiver and the throughput (or PRR equivalently) achieved by the corresponding wireless link. In [14], a methodology for estimating the packet error rate in the affected wireless network due to the interference from the interfering wireless network was presented. The throughput of the affected wireless network was found to increase continuously with the SINR attained at the corresponding receiver, which increased with the separation between the networks. Similarly, [2] derived expressions for the PRR as a function of distance, radio channel parameters, and the modulation/encoding scheme used by the radio. However, they did not provide analytical model on how the PRR function would impact the performance of the corresponding networks.
In [25], the throughput achieved by an M-link IEEE 802.11 network under physical layer capture was derived. While their analysis can be viewed as another case study of the effects of the partial interference over 802.11 networks, their approach only works for the case where all of the links are always saturated, that is, with infinite backlog at the transmitter side. In contrast, the approach proposed in Section 5 of this paper can handle unsaturated links and has provided explicit numerical solutions for the stability region of the 2-link case.
The study of the stability region of  -user infinite-buffer slotted ALOHA was initiated by the study in [17] decades before and is still an ongoing research. The authors in [17] obtained the exact stability region when
-user infinite-buffer slotted ALOHA was initiated by the study in [17] decades before and is still an ongoing research. The authors in [17] obtained the exact stability region when  under the collision channel (i.e., binary interference) model. References [18, 19] used stochastic dominance and derived the same result as in [17] for the case of
under the collision channel (i.e., binary interference) model. References [18, 19] used stochastic dominance and derived the same result as in [17] for the case of  .
.
For general  , there were attempts to find the exact stability region, but there was only limited success. Reference [21] established the boundary of the stability region, but it involves stationary joint queue statistics, which still do not have closed form to date. Instead, many researchers focused on finding bounds on the stability region for general
, there were attempts to find the exact stability region, but there was only limited success. Reference [21] established the boundary of the stability region, but it involves stationary joint queue statistics, which still do not have closed form to date. Instead, many researchers focused on finding bounds on the stability region for general  . Reference [17] obtained separate sufficient and necessary conditions for stability. References [18, 19] derived tighter bounds on the stability region by using stochastic dominance in different ways. Reference [22] introduced instability rank and used it to improve the bounds on the stability region. However, the bounds in [18, 22] are not always applicable. Also, the bounds obtained may not be piecewise linear.
. Reference [17] obtained separate sufficient and necessary conditions for stability. References [18, 19] derived tighter bounds on the stability region by using stochastic dominance in different ways. Reference [22] introduced instability rank and used it to improve the bounds on the stability region. However, the bounds in [18, 22] are not always applicable. Also, the bounds obtained may not be piecewise linear.
With the advances in multiuser detection, researchers also studied this problem with the multipacket reception (MPR) model. Reference [23] studied this problem in the infinite-user, single-buffer, and symmetric MPR case. Reference [16] considered the problem with finite users and infinite buffer. They obtained the boundary for the asymmetric MPR case with two users, and also the inner bound on the stability region for general  .
.
3. Partial Interference—Basic Idea
As an illustration to the methodology in [14], assume the underlying modulation scheme used is binary phase shift keying (BPSK). The distance between the transmitter and the receiver and that between the interferer and the receiver are  and
and  meters, respectively. The transmission power of the transmitter and the interferer are
meters, respectively. The transmission power of the transmitter and the interferer are  and
and  watts, respectively.
watts, respectively.
Assuming that the interfering signal can be modeled as additive white Gaussian noise (AWGN) and the background noise can be ignored, we use the two-ray ground reflection model

to represent the path loss, where  and
and  are the gain of transmitter and receiver antenna, respectively,
are the gain of transmitter and receiver antenna, respectively,  and
and  are the height of transmitter and receiver antenna, respectively, and
are the height of transmitter and receiver antenna, respectively, and  . The path loss exponent is 4 in this model. We let
. The path loss exponent is 4 in this model. We let  and
and  . Then, according to [26], the bit error rate (BER) is given by
. Then, according to [26], the bit error rate (BER) is given by

where  is the SINR attained at the receiver and is given by
is the SINR attained at the receiver and is given by

Define the packet-level normalized throughput  to be the ratio of the successful packet reception rate at the receiver when
to be the ratio of the successful packet reception rate at the receiver when  to the maximum packet reception rate of the link when
to the maximum packet reception rate of the link when  . As such,
. As such,  is actually the probability of a packet to be received without error when the SINR is
is actually the probability of a packet to be received without error when the SINR is  . Suppose that all packets consist of
. Suppose that all packets consist of  bits and bit errors are identically, independently distributed within each packet. We have
bits and bit errors are identically, independently distributed within each packet. We have

In general,  depends on the BER, which, in turn, is a function of the SINR at the receiver as well as the specific modulation scheme being used. While we use BPSK as an example here, the actual expression for
depends on the BER, which, in turn, is a function of the SINR at the receiver as well as the specific modulation scheme being used. While we use BPSK as an example here, the actual expression for  under other modulation schemes can be readily derived as shown in [2, Table
under other modulation schemes can be readily derived as shown in [2, Table  ].
].
Figure 1 shows a plot of such packet-level normalized throughput  against distance between the interferer and the receiver for
against distance between the interferer and the receiver for  dBm,
dBm,  meters,
meters,  ranging from 400 to 700 meters, and
ranging from 400 to 700 meters, and  bits (= 1500 bytes). Observe from the figure the nonbinary transitional region of
bits (= 1500 bytes). Observe from the figure the nonbinary transitional region of  as the separation between the interferer and the receiver increases. Such "partial interference" region is also consistent with the findings of many empirical studies discussed in Section 1.
as the separation between the interferer and the receiver increases. Such "partial interference" region is also consistent with the findings of many empirical studies discussed in Section 1.
In Figure 1, we also plot the variation of throughput against distance between the interferer and the receiver if the physical model is used. The SINR threshold  for the binary-interference model is set by assuming that when
for the binary-interference model is set by assuming that when  , the packet error rate is
, the packet error rate is  , that is,
, that is,

We observe that if the value we assign to  is too large (or the threshold distance is too large), we underestimate the throughput that the links can achieve. On the other hand, if
is too large (or the threshold distance is too large), we underestimate the throughput that the links can achieve. On the other hand, if  is too small (or the threshold distance is too small), we introduce excessive interference into the network. In other words, it is difficult to use a single threshold to describe accurately the relationship between interference and throughput of each link in a network.
is too small (or the threshold distance is too small), we introduce excessive interference into the network. In other words, it is difficult to use a single threshold to describe accurately the relationship between interference and throughput of each link in a network.
4. Capacity Gain When Partial Interference Is Considered
In this section, we demonstrate that there is a gain in system capacity when the effect of partial interference is considered. We consider one variation of the Manhattan network [27], that is, a network consisting of a rectangular grid extending to infinity in both dimensions. The horizontal and vertical separations between neighboring stations are denoted by  and
and  , respectively.
, respectively.
Under infinite transmitter backlog, the packet-level capacity of each link, that is, the maximum packet reception rate without interference, is denoted by  . We assume that differential binary phase shift keying (DBPSK) is employed and a packet consists of
. We assume that differential binary phase shift keying (DBPSK) is employed and a packet consists of  bits. We use the two-ray ground reflection model (1) as in previous section to model the path loss. To apply the physical model, we let the SINR threshold
bits. We use the two-ray ground reflection model (1) as in previous section to model the path loss. To apply the physical model, we let the SINR threshold  be the case that the packet error rate is
be the case that the packet error rate is  , that is,
, that is,  , where
, where  is the bit error rate of DBPSK [26]. We let
is the bit error rate of DBPSK [26]. We let  and
and  , therefore the SINR requirement is
, therefore the SINR requirement is  . Assuming that there is no interferer, this SINR requirement is met when the length of a link is smaller than 493 meters.
. Assuming that there is no interferer, this SINR requirement is met when the length of a link is smaller than 493 meters.
We use a Cartesian coordinate plane to represent the modified Manhattan network. One station is placed at every point with integral coordinates in the network. Suppose that we schedule flows in the modified Manhattan network from the South to the North using the pattern shown in Figure 2 and its shifted versions. In Figure 2, an arrow is used to represent an active link, where the tail and the head of an arrow denote the transmitter and the receiver of the link, respectively.
We use the capacity across unit cut as the performance metric, where
as the performance metric, where  is the ratio of the horizontal separation to the vertical separation. It is a measure on how much traffic we can send through a cut in a network on average while physically packing the links towards each other. Consider the SINR attained at the receiver marked with the blue circle, which has the position assigned as the origin in the Cartesian coordinate plane. We assume that all stations transmit with power
is the ratio of the horizontal separation to the vertical separation. It is a measure on how much traffic we can send through a cut in a network on average while physically packing the links towards each other. Consider the SINR attained at the receiver marked with the blue circle, which has the position assigned as the origin in the Cartesian coordinate plane. We assume that all stations transmit with power  , and each station has a background noise power of
, and each station has a background noise power of  . The SINR is defined by
. The SINR is defined by  , where
, where  is the received power from the intended transmitter and
is the received power from the intended transmitter and  is the power received from all interferers. The packet-level capacity achieved by each link, that is, the successful packet reception rate at the receiver, is
is the power received from all interferers. The packet-level capacity achieved by each link, that is, the successful packet reception rate at the receiver, is  under our partial interference model. On the other hand, under the physical interference model,
under our partial interference model. On the other hand, under the physical interference model,  if
if  and
and  otherwise. A cut
otherwise. A cut in the network is an infinitely long horizontal line. Let
in the network is an infinitely long horizontal line. Let  be the set of all active transmitters such that
be the set of all active transmitters such that  intersects the link used by
intersects the link used by  . We divide
. We divide  into segments
into segments  ,
,  , where
, where

and  is the Euclidean norm. Then the length
is the Euclidean norm. Then the length  of the cut occupied by an active transmitter is the length of
of the cut occupied by an active transmitter is the length of  , and the capacity across unit cut is therefore
, and the capacity across unit cut is therefore  , where
, where  is the fraction of time that a link is active.
is the fraction of time that a link is active.
In the following we assume that  meters,
meters,  dBm, and
dBm, and  dBm. For the schedule in Figure 2, the signal power is
dBm. For the schedule in Figure 2, the signal power is  . All transmitters in Figure 2 are located at positions
. All transmitters in Figure 2 are located at positions  , where
, where  and
and  are integers. The interference power is
are integers. The interference power is

Considering the physical model, if the schedule is allowed to be active, we need  , as listed in Table 1 and depicted in Figure 3 by the blue dashed line. The value of
, as listed in Table 1 and depicted in Figure 3 by the blue dashed line. The value of  is obtained from
is obtained from  . Each active transmitter occupies a cut of length
. Each active transmitter occupies a cut of length  , and each link is active for one quarter of a cycle. Therefore, for
, and each link is active for one quarter of a cycle. Therefore, for  , the maximum capacity across unit cut under the physical model is
, the maximum capacity across unit cut under the physical model is  bits per second per kilometer.
bits per second per kilometer.
If we allow partial interference, the active transmitters can be packed more closely. When  decreases, more spatial reuse is allowed. The increase in the density of active transmitters outweighs the degradation in capacity, so there is an increase in the capacity across unit cut. However, if
decreases, more spatial reuse is allowed. The increase in the density of active transmitters outweighs the degradation in capacity, so there is an increase in the capacity across unit cut. However, if  decreases further, interference will be the dominant factor in determining the capacity across unit cut. Therefore, the capacity across unit cut drops, and there exists
decreases further, interference will be the dominant factor in determining the capacity across unit cut. Therefore, the capacity across unit cut drops, and there exists  for the optimal performance under partial interference. This behavior is depicted by the blue solid line in Figure 3. The optimal value of
for the optimal performance under partial interference. This behavior is depicted by the blue solid line in Figure 3. The optimal value of  under partial interference is
under partial interference is  , and the capacity across unit cut is
, and the capacity across unit cut is  bits per second per kilometer. There is a percentage increase of 66.82% in the capacity across unit cut when the effect of partial interference is considered. Similar results are shown in Table 1 and Figure 3 for
bits per second per kilometer. There is a percentage increase of 66.82% in the capacity across unit cut when the effect of partial interference is considered. Similar results are shown in Table 1 and Figure 3 for  meters. The percentage increase is larger when the links are longer, but the capacity achieved by each link reduces. We can view
meters. The percentage increase is larger when the links are longer, but the capacity achieved by each link reduces. We can view  as the carrier sensing range in the modified Manhattan network with the scheduling pattern in Figure 2, as it is the smallest horizontal separation allowed by the physical model. We observe that if the length of the links increases, the carrier sensing range needs to be increased in a larger proportion. Also, this carrier sensing range is much larger than double of the length of the links, which is the usual convention used in defining the relationship between carrier sensing range and transmission range.
as the carrier sensing range in the modified Manhattan network with the scheduling pattern in Figure 2, as it is the smallest horizontal separation allowed by the physical model. We observe that if the length of the links increases, the carrier sensing range needs to be increased in a larger proportion. Also, this carrier sensing range is much larger than double of the length of the links, which is the usual convention used in defining the relationship between carrier sensing range and transmission range.
5. Partial Interference in 802.11
In this section, we study partial interference in 802.11 networks, the prevalent wireless random access networks. We present an analytical framework to characterize partial interference in a single-channel wireless network under unsaturated traffic conditions, which uses 802.11b with basic access scheme and DBPSK. We show that there is a partial interference region, in which the throughput of each link increases continuously with the separation between the links in the network. As a first attempt to relate the capacity-finding problem in wireless random access networks to the stability region of such networks, we derive the admissible (stability) region of an 802.11 network with two potentially unsaturated links numerically.
5.1. The 802.11 Model
We present our framework to characterize partial interference in a wireless network with random access protocols. In this framework, we derive the transmission probabilities and the packet corruption probabilities
and the packet corruption probabilities of the links in the network.
of the links in the network.  is the probability that a station transmits in a randomly chosen slot, while
is the probability that a station transmits in a randomly chosen slot, while  is the probability that a packet is received with error.
is the probability that a packet is received with error.
For illustration, we choose the MAC and PHY protocols to be 802.11b with basic access scheme and 1Mbps DBPSK. Our model can be readily extended to consider other modulation schemes. In addition, we make the following assumptions.
-
(i)
The network consists of two links
 and
and 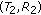 , where
, where  and
and  denote the transmitter and the receiver of the links, respectively,
denote the transmitter and the receiver of the links, respectively, 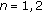 .
. -
(ii)
There are a constant buffer nonempty probability
 that the transmission buffer of
that the transmission buffer of  is nonempty and a constant channel idle probability
is nonempty and a constant channel idle probability that
that 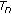 senses the channel to be idle,
senses the channel to be idle, 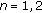 .
. -
(iii)
 transmits with power
transmits with power  , and the background noise power at
, and the background noise power at 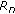 is
is  ,
, 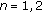 .
. -
(iv)
Channel defects like shadowing and fading are neglected, and a generic path loss model
 is used to model the wireless channel, where
is used to model the wireless channel, where 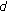 is the propagation distance,
is the propagation distance,  is the path loss exponent, and
is the path loss exponent, and 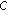 is a constant.
is a constant. -
(v)
The interference from other transmitters plus the receiver background noise is assumed to be Gaussian distributed.
-
(vi)
All bits in a packet must be received correctly for correct reception of the packet.
-
(vii)
The size of an acknowledgement is much smaller than that of the payload, so the bit errors on acknowledgement are negligible.
We follow the approach as in [15], using a discrete-time Markov chain to model the 802.11 Distributed Coordination Function (DCF) and obtain the transmission probability of a station. An ordered pair  is used to denote the state of the Markov chain, where
is used to denote the state of the Markov chain, where  represents the backoff stage and
represents the backoff stage and  is the current backoff counter value. In stage
is the current backoff counter value. In stage  ,
,  is in the range
is in the range  , where
, where  is the contention window size in stage
is the contention window size in stage  .
.  is the maximum number of backoff stages. However, there are some discrepancies between the model in [15] and the actual behavior of 802.11 DCF. First, the model assumes that a station retransmits indefinitely until the packet is successfully transmitted. This assumption is inconsistent with 802.11 basic access scheme. Also, the model does not account for the unsaturated traffic conditions, which is the scenario appeared in practical situations.
is the maximum number of backoff stages. However, there are some discrepancies between the model in [15] and the actual behavior of 802.11 DCF. First, the model assumes that a station retransmits indefinitely until the packet is successfully transmitted. This assumption is inconsistent with 802.11 basic access scheme. Also, the model does not account for the unsaturated traffic conditions, which is the scenario appeared in practical situations.
To overcome these limitations, we adopt and modify the Markov chain proposed by [15] to obtain an enhanced model. First, we take into account the limited number of retransmissions in 802.11 as in [28], by restricting the Markov chain to leave the  th backoff stage once the station transmits a packet in that backoff stage. Second, we follow [28] to modify the values of
th backoff stage once the station transmits a packet in that backoff stage. Second, we follow [28] to modify the values of  in accordance with the 802.11 MAC and PHY specifications [29], with
in accordance with the 802.11 MAC and PHY specifications [29], with  corresponding to the first backoff stage using the maximum contention window size
corresponding to the first backoff stage using the maximum contention window size

In addition, to handle the unsaturated traffic conditions, we follow [30] to augment the Markov chain by introducing new states  ,
,  . These new states represent the states of being in the post-backoff stage. The post-backoff stage is entered whenever the station has no packets queued in its transmission buffer after a successful transmission. The corresponding Markov chain is depicted in Figure 4.
. These new states represent the states of being in the post-backoff stage. The post-backoff stage is entered whenever the station has no packets queued in its transmission buffer after a successful transmission. The corresponding Markov chain is depicted in Figure 4.
Let  denote the stationary probability of the state
denote the stationary probability of the state  in the Markov chain. The transmission probability of a station is given by
in the Markov chain. The transmission probability of a station is given by

The details of the Markov chain and the derivation of this equation can be found in [31].
The packet corruption probability is calculated according to the modulation scheme used in the PHY layer, the distance between the transmitter and the receiver, and the existence of nearby interferer(s). For a fixed carrier sensing threshold , we differentiate into two cases, whether both transmitters can sense the transmission of each other or not.
, we differentiate into two cases, whether both transmitters can sense the transmission of each other or not.
If  can sense the transmission of
can sense the transmission of  , that is,
, that is,  , where
, where  is the distance between
is the distance between  and
and  , then the SINR at
, then the SINR at  is
is

The bit error rate attained by  is
is  , and the packet corruption probability for
, and the packet corruption probability for  is
is

where  ,
,  , and
, and  represent the number of bits in the PHY header, the MAC header, and the payload, respectively.
represent the number of bits in the PHY header, the MAC header, and the payload, respectively.
On the other hand, if  cannot sense the transmission of
cannot sense the transmission of  , that is,
, that is,  , then the SINR at
, then the SINR at  depends on whether
depends on whether  is active in transmission or not, that is,
is active in transmission or not, that is,

The packet corruption probability is calculated by the average bit error rate 

The channel idle probability is defined as follows. If  can sense the transmission of
can sense the transmission of  , then
, then  will consider the channel to be idle whenever
will consider the channel to be idle whenever  is inactive, that is,
is inactive, that is,  ; otherwise
; otherwise  always senses the channel to be idle and
always senses the channel to be idle and  .
.
Suppose that we want to schedule a flow of  bits per second on
bits per second on  and
and  bits per second is achieved by
bits per second is achieved by  ,
,  . We refer
. We refer  and
and  to the offered load and the carried load, respectively. We calculate
to the offered load and the carried load, respectively. We calculate  by
by

where  is the expected length of a slot as seen by
is the expected length of a slot as seen by  . Let
. Let  be the probability that at least one station is transmitting, and let
be the probability that at least one station is transmitting, and let  be the probability that there is at least one successful transmission given that at least one station is transmitting. Then
be the probability that there is at least one successful transmission given that at least one station is transmitting. Then  , where
, where  ,
,  , and
, and  are the time spent in an idle slot, a successful transmission, and an unsuccessful transmission, respectively. When
are the time spent in an idle slot, a successful transmission, and an unsuccessful transmission, respectively. When  can sense the transmission of
can sense the transmission of  , we consider both links to be one system:
, we consider both links to be one system:

Otherwise, we treat both links to be separate systems:

We approximate the packet arrival of  to be a Poisson process with rate
to be a Poisson process with rate  ,
,  , and estimate the buffer nonempty probability by
, and estimate the buffer nonempty probability by

In summary, if  can sense the transmission of
can sense the transmission of  , then we obtain the following set of equations for
, then we obtain the following set of equations for  :
:

Otherwise, we obtain another set of equations for 

Similarly, we can obtain three equations for link  . With these six equations we can solve for the variables
. With these six equations we can solve for the variables  ,
,  ,
,  ,
,  ,
,  ,
,  by Newton's method [32] and obtain the loadings of these two links by (14).
by Newton's method [32] and obtain the loadings of these two links by (14).
5.2. Some Analytical Results
We use the two-ray ground reflection model

to represent the path loss and the values in Table 2 to obtain numerical results from our model. These values are defined in or derived from the values in the 802.11 MAC and PHY specifications [29] or NS-2 [33].
In the following we attempt to find the maximum carried loads of each link in various scenarios. One observation from solving the system of equations in Section 5.1 is that the carried load will be smaller than the offered load when the offered load is too large. This corresponds to the instability of 802.11 observed in previous works (e.g., [15]). Therefore, we use binary search to find the maximum carried load under stable conditions. Initially, the search range for the offered load is between 0 and 1 Mbps. We choose the midpoint of the search range to be the offered load and solve the system of equations. If the resultant carried load is the same as the offered load, the offered load can be increased, and the next search range will be the upper half of the original one. Otherwise, the offered load results in instability, and the next search range will be the lower half of the original one. This procedure is repeated until the search range is sufficiently small.
We consider a network of two parallel links as shown in Figure 5, with  and
and  representing the length of the links and the link separation, respectively. The link separation is defined as the perpendicular distance between the links. We let
representing the length of the links and the link separation, respectively. The link separation is defined as the perpendicular distance between the links. We let  bits,
bits,  meters, and
meters, and  ,
,  ,
,  ,
,  dBm to solve for the maximum carried loads and obtain the curves as shown in Figures 6(a)–6(d).
dBm to solve for the maximum carried loads and obtain the curves as shown in Figures 6(a)–6(d).
Aggregate throughput for the topology in Figure 5 with length of links = 450 meters and various carrier sensing thresholds. 70 dBm
70 dBm 75 dBm−78 dBm−80 dBm
75 dBm−78 dBm−80 dBm
Consider the curve corresponding to the carrier sensing threshold of −78 dBm in Figure 6(c), which is a common value used in NS-2 simulation and the practical value used in Orinoco wireless LAN card. The corresponding carrier sensing range is 550 meters, which is in line with the carrier sensing range used in practice. In our model, we assume that carrier sensing works when the separation is within the carrier sensing range and fails otherwise and use two different sets of equations to model the system in these situations. Therefore there is an abrupt change in the aggregate throughput when the separation equals the carrier sensing range. If there is no carrier sensing in the system, the aggregate throughput will reduce to zero smoothly when the link separation reduces.
The curve in Figure 6(c) can be divided into three parts according to the link separation  . When
. When  meters, both transmitters are in the carrier sensing range of each other. As a result, at most only one transmitter is active at a time. If
meters, both transmitters are in the carrier sensing range of each other. As a result, at most only one transmitter is active at a time. If  meters, the transmitters are unaware of the existence of each other, and they contend for the wireless channel as if there were no interferers nearby. When
meters, the transmitters are unaware of the existence of each other, and they contend for the wireless channel as if there were no interferers nearby. When  meters, the separation is so large that there will not be any interference between the links. When
meters, the separation is so large that there will not be any interference between the links. When  lies between 550 and 800 meters, the aggregate throughput of the links increases smoothly as
lies between 550 and 800 meters, the aggregate throughput of the links increases smoothly as  increases. We label this range of
increases. We label this range of  as the partial interference region. The existence of this partial interference region suggests that the interference models proposed by [1] that a single threshold can represent the interference relationship in wireless networks may be overly simplified.
as the partial interference region. The existence of this partial interference region suggests that the interference models proposed by [1] that a single threshold can represent the interference relationship in wireless networks may be overly simplified.
The width of this partial interference region depends on the carrier sensing threshold  used. Smaller
used. Smaller  , for example, −80 dBm, results in a narrower partial interference region as in Figure 6(d). Simultaneous transmissions are allowed only for the links separated far enough, and the throughput is suppressed significantly. For larger
, for example, −80 dBm, results in a narrower partial interference region as in Figure 6(d). Simultaneous transmissions are allowed only for the links separated far enough, and the throughput is suppressed significantly. For larger  , for example, −75 and −70 dBm, more spatial reuse is allowed, and the width of the partial interference region is larger, as shown in Figures 6(a)-6(b). However, excessive interference is introduced for larger
, for example, −75 and −70 dBm, more spatial reuse is allowed, and the width of the partial interference region is larger, as shown in Figures 6(a)-6(b). However, excessive interference is introduced for larger  , so there is a reduction in the aggregate throughput.
, so there is a reduction in the aggregate throughput.
Besides carrier sensing threshold, the length of the links  also affects the partial interference region. We reduce
also affects the partial interference region. We reduce  to be 400 meters and obtain the results in Figures 7(a)–7(d). As shown in Figures 7(a)–7(d), the partial interference region becomes narrower for all values of carrier sensing threshold. Also, the aggregate throughput achieved by the links is larger for the same link separation when the links are shortened.
to be 400 meters and obtain the results in Figures 7(a)–7(d). As shown in Figures 7(a)–7(d), the partial interference region becomes narrower for all values of carrier sensing threshold. Also, the aggregate throughput achieved by the links is larger for the same link separation when the links are shortened.
Aggregate throughput for the topology in Figure 5 with length of links = 400 meters and various carrier sensing thresholds. 70 dBm
70 dBm 75 dBm
75 dBm 78 dBm
78 dBm 80 dBm
80 dBm
5.3. Admissible (Stability) Region
As an attempt to obtain the capacity of 802.11 networks under partial interference, we compute the admissible (stability) region predicted from our model. The admissible region includes all flow vectors  such that if
such that if  is located inside the admissible region, then a flow of
is located inside the admissible region, then a flow of  can be allocated on and achieved by
can be allocated on and achieved by  ,
,  . We use the same settings as above and choose the carrier sensing threshold to be −78 dBm. The link separations are chosen to be 500, 600, and 900 meters for illustrative purposes, because they correspond to different shapes of the admissible region. Figure 8 shows the admissible region for these three link separations. The link separation of 500 meters represents that the links are in mutual interference and the admissible region has a triangular shape. When the links are separated by 900 meters, the links do not interfere with each other, and the admissible region is rectangular. For the link separation of 600 meters, partial interference exists and the admissible region becomes convex.
. We use the same settings as above and choose the carrier sensing threshold to be −78 dBm. The link separations are chosen to be 500, 600, and 900 meters for illustrative purposes, because they correspond to different shapes of the admissible region. Figure 8 shows the admissible region for these three link separations. The link separation of 500 meters represents that the links are in mutual interference and the admissible region has a triangular shape. When the links are separated by 900 meters, the links do not interfere with each other, and the admissible region is rectangular. For the link separation of 600 meters, partial interference exists and the admissible region becomes convex.
Although we are able to compute the admissible region for a two-link 802.11 network numerically, the closed-form expression for the admissible region is unknown. Also, for an 802.11 network with two links, we have to solve a system of six nonlinear equations to compute the admissible region. When the number of links in the network grows, the number of equations involved will increase, and the system of equations will be more difficult to solve. Therefore the computation of the admissible region of general 802.11 networks seems to be forbiddingly intractable.
6. Partial Interference in Slotted ALOHA
In order to obtain insights in the stability region of general 802.11 networks, in this section, we study the stability of slotted ALOHA, which is a simpler random access protocol, under the assumptions of finite links and infinite buffer.
6.1. The Finite-Link Slotted ALOHA Model
Let  be the set of links in the slotted ALOHA system. Time is slotted. The following assumptions apply to all links
be the set of links in the slotted ALOHA system. Time is slotted. The following assumptions apply to all links  . Let
. Let  and
and  be the transmitter and the receiver of link
be the transmitter and the receiver of link  , respectively.
, respectively.  has an infinite buffer. The packet arrival process at
has an infinite buffer. The packet arrival process at  is Bernoulli with mean
is Bernoulli with mean  and is independent of the arrivals at other transmitters.
and is independent of the arrivals at other transmitters.  attempts a virtual transmission with probability
attempts a virtual transmission with probability  , that is, if its buffer is nonempty,
, that is, if its buffer is nonempty,  attempts an actual transmission with probability
attempts an actual transmission with probability  ; otherwise,
; otherwise,  always remains silent. Also define
always remains silent. Also define  .
.
In the system, each time slot is just enough for transmission of one packet. Packets are assumed to have equal lengths. We assume that transmission results are independent in each slot. For  , let
, let  be the probability that the transmission on link
be the probability that the transmission on link  is successful when
is successful when  is the set of active transmitters.
is the set of active transmitters.  depends on the SINR at the receiver and the modulation scheme used. We also assume that the transmitters know immediately the transmission results, so that the transmitters remove successfully transmitted packets and retain only those unsuccessful ones.
depends on the SINR at the receiver and the modulation scheme used. We also assume that the transmitters know immediately the transmission results, so that the transmitters remove successfully transmitted packets and retain only those unsuccessful ones.
We let  be the queue length in
be the queue length in  at the beginning of slot
at the beginning of slot  and use an
and use an  -dimensional Markov chain
-dimensional Markov chain  to represent the queue lengths in all transmitters. We denote by
to represent the queue lengths in all transmitters. We denote by  the number of packets arrived at
the number of packets arrived at  in slot
in slot  and
and  the number of packets successfully transmitted in slot
the number of packets successfully transmitted in slot  by
by  when
when  . Then
. Then  , where
, where  is used to account for the case that there is no packet transmitted when
is used to account for the case that there is no packet transmitted when  . We use the definition of stability in [16, 21, 22].
. We use the definition of stability in [16, 21, 22].
Definition 1.
An  - dimensional stochastic process
- dimensional stochastic process  is stable if for
is stable if for  the following holds:
the following holds:

If the following weaker condition holds instead,

then the process is substable. The process is unstable if it is neither stable nor substable.
The stability problem of slotted ALOHA we consider here is to determine whether the slotted ALOHA system with the set of links  is stable given the parameters
is stable given the parameters  and
and  . We use the result from [34]. On the assumption that the arrival and the service processes of a queue are stationary, the queue is stable if the average arrival rate is less than the average service rate, and the queue is unstable if the average arrival rate is larger than the average service rate. We also define the slotted ALOHA system to be stable when all queues in the system are stable.
. We use the result from [34]. On the assumption that the arrival and the service processes of a queue are stationary, the queue is stable if the average arrival rate is less than the average service rate, and the queue is unstable if the average arrival rate is larger than the average service rate. We also define the slotted ALOHA system to be stable when all queues in the system are stable.
6.2. Stability Region of 2-Link Slotted ALOHA under Partial Interference
We extend the model in [16] to capture the impact of partial interference on the capacity of a 2-link slotted ALOHA system with potentially unsaturated offered load. For  , let
, let  and
and  be the transmission power used by
be the transmission power used by  and the background noise power at
and the background noise power at  , respectively. Assume that the signal propagation follows the path loss model
, respectively. Assume that the signal propagation follows the path loss model  , where
, where  is the propagation distance,
is the propagation distance,  is the path loss exponent, and
is the path loss exponent, and  is a constant. We let
is a constant. We let  be the SINR attained at
be the SINR attained at  when
when  is the set of active transmitters. Assume that a packet consists of
is the set of active transmitters. Assume that a packet consists of  bits. Let
bits. Let  be the bit error rate when the SINR is
be the bit error rate when the SINR is  . In particular, if DBPSK is used in the physical layer,
. In particular, if DBPSK is used in the physical layer,  . Under binary interference, we let the SINR threshold
. Under binary interference, we let the SINR threshold  be the case that the packet error rate is
be the case that the packet error rate is  , that is,
, that is,  . Consider
. Consider  . When only
. When only  is active, the SINR attained at
is active, the SINR attained at  is
is  , and
, and

where  is the distance between
is the distance between  and
and  . When both
. When both  and
and  are active, then
are active, then  is the SINR attained at
is the SINR attained at  , and
, and

If we consider partial interference instead, we can calculate  as follows. When only
as follows. When only  is active,
is active,

When both  and
and  are active,
are active,

Similarly, we can derive expressions for  and
and  under binary and partial interference.
under binary and partial interference.
To evaluate the boundary of the stability region for the 2-link slotted ALOHA system, we use stochastic dominance as introduced in [18]. We use  to represent a dominant system of the original system
to represent a dominant system of the original system  , with
, with  being the persistent set. The transmitters of the links in this set transmit dummy packets when they decide to transmit but do not have packets queued in their buffer. The remaining transmitters behave identically as those in
being the persistent set. The transmitters of the links in this set transmit dummy packets when they decide to transmit but do not have packets queued in their buffer. The remaining transmitters behave identically as those in  . We first consider the dominant system
. We first consider the dominant system  . In this dominant system, the successful transmission probability of link 2 is
. In this dominant system, the successful transmission probability of link 2 is  . For link 1, the queue in
. For link 1, the queue in  is empty with probability
is empty with probability  ; in this case the successful transmission probability is
; in this case the successful transmission probability is  ; otherwise, the successful transmission probability is
; otherwise, the successful transmission probability is  . Hence, the average successful transmission probability of link 1 is
. Hence, the average successful transmission probability of link 1 is

With the following notations,

the stability region of  is
is

and by symmetry, the stability region of  is
is

The union of these two regions constitutes the inner bound on the stability region of the original system  .
.
The reason for the union of these two regions to be the outer bound on the stability region follows from the indistinguishability argument [16, 18]. Consider the dominant system  . With a particular initial condition on the length of the queues, if the queue in
. With a particular initial condition on the length of the queues, if the queue in  is unstable, it is equivalent to the case that the queue in
is unstable, it is equivalent to the case that the queue in  never empties with nonzero probability. Then
never empties with nonzero probability. Then  and
and  will be indistinguishable, in the sense that the packets transmitted from
will be indistinguishable, in the sense that the packets transmitted from  in
in  are always real packets and
are always real packets and  is also unstable. Therefore, the union of the regions defined by (29) and (30) is the exact stability region for
is also unstable. Therefore, the union of the regions defined by (29) and (30) is the exact stability region for  .
.
6.3. Some Illustrations
In this section, we depict the stability region derived in previous section by considering the parallel-link topology in Figure 5. We use the two-ray ground reflection model

to represent the path loss. The values of various parameters are shown in Table 3.
We first assume that  bits,
bits,  and vary the link separation, that is, the perpendicular distance between the links, to obtain the results under binary interference in Figure 9(a). The stability region has only two possible shapes. For the separations of 600, 800, and 1000 meters, the SINR attained at either receiver when both transmitters are active is smaller than the threshold. Therefore the underlying channel follows the collision channel model, and the stability region is nonconvex. When the separation is 1200 meters, the links are separated far enough so that transmissions on both links are independent. The channel can be regarded as the orthogonal channel, and the stability region is convex. Therefore, the threshold in binary interference determines when to switch between the collision channel and the orthogonal channel.
and vary the link separation, that is, the perpendicular distance between the links, to obtain the results under binary interference in Figure 9(a). The stability region has only two possible shapes. For the separations of 600, 800, and 1000 meters, the SINR attained at either receiver when both transmitters are active is smaller than the threshold. Therefore the underlying channel follows the collision channel model, and the stability region is nonconvex. When the separation is 1200 meters, the links are separated far enough so that transmissions on both links are independent. The channel can be regarded as the orthogonal channel, and the stability region is convex. Therefore, the threshold in binary interference determines when to switch between the collision channel and the orthogonal channel.
Figure 9(b) shows the corresponding results under partial interference. When the link separation is small, the amount of interference is so large that partial interference degenerates to the collision channel. As the link separation increases, the stability region expands gradually and changes from nonconvex to convex. At another extreme, when the links are sufficiently far apart, partial interference is identical to the orthogonal channel. Therefore, partial interference can be viewed as a generalization of binary interference that it interpolates the transition from the collision channel to the orthogonal channel. Notice that the results here are similar to the case in 802.11, therefore our results should be applicable to networks with practical random access protocols like 802.11.
Next, we assume that the links are separated by 800 meters. We let both links transmit with probability  and illustrate the effect of
and illustrate the effect of  on the convexity of the stability region under binary interference in Figure 10(a). When
on the convexity of the stability region under binary interference in Figure 10(a). When  is small, that is, 0.2 and 0.4, the links are too conservative in attempting transmissions. It leads to better channel utilization by adding one more link to the system, and the stability region is convex. On the other hand, when
is small, that is, 0.2 and 0.4, the links are too conservative in attempting transmissions. It leads to better channel utilization by adding one more link to the system, and the stability region is convex. On the other hand, when  is large, that is, 0.6 and 0.8, the links are too aggressive. When one more link is added to the system, it increases contention and hence reduces the loading supported by each link drastically. As a result, the stability region is nonconvex. The convexity of the stability region can therefore be regarded as a measure of the contention level in a network.
is large, that is, 0.6 and 0.8, the links are too aggressive. When one more link is added to the system, it increases contention and hence reduces the loading supported by each link drastically. As a result, the stability region is nonconvex. The convexity of the stability region can therefore be regarded as a measure of the contention level in a network.
Figure 10(b) illustrates the stability region when partial interference is considered instead, under the same settings. Although the SINR attained at a receiver when both transmitters are active is smaller than the threshold, the SINR is large enough to support a sustainable throughput probabilistically. Therefore, it is possible to receive more packets opportunistically under partial interference, thereby increasing the loading supported by each link and allowing the stability region to be convex. If we compare the stability region under binary and partial interference in identical settings, as shown in Figures 11(a)–11(d), the stability region under partial interference is always larger than that under binary interference. This implies that by considering partial interference, more combinations of flows on the links can be admitted, and the capacity of a wireless network can be potentially increased.
6.4. Partial Characterization of the Stability Region for the M-Link Case
In this section, we give in closed form a partial characterization on the boundary of the stability region of M-link slotted ALOHA under partial interference. First, for  ,
,  . Therefore, under binary interference,
. Therefore, under binary interference,

while under partial interference,

For each  , let
, let  be an
be an  -dimensional 0-1 vector such that
-dimensional 0-1 vector such that

where  is a set of persistent links and all other links are empty. Define
is a set of persistent links and all other links are empty. Define  , where
, where

to be a corner point corresponding to the case that  is the set of persistent links. Notice that RHS of (35) is zero when
is the set of persistent links. Notice that RHS of (35) is zero when  . Then we obtain the following theorem.
. Then we obtain the following theorem.
Theorem 2.
All corner points lie on the boundary of the stability region.
Proof.
Refer to Appendix A.
By using stochastic dominance and the indistinguishability argument, we obtain the following theorem.
Theorem 3.
Let  ,
,  be two corner points such that
be two corner points such that  . Then the line segment joining these two points lies on the boundary of the stability region. This line segment represents the case that
. Then the line segment joining these two points lies on the boundary of the stability region. This line segment represents the case that  is the set of persistent links while
is the set of persistent links while  is the only nonempty nonpersistent link in the system.
is the only nonempty nonpersistent link in the system.
Proof.
Refer to Appendix B.
We illustrate the results of these theorems by considering  with the ring topology in Figure 12(a). The distance between a receiver and the nearest interfering transmitter is 900 meters. Each link transmits with probability 0.6. Other parameters are the same as in Table 3. From Theorem 2, each of the eight 3-dimensional 0-1 vectors corresponds to a corner point shown in Figure 12(b), and their coordinates can be obtained from (35). By Theorem 3, the solid lines in Figure 12(b) are part of the boundary of the stability region. As another example, for
with the ring topology in Figure 12(a). The distance between a receiver and the nearest interfering transmitter is 900 meters. Each link transmits with probability 0.6. Other parameters are the same as in Table 3. From Theorem 2, each of the eight 3-dimensional 0-1 vectors corresponds to a corner point shown in Figure 12(b), and their coordinates can be obtained from (35). By Theorem 3, the solid lines in Figure 12(b) are part of the boundary of the stability region. As another example, for  , notice that (29) and (30) are special cases of (B.1). As a direct consequence of our Theorems 2 and 3, the stability region of slotted ALOHA with two links under partial interference is piecewise linear.
, notice that (29) and (30) are special cases of (B.1). As a direct consequence of our Theorems 2 and 3, the stability region of slotted ALOHA with two links under partial interference is piecewise linear.
7. Stability Region of the General M-Link Slotted ALOHA System under Partial Interference
Theorems 2 and 3 cover all cases with zero or one nonempty nonpersistent link in an M-link system, respectively. However, if there are at least two nonempty unsaturated links, the stationary joint queue statistics must be involved in calculating the boundary. Unless we are able to compute the stationary joint queue statistics in closed-form, we are unable to solve the capacity-finding problem, even assuming one of the simplest random access protocol, that is, slotted ALOHA. In fact, the characterization of the exact stability region of a general M-link slotted ALOHA system with nonpersistent links has remained to be a key open problem for decades when  [16–23] even under the simplified binary interference model.
[16–23] even under the simplified binary interference model.
To overcome the problem caused by the stationary joint queue statistics, we have introduced the FRASA (Feedback Retransmission Approximation for Slotted Aloha) model in [24] to obtain a closed-form approximation for the stability region of a general M-link slotted ALOHA system under binary interference (i.e., simple collision channel) assumptions. We refer the readers to [24, 31] for a detailed description of the FRASA approach. In the following subsection, we extend the model and analysis in [24] to cover the partial interference case. We remark that our results here automatically apply to the binary interference case if we allow  to be either zero or one only by comparing the corresponding SINR, that is,
to be either zero or one only by comparing the corresponding SINR, that is,  , against a predefined threshold
, against a predefined threshold  , as illustrated in (32) and (33).
, as illustrated in (32) and (33).
7.1. FRASA under Partial Interference
Assume identical settings as in [24]. There are  links in the network, and the set of links is denoted by
links in the network, and the set of links is denoted by  . Denote this FRASA system by
. Denote this FRASA system by  . Let
. Let  be the transmission probability vector. Define
be the transmission probability vector. Define  for all
for all  . We first consider a reduced FRASA system, in which we let
. We first consider a reduced FRASA system, in which we let  of the links have fixed aggregate arrival rates and the remaining link is assumed with infinite backlog. Take
of the links have fixed aggregate arrival rates and the remaining link is assumed with infinite backlog. Take  to be the link with infinite backlog and denote this reduced FRASA system by
to be the link with infinite backlog and denote this reduced FRASA system by  . Let
. Let  be the aggregate arrival rate of link
be the aggregate arrival rate of link  , where
, where  is between zero and one. Hence, link
is between zero and one. Hence, link  is active with probability
is active with probability  , while for
, while for  , link
, link  is active with probability
is active with probability  . Let
. Let  and
and  . Introduce the following notations:
. Introduce the following notations:



Equation (36) is the probability of successful transmission of link  given that link
given that link  is active but link
is active but link  is not. Equation (37) is the probability of successful transmission of link
is not. Equation (37) is the probability of successful transmission of link  given that both links
given that both links  and
and  are active. Equation (38) is the probability of successful transmission of link
are active. Equation (38) is the probability of successful transmission of link  given that link
given that link  is active. Then the parametric form of the stability region of
is active. Then the parametric form of the stability region of  will be
will be  ,
,  , where
, where

with  and
and  is between zero and one for all
is between zero and one for all  .
.  is the successful transmission probability vector under partial interference.
is the successful transmission probability vector under partial interference.
With this parametric form, we obtain the stability region of FRASA under partial interference as in the following theorem.
Theorem 4.
For each  , one constructs a hypersurface
, one constructs a hypersurface  , which is represented by
, which is represented by  ,
,  , where
, where

with  and
and  is between zero and one for all
is between zero and one for all  . Then
. Then  , the stability region of FRASA under partial interference, is enclosed by
, the stability region of FRASA under partial interference, is enclosed by  ,
,  in the positive orthant.
in the positive orthant.
Proof.
Refer to Appendix C.
An illustration of the results of Theorem 4 with the topology in Figure 12(a) is given in Figure 13. Figures 13(a), 13(b), and 13(c) depict  ,
,  , and
, and  , respectively. The union of these hypersurfaces, which is the boundary of the stability region of FRASA under partial interference, is shown in Figure 13(d).
, respectively. The union of these hypersurfaces, which is the boundary of the stability region of FRASA under partial interference, is shown in Figure 13(d).
Stability region of FRASA under partial interference with  , transmission probabilities 0.6 and topology in Figure 12(a) by Theorem 4.
, transmission probabilities 0.6 and topology in Figure 12(a) by Theorem 4. , boundary of stability region with link 1 infinitely backlogged
, boundary of stability region with link 1 infinitely backlogged , boundary of stability region with link 2 infinitely backlogged
, boundary of stability region with link 2 infinitely backlogged , boundary of stability region with link 3 infinitely backlogged
, boundary of stability region with link 3 infinitely backlogged , the whole stability region
, the whole stability region
7.2. Simulation Results
In this subsection, we demonstrate the effects of partial interference on the stability region of the general M-link slotted ALOHA systems by presenting results based on both simulation as well as the FRASA closed-form approximation approach. In particular, we perform simulations as in [24] to obtain the stability region of slotted ALOHA by considering the ring topology in Figure 12(a). We assume that all links transmit with probability 0.6. For illustrative purpose, we only show the cross-sections of the stability regions. In Figure 14(a), we depict the cross-sections of the stability region by fixing  , while in Figure 14(b) the cross-sections of the stability region are obtained by fixing
, while in Figure 14(b) the cross-sections of the stability region are obtained by fixing  . The solid lines represent the simulation results while the dash-dot lines are obtained from the FRASA closed-form approximation. Observe from the figures that, for the given set of system parameters, the curves derived from the FRASA approximation closely follow the simulation results. As a comparison against binary interference, we use the same set of input traffic parameters to obtain the stability region of slotted ALOHA under collision channel (i.e., binary interference model) via simulations. The corresponding cross-sections of the stability region are shown in Figures 14(c) and 14(d), respectively. These results also show a substantial expansion of the stability region by considering partial interference instead of binary ones as in Section 6. More importantly, one should note the qualitative changes in the shapes of the cross-sections of the stability region from concave to convex when the more realistic partial interference phenomenon is considered. This reinforces our argument that it is important to model the partial interference effects while analyzing the performance of wireless multiple access protocols.
. The solid lines represent the simulation results while the dash-dot lines are obtained from the FRASA closed-form approximation. Observe from the figures that, for the given set of system parameters, the curves derived from the FRASA approximation closely follow the simulation results. As a comparison against binary interference, we use the same set of input traffic parameters to obtain the stability region of slotted ALOHA under collision channel (i.e., binary interference model) via simulations. The corresponding cross-sections of the stability region are shown in Figures 14(c) and 14(d), respectively. These results also show a substantial expansion of the stability region by considering partial interference instead of binary ones as in Section 6. More importantly, one should note the qualitative changes in the shapes of the cross-sections of the stability region from concave to convex when the more realistic partial interference phenomenon is considered. This reinforces our argument that it is important to model the partial interference effects while analyzing the performance of wireless multiple access protocols.
Cross-section of stability region of the slotted ALOHA system with  and transmission probability 0. 6 under partial interference and binary interference (i.e., collision channel) models.
and transmission probability 0. 6 under partial interference and binary interference (i.e., collision channel) models. fixed, partial interference
fixed, partial interference fixed, partial interference
fixed, partial interference fixed, binary interference, collision channel
fixed, binary interference, collision channel fixed, binary interference, collision channel
fixed, binary interference, collision channel
8. Conclusion
In this paper, we have introduced the notion of partial interference in wireless multiple access systems and illustrated the potential gain in system capacity when the effect of partial interference is taken into account. In particular, we characterize the stability region of IEEE 802.11 networks under partial interference with two potentially unsaturated links numerically. We also derive the stability region of slotted ALOHA networks under partial interference with two links analytically and obtain a partial characterization of the boundary of the stability region for the case of more than two, potentially unsaturated links in a slotted ALOHA system. By extending the FRASA model, we provide a closed-form approximation for the stability region for general M-link slotted ALOHA system under partial interference effects. Our analyses demonstrate that partial interference considerations can result in not only significant quantitative differences in the predicted system capacity but also fundamental qualitative changes in the shape of the stability region of the systems. This highlights the need of capturing the partial interference effects instead of adopting the conventional, overly simplified binary interference models while analyzing wireless MAC protocols.
Appendices
A. Proof of Theorem 2
When  , (35) becomes
, (35) becomes  , which is obviously on the boundary. If
, which is obviously on the boundary. If  , each link
, each link  operates as
operates as  . If at a certain instant, only the links in
. If at a certain instant, only the links in  are active, which occurs with probability
are active, which occurs with probability  , the probability of successful transmission of link
, the probability of successful transmission of link  is
is  . Therefore, by unconditioning on
. Therefore, by unconditioning on  while noticing
while noticing  if
if  , the successful transmission probability of link
, the successful transmission probability of link  is
is

Therefore  lies on the boundary.
lies on the boundary.
B. Proof of Theorem 3
When  , it is trivial that the line segment between
, it is trivial that the line segment between  and
and  lies on the boundary because it is part of the positive
lies on the boundary because it is part of the positive  -axis. Assume that
-axis. Assume that  . We prove that
. We prove that

with

lies on the boundary of the stability region. For any  ,
,  has no packet, hence
has no packet, hence  . Therefore we consider the dominant system
. Therefore we consider the dominant system  , assuming that the system contains only the links in
, assuming that the system contains only the links in  . For the sufficiency part, the queue in
. For the sufficiency part, the queue in  in
in  is stable if
is stable if

For any  , the queue in
, the queue in  in
in  is stable if
is stable if

The necessity follows directly from the indistinguishability argument. We observe that  varies linearly with
varies linearly with  on the boundary,
on the boundary,  . It is trivial that
. It is trivial that  and
and  correspond to
correspond to  and
and  , respectively.
, respectively.
C. Proof of Theorem 4
Every point  with
with

where  is between zero and one for all
is between zero and one for all  lies in the stability region of FRASA under partial interference. Observe that when
lies in the stability region of FRASA under partial interference. Observe that when  , the corresponding
, the corresponding  lies in the interior of the stability region. Therefore we only need to consider those
lies in the interior of the stability region. Therefore we only need to consider those  with
with  for some
for some  . When
. When  , it means that link
, it means that link  has infinite backlog or operate in persistent conditions, while in nonpersistent conditions, we allow
has infinite backlog or operate in persistent conditions, while in nonpersistent conditions, we allow  to vary arbitrarily between zero and one. Notice that we can never reduce the successful transmission probabilities of all links by changing the links from operating in persistent conditions to nonpersistent conditions, because this reduces the amount of interference experienced by all links. Mathematically, we partition
to vary arbitrarily between zero and one. Notice that we can never reduce the successful transmission probabilities of all links by changing the links from operating in persistent conditions to nonpersistent conditions, because this reduces the amount of interference experienced by all links. Mathematically, we partition  into three disjoint sets
into three disjoint sets  . We first let
. We first let  be the set of persistent links. Then the successful transmission probability of link
be the set of persistent links. Then the successful transmission probability of link  is
is

If we let  be the set of persistent links, the successful transmission probability of link
be the set of persistent links, the successful transmission probability of link  is
is

It is easy to see that the successful transmission probability in (C.3) is larger than that in (C.2), because

where we assume that  , which is in general true because the probability of successful transmission is larger when there are less interferers. This implies that the stability region of FRASA obtained by assuming all links in
, which is in general true because the probability of successful transmission is larger when there are less interferers. This implies that the stability region of FRASA obtained by assuming all links in  in persistent conditions is contained inside the stability region of FRASA obtained by assuming all links in
in persistent conditions is contained inside the stability region of FRASA obtained by assuming all links in  in persistent conditions. Hence, to obtain the boundary of stability region of FRASA under partial interference, we only have to consider the case that only one link is persistent. Then we can use the parametric form (40) to obtain the boundary when
in persistent conditions. Hence, to obtain the boundary of stability region of FRASA under partial interference, we only have to consider the case that only one link is persistent. Then we can use the parametric form (40) to obtain the boundary when  . By repeating over all possible values of
. By repeating over all possible values of  , we get the desired result.
, we get the desired result.
References
Gupta P, Kumar PR: The capacity of wireless networks. IEEE Transactions on Information Theory 2000, 46(2):388-404. 10.1109/18.825799
Zuniga M, Krishnamachari B: Analyzing the transitional region in low power wireless links. Proceedings of the 1st Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks (SECON '04), June 2004, Santa Clara, Calif, USA 517-526.
Kim W, Lee J, Kwon T, Lee S-J, Choi Y: Quantifying the interference gray zone in wireless networks: A Measurement Study. Proceedings of the IEEE International Conference on Communications (ICC '07), June 2007, Glasgow, UK 3758-3763.
Maheshwari R, Jain S, Das SR: A measurement study of interference modeling and scheduling in low-power wireless networks. Proceedings of the 6th ACM Conference on Embedded Networked Sensor Systems (SenSys '08), November 2008, Raleigh, NC, USA
Padhye J, Agarwal S, Padmanabhan VN, Qiu L, Rao A, Zill B: Estimation of link interference in static multi-hop wireless networks. Proceedings of the Internet Measurement Conference, October 2005, Berkeley, Calif, USA
Mishra A, Rozner E, Banerjee S, Arbaugh W: Exploiting partially overlapping channels in wireless networks: turning a peril into an advantage. Proceedings of the Internet Measurement Conference, October 2005, Berkeley, Calif, USA
Maheshwari R, Cao J, Das SR: Physical interference modeling for transmission scheduling on commodity WiFi hardware. Proceedings of the 24th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '09), April 2009, Rio de Janeiro, Brazil 2661-2665.
Aguayo D, Bicket J, Biswas S, Judd G, Morris R: Link-level measurements from an 802.11b mesh network. Proceedings of the Conference on Computer Communications (SIGCOMM '04), September 2004, Portland, Ore, USA 121-131.
Camp J, Robinson J, Steger C, Knightly E: Measurement driven deployment of a two-tier urban mesh access network. Proceedings of the 4th International Conference on Mobile Systems, Applications and Services (MobiSys '06), June 2006, Uppsala, Sweden 96-109.
Lee J, Kim W, Lee S-J, Jo D, Ryu J, Kwon T, Choi Y: An experimental study on the capture effect in 802.11a networks. Proceedings of the 2nd ACM International Workshop on Wireless Network Testbeds, Experimental Evaluation and Characterization (WiNTECH '07), July 2007, Montreal, Canada 19-26.
Kochut A, Vasan A, Shankar AU, Agrawala A: Sniffing out the correct physical layer capture model in 802.11b. Proceedings of the 12th IEEE International Conference on Network Protocols (ICNP '04), October 2004, Berlin, Germany 252-261.
Lee J, Ryu J, Lee S-J, Kwon T: Improved modeling of IEEE 802.11a PHY through fine-grained measurements. Computer Networks 2010, 54(4):641-657. 10.1016/j.comnet.2009.08.003
Santi P, Maheshwari R, Resta G, Das S, Blough DM: Wireless link scheduling under a graded SINR interference model. Proceedings of the 2nd ACM international Workshop on Foundations of Wireless Ad hoc and Sensor Networking and Computing (FOWANC '09), 2009, New Orleans, La, USA 3-12.
Shellhammer SJ: Estimation of packet error rate caused by interference using analytic techniques—a coexistence assurance methodology. In IEEE 802.19 Technical Advisory Group Document Archive. Qualcomm, San Diego, Calif, USA; 2005.
Bianchi G: Performance analysis of the IEEE 802.11 distributed coordination function. IEEE Journal on Selected Areas in Communications 2000, 18(3):535-547. 10.1109/49.840210
Naware V, Mergen G, Tong L: Stability and delay of finite-user slotted ALOHA with multipacket reception. IEEE Transactions on Information Theory 2005, 51(7):2636-2656. 10.1109/TIT.2005.850060
Tsybakov BS, Mikhailov VA: Ergodicity of a slotted ALOHA system. Problems of Information Transmission 1979, 15(4):73-87.
Rao RR, Ephremides A: On the stability of interacting queues in a multiple-access system. IEEE Transactions on Information Theory 1988, 34(5):918-930. 10.1109/18.21216
Szpankowski W: Stability conditions for multidimensional queueing systems with computer applications. Operations Research 1988, 36(6):944-957. 10.1287/opre.36.6.944
Anantharam V: The stability region of the finite-user slotted ALOHA protocol. IEEE Transactions on Information Theory 1991, 37(3):535-540.
Szpankowski W: Stability conditions for some multiqueue distributed systems: buffered random access systems. Advances in Applied Probability 1994, 26: 498-515. 10.2307/1427448
Luo W, Ephremides A: Stability of N interacting queues in random-access systems. IEEE Transactions on Information Theory 1999, 45(5):1579-1587. 10.1109/18.771161
Ghez S, Verdú S, Schwartz SC: Stability properties of slotted aloha with multipacket reception capability. IEEE Transactions on Automatic Control 1988, 33(7):640-649. 10.1109/9.1272
Hui K-H, Yue O-C, Lau W-C: FRASA: feedback retransmission approximation for the stability region of finite-user slotted ALOHA. Proceedings of the International Conference on Network Protocols (ICNP '07), October 2007 330-331.
Chang H, Misra V, Rubenstein D: A general model and analysis of physical layer capture in 802.11 networks. Proceedings of the 25th IEEE International Conference on Computer Communications (INFOCOM '06), April 2006, Barcelona, Brazil
Rappaport TS: Wireless Communications: Principles and Practice. 2nd edition. Prentice Hall, Upper Saddle River, NJ, USA; 2002.
Mergen G, Tong L: Stability and capacity of regular wireless networks. IEEE Transactions on Information Theory 2005, 51(6):1938-1953. 10.1109/TIT.2005.847728
Wu H, Peng Y, Long K, Cheng S, Ma J: Performance of reliable transport protocol over IEEE 802.11 wireless LAN: analysis and enhancement. Proceedings of the 21st Annual Joint Conference of the IEEE Computer and Communications (INFOCOM '02), June 2002 599-607.
Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications IEEE Std. 802.11, 1999
Malone D, Duffy K, Leith D: Modeling the 802.11 distributed coordination function in nonsaturated heterogeneous conditions. IEEE/ACM Transactions on Networking 2007, 15(1):159-172.
Hui K-H: Characterizing Interference in Wireless Mesh Networks, M.S. thesis. The Chinese University of Hong Kong, Shatin, Hong Kong; 2007.
Kincaid D, Cheney W: Numerical Analysis: Mathematics of Scientific Computing. 3rd edition. Brooks/Cole, Pacific Grove, Calif, USA; 2002.
The Network Simulator—ns-2 http://www.isi.edu/nsnam/ns/
Loynes RM: The stability of a queue with non-independent interarrival and service times. Proceedings of the Cambridge Philosophical Society 1962, 58: 494-520.
Acknowledgments
The material in this paper was presented in part at the IEEE International Conference on Communications 2007, Glasgow, Scotland, June, 2007 and the 18th Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Athens, Greece, September, 2007.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hui, KH., Lau, W.C. & Yue, O. Partial Interference and Its Performance Impact on Wireless Multiple Access Networks. J Wireless Com Network 2010, 735083 (2010). https://doi.org/10.1155/2010/735083
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/735083



 and
and 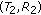 , where
, where  and
and  denote the transmitter and the receiver of the links, respectively,
denote the transmitter and the receiver of the links, respectively, 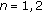 .
. that the transmission buffer of
that the transmission buffer of  is nonempty and a constant channel idle probability
is nonempty and a constant channel idle probability that
that 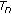 senses the channel to be idle,
senses the channel to be idle, 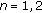 .
. transmits with power
transmits with power  , and the background noise power at
, and the background noise power at  is
is  ,
, 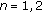 .
. is used to model the wireless channel, where
is used to model the wireless channel, where 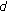 is the propagation distance,
is the propagation distance,  is the path loss exponent, and
is the path loss exponent, and 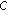 is a constant.
is a constant.





 with transmission probabilities 0. 8 under binary and partial interference.Binary interferencePartial interference
with transmission probabilities 0. 8 under binary and partial interference.Binary interferencePartial interference
 with link separation 800 meters under binary and partial interference. Binary interferencePartial interference
with link separation 800 meters under binary and partial interference. Binary interferencePartial interference
 under binary interference and partial interference with various transmission probabilities.
under binary interference and partial interference with various transmission probabilities.





 . A sample topologyPart of the exact boundary
. A sample topologyPart of the exact boundary
