- Research Article
- Open access
- Published:
Low-Complexity One-Dimensional Edge Detection in Wireless Sensor Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 751520 (2010)
Abstract
In various wireless sensor network applications, it is of interest to monitor the perimeter of an area of interest. For example, one may need to check if there is a leakage of a dangerous substance. In this paper, we model this as a problem of one-dimensional edge detection, that is, detection of a spatially nonconstant one-dimensional phenomenon, observed by sensors which communicate to an access point (AP) through (possibly noisy) communication links. Two possible quantization strategies are considered at the sensors: (i) binary quantization and (ii) absence of quantization. We first derive the minimum mean square error (MMSE) detection algorithm at the AP. Then, we propose a simplified (suboptimum) detection algorithm, with reduced computational complexity. Noisy communication links are modeled either as (i) binary symmetric channels (BSCs) or (ii) channels with additive white Gaussian noise (AWGN).
1. Introduction and Related Work
Sensor networks have been an active research field in the last years [1]. In particular, many civilian applications have been developed on the basis of this technology, for example, for environmental monitoring [2]. Several frameworks have been proposed for the analysis of sensor networks with a common binary phenomenon under observation [3–6]. While there are scenarios where the presence of a common phenomenon is meaningful, in other scenarios one may be interested in determining where the physical phenomenon changes its status (e.g., from presence to absence, or vice versa). As an illustrative example, consider the scenario shown in Figure 1(a). Suppose that in a given area there is a chemical facility where a dangerous gas is used. Obviously, it is of interest to detect any gas leakage. To this purpose, one may place a linear sensor network surrounding this area: in the example in Figure 1(a) there are six sensors. (In the remainder of this paper, by "sensor" we will denote the wireless transceiver which includes the sensing element. However, it has also (limited) processing capabilities and can communicate with the AP.) At a given time, it may happen that there is a leakage: some of the sensors (namely, sensors  ,
,  ,
,  , and
, and  in Figure 1(b)) thus detect the presence of the gas (namely, sensors
in Figure 1(b)) thus detect the presence of the gas (namely, sensors  ,
,  ,
,  , and
, and  ) whereas the remaining sensors (namely,
) whereas the remaining sensors (namely,  and
and  ) do not. This problem reduces to a distributed detection problem of a spatially nonconstant binary phenomenon, as shown in Figure 1(c) and described in more detail later. We remark that this is an illustrative example of a possible one-dimensional edge detection application. Our goal is to show how low-complexity distributed detection can be successfully applied to solve a general one-dimensional edge detection problem.
) do not. This problem reduces to a distributed detection problem of a spatially nonconstant binary phenomenon, as shown in Figure 1(c) and described in more detail later. We remark that this is an illustrative example of a possible one-dimensional edge detection application. Our goal is to show how low-complexity distributed detection can be successfully applied to solve a general one-dimensional edge detection problem.
In [7], the authors consider a scenario with a single phenomenon status change (denoted, in the following, as edge) and propose a framework, based on minimum mean square error (MMSE) estimation, to determine the position of this edge. In [8], under the assumption of proper regularity of the observed edge, a reduced complexity MMSE decoder is proposed. In [9], the authors show that an MMSE decoder is unfeasible for large-scale sensor networks, due to its computational complexity, and propose a distributed detection strategy based on factor graphs and the sum product algorithm. Moreover, MMSE-based distributed detection schemes have also been investigated in scenarios with (i) a common binary phenomenon under observation and (ii) bandwidth constraints [10]. In [11, 12], the authors examine the problem of determining edges of natural phenomena through proper processing of data collected by sensor networks. In these papers, particular attention is devoted to the estimation accuracy, given in terms of the confidence interval of the results obtained with the proposed framework.
The problem of edge detection is also well known in the realm of image processing, where it may be of interest to characterize the intensity changes in the processed image. In [13], the authors characterize, from a theoretical point of view, the types of possible intensity changes. In [14], using numerical optimization, optimal operators are preliminary derived for ridge and roof edges, and then specialized for step edges. In [15], the edge detection problem is tackled as a statistical inference problem. Other interesting approaches to edge detection, especially for noisy information fusion scenarios, are proposed in [16, 17].
In [18], we have proposed a preliminary analytical approach to the design of decentralized detection schemes for scenarios with spatially nonconstant binary phenomena, that is, phenomena with status (either "0" or "1") which may vary from sensor to sensor. We have also derived MMSE detection algorithms at the access point (AP), considering different quantization strategies at the sensors. In order to make our approach practical, a simplified detection algorithm, with a computational complexity much lower than that of the MMSE detection rule, has been proposed.
In this paper, we extend the approach presented in [18] to network scenarios where the communication links between the sensors and the AP may be noisy. These links are modeled either as binary symmetric channels (BSCs) or as additive white Gaussian noise (AWGN) channels. In particular, we study the relative impacts of communication and observation noises on the system performance, evaluated in terms of (i) distance between estimated and true phenomena and (ii) probability of local status estimation error (LSEE). As will be shown in the following, the proposed simplified detection algorithm incurs a limited performance loss with respect to the MMSE algorithm, yet guaranteeing a remarkable complexity reduction. Finally, the robustness and complexity of the proposed algorithms are investigated.
The structure of this paper is the following. In Section 2, we give preliminaries on decentralized detection. In Section 3, we derive the optimum MMSE detection rules at the AP in a scenario with noisy communication links and multiedge phenomena. In Section 4, we propose a simplified detection algorithm in order to reduce the computational complexity of the proposed decentralized detection scheme. In Section 5, numerical results on the performance of the proposed detection algorithms are presented. Finally, concluding remarks are given in Section 6.
2. Preliminaries on Decentralized Detection
As anticipated in Section 1, we focus on a network scenario where the status of the phenomenon under observation is characterized by a number  of "edges," that is, sensor positions where the phenomenon changes its status from "0" (e.g., absence of a critical gas) to "1" (e.g., presence of a critical gas) or vice versa. For the sake of simplicity, we assume that the status of the phenomenon is independent from sensor to sensor. The proposed approach, however, can be extended to take into account the presence of correlation between sensors. In general, the presence of correlation would limit the number of edges and, if properly exploited at the AP, improve the performance with respect to that obtained in the following. A pictorial description of the proposed scenario is given in Figure 1(c). In particular, we investigate the performance when the communication links between the sensors and the AP are noisy, that is, errors may be introduced during data transmission. Note that, under the assumption that the geographical positions are known, from the estimated edges' positions the real geographic structure of the phenomenon (e.g., area with gas leakage) can be immediately determined.
of "edges," that is, sensor positions where the phenomenon changes its status from "0" (e.g., absence of a critical gas) to "1" (e.g., presence of a critical gas) or vice versa. For the sake of simplicity, we assume that the status of the phenomenon is independent from sensor to sensor. The proposed approach, however, can be extended to take into account the presence of correlation between sensors. In general, the presence of correlation would limit the number of edges and, if properly exploited at the AP, improve the performance with respect to that obtained in the following. A pictorial description of the proposed scenario is given in Figure 1(c). In particular, we investigate the performance when the communication links between the sensors and the AP are noisy, that is, errors may be introduced during data transmission. Note that, under the assumption that the geographical positions are known, from the estimated edges' positions the real geographic structure of the phenomenon (e.g., area with gas leakage) can be immediately determined.
Denote the overall phenomenon status as  , where
, where  is the status at the
is the status at the  th sensor (
th sensor ( ). The signal observed at the
). The signal observed at the  th sensor can be expressed as
th sensor can be expressed as

where

and  are additive observation noise samples. Assuming that the noise samples
are additive observation noise samples. Assuming that the noise samples  are independent with the same Gaussian distribution
are independent with the same Gaussian distribution  , the common signal-to-noise ratio (SNR) at the sensors can be defined as follows:
, the common signal-to-noise ratio (SNR) at the sensors can be defined as follows:

Each sensor processes (through proper quantization) the observed signal and the value output by the  th sensor is denoted as
th sensor is denoted as  , where the function
, where the function  depends on the specific quantization strategy. In the following, we consider (i) binary quantization and (ii) absence of quantization. The analytical framework in the case of multilevel quantization can be easily derived from that presented in [18] for a scenario with ideal communication links. Upon reception of the messages sent by the sensors, the goal of the AP is to estimate, through MMSE or simplified detection strategies, the status of the binary phenomenon
depends on the specific quantization strategy. In the following, we consider (i) binary quantization and (ii) absence of quantization. The analytical framework in the case of multilevel quantization can be easily derived from that presented in [18] for a scenario with ideal communication links. Upon reception of the messages sent by the sensors, the goal of the AP is to estimate, through MMSE or simplified detection strategies, the status of the binary phenomenon  . As reference performance indicator, we will consider the quadratic distance (simply referred to as "distance")
. As reference performance indicator, we will consider the quadratic distance (simply referred to as "distance")  between the observed phenomenon
between the observed phenomenon  and its estimate
and its estimate  , that is,
, that is,

where the notation  stands for bit-by-bit EX-OR and
stands for bit-by-bit EX-OR and  is the estimated phenomenon. Given that
is the estimated phenomenon. Given that  are the true edges' positions,
are the true edges' positions,  can be directly derived from the estimated edges' positions
can be directly derived from the estimated edges' positions  . Therefore, our goal is to accurately estimate
. Therefore, our goal is to accurately estimate  . The particular expression for
. The particular expression for  depends on the chosen distributed detection strategy, as will be shown in the following. We will also consider, as a meaningful performance indicator, the probability of LSEE, that is, the probability that the estimated phenomenon status at a sensor is wrong. In Section 5.2, it will be shown how the probability of LSEE is related to
depends on the chosen distributed detection strategy, as will be shown in the following. We will also consider, as a meaningful performance indicator, the probability of LSEE, that is, the probability that the estimated phenomenon status at a sensor is wrong. In Section 5.2, it will be shown how the probability of LSEE is related to  .
.
3. MMSE One-Dimensional Edge Detection
The following assumptions are expedient to simplify the derivation of the MMSE one-dimensional edge detection strategy:
-
(i)
the edges cannot be in correspondence to the first sensor and the last sensor: the number of edges must then be such that
 (in particular,
(in particular, 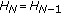 );
); -
(ii)
the phenomenon status is perfectly known at the first sensor: without loss of generality, we assume
 .
.
According to the above assumptions, the positions of the  edges
edges  have to satisfy the following conditions:
have to satisfy the following conditions:

Therefore, between positions 1 and  the phenomenon status is "0," between positions
the phenomenon status is "0," between positions  and
and  the phenomenon status is "1," and so on. The following bound on the position of the
the phenomenon status is "1," and so on. The following bound on the position of the  th edge must necessarily hold:
th edge must necessarily hold:

For each value of  , condition (6) formalizes the intuitive idea that the
, condition (6) formalizes the intuitive idea that the  th edge cannot fall beyond the
th edge cannot fall beyond the  th position, in order for the successive (remaining)
th position, in order for the successive (remaining)  edges to have admissible positions.
edges to have admissible positions.
In the remainder of this section, we derive the MMSE detection rules depending on the quantization strategy at the sensors.
3.1. Binary Quantization
In this scenario, the  th sensor makes a decision comparing its observation
th sensor makes a decision comparing its observation  with a threshold value
with a threshold value  , and computes a local binary decision
, and computes a local binary decision  , where
, where  is the unit step function. To optimize the system performance, the thresholds
is the unit step function. To optimize the system performance, the thresholds  need to be properly selected. In this paper, regardless of the value of
need to be properly selected. In this paper, regardless of the value of  , a common value
, a common value  at all sensors is considered [18].
at all sensors is considered [18].
In the presence of binary quantization at the sensors, the noisy communication links are modeled as BSCs. We denote as  the sequence of binary decisions at the sensors and
the sequence of binary decisions at the sensors and  as the sequence of binary decisions received at the AP. Under the assumption of BSCs, the received decisions
as the sequence of binary decisions received at the AP. Under the assumption of BSCs, the received decisions  might differ from
might differ from  (there could be "bit-flipping" in some of the links). In particular, the
(there could be "bit-flipping" in some of the links). In particular, the  th decision received at the AP (
th decision received at the AP ( ) can be expressed as
) can be expressed as

where  is the cross-over probability of the BSC.
is the cross-over probability of the BSC.
Theorem 1.
Assuming that  is known at the AP and denoting by
is known at the AP and denoting by  the positions of the edges, the
the positions of the edges, the  th (
th ( ) MMSE detected edge can be expressed as
) MMSE detected edge can be expressed as

(For ease of notational simplicity, in (8) we use the same symbol  to denote both the random variable (in the second term) and its realization (in the third and fourth terms). This simplified notational approach will be considered in the remainder of Section 3. The context should eliminate any ambiguity.)
to denote both the random variable (in the second term) and its realization (in the third and fourth terms). This simplified notational approach will be considered in the remainder of Section 3. The context should eliminate any ambiguity.)
Proof.
The MMSE detection strategy leads to the selection of the following vector of edges [19]:

The  th component (
th component ( ) of the vector
) of the vector  can then be written as
can then be written as

Taking into account the constraint (6), the upper and lower limits of the sum in (10) can be further refined, obtaining the right-hand side expression in (8).
The computation of the conditional probabilities appearing at the right-hand side of (8) can be carried out as outlined in Appendix A.1.
3.2. Absence of Quantization
In this case, a local likelihood value, such as the conditional probability density function (PDF) of the observable, is transmitted from each sensor to the AP. Obviously, this is not a practical approach, since an infinite bandwidth would be required to transmit a PDF value. However, investigating this case allows to derive useful information about the limiting performance of the considered detection schemes, since transmission of the PDFs of the observables does not entail any information loss at the sensors. Note that this limiting performance can be achieved by using multilevel quantization at the sensors with an increasing number of quantization bits [18]. Since the sensors transmit real numbers (the likelihood values) to the AP, the BSC model for noisy communication links does not apply. In order to obtain results comparable with those associated with a scenario with binary quantization, we consider AWGN communication links. In other words, the  th observable at the AP (
th observable at the AP ( ), denoted as
), denoted as  , can be written as
, can be written as

where  is the observable transmitted by the
is the observable transmitted by the  th sensor and
th sensor and  has a Gaussian distribution
has a Gaussian distribution  . The value of
. The value of  is set in order to make the AWGN scenario consistent with the BSC scenario. In particular, in the presence of uncoded binary phase shift keying (BPSK) transmission over AWGN links, the bit error rate is [20]
is set in order to make the AWGN scenario consistent with the BSC scenario. In particular, in the presence of uncoded binary phase shift keying (BPSK) transmission over AWGN links, the bit error rate is [20]

with  . Therefore, imposing that the BER in (12) is equal to the cross-over probability
. Therefore, imposing that the BER in (12) is equal to the cross-over probability  of the equivalent BSC, the corresponding value of
of the equivalent BSC, the corresponding value of  can be obtained. This makes the performance comparison between the cases with binary quantization and without quantization consistent.
can be obtained. This makes the performance comparison between the cases with binary quantization and without quantization consistent.
Theorem 2.
Assuming that  is known at the AP, the
is known at the AP, the  th (
th ( ) MMSE detected edge can be recursively computed from
) MMSE detected edge can be recursively computed from

Proof.
The proof follows exactly that of Theorem 1, but for replacing  with
with  .
.
The computation of the conditional probabilities appearing at the right-hand side of (13) can be carried out as outlined in Appendix A.2.
3.3. Remarks
We would like to remark that the MMSE strategy outlined above is based, regardless of the quantization strategy, on the assumption of knowledge of the number of edges  at the AP. However, in the scenario of interest, for example, monitoring of a gas leakage, this knowledge may not be a priori available and
at the AP. However, in the scenario of interest, for example, monitoring of a gas leakage, this knowledge may not be a priori available and  should be properly estimated. In this case, by averaging over all possible realizations of
should be properly estimated. In this case, by averaging over all possible realizations of  , the average performance, with respect to the number of edges, could be determined. This extension goes beyond the scope of this paper. In fact, the performance of the MMSE algorithm with knowledge of
, the average performance, with respect to the number of edges, could be determined. This extension goes beyond the scope of this paper. In fact, the performance of the MMSE algorithm with knowledge of  at the AP will be used as a benchmark for the performance of the simplified (and feasible) one-dimensional edge detection algorithms introduced in Section 4.
at the AP will be used as a benchmark for the performance of the simplified (and feasible) one-dimensional edge detection algorithms introduced in Section 4.
4. Simplified One-Dimensional Edge Detection
Since the computational complexity of the MMSE detection strategy increases very quickly with the number of phenomenon edges (see Section 5.4 for more details), the derivation of a simplified distributed detection algorithm with low complexity (but limited performance loss) is crucial. As considered in Section 3 for MMSE detection, we distinguish between scenarios with binary quantization and without quantization.
4.1. Binary Quantization
Define the following "reconstruction" function:

where  (
( ) and the conditional probabilities
) and the conditional probabilities  are evaluated in Appendix B.1. The key idea of our approach is the following. While the phenomenon does not change its status, the function
are evaluated in Appendix B.1. The key idea of our approach is the following. While the phenomenon does not change its status, the function  is a monotonically increasing (or decreasing) function of
is a monotonically increasing (or decreasing) function of  . In correspondence to each change of the phenomenon status, the function
. In correspondence to each change of the phenomenon status, the function  changes its monotonic behavior. More precisely, a phenomenon variation from "0" to "1" corresponds to a change, trendwise, from increasing to decreasing; a phenomenon variation from "1" to "0" corresponds to a change, trendwise, from decreasing to increasing. Therefore, through the monotonicity changes of
changes its monotonic behavior. More precisely, a phenomenon variation from "0" to "1" corresponds to a change, trendwise, from increasing to decreasing; a phenomenon variation from "1" to "0" corresponds to a change, trendwise, from decreasing to increasing. Therefore, through the monotonicity changes of  one can detect the positions of the edges. Moreover, since
one can detect the positions of the edges. Moreover, since 
 it follows that the term
it follows that the term  is always positive and, therefore, can be neglected to study the monotonicity of
is always positive and, therefore, can be neglected to study the monotonicity of  . An illustrative example of the behavior of
. An illustrative example of the behavior of  is shown in Figure 2, where the phenomenon under observation and the reconstruction function are shown, together with the detected edges. In this pictorial example, the estimated phenomenon coincides with the observed phenomenon.
is shown in Figure 2, where the phenomenon under observation and the reconstruction function are shown, together with the detected edges. In this pictorial example, the estimated phenomenon coincides with the observed phenomenon.
4.2. Absence of Quantization
In the absence of quantization at the sensors, one can define the following reconstruction function:

where  (
( ) and
) and  are computed in Appendix B.2. The edge detection algorithm at the AP is then identical to that presented in the case with binary quantization, but for the use of
are computed in Appendix B.2. The edge detection algorithm at the AP is then identical to that presented in the case with binary quantization, but for the use of  at the place of
at the place of  .
.
4.3. Remarks
One should observe that, unlike the MMSE strategy, our simplified edge detection algorithm (with binary quantization and no quantization, resp.) does not require knowledge of the number of edges  at the AP. Therefore, the simplified algorithm is suitable for area monitoring applications, since in this scenario
at the AP. Therefore, the simplified algorithm is suitable for area monitoring applications, since in this scenario  is not a priori known. Obviously, we expect that the proposed algorithm will incur a performance degradation with respect to the MMSE algorithm. However, this loss will be limited, as shown with simulation results in Section 5.
is not a priori known. Obviously, we expect that the proposed algorithm will incur a performance degradation with respect to the MMSE algorithm. However, this loss will be limited, as shown with simulation results in Section 5.
5. Numerical Results
5.1. Performance Analysis: Distance
The performance of the proposed detection schemes is first analyzed by evaluating of the distance  between the true phenomenon
between the true phenomenon  and the estimated phenomenon
and the estimated phenomenon  . More precisely, the Monte Carlo simulation results are obtained through the following steps:
. More precisely, the Monte Carlo simulation results are obtained through the following steps:
-
(1)
the number of edges is randomly generated—the AP is assumed to know this number in the MMSE case;
-
(2)
for a selected number of edges, their positions are randomly generated (From an operative viewpoint, in a scenario where the number of edges is larger than one, after the position of an edge is extracted, the following edge position is randomly chosen among the remaining positions. After all edges' positions are extracted, they are ordered.);
-
(3)
either the sensors' decisions or the PDFs of the observables, according to the chosen quantization strategy at the sensors, are transmitted to the AP;
-
(4)
a noisy version of the transmitted data is received at the AP;
-
(5)
the AP detects the edges' positions through either MMSE or simplified detection algorithms;
-
(6)
the distance
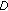 is evaluated, on the basis of the detected sequence of edges' positions;
is evaluated, on the basis of the detected sequence of edges' positions; -
(7)
steps (
 )
)  (
( ) are repeated for sufficiently large number of times in order to derive statistically meaningful results;
) are repeated for sufficiently large number of times in order to derive statistically meaningful results; -
(8)
the average distance
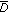 is finally computed as the arithmetic average of the distances computed at the previous iterations (in step (
is finally computed as the arithmetic average of the distances computed at the previous iterations (in step (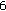 ) at each iteration).
) at each iteration).
In Figure 3, the distance is shown, as a function of the cross-over probability  , in a scenario with
, in a scenario with  sensors and binary quantization—in this case, the communication links are modeled as BSCs. Three values for the sensor SNR are considered: (i) −10 dB, (ii) 0 dB, and (iii) 10 dB. Both MMSE and simplified detection algorithms at the AP are considered. As expected, the use of the simplified detection algorithm at the AP leads to a performance worse than that with the MMSE detection algorithm. However, the higher is the sensor SNR, the lower is the difference between the performance of the two algorithms. Moreover, one can observe that the distance might not converge to zero (as in the case with ideal communication links), due to the presence of two independent noise components (i.e., observation and communication noises). For a sufficiently large value of the sensor SNR, however, the distance reduces to zero when
sensors and binary quantization—in this case, the communication links are modeled as BSCs. Three values for the sensor SNR are considered: (i) −10 dB, (ii) 0 dB, and (iii) 10 dB. Both MMSE and simplified detection algorithms at the AP are considered. As expected, the use of the simplified detection algorithm at the AP leads to a performance worse than that with the MMSE detection algorithm. However, the higher is the sensor SNR, the lower is the difference between the performance of the two algorithms. Moreover, one can observe that the distance might not converge to zero (as in the case with ideal communication links), due to the presence of two independent noise components (i.e., observation and communication noises). For a sufficiently large value of the sensor SNR, however, the distance reduces to zero when  tends to zero, in agreement with the results in [18].
tends to zero, in agreement with the results in [18].
In Figure 4, the distance  is shown, as a function of the sensor SNR, in a scenario with
is shown, as a function of the sensor SNR, in a scenario with  sensors and binary quantization at the sensors. Four different values of the cross-over probability
sensors and binary quantization at the sensors. Four different values of the cross-over probability  are considered: (i) 0.1, (ii) 0.2, (iii) 0.3, and (iv) 0.4. The performance with both MMSE and simplified detection algorithms at the AP is investigated. Unlike the results presented in [18] for a scenario with ideal communication links, there appears to be a distance floor (higher than zero) for larger and larger values of the sensor SNR. This is to be expected, since the communication noise (independent of the observation noise at the sensors) prevents the AP from correctly recovering the data sent by the sensors. In particular, when the cross-over probability is sufficiently large (e.g.,
are considered: (i) 0.1, (ii) 0.2, (iii) 0.3, and (iv) 0.4. The performance with both MMSE and simplified detection algorithms at the AP is investigated. Unlike the results presented in [18] for a scenario with ideal communication links, there appears to be a distance floor (higher than zero) for larger and larger values of the sensor SNR. This is to be expected, since the communication noise (independent of the observation noise at the sensors) prevents the AP from correctly recovering the data sent by the sensors. In particular, when the cross-over probability is sufficiently large (e.g.,  ), the performance does not depend on the value of the sensor SNR, since the noisy communication links make the data sent by the sensors very unreliable, regardless of the observation quality. Finally, one can observe that, for small values of the sensor SNR, the simplified detection algorithm shows a nonnegligible performance loss with respect to the MMSE detection algorithm. However, this loss reduces to zero, for increasing values of the sensor SNR, only for sufficiently small values of
), the performance does not depend on the value of the sensor SNR, since the noisy communication links make the data sent by the sensors very unreliable, regardless of the observation quality. Finally, one can observe that, for small values of the sensor SNR, the simplified detection algorithm shows a nonnegligible performance loss with respect to the MMSE detection algorithm. However, this loss reduces to zero, for increasing values of the sensor SNR, only for sufficiently small values of  . In other words, if the communication links are not reliable, then increasing the accuracy of the observations at the sensors is useless.
. In other words, if the communication links are not reliable, then increasing the accuracy of the observations at the sensors is useless.
In Figure 5 the distance  is shown, as a function of the sensor SNR, in a scenario with
is shown, as a function of the sensor SNR, in a scenario with  sensors and absence of quantization—in this case, the noisy communication links are modeled as AWGN channels. Two different values of the bit error rate
sensors and absence of quantization—in this case, the noisy communication links are modeled as AWGN channels. Two different values of the bit error rate  (corresponding to different values of
(corresponding to different values of  according to (12)) are considered: (i) 0.1 and (ii) 0.2. The performance of both MMSE and simplified detection algorithms at the AP is evaluated. One can observe that, unlike the case with binary quantization at the sensors, the distance reduces to zero when the sensor SNR increases, that is, no floor appears. Moreover, the distance with the simplified detection rule at the AP approaches that with the MMSE detection rule, that is, it reduces to zero. This means that the proposed simplified detection algorithm is (asymptotically) effective. Obviously, this is only a theoretical performance limit. In fact, even if the communication links were noisy, the transmission of the "exact" observables (requiring an infinite bandwidth) from the sensors would allow a correct estimation of the true phenomenon. This cannot happen in realistic scenarios with limited transmission bandwidths.
according to (12)) are considered: (i) 0.1 and (ii) 0.2. The performance of both MMSE and simplified detection algorithms at the AP is evaluated. One can observe that, unlike the case with binary quantization at the sensors, the distance reduces to zero when the sensor SNR increases, that is, no floor appears. Moreover, the distance with the simplified detection rule at the AP approaches that with the MMSE detection rule, that is, it reduces to zero. This means that the proposed simplified detection algorithm is (asymptotically) effective. Obviously, this is only a theoretical performance limit. In fact, even if the communication links were noisy, the transmission of the "exact" observables (requiring an infinite bandwidth) from the sensors would allow a correct estimation of the true phenomenon. This cannot happen in realistic scenarios with limited transmission bandwidths.
Distance, as a function of the sensor SNR, in a scenario with  sensors and absence of quantization. Two different values of the equivalent bit error rate
sensors and absence of quantization. Two different values of the equivalent bit error rate  (corresponding to different values of
(corresponding to different values of  according to (12)) are considered: (i) 0.1 and (ii) 0.2. Both MMSE and simplified detection algorithms at the AP are considered.
according to (12)) are considered: (i) 0.1 and (ii) 0.2. Both MMSE and simplified detection algorithms at the AP are considered.
In order to evaluate the loss incurred by the use of the simplified detection algorithm, it is expedient to introduce the following percentage loss:

where  and
and  correspond to the distances obtained with the simplified and MMSE detection algorithms, respectively. The intuition behind the definition of
correspond to the distances obtained with the simplified and MMSE detection algorithms, respectively. The intuition behind the definition of  in (16), corresponding to the geometric average of
in (16), corresponding to the geometric average of  and
and  , is the following.
, is the following.  represents the relative loss of the simplified detection rule with respect to the MMSE detection rule. However, using only this term could be misleading. In fact, for high sensor SNRs, the terms
represents the relative loss of the simplified detection rule with respect to the MMSE detection rule. However, using only this term could be misleading. In fact, for high sensor SNRs, the terms  and
and  are much lower than
are much lower than  (the maximum possible distance). Therefore, even if
(the maximum possible distance). Therefore, even if  (e.g.,
(e.g.,  and
and  with
with  ), both algorithms might perform very well. The introduction of
), both algorithms might perform very well. The introduction of  eliminates this ambiguity, since it represents the relative loss (between MMSE and simplified detection algorithms) with respect to the maximum (quadratic) distance, that is,
eliminates this ambiguity, since it represents the relative loss (between MMSE and simplified detection algorithms) with respect to the maximum (quadratic) distance, that is,  . In Figure 6, the behavior of
. In Figure 6, the behavior of  is shown, as a function of the sensor SNR, in a scenario with
is shown, as a function of the sensor SNR, in a scenario with  . In the region of interest (
. In the region of interest ( dB), one can observe that
dB), one can observe that  is lower than 20%, that is, the proposed simplified detection algorithm is effective.
is lower than 20%, that is, the proposed simplified detection algorithm is effective.
In Figure 7(a), we investigate the distance, as a function of the cross-over probability  , in a scenario with binary quantization. Three values for the number of sensors are considered: (i) 16, (ii) 32, and (iii) 64. For each number of sensors, the sensor SNR assumes three possible values: (i) −10 dB, (ii) 0 dB, and (iii) 10 dB. In these scenarios, only the simplified detection algorithm is considered, since the computational complexity of the MMSE detection algorithm becomes unfeasible (see Section 5.4). In all cases, the distance is a monotonically nondecreasing function of
, in a scenario with binary quantization. Three values for the number of sensors are considered: (i) 16, (ii) 32, and (iii) 64. For each number of sensors, the sensor SNR assumes three possible values: (i) −10 dB, (ii) 0 dB, and (iii) 10 dB. In these scenarios, only the simplified detection algorithm is considered, since the computational complexity of the MMSE detection algorithm becomes unfeasible (see Section 5.4). In all cases, the distance is a monotonically nondecreasing function of  , but it might not converge to zero for
, but it might not converge to zero for  , because of the residual observation noise. For a sufficiently high value of the sensor SNR, however, the distance becomes very low when
, because of the residual observation noise. For a sufficiently high value of the sensor SNR, however, the distance becomes very low when  , in agreement with the results in Figure 3. Moreover, note that for
, in agreement with the results in Figure 3. Moreover, note that for  the distance, for a given number of sensors, reaches the same value, regardless of the sensor SNR. This is due to the fact that, when
the distance, for a given number of sensors, reaches the same value, regardless of the sensor SNR. This is due to the fact that, when  , the AP receives "random" decisions and its estimate
, the AP receives "random" decisions and its estimate  is extracted randomly among all possible ones for the corresponding number of edges. This limit (for
is extracted randomly among all possible ones for the corresponding number of edges. This limit (for  ), denoted as
), denoted as  , depends only on
, depends only on  and in Appendix C we derive a simple analytical approximation for it.
and in Appendix C we derive a simple analytical approximation for it.
Distance, as a function of the cross-over probability  , in a scenario with binary quantization and simplified detection algorithm. Three values for the number of sensors are considered: (i) 16, (ii) 32, and (iii) 64. For a given number of sensors, three values for the sensor SNR are analyzed: (i) −10 dB, (ii) 0 dB, and (iii) 10 dB. In case (a), the distance is shown, whereas in case (b) the distance is normalized, for each value of
, in a scenario with binary quantization and simplified detection algorithm. Three values for the number of sensors are considered: (i) 16, (ii) 32, and (iii) 64. For a given number of sensors, three values for the sensor SNR are analyzed: (i) −10 dB, (ii) 0 dB, and (iii) 10 dB. In case (a), the distance is shown, whereas in case (b) the distance is normalized, for each value of  , to its corresponding maximum value (
, to its corresponding maximum value ( ).
).
In order to better understand the impacts of the communication and observation noises, it is expedient to normalize, sensor SNR by sensor SNR,  by
by  . In this way, the normalized distance
. In this way, the normalized distance  , denoted as
, denoted as  , assumes values in
, assumes values in  and allows to directly compare scenarios with different numbers of sensors. The normalized versions of the distance curves of Figure 7(a) are shown in Figure 7(b). Obviously, when
and allows to directly compare scenarios with different numbers of sensors. The normalized versions of the distance curves of Figure 7(a) are shown in Figure 7(b). Obviously, when  the distance goes to the same value (i.e., 1), regardless of the values of
the distance goes to the same value (i.e., 1), regardless of the values of  and
and  . As expected, for a given value of
. As expected, for a given value of  (i.e., the communication quality), the higher the sensor SNR is (i.e., the observation quality) the more pronounced is the performance degradation for increasing values of
(i.e., the communication quality), the higher the sensor SNR is (i.e., the observation quality) the more pronounced is the performance degradation for increasing values of  .
.
5.2. Performance Analysis: Probability of Local Status Estimation Error
Considering the same Monte Carlo simulation scenario described at the beginning of Section 5.1, the probability of LSEE can be approximated as follows:

where  is the number of simulation runs, and
is the number of simulation runs, and  is the probability of LSEE at the
is the probability of LSEE at the  th simulation run and can be written as
th simulation run and can be written as

where  is the distance at the
is the distance at the  th simulation run. It then follows:
th simulation run. It then follows:

Observing that  is a concave function and by using the Jensen inequality [21], one can write
is a concave function and by using the Jensen inequality [21], one can write

Therefore, the probability of LSEE can be upper bounded as follows:

In other words, the evaluation of the average distance  allows to directly derive un upper bound (UB) on the probability of LSEE. In Figure 8, the probability of LSEE is shown, as a function of the sensor SNR, for the same cases shown in Figure 5 (note that similar considerations hold for all other scenarios considered in Section 5.1). For the sake of graphical clarity, the exact performance is reported only for the scenario with the MMSE detection rule and
allows to directly derive un upper bound (UB) on the probability of LSEE. In Figure 8, the probability of LSEE is shown, as a function of the sensor SNR, for the same cases shown in Figure 5 (note that similar considerations hold for all other scenarios considered in Section 5.1). For the sake of graphical clarity, the exact performance is reported only for the scenario with the MMSE detection rule and  . However, in all cases the maximum SNR distance between the UB and the true curve is less than 2 dB (for
. However, in all cases the maximum SNR distance between the UB and the true curve is less than 2 dB (for  ). From the results in Figure 8, a bimodal behavior of the probability of LSEE can be observed. In fact, this probability decreases very slowly, for increasing SNRs, till a value around
). From the results in Figure 8, a bimodal behavior of the probability of LSEE can be observed. In fact, this probability decreases very slowly, for increasing SNRs, till a value around  , below which it drops very rapidly to zero. The knee of the probability of LSEE is placed at an SNR which depends on the chosen detection (MMSE or simplified) strategy and on the communication noise level. Note that at very low SNR the probability of LSEE tends to be 0.5, that is, it randomly decides on the phenomenon status at each sensor.
, below which it drops very rapidly to zero. The knee of the probability of LSEE is placed at an SNR which depends on the chosen detection (MMSE or simplified) strategy and on the communication noise level. Note that at very low SNR the probability of LSEE tends to be 0.5, that is, it randomly decides on the phenomenon status at each sensor.
Probability of LSEE, as a function of the sensor SNR, for the same cases shown in Figure 5. For the MMSE case with  , the exact performance and the UB are shown. For the other cases, only the UBs are shown.
, the exact performance and the UB are shown. For the other cases, only the UBs are shown.
5.3. System Robustness
We now investigate the robustness of the proposed simplified distributed detection algorithm with respect to possible mismatches between the actual system parameters and the used ones. In particular, we focus on a scenario with binary quantization at the sensors. Our conclusions hold also in other scenarios with different quantization strategies. In order to investigate the system robustness, we consider possible mismatches in the observation and communication phases, respectively.
-
(i)
In the observation phase, we assume that there could be an error in the decision threshold used at each sensor. More precisely, denoting by
 the optimized decision threshold (
the optimized decision threshold ( ), we assume that each sensor makes use of an actual decision threshold which is uniformly distributed in
), we assume that each sensor makes use of an actual decision threshold which is uniformly distributed in  , where
, where 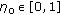 . The decision thresholds at different sensors are supposed to be independent.
. The decision thresholds at different sensors are supposed to be independent. -
(ii)
In the communication phase, we assume that, while the detection algorithm at the AP assumes a constant cross-over probability (denoted as
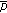 ) for all communication links, the actual cross-over probabilities in the various links are independent and uniformly distributed in the
) for all communication links, the actual cross-over probabilities in the various links are independent and uniformly distributed in the 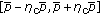 , where
, where 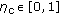 .
.
For the sake of simplicity, we consider a scenario with  sensors, binary quantization at the sensors, and simplified detection rule at the AP. In Figure 9, we show the performance results, in terms of distance versus (a)
sensors, binary quantization at the sensors, and simplified detection rule at the AP. In Figure 9, we show the performance results, in terms of distance versus (a)  and (b)
and (b)  , in the presence of mismatches in the (a) observation phase and (b) communication phases, respectively. In case (a), three values of the cross-over probability
, in the presence of mismatches in the (a) observation phase and (b) communication phases, respectively. In case (a), three values of the cross-over probability  of the communication links are considered: (i) 0, (ii) 0.2, and (iii) 0.5. In case (b), three values are considered for the average cross-over probability
of the communication links are considered: (i) 0, (ii) 0.2, and (iii) 0.5. In case (b), three values are considered for the average cross-over probability  : (i) 0.1, (ii) 0.2, and (iii) 0.5. For each value of
: (i) 0.1, (ii) 0.2, and (iii) 0.5. For each value of  or
or  , three values for the sensor SNR are considered: (i) −10 dB, (ii) 0 dB, and (iii) 10 dB.
, three values for the sensor SNR are considered: (i) −10 dB, (ii) 0 dB, and (iii) 10 dB.
Distance, as a function of (a)  and (b)
and (b)  , in the presence of mismatches in the (a) observation phase and (b) communication phases, respectively. In all cases, we consider
, in the presence of mismatches in the (a) observation phase and (b) communication phases, respectively. In all cases, we consider  sensors, binary quantization at the sensors, and simplified detection rule at the AP. Various combinations of the values of
sensors, binary quantization at the sensors, and simplified detection rule at the AP. Various combinations of the values of  (in case (a)),
(in case (a)),  (in case (b)), and the sensor SNR are considered.
(in case (b)), and the sensor SNR are considered.
In case (a), one can observe that, for sufficiently high values of the communication noise intensity  , there is a performance degradation (i.e., the distance increases) for increasing observation threshold mismatch (i.e., for increasing values of
, there is a performance degradation (i.e., the distance increases) for increasing observation threshold mismatch (i.e., for increasing values of  ), regardless of the sensor SNR. On the other hand, for low values of the communication noise intensity
), regardless of the sensor SNR. On the other hand, for low values of the communication noise intensity  and very high values of the sensor SNR (e.g.,
and very high values of the sensor SNR (e.g.,  dB), for increasing values of
dB), for increasing values of  the distance slightly increases. Finally, for low values of the communication noise intensity
the distance slightly increases. Finally, for low values of the communication noise intensity  and low/medium values of the sensor SNR, the distance slightly decreases for increasing values of
and low/medium values of the sensor SNR, the distance slightly decreases for increasing values of  —this is due to the fact that in the presence of strong observation noise, the considered local decision strategy is no longer optimized. In all possible situations, the distance saturates at
—this is due to the fact that in the presence of strong observation noise, the considered local decision strategy is no longer optimized. In all possible situations, the distance saturates at  . In other words, the proposed simplified detection strategy is robust against local decision threshold mismatches.
. In other words, the proposed simplified detection strategy is robust against local decision threshold mismatches.
In case (b), instead, the decision threshold  at the sensors is fixed to
at the sensors is fixed to  . As one can see, for high values of
. As one can see, for high values of  , for increasing variability of the communication link quality (i.e., for increasing values of
, for increasing variability of the communication link quality (i.e., for increasing values of  ) the performance rapidly degrades. For low values of
) the performance rapidly degrades. For low values of  , for increasing
, for increasing  there is a slight decrease of the distance, that is, a slight performance improvement—as previously commented, this depends on the fact that local sensor decision and AP detection strategies are no longer optimized. As in case (a), the performance with any scheme saturates at
there is a slight decrease of the distance, that is, a slight performance improvement—as previously commented, this depends on the fact that local sensor decision and AP detection strategies are no longer optimized. As in case (a), the performance with any scheme saturates at  , that is, the proposed simplified detection rule is robust also against mismatches in the communication phase.
, that is, the proposed simplified detection rule is robust also against mismatches in the communication phase.
As a final remark, we point out that the fact that the proposed simplified detection rule is insensitive to strong fluctuations of the observation and communication qualities means that the system performance basically depends on the average observation and communication conditions.
5.4. Computational Complexity
Finally, we evaluate the improvement, in terms of computational complexity reduction with respect to the MMSE detection rule, brought by the use of the simplified detection algorithms. As complexity indicators, we choose the numbers of additions and multiplications (referred to as  and
and  , resp.) required by the considered detection algorithms, evaluated as functions of the number of sensors
, resp.) required by the considered detection algorithms, evaluated as functions of the number of sensors  . In a scenario with noisy communication links, the same considerations carried out in [18] for a scenario with ideal communication links still hold. In fact, the structures of the proposed detection algorithms are the same in both scenarios, since only the expressions of the used probabilities and PDFs change. Therefore, it can be shown that the numbers of additions and multiplications required by the MMSE detection algorithm would be
. In a scenario with noisy communication links, the same considerations carried out in [18] for a scenario with ideal communication links still hold. In fact, the structures of the proposed detection algorithms are the same in both scenarios, since only the expressions of the used probabilities and PDFs change. Therefore, it can be shown that the numbers of additions and multiplications required by the MMSE detection algorithm would be  and
and  . On the other hand, the computational complexity of the proposed simplified detection algorithm is characterized by
. On the other hand, the computational complexity of the proposed simplified detection algorithm is characterized by  and
and  , showing a significant complexity reduction with respect to the MMSE detection algorithm—this also justifies the performance loss at small values of the sensor SNR.
, showing a significant complexity reduction with respect to the MMSE detection algorithm—this also justifies the performance loss at small values of the sensor SNR.
6. Concluding Remarks
In this paper, we have analyzed the problem of one-dimensional edge detection in wireless sensor networking scenarios with noisy communication links. This situation arises in many practical applications such as those where an area of interest needs to be actively monitored to detect the presence of a phenomenon, for example, the presence of a gas leakage. We have proposed an analytical framework considering two quantization strategies at the sensors: (i) no quantization at the sensors and (ii) binary quantization. In each case, the MMSE detection algorithm at the AP has been derived and the impacts of relevant network parameters (e.g., the sensor SNR, the communication noise level, and the number of sensors) have been investigated. Then, a low-complexity and feasible detection algorithm, which does not require any a priori information on the number of edges, has been derived. We have shown that the performance penalty induced by the use of the simplified detection algorithms is asymptotically (for high sensor SNR and low communication noise level) negligible. Moreover, the simplified detection algorithm has proved to be robust against system parameters' variations. Finally, we have quantified the relevant computational complexity reduction brought by the use of the simplified detection algorithms with respect to the MMSE ones.
Appendices
A. Details on the MMSE Distributed Detection Strategy
A.1. Binary Quantization
The probability  (
( ) can be obtained by marginalizing the joint probabilities of the edges' positions as follows:
) can be obtained by marginalizing the joint probabilities of the edges' positions as follows:

where  and the notation
and the notation  indicates all sequences
indicates all sequences  with
with  at the
at the  th position.
th position.
At this point, one needs to evaluate the joint conditional probability mass functions (PMFs) at the right-hand side of (A.1). By applying the Bayes formula and the total probability theorem [22], after a few manipulations one obtains

We now characterize the three multiplicative terms at the right-hand side of (A.2). The first multiplicative term at the right-hand side of (A.2) can be written as

where we have used the fact that the sensors' decisions are conditionally independent. Note that  if
if  is even, whereas
is even, whereas  if
if  is odd. The component conditional probabilities at the right-hand side of (A.3) can be expressed as follows:
is odd. The component conditional probabilities at the right-hand side of (A.3) can be expressed as follows:

where

After a few manipulations, one obtains:

where

with  .
.
The second multiplicative term at the right-hand side of (A.2) can be written, using the chain rule [22], as

where we have used the fact that the position of the  th edge depends only on the position of the (previous)
th edge depends only on the position of the (previous)  th edge. The multiplicative terms at the right-hand side of (A.8) can be evaluated by observing that each edge is spatially distributed according to the constraints in (6). In particular, by using combinatorics, it follows that
th edge. The multiplicative terms at the right-hand side of (A.8) can be evaluated by observing that each edge is spatially distributed according to the constraints in (6). In particular, by using combinatorics, it follows that

The last term at the right-hand side of (A.2) (i.e., the denominator) can be easily computed by observing that it is composed of terms similar to those evaluated in (A.3) and (A.8).
A.2. Absence of Quantization
The conditional probabilities at the right-hand side of (13) can be obtained, as in Appendix A.1, through proper marginalization of joint conditional PMFs of the following type:

Since sensors' observations are independent, it holds that

where

One can notice that the effects of observation and communication AWGNs add directly.
B. Details on the Simplified One-Dimensional Edge Detection Strategy
B.1. Binary Quantization
The conditional PMFs  (
( ;
;  ) in (14) can be written, by applying the Bayes formula, as
) in (14) can be written, by applying the Bayes formula, as

where we have used the fact that  and
and

B.2. Absence of Quantization
The conditional PMFs  at the right-hand side in (15) can be computed as follows
at the right-hand side in (15) can be computed as follows

and  has been defined in Appendix A.2.
has been defined in Appendix A.2.
C. Limiting Distance for High Communication Noise
The limiting distance when  can be computed, by averaging over the possible (equiprobable) values for the number of edges
can be computed, by averaging over the possible (equiprobable) values for the number of edges  , as
, as

where  is the average distance in the presence of
is the average distance in the presence of  edges. The value of
edges. The value of  can in turn be computed by averaging over all possible pair-wise distances between the true phenomenon configurations and all possible configurations with
can in turn be computed by averaging over all possible pair-wise distances between the true phenomenon configurations and all possible configurations with  edges for the (randomly) estimated phenomenon at the AP. We denote these sets of edges as
edges for the (randomly) estimated phenomenon at the AP. We denote these sets of edges as  and
and  , respectively. The distance between the phenomena (true and estimated) associated to a pair of these sequences is
, respectively. The distance between the phenomena (true and estimated) associated to a pair of these sequences is

The number of all possible sequences of  edges can be computed by simply counting all possible configurations for the edges' positions, that is, as follows:
edges can be computed by simply counting all possible configurations for the edges' positions, that is, as follows:

Therefore, one can write

Finally, the limiting distance in (C.1) is

The computation of the above expression is analytically very cumbersome. However, as shown in Figure 7(a) , it can be obtained out through simulations. In particular, our results show that an accurate approximation (through interpolation) is given by  , where
, where  —in this case, the relative error between
—in this case, the relative error between  and
and  is lower than 2.4% for
is lower than 2.4% for  .
.
References
Akyildiz IF, Su W, Sankarasubramaniam Y, Cayirci E: A survey on sensor networks. IEEE Communications Magazine 2002, 40(8):102-114. 10.1109/MCOM.2002.1024422
Simic SN, Sastry S: Distributed environmental monitorning using random sensor networks. Proceedings of the 2nd International Workshop on Information Processing in Sensor Networks, April 2003, Palo Alto, Calif, USA 582-592.
Viswanathan R, Varshney PK: Distributed detection with multiple sensors—part I: fundamentals. Proceedings of the IEEE 1997, 85(1):54-63. 10.1109/5.554208
Hoballah IY, Varshney PK: Information theoretic approach to the distributed detection problem. IEEE Transactions on Information Theory 1989, 35(5):988-994. 10.1109/18.42216
Gnanapandithan N, Natarajan B: Joint optimization of local and fusion rules in a decentralized sensor network. Journal of Communications 2006, 1(6):9-17.
Ferrari G, Pagliari R: Decentralized binary detection with noisy communication links. IEEE Transactions on Aerospace and Electronic Systems 2006, 42(4):1554-1563.
Nowak R, Mitra U: Boundary estimation in sensor networks: theory and methods. Proceedings of the 2nd International Workshop on Information Processing in Sensor Networks, April 2003, Palo Alto, Calif, USA 80-95.
Nowak R, Mitra U, Willett R: Estimating inhomogeneous fields using wireless sensor networks. IEEE Journal on Selected Areas in Communications 2004, 22(6):999-1006. 10.1109/JSAC.2004.830893
Barros J, Tüchler M: Scalable decoding on factor trees: a practical solution for wireless sensor networks. IEEE Transactions on Communications 2006, 54(2):284-294.
Luo Z-Q: An isotropic universal decentralized estimation scheme for a bandwidth constrained ad hoc sensor network. IEEE Journal on Selected Areas in Communications 2005, 23(4):735-744.
Duttagupta S, Ramamritham K: Distributed boundary estimation using sensor networks. Indian Institute of Technology, Mumbai, India; 2006.http://www.it.iitb.ac.in/research/techreport/
Duttagupta S, Ramamritham K, Ramanathan P: Distributed boundary estimation using sensor networks. Proceedings of the International Conference on Mobile Ad-hoc and Sensor Systems (MASS '06), October 2006, Vancouver, Canada 316-325.
Torre V, Poggio TA: On edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence 1986, 8(2):147-163.
Canny J: A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence 1986, 8(6):679-698.
Konishi S, Yuille AL, Coughlan JM, Song CZ: Statistical edge detection: learning and evaluating edge cues. IEEE Transactions on Pattern Analysis and Machine Intelligence 2003, 25(1):57-74. 10.1109/TPAMI.2003.1159946
Khashman A: Noise-dependent optimal scale in edge detection. Proceedings of the International Symposium on Industrial Electronics (ISIE '02), July 2002, L'Aquila, Italy 2: 467-471.
Jia L, Xiaojun J: Edge detection based on decision-level information fusion and its application in hybrid image filtering. Proceedings of the International Conference on Image Processing (ICIP '04), October 2004, Singapore 1: 251-254.
Ferrari G, Martalò M, Sarti M: Sensor networks as data acquisition devices—reduced-complexity decentralized detection of spatially non-constant phenomena. In Grid Enabled Instrumentation and Measurement, Signals and Communication Technology. Edited by: Davoli F, Meyer N, Pugliese R, Zappatore S. Springer, New York, NY, USA; 2008:33-54.
Kay SM: Fundamentals of Statistical Signal Processing, Volume I: Estimation Theory. Prentice-Hall, Upper Saddle River, NJ, USA; 1993.
Proakis JG: Digital Communications. 4th edition. McGraw-Hill, New York, NY, USA; 2001.
Cover TM, Thomas JA: Elements of Information Theory. John Wiley & Sons, New York, NY, USA; 1991.
Papoulis A: Probability, Random Variables and Stochastic Processes. McGraw-Hill, New York, NY, USA; 1991.
Acknowledgment
The authors would like to thank Marco Sarti (Elettric 80 S.p.A., Viano, Reggio Emilia, Italy) for his help in the derivation of part of the simulator.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Martalò, M., Ferrari, G. Low-Complexity One-Dimensional Edge Detection in Wireless Sensor Networks. J Wireless Com Network 2010, 751520 (2010). https://doi.org/10.1155/2010/751520
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/751520

 (in particular,
(in particular, 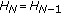 );
); .
.
 in (14) (dashed arrows). The estimated edges are indicated by vertical arrows.
in (14) (dashed arrows). The estimated edges are indicated by vertical arrows. is evaluated, on the basis of the detected sequence of edges' positions;
is evaluated, on the basis of the detected sequence of edges' positions;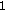 )
)  (
(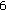 ) are repeated for sufficiently large number of times in order to derive statistically meaningful results;
) are repeated for sufficiently large number of times in order to derive statistically meaningful results;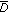 is finally computed as the arithmetic average of the distances computed at the previous iterations (in step (
is finally computed as the arithmetic average of the distances computed at the previous iterations (in step (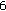 ) at each iteration).
) at each iteration).
 , in a scenario with
, in a scenario with  sensors and binary quantization. Three values for the sensor SNR are considered: (i) −10 dB, (ii) 0 dB, and (iii) 10 dB. Both MMSE and simplified detection algorithms at the AP are considered.
sensors and binary quantization. Three values for the sensor SNR are considered: (i) −10 dB, (ii) 0 dB, and (iii) 10 dB. Both MMSE and simplified detection algorithms at the AP are considered.
 sensors and binary quantization. Four different values of the cross-over probability
sensors and binary quantization. Four different values of the cross-over probability  are considered: (i) 0.1, (ii) 0.2, (iii) 0.3, and (iv) 0.4. Both MMSE and simplified detection algorithms at the AP are considered.
are considered: (i) 0.1, (ii) 0.2, (iii) 0.3, and (iv) 0.4. Both MMSE and simplified detection algorithms at the AP are considered.

 and simplified detection algorithm at the AP. Both absence of quantization and binary quantization at the sensors. Three values for
and simplified detection algorithm at the AP. Both absence of quantization and binary quantization at the sensors. Three values for  are considered: (i) 0 (ideal communication links), (ii) 0.1, and (iii) 0.2.
are considered: (i) 0 (ideal communication links), (ii) 0.1, and (iii) 0.2.

 the optimized decision threshold (
the optimized decision threshold ( ), we assume that each sensor makes use of an actual decision threshold which is uniformly distributed in
), we assume that each sensor makes use of an actual decision threshold which is uniformly distributed in  , where
, where 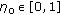 . The decision thresholds at different sensors are supposed to be independent.
. The decision thresholds at different sensors are supposed to be independent.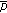 ) for all communication links, the actual cross-over probabilities in the various links are independent and uniformly distributed in the
) for all communication links, the actual cross-over probabilities in the various links are independent and uniformly distributed in the 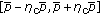 , where
, where 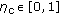 .
.