- Research Article
- Open access
- Published:
Joint Utility-Based Power Control and Receive Beamforming in Decentralized Wireless Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 751893 (2010)
Abstract
This paper addresses the problem of joint resource allocation in general wireless networks and its practical implementation aspects. The objective is to allocate transmit powers and receive beamformers to the users in order to maximize a network-wide utility that represents the attained QoS and is a function of the signal-to-interference ratios. This problem is much more intricate than the corresponding QoS-based power control problem. In particular, it is not known which class of utility functions allows for a convex formulation of this problem. In case of perfect synchronization, the joint power and receiver control problem can be reformulated as a power control problem under optimal receivers. Standard gradient projection methods can be applied to solve this problem. However, these algorithms are not applicable in decentralized wireless networks. Therefore, we decompose the problem and propose a convergent alternate optimization that is amenable to distributed implementation. In addition, in real-world networks noisy measurements and estimations occur. Thus, the proposed algorithm has to be investigated in the framework of stochastic approximation. We discuss practical implementation aspects of the proposed stochastic algorithm and investigate its convergence properties by simulations.
1. Introduction
Two central mechanisms for resource allocation and interference management in wireless networks are power control and beamforming. In order to ensure a high utilization of wireless resources, transmit powers and beamformers should be optimized jointly to exploit interdependencies between them. As is widely known the overall network can be optimized with respect to different optimization goals. In general, there exist two main approaches that are typically used. The classical QoS-based approach aims at satisfying a certain quality-of-service (QoS) requirement with minimum power. To circumvent the feasibility problem a related approach is to solve the so-called max-min SIR-balancing problem. In contrast to this stands the utility-based resource allocation problem where the network operator aims at optimizing a weighted aggregate utility so as to maximize the overall network performance. By appropriately choosing the utility function one can trade overall system efficiency against fairness. Widely known are the  -fair strictly concave utility functions introduced by [1].
-fair strictly concave utility functions introduced by [1].
In decentralized wireless networks, however, in addition to efficiently managing wireless resources the two challenging tasks are to distributedly assign these resources and to apply stochastic algorithms that deal with noisy measurements and estimations. Thus in this paper we focus on the following problem: maximizing an aggregate utility jointly over powers and receive beamformers in real-world decentralized wireless networks.
1.1. Related Work
Classical QoS-based power control has been studied extensively (e.g., [2–4]). It aims at allocating transmit powers to the users such that each user meets its SIR target. Provided that the SIR requirements are feasible there exist iterative distributed algorithms that attain the target SIR [3, 5, 6]. Note, that a closely related approach to the classical approach is to maximize the minimum SIR [7–10]. In contrast to the classical QoS-based power control, the objective of utility-based power control is to optimize the overall network performance with respect to some aggregate utility function [11–18]. Recently distributed utility-based power control algorithms have been developed by [14, 16–18]. In [17] the problem of joint power control and end-to-end congestion control is addressed where the power control part is a special case of the power control problem in [14]. The approach of [16] is a game-theoretic one. References [16, 17] apply a flooding protocol to pass locally available quantities to other nodes. The authors of [18] interpret the utility-based power control problem as a joint optimization of powers and SIR assignment over the feasibility region. They proposed a distributed power control and SIR assignment algorithm for the uplink in a multicell wireless network. In contrast [14] proposed a distributed utility-based power control algorithm for general wireless networks applying the notion of the adjoint network and thus avoiding to use a relatively expensive flooding protocol. In addition, the authors touched the problem of stochastic approximation and show how to deal with it in practice.
Independently from and simultaneously to our work the authors of [19] have proposed a distributed utility-based joint power control and receive beamforming algorithm for cellular uplinks applying the scheme of [18]. Apart from that, so far most work on joint power control and beamforming has focused on the QoS-based resource allocation, especially on the so-called max-min SIR-balancing and its related problem. For example in [20–22] the duality between uplink and downlink channels is exploited. Another strategy was proposed by [23, 24] showing that the problem can be embedded in semidefinite and conic optimization programs. The work of [25] extended the publication [22] to solve the max-min SIR-balancing problem under general power constraints.
However, apart from [15] the above set of publications considered only the deterministic case. First works incorporating imprecise knowledge of received waveforms can be found in [26–28]. Recently, stochastic algorithms for joint QoS-based power control and receive beamforming and their convergence analysis have been proposed by [29, 30].
1.2. Summary of Main Results and Paper Organization
In the following we consider the problem of joint power control and receive beamforming in order to maximize a certain aggregate utility function that represents the QoS attained and is a function of the SIR. However, in contrast to the pure power control problem [14], it is not known which class of utility functions allows a convex formulation of this joint optimization problem and thus enables an efficient global solution in distributed wireless networks. In particular, in case of the logarithmic function, the aggregate utility function appears to have relatively many local maxima.
Now, in this paper, under the assumption of perfect synchronization we first reformulate the joint power and receiver control problem as a pure power control problem under optimal receivers. This follows from the fact that an optimal receiver can be obtained in closed-form solution for any power vector. However, an efficient implementation of the equivalent gradient projection algorithm is notoriously difficult to achieve in decentralized wireless networks. Thus, we decompose the problem into two coupled subproblems and propose an alternating algorithm that converges to a stationary point. If we confine our attention to utility functions whose relative concavity is larger than that of the logarithmic function, numerical experiments suggest that then the proposed algorithm may converge to a global maximum for a large set of initial SIRs.
In contrast to [15] which touches the problem briefly this paper provides a more detailed analysis. In addition it is devoted to practical implementation aspects that are completely missing so far. As already mentioned, in real-world networks noisy measurements and estimations occur. We embed the proposed alternating algorithm into the framework of stochastic approximation. In particular, we discuss in detail the imprecise knowledge of received waveforms and the influence of step size control on the convergence properties. Finally we provide extensive simulations on the convergence behavior as well as performance comparisons with pure power control schemes.
Potential applications of the resource allocation scheme presented in this paper are envisaged for example in wireless mesh networks to control transmit powers and beamformers of base stations (mesh routers). These base stations create a wireless backbone via multihop ad hoc networking and have practically unlimited energy supply.
2. System Model and Problem Statement
2.1. System Model
We consider a general multiple-antenna wireless network with an established network topology, in which all links share a common wireless spectrum. All users are equipped with  antennas. Let
antennas. Let  users compete for access to the wireless links and let
users compete for access to the wireless links and let  denote the index set of all users. Assume that
denote the index set of all users. Assume that  is arbitrary but fixed and define
is arbitrary but fixed and define  to be the effective transmit vector of transmitter
to be the effective transmit vector of transmitter  associated with receiver
associated with receiver  . The effective transmit vector
. The effective transmit vector  is the product of the channel matrix between transmitter
is the product of the channel matrix between transmitter  and receiver
and receiver  and its transmit beamformer. It determines the "direction" of the transmit signal. The effective transmit vector is assumed to be arbitrary but fixed, which implies that the channels and transmit beamformers are fixed. In contrast, the receive beamformers acting as linear receivers should be jointly optimized with transmit powers of the users. We use
and its transmit beamformer. It determines the "direction" of the transmit signal. The effective transmit vector is assumed to be arbitrary but fixed, which implies that the channels and transmit beamformers are fixed. In contrast, the receive beamformers acting as linear receivers should be jointly optimized with transmit powers of the users. We use  and
and  to denote the receive beamformer and transmit power of user
to denote the receive beamformer and transmit power of user  , respectively. The receive beamformers of all users are collected in the receive beamforming matrix
, respectively. The receive beamformers of all users are collected in the receive beamforming matrix  and their transmit powers in the power vector
and their transmit powers in the power vector  (In what follows,
(In what follows,  and
and  denote the set of nonnegative reals and positive reals, resp.). The transmit powers of the users are subject to individual power constraints
denote the set of nonnegative reals and positive reals, resp.). The transmit powers of the users are subject to individual power constraints  so that
so that  must hold, where
must hold, where  . Furthermore, since the signal-to-interference ratio (SIR) is independent of the norm of the receive beamformers, we can assume that
. Furthermore, since the signal-to-interference ratio (SIR) is independent of the norm of the receive beamformers, we can assume that  for each
for each  , and hence
, and hence  denotes the set of all beamforming matrices. Note that both
denotes the set of all beamforming matrices. Note that both  and
and  are compact sets, so is also their Cartesian product
are compact sets, so is also their Cartesian product  . Finally, we define
. Finally, we define  . In words,
. In words,  is the set of positive power vectors satisfying the power constraints.
is the set of positive power vectors satisfying the power constraints.
The main figure of merit is the SIR at the output of each receiver. Using the above notation and considering the fact that all users are perfectly synchronized, the SIR of user  is given by
is given by

where  is the variance of independent zero-mean additive Gaussian noise, and
is the variance of independent zero-mean additive Gaussian noise, and  is the attenuation of the power from transmitter of user
is the attenuation of the power from transmitter of user  to receiver of user
to receiver of user  where
where  denotes the inner product of the vectors
denotes the inner product of the vectors  . Note that the SIR of user
. Note that the SIR of user  depends only on the
depends only on the  th receive beamformer
th receive beamformer  .
.
2.2. Problem Statement
One way to control both transmit powers of the users and their receive beamformers is to apply a utility-based framework. Let  be the utility of user
be the utility of user  that represents the QoS level of user
that represents the QoS level of user  under power vector
under power vector  and receive beamformer
and receive beamformer  . Other typical interpretations include the degree of user satisfaction with the received SIR or the revenue of the network operator. Throughout the paper we assume that
. Other typical interpretations include the degree of user satisfaction with the received SIR or the revenue of the network operator. Throughout the paper we assume that  satisfies the following conditions.
satisfies the following conditions.
-
(A.1)
 is a twice continuously differentiable, strictly increasing and strictly concave function of the SIR where
is a twice continuously differentiable, strictly increasing and strictly concave function of the SIR where  is an open interval on the real line such that
is an open interval on the real line such that 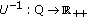 .
. -
(A.2)
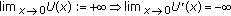 .
. -
(A.3)
 is convex on
is convex on  .
.
Since  is an open set, all these assumptions imply that the first derivative
is an open set, all these assumptions imply that the first derivative  is positive on
is positive on  , that is, there are no isolated points
, that is, there are no isolated points  such that
such that  .
.
The joint utility-based power control and receive beamforming problem can be written as follows. Given any weight vector  , we search for a power vector
, we search for a power vector  and a beamforming matrix
and a beamforming matrix  such that
such that

where

Since the noise variance is strict positive, standard arguments can be used to show that with our choice of the utility functions, the maximum exists. The convexity discussion of this problem, the development of a distributed algorithm, and its implementation in real-world environments with noisy measurements together with the performance evaluation by simulations will be the main tasks of this paper.
3. A Class of Utility Functions
Suppose that the utility function  is further confined to satisfy
is further confined to satisfy

where  and
and  denote the first and second derivatives of
denote the first and second derivatives of  , respectively. Then, we know that [15], for any fixed
, respectively. Then, we know that [15], for any fixed  ,
,  is concave in the logarithmic power vector
is concave in the logarithmic power vector  with
with  and
and

Here and hereafter,  and
and  are defined component-wise. Since the logarithm is a bijection from
are defined component-wise. Since the logarithm is a bijection from  onto
onto  and
and  , there is a one-to-one relationship
, there is a one-to-one relationship  between optimal power vectors
between optimal power vectors  and optimal logarithmic power vectors
and optimal logarithmic power vectors  . The motivation beyond this substitution is the following fact [15].
. The motivation beyond this substitution is the following fact [15].
Lemma 1.
 if and only if
if and only if  is concave on
is concave on  .
.
Since  is twice continuously differentiable,
is twice continuously differentiable,  is concave if and only if
is concave if and only if  . This in turn holds if and only if
. This in turn holds if and only if  , which is equivalent to (11) since
, which is equivalent to (11) since  for all
for all  .
.
Therefore, for  to be concave in
to be concave in  , it is sufficient that
, it is sufficient that  is a log-concave function of
is a log-concave function of  . In economics, the quantity
. In economics, the quantity  is known as the coefficient of relative risk aversion [31] and is used to measure the relative concavity of
is known as the coefficient of relative risk aversion [31] and is used to measure the relative concavity of  . The larger the value of
. The larger the value of  is, the larger is the relative concavity of
is, the larger is the relative concavity of  at
at  , and therefore a better fairness performance (at the cost of the throughput performance) can be expected. A prominent example of a function that satisfies (4) is the logarithmic function
, and therefore a better fairness performance (at the cost of the throughput performance) can be expected. A prominent example of a function that satisfies (4) is the logarithmic function  , in which case
, in which case  .
.
Now the question is what happens if we use this class of utility functions in the joint power control and receive beamforming problem (2). First note that this problem can be written as a power control problem because

where  is used to denote an optimal receive beamforming matrix for a given
is used to denote an optimal receive beamforming matrix for a given  and the last step follows from (A.2). Obviously, since the SIR of user
and the last step follows from (A.2). Obviously, since the SIR of user  depends only on the
depends only on the  th receive beamformer, one obtains
th receive beamformer, one obtains

where

is the SIR under an optimal receive beamforming (see Section 4) and the last step follows since  is a strictly increasing function and
is a strictly increasing function and  is a positive vector. Now, using the substitution
is a positive vector. Now, using the substitution  (in accordance with the power control problem of [15]) and
(in accordance with the power control problem of [15]) and

it follows that a solution to (2) is any pair  given by
given by  and
and  where
where

In words, as in [15], the problem reduces to a power control problem except that now each SIR is assumed to attain its maximum overall receive beamformers.
Unfortunately, the condition (4) is not sufficient for  defined by (9) to be a concave function of
defined by (9) to be a concave function of  . A simple counter example is constructed in the appendix for
. A simple counter example is constructed in the appendix for  . Numerical experiments show that if
. Numerical experiments show that if  then the gradient projection algorithm is not globally convergent, that is, it in general converges to a local maximum which is not global. Given
then the gradient projection algorithm is not globally convergent, that is, it in general converges to a local maximum which is not global. Given  and
and  , the aggregate utility function seems to have relatively many local maxima.
, the aggregate utility function seems to have relatively many local maxima.
A simple idea is to further restrict the class of utility functions by requiring larger values of  for all
for all  . For instance, we could demand that
. For instance, we could demand that

This excludes the logarithmic function and implies that  is strictly concave. A class of utility functions that satisfies (11) are the following functions
is strictly concave. A class of utility functions that satisfies (11) are the following functions

Indeed, it may be easily verified that  , and hence (11) holds for all
, and hence (11) holds for all  . Another example is
. Another example is

in which case  . So, at low values of
. So, at low values of  , the function in (13) behaves like the logarithmic function. In contrast, as
, the function in (13) behaves like the logarithmic function. In contrast, as  increases, it is similar to the negative inverse function. Numerical experiments with the utility function (13) suggest that in this case, the gradient projection algorithm (see Section 4.1) converges to a global maximum for a relatively large set of initial SIR values. When compared with the logarithmic utility function, convergence to a local point was observed in significantly fewer cases. However, we can show that
increases, it is similar to the negative inverse function. Numerical experiments with the utility function (13) suggest that in this case, the gradient projection algorithm (see Section 4.1) converges to a global maximum for a relatively large set of initial SIR values. When compared with the logarithmic utility function, convergence to a local point was observed in significantly fewer cases. However, we can show that  with (13) is not concave in general and the standard gradient projection algorithms are not globally convergent for all initial SIR levels.
with (13) is not concave in general and the standard gradient projection algorithms are not globally convergent for all initial SIR levels.
An interesting problem is whether a global convergence (if not for all starting points, then at least for most of them) of the gradient projection algorithm can be achieved by requiring that  for some sufficiently large constant
for some sufficiently large constant  . Increasing the constant
. Increasing the constant  leads to utility functions with larger relative concavities. In particular, as shown below, if there is a utility function for which each addend in (9) is concave on
leads to utility functions with larger relative concavities. In particular, as shown below, if there is a utility function for which each addend in (9) is concave on  , then
, then  is concave for all utility functions with a larger coefficient
is concave for all utility functions with a larger coefficient  .
.
Observation 1.
Let  be any utility function for which (4) holds, and suppose that each addend in
be any utility function for which (4) holds, and suppose that each addend in  with
with  is concave on
is concave on  . Then,
. Then,  with
with  is concave for any utility function
is concave for any utility function  such that
such that  for all
for all  .
.
Since  and
and  are bijective utility functions, there is a twice continuously differentiable and strictly increasing function
are bijective utility functions, there is a twice continuously differentiable and strictly increasing function  such that
such that  . So, the observation follows if
. So, the observation follows if  is concave. Considering the fact that
is concave. Considering the fact that  with
with  for all
for all  , the second derivative of
, the second derivative of  yields
yields  . By
. By  , we have
, we have  , so that
, so that  . This implies that
. This implies that  , and hence one obtains
, and hence one obtains  due to the bijectivity of
due to the bijectivity of  .
.
Applying this observation to the class in (12) reveals that if there was some  such that
such that  is concave on
is concave on  for each
for each  , then the problem (10) would be a convex problem for all
, then the problem (10) would be a convex problem for all  with
with  . Then, as discussed in the following section, we would be able to efficiently and arbitrarily close approximate the max-min fair rate allocation for any power constraints.
. Then, as discussed in the following section, we would be able to efficiently and arbitrarily close approximate the max-min fair rate allocation for any power constraints.
3.1. An Arbitrarily Close Approximation of the Max-Min Fair Allocation
Reference [1] introduced the class of utility functions in (12) to obtain different tradeoffs between throughput and fairness performance in wireline communications networks. In particular, it was shown that if each source is assigned the utility function  , then the corresponding rate allocation tends to the max-min rate allocation as
, then the corresponding rate allocation tends to the max-min rate allocation as  . For a large family of modulations determining the relationship between data rates attainable on wireless links and the SIR at the receiver output, this result carries over to our setting. To be precise, assume that
. For a large family of modulations determining the relationship between data rates attainable on wireless links and the SIR at the receiver output, this result carries over to our setting. To be precise, assume that  is a one-to-one continuously differentiable function that maps the SIR values onto the data rates. A common assumption is that
is a one-to-one continuously differentiable function that maps the SIR values onto the data rates. A common assumption is that  . By this model, the set of all simultaneously achievable data rates is
. By this model, the set of all simultaneously achievable data rates is

which is a (connected) compact set since  is continuous on the compact set
is continuous on the compact set  , where
, where  is the unit sphere in
is the unit sphere in  . This yields the following observation (see [15] and [1, Lemma
. This yields the following observation (see [15] and [1, Lemma  ]).
]).
Observation 2.
Let  be arbitrary, and let
be arbitrary, and let  be given by (12). Then,
be given by (12). Then,  converges to a max-min fair rate allocation as
converges to a max-min fair rate allocation as  .
.
By the observation,  with
with  converges to the max-min power allocation as
converges to the max-min power allocation as  tends to infinity [22]. Moreover, for every
tends to infinity [22]. Moreover, for every  ,
,  exists and is continuous on
exists and is continuous on  so that efficient gradient projection algorithms could be used to approximate the max-min power allocation for any power constraints if the algorithms were global convergent for some sufficiently large
so that efficient gradient projection algorithms could be used to approximate the max-min power allocation for any power constraints if the algorithms were global convergent for some sufficiently large  (as discussed before).
(as discussed before).
4. Utility-Based Power Control and Beamforming Algorithm
In this section, we derive a gradient projection algorithm for the problem (19) and prove its convergence. To this end, let us first identify optimal receive beamformers. By (8), an optimal receive beamformer of user  is exactly that beamformer for which the
is exactly that beamformer for which the  th SIR attains its maximum. Hence,
th SIR attains its maximum. Hence,

where

is positive definite since  is positive. As a consequence, the inverse matrix of
is positive. As a consequence, the inverse matrix of  exists regardless of the choice of the effective transmit vectors
exists regardless of the choice of the effective transmit vectors  and
and  . Note that the SIR can be written in this compact form due to the assumption of perfect synchronization. An optimal receive beamformer
. Note that the SIR can be written in this compact form due to the assumption of perfect synchronization. An optimal receive beamformer  can be easily found when the
can be easily found when the  is rewritten as a Rayleigh quotient to obtain [32]
is rewritten as a Rayleigh quotient to obtain [32]

where  is a constant chosen such that
is a constant chosen such that  . Consequently, with an optimal beamformer, the SIR of user
. Consequently, with an optimal beamformer, the SIR of user  is equal to
is equal to

From this, it follows that

and ( ),
),

with appropriately chosen constants  .
.
If we assume the utility function (13) or the functions (12), then  in (19) can be written using the inverse of
in (19) can be written using the inverse of

which is independent of the index  . Indeed, by the Sherman-Morrison formula [33], it follows that
. Indeed, by the Sherman-Morrison formula [33], it follows that

and hence

So, if  the aggregate utility function in (9) yields
the aggregate utility function in (9) yields

Choosing  given by (12) gives
given by (12) gives

where  and the constant
and the constant  can be neglected as it has no impact on the maximizer.
can be neglected as it has no impact on the maximizer.
4.1. Gradient Projection Algorithm
All partial derivatives of  with
with  given by (18) exist and are continuous functions on
given by (18) exist and are continuous functions on  because the inverse matrix
because the inverse matrix  exists for all
exists for all  , regardless of the choice of the effective transmit vectors, and the entries in
, regardless of the choice of the effective transmit vectors, and the entries in  vary continuously with the entries in
vary continuously with the entries in  . Hence, we can consider a gradient projection algorithm with a constant step size
. Hence, we can consider a gradient projection algorithm with a constant step size  (sufficiently small)
(sufficiently small)

where  is the projection of
is the projection of  on the closed convex set
on the closed convex set  [34, 35] and the
[34, 35] and the  th partial derivative
th partial derivative  yields
yields

where the following identity was used. For an invertible and differentiable matrix function  , there holds
, there holds

Hence, due to the individual power constraints on each user  , the algorithm (26) takes the form
, the algorithm (26) takes the form

where  is defined by (18).
is defined by (18).
Lemma 2.
For a sufficiently small step size  , the sequence
, the sequence  generated by the algorithm (29) with
generated by the algorithm (29) with  converges to a local stationary point.
converges to a local stationary point.
Proof.
By standard results [34, 35], the gradient projection algorithm converges to a stationary point for sufficiently small values of  if
if  is bounded above, continuously differentiable on
is bounded above, continuously differentiable on  , and the gradient
, and the gradient  is Lipschitz continuous on any bounded subset of
is Lipschitz continuous on any bounded subset of  . The first condition is clearly satisfied due to the power constraints. The second condition holds as well since, by assumption, the utility function
. The first condition is clearly satisfied due to the power constraints. The second condition holds as well since, by assumption, the utility function  is twice continuously differentiable. Hence, the Hessian of
is twice continuously differentiable. Hence, the Hessian of  is bounded in the matrix
is bounded in the matrix  -norm on any bounded subset of
-norm on any bounded subset of  . This implies that
. This implies that  is Lipschitz continuous on any bounded subset of
is Lipschitz continuous on any bounded subset of  [36, page 70].
[36, page 70].
Note that the maximum feasible step size in the algorithm may depend on the choice of the starting point  .
.
5. Distributed Implementation
The computation of the gradient in (29) might be too expensive to be implemented in a distributed environment. In this section, we slightly modify the algorithm so that it can be implemented in a distributed manner. The basic idea is to increase the value of the function  in the following alternating fashion. For some given receive beamforming matrix
in the following alternating fashion. For some given receive beamforming matrix  and power vector
and power vector  , a new power vector
, a new power vector  is chosen such that
is chosen such that  . Then, the beamforming matrix is updated by
. Then, the beamforming matrix is updated by  such that
such that  . This alternating process is repeated until convergence.
. This alternating process is repeated until convergence.
Let us first consider the power vector update. To this end, let  be fixed and define
be fixed and define  . Then, the power vector can be updated according to the following algorithm
. Then, the power vector can be updated according to the following algorithm

for some  , where, with some abuse of notation,
, where, with some abuse of notation,  is used to denote a noisy estimation of the gradient vector
is used to denote a noisy estimation of the gradient vector  and
and  with
with  is an appropriately chosen sequence of diminishing step sizes [37]. If
is an appropriately chosen sequence of diminishing step sizes [37]. If  is a sequence generated by (30) for some
is a sequence generated by (30) for some  , then we put
, then we put  . Note that the estimate
. Note that the estimate  can be computed in a distributed manner using the adjoint network of [15]. This scheme enables each transmitter to estimate its current update direction from the received signal power. This mitigates the problem of global coordination of the transmitters when carrying out gradient-projection algorithms in distributed wireless networks. More precisely, instead of each node sending its message separately as in case of classical flooding protocols, nodes transmit simultaneously (only coarse synchronization is required) over the adjoint network such that each node can estimate its gradient component from the received power. The price for this are possible estimation errors that usually can be dealt with a diminishing step size [37] as is shortly discussed in the following Section 5.1.
can be computed in a distributed manner using the adjoint network of [15]. This scheme enables each transmitter to estimate its current update direction from the received signal power. This mitigates the problem of global coordination of the transmitters when carrying out gradient-projection algorithms in distributed wireless networks. More precisely, instead of each node sending its message separately as in case of classical flooding protocols, nodes transmit simultaneously (only coarse synchronization is required) over the adjoint network such that each node can estimate its gradient component from the received power. The price for this are possible estimation errors that usually can be dealt with a diminishing step size [37] as is shortly discussed in the following Section 5.1.
Now assume that  is fixed. Distributed algorithms for computing optimal receive beamformers defined by (17) are widely established. These algorithms are based either on blind or pilot-based estimation methods [38]. In the latter case, if
is fixed. Distributed algorithms for computing optimal receive beamformers defined by (17) are widely established. These algorithms are based either on blind or pilot-based estimation methods [38]. In the latter case, if  is a pilot symbol of user
is a pilot symbol of user  with zero mean and
with zero mean and  , and
, and  represents the observations at receiver
represents the observations at receiver  , then
, then  given by (17) minimizes the mean square error
given by (17) minimizes the mean square error  over
over  , where
, where  is a normalizing constant chosen such that, in the minimum,
is a normalizing constant chosen such that, in the minimum,  . For practical implementation, we can assume
. For practical implementation, we can assume  , and then normalize the beamformers so that their
, and then normalize the beamformers so that their  -norms are equal to one. Besides note that the expectation is taken with respect to
-norms are equal to one. Besides note that the expectation is taken with respect to  , which depends on the logarithmic power vector
, which depends on the logarithmic power vector  . Now if the convex function
. Now if the convex function  was explicitly known, then the algorithm (with the complex gradient operator
was explicitly known, then the algorithm (with the complex gradient operator  which gives the direction of steepest ascent of
which gives the direction of steepest ascent of  )
)

would converge to  defined by (17) for a sufficiently small step size
defined by (17) for a sufficiently small step size  . The problem is that the function
. The problem is that the function  is usually not known since the distribution of
is usually not known since the distribution of  is not known [38]. Therefore,
is not known [38]. Therefore,  cannot be computed and the algorithm must be modified using the framework of stochastic approximation [37]. The idea is to consider the functions
cannot be computed and the algorithm must be modified using the framework of stochastic approximation [37]. The idea is to consider the functions  for all
for all  as noisy estimations of
as noisy estimations of  . Then, under some conditions on the estimation error and for any
. Then, under some conditions on the estimation error and for any  , the algorithm
, the algorithm

converges to  (in some probabilistic sense), provided that the step size
(in some probabilistic sense), provided that the step size  with
with  and
and  is chosen suitably [26].
is chosen suitably [26].
Now combining these two ingredients leads to the following joint power control and receive beamforming algorithm. At the beginning of every frame,  and
and  are set to be equal to the current transmit powers and receive beamformers. Then, all users concurrently execute
are set to be equal to the current transmit powers and receive beamformers. Then, all users concurrently execute  updates of their transmit powers and receive beamformers. The
updates of their transmit powers and receive beamformers. The  th update consists of the following intermediate steps.
th update consists of the following intermediate steps.
-
(i)
For fixed
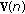 and some
and some 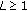 , each user
, each user  generates a sequence
generates a sequence 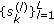 by carrying out (30) and defines
by carrying out (30) and defines 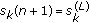 .
. -
(ii)
For some
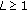 and with
and with  , each user
, each user  executes
executes 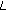 iterations of the algorithm (32) to obtain the sequence
iterations of the algorithm (32) to obtain the sequence 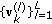 . It defines
. It defines 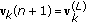 .
.
The convergence of the algorithm (in some probabilistic sense) strongly depends on the choice of the step sizes in (30) and (32) as well as on the properties of the estimation errors in (30) and (32). However, we point out that the algorithm is motivated by the following observation. If the estimates in (30) are known perfectly meaning that we can use  for sufficiently small
for sufficiently small  and (31) is used instead of (32), then the sequence
and (31) is used instead of (32), then the sequence  generated by the resulting algorithm converges to a stationary point. This is because, under this assumption, (30) and (31) are both monotonic, and hence we have (for all
generated by the resulting algorithm converges to a stationary point. This is because, under this assumption, (30) and (31) are both monotonic, and hence we have (for all  )
)

This implies that the sequence  is monotonically increasing, provided that the step sizes are sufficiently small. Moreover, it is bounded since
is monotonically increasing, provided that the step sizes are sufficiently small. Moreover, it is bounded since  for all
for all  . Therefore, the algorithm converges to a stationary point. In addition, verifying the second order sufficiency conditions would show that this stationary point is also a local maximizer for the problem (2).
. Therefore, the algorithm converges to a stationary point. In addition, verifying the second order sufficiency conditions would show that this stationary point is also a local maximizer for the problem (2).
Due to scarce resources in wireless networks, it is reasonable to choose the number of updates  in every frame. In addition, instead of transmitting pilot signals in the intermediate step (ii), the optimal receive beamformers can be estimated during the data transmission using some blind estimation method (see [38] and references therein). So, at the beginning of every frame, the step (i) is executed only once. Then, the resulting transmit powers are used for data transmission. During this time, the receive beamformers are updated online after each transmitted symbol. However, numerical experiments suggest that the scheme should not exclusively rely on blind methods to estimate the optimal receivers with a sufficient accuracy.
in every frame. In addition, instead of transmitting pilot signals in the intermediate step (ii), the optimal receive beamformers can be estimated during the data transmission using some blind estimation method (see [38] and references therein). So, at the beginning of every frame, the step (i) is executed only once. Then, the resulting transmit powers are used for data transmission. During this time, the receive beamformers are updated online after each transmitted symbol. However, numerical experiments suggest that the scheme should not exclusively rely on blind methods to estimate the optimal receivers with a sufficient accuracy.
5.1. Stochastic Approximation View
As already mentioned, in real-world networks estimation errors and other distorting factors as quantization noise occur. Now the interesting question is, what is the impact of these stochastic noisy measurements on the convergence properties. Does the proposed algorithm still converge and under what conditions? In the case of such uncertainties, the proposed algorithm has to be analyzed in the context of stochastic approximation theory. In the following we give several interesting insights. However, the topic is too broad to be discussed in all details. We also refer to [37] as a comprehensive reference.
We assume that the estimated gradient component  is a random variable of the form
is a random variable of the form

where  is the estimation noise process that fulfills the following conditions:
is the estimation noise process that fulfills the following conditions:
-
(A.4)
The estimation noise process depends on the receiver noise process which is assumed to be a martingale difference that is uncorrelated with transmit symbols and has a finite variance.
-
(A.5)
The estimation noise is zero mean and exogeneous, in the sense that
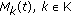 is independent of the iterate value.
is independent of the iterate value.
Assuming these two conditions one can deal with the estimation noise applying a diminishing step size sequence that satisfies  with
with  and
and  . A typical choice for a step size sequence is for instance
. A typical choice for a step size sequence is for instance  for some
for some  . The choice of the step size is central to the effectiveness of the algorithm as is shown by simulations in the next section.
. The choice of the step size is central to the effectiveness of the algorithm as is shown by simulations in the next section.
In the previous algorithm the powers and beamformers are updated in parallel, meaning that the power control algorithm does not wait for the convergence of the receive beamformers and vice versa. Thus the convergence of this practical stochastic algorithm is only verified by simulations presented in the following section. In addition, note that condition ( ) is not necessarily fulfilled by the distributed power control algorithm. Thus the estimates
) is not necessarily fulfilled by the distributed power control algorithm. Thus the estimates  may be biased by some
may be biased by some  meaning that
meaning that  . Simulation results indicate that the algorithm still converges to a contraction region around the optimal point provided that the bias is bounded by a scaled version of the true gradients.
. Simulation results indicate that the algorithm still converges to a contraction region around the optimal point provided that the bias is bounded by a scaled version of the true gradients.
6. Numerical Results
6.1. Influence of Step Size Control
In the following, we show exemplarily the convergence behavior of the proposed scheme for  and a random channel realization. We consider a wireless system with
and a random channel realization. We consider a wireless system with  transmit and receive antennas, and
transmit and receive antennas, and  users operating at a SNR level of
users operating at a SNR level of  dB. The weight vector is
dB. The weight vector is  . The noisy measurements of the gradient are assumed to be
. The noisy measurements of the gradient are assumed to be  , where
, where  is an independent zero-mean Gaussian random variable (and thus fulfils the conditions of a martingale difference noise) whose variance
is an independent zero-mean Gaussian random variable (and thus fulfils the conditions of a martingale difference noise) whose variance  depends on
depends on  and is
and is  percent of the absolute gradient value. We have
percent of the absolute gradient value. We have  and
and  steps in (i) and (ii), respectively. Hence, during each iteration step
steps in (i) and (ii), respectively. Hence, during each iteration step  , the algorithm performs
, the algorithm performs  power control step and estimates the beamformers using
power control step and estimates the beamformers using  pilot symbols. The diminishing step sizes for the intermediate steps are
pilot symbols. The diminishing step sizes for the intermediate steps are  and
and  for some positive constants
for some positive constants  and some exponent
and some exponent  . Figure 1 depicts the aggregate utility, the mean square error of the SIR, and the SIR for two users over the number of iterations
. Figure 1 depicts the aggregate utility, the mean square error of the SIR, and the SIR for two users over the number of iterations  for different values of
for different values of  to show the influence of the diminishing step size. As can be easily seen, if the step size vanishes fast the algorithm converges much slower than with a slowly decreasing step size. However, the behavior is very smooth causing nearly no oscillations in contrast to a slowly decreasing step size. Figure 2 depicts the aggregate utility, the mean square error of the SIR, and the SIR for two users over the number of iterations
to show the influence of the diminishing step size. As can be easily seen, if the step size vanishes fast the algorithm converges much slower than with a slowly decreasing step size. However, the behavior is very smooth causing nearly no oscillations in contrast to a slowly decreasing step size. Figure 2 depicts the aggregate utility, the mean square error of the SIR, and the SIR for two users over the number of iterations  for different values of
for different values of  and
and  and a fixed
and a fixed  to show the influence of the start step size values. Here a higher (but sufficiently small) start step size leads to a faster but oscillating convergence compared to lower start step sizes with a slow but smooth convergence behavior.
to show the influence of the start step size values. Here a higher (but sufficiently small) start step size leads to a faster but oscillating convergence compared to lower start step sizes with a slow but smooth convergence behavior.
Summarizing, we state the following. It is important, that the step sizes  and
and  are sufficiently small to ensure that the algorithm does not diverge. Besides the decrease of the step sizes adjusted by exponent
are sufficiently small to ensure that the algorithm does not diverge. Besides the decrease of the step sizes adjusted by exponent  should be not too small to avoid a very slow convergence speed. In case of a dynamic environment where the channel changes over time,
should be not too small to avoid a very slow convergence speed. In case of a dynamic environment where the channel changes over time,  should be chosen to be able to follow the channel changes. This is paid with a more oscillating behavior. Finally note that the length of the pilot sequences also depends on the number of users because the link-specific pilot sequence is typically a pseudo-noise sequence with good autocorrelation properties.
should be chosen to be able to follow the channel changes. This is paid with a more oscillating behavior. Finally note that the length of the pilot sequences also depends on the number of users because the link-specific pilot sequence is typically a pseudo-noise sequence with good autocorrelation properties.
6.2. Influence of Biased Gradient Estimators
In Figure 3 a convergence example is depicted for the case that the estimates  are biased by some
are biased by some  . Further independent simulations suggest that the proposed algorithm converges to a contraction region around the optimal point if the bias is small enough. Otherwise the algorithm may diverge. However, the conditions on the bias to ensure convergence to a contraction region remain an open question.
. Further independent simulations suggest that the proposed algorithm converges to a contraction region around the optimal point if the bias is small enough. Otherwise the algorithm may diverge. However, the conditions on the bias to ensure convergence to a contraction region remain an open question.
6.3. Comparison with Pure Utility-Based Power Control
In this last section, we compare utility-based power control with joint utility-based power control and receive beamforming. In Figure 4 the maximum and minimum SIRs are depicted as a function of  representing the concavity of the utility function chosen. The figures show that a significant performance gain can be achieved by a joint optimization. Note that in this simulation example only a total throughput of 4.3 can be supported if the users transmit with maximum power and receive with a filter that is matched to the channel. In addition, the simulations confirm that with increasing concavity (
representing the concavity of the utility function chosen. The figures show that a significant performance gain can be achieved by a joint optimization. Note that in this simulation example only a total throughput of 4.3 can be supported if the users transmit with maximum power and receive with a filter that is matched to the channel. In addition, the simulations confirm that with increasing concavity ( ) the utility-based resource allocation strategy achieves fairness at the expense of a decreasing throughput performance. For
) the utility-based resource allocation strategy achieves fairness at the expense of a decreasing throughput performance. For  max-min fairness is achieved.
max-min fairness is achieved.
Finally, in Figure 5 we show the performance gains that can be achieved in an exemplary wireless mesh network (Downlink) where the base stations are connected wirelessly with an Access Point (AP). More precisely, the total network throughput and the delay performance are depicted over the arrival rate. For a fixed routing and a fixed scheduling strategy we compare the static resource allocation, that adapts the beamformers to the channel and transmits with maximum available transmit powers, with the utility-based power control and with the joint utility-based power control and receive beamforming for  . The weights are chosen to represent the queue differences in order to support low delays. As can be easily seen the joint resource allocation outperforms the utility-based power control.
. The weights are chosen to represent the queue differences in order to support low delays. As can be easily seen the joint resource allocation outperforms the utility-based power control.
7. Conclusions
We proposed a framework for joint power control and receive beamforming in wireless networks, with the goal to maximize some aggregate utility function of the SIRs. The paper is a step to better understand the problem of utility-based power control and receive beamforming. We especially give insights into practical implementation issues and exemplarily show the effects of noisy estimations (unbiased and biased) as well as the influence of step size control on the convergence properties. However, the interesting theoretical issue of global convergence seems to be further unresolved.
Appendix
We show that  given by (9) is not concave in general when
given by (9) is not concave in general when  . To this end, consider the
. To this end, consider the  -user case with
-user case with  so that
so that  where
where  and
and  . Define
. Define  and
and  . Without loss of generality, assume
. Without loss of generality, assume  . Using the Sherman-Morrison formula [33] yields
. Using the Sherman-Morrison formula [33] yields  and
and  is obtained in an equivalent way. Therefore,
is obtained in an equivalent way. Therefore,

where  . Assume that
. Assume that  and
and  , in which case
, in which case  . Now taking the second derivative either with respect to
. Now taking the second derivative either with respect to  or
or  shows that
shows that  is not concave in general.
is not concave in general.
References
Mo J, Walrand J: Fair end-to-end window-based congestion control. IEEE/ACM Transactions on Networking 2000, 8(5):556-567. 10.1109/90.879343
Wu Q: Optimum transmitter power control in cellular systems with heterogeneous SIR thresholds. IEEE Transactions on Vehicular Technology 2000, 49(4):1424-1429. 10.1109/25.875275
Bambos N, Chen SC, Pottie GJ: Channel access algorithms with active link protection for wireless communication networks with power control. IEEE/ACM Transactions on Networking 2000, 8(5):583-597. 10.1109/90.879345
Feiten A, Mathar R: Optimal power control for multiuser CDMA channels. Proceedings of the IEEE International Symposium on Information Theory (ISIT '05), September 2005, Adelaide, Australia 1903-1907.
Foschini GJ, Miljanic Z: A simple distributed autonomous power control algorithm and its convergence. IEEE Transactions on Vehicular Technology 1993, 42(4):641-646. 10.1109/25.260747
Yates RD: A framework for uplink power control in cellular radio systems. IEEE Journal on Selected Areas in Communications 1995, 13(7):1341-1347. 10.1109/49.414651
Zander J: Distributed cochannel interference control in cellular radio systems. IEEE Transactions on Vehicular Technology 1992, 41(3):305-311. 10.1109/25.155977
Zander J: Performance of optimum transmitter power control in cellular radio systems. IEEE Transactions on Vehicular Technology 1992, 41(1):57-62. 10.1109/25.120145
Bambos N: Toward power-sensitive network architectures in wireless communications: concepts, issues, and design aspects. IEEE Personal Communications 1998, 5(3):50-59. 10.1109/98.683739
Koskie S, Gajic Z: A Nash game algorithm for SIR-based power control in 3G wireless CDMA networks. IEEE/ACM Transactions on Networking 2005, 13(5):1017-1026.
Goodman D, Mandayam N: Power control for wireless data. IEEE Personal Communications 2000, 7(2):48-54. 10.1109/98.839331
Saraydar CU, Mandayam NB, Goodman DJ: Efficient power control via pricing in wireless data networks. IEEE Transactions on Communications 2002, 50(2):291-303. 10.1109/26.983324
Xiao M, Shroff NB, Chong EKP: A utility-based power-control scheme in wireless cellular systems. IEEE/ACM Transactions on Networking 2003, 11(2):210-221. 10.1109/TNET.2003.810314
Stańczak S, Wiczanowski M, Boche H: Distributed utility-based power control: objectives and algorithms. IEEE Transactions on Signal Processing 2007, 55(10):5058-5068.
Stanczak S, Wiczanowski M, Boche H: Fundamentals of Resource Allocation in Wireless Networks. Volume 3. Springer, Berlin, Germany; 2009.
Huang J, Berry RA, Honig ML: Distributed interference compensation for wireless networks. IEEE Journal on Selected Areas in Communications 2006, 24(5):1074-1084.
Chiang M: Balancing transport and physical layers in wireless multihop networks: jointly optimal congestion control and power control. IEEE Journal on Selected Areas in Communications 2005, 23(1):104-116.
Hande P, Rangan S, Chiang M, Wu X: Distributed uplink power control for optimal SIR assignment in cellular data networks. IEEE/ACM Transactions on Networking 2008, 16(6):1420-1433.
Lan T, Hande P, Chiang M: Joint beamforming and power control for optimal SIR assignment in cellular uplinks. Proceedings of the IEEE International Symposium on Information Theory (ISIT '07), June 2007, Nice, France 2436-2440.
Rashid-Farrokhi F, Tassiulas L, Liu KJR: Joint optimal power control and beamforming in wireless networks using antenna arrays. IEEE Transactions on Communications 1998, 46(10):1313-1324. 10.1109/26.725309
Schubert M, Boche H: Solution of the multiuser downlink beamforming problem with individual SINR constraints. IEEE Transactions on Vehicular Technology 2004, 53(1):18-28. 10.1109/TVT.2003.819629
Schubert M, Boche H: QoS-based resource allocation and transceiver optimization. Foundations and Trends in Communications and Information Theory 2006, 2(6):383-529.
Bengtsson M, Ottersten B: Optimal and suboptimal transmit beamforming. In Handbook of Antennas in Wireless Communications. CRC Press, Boca Raton, Fla, USA; 2001.
Wiesel A, Eldar YC, Shamai S: Linear precoding via conic optimization for fixed MIMO receivers. IEEE Transactions on Signal Processing 2006, 54(1):161-176.
Feistel A, Stanczak S, Kaliszan M: Resource allocation in multiantenna systems under general power constraints. Proceedings of the ITG/IEEE International Workshop on Smart Antennas (WSA '09), February 2009, Berlin, Germany
Honig M, Madhow U, Verdu S: Blind adaptive multiuser detection. IEEE Transactions on Information Theory 1995, 41(4):944-960. 10.1109/18.391241
Ulukus S, Yates RD: Stochastic power control for cellular radio systems. IEEE Transactions on Communications 1998, 46(6):784-798. 10.1109/26.681417
Varanasi MK: Nonlinear multiuser receivers with distributed power control in cellular radio networks. Proceedings of the 37th Annual Allerton Conference on Communication, Control and Computing, September 1999, Monticello, Ill, USA 820-830.
Luo J, Ulukus S, Ephremides A: Standard and quasi-standard stochastic power control algorithms. IEEE Transactions on Information Theory 2005, 51(7):2612-2624. 10.1109/TIT.2005.850105
Das D, Varanasi MK: Distributed algorithms for joint optimization of multiuser receivers and power control. IEEE Transactions on Wireless Communications 2007, 6(9):3374-3383.
Mas-Colell A, Whinston MD, Green JR: Microeconomic Theory. Oxford University Press, Oxford, UK; 1995.
Viswanath P, Anantharam V, Tse DNC: Optimal sequences, power control, and user capacity of synchronous CDMA systems with linear MMSE multiuser receivers. IEEE Transactions on Information Theory 1999, 45(6):1968-1983. 10.1109/18.782119
Meyer CD: Matrix Analysis and Applied Linear Algebra. SIAM, Philadelphia, Pa, USA; 2000.
Bertsekas DP: Nonlinear Programming. Athena Scientific, Belmont, Mass, USA; 1995.
Bertsekas DP, Tsitsiklis JN: Parallel and Distributed Computation. Prentice Hall, Englewood Cliffs, NJ, USA; 1989.
Ortega JM, Rheinboldt WC: Iterative Solution of Nonlinear Equations in Several Variables, Classics in Applied Mathematics 30. SIAM, Philadelphia, Pa, USA; 2000.
Kushner HJ, Yin GG: Stochastic Approximation and Recursive Algorithms and Applications. Springer, Berlin, Germany; 2003.
Verdu S: Multiuser Detection. Cambridge University Press, Cambridge, UK; 1998.
Acknowledgments
This paper was supported in part by the German Ministry for Education and Research (BMBF) under Grant 01BU680 and in part by the Deutsche Forschungsgemeinschaft (DFG) under Grant STA 8653-1. The paper was partly presented at the 2007 Conference on Information Sciences and Systems (CISS), Washington, USA.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Feistel, A., Stańczak, S. & Tomecki, D. Joint Utility-Based Power Control and Receive Beamforming in Decentralized Wireless Networks. J Wireless Com Network 2010, 751893 (2010). https://doi.org/10.1155/2010/751893
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/751893
 is a twice continuously differentiable, strictly increasing and strictly concave function of the SIR where
is a twice continuously differentiable, strictly increasing and strictly concave function of the SIR where  is an open interval on the real line such that
is an open interval on the real line such that 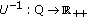 .
.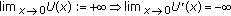 .
. is convex on
is convex on  .
.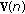 and some
and some 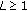 , each user
, each user  generates a sequence
generates a sequence 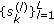 by carrying out (30) and defines
by carrying out (30) and defines 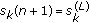 .
.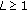 and with
and with  , each user
, each user  executes
executes 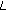 iterations of the algorithm (32) to obtain the sequence
iterations of the algorithm (32) to obtain the sequence 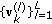 . It defines
. It defines 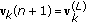 .
.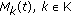 is independent of the iterate value.
is independent of the iterate value.
 ,
,  and
and  .
.
 and
and  .
.
 ,
,  ,
,  for the biased and unbiased case.
for the biased and unbiased case.
 for utility-based power control (dashed lines) and utility-based joint power and receiver control (solid lines).
for utility-based power control (dashed lines) and utility-based joint power and receiver control (solid lines).