- Research Article
- Open access
- Published:
Effects of Channel Estimation on Multiuser Virtual MIMO-OFDMA Relay-Based Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 764784 (2010)
Abstract
A practical multiuser cooperative transmission scheme denoted as Virtual Maximum Ratio Transmission (VMRT) for multiple-input multiple-output-orthogonal frequency division multiple access (MIMO-OFDMA) relay-based networks is proposed and evaluated in the presence of a realistic channel estimation algorithm and using low-density parity-check (LDPC) codes. It is shown that this scheme is robust against channel estimation errors. It offers diversity and array gain, keeping the complexity low with a multiuser and multiantenna channel estimation algorithm that is simple and efficient. In addition, the combination with LDPC codes provides improved gains; diversity gains larger than 6 dB can be easily obtained with a reduced number of relays. Thus, this scheme can be used to extend coverage or increase system throughput by using simple cooperative OFDMA-based relays.
1. Introduction
The idea of increasing reliability, coverage, and/or capacity in future wireless networks by using cooperative single-antenna relays to reach users' terminals has recently attracted much attention [1–15]. In addition, Multiple-Input Multiple-Output (MIMO) technology has demonstrated that it is a good approach to increase capacity [16, 17]; together with Orthogonal Frequency Division Multiplexing (OFDM) [18] or Orthogonal Frequency Division Multiple Access (OFDMA) [19], MIMO techniques can also provide increased reliability. The right combination of all these elements would lead to a considerable improvement of system performance.
Relay schemes can be categorized into three different groups: Amplify-and-Forward (AF) [3, 4, 8, 10–13], Compress-and-Forward (CF) [5, 20], and Decode-and-Forward (DF) [1–3, 6, 7, 9, 15]. In the AF schemes, relays amplify (and maybe transform [4]) the received signal and broadcast it to the destination. These schemes can be appropriate to extend coverage or to solve the problem of attenuation faced by receivers. Furthermore, some spatial diversity can be provided [1, 6]. In the CF, the relay transmits a quantized and compressed version of the received signal to the destination, and the destination decodes the signal by combining it with its own received signal. These schemes can exploit the redundancy between source and destination, and they assume that the source is able to reach the destination. In the last group, relays in the DF strategy decode the received signal and re-encode (and possibly transform/adapt) the information and send it to destinations. In [5], it is shown that CF strategies outperform DF when the relays are closer to the destination, and DF obtains larger throughput when relays are closer to the source. Since among the applications of our scheme is coverage extension (which imposes that the source cannot directly reach the destinations) and the use of simple relays, in this paper, we adopt this last strategy because in these scenarios better performance can be achieved by DF.
In [8], it is shown that the conventional Maximum Ratio Combining (MRC) is the optimum detection scheme for the AF strategy and also that it can achieve full diversity order of  , where
, where  is the number of relays, whereas for the DF strategy, the optimum is the Maximum Likelihood (ML) detector [1, 9]. As recognized in [1], performance analysis and implementation of said detector are quite complicated and thus a suboptimum combiner termed as
is the number of relays, whereas for the DF strategy, the optimum is the Maximum Likelihood (ML) detector [1, 9]. As recognized in [1], performance analysis and implementation of said detector are quite complicated and thus a suboptimum combiner termed as  -MRC was derived. Another suboptimum detector is the cooperative MRC (C-MRC) [10] and link adaptive regeneration (LAR) [11]. In these works, collaboration is performed at the destination, namely, the receiver treats the relays as a multiple-source transmitter and combines the multiple received signal adequately to obtain the best performance. If we also take relays into account in the design, we can improve the throughput and lower the outage probability by selecting the best relays to transmit from [12, 13] (for the AF strategy) and [7] (for the DF). Going further, we can consider the relays as a virtual multiple-input transmitter (if cooperation is used), and thus leverage on it to improve destination (user) performance. In [14, 15], the relays are used as a beamformer where full or partial channel state information (CSI) is needed on all the elements, and a joint optimization is performed to obtain the best results at the destination. However, in a practical scenario, knowledge of CSI (even partial) from all the network elements at the source (CSI-T) is not possible, and moreover, it needs to be estimated and errors might occur.
-MRC was derived. Another suboptimum detector is the cooperative MRC (C-MRC) [10] and link adaptive regeneration (LAR) [11]. In these works, collaboration is performed at the destination, namely, the receiver treats the relays as a multiple-source transmitter and combines the multiple received signal adequately to obtain the best performance. If we also take relays into account in the design, we can improve the throughput and lower the outage probability by selecting the best relays to transmit from [12, 13] (for the AF strategy) and [7] (for the DF). Going further, we can consider the relays as a virtual multiple-input transmitter (if cooperation is used), and thus leverage on it to improve destination (user) performance. In [14, 15], the relays are used as a beamformer where full or partial channel state information (CSI) is needed on all the elements, and a joint optimization is performed to obtain the best results at the destination. However, in a practical scenario, knowledge of CSI (even partial) from all the network elements at the source (CSI-T) is not possible, and moreover, it needs to be estimated and errors might occur.
In addition, the time-frequency structure of OFDMA offers flexibility in terms of multiuser resource management and advantages in terms of dealing with multipath wireless channel effects. Moreover, next generation wireless mobile networks will use some combination of the OFDMA transmission technique [21]. For this reason, in this paper OFDMA has been selected in combination with MIMO to offer a global system design with high data rate capacity and flexibility in terms of accommodating multiple users.
On the other hand, channel-coding schemes are able to drastically improve performance, while channel estimation errors may seriously affect them. Although capacity-approaching codes such as the low-density parity-check (LDPC) were proposed long ago [22], these codes have recently attracted much attention due to their efficient implementations [23] and large coding gains [24].
In [25], the authors propose and analyze a practical transmission scheme with the DF strategy taking the relays as a Virtual Multiple-Input Transceiver (VMIT). However, perfect and instantaneous CSI is assumed and no channel code is used. In this paper, we design and examine the performance of this scheme in the presence of a realistic and practical channel estimation algorithm and with the use of powerful LDPC codes. The acquisition of channel state information in a multiuser VMIT must be carried out in an efficient and simple way in order not to have a serious impact on bandwidth efficiency. Lowering the pilot overhead and the complexity of the channel estimation scheme adopted in all the receivers in the system is of paramount importance, and as the number of users and relays increases, it becomes mandatory. Thus, the proposal in [26] is used to fit requirements.
Our contributions in this paper are
-
(i)
the comparison of different practical transmission schemes in a MIMO-OFDMA-relay-based network with a base station with
 transmit antennas, using the Decode-and-Forward strategy, and LDPC channel codes and keeping the complexity low;
transmit antennas, using the Decode-and-Forward strategy, and LDPC channel codes and keeping the complexity low; -
(ii)
a proposal for the transmission over this network that obtains diversity and array gain at the users' terminals with increase in system performance and reliability with no CSI-T either at the base station or at the relays and with low complexity;
-
(iii)
the evaluation of these schemes when there is degradation in the CSI due to the use of a realistic channel estimation algorithm;
-
(iv)
the evaluation of the LDPC codes in such two-hop distributed systems.
The remainder of this paper is organized as follows. First, in Section 2, a description of the scenario and the system model is presented. Next, in Sections 3 and 4, the proposed scheme and the proposed channel estimation are described and summarized, respectively. In Section 5, the results are presented and discussed. Finally, some conclusions are drawn in Section 6.
Notations
Throughout the paper the following notation will be used. Bold capitals and bold face for matrices and vectors, respectively.  denotes expectation of
denotes expectation of  over
over  and
and  and
and  account for the absolute value and the square of the 2-norm of
account for the absolute value and the square of the 2-norm of  , respectively. The square of this norm will be denoted in the paper as gain (
, respectively. The square of this norm will be denoted in the paper as gain ( ).
).  is the identity matrix of size
is the identity matrix of size  , and
, and  is a diagonal matrix containing
is a diagonal matrix containing  in its diagonal and 0 elsewhere.
in its diagonal and 0 elsewhere.
2. Description of the Scenario and System Model
The reference scenario is shown in Figure 1 and is based on a base station (BS) with  transmit antennas,
transmit antennas,  cooperative relay stations (RSs), each one with only one antenna for transmission and reception, and
cooperative relay stations (RSs), each one with only one antenna for transmission and reception, and  user's terminals (UT), also with one receive antenna each. We assume that the users cannot be reached by the BS directly. The strategy used is the Decode-and-Forward in a half-duplex transmission; that is, in phase I, the BS transmits and RSs receive first link/hop and, in phase II, the relays transmit and UTs receive second link/hop. The system uses
user's terminals (UT), also with one receive antenna each. We assume that the users cannot be reached by the BS directly. The strategy used is the Decode-and-Forward in a half-duplex transmission; that is, in phase I, the BS transmits and RSs receive first link/hop and, in phase II, the relays transmit and UTs receive second link/hop. The system uses  subcarriers that can be allocated to different users in an OFDMA transmission; that is, different UTs use disjoint sets of
subcarriers that can be allocated to different users in an OFDMA transmission; that is, different UTs use disjoint sets of  orthogonal subcarriers. We assume, for simplicity and without loss of generality, that the subcarriers used in the link BS-RS are the same as in the link RS-UT. The algorithm or policy for the scheduler to assign subcarriers is beyond the scope of the paper. We will consider the transmission of
orthogonal subcarriers. We assume, for simplicity and without loss of generality, that the subcarriers used in the link BS-RS are the same as in the link RS-UT. The algorithm or policy for the scheduler to assign subcarriers is beyond the scope of the paper. We will consider the transmission of  OFDMA symbols as a block and denote a packet as a group of several blocks. In general,
OFDMA symbols as a block and denote a packet as a group of several blocks. In general,  can take any value. However, for the space-time block code-(STBC-) based schemes that we are proposing, the block size must necessarily equal the number of transmit antennas, that is,
can take any value. However, for the space-time block code-(STBC-) based schemes that we are proposing, the block size must necessarily equal the number of transmit antennas, that is,  . This is because we are proposing the use of full-rate STBC.
. This is because we are proposing the use of full-rate STBC.
The frequency-domain transmitted signal from the BS is

where  is the signal transmitted from the
is the signal transmitted from the  antennas at
antennas at  th subcarrier during block of
th subcarrier during block of  OFDMA symbols,
OFDMA symbols,  is a generic precoding matrix
is a generic precoding matrix  , and
, and  are the complex base band data to be sent on the
are the complex base band data to be sent on the  th subcarrier by all the transmit antennas, assumed here to be
th subcarrier by all the transmit antennas, assumed here to be  -QAM or
-QAM or  -PSK modulated without loss of generality.
-PSK modulated without loss of generality.
Next, the frequency-domain received signal at the  th relay on the
th relay on the  th subcarrier after discrete fourier transform (DFT) and discarding the cyclic prefix (CP) can be written as
th subcarrier after discrete fourier transform (DFT) and discarding the cyclic prefix (CP) can be written as

where  is the received signal by relay
is the received signal by relay  at subcarrier
at subcarrier  ,
,  is the channel frequency response for relay
is the channel frequency response for relay  at subcarrier
at subcarrier  from all the transmit antennas (
from all the transmit antennas ( ), and
), and  is the zero-mean additive white Gaussian noise (AWGN) vector, with each component (
is the zero-mean additive white Gaussian noise (AWGN) vector, with each component ( ) with variance
) with variance  . We can arrange the signal received by all the relays in a matrix form as
. We can arrange the signal received by all the relays in a matrix form as

where  is the received signal by all the relays at
is the received signal by all the relays at  th subcarrier during a block of
th subcarrier during a block of  OFDMA symbols, the matrix
OFDMA symbols, the matrix  accounts for the channel frequency response on
accounts for the channel frequency response on  th subcarrier, and
th subcarrier, and  contains the zero-mean AWGN. The
contains the zero-mean AWGN. The  th subcarrier can be assigned to any user by the scheduler.
th subcarrier can be assigned to any user by the scheduler.
For the second hop, namely, from RS to UT, the frequency-domain joint transmitted signal (It should be noted that each relay transmits one of the rows of the joint matrix  . Thus, the precoding matrix
. Thus, the precoding matrix  must be diagonal, otherwise relays would have to share transmission information, and therefore the complexity would increase, which is not the case) is
must be diagonal, otherwise relays would have to share transmission information, and therefore the complexity would increase, which is not the case) is

where  is the signal transmitted by relays at
is the signal transmitted by relays at  th subcarrier during the block of
th subcarrier during the block of  OFDMA symbols,
OFDMA symbols,  is a new generic precoding matrix for the second hop, and
is a new generic precoding matrix for the second hop, and  is the estimated
is the estimated  from received
from received  and the remodulated transmitted signal. Since the relays are equipped with only one antenna, the estimated signal is performed in a multiple-input single-output (MISO) way by each relay. In this paper, a simple zero-forcing (ZF) equalization and detection is used for reducing complexity at relays and user's terminals. This yields the following frequency-domain received signal at user's terminal
and the remodulated transmitted signal. Since the relays are equipped with only one antenna, the estimated signal is performed in a multiple-input single-output (MISO) way by each relay. In this paper, a simple zero-forcing (ZF) equalization and detection is used for reducing complexity at relays and user's terminals. This yields the following frequency-domain received signal at user's terminal 

where  is the received signal for user
is the received signal for user  at
at  th subcarrier during the block of
th subcarrier during the block of  OFDM symbols,
OFDM symbols,  is the channel frequency response for user
is the channel frequency response for user  from the
from the  relays at
relays at  th subcarrier, and
th subcarrier, and  is a second AWGN noise vector for subcarrier
is a second AWGN noise vector for subcarrier  with each component of variance
with each component of variance  . Again, grouping all the received signals by users into a matrix yields
. Again, grouping all the received signals by users into a matrix yields

 being the received signal by all the users on subcarrier
being the received signal by all the users on subcarrier  during the block of
during the block of  , the matrix
, the matrix  the channel frequency response from relays to users at
the channel frequency response from relays to users at  th subcarrier, and
th subcarrier, and  a second AWGN matrix. Note that since the system uses OFDMA, at reception, each UT selects the subcarriers with data allocated to it among all the received subcarriers.
a second AWGN matrix. Note that since the system uses OFDMA, at reception, each UT selects the subcarriers with data allocated to it among all the received subcarriers.
In this paper, the evaluation of the performance is based on the bit error rate (BER) as a measurement over different Signal-to-noise ratios (SNR). In the scenarios, there are two different links, one from BS to RS and another from RS to UT. Thus, we define the SNR for each link separately. In addition, since the system is MIMO-OFDMA-based, there will exist  different channels (in the first link) over
different channels (in the first link) over  different subcarriers. For these reasons, the average SNR per link is defined as
different subcarriers. For these reasons, the average SNR per link is defined as

Looking at (7), the SNR is calculated, averaging the signal  over the transmit antennas and the subcarriers. In this way, a single value per link is obtained to associate with the performance in a given scenario. When transmitting from relays, we will have
over the transmit antennas and the subcarriers. In this way, a single value per link is obtained to associate with the performance in a given scenario. When transmitting from relays, we will have  different channels, and in (7),
different channels, and in (7),  should be replaced by the number of transmitting relays for the scheme (
should be replaced by the number of transmitting relays for the scheme ( ) and
) and  by
by  .
.
It should be noted here that the SNR is used as a way of describing different scenarios for evaluation purposes, but it is not a parameter that needs to be estimated to perform the transmission.
2.1. A Non-CSI-T Scheme: 2-Hop Space-Time Block Code (2h-STBC)
Although Virtual Maximum Ratio Transmission (VMRT) does not need CSI-T at the relays because the UTs compute the beamforming weights (see Section 3), the selected terminal (and only the selected one) must send its weights to the relays regularly. For this reason, in order to compare and evaluate the impact of channel estimation errors and the use of LDPC codes of the proposed VMRT with the case where no CSI-T is needed, a 2-hop space-time block code is used, denoted as 2h-STBC throughout the paper; this encoding scheme uses STBC codes in both links. In phase I the BS transmits using Alamouti [27] when using 2 antennas or when using 4 or 8 antennas, [28, 29] which is denoted as "Alamoutitation" in [29]. For this scheme, the precoding matrix in (1) is  and the number of OFDMA symbols per block (
and the number of OFDMA symbols per block ( ) is set to
) is set to  . Thus, the transmitted signal can be written as
. Thus, the transmitted signal can be written as

with  when
when  , or 8, respectively, and
, or 8, respectively, and

being the matrices containing the data to be sent.  are the data on subcarrier
are the data on subcarrier  at OFDMA symbol
at OFDMA symbol  .
.
All the relays will receive the signal, and thus they are able to decode it, that is,  in (2). Grouping all the received signals by all relays, (3) yields
in (2). Grouping all the received signals by all relays, (3) yields

Therefore, a cooperative Virtual STBC transmission can be carried out from RS in phase II, assuming that the RSs are numbered and perfectly synchronized. Now, each relay, or a group of  relays, acts as an antenna re-encoding the received signal
relays, acts as an antenna re-encoding the received signal  into
into  . Again, in the general expression of (4), the pre-coding matrix is
. Again, in the general expression of (4), the pre-coding matrix is  , and thus arranging all the transmitted signals from the relays into a matrix form, we obtain
, and thus arranging all the transmitted signals from the relays into a matrix form, we obtain

with  for
for  , or 8, respectively, and
, or 8, respectively, and

with  being the re-encoded signal transmitted by the RS
being the re-encoded signal transmitted by the RS  at
at  th OFDMA symbol (
th OFDMA symbol ( ). Some observations must be pointed out here. The first one is that a different number of transmit elements can be used on each link; that is,
). Some observations must be pointed out here. The first one is that a different number of transmit elements can be used on each link; that is,  can be different from
can be different from  and
and  ; in fact, usually
; in fact, usually  . Since all the relays decode the transmitted signal by BS, the increase in the number of virtual transmitters (relays) will exploit diversity and array gains, and the second one is that the transmitted information by relays may not be orthogonal anymore because each relay decodes the received data and some errors can appear. Thus, some degradation in the performance can be expected at the user's end, especially for the channel estimation algorithm and/or LDPC codes. This scheme is the simplest method to obtain diversity from both links, so we will use it as a reference. Moreover, it can be noted that no CSI-T is needed, but rather only channel state information at the receiver (CSI-R) for coherent demodulation, at both links.
. Since all the relays decode the transmitted signal by BS, the increase in the number of virtual transmitters (relays) will exploit diversity and array gains, and the second one is that the transmitted information by relays may not be orthogonal anymore because each relay decodes the received data and some errors can appear. Thus, some degradation in the performance can be expected at the user's end, especially for the channel estimation algorithm and/or LDPC codes. This scheme is the simplest method to obtain diversity from both links, so we will use it as a reference. Moreover, it can be noted that no CSI-T is needed, but rather only channel state information at the receiver (CSI-R) for coherent demodulation, at both links.
3. Virtual Maximum Ratio Transmission (VMRT)
In order to obtain diversity in both links with reduced complexity and CSI in all the elements in the network, in [25], the following scheme is proposed, denoted as Virtual Maximum Ratio Transmission, because the relays are used as a cooperative virtual beamformer. In this scheme, the BS uses STBC (2, 4, or 8 scheme) to transmit to relays as in the 2h-STBC scheme. Therefore, the signal model is the same until the first hop as in 2h-STBC. In the second hop, instead of using an STBC again, here, the relays are configured as a virtual beamformer, and they conform the signal to the user with the best quality. The beamformer can be performed with all the relays or a group of  . In order to reduce the complexity at the relays and the CSI requirements, we use an approach similar to the one of [30]. The step-by-step procedure is as follows.
. In order to reduce the complexity at the relays and the CSI requirements, we use an approach similar to the one of [30]. The step-by-step procedure is as follows.
-
(1)
Users' terminals estimate the channel matrix and compute the Maximum Ratio Transmission (MRT) weights.
-
(2)
Each UT computes the link quality (
 ), only over its subcarriers; that is,
), only over its subcarriers; that is,  , where
, where  is the set of subcarriers allocated to user
is the set of subcarriers allocated to user 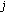 and
and  is the estimated BER at subcarrier
is the estimated BER at subcarrier 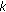 for
for  th terminal. (e.g., for QPSK modulation, BER at subcarrier
th terminal. (e.g., for QPSK modulation, BER at subcarrier 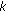 for
for  th terminal (
th terminal ( ) can be estimated as
) can be estimated as 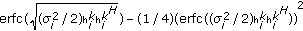 , whereas for 64-QAM, BER can be estimated as
, whereas for 64-QAM, BER can be estimated as  , where
, where  .)
.) -
(3)
UTs broadcast their quality to relays; it should be noted that this value is only a scalar per user.
-
(4)
All RSs receive this value from each UT, and according to the minimax BER criterion, the one with the minimum maximum BER is scheduled to transmit. As was shown in [25], this metric is the one which obtains the performance closest to the optimum. If qualities are sorted out in ascending order so that
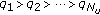 , the UT with
, the UT with  is selected.
is selected. -
(5)
One RS can act as coordinator and informs the selected UT.
-
(6)
The selected user sends the pre-coding weights vector to relays to obtain the already calculated fed-back quality (
 )
) -
(7)
Each RS uses the adequate weight to perform the cooperative Virtual Maximum Ratio Transmission.
Thus, transmitted signal  in (4) will use (10) with
in (4) will use (10) with  , calculated by using the minimax BER criterion
, calculated by using the minimax BER criterion

It should be noted that, although it is a multicarrier system, only one weight per transmit antenna is needed since using the minimax BER criterion, the best weight per transmit antenna for all the subcarriers is obtained (Note that  is not dependent on the subcarrier index
is not dependent on the subcarrier index  .). In this way, the required feedback is reduced and is independent of the number of subcarriers.
.). In this way, the required feedback is reduced and is independent of the number of subcarriers.
Statistically, if the average SNR is the same for all terminals and if the channel is ergodic, then the performance is identical for all users since all of them will sometimes experience the best quality channel on the average. By using this scheme, diversity is exploited in both links, especially on the second one, since usually the number of RS is higher than the number of transmit antennas. The reader is referred to [25] for more details.
4. Channel Estimation
The use of coherent demodulation implies the knowledge of the CSI-R at the receivers. The initial proposals for pilot-aided channel estimation schemes for MIMO-OFDM transformed the problem of estimating overlapping channels in the estimation of multiple single-input single-output (SISO) OFDM channels. This was achieved by allocating dedicated pilot subcarriers to each transmit antenna. The receiver estimates each channel from the pilot subcarriers belonging to each transmit antenna, and then it applies an interpolator to get the full channel estimate [31, 32]. This type of pilot allocation can be found in the fixed WIMAX standard [33]. Although this type of pilot allocation simplifies the channel estimation, it presents some drawbacks. As the number of transmit antennas increases, the spectral efficiency decreases considerably since a large number of subcarriers will be assigned exclusively to transmit pilots. Moreover, the fact that the pilot subcarriers are not loaded in any except the transmit antenna for which the subcarrier is allocated increases the critical peak-to-average power ratio (PAPR) parameter [34], which strongly impacts on the performance of the power amplifier.
In our scenario, where the BS can be equipped with several antennas or the VMIT can be configured as a large number of transmit antennas ( ), the pilots must be sent efficiently to minimize the decrease in the system's efficiency but still enable the receivers to estimate all the channels accurately, with minimum cochannel interference.
), the pilots must be sent efficiently to minimize the decrease in the system's efficiency but still enable the receivers to estimate all the channels accurately, with minimum cochannel interference.
A pilot-aided channel estimation scheme that attempted to minimize the cochannel interference was published in [35]. The proposed algorithm exhibits a high computational load. A simplified and enhanced algorithm, introducing a data-aided scheme for the data transmission mode, is presented in [36]. In [37], overlapped pilots are proposed for channel estimation where different transmitters use the same pilot subcarriers, avoiding the decrease in efficiency with an increasing number of transmitters. However, the performance results are not very favorable. The topic attracted significant attention and has been the focus of research in multiple publications [38–40] and references therein.
The design of training symbols and pilot sequences with the ability to decouple the cochannel interference and minimize the channel estimation mean square error (MSE) for MIMO-OFDM was addressed in several publications [36, 41, 42]. In addition, the use of different orthogonal sequences was addressed in several works. The use of Hadamard sequences was proposed in [34, 43], while the Golay sequences were considered in [44] and complex exponential sequences were investigated in [45, 46]. The time-domain channel estimation schemes have not received much attention due to the insurmountable fact that the equalization is performed in the frequency domain. Nevertheless, some research on the topic can be found in the literature.
The design of the pilot sequences is explored in [47, 48]. The pilot-carrying received symbols are processed to explore the correlation among the several channel impulse response (CIR) replicas to reduce the noise in the estimate. The use of superimposed pseudorandom pilot sequences was investigated in [47, 49]. In these schemes, the CIR estimate is obtained through the correlation of the received symbols with copies of transmitted pseudorandom sequences that are stored in the receiver (known a priori).
Although published work on time-domain channel estimation showed that the estimation process can be performed directly in time domain, due to the common frequency-domain pilot arrangement, most of the publications on the topic of pilot-aided channel estimation use the frequency-domain least squares (LS) estimates as the starting point for the estimation process. The results in [50] show that this operation can be performed in time-domain by a simple linear operation on the received signal.
In this paper, we adopt the MIMO-OFDM pilot sequence design, where the same set of subcarriers conveys pilots for all antennas, and the pilot sequence corresponding to each transmit antenna is coded with different orthogonal phase-shifting sequences. This sequence design is proven to be optimal in [42]. The pilot design, together with the associated channel estimation method [26], succeeds in estimating all the channels involved in the transmission process and eliminate the cochannel interference, under given conditions, with minimal computational load, directly from the time-domain received samples, with no DFT/IDFT operations performed prior to the estimation filter. In this way, a large amount of computational load is saved. In the following, a summary of the proposed channel estimator is shown.
The first OFDMA symbol of the transmission packet (preamble) is used to transmit pilots. In our MIMO system,  or
or  channels need to be estimated and so, in order to improve the system's efficiency, we propose that the preamble be shared among all transmit paths. From BS or RS, superimposed pilots sequences are sent by the different
channels need to be estimated and so, in order to improve the system's efficiency, we propose that the preamble be shared among all transmit paths. From BS or RS, superimposed pilots sequences are sent by the different  transmit antennas (in the case of relays, different
transmit antennas (in the case of relays, different  relays). To mitigate the resulting cochannel interference, orthogonal phase-shift sequences are used in each path, where each transmit antenna path uses a distinct pilot sequence
relays). To mitigate the resulting cochannel interference, orthogonal phase-shift sequences are used in each path, where each transmit antenna path uses a distinct pilot sequence  according to
according to

where  is the index of the BS transmit antenna and
is the index of the BS transmit antenna and  is the subcarrier index. For the relay-user link,
is the subcarrier index. For the relay-user link,  in (14) must be replaced by
in (14) must be replaced by  . Denoting
. Denoting  as the time-domain received signal at relay
as the time-domain received signal at relay  (after removing the cyclic prefix), and considering that in the most common channel models, the taps of the time-domain channel impulse response are uncorrelated and typically limited to a number of nonvanishing terms much lower than the Fast Fourier Transform (FFT) length, since the amplitude of the sequence in (14) is one, at the receiver, the time-domain channel impulse response estimate from transmit antenna
(after removing the cyclic prefix), and considering that in the most common channel models, the taps of the time-domain channel impulse response are uncorrelated and typically limited to a number of nonvanishing terms much lower than the Fast Fourier Transform (FFT) length, since the amplitude of the sequence in (14) is one, at the receiver, the time-domain channel impulse response estimate from transmit antenna  to relay
to relay  ,
,  , is
, is

where  represents the number of samples that are collected from each antenna, and
represents the number of samples that are collected from each antenna, and  . It should be noted that
. It should be noted that  is also the limit for the maximum channel delay (normalized to the system's sampling interval). This value is especially important on the second hop, limiting the number of relay channels that can be estimated using only one OFDMA symbol. Going over this limit will result in some performance degradation due to the distortion caused by the cochannel interference. To obtain the frequency-domain channel response, a FFT is applied on
is also the limit for the maximum channel delay (normalized to the system's sampling interval). This value is especially important on the second hop, limiting the number of relay channels that can be estimated using only one OFDMA symbol. Going over this limit will result in some performance degradation due to the distortion caused by the cochannel interference. To obtain the frequency-domain channel response, a FFT is applied on  . Since we use OFDMA, the multiuser channel estimation is performed using only the desired frequencies. This channel estimator will be denoted throughout the paper as LS, since it follows the LS criterion.
. Since we use OFDMA, the multiuser channel estimation is performed using only the desired frequencies. This channel estimator will be denoted throughout the paper as LS, since it follows the LS criterion.
If the channel impulse response estimate contains more samples than the normalized channel length, some of them will only contain noise, and thus these samples will degrade the channel estimation performance. For this reason, we also implement the Most Significant Tap (MST) channel estimation [48], applied to [26], where we only take the most significant  taps. This low cost improvement of (15) will be denoted as MST throughout the text, and it provides significant performance improvements, especially in the case of LDPC codes, as will be seen in Section 5.
taps. This low cost improvement of (15) will be denoted as MST throughout the text, and it provides significant performance improvements, especially in the case of LDPC codes, as will be seen in Section 5.
5. Simulation Results
Several simulations have been carried out using the Monte Carlo method to evaluate the proposed scheme under realistic channel conditions. All simulations use  subcarriers and a cyclic prefix of 16 samples over a SUI-3 [51] or HiperLAN 2 B channel model [52]. Since we are not focusing on subcarrier scheduling policies, a block of
subcarriers and a cyclic prefix of 16 samples over a SUI-3 [51] or HiperLAN 2 B channel model [52]. Since we are not focusing on subcarrier scheduling policies, a block of  contiguous subcarriers is assigned to each user. Only user 1 results are presented because similar performance is obtained by the different users, as explained before. In [25], it is shown that we can obtain diversity and array gain on both hops, and this gain increases as the number of RS does. Since this paper is focused on the performance of channel estimation and LDPC codes, we fixed the number of transmit antennas at the BS to 4, the number of relays to 8 (and 8, 16, 32 for LDPC codes), and the number of users to 4. Obtained results can be extrapolated to other configurations because they do not depend on these parameters. The two channel estimation algorithms proposed in the paper, namely, the LS and the MST, have been evaluated in two different scenarios:
contiguous subcarriers is assigned to each user. Only user 1 results are presented because similar performance is obtained by the different users, as explained before. In [25], it is shown that we can obtain diversity and array gain on both hops, and this gain increases as the number of RS does. Since this paper is focused on the performance of channel estimation and LDPC codes, we fixed the number of transmit antennas at the BS to 4, the number of relays to 8 (and 8, 16, 32 for LDPC codes), and the number of users to 4. Obtained results can be extrapolated to other configurations because they do not depend on these parameters. The two channel estimation algorithms proposed in the paper, namely, the LS and the MST, have been evaluated in two different scenarios:
-
(i)
Scenario A: the two links have the same SNR.
-
(ii)
Scenario B: the SNR of the first link is fixed to 20 and 30 dB for QPSK and 64-QAM, respectively.
-
(iii)
Scenario C: when using LDPC codes, performance is usually given as a function of the
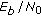 (the energy per uncoded bit over the noise). For this reason, results on LDPC will use the
(the energy per uncoded bit over the noise). For this reason, results on LDPC will use the 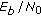 instead of the SNR. In these cases, the
instead of the SNR. In these cases, the 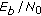 for the first link has been fixed to 3 dB.
for the first link has been fixed to 3 dB.
5.1. Maximum Ratio Transmission-Single Link (MRT-SL)
Before presenting the results, in the following, a comparison model is introduced. In [7], an optimized transmission scheme based on relays is proposed. The BS uses a single antenna and selects the best relay to transmit to. Then, from this relay the signal is forwarded to the destination. Adapting [7] to be used with multiple antennas at the BS, we have the Maximum Ratio Transmission-Single Link (MRT-SL). In this scheme, the BS, based on the channel state information in the link BS-RS, selects the best relay to transmit to and beamforms the transmission to it according to the maximum ratio transmission criterion [53]. Thus, transmitted signal can be written as

with  ,
,  (a column vector with the
(a column vector with the  data to be sent in this block on subcarrier
data to be sent in this block on subcarrier  ), and
), and  being the matrix formed by the repetition of
being the matrix formed by the repetition of  times vector
times vector  , which are the beamforming weights, again, according to the minimax criterion. Thus
, which are the beamforming weights, again, according to the minimax criterion. Thus

Again,  . It should be noted that here the search is over the whole subcarrier set because the relays need to receive the signal in the whole bandwidth. In this way, only the
. It should be noted that here the search is over the whole subcarrier set because the relays need to receive the signal in the whole bandwidth. In this way, only the  th relay is able to decode the data. Then, from this relay, data are sent to the users in a single-Input single-output (SISO) link; that is,
th relay is able to decode the data. Then, from this relay, data are sent to the users in a single-Input single-output (SISO) link; that is,  in (4) is
in (4) is  ,
,  ,
,  , and
, and  .
.
This scheme follows [7] but is adapted for a scenario with multiple transmit antennas and without MRC performed at the destination. As will be seen later, this scheme does not exploit diversity on the second hop. Indeed, the best relay from the point of view of BS might not be the best one to reach users. It has the advantage that CSI-T is needed at the BS only for the link BS-RS instead of the whole link CSI-T as in [14]. This scheme will be used for comparison purposes.
5.2. Effect of the Channel Estimation
Results have been obtained using the channel estimated by the proposed algorithms at each of the steps in the transmission link. For clarity reasons, in the following, the places and purposes of channel estimation are summarized as follows:
-
(i)
2h- STBC—where: at the reception of RS and UT. Reason: for coherent demodulation.
-
(ii)
MRT-SL—where: at the RS receiver. Reasons: to calculate the beamforming weights and for coherent demodulation. Where: at the reception of UT receiver. Reason: for coherent demodulation.
-
(iii)
VMRT—where: at the reception of RS. Reason: for coherent demodulation. Where: at the UT receiver. Reasons: to calculate the beamforming weights and for coherent demodulation.
It should be noted that for schemes using MRT, the channel estimation errors will produce a twofold effect: first, the beamforming weights will be corrupted by these errors, and second, the coherent demodulation will also be affected.
In Figure 2, the channel estimation effect on different schemes is shown for a QPSK modulation over a SUI-3 channel and the two scenarios. It can be observed that the VMRT scheme outperforms the others. A diversity gain and an array gain can be observed, due to the multiple transmit elements (relays) on the second hop as stated in [25]. In addition, in Figure 2(a), it can be seen that all the schemes behave similarly when the proposed LS channel estimation is used (around 3 dB of loss in SNR with respect to a perfect CSI). However, in the case of MST estimation, the gain obtained depends on the scheme and the scenario. In scenario A, by using MST estimation with VMRT, we obtain a gain (with respect to the LS estimation) of around 1.5 dB, whereas for the 2h-STBC, it is around 1 dB, and for the MRT-SL, the gain is less than 0.5 dB. This means that the VMRT scheme is more robust to channel estimation errors, but it is also more sensitive to the algorithm used to estimate the channel. Indeed, the proposed design with MST channel estimation obtains only a degradation of around 1 dB with respect to a perfect CSI. For the results on Scenario B in Figure 2(b), there is a gain of 3 dB for the VMRT, around 2 dB in the case of 2h-STBC and 1 dB for the MRT-SL. Thus, it can be concluded that channel estimation errors affect the coherent demodulation more than the weight calculation. The reason is because for the 2h-STBC (which will only ehibit the coherent demodulation effect), once the SNR in the first link has been fixed to a realtively good value, the MST obtains 0.5 dB of degradation with respect to the perfect CSI knowledge, whereas for the VMRT (which calculates the weights in the second hop), the degradation of MST performance with respect to the perfect CSI is around 0.2 dB. This is mainly due to the coherent demodulation errors in the first link. Furthermore, it can also be observed that there is an error floor caused by the errors on the first link that cannot be recovered, although this error floor is lower (around  ) for the VMRT than for the other schemes (around
) for the VMRT than for the other schemes (around  ).
).
Similar results are obtained when 64-QAM modulation is used over a SUI-3 channel, as can be observed in Figure 3, which is interesting since results do not depend on the modulation order; there is only a shift in the SNR values for QPSK with respect to 64-QAM.
Next, in Figure 4(a), the same results as in Figure 3(a) are presented but over an HiperLAN 2 B channel (more frequency selective behavior, used to check the robustness of the scheme and the channel estimator). It can be observed that the estimator is robust and accurate even for a highly frequency-selective channel.
5.3. LDPC and Channel Estimation
Recently, capacity-approaching LDPC codes [24] have attracted much attention. Their application to relay-based networks has also recently attracted interest [54–59], although, to the authors' knowledge, the performance has always been evaluated in AWGN scenarios: for single-carrier, single-relay and single-antenna half-duplex transmission in [54, 57], when relays re-encode the signal, and in [58] when they do not, and for multiple-antenna in [55]. If there are many relays conforming a virtual transmitter (although scenarios proposed by those authors only take into account a few), in [56], the increase in performance is noticeable. In [59], the work in [57] is applied to multicarrier signals.
It is well known that random puncturing degrades the LDPC codes performance, and so, in a relay-based system with a realistic channel estimation algorithm, this situation might occur very often. It would be interesting to show how the global performance, when using powerful forward error correction (FEC) such as LDPC codes in the system, would be affected by the channel estimation strategies, and how it does so in the proposed transmission schemes. A similar rate  LDPC code as in IEEE 802.16e standard [60] is used. As can be seen in Figures 4(b) and 5, several interesting aspects can be found. The first one is that our proposed scheme, combined with LDPC, in AWGN channels, obtains a large gain. The coding gain of LDPC together with our diversity and array gains gives a relay-based system that is able to work with very low
LDPC code as in IEEE 802.16e standard [60] is used. As can be seen in Figures 4(b) and 5, several interesting aspects can be found. The first one is that our proposed scheme, combined with LDPC, in AWGN channels, obtains a large gain. The coding gain of LDPC together with our diversity and array gains gives a relay-based system that is able to work with very low  in both links. The second one is that the scheme still works in wireless channels such as SUI-3, although with an increase in BER and a decrease in diversity gain. The third one is that the channel estimation errors seriously affect the global performance of LDPC codes, and thus it is important to improve channel estimation algorithms to boost performance. Our proposed efficient and simple MST algorithm is able to improve the performance, although there is still a 3 dB penalty with respect to a perfect CSI.
in both links. The second one is that the scheme still works in wireless channels such as SUI-3, although with an increase in BER and a decrease in diversity gain. The third one is that the channel estimation errors seriously affect the global performance of LDPC codes, and thus it is important to improve channel estimation algorithms to boost performance. Our proposed efficient and simple MST algorithm is able to improve the performance, although there is still a 3 dB penalty with respect to a perfect CSI.
5.4. Effect of the Feedback Quantization
Another important aspect is the number of bits needed for the quantization of the weights in the VMRT scheme. In Figure 6, the effect of the number of bits on a fixed point feedback is shown. It can be observed that if the number of bits is too low there is a degradation in the performance (an error floor may even appear), but once the number of bits is sufficient (and not very high), the system performs almost the same as in the case of using full precision. In addition, it can also be appreciated that the degradation decreases with a large number of relays. The reason is because when increasing the number of relays, quantization errors may compensate one another. It should be noted that, although it is a multiuser MIMO system, on the second hop, only one user feeds the weights back (the selected one), so the feedback does not depend on the number of users but only on the number of transmit elements ( ). This is indeed another advantage of this cooperative scheme.
). This is indeed another advantage of this cooperative scheme.
Moreover, in order to compress the feedback requirements even more, the value of the quality of each user can be quantized. It has been shown in [61] that with one or two bits (per user) it is enough to reach more than 95% of the possible throughput.
6. Conclusions
In this paper, the scheme denoted as Virtual Maximum Ratio Transmission for a cooperative MIMO-OFDMA-relay-based network is evaluated in the presence of realistic propagation channels such as SUI-3 or HiperLAN 2 B channel models. A practical, simple, and efficient multiuser MIMO channel estimation algorithm and the use of LDPC codes are also analyzed.
It has been shown that the scheme is robust against channel estimation errors and it still provides diversity and array gains in such scenarios. Furthermore, when combined with powerful channel codes such as LDPC, the joint advantages result in a significant improvement, allowing the coverage extension even if the first-link SNR is very low. Thus, the VMRT is a cooperative transmission scheme that can increase coverage and system throughput without increasing users' hardware and/or complexity.
References
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part I: system description. IEEE Transactions on Communications 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part II: implementation aspects and performance analysis. IEEE Transactions on Communications 2003, 51(11):1939-1948. 10.1109/TCOMM.2003.819238
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Krishna R, Xiong Z, Lambotharan S: A cooperative MMSE relay strategy for wireless sensor networks. IEEE Signal Processing Letters 2008, 15: 549-552.
Kramer G, Gastpar M, Gupta P: Cooperative strategies and capacity theorems for relay networks. IEEE Transactions on Information Theory 2005, 51(9):3037-3063. 10.1109/TIT.2005.853304
Janani M, Hedayat A, Hunter TE, Nosratinia A: Coded cooperation in wireless communications: space-time transmission and iterative decoding. IEEE Transactions on Signal Processing 2004, 52(2):362-371. 10.1109/TSP.2003.821100
Yi Z, Kim ILM: Diversity order analysis of the decode-and-forward cooperative networks with relay selection. IEEE Transactions on Wireless Communications 2008, 7(5):1792-1799.
Anghel PA, Kaveh M: Exact symbol error probability of a cooperative network in a rayleigh-fading environment. IEEE Transactions on Wireless Communications 2004, 3(5):1416-1421. 10.1109/TWC.2004.833431
Chen D, Laneman JN: Modulation and demodulation for cooperative diversity in wireless systems. IEEE Transactions on Wireless Communications 2006, 5(7):1785-1794.
Wang T, Cano A, Giannakis GB, Laneman JN: High-performance cooperative demodulation with decode-and-forward relays. IEEE Transactions on Communications 2007, 55(7):1427-1438.
Wang T, Giannakis GB, Wang R: Smart regenerative relays for link-adaptive cooperative communications. IEEE Transactions on Communications 2008, 56(11):1950-1960.
Zhao Y, Adve R, Lim TJ: Symbol error rate of selection amplify-and-forward relay systems. IEEE Communications Letters 2006, 10(11):757-759.
Yi Z, Adve R, Teng JL: Improving amplify-and-forward relay networks: optimal power allocation versus selection. IEEE Transactions on Wireless Communications 2007, 6(8):3114-3123.
Yi Z, Kim IM: Joint optimization of relay-precoders and decoders with partial channel side information in cooperative networks. IEEE Journal on Selected Areas in Communications 2007, 25(2):447-458.
Alexiou A, Yu K, Boccardi F: Combining MIMO and relaying gains for highly efficient wireless backhaul. IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '08), 2008 1-5.
Gong J, Soleymani MR, Hayes JF: A rigorous proof of MIMO channel capacity's increase with antenna number. Wireless Personal Communications 2009, 49(1):81-86. 10.1007/s11277-008-9558-2
Katalinić A, Nagy R, Zentner R: Benefits of MIMO systems in practice: increased capacity, reliability and spectrum efficiency. 48th International Symposium ELMAR focused on Multimedia Signal Processing and Communications, 2006 263-266.
Sampath H, Talwar S, Tellado J, Erceg V, Paulraj A: A fourth-generation MIMO-OFDM broadband wireless system: design, performance, and field trial results. IEEE Communications Magazine 2002, 40(9):143-149. 10.1109/MCOM.2002.1031841
Han C, Doufexi A, Armour S, Ng KH, McGeehan J: Adaptive MIMO OFDMA for future generation cellular systems in a realistic outdoor environment. Proceedings of the IEEE 63rd Vehicular Technology Conference (VTC '06), July 2006 142-146.
Cover TM, Gamal AAEL: Capacity theorems for the relay channel. IEEE Transactions on Information Theory 1979, 25(5):572-584. 10.1109/TIT.1979.1056084
Sternad M, Svensson T, Ottosson T, Ahlen A, Svensson A, Brunstrom A: Towards systems beyond 3G based on adaptive OFDMA transmission. Proceedings of the IEEE 2007, 95(12):2432-2455.
Gallager RG: Low-density parity-check codes. IEEE Transactions on Information Theory 1962, 8: 21-28. 10.1109/TIT.1962.1057683
Richardson TJ, Urbanke RL: Efficient encoding of low-density parity-check codes. IEEE Transactions on Information Theory 2001, 47(2):638-656. 10.1109/18.910579
Richardson TJ, Shokrollahi MA, Urbanke RL: Design of capacity-approaching irregular low-density parity-check codes. IEEE Transactions on Information Theory 2001, 47(2):619-637. 10.1109/18.910578
Gil Jiménez VP, Gameiro A, García Armada A: Virtual maximum ratio transmission for downlink OFDMA relay-based networks. Wireless Personal Communications 2010, 1-19.
Ribeiro C, Gameiro A: Estimation of CFO and channels in phase-shift orthogonal pilot-aided OFDM systems with transmitter diversity. Eurasip Journal on Wireless Communications and Networking 2009, 2009:-10.
Alamouti SM: A simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998, 16(8):1451-1458. 10.1109/49.730453
Tarokh V, Jafarkhani H, Calderbank AR: Space-time block codes from orthogonal designs. IEEE Transactions on Information Theory 1999, 45(5):1456-1467. 10.1109/18.771146
Mecklenbräuker CF, Rupp M: Generalized alamouti codes for trading quality of service against data rate in MIMO UMTS. EURASIP Journal on Applied Signal Processing 2004, 2004(5):662-675. 10.1155/S1110865704310061
Ko JY, Oh DC, Lee YH: Coherent opportunistic beamforming with partial channel information in multiuser wireless systems. IEEE Transactions on Wireless Communications 2008, 7(2):705-713.
Jeon WG, Paik KH, Cho YS: An efficient channel estimation technique for OFDM systems with transmitter diversity. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '00) 2000, 2: 1246-1250.
Dowler A, Doufexi A, Nix A: Performance evaluation of channel estimation techniques for a mobile fourth generation wide area OFDM system. Proceedings of the IEEE Vehicular Technology Conference, 2002 56(4):2036-2040.
IEEE 802.16-2004: IEEE Standard for Local and metropolitan area networks Part 16: Air Interface for Fixed Broadband Wireless Access Systems IEEE; 2004.
Dowler A, Nix A: Performance evaluation of channel estimation techniques in a multiple antenna OFDM system. Proceedings of the IEEE Vehicular Technology Conference, 2003 58(2):1214-1218.
Li Y, Seshadri N, Ariyavisitakul S: Channel estimation for OFDM systems with transmitter diversity in mobile wireless channels. IEEE Journal on Selected Areas in Communications 1999, 17(3):461-471. 10.1109/49.753731
Li Y: Simplified channel estimation for OFDM systems with multiple transmit antennas. IEEE Transactions on Wireless Communications 2002, 1(1):67-75. 10.1109/7693.975446
Sternad M, Aronsson D: Channel estimation and prediction for adaptive OFDMA/TDMA uplinks, based on overlapping pilots. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '05), 2005 3: 861-864.
Shin M, Lee H, Lee C: Enhanced channel-estimation technique for MIMO-OFDM systems. IEEE Transactions on Vehicular Technology 2004, 53(1):261-265. 10.1109/TVT.2003.822002
Zhang H, Li Y, Reid A, Terry J: Channel estimation for MIMO OFDM in correlated fading channels. Proceedings of the IEEE International Conference on Communications, 2005 4: 2626-2630.
Zamiri-Jafarian H, Pasupathy S: Robust and improved channel estimation algorithm for MIMO-OFDM systems. IEEE Transactions on Wireless Communications 2007, 6(6):2106-2113.
Barhumi I, Leus G, Moonen M: Optimal training design for MIMO OFDM systems in mobile wireless channels. IEEE Transactions on Signal Processing 2003, 51(6):1615-1624. 10.1109/TSP.2003.811243
Minn H, Al-Dhahir N: Optimal training signals for MIMO OFDM channel estimation. IEEE Transactions on Wireless Communications 2006, 5(5):1158-1168.
Shao L, Roy S: A rate-one non-orthogonal space-time coded OFDM system with estimation for frequency selective channels. Proceedings of the IEEE Global Telecommunications Conference, 2002 1: 676-680.
Suh C, Hwang C-S, Choi H: Preamble design for channel estimation in MIMO-OFDM systems. Proceedings of the IEEE Global Telecommunications Conference, 2003 1: 317-321.
Minn H, Kim DI, Bhargava VK: A reduced complexity channel estimation for OFDM systems with transmit diversity in mobile wireless channels. IEEE Transactions on Communications 2002, 50(5):799-807. 10.1109/TCOMM.2002.1006561
Auer G: Channel estimation in two dimensions for OFDM systems with multiple transmit antennas. Proceedings of the IEEE Global Telecommunications Conference, 2003 1: 322-326.
Yeh CS, Lin Y: Channel estimation using pilot tones in OFDM systems. IEEE Transactions on Broadcasting 1999, 45(4):400-409. 10.1109/11.825535
Minn H, Bhargava VK: An investigation into time-domain approach for OFDM channel estimation. IEEE Transactions on Broadcasting 2000, 46(4):240-248. 10.1109/11.898744
Wang D, Zhu G, Hu Z: A combined channel estimation in time-frequency domain for OFDM system in mobile channel. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '03), 2003, Beijing, China 1: 940-944.
Ribeiro C, Gameiro A: Direct time-domain channel impulse response estimation for OFDM-based systems. Proceedings of the IEEE Vehicular Technology Conference, 2007 1082-1086.
Hari KVS, Sheikh KP, Bushue C: Interim channel models for G2 MMDS fixed wireless applications. IEEE; 2000.
ETSI-BRAN : Channel models for HiperLAN 2 in different indoor scenarios. ETSI-BRAN; 1998.
Lo TKY: Maximum ratio transmission. IEEE Transactions on Communications 1999, 47(10):1458-1461. 10.1109/26.795811
Wu M, Weitkemper P, Wubben D, Kammeyer KD: Comparison of distributed LDPC coding schemes for decode-and-forward relay channels. Proceedings of the International ITG Workshop on Smart Antennas (WSA '10), February 2010 127-134.
He Z, Roy S: LDPC coded two-way MIMO relay networks with physical layer network coding. Proceedings of the WSA 25th Queen's Biennial Symposium on Communications (QBSC '10), May 2010 301-304.
Li C, Yue G, Khojastepour MA, Wang X, Madihian MM: LDPC-coded cooperative relay systems: performance analysis and code design. IEEE Transactions on Communications 2008, 56(3):485-496.
Li C, Yue G, Wang X, Khojastepour MA: LDPC code design for half-duplex cooperative relay. IEEE Transactions on Wireless Communications 2008, 7(11):4558-4567.
Chen Z, Ouyang S, Xiao H: The design of efficiently-encodable LDPC codes for coded cooperation in relay channel. Proceedings of the QBSC WRI International Conference on Communications and Mobile Computing (CMC '10), 2010 2: 221-223.
Kim KJ, Wang P, Kwak D, Kwak KS: Distributed LDPC coders in cooperative relay networks. Proceedings of the 9th International Symposium on Communications and Information Technology (ISCIT '09), September 2009 949-953.
IEEE : IEEE 802.16e-2005: IEEE Standard for local and metropolitan area networks—part 16: air interface for fixed and mobile broadband wireless access systems. Amendment 2: physical and medium access control layers for combined fixed and mobile operation in licensed bands and corrigendum 1. IEEE; 2005.
Florén F, Edfors O, Molin B-A: The effect of feedback quantization on the throughput of a multiuser diversity scheme. Proceedings of the IEEE Global Telecommunications Conference, 2003 1: 497-501.
Acknowledgments
The authors would like to thank Jae-Yun Ko for his valuable help at the beginning of our work. This work has been partly funded by the projects MULTIADAPTIVE (TEC2008-06327-C03-02), COMONSENS (CSD2008-00010) and CODIV (ICT-2007-215477).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gil Jiménez, V.P., Ribeiro, C., Gameiro, A. et al. Effects of Channel Estimation on Multiuser Virtual MIMO-OFDMA Relay-Based Networks. J Wireless Com Network 2010, 764784 (2010). https://doi.org/10.1155/2010/764784
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/764784
 transmit antennas, using the Decode-and-Forward strategy, and LDPC channel codes and keeping the complexity low;
transmit antennas, using the Decode-and-Forward strategy, and LDPC channel codes and keeping the complexity low;
 ), only over its subcarriers; that is,
), only over its subcarriers; that is,  , where
, where  is the set of subcarriers allocated to user
is the set of subcarriers allocated to user 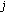 and
and  is the estimated BER at subcarrier
is the estimated BER at subcarrier 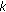 for
for  th terminal. (e.g., for QPSK modulation, BER at subcarrier
th terminal. (e.g., for QPSK modulation, BER at subcarrier 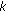 for
for  th terminal (
th terminal ( ) can be estimated as
) can be estimated as 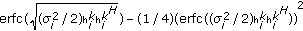 , whereas for 64-QAM, BER can be estimated as
, whereas for 64-QAM, BER can be estimated as  , where
, where  .)
.)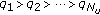 , the UT with
, the UT with  is selected.
is selected. )
) (the energy per uncoded bit over the noise). For this reason, results on LDPC will use the
(the energy per uncoded bit over the noise). For this reason, results on LDPC will use the 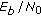 instead of the SNR. In these cases, the
instead of the SNR. In these cases, the 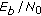 for the first link has been fixed to 3 dB.
for the first link has been fixed to 3 dB.
 ,
,  ,
,  ,
,  . Scenario AScenario B
. Scenario AScenario B
 ,
,  ,
,  ,
,  . Scenario AScenario B
. Scenario AScenario B
 ,
,  ,
,  ,
,  . HiperLAN 2 B channel. Scenario ABPSK with LDPC codes. SUI-3 channel. Scenario C
. HiperLAN 2 B channel. Scenario ABPSK with LDPC codes. SUI-3 channel. Scenario C
 ,
,  ,
,  . Scenario C.
. Scenario C.


 ,
,  , and
, and  . full precision (FP) and the number of bits for precision.
. full precision (FP) and the number of bits for precision.