- Research Article
- Open access
- Published:
Resource Allocation for the Multiband Relay Channel: A Building Block for Hybrid Wireless Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 792410 (2010)
Abstract
We investigate optimal resource allocation for the multiband relay channel. We find the optimal power and bandwidth allocation strategies that maximize the bounds on the capacity, by solving the corresponding max-min optimization problem. We provide sufficient conditions under which the associated max-min problem is equivalent to a supporting plane problem, which renders the solution for an arbitrary number of bands tractable. In addition, the sufficient conditions derived are general enough so that a class of utility functions can be accommodated with this formulation. As an example, we concentrate on the case where the source has two bands and the relay has a single band available and find the optimal resource allocation. We observe that joint power and bandwidth optimization always yields higher achievable rates than power optimization alone, establishing the merit of bandwidth sharing. Motivated by our analytical results, we examine a simple scenario where new channels become available for a transmitter to communicate; that is, new source to relay bands are added to a frequency division relay network. Given the channel conditions of the network, we establish the guidelines on how to allocate resources in order to achieve higher rates, depending on the relative quality of the available links.
1. Introduction
Future wireless networks are expected to enable nodes to communicate over multiple technologies and hops. Recent advances in the development of software defined radios support the vision where agile radios are employed at each node that utilize multiple standards and communicate seamlessly. Indeed, an intense research effort is directed towards having multiple communication standards coexist within one system, for example, the cellular network and IEEE 802.11 WLAN as in [1, 2]. We refer to a group of nodes capable of employing a number of communication technologies to find the best multihop route between the source-destination pairs, as a hybrid wireless network.
In this paper, we consider a simple hybrid wireless network with a source destination pair and aim at understanding its performance limits, that is, information theoretic rates with optimal resource allocation. In particular, we consider a scenario where a source node can communicate over multiple frequency bands to its destination, and a node that overhears the source transmission acts as a relay. We assume that the frequency bands that the source utilizes as well the ones used by the relay node are mutually orthogonal. The different bands are envisioned to represent links that operate with different wireless communication standards.
There has been considerable research effort up to date towards characterizing the information theoretic capacity of relay channels [3–7]. Most of the earlier work on relay channel capacity assumes that simultaneous transmission and reception at the relay is possible [4]. Since this is difficult to implement, recent work considers employing orthogonality at the relay via time-division [5, 8–10], frequency-division [11, 12], or code-division [13, 14]. To compensate the loss of spectral efficiency caused by this architecture and to increase the capacity, optimal resource allocation has been considered in [5, 8, 10, 11, 15, 16]. The optimal power and time slot duration allocation for the time-division relay channel has been considered in [5]. The work in [8] investigates three half-duplex time-division protocols that vary in the method of broadcasting they employ and the existence of receiver collision. The optimal power and time-slot allocation has been investigated for the protocol with the maximum degree of broadcasting and no receiver collision in [5].
We note that resource allocation in wireless relay networks is employed by utilizing the received SNR and the channel state information which are typically assumed to be available at the source and the relay node [5, 8, 10, 11, 16]. Notably, [16] studies optimal power and bandwidth allocation strategies for collaborative transmit diversity schemes for the situation when the source and the relay know only the magnitudes of the channel gains. The outage minimization and the corresponding optimal power control are considered when the network channel state is available at the source and the relay [10]. The model considered in this paper is in accordance with previous work and utilizes the received SNRs that are available at the source and the relay in order to find optimal resource allocation strategy.
In this paper, we investigate the optimal resource allocation strategies that maximize the capacity bounds for a simple hybrid wireless relay network. The channel model in this work can be traced back to a class of orthogonal relay networks first proposed in [11]. The three-node relay network in [11] is composed of two parts: a broadcast channel from the source node to the relay and destination node, and a separate orthogonal link from the relay node to the destination node. The parallel channel counterpart of [11] is later examined in [15]. A sum power constraint is imposed on the source node, and the relay node is restricted to perform a partial decode and forward operation. The sum rate from the source to the destination is then maximized by performing power allocation among different subchannels and the time sharing factor between the two parts of the network. A supporting plane technique is proposed in [15] to solve the associated max-min optimization problem. The results for the parallel network are then applied to the block fading model [15].
The model considered in this work is similar to the parallel relay network in [15]; yet, for the hybrid wireless network considered, the rate maximization leads to a different optimization problem than [15]: in a hybrid network, in addition to power allocation among different bands, it is conceivable to consider bandwidth allocation as well, and we find that the joint optimal power and bandwidth allocation yields higher rate than power optimization only. It is worth mentioning that dynamic bandwidth allocation is beneficial for a hybrid wireless network even in a scenario of a flat overall band. This is because different systems (standards) may exhibit different received SNR behavior even if the underlying channel gain and noise level are the same. This can be caused, for example, by different coding schemes or different requirements on feedback. Thus, one system will not, in general, be invariably better than all the others over all links.
At the outset, the joint power and bandwidth optimization appears challenging. Luckily, the resulting max-min optimization problem, we show, conforms to a set of sufficient conditions that render the solution manageable, even for an arbitrarily large number of bands. The technique that we can use under these sufficient conditions is the supporting plane technique used in [15]. We remark that the sufficient conditions are general enough that a class of utility functions can be optimized using the technique although our focus is on the information theoretic rates. This implies that the optimization technique used in this paper can be incorporated as a building block in a variety of resource allocation settings.
Lastly, in order to gain insight into the impact of optimal resource allocation on the construction of a hybrid wireless network, we examine a scenario where new wireless links can be added to the classical frequency division relay network to form a simple hybrid wireless network. Given the channel conditions between nodes, we study how to allocate resources to achieve the higher achievable rate. We observe that the source node is encouraged to communicate over the best network by dedicating all resources exclusively when condition of source-to-relay (SR) link and source-to-destination (SD) link of the new network is better (or worse) than that of SD link and SR link of the current network. Otherwise, it is beneficial to share resource between the current network and the new network to achieve a higher rate.
2. The Multiband Relay Channel
We consider the multiband relay channel (MBRC), which models a three-node hybrid wireless network where multiple frequency bands available from the source and the relay are mutually orthogonal. In particular, the situation where, among total  channels, there are
channels, there are  channels available for the source node and
channels available for the source node and  for the relay node, shown in Figure 1, is termed the
for the relay node, shown in Figure 1, is termed the  -MBRC.
-MBRC.
The source node transmits information over  orthogonal channels to the relay and the destination node. The relay node uses a decode-and-forward scheme [4]. The
orthogonal channels to the relay and the destination node. The relay node uses a decode-and-forward scheme [4]. The  -MBRC input-output signal model is thus given by
-MBRC input-output signal model is thus given by

where and
and  are the transmitted signal vectors from the source node and the relay node, respectively.
are the transmitted signal vectors from the source node and the relay node, respectively.  and
and  are the received signal vectors at the destination node and the relay node when the signal is transmitted from the source node.
are the received signal vectors at the destination node and the relay node when the signal is transmitted from the source node.  is the received signal vector at the destination from the relay.
is the received signal vector at the destination from the relay.  =
=  is the zero-mean independent additive white Gaussian noise (AWGN) vector with covariance matrix
is the zero-mean independent additive white Gaussian noise (AWGN) vector with covariance matrix  at the relay node.
at the relay node.  and
and  are the zero-mean independent AWGN vectors with covariance matrices
are the zero-mean independent AWGN vectors with covariance matrices  , and
, and  at the destination node.
at the destination node.  denotes the transpose operation, and
denotes the transpose operation, and  is an
is an  diagonal matrix. Since channels are independent, the channel transition probability mass function is given by
diagonal matrix. Since channels are independent, the channel transition probability mass function is given by

and we have the following theorem.
Theorem 1.
The upper and lower bounds for the capacity of  -MBRC are
-MBRC are


where  is the mutual information between
is the mutual information between  and
and  . The input distribution
. The input distribution  is
is

Proof.
The lower bound is obtained by taking the maximum of all possible transmission rates given the total number of bands; that is, the lower bound includes all possible transmission schemes which depend on whether the transmission from the source band(s) is decoded at the relay.
We define  as the set of bands in which the transmission from the source is decoded at the relay.
as the set of bands in which the transmission from the source is decoded at the relay.  is the complement of
is the complement of  and includes the set of bands for direct communication. For
and includes the set of bands for direct communication. For  -MBRC, the lower bound is given by
-MBRC, the lower bound is given by

where  is the transmitted signal vector from the source and
is the transmitted signal vector from the source and  is the transmitted signal vector from the source intended for direct transmission. Similarly,
is the transmitted signal vector from the source intended for direct transmission. Similarly,  is the transmitted signal from the relay.
is the transmitted signal from the relay.  is the received signal vector at the relay.
is the received signal vector at the relay.  is the received signal vector at the destination.
is the received signal vector at the destination.  is the received signal vector at the destination as a result of direct transmission.
is the received signal vector at the destination as a result of direct transmission.  and
and  are given by
are given by


where  is the input joint distribution with respect to
is the input joint distribution with respect to  . Similarly,
. Similarly,  is the input joint distribution with respect to
is the input joint distribution with respect to  . We note that (7) can be readily obtained by using the results in [4] by taking
. We note that (7) can be readily obtained by using the results in [4] by taking  ,
,  ,
,  , and
, and  . Applying the same approach, we obtain the following from the cut set bound [17]:
. Applying the same approach, we obtain the following from the cut set bound [17]:

where  . Following a similar approach to [11], (5) can be shown to maximize the mutual information in (7)–(9), and the optimization over (5) leads to (3)-(4).
. Following a similar approach to [11], (5) can be shown to maximize the mutual information in (7)–(9), and the optimization over (5) leads to (3)-(4).
3. Capacity Bounds and Optimal Resource Allocation
In the remainder of the paper, we will consider optimal resource allocation on the bounds obtained for the MBRC, that is, for hybrid wireless networks where the source node has access to distinct bands (standards) and a second node that overhears the source information relays to the destination using additional orthogonal bands. We consider the Gaussian case, where all the transmitted signals are corrupted by additive white Gaussian noises.
We have the input-output signal model given by (1) under source and relay power constraints:

where  and
and  are the total available power at the source and relay node.
are the total available power at the source and relay node.  and
and  are the nonnegative power allocation parameters for each orthogonal band at the source and relay node, and
are the nonnegative power allocation parameters for each orthogonal band at the source and relay node, and  . Unlike [5, 10], we do not have a total power constraint between the source and the relay and assume that each has its own battery.
. Unlike [5, 10], we do not have a total power constraint between the source and the relay and assume that each has its own battery.
We assume that the system has total bandwidth  . We define the received SNRs at the relay and the destination over channel
. We define the received SNRs at the relay and the destination over channel  as
as

Note that the actual received SNR values are the scaled versions of (11) depending on the power and bandwidth allocation. For example, the actual received SNR at the relay from channel 1, which is allocated  fraction of the source power and
fraction of the source power and  fraction of the bandwidth, simply is
fraction of the bandwidth, simply is  . Given the received SNRs which are available at the source and relay, our aim is to find the optimal resource allocation parameters that maximize capacity lower bound in terms of the transmitted power and the total bandwidth for
. Given the received SNRs which are available at the source and relay, our aim is to find the optimal resource allocation parameters that maximize capacity lower bound in terms of the transmitted power and the total bandwidth for  -MBRC, which leads to optimally allocating the source power among
-MBRC, which leads to optimally allocating the source power among  source bands, the relay power among
source bands, the relay power among  relay bands, and the total bandwidth among
relay bands, and the total bandwidth among  bands. We can obtain the capacity lower and upper bounds of
bands. We can obtain the capacity lower and upper bounds of  -MBRC from Theorem 1 as follows.
-MBRC from Theorem 1 as follows.
Theorem 2.
The upper and lower bounds for the capacity of the Gaussian  -MBRC are
-MBRC are


We omit the proof for Theorem 2 since the derivation for each mutual information follows directly from [15]. For each broadcast channel, if the relay node sees a higher received SNR than the destination node, then a superposition coding scheme [17] is used to convey independent information to the relay node, which cannot be decoded by the destination directly. The relay node then collects this information from all the channels where superposition coding is used, and transmits it to the destination at the appropriate rate.
Based on whether the relay node is utilized by a certain channel (band), we note that there are  possible schemes. We observe that these
possible schemes. We observe that these  schemes are not exclusive to each other, since a superposition coding scheme may be reduced to a direct source-to-destination transmission if no band is allocated to the relay-to-destination link. We also note that which scheme yields the largest rate is completely decided by the SNR relationship, namely, the componentwise relationship between the received SNRs of the source-to-relay links, that is,
schemes are not exclusive to each other, since a superposition coding scheme may be reduced to a direct source-to-destination transmission if no band is allocated to the relay-to-destination link. We also note that which scheme yields the largest rate is completely decided by the SNR relationship, namely, the componentwise relationship between the received SNRs of the source-to-relay links, that is,  and the received SNRs of the source-to-destination links, that is,
and the received SNRs of the source-to-destination links, that is,  .
.
If  ,
,  , then for any bandwidth allocation, the signal received by the relay over this broadcast channel can be viewed as a degraded version of the signal received by the destination. Therefore, direct link transmission should be used for this band, regardless of what scheme is used for the other bands. On the other hand, if
, then for any bandwidth allocation, the signal received by the relay over this broadcast channel can be viewed as a degraded version of the signal received by the destination. Therefore, direct link transmission should be used for this band, regardless of what scheme is used for the other bands. On the other hand, if  , then the relay node can always learn something more than the destination node over this band and uses the superposition code scheme, and although the superposition scheme may be reduced to a direct link transmission scheme, optimizing under this scheme does not incur any rate loss. Based on these observations, we conclude that there is no need to examine all the schemes to find the best rate and the corresponding resource allocation. That is, practically, the system checks the received SNRs and chooses one of
, then the relay node can always learn something more than the destination node over this band and uses the superposition code scheme, and although the superposition scheme may be reduced to a direct link transmission scheme, optimizing under this scheme does not incur any rate loss. Based on these observations, we conclude that there is no need to examine all the schemes to find the best rate and the corresponding resource allocation. That is, practically, the system checks the received SNRs and chooses one of  schemes satisfying the relationship of the received SNRs to communicate and the rate with optimized resource allocation for the chosen scheme is the maximum achievable rate, and the corresponding resource allocation is the globally optimal solution.
schemes satisfying the relationship of the received SNRs to communicate and the rate with optimized resource allocation for the chosen scheme is the maximum achievable rate, and the corresponding resource allocation is the globally optimal solution.
Next, we maximize the capacity lower bound in (12). To achieve this goal, we introduce the following general max-min optimization problem. We define  and
and  as any utility function with any resource allocation vector
as any utility function with any resource allocation vector  over the convex set
over the convex set  :
:

Proposition 1.
If  and
and  are nonnegative and concave over
are nonnegative and concave over  , there must exist
, there must exist  such that maximizing the following equation with respect to
such that maximizing the following equation with respect to  is equivalent to (14):
is equivalent to (14):

Proof.
See Appendix A.
Note that the optimization problem in (14) corresponds to finding  and
and  maximizing the minimum of two end points in
maximizing the minimum of two end points in  . One possible technique to solve the max-min optimization problem in (14) is given by the following proposition [15], which we will also utilize.
. One possible technique to solve the max-min optimization problem in (14) is given by the following proposition [15], which we will also utilize.
Proposition 2 ([15, Proposition  ]).
]).
The relationship between optimal resource allocation parameters  and the corresponding optimal point
and the corresponding optimal point  is given by the following.
is given by the following.
Case 1:If  ,
, 
Case 2:If  ,
,  .
.
Case 3:Neither case 1 nor 2 occurs; under this case, if  ,
,  .
.
Now, one can restate our max-min optimization problem given in Theorem 2 as follows:

where  and
and  are the first and the second terms of max-min optimization problem in (12). Next, one needs to prove that
are the first and the second terms of max-min optimization problem in (12). Next, one needs to prove that  and
and  are concave over
are concave over  in (16). Define
in (16). Define

It is easy to see that  is continuous over
is continuous over  . Then, one has the following proposition.
. Then, one has the following proposition.
Proposition 3.
 is concave over
is concave over  .
.
Proof.
First, note that due to the continuity of  , we only need to prove that
, we only need to prove that  is concave over the interior of the region, that is,
is concave over the interior of the region, that is,  . This is done by examining the Hessian,
. This is done by examining the Hessian,  , of (17). The second-order derivatives of (17) with respect to
, of (17). The second-order derivatives of (17) with respect to  and
and  are
are


We note that  .
.
The Hessian is the  block diagonal matrix with the following matrix in its
block diagonal matrix with the following matrix in its  th diagonal:
th diagonal:

It is readily seen that  is singular. Since
is singular. Since  for
for  from (18),
from (18),  is the negative semidefinite. Thus,
is the negative semidefinite. Thus,  is concave over
is concave over  . Since
. Since  is continuous over
is continuous over  ,
,  is concave over
is concave over  .
.
We note that for any choice of set  ,
,  corresponds to
corresponds to  in (17) with
in (17) with  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  ,
,  . For
. For  , the Hessian is a
, the Hessian is a  block diagonal matrix. Similarly,
block diagonal matrix. Similarly,  corresponds to
corresponds to  with
with  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  ,
,  . For
. For  , the Hessian is a
, the Hessian is a  block diagonal matrix.
block diagonal matrix.
Remark 1.
Since  is concave over the set
is concave over the set  , it is also concave over any convex subset of it. Thus,
, it is also concave over any convex subset of it. Thus,  and
and  are concave over
are concave over  . (It is readily seen that the sum constraints define a convex set.) This establishes that the local optimal for (16) is also the global optimal [18, Theorem
. (It is readily seen that the sum constraints define a convex set.) This establishes that the local optimal for (16) is also the global optimal [18, Theorem  , page 125-126].
, page 125-126].
Remark 2.
We further find that  is strictly concave over any convex subset of
is strictly concave over any convex subset of 
 ,
,  , jointly when
, jointly when  , are held constant. Note that when all
, are held constant. Note that when all  , are held constant, that is,
, are held constant, that is,  , we have
, we have  as a function of
as a function of  ,
,  . In this case, it is easily seen that the Hessian is the
. In this case, it is easily seen that the Hessian is the  diagonal matrix in which
diagonal matrix in which  th diagonal term is given by
th diagonal term is given by  ,
,  ,
,  . Since now all of the diagonal terms are strictly negative when
. Since now all of the diagonal terms are strictly negative when  ,
,  ,
,  is strictly concave over all
is strictly concave over all  ,
,  , jointly when all
, jointly when all  ,
,  , are held constant. Similarly,
, are held constant. Similarly,  is strictly concave over
is strictly concave over  ,
,  , jointly when all
, jointly when all  ,
,  , are held constant. Since if a function is strictly concave over a set, it is also strictly concave over any convex subset of that set, the preceding argument implies that
, are held constant. Since if a function is strictly concave over a set, it is also strictly concave over any convex subset of that set, the preceding argument implies that  is strictly concave over any convex subset of
is strictly concave over any convex subset of  , when all
, when all  , are held constant. This fact will be useful in the sequel.
, are held constant. This fact will be useful in the sequel.
Based on Proposition 1 and Proposition 3, the methodology given in Proposition 2 can be applied to our max-min optimization problem in (16) for an arbitrary  . That said, in the remainder of the paper, we will examine the optimal resource allocation for
. That said, in the remainder of the paper, we will examine the optimal resource allocation for  -MBRC where the source has two bands and the relay has a single band available to communicate and uses its own full power
-MBRC where the source has two bands and the relay has a single band available to communicate and uses its own full power  . We find this network model representative and meaningful because of the following two observations. First, if there is more than one band available for the link between the relay and the destination, then only the best band among them will be used. This can be seen by fixing the overall band for this link and performing joint power and bandwidth optimization. Therefore, as long as the relay-to-destination SNRs are different, which is usually the case in practice,
. We find this network model representative and meaningful because of the following two observations. First, if there is more than one band available for the link between the relay and the destination, then only the best band among them will be used. This can be seen by fixing the overall band for this link and performing joint power and bandwidth optimization. Therefore, as long as the relay-to-destination SNRs are different, which is usually the case in practice,  -MBRC will have the same resource allocation parameters as those of
-MBRC will have the same resource allocation parameters as those of  -MBRC. Secondly, the case with
-MBRC. Secondly, the case with  is similar to the case with
is similar to the case with  except that there are more schemes to choose from. Therefore, we focus on the
except that there are more schemes to choose from. Therefore, we focus on the  -MBRC in the sequel.
-MBRC in the sequel.
3.1. Maximization of Capacity Bounds for the Gaussian  -MBRC
-MBRC
For  -MBRC, there are four schemes to choose from. Let us label them Schemes I through IV. From Theorem 2, upper and lower bounds for the capacity of the Gaussian
-MBRC, there are four schemes to choose from. Let us label them Schemes I through IV. From Theorem 2, upper and lower bounds for the capacity of the Gaussian  -MBRC are
-MBRC are


where  =
=  ,
,  ,
,  , and
, and  for schemes I to IV, respectively. Each scheme materializes as a function of the received SNRs as follows.
for schemes I to IV, respectively. Each scheme materializes as a function of the received SNRs as follows.
Scheme  :
:  , the scenario where transmission from the source node over both links is decoded at the relay node. This scheme is chosen if
, the scenario where transmission from the source node over both links is decoded at the relay node. This scheme is chosen if  and
and  .
.
Scheme II:  , the scenario where transmission from the source node over band 1 is decoded at the relay node while band 2 is used for direct transmission only. This scheme is chosen if
, the scenario where transmission from the source node over band 1 is decoded at the relay node while band 2 is used for direct transmission only. This scheme is chosen if  and
and  .
.
Scheme III:  , the scenario where transmission from the source node over band 2 is decoded at the relay node while band 1 is used for direct transmission only. This scheme is chosen if
, the scenario where transmission from the source node over band 2 is decoded at the relay node while band 1 is used for direct transmission only. This scheme is chosen if  and
and  .
.
Scheme IV:  , the scenario where transmissions from the source node from both bands are used only for direct transmission. This scheme is chosen if
, the scenario where transmissions from the source node from both bands are used only for direct transmission. This scheme is chosen if  and
and  .
.
We define  as the optimal resource allocation parameters for (21).
as the optimal resource allocation parameters for (21).  and
and  are the first and second terms in (21). From (21), we note that the capacity for scheme IV is given by
are the first and second terms in (21). From (21), we note that the capacity for scheme IV is given by

In this case, the max-min optimization problem reduces to a maximization problem and it is readily shown that the optimal resource allocation for the rate of scheme IV is given by

For schemes I, II, III, once the appropriate scheme is decided upon, parameters  can be substituted accordingly and we can examine
can be substituted accordingly and we can examine  for each of the cases in Proposition 2.
for each of the cases in Proposition 2.
Case 1.
 , and
, and  maximizes
maximizes  .
.
This case holds if the following condition is satisfied:

and we obtain

The received SNRs must satisfy


Proof.
See Appendix B.
Case 2.
 , and
, and  maximizes
maximizes  .
.
This case holds if the following condition is satisfied:

and we obtain

Proof.
See Appendix B.
Remark 3.
By substituting the appropriate parameters for  for each scheme into (30), we observe that Case 2 does not ever materialize for schemes I, II, III.
for each scheme into (30), we observe that Case 2 does not ever materialize for schemes I, II, III.
Case 3.
 , and
, and  maximizes
maximizes  for a fixed
for a fixed  .
.
This case occurs when (25) or (29) doES not hold. The closed form solution for this optimization problem does not exist. Thus, we have to rely on an iterative algorithm. We propose to use alternating maximization algorithm that calls for optimizing  =
=  in one stage, followed by optimizing
in one stage, followed by optimizing  in the next stage. The iterations are obtained by finding KKT points of the corresponding optimization problem with the variable vector
in the next stage. The iterations are obtained by finding KKT points of the corresponding optimization problem with the variable vector  or
or  . We note that the objective function is not differentiable at the boundary of the feasible region, that is, for
. We note that the objective function is not differentiable at the boundary of the feasible region, that is, for  ,
,  and the corresponding KKT points are not defined. Thus, we need to introduce a small positive value,
and the corresponding KKT points are not defined. Thus, we need to introduce a small positive value,  , and define a modified feasible region as illustrated in (B.3) and (B.4) that excludes the boundary point. Every time an iteration reaches the boundary of the new feasible region, we expand the feasible region by successively reducing
, and define a modified feasible region as illustrated in (B.3) and (B.4) that excludes the boundary point. Every time an iteration reaches the boundary of the new feasible region, we expand the feasible region by successively reducing  so that we can continue with the iterations until convergence. The detailed description of the following proposed iterative algorithm and proof of its convergence to the global optimal solution is given in Appendix C.
so that we can continue with the iterations until convergence. The detailed description of the following proposed iterative algorithm and proof of its convergence to the global optimal solution is given in Appendix C.
Step 1.
-
(i)
Initialization: for initial values of
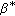 ,
,  ,
, 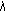 ,
,  ,
, 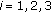 ,
,  ,
, 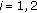 , and assign values to
, and assign values to  , such that
, such that 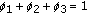 .
. -
(ii)
Iteration
 : update
: update 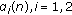 by finding the solution of KKT condition of (C.2) with respect to
by finding the solution of KKT condition of (C.2) with respect to 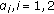 ; find
; find 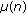 and
and 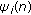 ,
, 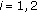 such that
such that  and
and 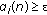 ,
, 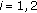 .
. -
(iii)
Iteration
 : update
: update  ,
, 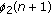 , and
, and  by finding the solution of KKT condition of (C.2) with respect to
by finding the solution of KKT condition of (C.2) with respect to 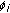 ,
, 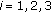 ; find
; find  and
and 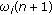 ,
,  such that
such that  , and
, and  ,
, 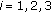 .
. -
(iv)
Repeat step (ii) until the optimal
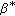 is found by
is found by 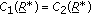 in (C.3).
in (C.3).
Step 2.
If the iteration does not reach the boundary of the feasible region of (B.3) and (B.4), the algorithm terminates.
Step 3.
Otherwise, set  ,
,  in (B.3) and (B.4) and repeat Steps (1) to (2) by using the KKT points from the previous iteration as the initial points. (For numerical results, we use
in (B.3) and (B.4) and repeat Steps (1) to (2) by using the KKT points from the previous iteration as the initial points. (For numerical results, we use  .)
.)
We reiterate that based on the scheme at hand, we would substitute the correct parameters for  to find the optimal resource allocation strategy.
to find the optimal resource allocation strategy.
3.2. Upper Bound on Capacity
Recall that the upper bound given by (13) is obtained by the max-flow min-cut theorem. The maximization for the upper bound follows same steps to that of the lower bound, details of which we will omit here. In general, the upper bound is not tight. One exception is that for  -MBRC, since Case 2 for schemes I, II, and III is not possible, the optimal resource allocation parameters
-MBRC, since Case 2 for schemes I, II, and III is not possible, the optimal resource allocation parameters  maximize
maximize  (Case 1) or
(Case 1) or  (Case 3). There exists a
(Case 3). There exists a  such that
such that  if
if  , otherwise
, otherwise  . Since the first term of the upper bound in (22) is the same as
. Since the first term of the upper bound in (22) is the same as  , we know that for
, we know that for  -MBRC,
-MBRC,  maximizes
maximizes  for
for  and the resulting optimized rate is the capacity of
and the resulting optimized rate is the capacity of  -MBRC. A similar observation was made for the frequency division relay network, that is, when one band exists from the source in [11]. It is interesting to observe that the same observation extends to the multiband case.
-MBRC. A similar observation was made for the frequency division relay network, that is, when one band exists from the source in [11]. It is interesting to observe that the same observation extends to the multiband case.
4. Numerical Results and Discussion
4.1. Capacity Bounds
In this section, we present numerical results to support our analysis described in Section 3. Specifically, for  -MBRC, we plot the capacity lower bound (LB) obtained by optimal resource allocation as well as the capacity upper bound (UB) with the same resource allocation parameters. For comparison purposes, we also consider the case where overall bandwidth
-MBRC, we plot the capacity lower bound (LB) obtained by optimal resource allocation as well as the capacity upper bound (UB) with the same resource allocation parameters. For comparison purposes, we also consider the case where overall bandwidth  is equally divided between the three bands and only optimal power allocation is done.
is equally divided between the three bands and only optimal power allocation is done.
Figure 2 shows the capacity UB and LB for  -MBRC with optimal power allocation only. When the source-to-relay (SR) SNRs
-MBRC with optimal power allocation only. When the source-to-relay (SR) SNRs  and
and  are smaller than or equal to the source-to-destination (SD) SNRs
are smaller than or equal to the source-to-destination (SD) SNRs  and
and  , respectively, the lower bound does not increase and saturate even if the relay-to-destination (RD) SNR
, respectively, the lower bound does not increase and saturate even if the relay-to-destination (RD) SNR  increases. This is expected, since using the relay is not beneficial when the source-to-relay channel is worse than the source-to-destination channel.
increases. This is expected, since using the relay is not beneficial when the source-to-relay channel is worse than the source-to-destination channel.
In contrast, when  and
and  are larger than
are larger than  and
and  , respectively, the lower bound increases as
, respectively, the lower bound increases as  increases and saturates after a certain threshold of
increases and saturates after a certain threshold of  . This threshold becomes larger as the quality of the SR links improves as compared to the SD links, that is, as
. This threshold becomes larger as the quality of the SR links improves as compared to the SD links, that is, as  and
and  get larger compared to
get larger compared to  and
and  . Indeed, the fact that we can achieve higher rates when the SR channel is better than the SD channel is intuitively pleasing as the power allocation becomes more effective when we have a better SR channel. It is noticeable that the upper and lower bounds approach each other as the SR link quality improves as compared to that of SD.
. Indeed, the fact that we can achieve higher rates when the SR channel is better than the SD channel is intuitively pleasing as the power allocation becomes more effective when we have a better SR channel. It is noticeable that the upper and lower bounds approach each other as the SR link quality improves as compared to that of SD.
Figure 3 shows the capacity UB and LB for  -MBRC with joint optimal power and bandwidth allocation. We observe that the lower bound does not saturate when the SR links are better than the SD links. This additional improvement is thanks to the dynamic bandwidth allocation. By comparing Figure 2 and 3, we observe that the achievable rate of MBRC with joint optimal power and bandwidth is always larger than that of power optimization only, sometimes by a significant margin. This points to the advantage of joint power and bandwidth optimization, promoting the idea of different wireless technologies lending each other frequency resources to improve capacity.
-MBRC with joint optimal power and bandwidth allocation. We observe that the lower bound does not saturate when the SR links are better than the SD links. This additional improvement is thanks to the dynamic bandwidth allocation. By comparing Figure 2 and 3, we observe that the achievable rate of MBRC with joint optimal power and bandwidth is always larger than that of power optimization only, sometimes by a significant margin. This points to the advantage of joint power and bandwidth optimization, promoting the idea of different wireless technologies lending each other frequency resources to improve capacity.
4.2. Guidelines for Hybrid Network Design
When a new wireless link becomes available at the source in addition to the existing single band relay network, a hybrid wireless network can be formed. In this case, a meaningful question is how to allocate resources between links in order to maximize the data rate. It is evident that the resource allocation strategy is a function of the channel quality of the available links (SD/SR/RD). To answer this question, we compare the achievable rates with optimal resource allocation for  and
and  and observe the effect of adding a new link on the maximum achievable rate.
and observe the effect of adding a new link on the maximum achievable rate.
Figure 4 shows the achievable rates when the new SR ink is better than the current SR link, and the new SD link is better than the current SD link. Comparing  and
and  , we observe that the achievable rate of
, we observe that the achievable rate of  is better than that of
is better than that of  . This is because quality of the new link is better than that of the current link, and all resources are allocated to the new link. If the new links were worse, the maximum achievable rates would stay the same since all resources would be allocated to the current link.
. This is because quality of the new link is better than that of the current link, and all resources are allocated to the new link. If the new links were worse, the maximum achievable rates would stay the same since all resources would be allocated to the current link.
Figure 5 shows the achievable rates when the new SR link is better than the current SR link, and the new SD link is worse than the current SD link. We observe that the achievable rates for  and
and  are almost same for low RD SNR. This is because when the RD link is poor, the relay becomes less useful, and most of bandwidth and power are allocated into channel with the best direct link. As the RD SNR increases, we observe that the achievable rate for
are almost same for low RD SNR. This is because when the RD link is poor, the relay becomes less useful, and most of bandwidth and power are allocated into channel with the best direct link. As the RD SNR increases, we observe that the achievable rate for  is larger than that of
is larger than that of  . This is because it is optimal resource allocation that we allocate more bandwidth and power to the new link with the best SR link. The observation is justified by examining bandwidth allocation (the power allocation follows a similar pattern) for
. This is because it is optimal resource allocation that we allocate more bandwidth and power to the new link with the best SR link. The observation is justified by examining bandwidth allocation (the power allocation follows a similar pattern) for  shown in Figure 6. We see that more bandwidth is allocated to the current link (
shown in Figure 6. We see that more bandwidth is allocated to the current link ( for
for  ) for low received RD SNR. More bandwidth is allocated to the new link (
) for low received RD SNR. More bandwidth is allocated to the new link ( for
for  ) when the RD link becomes better. We also observe that Case 1 and Case 3 of our proposed optimal resource allocation occur depending on the RD SNR: with both SR SNRs better than both SD SNRs, Case 1 occurs at low RD SNR (from 0 dB to 10 dB); otherwise, the optimal resource allocation corresponds to Case 3. We note that the optimal resource allocation scheme would be reversed if the new SR link were worse than the current SR link, and the new SD link were better than the current SD link.
) when the RD link becomes better. We also observe that Case 1 and Case 3 of our proposed optimal resource allocation occur depending on the RD SNR: with both SR SNRs better than both SD SNRs, Case 1 occurs at low RD SNR (from 0 dB to 10 dB); otherwise, the optimal resource allocation corresponds to Case 3. We note that the optimal resource allocation scheme would be reversed if the new SR link were worse than the current SR link, and the new SD link were better than the current SD link.
We note that the given received SNRs in the numerical results correspond to scheme I (i.e.,  ,
,  ). Similarly, we can examine the effect of adding a new link under different received SNR relationship between
). Similarly, we can examine the effect of adding a new link under different received SNR relationship between  and
and  which corresponds to scheme II or scheme III, and we could readily apply the optimal resource allocation solution found in Section 3.1.
which corresponds to scheme II or scheme III, and we could readily apply the optimal resource allocation solution found in Section 3.1.
5. Conclusions
In this paper, we have investigated the optimal resource allocation for a hybrid three-node relay network where the source, with the help of a relay node, communicates to the destination via multiple orthogonal channels (MBRCs). In particular, we have studied joint optimal power and bandwidth allocation strategies that maximize the bounds on the capacity, which results in a max-min optimization problem. We have solved this problem using a supporting plane technique [15]. In particular, we have provided sufficient conditions for when this max-min optimization problem can be solved using this technique. It is worthwhile to mention that these sufficient conditions are general enough so that other utility functions that rely on SNR can be considered as well as the information theoretic rates considered in this paper.
For  -MBRC, we have found the joint power and bandwidth allocation. We have observed that the upper and lower bounds approach each other as the source-to-relay channel condition improves as compared to the source-to-destination channel condition, and joint power and bandwidth optimization always yields better performance than power optimization only.
-MBRC, we have found the joint power and bandwidth allocation. We have observed that the upper and lower bounds approach each other as the source-to-relay channel condition improves as compared to the source-to-destination channel condition, and joint power and bandwidth optimization always yields better performance than power optimization only.
Our numerical results have also investigated the scenario where a new link at the source becomes available for an existing frequency division relay network, and the power and bandwidth resources are to be reallocated. We have observed that the source node is encouraged to communicate over the best link by dedicating all resources when the new SR link and SD link are better (or worse) than the current SD link and SR link. Otherwise, it is beneficial to share resources between the current link and the new link to achieve the higher rate.
The simple MBRC investigated in this paper can be considered as a building block for more complex hybrid wireless networks. From the system design point of view, we conclude that, for this two-hop, simple network, higher achievable rates can be obtained by optimally allocating resources between multiple standards. It would be of interest to gain an understanding of the set of conditions under which using multiple communication links (standards) and optimal sharing of resources would be beneficial for multihop hybrid wireless networks.
Appendices
A. Proof of Proposition 1
Proof.
Suppose that both  and
and  are nonnegative and concave over convex set
are nonnegative and concave over convex set  . Then, we claim that the optimization problem (14) can be relaxed as follows:
. Then, we claim that the optimization problem (14) can be relaxed as follows:






To see that, we devise the following notion of dominance: pair ( ) is said to be dominated by (
) is said to be dominated by ( ) if
) if  and
and  . We say that a set
. We say that a set  is dominated by the other set
is dominated by the other set  , or
, or  if every point in
if every point in  is dominated by some point in
is dominated by some point in  . Since
. Since  and
and  are concave over
are concave over  , we realize that
, we realize that  dominates its convex closure
dominates its convex closure  . Furthermore, from the definition of dominance closure in (A.5), it is easy to see
. Furthermore, from the definition of dominance closure in (A.5), it is easy to see  . Since
. Since  and
and  , we have
, we have  . We note that adding dominated points to
. We note that adding dominated points to  does not change the value of optimization problem (14), which allows us to consider problem (A.1)–(A.6) instead.
does not change the value of optimization problem (14), which allows us to consider problem (A.1)–(A.6) instead.
Set  has the following properties. (
has the following properties. ( ) It is a closed convex set. To see that, consider two points in
) It is a closed convex set. To see that, consider two points in  :
:  and
and  . Then we must have
. Then we must have  . (
. ( ) Consider any supporting plane of this set, which is a line in
) Consider any supporting plane of this set, which is a line in  in this case. The slope of this line cannot be both positive and finite. Otherwise, suppose the supporting plane passes through point
in this case. The slope of this line cannot be both positive and finite. Otherwise, suppose the supporting plane passes through point  in
in  , then
, then  , defined by (A.6), will not be in
, defined by (A.6), will not be in  .
.
We then observe that (A.1)–(A.6) must be solved when  and
and  is at the boundary of
is at the boundary of  . The maximum of (A.1)–(A.6) should be attained at the boundary of
. The maximum of (A.1)–(A.6) should be attained at the boundary of  since every interior point of
since every interior point of  must be dominated by some point at its boundary. Also, there must be such a point on the boundary with
must be dominated by some point at its boundary. Also, there must be such a point on the boundary with  . We then show that the point with
. We then show that the point with  must be a local maximal point. This is because any improvement over this point would require increasing
must be a local maximal point. This is because any improvement over this point would require increasing  simultaneously. Suppose such improved point exists. Then it will be strictly separated from set
simultaneously. Suppose such improved point exists. Then it will be strictly separated from set  by the support plane passing through
by the support plane passing through  , since no supporting plane has finite positive slope. Since
, since no supporting plane has finite positive slope. Since  is a closed convex set and
is a closed convex set and  is a concave function over
is a concave function over  , any local maximum must be globally optimal [18,Theorem
, any local maximum must be globally optimal [18,Theorem  , page 125-126]. This completes our claim that optimality must be attained at the diagonal line. We observe that this point may not be in
, page 125-126]. This completes our claim that optimality must be attained at the diagonal line. We observe that this point may not be in  . Therefore, it may not be parameterizable by
. Therefore, it may not be parameterizable by  . This necessitates consideration of the three cases as we will show later.
. This necessitates consideration of the three cases as we will show later.
Since optimality must be attained at the boundary of the convex set  , we observe that (A.1)–(A.6) is equivalent to (A.7) for a certain
, we observe that (A.1)–(A.6) is equivalent to (A.7) for a certain  :
:

(A.7) can be solved by examining three cases:  ,
,  ,
,  .
.
For  and
and  , we have
, we have

For  , we prove below that (A.7) is equivalent to (A.9). Let the optimal solution of (A.7) be
, we prove below that (A.7) is equivalent to (A.9). Let the optimal solution of (A.7) be  . Since
. Since  ,
,  cannot be dominated by any point in
cannot be dominated by any point in  other than itself. (If such a point exists, it would be separated from
other than itself. (If such a point exists, it would be separated from  by the supporting plane passing through
by the supporting plane passing through  .) Since
.) Since  and
and  , we must have
, we must have  . This means that we can solve (A.9) instead:
. This means that we can solve (A.9) instead:

Since all points in  can be parameterized by
can be parameterized by  , problem (A.9) is equivalent to (A.10).
, problem (A.9) is equivalent to (A.10).  is adjusted until the solution to (A.10) yields
is adjusted until the solution to (A.10) yields  :
:

In summary, we proved that there must exist a  such that (14) is equivalent to (A.7) if
such that (14) is equivalent to (A.7) if  and
and  are nonnegative and concave over convex set
are nonnegative and concave over convex set  . Depending on the value of
. Depending on the value of  , we find that there are three cases for the max-min optimization (A.7) as given in Proposition 2.
, we find that there are three cases for the max-min optimization (A.7) as given in Proposition 2.
B. Optimal Resource Allocation
Proof.
We provide the proof for optimal resource allocation for  -MBRC. To do so, we utilize the following theorem which we restate here with our notation for convenience.
-MBRC. To do so, we utilize the following theorem which we restate here with our notation for convenience.
Theorem 3 ([19, Proposition  , pages 219–221]).
, pages 219–221]).
Suppose that  is continuously differentiable and concave on the set
is continuously differentiable and concave on the set  , a Cartesian product of sets
, a Cartesian product of sets  , where each
, where each  is a closed convex subset of
is a closed convex subset of 
 . Furthermore, suppose that for
. Furthermore, suppose that for  ,
,  ,
,  is a strictly concave function of each
is a strictly concave function of each  , when the other components of
, when the other components of  are held constant. Let
are held constant. Let  be the sequence generated by the iterative algorithm obtained by optimizing
be the sequence generated by the iterative algorithm obtained by optimizing  over one vector variable at a time. Then, every limit point of
over one vector variable at a time. Then, every limit point of  maximizes
maximizes  over
over  .
.
For a fixed  , the objective function of our max-min problem corresponds to
, the objective function of our max-min problem corresponds to

where  corresponds to
corresponds to  .
.
Based on Proposition 3, we know that the objective function (B.1) of our max-min optimization problem given in (21) is concave over the constraint set  , which is a Cartesian product of the following two sets,
, which is a Cartesian product of the following two sets,  and
and  , which are closed convex subset of
, which are closed convex subset of  :
:

Also, for the interior points of the feasible region of  , we note that (B.1) is strictly concave over
, we note that (B.1) is strictly concave over  when
when  are fixed; see Remark 2. We note that the objective function (B.1) is not differentiable at the boundary of the feasible region, that is, for
are fixed; see Remark 2. We note that the objective function (B.1) is not differentiable at the boundary of the feasible region, that is, for  ,
,  . Therefore, we cannot directly apply Theorem 3. We define a modified feasible region as follows:
. Therefore, we cannot directly apply Theorem 3. We define a modified feasible region as follows:


with a small  . Since (B.1) is continuously differentiable over the new feasible region given by (B.3) and (B.4), we can now apply Theorem 3. Thus, we can devise an iterative algorithm to maximize the function, by maximizing over
. Since (B.1) is continuously differentiable over the new feasible region given by (B.3) and (B.4), we can now apply Theorem 3. Thus, we can devise an iterative algorithm to maximize the function, by maximizing over  for fixed
for fixed  (
( for fixed
for fixed  ) and then maximizing
) and then maximizing  for fixed
for fixed  (
( for fixed
for fixed  ). The iterative method, by Theorem 3, will converge to the maximizer of
). The iterative method, by Theorem 3, will converge to the maximizer of  over (B.3) and (B.4), which is the global optimal. If the iterative algorithm converges to a point that is at the boundary of the new feasible region given by (B.3) and (B.4), we need to reduce
over (B.3) and (B.4), which is the global optimal. If the iterative algorithm converges to a point that is at the boundary of the new feasible region given by (B.3) and (B.4), we need to reduce  further and repeat the iteration using the KKT points from the previous iteration as the initial point. By repeating this procedure, the iterative algorithm converges to the global optimal solution.
further and repeat the iteration using the KKT points from the previous iteration as the initial point. By repeating this procedure, the iterative algorithm converges to the global optimal solution.
For Case 1 ( in (B.1)) and Case 2 (
in (B.1)) and Case 2 ( in (B.1)), we provide the closed form solution below. For Case 3 (
in (B.1)), we provide the closed form solution below. For Case 3 ( in (B.1)), we provide the iterative algorithm in Appendix C.
in (B.1)), we provide the iterative algorithm in Appendix C.
Case 1.
 maximizes
maximizes  . Using
. Using  and
and  ,
,  in (21) can be rewritten as
in (21) can be rewritten as

Differentiating (B.5) with respect to  , we obtain
, we obtain  . Observe that
. Observe that  for
for  and
and  . Substituting this expression for
. Substituting this expression for  into (B.5), we obtain
into (B.5), we obtain

For fixed  , we can maximize (B.6) in terms of
, we can maximize (B.6) in terms of  by
by

Substituting (B.7) into (B.6), we have

Maximizing (B.8) with respect to  leads to
leads to  . The optimal power allocation parameter in (B.7) indicates that one of channels whose received SNR at the destination is smaller is not used. Thus, for the case where
. The optimal power allocation parameter in (B.7) indicates that one of channels whose received SNR at the destination is smaller is not used. Thus, for the case where  ,
,  . On the other hand, for the case where
. On the other hand, for the case where  ,
,  . Thus, using
. Thus, using  , the optimal resource allocation parameter for Case 1 is given by (26). By Remark 1, this is the global optimal solution. The condition of the received SNRs given by (27) and (28) for Case 1 to occur can be readily found by substituting (26) into (25).
, the optimal resource allocation parameter for Case 1 is given by (26). By Remark 1, this is the global optimal solution. The condition of the received SNRs given by (27) and (28) for Case 1 to occur can be readily found by substituting (26) into (25).
Case 2.
 maximizes
maximizes  . By applying the same technique as in Case 1, we find the optimal resource allocation parameters given in (30). By Remark 1, this is the global optimal solution.
. By applying the same technique as in Case 1, we find the optimal resource allocation parameters given in (30). By Remark 1, this is the global optimal solution.
C. Iterative Algorithm for Case 3
Proof.
For Case 3,  maximizes the following.
maximizes the following.

Since the closed form solution does not exist for case 3, we rely on the iterative algorithm given in Theorem 3. As we noted in Appendix B, (C.1) is not differentiable at the boundary of the feasible region. Thus, we start with the new feasible region given in (B.3) and (B.4). Then, the Lagrangian is

where  and
and  are Lagrange multipliers corresponding to sum constraints for bandwidth and power allocation, respectively.
are Lagrange multipliers corresponding to sum constraints for bandwidth and power allocation, respectively.  and
and  are inequality constraints for bandwidth and power allocation, respectively, that is,
are inequality constraints for bandwidth and power allocation, respectively, that is,  ,
,  , and
, and  ,
,  . For a fixed
. For a fixed  , we start with values of
, we start with values of  ,
,  , and
, and  such that
such that  = 1 and find the optimal
= 1 and find the optimal  such that
such that  . In iteration
. In iteration  , we update
, we update  by optimizing the objective function over
by optimizing the objective function over  while keeping the total power constraints satisfied, and fixing
while keeping the total power constraints satisfied, and fixing  . In iteration
. In iteration  ,
,  is found by optimizing the objective function with respect to
is found by optimizing the objective function with respect to  while keeping the bandwidth constraints satisfied, and fixing
while keeping the bandwidth constraints satisfied, and fixing  . By Remark 1 and 2, and Theorem 3, this algorithm converges to the global optimal solution. Note that the optimal solution
. By Remark 1 and 2, and Theorem 3, this algorithm converges to the global optimal solution. Note that the optimal solution  satisfies (see Proposition 2)
satisfies (see Proposition 2)

References
Luo H, Ramjee R, Sinha P, Li L, Lu S: UCAN: a unified cellular and ad-hoc network architecture. Proceedings of the Annual International Conference on Mobile Computing and Networking (MOBICOM '03), September 2003 353-367.
Wu H, Qiao C, De S, Tonguz O: Integrated cellular and ad hoc relaying systems: iCAR. IEEE Journal on Selected Areas in Communications 2001, 19(10):2105-2115. 10.1109/49.957326
van der Meulen EC: Three- terminal communication channels. Advances in Applied Probability 1971, 3(1):120-154. 10.2307/1426331
Cover TM, El Gamal AA: Capacity theorems for the relay channel. IEEE Transactions on Information Theory 1979, 25(5):572-584. 10.1109/TIT.1979.1056084
Høst-Madsen A, Zhang J: Capacity bounds and power allocation for wireless relay channels. IEEE Transactions on Information Theory 2005, 51(6):2020-2040. 10.1109/TIT.2005.847703
Boyer J, Falconer DD, Yanikomeroglu H: Multihop diversity in wireless relaying channels. IEEE Transactions on Communications 2004, 52(10):1820-1830. 10.1109/TCOMM.2004.836447
Kramer G, Gastpar M, Gupta P: Cooperative strategies and capacity theorems for relay networks. IEEE Transactions on Information Theory 2005, 51(9):3037-3063. 10.1109/TIT.2005.853304
Nabar RU, Bölcskei H, Kneubühler FW: Fading relay channels: performance limits and space-time signal design. IEEE Journal on Selected Areas in Communications 2004, 22(6):1099-1109. 10.1109/JSAC.2004.830922
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Ahmed N, Khojastepour MA, Aazhang B: Outage minimization and optimal power control for the fading relay channel. Proceedings of the IEEE Information Theory Workshop (ITW '04), October 2004, San Antonio, Tex, USA 458-462.
Liang Y, Veeravalli VV: Gaussian orthogonal relay channels: optimal resource allocation and capacity. IEEE Transactions on Information Theory 2005, 51(9):3284-3289. 10.1109/TIT.2005.853305
El Gammal A, Mohseni M, Zahedi S: Bounds on capacity and minimum energy-per-bit for AWGN relay channels. IEEE Transactions on Information Theory 2006, 52(4):1545-1561.
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part I: system description. IEEE Transactions on Communications 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part II: implementation aspects and performance analysis. IEEE Transactions on Communications 2003, 51(11):1939-1948. 10.1109/TCOMM.2003.819238
Liang Y, Veeravalli VV, Poor HV: Resource allocation for wireless fading relay channels: max-min solution. IEEE Transactions on Information Theory 2007, 53(10):3432-3453.
Larsson EG, Cao Y: Collaborative transmit diversity with adaptive radio resource and power allocation. IEEE Communications Letters 2005, 9(6):511-513. 10.1109/LCOMM.2005.1437354
Cover TM, Thomas JA: Elements of Information Theory. Wiley Interscience, New York, NY, USA; 2006.
Bazaraa MS, Sherali HD, Shetty CM: Nonlinear Programming: Theory and Algorithms. Wiley-Interscience, New York, NY, USA; 2006.
Bertsekas DP, Tsitsiklis JN: Parallel and Distributed Computation: Numerical Methods. Athena Scientific, Nashua, NH, USA; 1997.
Acknowledgments
This work was supported in part by NSF Grants CNS-0626905 and CNS-0721445 and DARPA ITMANET Program via Grant W911NF-07-1-0028. An earlier version of this work was presented in part in Conference on Information Sciences and Systems (CISS), 2005, and in International Conference on Wireless Networks, Communications, and Mobile Computing (WirelessCom), 2005.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lee, K., Yener, A. & He, X. Resource Allocation for the Multiband Relay Channel: A Building Block for Hybrid Wireless Networks. J Wireless Com Network 2010, 792410 (2010). https://doi.org/10.1155/2010/792410
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/792410

 Multiband Relay Channel.
Multiband Relay Channel.
 -MBRC
-MBRC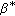 ,
,  ,
, 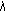 ,
,  ,
, 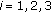 ,
,  ,
, 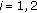 , and assign values to
, and assign values to  , such that
, such that 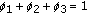 .
. : update
: update 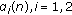 by finding the solution of KKT condition of (C.2) with respect to
by finding the solution of KKT condition of (C.2) with respect to 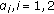 ; find
; find 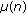 and
and 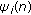 ,
, 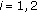 such that
such that  and
and 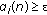 ,
, 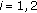 .
. : update
: update  ,
, 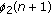 , and
, and  by finding the solution of KKT condition of (C.2) with respect to
by finding the solution of KKT condition of (C.2) with respect to 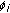 ,
, 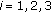 ; find
; find  and
and  ,
,  such that
such that  , and
, and  ,
,  .
.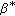 is found by
is found by 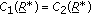 in (C.3).
in (C.3).
 -MBRC with power optimization only: SNRs at SD,
-MBRC with power optimization only: SNRs at SD,
 = 10 dB and
= 10 dB and
 = 5 dB.
= 5 dB.

 -MBRC with joint power and bandwidth optimization: SNRs at SD,
-MBRC with joint power and bandwidth optimization: SNRs at SD,
 = 10 dB and
= 10 dB and
 = 5 dB.
= 5 dB.


