- Research Article
- Open access
- Published:
Analysis and Construction of Full-Diversity Joint Network-LDPC Codes for Cooperative Communications
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 805216 (2010)
Abstract
Transmit diversity is necessary in harsh environments to reduce the required transmit power for achieving a given error performance at a certain transmission rate. In networks, cooperative communication is a well-known technique to yield transmit diversity and network coding can increase the spectral efficiency. These two techniques can be combined to achieve a double diversity order for a maximum coding rate  on the Multiple-Access Relay Channel (MARC), where two sources share a common relay in their transmission to the destination. However, codes have to be carefully designed to obtain the intrinsic diversity offered by the MARC. This paper presents the principles to design a family of full-diversity LDPC codes with maximum rate. Simulation of the word error rate performance of the new proposed family of LDPC codes for the MARC confirms the full diversity.
on the Multiple-Access Relay Channel (MARC), where two sources share a common relay in their transmission to the destination. However, codes have to be carefully designed to obtain the intrinsic diversity offered by the MARC. This paper presents the principles to design a family of full-diversity LDPC codes with maximum rate. Simulation of the word error rate performance of the new proposed family of LDPC codes for the MARC confirms the full diversity.
1. Introduction
Multipath propagation (small-scale fading) is an important salient effect of wireless channels, causing possible destructive adding of signals at the receiver. When the fading varies very slowly, error-correcting codes cannot combat the detrimental effect of the fading on a point-to-point channel. Space diversity, that is, transmitting information over independent paths in space, is a means to mitigate the effects of slowly varying fading. Cooperative communication [1–4] is a well-known technique to yield transmit diversity. The most elementary example of a cooperative network is the relay channel, consisting of a source, a relay, and a destination [3, 5]. The task of the relay is specified by the strategy or protocol. In the case of coded cooperation [4], the relay decodes the message received from the source, and then transmits to the destination additional parity bits related to the message; this results in a higher information theoretic spectral efficiency than simply repeating the message received from the source [6]. The resulting outage probability [7] exhibits twice the diversity, as compared to point-to-point transmission. However, the overall error-correcting code should be carefully designed in order to guarantee full diversity [8].
We focus on capacity achieving codes, more precisely, low-density parity-check (LDPC) codes [9], because their word error rate (WER) performance is quasi-independent of the block length [10] when the block length is becoming very large.
Considering two users,  and
and  , and a common destination
, and a common destination  , a double diversity order can be obtained by cooperating. When no common relay
, a double diversity order can be obtained by cooperating. When no common relay  is used, the maximum achievable coding rate that allows to achieve full diversity is
is used, the maximum achievable coding rate that allows to achieve full diversity is  (according to the blockwise Singleton bound [7, 11]). However, when one common relay
(according to the blockwise Singleton bound [7, 11]). However, when one common relay  for two users is used (a Multiple Access Relay Channel—MARC), it can be proven that the maximum achievable coding rate yielding full diversity is
for two users is used (a Multiple Access Relay Channel—MARC), it can be proven that the maximum achievable coding rate yielding full diversity is  [12]. The increase of the maximum coding rate yielding full diversity from
[12]. The increase of the maximum coding rate yielding full diversity from  to
to  is achieved through network coding [13] at the physical layer, that is,
is achieved through network coding [13] at the physical layer, that is,  sends a transformation of its incoming bit packets to
sends a transformation of its incoming bit packets to  (only linear transformations over GF(5) are considered here). From a decoding point of view, this linear transformation can be interpreted as additional parity bits of a linear block code. Hence, the destination will decode a joint network-channel code. Therefore, the problem formulation is how to design a full-diversity joint network-channel code construction for a rate
(only linear transformations over GF(5) are considered here). From a decoding point of view, this linear transformation can be interpreted as additional parity bits of a linear block code. Hence, the destination will decode a joint network-channel code. Therefore, the problem formulation is how to design a full-diversity joint network-channel code construction for a rate  .
.
Up till now, no family of full-diversity LDPC codes with  for coded cooperation on the MARC has been published. Chebli, Hausl, and Dupraz obtained interesting results on joint network-channel coding for the MARC with turbo codes [14] and LDPC codes [15, 16], but these authors do not elaborate on a structure to guarantee full diversity at maximum rate, which is the most important criterion for a good performance on fading channels. A full-diversity code structure describes a family of LDPC codes or an ensemble of LDPC codes, permitting to generate many specific instances of LDPC codes.
for coded cooperation on the MARC has been published. Chebli, Hausl, and Dupraz obtained interesting results on joint network-channel coding for the MARC with turbo codes [14] and LDPC codes [15, 16], but these authors do not elaborate on a structure to guarantee full diversity at maximum rate, which is the most important criterion for a good performance on fading channels. A full-diversity code structure describes a family of LDPC codes or an ensemble of LDPC codes, permitting to generate many specific instances of LDPC codes.
In this paper, we present a strategy to produce excellent LDPC codes for the MARC. First, we outline the physical layer network coding framework. Then, we derive the conditions on the MARC model and the coding rate necessary to achieve a double diversity order. In the second part of the paper, we elaborate on the code construction. A joint network-channel code construction is derived that guarantees full diversity, irrespective of the parameters of the LDPC code (the degree distributions). Finally, the coding gain can be improved by selecting the appropriate degree distributions of the LDPC code [17] or using the doping technique [18] as shown in Section 7.2. Simulation results for finite and infinite length (through density evolution) are provided. To the best of authors' knowledge, this is the first time that a joint full-diversity network-channel LDPC code construction for maximum rate is proposed.
Channel-State Information is assumed to be available only at the decoder. In order to simplify the analysis, we consider orthogonal half-duplex devices that transmit in separate timeslots.
2. System Model and Notation
2.1. Multiple Access Relay Channel
We consider a Multiple Access Relay Channel (MARC) with two users  and
and  , a common relay
, a common relay  , and a common destination
, and a common destination  . Each of the three transmitting devices transmits in a different timeslot:
. Each of the three transmitting devices transmits in a different timeslot:  in timeslot 1,
in timeslot 1,  in timeslot 2, and
in timeslot 2, and  in timeslot 3 (Figure 1). In this paper, we limit the scheme to two sources, but any extension to a larger number of sources is possible by applying the principles explained in the paper. We consider a joint network-channel code over this network, that is, an overall codeword
in timeslot 3 (Figure 1). In this paper, we limit the scheme to two sources, but any extension to a larger number of sources is possible by applying the principles explained in the paper. We consider a joint network-channel code over this network, that is, an overall codeword  is received at the destination during timeslot 1, timeslot 2, and timeslot 3, which form together one coding block. The codeword is partitioned into three parts:
is received at the destination during timeslot 1, timeslot 2, and timeslot 3, which form together one coding block. The codeword is partitioned into three parts:  , where
, where  ,
,  , and
, and  , and where
, and where  and
and  transmit
transmit  bits (note that each user is given an equal slot length because of fairness), and
bits (note that each user is given an equal slot length because of fairness), and  transmits
transmits  bits, so that
bits, so that  . We define the level of cooperation,
. We define the level of cooperation,  , as the ratio
, as the ratio  . Because the users do not communicate between each other, the bits
. Because the users do not communicate between each other, the bits  , transmitted by
, transmitted by  , and the bits
, and the bits  , transmitted by
, transmitted by  , are independent.
, are independent.
Since the focus in this paper is on coding, BPSK signaling is used for simplicity, so that the transmitters send symbols  , where
, where  stands for the timeslot number and
stands for the timeslot number and  is the symbol time index in timeslot
is the symbol time index in timeslot  . The channel is memoryless with real additive white Gaussian noise and multiplicative real fading. The fading coefficients are only known at the decoder side where the received signal vector at the destination
. The channel is memoryless with real additive white Gaussian noise and multiplicative real fading. The fading coefficients are only known at the decoder side where the received signal vector at the destination  is
is

where  ,
,  , and
, and  are the received complex signal vectors in timeslots
are the received complex signal vectors in timeslots  ,
,  , and
, and  , respectively. The noise vector
, respectively. The noise vector  consists of independent noise samples which are real Gaussian distributed, that is,
consists of independent noise samples which are real Gaussian distributed, that is,  , where
, where  is the average signal-to-noise ratio
is the average signal-to-noise ratio  . The Rayleigh distributed fading coefficients
. The Rayleigh distributed fading coefficients  ,
,  and
and  are independent and identically distributed. (The average signal-to-noise ratios on the
are independent and identically distributed. (The average signal-to-noise ratios on the  -
- ,
,  -
- ; and
; and  -
- channels are the same.) The channel model is illustrated in Figure 2. In some parts of the paper, a block binary erasure channel (block BEC) [19, 20] will be assumed, which is a special case of block fading. In a block BEC, the fading gains belong to the set
channels are the same.) The channel model is illustrated in Figure 2. In some parts of the paper, a block binary erasure channel (block BEC) [19, 20] will be assumed, which is a special case of block fading. In a block BEC, the fading gains belong to the set  , where
, where  means the link is a complete erasure, while
means the link is a complete erasure, while  means the link is perfect.
means the link is perfect.
We assume that no errors occur on the  -
- and
and  -
- channels. This simplifies the analysis and does not change the criteria for the code to attain full-diversity, as will be shown in Section 3.2.
channels. This simplifies the analysis and does not change the criteria for the code to attain full-diversity, as will be shown in Section 3.2.
2.2. LDPC Coding
We focus on binary LDPC codes  with block length
with block length  and dimension
and dimension  , and coding rate
, and coding rate  . (We consider two sources each with
. (We consider two sources each with  information bits and an overall error-correcting code with
information bits and an overall error-correcting code with  codebits.) The code
codebits.) The code  is defined by a parity-check matrix
is defined by a parity-check matrix  , or equivalently, by the corresponding Tanner graph [7, 9]. Regular
, or equivalently, by the corresponding Tanner graph [7, 9]. Regular  LDPC codes have a parity-check matrix with
LDPC codes have a parity-check matrix with  ones in each column and
ones in each column and  ones in each row. For irregular
ones in each row. For irregular  LDPC codes, these numbers are replaced by the so-called degree distributions [9]. These distributions are the standard polynomials
LDPC codes, these numbers are replaced by the so-called degree distributions [9]. These distributions are the standard polynomials  and
and  [21]:
[21]:

where  (resp.,
(resp.,  ) is the fraction of all edges in the Tanner graph, connected to a bit node (resp., check node) of degree
) is the fraction of all edges in the Tanner graph, connected to a bit node (resp., check node) of degree  . Therefore,
. Therefore,  and
and  are sometimes referred to as left and right degree distributions from an edge perspective. In Section 6, the polynomials
are sometimes referred to as left and right degree distributions from an edge perspective. In Section 6, the polynomials  and
and  , which are the left and right distributions from a node perspective, will also be adopted:
, which are the left and right distributions from a node perspective, will also be adopted:

where  (resp.,
(resp.,  ) is the fraction of all bit nodes (resp., check nodes) in the Tanner graph of degree
) is the fraction of all bit nodes (resp., check nodes) in the Tanner graph of degree  , hence
, hence  and likewise with
and likewise with  .
.
The goal of this research is to design a full-diversity ensemble of LDPC codes for the MARC. An ensemble of LDPC codes is the set of all LDPC codes that satisfy the left degree distribution  and right degree distribution
and right degree distribution  .
.
In this paper, not all bit nodes and check nodes in the Tanner graph will be treated equally. To elucidate the different classes of bit nodes and check nodes, a compact representation of the Tanner graph, adopted from [22] and also known as protograph representation [9, 23, 24] (and the references therein), will be used. In this compact Tanner graph, bit nodes and check nodes of the same class are merged into one node.
2.3. Physical Layer Network Coding
The coded bits transmitted by  are a linear transformation of the information bits from
are a linear transformation of the information bits from  and
and  , denoted as
, denoted as  and
and  , where both vectors are of length
, where both vectors are of length  . (In some papers, the coded bits transmitted by
. (In some papers, the coded bits transmitted by  are a linear transformation of the transmitted bits from
are a linear transformation of the transmitted bits from  and
and  , which boils down to the same as the information bits, since the transmitted bits (parity bits and information bits) are a linear transformation of the information bits.) Let
, which boils down to the same as the information bits, since the transmitted bits (parity bits and information bits) are a linear transformation of the information bits.) Let  stand for a matrix multiplication in GF(5);
stand for a matrix multiplication in GF(5);

The matrix  represents the network code, which has to be designed. Let us split
represents the network code, which has to be designed. Let us split  into two matrices
into two matrices  and
and  such that
such that  , where
, where  is an
is an  matrix and
matrix and  is an
is an  matrix. Now we have the following relation:
matrix. Now we have the following relation:

Equation (5) can be inserted into the parity-check matrix defining the overall error-correcting code. Instead of designing  , we can design
, we can design  and
and  using principles from coding theory.
using principles from coding theory.
3. Diversity and Outage Probability of MARC
3.1. Achievable Diversity Order
The formal definition of diversity order on a block fading channel is well known [25].
Definition 1.
The diversity order attained by a code  is defined as
is defined as

where  is the word error rate after decoding.
is the word error rate after decoding.
However, in this document, as far as the diversity order is concerned, we mostly use a block BEC. It has been proved that a coding scheme is of full diversity on the block fading channel if and only if it is of full diversity on a block BEC [22]. The channel model is the same as for block fading, except that the fading gains belong to the set  . Suppose that on the
. Suppose that on the  -
- ,
,  -
- , and
, and  -
- links, the probability of a complete erasure, that is,
links, the probability of a complete erasure, that is,  , is
, is  .
.
Definition 2.
A code  achieves a diversity order
achieves a diversity order  on a block BEC if and only if [26]
on a block BEC if and only if [26]

where  is the word error rate after decoding and
is the word error rate after decoding and  means proportional to.
means proportional to.
Therefore, it is sufficient to show that two erased channels cause an error event to prove that  , because the probability of this event is proportional to
, because the probability of this event is proportional to  . Consider, for example, that the
. Consider, for example, that the  -
- channel has been erased, as well as the
channel has been erased, as well as the  -
- channel. Then, the information from
channel. Then, the information from  can never reach
can never reach  , because
, because  does not communicate with
does not communicate with  . Therefore, the diversity order
. Therefore, the diversity order  .
.
A diversity order of two is achieved if the destination is capable of retrieving the information bits from  and
and  , when exactly one of the
, when exactly one of the  -
- ,
,  -
- , or
, or  -
- channels is erased. The maximum coding rate allowing the destination to do so will be derived in Section 3.4.
channels is erased. The maximum coding rate allowing the destination to do so will be derived in Section 3.4.
3.2. Perfect Source-Relay Channels
Here, we will show that the achieved diversity at  does not depend on the quality of the source-relay (
does not depend on the quality of the source-relay ( -
- ) channel. Therefore, in the remainder of the paper, we will assume errorless
) channel. Therefore, in the remainder of the paper, we will assume errorless  -
- channels to simplify the analysis.
channels to simplify the analysis.
Let us consider a simple block fading relay channel with one source  , one relay
, one relay  , and one destination
, and one destination  . All considered point-to-point channels (
. All considered point-to-point channels ( -
- ,
,  -
- ,
,  -
- ) have an intrinsic diversity order of one. In a cooperative protocol, where
) have an intrinsic diversity order of one. In a cooperative protocol, where  has to decode the transmission from
has to decode the transmission from  in the first slot, two cases can be distinguished: (
in the first slot, two cases can be distinguished: ( )
)  is able to decode the transmission from
is able to decode the transmission from  and cooperates with
and cooperates with  in the second slot, hence
in the second slot, hence  receives two messages carrying information from
receives two messages carrying information from  ; (
; ( )
)  is not able to decode the transmission from
is not able to decode the transmission from  and therefore does not transmit in the second slot, hence
and therefore does not transmit in the second slot, hence  receives only one message carrying information from
receives only one message carrying information from  , namely, on the
, namely, on the  -
- channel. Now, the decoding error probability, that is, the WER
channel. Now, the decoding error probability, that is, the WER  , at
, at  can be written as follows:
can be written as follows:

The probability  is equal to the probability of erroneous decoding at
is equal to the probability of erroneous decoding at  . For large
. For large  , we have
, we have  and
and  [25], where
[25], where  is a constant. The probability
is a constant. The probability  is equal to the probability of erroneous decoding on the
is equal to the probability of erroneous decoding on the  -
- channel; hence for large
channel; hence for large  ,
,  . Now, the error probability
. Now, the error probability  at large
at large  is proportional to
is proportional to

where  is a positive constant. According to Definition 1, full-diversity requires that at large
is a positive constant. According to Definition 1, full-diversity requires that at large  ,
,  . We see that this only depends on the behavior of
. We see that this only depends on the behavior of  at large
at large  , because the second case where the relay cannot decode the transmission from the source in the first slot does automatically give rise to a double diversity order without the need for any code structure. This means that as far as the diversity order is concerned, it is sufficient to assume errorless
, because the second case where the relay cannot decode the transmission from the source in the first slot does automatically give rise to a double diversity order without the need for any code structure. This means that as far as the diversity order is concerned, it is sufficient to assume errorless  -
- channels (yielding
channels (yielding  ). Furthermore, techniques [8] are known to extend the proposed code construction to nonperfect source-relay channels, so that, for the clarity of the presentation, perfect source-relay channels are assumed in the remainder of the paper.
). Furthermore, techniques [8] are known to extend the proposed code construction to nonperfect source-relay channels, so that, for the clarity of the presentation, perfect source-relay channels are assumed in the remainder of the paper.
3.3. Outage Probability of the MARC
We denote an outage event of the MARC by  . An outage event is the event that the destination cannot retrieve the information from
. An outage event is the event that the destination cannot retrieve the information from  or
or  , that is, the transmitted rate is larger than or equal to the instantaneous mutual information. The transmitted rate
, that is, the transmitted rate is larger than or equal to the instantaneous mutual information. The transmitted rate  is the average spectral efficiency of user
is the average spectral efficiency of user  whereas
whereas  is the overall spectral efficiency, so that
is the overall spectral efficiency, so that  . (The average spectral efficiency denotes the average number of bits per overall channel uses, including the channel uses of the other devices, that is, transmitted over the MARC channel.) We can interprete
. (The average spectral efficiency denotes the average number of bits per overall channel uses, including the channel uses of the other devices, that is, transmitted over the MARC channel.) We can interprete  as the total spectral efficiency, that is, transmitted over the network. The MARC block fading channel has a Shannon capacity, that is, essentially zero since the fading gains make the mutual information a random variable which does not allow to achieve an arbitrarily small word error probability under a certain spectral efficiency. This word error probability is called information outage probability in the limit of large block length, denoted by
as the total spectral efficiency, that is, transmitted over the network. The MARC block fading channel has a Shannon capacity, that is, essentially zero since the fading gains make the mutual information a random variable which does not allow to achieve an arbitrarily small word error probability under a certain spectral efficiency. This word error probability is called information outage probability in the limit of large block length, denoted by

The outage probability is a lower bound on the average word error rate of coded systems [27].
The mutual information from user 1 to the destination is the weighted sum of the mutual informations from the channels from  -
- and
and  -
- . (The transmission of
. (The transmission of  corresponds to redundancy for
corresponds to redundancy for  and
and  at the same time. From the point of view of
at the same time. From the point of view of  , the transmission of
, the transmission of  contains interference from
contains interference from  . By using the observations from
. By using the observations from  , the decoder at the destination can at most cancel the interference from
, the decoder at the destination can at most cancel the interference from  in the transmission from
in the transmission from  .) Hence the spectral efficiency
.) Hence the spectral efficiency  is upper bounded as
is upper bounded as

where  and
and  are the fractions of the time during which
are the fractions of the time during which  and
and  are active [25, Section
are active [25, Section  ]. The same holds for user 2:
]. The same holds for user 2:

Combining (11) and (12) yields

However, there is a tighter bound for  . Indeed, (11) and (12) both rely on the fact that the destination can cancel the interference from the other user on the relay-to-destination channel, but therefore, the destination must be able to decode one of the users' information from their respective transmission. Hence, there exist two scenarios: (
. Indeed, (11) and (12) both rely on the fact that the destination can cancel the interference from the other user on the relay-to-destination channel, but therefore, the destination must be able to decode one of the users' information from their respective transmission. Hence, there exist two scenarios: ( ) in the first scenario,
) in the first scenario,  decodes the information of
decodes the information of  from the transmission of
from the transmission of  (
( ), so that it can cancel the interference from
), so that it can cancel the interference from  in the transmission from
in the transmission from  ((11) holds); (
((11) holds); ( ) the second scenario is the symmetric case (
) the second scenario is the symmetric case ( and (12) holds). Both scenarios lead to a tighter bound for
and (12) holds). Both scenarios lead to a tighter bound for  :
:

Bound (14) can be verified when considering the instantaneous mutual information between the sources and the sinks in the network. We denote the instantaneous mutual information of the MARC as  , which is a function of the set of fading gains
, which is a function of the set of fading gains  and average SNR
and average SNR  . The overall mutual information is
. The overall mutual information is

because the three timeslots behave as parallel Gaussian channels whose mutual informations add together. Of course, the timeslots timeshare a time-interval, which gives a weight to each mutual information term [25, Section  ]. The total transmitted rate must be smaller than
]. The total transmitted rate must be smaller than  , which yields (14).
, which yields (14).
From the above analysis, we can now write the expression of an outage event:

The three terms  ,
,  , and
, and  are each the average mutual information of a point-to-point channel with input
are each the average mutual information of a point-to-point channel with input  , received signal
, received signal  with
with  , conditioned on the channel realization
, conditioned on the channel realization  , which is determined by the following well-known formula [28]:
, which is determined by the following well-known formula [28]:

where  is the mathematical expectation over
is the mathematical expectation over  given
given  and
and  . Therefore, three terms
. Therefore, three terms  ,
,  , and
, and  are
are

Now, the outage probability can be easily determined through Monte-Carlo simulations to average over the fading gains and to average over the noise. (Averaging over the noise can be done more efficiently using Gauss-Hermite quadrature rules [29].)
3.4. Maximum Achievable Coding Rate for Full Diversity
In Section 3.1, we established that the maximum achievable diversity order is two. Here, we will derive an upper bound on the coding rate yielding full diversity, valid for all discrete constellations (assume a discrete constellation with M bits per symbol).
It has been proved that a coding scheme is of full diversity on the block fading channel if and only if it is of full diversity on a block BEC [22]. So let us assume a block BEC, hence  ,
,  . The strategy to derive the maximum achievable coding rate is as follows: erase one of the three channels (see Figure 3), and derive the maximum spectral efficiency that allows successful decoding at the destination. (Another approach from a coding point of view has been made in [30].)
. The strategy to derive the maximum achievable coding rate is as follows: erase one of the three channels (see Figure 3), and derive the maximum spectral efficiency that allows successful decoding at the destination. (Another approach from a coding point of view has been made in [30].)
The criteria for successful decoding at the destination are given in the previous subsection see (11), (12), and (14). Because one of the three channels has been erased (see Figure 3), one of the mutual informations is zero. The channels that are not erased have a maximum mutual information  (discrete signaling). A user's spectral efficiency allows successful decoding if and only if
(discrete signaling). A user's spectral efficiency allows successful decoding if and only if


It can be easily seen that (20) is a looser bound than (19) ( ), so that finally
), so that finally

which is maximized if  , such that
, such that  . The destination decodes all the information bits on one graph that represents an overall code with coding rate
. The destination decodes all the information bits on one graph that represents an overall code with coding rate  . Hence the maximum achievable overall coding rate is
. Hence the maximum achievable overall coding rate is  . It is clear that to maximize
. It is clear that to maximize  , the spectral efficiencies
, the spectral efficiencies  and
and  should be equal, that is, all users in the network transmit at the same rate. In this case, (21) and (19) are equivalent and it is sufficient to bound the sum-rate only. In our design, we will take
should be equal, that is, all users in the network transmit at the same rate. In this case, (21) and (19) are equivalent and it is sufficient to bound the sum-rate only. In our design, we will take  , so that the maximum achievable coding rate can be achieved.
, so that the maximum achievable coding rate can be achieved.
4. Full-Diversity Coding for Channels with Multiple Fading States
In the first part of the paper, we established the channel model, the physical layer network coding framework, the maximum achievable diversity order, and the maximum achievable coding rate yielding full diversity. In a nutshell, if the relay transmits a linear transformation of the information bits from both sources during  of the time, a double diversity order can be achieved with one overall error-correcting code with a maximum coding rate
of the time, a double diversity order can be achieved with one overall error-correcting code with a maximum coding rate  . Now, in the second part of the paper, this overall LDPC code construction that achieves full diversity for maximum rate will be designed. First, in this section, rootchecks will be introduced, a basic tool to achieve diversity on fading channels under iterative decoding [22]. Then, in the following section, application of these rootchecks to the MARC will define the network code, that is,
. Now, in the second part of the paper, this overall LDPC code construction that achieves full diversity for maximum rate will be designed. First, in this section, rootchecks will be introduced, a basic tool to achieve diversity on fading channels under iterative decoding [22]. Then, in the following section, application of these rootchecks to the MARC will define the network code, that is,  and
and  , such that a double-diversity order is achieved. Finally, these claims will be verified by means of simulations for finite length and infinite length codes.
, such that a double-diversity order is achieved. Finally, these claims will be verified by means of simulations for finite length and infinite length codes.
4.1. Diversity Rule
In order to perform close to the outage probability, an error-correcting code must fulfil two criteria:
-
(1)
full-diversity, that is, the slope of the WER is the same as the slope of the outage probability at
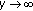 ;
; -
(2)
coding gain, that is, minimizing the gap between the outage probability and the WER performance at high SNR.
The criteria are given in order of importance. The first criterion is independent of the degree distributions of the code [22], hence serves to construct the skeleton of the code. It guarantees that the gap between the outage probability and the WER performance is not increasing at high SNR. The second criterion can be achieved selecting the appropriate degree distributions or applying the doping techniques (see Section 7.2). In this paper, the most attention goes to the first criterion.
In the belief propagation (BP) algorithm, probabilistic messages (log-likelihood ratios) are propagating on the Tanner graph. The behavior of the messages for  determines whether the diversity order can be achieved [17]. However, the BP algorithm is numerical and messages propagating on the graph are analytically intractable. Fortunately, there is another much simpler approach to prove full diversity. Diversity is defined at
determines whether the diversity order can be achieved [17]. However, the BP algorithm is numerical and messages propagating on the graph are analytically intractable. Fortunately, there is another much simpler approach to prove full diversity. Diversity is defined at  . In this region the fading can be modeled by a block BEC, an extremal case of block-Rayleigh fading. Full diversity on the block BEC is a necessary and sufficient condition for full diversity on the block-Rayleigh fading channel [22]. The analysis on a block BEC channel is a very simple (bits are erased or perfectly known) but very powerful means to check the diversity order of a system.
. In this region the fading can be modeled by a block BEC, an extremal case of block-Rayleigh fading. Full diversity on the block BEC is a necessary and sufficient condition for full diversity on the block-Rayleigh fading channel [22]. The analysis on a block BEC channel is a very simple (bits are erased or perfectly known) but very powerful means to check the diversity order of a system.
Proposition 1.
One obtains a diversity order  on the MARC, provided that all information bits can be recovered, when any single timeslot is erased.
on the MARC, provided that all information bits can be recovered, when any single timeslot is erased.
This rule will be used in the remainder of the paper to derive the skeleton of the code.
4.2. Rootcheck
Applying Proposition 1 to the MARC leads to three possibilities (Figure 3).
Case 1.
The  -
- channel is erased:
channel is erased:  ,
,  ,
, 
Case 2.
The  -
- channel is erased:
channel is erased:  ,
,  ,
, 
Case 3.
The  -
- channel is erased:
channel is erased:  ,
,  ,
,  .
.
Let us zoom on the decoding algorithm to see what is happening. We illustrate the decoding procedure on a decoding tree, which represents the local neighborhood of a bit node in the Tanner graph (the incoming messages are assumed to be independent). When decoding, bit nodes called leaves pass extrinsic information through a check node to another bit node called root (Figure 4). Because we consider a block BEC channel, the check node operation becomes very simple. If all leaf bits are known, the root bit becomes the modulo-2 sum of the leaf bits, otherwise, the root bit is undetermined (P(bit=1)=P(bit=0)=0.5). Dealing with Case 3 is simple: let every source send its information uncoded and  sends extra parity bits. If
sends extra parity bits. If  receives the transmissions of
receives the transmissions of  and
and  perfectly, it has all the information bits. So the challenging cases are the first two possibilities. Let us assume that the nodes corresponding to the bits transmitted by
perfectly, it has all the information bits. So the challenging cases are the first two possibilities. Let us assume that the nodes corresponding to the bits transmitted by  ,
,  , and
, and  are filled red, blue, and white, respectively. Assume that all red (blue) bits are erased at
are filled red, blue, and white, respectively. Assume that all red (blue) bits are erased at  . A very simple way to guarantee full diversity is to connect a red (blue) information bit node to a rootcheck (Figures 4(a) and 4(b)).
. A very simple way to guarantee full diversity is to connect a red (blue) information bit node to a rootcheck (Figures 4(a) and 4(b)).
Two examples of a decoding tree, where we distinguish a root and the leaves. While decoding, the leaves pass extrinsic information to the root. Both examples are rootchecks; the root can be recovered if bits corresponding to other colors are not erased. (a) recovers the red root bit if all red bits are erased. (b) recovers the blue root bit if all blue bits are erased.
Definition 3.
A rootcheck is a special type of check node, where all the leaves have colors that are different from the color of its root.
Assigning rootchecks to all the information bits is the key to achieve full diversity. This solution has already been applied in some applications, for example, the cooperative multiple access channel (without external relay) [8]. Note that a check node can be a rootcheck for more than one bit node, for example, the second rootcheck in Figure 4.
4.3. An Example for the MARC
The sources  and
and  transmit information bits and parity bits that are related to their own information, and
transmit information bits and parity bits that are related to their own information, and  transmits information bits and parity bits related to the information from
transmits information bits and parity bits related to the information from  and
and  . The previous description naturally leads to 8 different classes of bit nodes. Information bits of
. The previous description naturally leads to 8 different classes of bit nodes. Information bits of  are split into two classes: one class of bits is transmitted on fading gain
are split into two classes: one class of bits is transmitted on fading gain  (red) and is denoted as
(red) and is denoted as  , the other class is transmitted on
, the other class is transmitted on  (white) and denoted as
(white) and denoted as  ; similarly, red and white parity bits derived from the message of
; similarly, red and white parity bits derived from the message of  are of the classes
are of the classes  and
and  , respectively. Likewise, bits related to
, respectively. Likewise, bits related to  are split into four classes: blue bits
are split into four classes: blue bits  and
and  (transmitted on
(transmitted on  ), and white bits
), and white bits  and
and  (transmitted on
(transmitted on  ). The subscripts of a class refer to the associated user. In the remainder of the paper, the vectors
). The subscripts of a class refer to the associated user. In the remainder of the paper, the vectors  ,
,  ,
,  , and
, and  collect the bits of the classes
collect the bits of the classes  ,
,  ,
,  , and
, and  , respectively. A similar notation holds for
, respectively. A similar notation holds for  . This notation is illustrated in Figure 5.
. This notation is illustrated in Figure 5.
Above, we concluded that all information bits should be the root of a rootcheck. The class of rootchecks for  is denoted as
is denoted as  . Translating Figure 4 to its matrix representation renders
. Translating Figure 4 to its matrix representation renders

The identity matrix concatenated with a matrix of zeros assures that bits of the class  are the only red bits connected to check nodes of the class
are the only red bits connected to check nodes of the class  . (Note that the identity matrix can be replaced by a permutation matrix. For the simplicity of the notation, in the rest of the paper
. (Note that the identity matrix can be replaced by a permutation matrix. For the simplicity of the notation, in the rest of the paper  will be used.) As the bits from
will be used.) As the bits from  and
and  are independent, the matrix representation can be further detailed:
are independent, the matrix representation can be further detailed:

Hence, a full-diversity code construction for the MARC can be formed by assigning this type of rootchecks (introducing new classes  ,
,  , and
, and  ) to all information bits:
) to all information bits:

(The reader can verify that this is a straightforward extension of full-diversity codes for the block fading channel [22].)  transmits
transmits  and
and  ,
,  transmits
transmits  and
and  , and the common relay first transmits
, and the common relay first transmits  and
and  and then transmits
and then transmits  and
and  , hence the level of cooperation is
, hence the level of cooperation is  . The reader can easily verify that if only one color is erased, all information bits can be retrieved after one decoding iteration. Note that both sources do not transmit all information bits, but the relay transmits a part of the information bits. This is possible because if
. The reader can easily verify that if only one color is erased, all information bits can be retrieved after one decoding iteration. Note that both sources do not transmit all information bits, but the relay transmits a part of the information bits. This is possible because if  receives
receives  and
and  perfectly it can derive
perfectly it can derive  (because of the rootchecks
(because of the rootchecks  ) and consequently
) and consequently  (after reencoding). (This code construction can be easily extended to nonperfect relay channels using techniques described in [8].) The same holds for
(after reencoding). (This code construction can be easily extended to nonperfect relay channels using techniques described in [8].) The same holds for  . It turns out that splitting information bits in two parts and letting one part to be transmitted on the first fading gain and the other part on the second fading gain is the only way to guarantee full diversity for maximum coding rate [22]. This code construction is semirandom, because only parts of the parity-check matrix are randomly generated. However, every set of rows and set of columns contains a randomly generated matrix and, therefore, can conform to any degree distribution. It has been shown that despite the semirandomness (due to the presence of deterministic blocks), these LDPC codes are still very powerful in terms of decoding threshold [22]. No network coding has been used to obtain the code construction discussed above. The aim of this subsection was to show that through rootchecks, it is easy to construct a full-diversity code construction. However, when applying network coding, as will be discussed in Section 5, the spectral efficiency can be increased.
. It turns out that splitting information bits in two parts and letting one part to be transmitted on the first fading gain and the other part on the second fading gain is the only way to guarantee full diversity for maximum coding rate [22]. This code construction is semirandom, because only parts of the parity-check matrix are randomly generated. However, every set of rows and set of columns contains a randomly generated matrix and, therefore, can conform to any degree distribution. It has been shown that despite the semirandomness (due to the presence of deterministic blocks), these LDPC codes are still very powerful in terms of decoding threshold [22]. No network coding has been used to obtain the code construction discussed above. The aim of this subsection was to show that through rootchecks, it is easy to construct a full-diversity code construction. However, when applying network coding, as will be discussed in Section 5, the spectral efficiency can be increased.
4.4. Rootchecks for Punctured Bits
In the previous subsection, we have illustrated that, through rootchecks, full-diversity can be achieved. Another feature of rootchecks is to retrieve bits that have not been transmitted, which are called punctured bits. Punctured bits are very similar to erased bits, because both are not received by the destination. However, the transmitter knows the exact position of the punctured bits inside the codeword which is not the case for erased bits. Formally, we can state that from an algebraic decoding or a probabilistic decoding point of view, puncturing and erasing are identical, an erased/punctured bit is equivalent to an error with known location but unknown amplitude. From a transmitter point of view, punctured bits have always fixed position in the codeword whereas channel erased bits have random locations.
When punctured bits are information bits, the destination must be able to retrieve them. There are two ways to protect punctured bits.
-
(i)
The punctured bit nodes are connected to one or more rootchecks. If the leaves are erased or punctured, the punctured root bit cannot be retrieved after the first decoding iteration. The erased or punctured leaves on their turn must be connected to rootchecks, such that they can be retrieved after the first iteration. Then, in the second iteration the punctured root bit can be retrieved. These rootchecks are denoted as second-order rootchecks (see Figure 6). Similarly, higher-order rootchecks can be used.
-
(ii)
The punctured bit nodes are connected to at least two rootchecks where both rootchecks have leaves with different colors (see Figure 6). If one color is erased, there will always be a rootcheck without erased leaves to retrieve the punctured bit node.
Two special rootchecks for punctured bits (shaded bit nodes). (a) is a second-order rootcheck. Imagine that all blue bits are erased, than the shaded bit node will be retrieved in the second iteration. (b) represents two rootchecks where both rootchecks have leaves with other colors. Imagine that one color has been erased, than the shaded bit node will still be recovered after the first iteration.
Combinations of both types of rootchecks are also possible.
5. Full-Diversity Joint Network-Channel Code
In this section, we join the principles of the previous section with the physical layer network coding framework. We will use the same bit node classes as in the previous section, hence  transmits
transmits  and
and  , and
, and  transmits
transmits  and
and  . The bits transmitted by the relay are determined by (5) and are of the class
. The bits transmitted by the relay are determined by (5) and are of the class  . Adapting (5) to the classes of bit nodes gives
. Adapting (5) to the classes of bit nodes gives

where the dimensions of  are
are  . Please note that
. Please note that  ,
,  ,
,  , and
, and  are not transmitted anymore (these bits are punctured). The number of transmitted bits
are not transmitted anymore (these bits are punctured). The number of transmitted bits  by the relay is determined by the coding rate. There are
by the relay is determined by the coding rate. There are  information bits. The sources
information bits. The sources  and
and  each transmit
each transmit  bits, hence to obtain a coding rate
bits, hence to obtain a coding rate  , the relay can transmit
, the relay can transmit  bits. We will include the punctured information bits
bits. We will include the punctured information bits  and
and  in the parity-check matrix for two reasons:
in the parity-check matrix for two reasons:
-
(i)
without
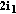 and
and 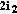 , we cannot insert (25) in the parity-check matrix;
, we cannot insert (25) in the parity-check matrix; -
(ii)
the destination wants to recover all information bits, that is,
 ,
,  ,
, 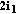 , and
, and  , so
, so 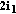 and
and 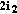 must be included in the decoding graph.
must be included in the decoding graph.
(The matrices in the following of the paper correspond to codewords that must be punctured to obtain the bits actually transmitted.) The parity-check matrix now has the following form:

Because the nodes  and
and  have been added, we have now
have been added, we have now  columns and
columns and  rows.
rows.  rows are used to implement (25), while the other
rows are used to implement (25), while the other  rows define
rows define  in terms of the information bits
in terms of the information bits  and
and  (used for encoding at
(used for encoding at  ), and
), and  in terms of the information bits
in terms of the information bits  and
and  (used for encoding at
(used for encoding at  ). The first two set of rows
). The first two set of rows  and
and  are rootchecks for
are rootchecks for  and
and  ; see Section 4. Now it boils down to design the matrices
; see Section 4. Now it boils down to design the matrices  ,
,  ,
,  ,
,  , and
, and  , such that the set of rows
, such that the set of rows  and
and  represent rootchecks of the first or second order for all information bits. There exist 8 possible parity-check matrices that conform to this requirement; see Appendix A. With the exception of matrix (A.7), all matrices have one or both of the following disadvantages.
represent rootchecks of the first or second order for all information bits. There exist 8 possible parity-check matrices that conform to this requirement; see Appendix A. With the exception of matrix (A.7), all matrices have one or both of the following disadvantages.
-
(i)
There is no random matrix in each set of columns, such that
 cannot conform to any degree distribution.
cannot conform to any degree distribution. -
(ii)
There is an asymmetry wrt.
 and
and 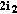 and/or wrt.
and/or wrt. 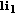 and
and 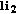 and/or
and/or  and
and  which results in a loss of coding gain.
which results in a loss of coding gain.
Therefore, we select the matrix (A.7). The parity-check matrix (A.7) of the overall decoder at  shows that the bits transmitted by
shows that the bits transmitted by  are a linear transformation of all the information bits
are a linear transformation of all the information bits  ,
,  ,
,  , and
, and  . Furthermore, the checks
. Furthermore, the checks  represent rootchecks for all the information bits, guaranteeing full diversity. The checks
represent rootchecks for all the information bits, guaranteeing full diversity. The checks  are necessary because the bits
are necessary because the bits  are not transmitted. Note that the punctured bits
are not transmitted. Note that the punctured bits  have two rootchecks that have leaves with different colors. One of the rootchecks is a second-order rootcheck. For example, the punctured bits of the class
have two rootchecks that have leaves with different colors. One of the rootchecks is a second-order rootcheck. For example, the punctured bits of the class  have two rootchecks, one of the class
have two rootchecks, one of the class  and one of the class
and one of the class  . The rootcheck of the class
. The rootcheck of the class  has only red leaves, while the rootcheck of the class
has only red leaves, while the rootcheck of the class  has white and blue leaves. All but one blue leaves are punctured such that the rootcheck of the class
has white and blue leaves. All but one blue leaves are punctured such that the rootcheck of the class  is a second-order rootcheck.
is a second-order rootcheck.
6. Density Evolution for the MARC
In this section, we develop the density evolution (DE) framework, to simulate the performance of infinite length LDPC codes. In classical LDPC coding, density evolution [9, 24, 31] is used to simulate the threshold of an ensemble of LDPC codes. (Richardson and Urbanke [9, 31] established that, if the block length is large enough, (almost) all codes in an ensemble of codes behave alike, so the determination of the average behavior is sufficient to characterize a particular code behavior. This average behavior converges to the cycle-free case if the block length augments and it can be found in a deterministic way through density evolution (DE).) The threshold of an ensemble of codes is the minimum SNR at which the bit error rate converges to zero [31].
This technique can also be used to predict the word error rate of an ensemble of LDPC codes [22]. We refer to the event where the bit error probability does not converge to 0 by Density Evolution Outage (DEO). By averaging over a sufficient number of fading instances, we can determine the probability of a Density Evolution Outage  . Now, it is possible to write the word error probability
. Now, it is possible to write the word error probability  of the ensemble as
of the ensemble as

where  is the word error rate given a DEO event and
is the word error rate given a DEO event and  is the word error rate when DE converges. If the bit error rate does not converge to zero, then the word error rate equals one, so that
is the word error rate when DE converges. If the bit error rate does not converge to zero, then the word error rate equals one, so that  . On the other hand,
. On the other hand,  depends on the speed of convergence of density evolution and the population expansion of the ensemble with the number of decoding iterations [32, 33], but in any case
depends on the speed of convergence of density evolution and the population expansion of the ensemble with the number of decoding iterations [32, 33], but in any case  , so that the performance simulated via DE is a lower bound on the word error rate. Finite length simulations confirm the tightness of this lower bound.
, so that the performance simulated via DE is a lower bound on the word error rate. Finite length simulations confirm the tightness of this lower bound.
In summary, a tight lower bound on the word error rate of infinite length LDPC codes can be obtained by determining the probability of a Density Evolution Outage  . Given a triplet
. Given a triplet  , one needs to track the evolution of message densities under iterative decoding to check whether there is DEO. (Messages are under the form of log-likelihood ratios (LLRs).) The evolution of message densities under iterative decoding is described through the density evolution equations, which are derived directly through the evolution trees. The evolution trees represent the local neighborhood of a bit node in an infinite length code whose graph has no cycles, hence incoming messages to every node are independent.
, one needs to track the evolution of message densities under iterative decoding to check whether there is DEO. (Messages are under the form of log-likelihood ratios (LLRs).) The evolution of message densities under iterative decoding is described through the density evolution equations, which are derived directly through the evolution trees. The evolution trees represent the local neighborhood of a bit node in an infinite length code whose graph has no cycles, hence incoming messages to every node are independent.
6.1. Tanner Graph and Notation
The proposed code construction has 7 variable node types and 4 check node types. Consequently, the evolution of message densities under iterative decoding has to be described through multiple evolution trees, which can be derived from the Tanner graph. A Tanner graph is a representation of the parity-check matrices of an error-correcting code. In a Tanner graph, the focus is more on its degree distributions. In Figure 7, the Tanner graph of matrix (A.7) is shown. The new polynomials  and
and  are derived in Proposition 2.
are derived in Proposition 2.
Proposition 2.
In a Tanner graph with a left degree distribution  , isolating one edge per bit node yields a new left degree distribution described by the polynomial
, isolating one edge per bit node yields a new left degree distribution described by the polynomial  :
:

Proof.
Let us define  as the number of edges connected to a bit node of degree
as the number of edges connected to a bit node of degree  . Similarly, the number of all edges is denoted
. Similarly, the number of all edges is denoted  . From Section 2, we know that
. From Section 2, we know that  expresses the left degree distribution, where
expresses the left degree distribution, where  is the fraction of all edges in the Tanner graph, connected to a bit node of degree
is the fraction of all edges in the Tanner graph, connected to a bit node of degree  . So finally
. So finally  . A similar reasoning can be followed to determine
. A similar reasoning can be followed to determine  :
:

-
(a)
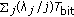 is equal to the number of edges that are removed which is equal to the number of bits.
is equal to the number of edges that are removed which is equal to the number of bits. -
(b)
 is equal to the number of edges connected to a bit of degree
is equal to the number of edges connected to a bit of degree  .
.
Similarly, we can determine  , where
, where  . It can be shown that
. It can be shown that  is the same as applying the transformation
is the same as applying the transformation  two times consecutively, hence first on
two times consecutively, hence first on  , and then on
, and then on  .
.
6.2. DE Trees and DE Equations
The proposed code construction has 7 variable node types and 4 check node types. But not all variable node types are connected to all check node types. Therefore, there are 14 evolution trees. But it is sufficient to draw only 7 of them because of symmetry. To write down the equations we adopt the following notation.
Let  and
and  be two independent real random variables. The density function of
be two independent real random variables. The density function of  is obtained by convolving the two original densities, written as
is obtained by convolving the two original densities, written as  . The notation
. The notation  denotes the convolution of
denotes the convolution of  with itself
with itself  times.
times.
The density function  of the variable
of the variable  , obtained through a check node with
, obtained through a check node with  and
and  at the input, is obtained through the R-convolution [9], written as
at the input, is obtained through the R-convolution [9], written as  . The notation
. The notation  denotes the tangent hyperbolic function and
denotes the tangent hyperbolic function and  denotes the
denotes the  -convolution of
-convolution of  with itself
with itself  times.
times.
To simplify the notations, we use the following definitions:

Next, we will use the following definitions:

The first definition is necessary because of the nonlinearity of the R-convolution. Therefore, the first equation is not equal to  .
.
The following message densities at the  iteration are distinguished:
iteration are distinguished:

Proposition 3.
The DE equations in the neighborhood of  ,
,  ,
,  , and
, and  for all
for all  are listed in (33)–(34),
are listed in (33)–(34),


where









Note that the message densities propagating from bits of the class  do not contain a channel observation
do not contain a channel observation  because these information bits are punctured.
because these information bits are punctured.
Proof.
See Appendix B.
7. Numerical Results
7.1. Full-Diversity LDPC Ensembles
We evaluated the finite length performance of full-diversity LDPC codes and the asymptotic performance by applying DE on the proposed code construction. The parity-check matrix (A.7) is used by the destination to decode the information bits. This paper focuses on full diversity, rather than coding gain. Therefore, one of the codes is a simple regular  LDPC code. This means that all the random matrices in (A.7) are randomly generated satisfying an overall row weight of
LDPC code. This means that all the random matrices in (A.7) are randomly generated satisfying an overall row weight of  and an overall column weight of
and an overall column weight of  . This matrix corresponds to a coding rate of
. This matrix corresponds to a coding rate of  , but because
, but because  are punctured, the actual coding rate is
are punctured, the actual coding rate is  . The other code, that is, simulated and is denoted as code 2 is an irregular
. The other code, that is, simulated and is denoted as code 2 is an irregular  LDPC ensemble [22] with left and right degree distributions given by the polynomials
LDPC ensemble [22] with left and right degree distributions given by the polynomials

We studied the following scenario.
-
(i)
The
 -
-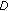 ,
, 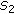 -
-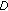 , and
, and 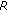 -
- links have the same average SNR.
links have the same average SNR. -
(ii)
The
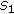 -
-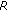 and
and  -
-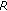 links are perfect.
links are perfect. -
(iii)
The coding rate is
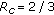 and the cooperation level is
and the cooperation level is 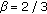 .
.
Figure 8 shows the main results: the word error rate (WER) of a regular  LDPC ensemble and of an irregular
LDPC ensemble and of an irregular  LDPC ensemble, which are both of full diversity.
LDPC ensemble, which are both of full diversity.
It is clear that the DE results are a lower bound on the actual word error rates (a tight lower bound for the regular code and a less tight lower bound for the irregular code). The word error rate of a regular  LDPC code is only about
LDPC code is only about  worse than the outage probability. The irregular LDPC code is only slightly better than the regular
worse than the outage probability. The irregular LDPC code is only slightly better than the regular  LDPC code in terms of word error rate.
LDPC code in terms of word error rate.
7.2. Full-Diversity RA Codes with Improved Coding Gain
Another technique, suggested in [17], that improves the coding gain is called doping. For all the Rootcheck based LDPC codes the reliability of the messages exchanged by the belief propagation algorithm can be improved by increasing the reliability of parity bits (which are not protected by rootchecks). In fact the LLR values of the messages exchanged by the belief propagation algorithm are in the form [17]:

where  are the fading coefficients,
are the fading coefficients,  are positive constants, and
are positive constants, and  represents the noise. The higher the coefficients
represents the noise. The higher the coefficients  , the more reliable are the LLR messages. Since the output messages of the check node are limited by the lowest LLR values of the incoming messages, that is, the messages coming from parity bits, the doping technique aims to increase those values. The least reliable variable nodes are the parity bits sent on a channel in a deep fade.
, the more reliable are the LLR messages. Since the output messages of the check node are limited by the lowest LLR values of the incoming messages, that is, the messages coming from parity bits, the doping technique aims to increase those values. The least reliable variable nodes are the parity bits sent on a channel in a deep fade.
In case of block BEC, consider the parity bits sent on a channel with fading coefficient  and suppose that all the other fading coefficients are
and suppose that all the other fading coefficients are  with
with  . Consider the parity-check matrix (A.7). The doping technique consists in fixing the random matrix
. Consider the parity-check matrix (A.7). The doping technique consists in fixing the random matrix  such that, under BP, all the variable nodes can be recovered after a certain number of iterations. This is equivalent to having reliable parity bits, that is, connected to rootchecks of a certain order, and it guarantees to increase the coefficients
such that, under BP, all the variable nodes can be recovered after a certain number of iterations. This is equivalent to having reliable parity bits, that is, connected to rootchecks of a certain order, and it guarantees to increase the coefficients  .
.
While the aforementioned doping technique has been proposed and investigated for infinite length LDPC codes, finite length rootcheck based LDPC codes that get advantage of the doping technique have not been published yet. Ongoing studies have revealed construction problems with doped finite length Root-LDPC codes, so that their performance cannot be included here. An important issue, that is often not considered, is the encoding complexity. This suggests to embed the well-known repeat-accumulate (RA) structure in the parity-check matrix, which results in linear-time encoding. Hence, regardless the degree distribution, we substitute the matrices  ,
,  , and
, and  with staircase matrices (46)
with staircase matrices (46)

Figure 9 reports the simulation results for a regular RA code that show a 0.5 dB improvement compared to the proposed regular (3,6) code. Together with the fact that this simple code is now linear-time encoding, this result is impressive because we have lowered the complexity and improved the performance at the same time. As a benchmark the outage probability has been plotted. We have also included the best known LDPC code for the MARC in literature: the rate  network code proposed in [16]; it reports a loss of almost 2.5 dB wrt. the proposed full-diversity RA code.
network code proposed in [16]; it reports a loss of almost 2.5 dB wrt. the proposed full-diversity RA code.
8. Conclusions and Remarks
We have studied LDPC codes for the multiple access relay channel in a slowly varying fading environment under iterative decoding. LDPC codes must be carefully designed to achieve full diversity on this channel and network coding must be applied to increase the achievable coding rate to a maximum rate  . Combining network coding with of full diversity channel coding gave rise to a new family of semirandom full-diversity joint network-channel LDPC codes for all rates not exceeding
. Combining network coding with of full diversity channel coding gave rise to a new family of semirandom full-diversity joint network-channel LDPC codes for all rates not exceeding  . A code that is only
. A code that is only  away from the outage probability limit has been presented.
away from the outage probability limit has been presented.
For a block fading channel with several fading states per codeword, it has been pointed out that the poor reliability of the parity bits in full-diversity LDPC codes (where especially the information bits are well protected) causes the actual gap with the outage probability limit. We increased the reliability of the parity bits by using a repeat-accumulate structure and have improved the coding gain of the presented code construction for the MARC.
Appendices
A. Full-Diversity Parity-Check Matrices
The reader can find here a list of full-diversity parity-check matrices  , that is, matrices where all information bits are assigned to a rootcheck in the last two set of rows
, that is, matrices where all information bits are assigned to a rootcheck in the last two set of rows  and
and  . Matrix (A.7) performs the best for reasons of symmetry and randomness,
. Matrix (A.7) performs the best for reasons of symmetry and randomness,








B. Proof of Proposition 3
Equations (33)–(40) are directly derived from the local neighborhood trees (see e.g., Figures 11 and 12). The proportionality factors (35)–(40) can easily be determined by analyzing the Tanner graph. Let  denote the total number of edges between the variable nodes
denote the total number of edges between the variable nodes  and the check nodes
and the check nodes  . Figure 10 illustrates how
. Figure 10 illustrates how  and
and  are obtained:
are obtained:



-
(a)
The fraction of check nodes connected to
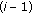 edges of
edges of  is
is 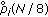 . A similar reasoning proves (B.2).
. A similar reasoning proves (B.2). -
(b)
The fraction of edges
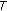 connecting
connecting 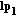 to
to  is
is 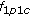 and the fraction of edges
and the fraction of edges 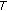 connecting
connecting  to
to 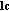 is
is 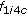 .
.
Note that in the first iteration,  ,
,  ,
,  , and
, and  are equal to
are equal to  , because the received messages come from check nodes where one of the leaves corresponds to a punctured information bit (so that their message density is a Dirac function on
, because the received messages come from check nodes where one of the leaves corresponds to a punctured information bit (so that their message density is a Dirac function on  ). Therefore, the message densities coming from the check nodes are also Dirac functions on
). Therefore, the message densities coming from the check nodes are also Dirac functions on  . (The output of a check node
. (The output of a check node  is determined through its inputs
is determined through its inputs  ,
,  via the following formula:
via the following formula:  . If one of the inputs
. If one of the inputs  is always zero because its distribution is a Dirac function on
is always zero because its distribution is a Dirac function on  , then the output
, then the output  will always be zero, so that its distribution will also be a Dirac function on
will always be zero, so that its distribution will also be a Dirac function on  .) But
.) But  and
and  are different from a Dirac function on
are different from a Dirac function on  after the first iteration, so that the next iteration also
after the first iteration, so that the next iteration also  becomes different from a Dirac function on
becomes different from a Dirac function on  .
.
The factor  in (42) and (43) takes into account that
in (42) and (43) takes into account that  counts
counts  variable nodes while
variable nodes while  and
and  count only
count only  parity check equations. Solving together (40)–(43), it is possible to prove that for any degree distribution
parity check equations. Solving together (40)–(43), it is possible to prove that for any degree distribution

References
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part I: system description. IEEE Transactions on Communications 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part II: implementation aspects and performance analysis. IEEE Transactions on Communications 2003, 51(11):1939-1948. 10.1109/TCOMM.2003.819238
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Hunter T: Coded cooperation: a new framework for user cooperation in wireless systems, Ph.D. dissertation. University of Texas at Dallas, Richardson, Tex, USA; 2004.
Van Der Meulen E: Three-terminal communication channels. Advances in Applied Probability 1971, 3(1):120-154. 10.2307/1426331
Cover TM, Gamal AA: Capacity theorems for the relay channel. IEEE Transactions on Information Theory 1979, 25(5):572-584. 10.1109/TIT.1979.1056084
Biglieri E: Coding for the Wireless Channel. Springer, New York, NY, USA; 2005.
Duyck D, Boutros J, Moeneclaey M: Low-density graph codes for slow fading relay channels. IEEE Transactions on Information Theory, . In press http://telin.ugent.be/~dduyck/publications/paper_ldpc_cooperative.pdf
Richardson T, Urbanke R: Modern Coding Theory. Cambridge University Press, Cambridge, UK; 2008.
Boutros J, Fàbregas GI, Calvanese-Strinati E: Analysis of coding on non-ergodic channels. Proceedings of the Allerton Conference on Communication, Control and Computing, 2005
Knopp R, Humblet PA: On coding for block fading channels. IEEE Transactions on Information Theory 2000, 46(1):189-205. 10.1109/18.817517
Hausl C: Joint network-channel coding for wireless relay networks, Ph.D. dissertation. Technische Universität München, München, Germany; November 2008.
Ahlswede R, Cai N, Li S-YR, Yeung RW: Network information flow. IEEE Transactions on Information Theory 2000, 46(4):1204-1216. 10.1109/18.850663
Hausl C, Dupraz P: Joint network-channel coding for the multiple-access relay channel. Proceedings of the 3rd Annual IEEE Communications Society on Sensor and Ad Hoc Communications and Networks (Secon '06), September 2006 3: 817-822.
Hausl C, Schreckenbach F, Oikonomidis I, Bauch G: Iterative network and channel decoding on a tanner graph. Proceedings of the Allerton Conference on Communication, Control and Computing, 2005
Chebli L, Hausl C, Zeitler G, Koetter R: Cooperative uplink of two mobile stations with network coding based on the WiMax LDPC code. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '09), 2009
Boutros JJ: Diversity and coding gain evolution in graph codes. Proceedings of the Information Theory and Applications Workshop (ITA '09), February 2009 34-43.
Capirone D, Duyck D, Moeneclaey M: Repeat-accumulate and Quasi-Cyclic Root-LDPC codes for block fading channels. IEEE Communications Letters. In press
Lapidoth A: The performance of convolutional codes on the block erasure channel using various finite interleaving techniques. IEEE Transactions on Information Theory 1994, 40(5):1459-1473. 10.1109/18.333861
McEliece RJ, Stark WE: Channels with block interference. IEEE Transactions on Information Theory 1984, 30(1):44-53. 10.1109/TIT.1984.1056848
Richardson TJ, Shokrollahi MA, Urbanke RL: Design of capacity-approaching irregular low-density parity-check codes. IEEE Transactions on Information Theory 2001, 47(2):619-637. 10.1109/18.910578
Boutros JJ, Fàbregas AGI, Biglieri E, Zémor G: Low-density parity-check codes for nonergodic block-fading channels. IEEE Transactions on Information 2009, 56(9):4286-4300.
Thorpe J: Low-density parity-check (LDPC) codes constructed from protographs. JPL INP Progress Report 2003, 42(154):1-7.
Ryan W, Lin S: Channel Codes, Classical and Modern. Cambridge University Press, Cambridge, UK; 2009.
Tse D, Viswanath P: Fundamentals of Wireless Communication. Cambridge University Press, Cambridge, UK; 2005.
Fàbregas GI: Coding in the block-erasure channel. IEEE Transactions on Information Theory 2006, 52(11):5116-5121.
Biglieri E, Proakis J, Shamai S: Fading channels: information-theoretic and communications aspects. IEEE Transactions on Information Theory 1998, 44(6):2619-2692. 10.1109/18.720551
Ungerboeck G: Channel coding with multilevel/phase signals. IEEE Transactions on Information Theory 1982, 28(1):55-67. 10.1109/TIT.1982.1056454
Abramowitz M, Stegun I: Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables. Courier Dover, New York, NY, USA; 1965.
Duyck D, Capirone D, Moeneclaey M, Boutros JJ: A full-diversity joint network-channel code construction for cooperative communications. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '09), 2009
Richardson T, Urbanke R: The capacity of low-density paritycheck codes undermessage-passing decoding. IEEE Transactions on Information Theory 2001, 47(2):599-618. 10.1109/18.910577
Jin H, Richardson T, Technol F, Bedminster N: Block error iterative decoding capacity for LDPC codes. Proceedings of the IEEE International Symposium on Information Theory (ISIT '05), 2005 52-56.
Lentmaier M, Truhachev DV, Zigangirov KS, Costello DJ Jr.: An analysis of the block error probability performance of iterative decoding. IEEE Transactions on Information Theory 2005, 51(11):3834-3855. 10.1109/TIT.2005.856942
Acknowledgments
D. Capirone wants to acknowledge professor Benedetto for helpful and stimulating discussions. This work was supported by the European Commission in the framework of the FP7 Network of Excellence in Wireless COMmunications NEWCOM++ (Contract no. 216715).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Duyck, D., Capirone, D., Boutros, J. et al. Analysis and Construction of Full-Diversity Joint Network-LDPC Codes for Cooperative Communications. J Wireless Com Network 2010, 805216 (2010). https://doi.org/10.1155/2010/805216
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/805216


 ,
,  , and
, and  are independent.
are independent.
 and
and
 .
.
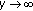 ;
;


 and
and  , we cannot insert (25) in the parity-check matrix;
, we cannot insert (25) in the parity-check matrix; ,
,  ,
,  , and
, and  , so
, so  and
and 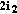 must be included in the decoding graph.
must be included in the decoding graph. cannot conform to any degree distribution.
cannot conform to any degree distribution. and
and 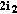 and/or wrt.
and/or wrt. 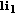 and
and 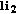 and/or
and/or  and
and  which results in a loss of coding gain.
which results in a loss of coding gain.
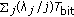 is equal to the number of edges that are removed which is equal to the number of bits.
is equal to the number of edges that are removed which is equal to the number of bits. is equal to the number of edges connected to a bit of degree
is equal to the number of edges connected to a bit of degree  .
. -
-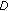 ,
, 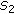 -
-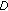 , and
, and 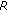 -
- links have the same average SNR.
links have the same average SNR.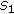 -
-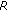 and
and  -
-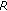 links are perfect.
links are perfect.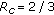 and the cooperation level is
and the cooperation level is 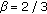 .
.
 with iterative decoding on a MARC.
with iterative decoding on a MARC. is the average information bit energy-to-noise ratio on the
is the average information bit energy-to-noise ratio on the  -
- ,
,  -
- , and
, and  -
- links.
links.
 is the average information bit energy-to-noise ratio on the
is the average information bit energy-to-noise ratio on the  -
- ,
,  -
- , and
, and  -
- links.
links.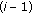 edges of
edges of  is
is 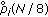 . A similar reasoning proves (B.2).
. A similar reasoning proves (B.2).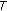 connecting
connecting  to
to  is
is  and the fraction of edges
and the fraction of edges 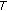 connecting
connecting  to
to  is
is  .
.
 to
to  is
is  . The number of edges connecting
. The number of edges connecting  to
to  is
is  . The number of edges connecting
. The number of edges connecting  to
to  is
is  .
.
 . This tree is used to determine
. This tree is used to determine  .
.
 . This tree is used to determine
. This tree is used to determine  .
.