- Research Article
- Open access
- Published:
Adaptive Power Allocation in Wireless Sensor Networks with Spatially Correlated Data and Analog Modulation: Perfect and Imperfect CSI
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 817961 (2010)
Abstract
We address the problem of power allocation in a wireless sensor network where distributed sensors amplify and forward their partial and noisy observations of a Gaussian random source to a remote fusion center (FC). The FC reconstructs the source based on linear minimum mean-squared error (LMMSE) estimation rule. Motivated by the availability of limited energy in the sensor networks, we undertake the design of power allocation based on minimization of the reconstruction distortion subject to a constraint on the network transmit power. The design is based on the following two cases: (i) exact knowledge of the channel gains and (ii) the estimates of the channel gains. We show that the distortion can be represented as a convex function of the transmit powers of the sensors. Moreover, we show that the power allocation based on this distortion function does not bear any closed form solution. To this end, we propose a novel design based on the successive approximation of the LMMSE distortion, which turns out to be simple, computationally efficient, and exhibits excellent convergence properties. The simulation examples illustrate that the proposed design holds considerable performance gain compared to a uniform power allocation scheme.
1. Introduction
Wireless sensor networking is an emerging technology which finds application in many fields including environment and habitat monitoring, health care, automation, military applications such as battlefield monitoring and surveillance, and underwater wireless sensor networks (UWSNs) for marine environment monitoring [1, 2]. A wireless sensor network (WSN) consists of spatially distributed sensors that cooperatively monitor physical or environmental conditions, for example, temperature, vibration, pressure, motion, or pollutants.
We consider a system in star topology where sensors amplify and transmit their noisy observations of a common source, via some orthogonal multiple access scheme such as frequency division multiple-access (FDMA), to a central processing unit called fusion center (FC) which reconstructs the source in a way that the overall distortion (e.g., mean squared error) be minimized. Conceptually, the system is similar to the CEO problem [3, 4].
The sensors in the network have partial and spatially correlated observations of the underlying source. The correlation exists where sensors measure data in same geographical location, for example, acoustic sensors that are sensing a common event produce measurements that are correlated. In addition, observation noise and communication channel may not have same conditions across the sensors. Therefore, transmission of the observations based on uniform power allocation is not an optimal strategy.
In this paper, we study the problem of adaptive power allocation given a network power constraint with the objective to minimize the reconstruction MSE. The optimal power allocations are jointly determined at the FC which are then conveyed to the individual sensors via feedback channels. The communication channels from the sensors to the FC experience independent flat fading. The channel from the sensor to the FC is usually estimated using some training sequence. The receiver noise and the limited available power means that the channel estimation always incurs some estimation error. Consequently, the design of power allocation scheme should also take into account the channel estimation errors [5, 6]. In this paper, first we design the power allocation scheme based on perfect knowledge of the channel state information (CSI) and subsequently, in the design, we incorporate the effect of imperfect CSI.
In a sensor network measuring a memoryless Gaussian source uncoded transmission, that is, amplify and forward (AF), outperforms the separate coding and transmission over the multiple-access channel [7–9]. Motivated by this result, Vuran et al. in [10] considered the estimation of a random source with distributed sensors and suggested a sensor selection procedure which exploits the spatial correlation to minimize the estimation error (based on the LMMSE estimation criterion). The sensor selection procedure suggests that the sensors with high correlation with the source and low cross-correlations should be selected. The procedure does not take into account the fact that even if a sensor has high correlation with the source and low cross-correlations with the other sensors, it can still be a bad selection in terms of energy efficiency if its observation noise is high and/or the communication channel to the FC is bad. A recent related work appears in [11]. Bahceci and Khandani in [12] proposed a power allocation scheme where each sensor observes a separate source albeit correlated. Reference [13] presented a power scheduling scheme for sensor networks to detect a source based on the binary hypothesis testing rule which exploits the correlation in the observation noises at the sensors. Other works like [14–18] proposed power allocation schemes for parameter estimation in wireless sensor networks without considering the spatial correlation. In this paper, we present a novel framework which incorporates adaptive power allocation (APA) in the network by taking into account the spatial correlation and cross-correlations of the observations, observation quality, and communication channel to the FC. The power allocation design also takes into account the channel estimation errors.
We assume that the FC reconstructs the underlying source using linear minimum mean squared error (LMMSE) estimation rule. The power allocation design is based on minimization of the reconstruction distortion subject to a constraint on the total transmit power of the sensors. Due to the spatial correlation among the sensor observations, the design of the power allocation scheme based on the given optimization problem presents a unique challenge because the LMMSE estimation/reconstruction error of the underlying source contains nonlinearly coupled optimization variables. Herein, first we prove that the estimation distortion can be represented as a convex function of the sensor transmit powers, then we show that the power allocation design based on this distortion function turns out to be complicated and does not bear a closed solution. Subsequently, we propose a novel design based on the successive approximation of the LMMSE estimation distortion. The resulting power allocation algorithm is simple, computationally efficient, and exhibits excellent convergence properties. The proposed designs hold considerable performance gain compared to a uniform power allocation scheme. To the best of our knowledge, in the present literature, there is no such work on the design of power allocation for the sensor network under consideration which jointly exploits spatial correlation, observation noises, channel gains, and their estimation errors.
The rest of the paper is organized as follows. Section 2 describes the system set-up. The power allocation problems and their solutions are presented in Sections 3 and 4, respectively for perfect and imperfect knowledge of the CSI. Section 5 evaluates performance of the power allocation designs. Section 6 concludes the work.
2. System Model
Consider the system model shown in Figure 1 in which  spatially distributed sensors observe an unknown zero-mean real Gaussian random source
spatially distributed sensors observe an unknown zero-mean real Gaussian random source  , and communicate with the fusion center (FC) via orthogonal multiple-access channels. Each sensor has a partial and noisy observation of the source, and sends an amplified version of it to the FC. The FC collects the signals from all sensors and reconstructs the source according to a given fidelity criterion, for example, minimum mean-squared estimation error. The
, and communicate with the fusion center (FC) via orthogonal multiple-access channels. Each sensor has a partial and noisy observation of the source, and sends an amplified version of it to the FC. The FC collects the signals from all sensors and reconstructs the source according to a given fidelity criterion, for example, minimum mean-squared estimation error. The  and
and  respectively, denote the partial observation of the source
respectively, denote the partial observation of the source  and the noise corrupting this observation such that the noisy observation at sensor
and the noise corrupting this observation such that the noisy observation at sensor  is
is

The estimation of the source is done on a sample by sample basis, and its procedure is same for all samples. Therefore, for clarity, in the subsequent formulation we drop the time index. We assume that the sensors amplify and forward their observations to the FC via orthogonal channels where each channel experiences flat fading independent over time and across sensors.
The optimality of the AF scheme is established for the Gaussian network with nonorthogonal multiple-access channel from the sensors to the FC [7]. However, for the network with orthogonal multiple-access channel it has been shown in [19, 20] that the separate source channel coding outperforms the AF scheme. The optimality of the coded source-channel communication in general requires coding over long block lengths and will require some data processing at the sensors. This will increase the power consumption at the sensors and will lead to longer processing delays which may not be tolerable in many applications. Therefore, due to simplicity, low latency, and ease of implementation, in this paper we adopt the AF transmission strategy.
The received signal at FC from sensor  is
is

where  is a amplifying factor and
is a amplifying factor and  is a circularly-symmetric Gaussian receiver noise. The fading channels
is a circularly-symmetric Gaussian receiver noise. The fading channels  between the sensors and the FC are
between the sensors and the FC are  with gain factors
with gain factors  which are Rayleigh distributed. Noting that
which are Rayleigh distributed. Noting that  , we can write (2) as
, we can write (2) as

where the exponential term  can be merged into the variable
can be merged into the variable  without changing its statistical properties—due to the circular-symmetry property of
without changing its statistical properties—due to the circular-symmetry property of  [21]. Since the underlying source
[21]. Since the underlying source  and the noisy observation
and the noisy observation  are real-valued, therefore, we only need to consider the component of the noise
are real-valued, therefore, we only need to consider the component of the noise  which is in-phase with the observation
which is in-phase with the observation  , that is,
, that is,

where  and
and  .
.
For the analysis in this work, we assume that the observation noise  ,
,  (similarly the receiver noise
(similarly the receiver noise  ,
,  ) is independent across the sensors and is also independent of
) is independent across the sensors and is also independent of  ,
,  (
( ). Moreover, we assume that the source
). Moreover, we assume that the source  , the observation
, the observation  at sensor
at sensor  , the observation
, the observation  at sensor
at sensor  , the observation noise
, the observation noise  at the sensor, and the receiver noise
at the sensor, and the receiver noise  at the FC are jointly Gaussian across sensors (
at the FC are jointly Gaussian across sensors ( and
and  ) with zero mean and covariance (
) with zero mean and covariance ( ) specified by
) specified by

We also assume that the samples of  ,
,  ,
,  and
and  are individually independent in time.
are individually independent in time.
In (5), the correlation coefficient  represents the correlation between
represents the correlation between  and
and  and the coefficient
and the coefficient  denotes the correlation between
denotes the correlation between  and
and  . The values of these correlation coefficients depend on the distance of the sensors w.r.t. the position of the source
. The values of these correlation coefficients depend on the distance of the sensors w.r.t. the position of the source  and w.r.t. each other, respectively, and can be characterized as follows:
and w.r.t. each other, respectively, and can be characterized as follows:

which is a power exponential model for correlation [10, 22]. In (6),  is the distance between the source
is the distance between the source  and sensor
and sensor  , and
, and  is the distance between the sensors
is the distance between the sensors  and
and  . The parameter
. The parameter  controls how fast the correlation decays with distance and is called range parameter. The other parameter
controls how fast the correlation decays with distance and is called range parameter. The other parameter  is called a smoothness or roughness parameter which is
is called a smoothness or roughness parameter which is  . Equation (6) shows that the correlation decays with distance with limiting values of 1 and 0 as
. Equation (6) shows that the correlation decays with distance with limiting values of 1 and 0 as  and
and  respectively. Therefore, the correlation changes with the change in the elative positions of the source and the sensors. The change may happen due to movement of either the sensors or the source or both, for example, an animal may kick a sensor node to a different location. We assume that the relative positions of the sensors with respect to each other and the underlying source are perfectly known. Moreover, we assume that the positions remain unchanged for at least one estimation cycle.
respectively. Therefore, the correlation changes with the change in the elative positions of the source and the sensors. The change may happen due to movement of either the sensors or the source or both, for example, an animal may kick a sensor node to a different location. We assume that the relative positions of the sensors with respect to each other and the underlying source are perfectly known. Moreover, we assume that the positions remain unchanged for at least one estimation cycle.
Based on the correlation model, therefore, we can say that the FC in essence is interested to reconstruct the source  which is located at a specific location by collecting observations from spatially distributed sensors where correlation of the observations with the source and among the sensors, respectively, depends on the spatial location of the sensors w.r.t. the source and w.r.t. each other. Note that the location of the source and the sensors can be in two or three dimensional space.
which is located at a specific location by collecting observations from spatially distributed sensors where correlation of the observations with the source and among the sensors, respectively, depends on the spatial location of the sensors w.r.t. the source and w.r.t. each other. Note that the location of the source and the sensors can be in two or three dimensional space.
The equation (4) can be written equivalently in matrix-vector notation as follows:

where  denotes the matrix-vector transpose operation. At the FC, the optimal estimator in minimum mean-squared error (MMSE) sense is the conditional mean of
denotes the matrix-vector transpose operation. At the FC, the optimal estimator in minimum mean-squared error (MMSE) sense is the conditional mean of  given the observation
given the observation  , that is,
, that is,  , where
, where  denotes the mathematical expectation. Under the jointly Gaussian assumption of the
denotes the mathematical expectation. Under the jointly Gaussian assumption of the  and
and  , the conditional mean estimator turns out to be linear and is called linear minimum mean-squared error estimator (LMMSEE). Therefore, we seek the estimate of the source like
, the conditional mean estimator turns out to be linear and is called linear minimum mean-squared error estimator (LMMSEE). Therefore, we seek the estimate of the source like  which can be written as [23]
which can be written as [23]

where  is a row-vector of LMMSEE weighting coefficients. The resultant distortion of the estimate
is a row-vector of LMMSEE weighting coefficients. The resultant distortion of the estimate  in comparison to the original signal
in comparison to the original signal  is measured by the mean-squared error and is given by [23]
is measured by the mean-squared error and is given by [23]

where  ,
,  ,
,  ,
,  and
and  . The estimation distortion
. The estimation distortion  can also be written as follows:
can also be written as follows:

which is obtained by using the Woodbury identity for matrix inversion [24] (see Appendix A). Let  , where
, where  . Now we can write (10) as
. Now we can write (10) as

Theorem 1.
The estimation distortion function in (11) is convex over  for
for  .
.
Let  be a vector of the transmit power of the sensors. The proof of the theorem consists in showing that the Hessian of the distortion function in (11) with respect to
be a vector of the transmit power of the sensors. The proof of the theorem consists in showing that the Hessian of the distortion function in (11) with respect to  is positive semidefinite. To this end, a detailed proof is given in Appendix B.
is positive semidefinite. To this end, a detailed proof is given in Appendix B.
Remark 1.
The reconstruction distortion is upper bounded by the variance of the source  , and lower bounded by the variances of the observation noises and spatial correlation and cross-correlation values as given by
, and lower bounded by the variances of the observation noises and spatial correlation and cross-correlation values as given by

The lower-bound distortion is achieved when the observations of the sensors are received at the FC via ideal communication channels which can be verified by setting  ,
,  in (11). Note that it is not possible to achieve distortion less than
in (11). Note that it is not possible to achieve distortion less than  . Moreover, when observation noise variances are
. Moreover, when observation noise variances are  then the lower bound distortion reduces to
then the lower bound distortion reduces to  . The achieved distortion is equal to the upper bound value (i.e.,
. The achieved distortion is equal to the upper bound value (i.e.,  ) when either no signal is received at the FC from the sensors or the observations are uncorrelated with the source
) when either no signal is received at the FC from the sensors or the observations are uncorrelated with the source  or both, which can be verified from (11).
or both, which can be verified from (11).
3. Power Allocation with Perfect CSI
In this section, we assume that the channel state information (CSI), that is, the channel gains  are perfectly known at the FC. The case of imperfect CSI is considered in the next section.
are perfectly known at the FC. The case of imperfect CSI is considered in the next section.
3.1. Minimization of the Distortion Subject to the Power Constraint
We base our adaptive power allocation design on the following optimization problem.
Prob
Minimize the distortion
 subject to
subject to

where denotes the total power in the transmitted signal of sensor
denotes the total power in the transmitted signal of sensor  . The sum power constraint in (13) enables a fair comparison between the networks of different sizes. Moreover, for a sensor network which forms part of a bigger network where each subnetwork performs different sensing task but share the same frequency band to transmit observations, to limit the interference between the subnetworks, the total power emitted from each subnetwork is upper bounded. Furthermore, recent studies have shown that the ICT (Information and Communication Technology) power consumption is a significant contributor to the global warming [25]. Therefore, in the context of sensor networks, putting cap on the total power consumption conserves energy and limits the contribution to the global warming.
. The sum power constraint in (13) enables a fair comparison between the networks of different sizes. Moreover, for a sensor network which forms part of a bigger network where each subnetwork performs different sensing task but share the same frequency band to transmit observations, to limit the interference between the subnetworks, the total power emitted from each subnetwork is upper bounded. Furthermore, recent studies have shown that the ICT (Information and Communication Technology) power consumption is a significant contributor to the global warming [25]. Therefore, in the context of sensor networks, putting cap on the total power consumption conserves energy and limits the contribution to the global warming.
Since the optimization problem in (13) is convex (the objective is convex and the constraints are linear), therefore we can use the Lagrangian method of multipliers to find the optimal  's [26]. The Lagrangian cost function is
's [26]. The Lagrangian cost function is

where  and
and  are dual variables or Lagrange multipliers. The associated Karush-Kuhn-Tucker (KKT) conditions are
are dual variables or Lagrange multipliers. The associated Karush-Kuhn-Tucker (KKT) conditions are



where  is a diagonal matrix with unity at
is a diagonal matrix with unity at  place and all other elements are equal to zero.
place and all other elements are equal to zero.
The expression in (15) is a complicated function of the optimization variables. Therefore, a closed form solution for this problem is not tractable. However, we can resort to numerical methods (e.g., bisectional search over  's in (15) and gradient method to update
's in (15) and gradient method to update  ) to find the optimal
) to find the optimal  in an iterative manner as outlined under Algorithm 1. From (17), note that the active sensors
in an iterative manner as outlined under Algorithm 1. From (17), note that the active sensors  have corresponding Lagrangian multipliers
have corresponding Lagrangian multipliers  . The sensors with
. The sensors with  are removed from the system. The parameter
are removed from the system. The parameter  in * denotes the step-size. Since the objective function of the optimization problem is convex and bounded and the constraints are linear, therefore the algorithm can achieve convergence to the absolute minimum (the KKT point) of the problem provided the step-size
in * denotes the step-size. Since the objective function of the optimization problem is convex and bounded and the constraints are linear, therefore the algorithm can achieve convergence to the absolute minimum (the KKT point) of the problem provided the step-size  is selected properly [27]. Unfortunately, Algorithm 1 will be computationally quite expensive (unless the network size is small) due to
is selected properly [27]. Unfortunately, Algorithm 1 will be computationally quite expensive (unless the network size is small) due to
-
(i)
a number of matrix inversions involved in (15) while numerically searching for
 in each iteration;
in each iteration; -
(ii)
the dependence of the convergence properties on the step-size
 [27, 28].
[27, 28].
Algorithm 1:
1: Initialize  and
and  for
for 
2: Set 
3: While  where
where  denotes the
denotes the
while loop iteration index
4: 
5: Find  ,
,  , by numerically solving (15),
, by numerically solving (15),
for example, using bisectional search method
6: Update  using gradient method as follows:
using gradient method as follows:
 *
*
7: Calculate 
8: end while
In the sequel, based on a successive approximation (SA) principle, we present a novel quasianalytical solution of the optimization problem which is simple and the associated algorithm is computationally efficient compared to Algorithm 1, exhibits remarkable convergence properties, and achieves distortion very close to the global optimum of the Algorithm 1 with no appreciable performance gap. This so-called SA-based design can be viewed as the joint optimization of the transmit powers and the modified LMMSE coefficients as we will see in the subsequent development.
According to the idea of successive approximation, a modified function is constructed from the given function in some special way [29–31]. Then that modified function is solved iteratively/successively to find the solution for the underlying problem. The solution obtained by the SA approach can be viewed as quasianalytical solution. We apply the idea of successive approximation to the reconstruction distortion function and solve the problem of power allocation in the sensor network. To this end, at the FC, to form the estimate  of the source
of the source  and to characterize the resultant mean-squared distortion
and to characterize the resultant mean-squared distortion  , we proceed as follows. We can write the distortion
, we proceed as follows. We can write the distortion  as
as

and by solving  we get the following expression for the LMMSE weighting coefficients:
we get the following expression for the LMMSE weighting coefficients:

The variables  and
and  are, respectively, defined as follows:
are, respectively, defined as follows:


where  . With (20) and (21), the distortion in (18) simplifies to
. With (20) and (21), the distortion in (18) simplifies to

Equation (21) forms a set of  coupled equations which constitute the Wiener-Hopf equation for the LMMSE filter coefficients (
coupled equations which constitute the Wiener-Hopf equation for the LMMSE filter coefficients ( ,
,  ). If we know the transmit powers
). If we know the transmit powers  then for given covariance
then for given covariance  and the channel gains
and the channel gains  , we can find the coefficients
, we can find the coefficients  by solving (21). For the solution, it is convenient to employ the matrix-vector form as follows:
by solving (21). For the solution, it is convenient to employ the matrix-vector form as follows:

where  ,
,  ,
,  for
for  and
and  for
for  . Note that
. Note that  denotes the
denotes the  element of the matrix
element of the matrix  . However, the point here is that we do not know the transmit powers
. However, the point here is that we do not know the transmit powers  . The following subsection presents an alternative solution to the problem of optimizing the transmit powers of the sensors under the network-wide power constraint such that the distortion
. The following subsection presents an alternative solution to the problem of optimizing the transmit powers of the sensors under the network-wide power constraint such that the distortion  be minimized. Therein, to derive an algorithm for the solution of
be minimized. Therein, to derive an algorithm for the solution of  , the underlying idea is to assume
, the underlying idea is to assume  as constant. Based on this assumption, we derive an iterative algorithm which computes
as constant. Based on this assumption, we derive an iterative algorithm which computes  using the values of
using the values of  from the previous iteration. This successive approximation (SA) of the distortion function in (22) makes the solution of the power allocation problem simple and easy to compute as will be seen in the ensuing development. Note that the resulting design for power allocation can be viewed as a joint optimization of
from the previous iteration. This successive approximation (SA) of the distortion function in (22) makes the solution of the power allocation problem simple and easy to compute as will be seen in the ensuing development. Note that the resulting design for power allocation can be viewed as a joint optimization of  and
and  .
.
3.2. Minimization of the Distortion Subject to the Power Constraint-SA
Herein, we solve the optimization problem in (13) based on the distortion function  in (22) and using the successive-approximation principle outlined in the preceding subsection. For given
in (22) and using the successive-approximation principle outlined in the preceding subsection. For given  , it is easy to verify that the distortion function is convex with respect to the optimization variables
, it is easy to verify that the distortion function is convex with respect to the optimization variables  . Therefore, the KKT conditions are sufficient for optimality [26] which are given as follows:
. Therefore, the KKT conditions are sufficient for optimality [26] which are given as follows:



Solving (24) for active sensor  (i.e.,
(i.e.,  ,
,  from (26)), we get
from (26)), we get

for  , where
, where  denotes the channel SNR for sensor
denotes the channel SNR for sensor  and
and  . Based on (27), following observations are in order.
. Based on (27), following observations are in order.
-
(1)
There exists a cut-off value
 such that for
such that for 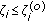 , the power allocation policy follows waterfilling on channel SNR, that is,
, the power allocation policy follows waterfilling on channel SNR, that is, 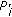 increases with increasing
increases with increasing  ; and for
; and for 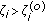 , the power allocation is according to inversion in the channel SNR, that is, increasing
, the power allocation is according to inversion in the channel SNR, that is, increasing  decreases
decreases 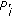 .
. -
(2)
The sensors with higher observation noise variances are given less power. For sensor
 , in the limiting case
, in the limiting case  (i.e.,
(i.e.,  ) then
) then 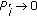 .
. -
(3)
The sensors with weak correlation with the source are allotted less power. For instance, if
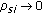 then
then 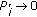 .
.
Combining the aforementioned points we can see that the final power allocation policy for the sensors depends on the spatial correlations, variance of the observation noises, and the channel SNRs. Moreover, we see that depending on the values of these system parameters some of the sensors may be switched-off altogether. For sensor  to be active, following condition must hold:
to be active, following condition must hold:

which stems from the fact that  if sensor
if sensor  is active. Let
is active. Let  denotes the set of active sensors defined as follows:
denotes the set of active sensors defined as follows:

Since the problem is convex, the minimum of the objective function occurs at the sum power constraint boundary, that is, the constraint is active. Therefore, the transmit powers  must satisfy the power constraint with equality, that is,
must satisfy the power constraint with equality, that is,  , which gives
, which gives

Based on the solution from (27) through (30), Algorithm 2 can be proposed which iteratively optimizes the transmit powers  and the variables
and the variables  , while minimizing the reconstruction distortion subject to the power constraint. If during iterations any sensor does not fulfill the condition in (28), it is switched off and the algorithm continues with the remaining sensors until the convergence criterion is fulfilled. Regarding the convergence properties of the algorithm, consider the following.
, while minimizing the reconstruction distortion subject to the power constraint. If during iterations any sensor does not fulfill the condition in (28), it is switched off and the algorithm continues with the remaining sensors until the convergence criterion is fulfilled. Regarding the convergence properties of the algorithm, consider the following.
-
(i)
Since in each iteration (successive approximation) we are minimizing a convex function over the convex-set of the transmit powers
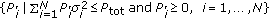 , therefore the optimality of the transmit powers
, therefore the optimality of the transmit powers 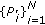 in each approximation (for given
in each approximation (for given 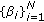 ) combined with the optimality of
) combined with the optimality of 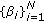 for given
for given 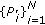 as per (23) means that the algorithm achieves monotonic decrease in the distortion, that is,
as per (23) means that the algorithm achieves monotonic decrease in the distortion, that is,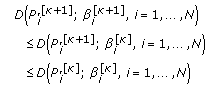 (31)
(31)and consequently it does converge to a unique minimum point.
-
(ii)
The algorithm consistently arrives at the same combination of the transmit power tuple
 and achieves the same minimum distortion for a wide range of different initialization points. In other words, we can say that the algorithm exhibits start point independence (for a wide range of initialization points). Moreover, the algorithm asymptotically achieves the lower-bound distortion
and achieves the same minimum distortion for a wide range of different initialization points. In other words, we can say that the algorithm exhibits start point independence (for a wide range of initialization points). Moreover, the algorithm asymptotically achieves the lower-bound distortion 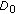 with increasing transmit power
with increasing transmit power 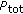 . In Section 5, we illustrate the monotonic decrease, start point insensitivity, and the asymptotic convergence to
. In Section 5, we illustrate the monotonic decrease, start point insensitivity, and the asymptotic convergence to 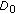 with several simulation examples. There we also show that the convergence may be achieved in as few as two or three iterations.
with several simulation examples. There we also show that the convergence may be achieved in as few as two or three iterations. -
(iii)
We have shown that the original problem is convex and therefore the objective function has a global minima under the power constraint which can be achieved by Algorithm 1. Now the question is how closely does the successive approximation-based algorithm converge to the global minimum value? The simulation examples in Section 5 show that the distortion achieved by both algorithms are extremely close and the performance gap between the full-optimization and the successive approximation based algorithms is virtually negligible.
Algorithm 2:
1: Initialize  for
for 
2: Calculate  for
for 
3: Set 
4:while do
do where
where  denotes the
denotes the
while loop iteration index
5: 
6: For  determine transmit power as follows:
determine transmit power as follows:
7: if Condition in (28) is true then
8: Determine  from (27)
from (27)
9: else
10: 
11: end if
12: For  update
update  from (23)
from (23)
13: Calculate 
14: end while
It is a quite remarkable that the algorithm exhibits such excellent convergence properties which illustrates that the proposed successive approximation strategy works quite well. Finally, compared to the power allocation Algorithm 1, the ease of computation and simplicity of the design based on the successive approximation principle can be appreciated from the simple and elegant structure of (27)–(30).
4. Power Allocation with Imperfect CSI
Heretofore, we have assumed perfect knowledge of the channel gains  . However, in practice, we have estimates
. However, in practice, we have estimates  of the actual channel gains. One way to estimate the channel is by a training sequence whereby each sensor transmits a known sequence of data symbols called pilots. Then based on the received data, the FC estimates the channel. Let
of the actual channel gains. One way to estimate the channel is by a training sequence whereby each sensor transmits a known sequence of data symbols called pilots. Then based on the received data, the FC estimates the channel. Let  denote the pilot symbol transmitted by sensor
denote the pilot symbol transmitted by sensor  in the channel estimation phase. The corresponding received signal is
in the channel estimation phase. The corresponding received signal is  and based on which the LMMSE estimate
and based on which the LMMSE estimate  of
of  is
is

where  denotes the complex conjugate operation. The variance of the estimation error
denotes the complex conjugate operation. The variance of the estimation error  is
is

wherein  is power of the transmitted pilot. Note that the variance of channel estimation error is finite for finite
is power of the transmitted pilot. Note that the variance of channel estimation error is finite for finite  and
and  . The actual channel can be represented as a sum of the estimate and the estimation error, that is,
. The actual channel can be represented as a sum of the estimate and the estimation error, that is,

where  . Such an approach to model the channel estimation error can be viewed as the Bayesian approach [6].
. Such an approach to model the channel estimation error can be viewed as the Bayesian approach [6].
One way to design the power-scheduling scheme is by replacing  and
and  respectively, by
respectively, by  and
and  in the formulations of the foregoing section. This constitutes a naive-approach because it ignores the error in the channel estimate. An alternative design originates by substituting (34) in (2) as follows:
in the formulations of the foregoing section. This constitutes a naive-approach because it ignores the error in the channel estimate. An alternative design originates by substituting (34) in (2) as follows:

in which  can be viewed as total receiver noise corresponding to sensor
can be viewed as total receiver noise corresponding to sensor  with
with  ,
,  ,
,  and
and  ,
,  . Noting that
. Noting that  , we can write
, we can write

where the exponential term  can be absorbed into
can be absorbed into  , that is, into the Gaussian variables
, that is, into the Gaussian variables  and
and  without changing their statistical properties—thanks to their circular symmetry. Since the underlying source
without changing their statistical properties—thanks to their circular symmetry. Since the underlying source  and the observation
and the observation  are real-valued, as a consequence only the part of the noise
are real-valued, as a consequence only the part of the noise  in-phase with the sensor observation is relevant for estimation of the source
in-phase with the sensor observation is relevant for estimation of the source  . Therefore, we can write
. Therefore, we can write

where  ,
,  and
and  . Following a procedure similar to Section 3, it can be shown that the mean-squared reconstruction distortion of the estimate
. Following a procedure similar to Section 3, it can be shown that the mean-squared reconstruction distortion of the estimate  with respect to
with respect to  is given by
is given by

where

The solution of the optimization problem in (13) with the objective to minimize the distortion  defined in (38) subject to the constraint on the total network power can be obtained by using the method of Lagrangian multipliers and is outlined as follows.
defined in (38) subject to the constraint on the total network power can be obtained by using the method of Lagrangian multipliers and is outlined as follows.

-
(1)
The power allotted to sensor
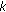 is for
is for 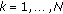 , where
, where 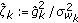 defines the channel SNR based on the channel estimate.
defines the channel SNR based on the channel estimate. -
(2)
For sensor
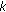 to be active, that is,
to be active, that is, 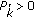 , the following condition:
, the following condition: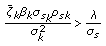 (41)
(41)must hold, otherwise it is switched-off.
-
(3)
The index-set
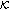 of the active sensors is
of the active sensors is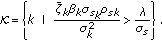 (42)
(42) -
(4)
The Lagrangian multiplier
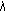 is
is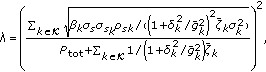 (43)
(43)
which is determined such that the power constraint be satisfied with equality.
Based on (40)–(43), the power allocation for the sensors can be obtained using the procedure outlined under Algorithm 2. (The power allocation design under Algorithm 1 can similarly be extended to the imperfect CSI case.) Note that the convergence properties of the algorithm with perfect CSI also applies to the imperfect CSI case. Moreover, the above power allocation design exhibits robustness to the channel estimation errors compared to the naive approach as shown in the subsequent section.
Remark 2.
We can observe that as
 then
then
 for
for
 and ( 40 )–( 43 ), respectively, converges to the power allocation design with perfect CSI in ( 27 )–( 30 ).
and ( 40 )–( 43 ), respectively, converges to the power allocation design with perfect CSI in ( 27 )–( 30 ).
5. Performance Evaluation and Discussion
Through simulation examples, this section corroborates the analytical findings and illustrates the effectiveness of the proposed adaptive power allocation (APA) designs under Algorithms 1 and 2 for the perfect and imperfect CSI cases. We assume without any loss of generality that  . In the simulations, the distortion is calculated from
. In the simulations, the distortion is calculated from  realizations of the underlying source, partial observations, and observation and receiver noises according to the covariance
realizations of the underlying source, partial observations, and observation and receiver noises according to the covariance  . The simulation examples focus on the successive approximation-based power allocation design unless stated otherwise. In the figures,
. The simulation examples focus on the successive approximation-based power allocation design unless stated otherwise. In the figures,  denotes the logarithm with base 10.
denotes the logarithm with base 10.
5.1. Spatial Correlation
In order to show the efficacy of our design, we compare its performance with a uniform power allocation-based design. In the figures, the designs are, respectively, denoted as APA (Adaptive Power Allocation) and UPA (Uniform Power Allocation). Moreover,  for the UPA design.
for the UPA design.
We consider two sensor networks, respectively, comprising  and
and  sensors which are uniformly distributed in a
sensors which are uniformly distributed in a  grid with the source
grid with the source  at its center. Figure 2 plots the distortion achieved by the SA-based APA design and compares it with the UPA design. The distortion is averaged over
at its center. Figure 2 plots the distortion achieved by the SA-based APA design and compares it with the UPA design. The distortion is averaged over  independent realizations (drawn from a uniform distribution) of the sensors deployment. The figure shows that our proposed design outperforms the UPA scheme and the achieved distortion monotonically approaches the lower-bound distortion value
independent realizations (drawn from a uniform distribution) of the sensors deployment. The figure shows that our proposed design outperforms the UPA scheme and the achieved distortion monotonically approaches the lower-bound distortion value  with increasing
with increasing  . For given
. For given  , we can observe that the distortion decreases with increasing the number of sensors and the performance gap between the APA and UPA designs also increases. Moreover, we can see that increasing the value of
, we can observe that the distortion decreases with increasing the number of sensors and the performance gap between the APA and UPA designs also increases. Moreover, we can see that increasing the value of  decreases the distortion. This is because, for given deployment, the spatial correlation of the sensors with the source (and with each other) improves with increasing
decreases the distortion. This is because, for given deployment, the spatial correlation of the sensors with the source (and with each other) improves with increasing  [c.f. (6)]. Note that at low value of
[c.f. (6)]. Note that at low value of  , the distortion is high and the performance gap between the APA and UPA designs is very small. However, as the value of
, the distortion is high and the performance gap between the APA and UPA designs is very small. However, as the value of  increases the distortion decreases and the performance gap between the APA and UPA increases. However, we can see that with increasing the value of
increases the distortion decreases and the performance gap between the APA and UPA increases. However, we can see that with increasing the value of  further the performance gap starts decreasing. This is because for very small value of
further the performance gap starts decreasing. This is because for very small value of  the sensors have very low correlation with the source and for very large value of
the sensors have very low correlation with the source and for very large value of  the correlation is high for all sensors, and in these extreme cases the UPA scheme is as good as the APA scheme.
the correlation is high for all sensors, and in these extreme cases the UPA scheme is as good as the APA scheme.
Next, for the sake of illustration, we focus on the network with three sensors, that is,  , and we consider the following two examples:
, and we consider the following two examples:
-
(i)
Ex
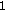 :
: 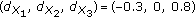 and
and 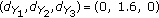 ,
, -
(ii)
Ex
 :
: 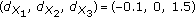 and
and 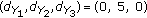 ,
,
where  gives the position of sensor
gives the position of sensor  with respect to the origin in the
with respect to the origin in the  -plane. Note that we can view these examples as specific realizations of the deployment of the sensors. Assuming the source at the origin and for
-plane. Note that we can view these examples as specific realizations of the deployment of the sensors. Assuming the source at the origin and for  in (6), we obtain the following spatial correlation values:
in (6), we obtain the following spatial correlation values:
-
(i)
Ex
 :
:  and
and 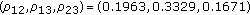 ,
, -
(ii)
Ex
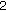 :
: 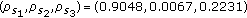 and
and 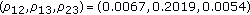 .
.
The simulations in the sequel are based on these two examples. We have taken these examples for purely illustrative purpose and they in no way limit the generality of our designs. For zero-observation noise variances, the spatial correlation lower bounds the reconstruction distortion at  , where first value is for Ex1 and the second value is for Ex2. The distortion in the subsequent simulation examples cannot be below this value no matter how high the transmit power becomes.
, where first value is for Ex1 and the second value is for Ex2. The distortion in the subsequent simulation examples cannot be below this value no matter how high the transmit power becomes.
Figure 3 shows that the proposed design gives reconstruction distortion which is less than that achieved by the uniform power allocation. This superior performance originates from the reason that the proposed design assigns all or more power to the sensor(s) with better correlation properties. This is contrary to the UPA scheme which gives equal importance to all sensors regardless of the correlation structure and thereby wasting power. For both examples, note that the achieved distortion decreases monotonically with increasing  but is never less than the lower-bound value
but is never less than the lower-bound value  .
.
For Ex1 and Ex2, Figure 4 shows that with different initial values of  , Algorithm 2 converges to the same distortion value (0.5817 for Ex1 and 0.2646 for Ex2). Moreover, at the convergence, the power distribution among the sensors is
, Algorithm 2 converges to the same distortion value (0.5817 for Ex1 and 0.2646 for Ex2). Moreover, at the convergence, the power distribution among the sensors is  and
and  respectively, for Ex1 and Ex2 in all cases irrespective of the initialization point of the algorithm. Note that in one iteration the distortion reaches fairly close to the minimum value. Nevertheless, after the second or third iteration there is virtually no appreciable change in these values. This observation extends to all simulation examples presented herein.
respectively, for Ex1 and Ex2 in all cases irrespective of the initialization point of the algorithm. Note that in one iteration the distortion reaches fairly close to the minimum value. Nevertheless, after the second or third iteration there is virtually no appreciable change in these values. This observation extends to all simulation examples presented herein.
Figure 5 compares performance of the proposed APA designs under Algorithms 1 and 2 which shows that the distortion curves produced by the two algorithms are extremely close and the performance gap is negligible. This is quite remarkable result especially when viewed in combination with the simplicity and computational efficiency of Algorithm 2 compared to Algorithm 1.
The simulation examples in the sequel only treat the APA design based on the successive approximation (SA) without including comparison with the APA design under Algorithm 1 and the UPA scheme. Nevertheless, in all the instances, the SA-based design closely achieves the performance of the design in Algorithm 1 and outperforms the UPA scheme except in a symmetric case where both designs (APA and UPA) converge. In the symmetric case, the correlations, variances of the observation and the receiver noises, and the channel gains are same across all sensors.
5.2. Channel SNR
Assuming fixed channel gains (no fading),  and
and  , we consider the following cases:
, we consider the following cases: 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 and
and 
 . Figure 6 shows that for given
. Figure 6 shows that for given  the distortion decreases with increase in the so-called channel SNR and vice versa. Note that in each case the achieved distortion monotonically approaches the lower-bound value (
the distortion decreases with increase in the so-called channel SNR and vice versa. Note that in each case the achieved distortion monotonically approaches the lower-bound value ( ) with increasing
) with increasing  . Figure 6(b) shows how the total power
. Figure 6(b) shows how the total power  is distributed among the sensors in
is distributed among the sensors in  and
and  . The figure shows that in
. The figure shows that in  , the sensors with better correlation properties are given more power, which is due to the fact that, in this case, the system is symmetric with respect to all other system parameters. However, the case
, the sensors with better correlation properties are given more power, which is due to the fact that, in this case, the system is symmetric with respect to all other system parameters. However, the case  is different where the channel SNRs are not same across the sensors. For this case the figure shows that the power allocation policy follows sensor selection and waterfilling with respect to the SNR until the next sensor is turned on, after which point the power allocation is according to the channel inversion. These examples show that the power allocation policy is jointly determined by the spatial correlation values, variance of the observation noises, and the channel SNRs.
is different where the channel SNRs are not same across the sensors. For this case the figure shows that the power allocation policy follows sensor selection and waterfilling with respect to the SNR until the next sensor is turned on, after which point the power allocation is according to the channel inversion. These examples show that the power allocation policy is jointly determined by the spatial correlation values, variance of the observation noises, and the channel SNRs.
5.3. Observation Noise
Herein, we assume that  ,
,  and consider the following cases:
and consider the following cases: 
 and
and  ,
, 
 and
and  ,
, 
 and
and  ,
, 
 and
and  . Figure 7 shows that increasing the variances of the observation noise at the sensors, increases the reconstruction distortion. Moreover, in each case, the achieved distortion
. Figure 7 shows that increasing the variances of the observation noise at the sensors, increases the reconstruction distortion. Moreover, in each case, the achieved distortion  decreases monotonically with the transmit power
decreases monotonically with the transmit power  and approaches
and approaches  at high transmit power.
at high transmit power.
5.4. Imperfect CSI
We assume that the communication channels  from the sensors to the FC undergo independent Rayleigh fading such that
from the sensors to the FC undergo independent Rayleigh fading such that  . Moreover, we assume that
. Moreover, we assume that  and
and  . The simulations in Figure 8 illustrate the achieved distortion when we have (i) perfect knowledge of the CSI, that is,
. The simulations in Figure 8 illustrate the achieved distortion when we have (i) perfect knowledge of the CSI, that is,  and (ii) the estimates of the channels with estimation error variances
and (ii) the estimates of the channels with estimation error variances  and
and  . The distortion is averaged over
. The distortion is averaged over  realizations of the source and the corresponding partial observations, the observation and receiver noises, and the channel gains. From the figure we can see that the channel errors increase the reconstruction distortion. Moreover, the proposed design (Rob in the figure) shows robustness to the channel estimation errors compared to the naive approach (Nav in the figure).
realizations of the source and the corresponding partial observations, the observation and receiver noises, and the channel gains. From the figure we can see that the channel errors increase the reconstruction distortion. Moreover, the proposed design (Rob in the figure) shows robustness to the channel estimation errors compared to the naive approach (Nav in the figure).
6. Conclusions
In this paper we have investigated the joint adaptive power allocation design for the sensors to transmit their observations to the FC with the goal to reconstruct the underlying source with minimum distortion subject to a constraint on the total network power. We demonstrated the effectiveness of our proposed design with a few simple examples where we vary one parameter while keeping all others the same across sensors. In practice, the correlation, observation noises, and the SNRs of the communication channels may simultaneously vary across sensors. Consequently, the power allocation policy is a nontrivial function of all these factors. Our proposed design incorporates them in (quasi)analytical expressions. We showed that the power allocation problem is convex which does not bear closed-form analytical solution. We showed that the problem can be solved by an iterative numerical procedure which is computationally expensive unless the network size is small. Then, based on the successive approximation principle, we proposed a novel power allocation design which is simple and easy to compute, and exhibits excellent convergence properties. We demonstrated that our proposed design outperforms a scheme based on the uniform power allocation except in a symmetric case where both designs converge. The performance gain may be large for a relatively large sensor network with high heterogeneity in the spatial correlation, observation quality, and the channel gains. In the proposed design, we also incorporated the case when imperfect knowledge of the channel gains is available. We demonstrated that the proposed design exhibits robustness to the channel estimation errors relative to a naive approach. The future work may consider the extension to the nonorthogonal channels from the sensors to the FC. Moreover, optimizing the performance such as reconstruction distortion or the power consumption over a priori given network life can be investigated. We only considered the power required for transmitting the observations to the FC, where as the future work may also include the power consumed in the sensing, preparing the observation for transmission and in the receiving processes.
Appendices
A. Proof of Reconstruction Distortion in (10)
From (9), we can write

Let  (where
(where  denotes identity matrix),
denotes identity matrix),  ,
,  and
and  then the Woodbury identity [24]
then the Woodbury identity [24]

gives

which after substitution in (A.1) gives (10).
B. Proof of Theorem 1
The vector of the transmit powers is  and we know that the estimation distortion is given by
and we know that the estimation distortion is given by

which can be written as

where  and
and  denotes the trace of matrix
denotes the trace of matrix  . In moving from (B.4) to (B.5) we have used the invariance property of Tr under cyclic permutations, that is
. In moving from (B.4) to (B.5) we have used the invariance property of Tr under cyclic permutations, that is  [24].
[24].
In order to prove that the function  is convex over
is convex over  , we derive its Hessian and then show that it is positive semidefinite. To this end, first we calculate the first-order derivative of
, we derive its Hessian and then show that it is positive semidefinite. To this end, first we calculate the first-order derivative of  with respect to each component of
with respect to each component of  , that is,
, that is,  for
for  as follows:
as follows:

In (B.6), we have used  where
where  with
with  for
for  and
and  for
for  [24].
[24].
Now we take the derivative of (B.6) with respect to  for
for  as follows:
as follows:

where we have used  and
and  . Now let
. Now let  and
and  then the Hessian of
then the Hessian of  can be written in the following form:
can be written in the following form:

where  denotes the Hadamard or Schur product of
denotes the Hadamard or Schur product of  and
and  . Note that
. Note that  ,
,  ,
,  and
and  are positive semidefinite matrices. We know that the product of the positive semidefinite matrices is also a positive semidefinite matrix and the Hadamard product of positive semidefinite matrices is also a positive semidefinite matrix. Therefore, we can conclude that the Hessian
are positive semidefinite matrices. We know that the product of the positive semidefinite matrices is also a positive semidefinite matrix and the Hadamard product of positive semidefinite matrices is also a positive semidefinite matrix. Therefore, we can conclude that the Hessian  is also positive semidefinite which establish, the convexity of the function in (11) with respect to the transmit powers
is also positive semidefinite which establish, the convexity of the function in (11) with respect to the transmit powers  .
.
References
Akyildiz IF, Su W, Sankarasubramaniam Y, Cayirci E: Wireless sensor networks: a survey. Computer Networks 2002, 38(4):393-422. 10.1016/S1389-1286(01)00302-4
Akyildiz IF, Pompili D, Melodia T: Underwater acoustic sensor networks: research challenges. Elsevier Journal on Ad Hoc Networks 2005, 3(3):257-279. 10.1016/j.adhoc.2005.01.004
Berger T, Zhang Z, Viswanathan H: The CEO problem. IEEE Transactions on Information Theory 1996, 42(5):887-902.
Viswanathan H, Berger T: The quadratic Gaussian CEO problem. IEEE Transactions on Information Theory 1997, 43(5):1549-1559. 10.1109/18.623151
Duplicy J, Vandendorpe L: Robust MMSE precoding for the MIMO compex Gaussian broadcast channel. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '07), April 2007, Honolulu, Hawaii, USA 421-424.
Palomar DP: A unified framework for communications through MIMO channels, PhD Dissertation. Universitat Politechnica de Catalunya, Spain; May 2003.
Gastpar M: Uncoded transmission is exactly optimal for a simple Gaussian sensor network. IEEE Transactions on Information 2008., 54(11):
Gastpar M, Vetterli M, Dragotti PL: Sensing reality and communicating bits: a dangerous liaison. IEEE Signal Processing Magazine 2006, 23(4):70-83.
Dragotti PL, Gastpar M: Distributed Source Coding: Theory, Algorithms and Applications. Elsevier, Amsterdam, The Netherlands; 2009.
Vuran MC, Akan OB, Akylidiz IF: Spatio-temporal correlation: theory and applications for wireless sensor networks. Elsevier Journal on Computer Networks 2004, 45(3):245-259. 10.1016/j.comnet.2004.03.007
Davoli F, Marchese M, Mongelli M: A decision theoretic approach to Gaussian sensor networks. Proceedings of the IEEE International Conference on Communications (ICC '09), June 2009, Genova, Italy
Bahceci I, Khandani AK: Linear estimation of correlated data in wireless sensor networks with optimum power allocation and analog modulation. IEEE Transactions on Communications 2008, 56(7):1146-1156.
Wimalajeewa T, Jayaweera SK: Optimal power scheduling for correlated data fusion in wireless sensor networks via constraint PSO. IEEE Transaction on Wireless Communications 2008, 7(9):3608-3618.
Xiao J-J, Luo Z-Q, Cui S, Goldsmith AJ: Power-efficient analog forwarding transmission in an inhomogeneous gaussian sensor network. Proceedings of the 6th IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '05), June 2005, Minneapolis, Minn, USA 121-125.
Cui S, Xiao J-J, Goldsmith AJ, Luo Z-Q, Poor HV: Estimation diversity and energy efficiency in distributed sensing. IEEE Transactions on Signal Processing 2007, 55(9):4683-4695.
Senol H, Tepedelenlioglu C: Performance of distributed estimation over unknown parallel fading channels. IEEE Transactions on Signal Processing 2008, 56(12):6057-6068.
Bai K, Tepedelenlioǧlu C, Şenol H: Outage diversity for distributed estimation over parallel fading channels. Proceedings of the 42nd Asilomar Conference on Signals, Systems and Computers, October 2008 863-867.
Thatte G, Mitra U: Sensor selection and power allocation for distributed estimation in sensor networks: beyond the star topology. IEEE Transactions on Signal Processing 2008, 56(7):2649-2661.
Xiao J-J, Luo Z-Q: Multiterminal source-channel communication over an orthogonal multiple-access channel. IEEE Transactions on Information Theory 2007, 53(9):3255-3264.
Behroozi H, Soleymani MR: Source-channel communication in one-helper problem. Proceedings of the 64th IEEE Vehicular Technology Conference (VTC '06), September 2006, Quebec, Canada 1748-1752.
Tse D, Viswanath P: Fundamentals of Wireless Communication. Cambridge University Press, Cambridge, UK; 2005.
Berger JO, Oliveira VD, Sansó B: Objective bayesian analysis of spatially correlated data. Journal of the American Statistical Association 2001, 96(456):1361-1374. 10.1198/016214501753382282
Kay SM: Fundamentals of Statistical Signal Processing:Estimation Theory. Prentice-Hall, Upper Saddle River, NJ, USA; 1993.
Petersen KB, Pedersen MS: The Matrix Cookbook. Technical University of Denmark; 2008.
Special theme: towards green ICT ERCIM News October 2009., (79):
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, UK; 2008.
Bertsekas DP: Nonlinear Programming. 2nd edition. Athena Scientific, Belmont, Mass, USA; 1999.
Palomar DP, Chiang M: A tutorial on decomposition methods for network utility maximization. IEEE Journal on Selected Areas in Communications 2006, 24(8):1439-1451.
Barthelemy J-FM, Haftka RT: Approximation concepts for optimum structural design—a review. Springer Journal on Structural and Multidisciplinary Optimization 1993, 5(3):129-144.
Bertsekas DP, Tsitsiklis JN: Parallel and Distributed Computation: Numerical Methods. Athena Scientific, Belmont, Mass, USA; 1997.
Rontó M: Numerical-analytic successive approximation method for non-linear boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 1997, 30(5):3179-3188. 10.1016/S0362-546X(96)00355-0
Acknowledgments
The authors would like to thank the Walloon Region Ministry DGTRE framework program COSMOS/TSARINE and EU project FP7 NEWCOM++ for the financial support and the scientific inspiration.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chaudhary, M., Vandendorpe, L. Adaptive Power Allocation in Wireless Sensor Networks with Spatially Correlated Data and Analog Modulation: Perfect and Imperfect CSI. J Wireless Com Network 2010, 817961 (2010). https://doi.org/10.1155/2010/817961
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/817961

 in each iteration;
in each iteration; [
[ such that for
such that for 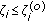 , the power allocation policy follows waterfilling on channel SNR, that is,
, the power allocation policy follows waterfilling on channel SNR, that is, 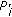 increases with increasing
increases with increasing  ; and for
; and for 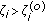 , the power allocation is according to inversion in the channel SNR, that is, increasing
, the power allocation is according to inversion in the channel SNR, that is, increasing  decreases
decreases 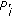 .
. , in the limiting case
, in the limiting case  (i.e.,
(i.e.,  ) then
) then 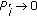 .
.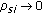 then
then 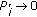 .
.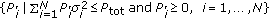 , therefore the optimality of the transmit powers
, therefore the optimality of the transmit powers 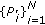 in each approximation (for given
in each approximation (for given 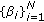 ) combined with the optimality of
) combined with the optimality of 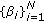 for given
for given 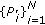 as per (23) means that the algorithm achieves monotonic decrease in the distortion, that is,
as per (23) means that the algorithm achieves monotonic decrease in the distortion, that is,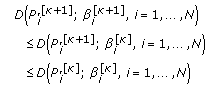
 and achieves the same minimum distortion for a wide range of different initialization points. In other words, we can say that the algorithm exhibits start point independence (for a wide range of initialization points). Moreover, the algorithm asymptotically achieves the lower-bound distortion
and achieves the same minimum distortion for a wide range of different initialization points. In other words, we can say that the algorithm exhibits start point independence (for a wide range of initialization points). Moreover, the algorithm asymptotically achieves the lower-bound distortion 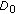 with increasing transmit power
with increasing transmit power 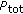 . In Section 5, we illustrate the monotonic decrease, start point insensitivity, and the asymptotic convergence to
. In Section 5, we illustrate the monotonic decrease, start point insensitivity, and the asymptotic convergence to 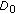 with several simulation examples. There we also show that the convergence may be achieved in as few as two or three iterations.
with several simulation examples. There we also show that the convergence may be achieved in as few as two or three iterations.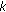 is for
is for 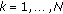 , where
, where 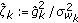 defines the channel SNR based on the channel estimate.
defines the channel SNR based on the channel estimate.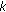 to be active, that is,
to be active, that is, 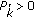 , the following condition:
, the following condition: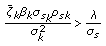
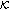 of the active sensors is
of the active sensors is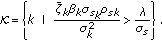
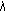 is
is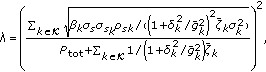

 ,
,  and
and 
 ,
, 
 ,
, 
 and
and 
 .
. sensors
sensors sensors
sensors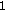 :
: 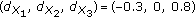 and
and 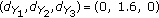 ,
, :
: 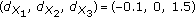 and
and 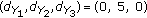 ,
, :
:  and
and 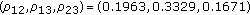 ,
, :
: 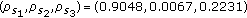 and
and 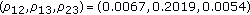 .
.
 Reconstruction distortionPower allocation
Reconstruction distortionPower allocation

 . Ex1:
. Ex1:  Ex2:
Ex2: 



