- Research Article
- Open access
- Published:
A Precoded OFDMA System with User Cooperation
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 843745 (2010)
Abstract
A new cooperative scheme for a two-user orthogonal frequency division multiple access (OFDMA) uplink communication scenario is proposed. Each user is equipped with one transmit/receive antenna. Before transmission, inter-block linear precoding is introduced to pairs of blocks. The cooperative transmission is implemented in cycles of three time slots. During each slot, a user transmits either his data, or a weighted mixture of his data and the data that he received in previous slots of the same cycle. The weights are obtained in an optimum fashion, so that a user that faces deep fading on certain subcarriers can benefit from the other user's channel, without taxing significantly the resources of that user. It is shown that the proposed scheme achieves the maximum available diversity for both users (full cooperation), or for the weak user (half cooperation) without increasing the number of antennas needed as compared to an energy-equivalent noncooperative OFDMA system that also uses inter-block precoding. Further, the proposed use of inter-block precoding allows one to exploit the cooperation induced diversity in 1.5 slots on the average; 2 slots would be needed if intra-block precoding was used instead.
1. Introduction
Multiuser Cooperation is a promising technology for improving the performance of wireless communication systems, as it has the potential to increase the data rate [1, 2], and achieve diversity order equal to the number of cooperating users [3]. Three types of cooperation have been used in the past, decode-and-forward (DF) [1, 4], amplify-and-forward (AF) [5], and coded cooperation [6]. In [4], a two-user cooperative system was considered and in that context it was shown that the AF approach performs better than the DF, with the performance gap closing as the SNR increases. Also in [4], it was shown that coded cooperation based on channel coding can in general outperform both AF and DF schemes at all SNR levels, while it is comparable to the noncooperative system at low SNR.
OFDM systems have gained popularity due to their ability to handle frequency selective fading. Various forms of cooperation in the context of OFDM systems have been considered. In [5], a hybrid forwarding scheme was proposed for cooperative relaying in OFDM-based networks that adaptively decides between AF, DF, or no relaying at all, based on the instantaneous SNR on each subcarrier. An OFDM cooperative scheme for multihop networks was proposed in [7], where in order to achieve full spatial diversity, relay selection is performed on a per-subcarrier basis instead of the entire block. Each subcarrier can determine the best relay independently at each hop, so that different subcarriers experience different paths. In [8] (Chapter 17), a general two-phase cooperative protocol for OFDM networks was studied, where in phase 1 each user transmits its own data and in phase 2 the relay decodes the source symbols that are not decoded successfully by the central node, according to feedback information sent by the central node. In order to resolve multiple users at the central code, the users can send their information in different time slots or utilize different sets of subcarriers in phase 1. It was shown in [8] that the performance of the cooperative protocol depends on the number of relays and relay selection. In [9], a multiuser OFDM network was considered where some users serve as AF relays by offering some of their subcarriers to other users. Optimal schemes of power control, subcarrier allocation, and relay selection were considered in the same paper. A DF cooperation strategy and resource-allocation algorithm for two-user OFDMA systems was proposed in [10] and was shown to achieve the capacity region upper bound of two-user OFDMA systems.
It is well known that OFDM systems loose multipath diversity as each symbol is transmitted on one subcarrier only. Several ways have been proposed in the literature for introducing path diversity in OFDM systems. Suppose that the multipath channel is finite impulse response (FIR) with  taps. Maximum diversity gain,
taps. Maximum diversity gain,  , was achieved in [11, 12] via a linear receiver using redundant precoding, or oversampling at the receiver. In [13] it was shown that a single user OFDM system with nonredundant block precoding can achieve diversity gain up to
, was achieved in [11, 12] via a linear receiver using redundant precoding, or oversampling at the receiver. In [13] it was shown that a single user OFDM system with nonredundant block precoding can achieve diversity gain up to  . The performance gain is exploitable using a Maximum Likelihood (ML) decoder. Reduced complexity decoding at the receiver is possible via subcarrier grouping [13], which may result in smaller than
. The performance gain is exploitable using a Maximum Likelihood (ML) decoder. Reduced complexity decoding at the receiver is possible via subcarrier grouping [13], which may result in smaller than  diversity gains. Other nonredundant precoding techniques were also considered in [14–16]. A multirelay cooperative OFDM system with nonredundant precoding and AF relaying was investigated in [17]. Based on the expression of pairwise error probability (PEP), it was demonstrated that the maximum diversity order is the sum of the source-to-destination channel length and the length of the shortest channel among the relay links.
diversity gains. Other nonredundant precoding techniques were also considered in [14–16]. A multirelay cooperative OFDM system with nonredundant precoding and AF relaying was investigated in [17]. Based on the expression of pairwise error probability (PEP), it was demonstrated that the maximum diversity order is the sum of the source-to-destination channel length and the length of the shortest channel among the relay links.
In this paper we propose a cooperative approach for a two-user OFDMA system that combines linear interblock precoding and user cooperation. The transmission occurs in cycles of three time slots each; two new precoded data blocks for each user are transmitted in each cycle. In the first slot, both users transmit their own data. In the two subsequent slots, each user transmits a weighted combination of the user's own precoded data and also data from the other user that were received in the previous slot. The weights are obtained as the solution of a constrained optimization problem that allows the user that faces a bad channel on certain subcarriers to benefit from the user that has a better channel, without taxing significantly the resources of that user. Two methods are proposed to implement this scheme: the full cooperation and the half cooperation. In the full-cooperation scheme, both users are involved in the cooperation. The base station (BS) recovers the transmitted symbols after it has collected data from both users in the three slots. In the half-cooperation scheme, only the strong user transmits cooperative information. We show that the proposed cooperative schemes combined with interblock precoding can achieve the maximum available diversity, that is, twice the length of the multipath channel. To achieve the same diversity order, a noncooperative OFDMA system that uses the same transmission energy per block pair and the same interblock precoding scheme would require at least two transmit antennas. Further, the proposed use of interblock precoding allows one to exploit the diversity induced by cooperation in 1.5 slots on the average; 2 slots would be needed if intrablock precoding was used instead.
1.1. Relation of Contribution to the Literature
For most existing cooperative OFDM techniques [5, 7–10, 17], the users serving as relays transmit only the data of other users during the cooperation phase. The main difference between the proposed approach and these techniques lies in the fact that each cooperating user transmits a linear combination of the user's own data and also data from the other user. Superposing user's own data and data from the other user can double the maximum diversity gain of each user.
In this paper, we propose to use interblock precoding for our proposed cooperation scheme. Inter-block precoding was previously applied to channel estimation for OFDM systems in [16] to exploit time diversity introduced by time varying channels. However, here, even if the channel is completely static, interblock precoding allows one to exploit the spatial diversity that is introduced by cooperation. In [17], intrablock precoding [13] was employed to achieve multipath diversity for multirelay cooperative OFDM system. The proposed use of interblock precoding allows one to exploit the diversity induced by cooperation in  slots on the average;
slots on the average;  slots would be needed if intrablock precoding was used instead.
slots would be needed if intrablock precoding was used instead.
1.2. Paper Organization
The paper is organized as follows. In Section 2 we describe the signal model of a multiuser OFDM system. In Section 3, we propose a full-cooperation scheme and a half-cooperation scheme for a two-user OFDMA system and provide diversity analysis. Further, we describe a modified ML decoder based on subcarrier grouping. We provide simulation results of two cooperative schemes in Section 4, and finally make some concluding remarks in Section 5.
1.3. Notation
The small and capital letters in bold denote vectors and matrices. We denote the  identity matrix as
identity matrix as  and all-zero matrix as
and all-zero matrix as  . The statistical expectation of a random variable is denoted by
. The statistical expectation of a random variable is denoted by  . The superscripts
. The superscripts  and
and  denote the conjugation and Hermitian respectively. We use
denote the conjugation and Hermitian respectively. We use  to denote element-wise multiplication.
to denote element-wise multiplication.
2. Signal Model and Assumptions
Let us consider a two-user OFDMA system where users communicate with a BS. The users are assigned disjoint carriers. User 1 transmits over subcarriers in set  and receives over subcarriers in set
and receives over subcarriers in set  , where
, where  and
and  . User 2 transmits over subcarriers in set
. User 2 transmits over subcarriers in set  and receives over subcarriers in set
and receives over subcarriers in set  .
.  denotes the cardinality of set
denotes the cardinality of set  . We assume that
. We assume that  . Let
. Let  denote the
denote the  th OFDM block of user
th OFDM block of user  with the length
with the length  , that is transmitted over the subcarriers in
, that is transmitted over the subcarriers in  , and
, and  denote the corresponding signal received by user
denote the corresponding signal received by user  in the
in the  th time slot over the carriers in set
th time slot over the carriers in set  .
.
The time-domain multipath channel between user  and user
and user  is denoted by
is denoted by  ,
,  ; each channel tap is assumed to be zero-mean i.i.d. Gaussian with unit variance. The taps
; each channel tap is assumed to be zero-mean i.i.d. Gaussian with unit variance. The taps  are assumed to be uncorrelated for different
are assumed to be uncorrelated for different  pairs, and also for different discrete times
pairs, and also for different discrete times  . We assume that the channel is slowly varying, that is, the channel remains constant over several OFDM blocks. The BS has perfect knowledge of the interuser and user-to-BS channel. Let the frequency-domain channel be
. We assume that the channel is slowly varying, that is, the channel remains constant over several OFDM blocks. The BS has perfect knowledge of the interuser and user-to-BS channel. Let the frequency-domain channel be  ,
,  . Then the received signal by user
. Then the received signal by user  from user
from user  in the
in the  th slot is given by
th slot is given by

where

with  denoting the
denoting the  th element of the set
th element of the set  according to some predefined ordering;
according to some predefined ordering;  denotes noise at user
denotes noise at user  during the transmission of the
during the transmission of the  th block from user
th block from user  with the variance of its entries being
with the variance of its entries being  . We assume that the noise is circularly complex Gaussian with zero mean, temporally and spatially white, that is,
. We assume that the noise is circularly complex Gaussian with zero mean, temporally and spatially white, that is,

For simplicity we assume that for the noise variance it holds:  .
.
The signal-to-noise ratio (SNR) throughout this paper is defined as the ratio of the power of transmitted signal to the power of additive noise as

It is well known that a good interuser channel is a pre-requisite for cooperation. In a multiuser system, the partners are selected to have a good channel between them. Therefore, throughout this paper we assume that the interuser channels are sufficiently good.
We will next discuss a scenario where both users transmit and receive simultaneously using the same antenna, that is, in full duplex mode. Since there could be practical difficulties in such scenario, we will later discuss an approach where time division multiplexing is used to achieve full duplex operation. As that approach does not change the following analysis nor the conclusions drawn in this paper, for simplicity, we continue to present our methods assuming full duplex operation.
3. The Precoded Cooperation Scheme
First, the users perform interblock precoding on pairs of successive data blocks before they enter the OFDM system. As it will be shown in a subsequent subsection, the purpose of the precoding is to exploit the multipath diversity and spatial diversity that is introduced by the cooperative retransmissions.
Let us express  be the unitary precoding matrix for user
be the unitary precoding matrix for user  as
as

where  contains the first half of the rows of
contains the first half of the rows of  while
while  contains the other half. On denoting the uncoded blocks of user
contains the other half. On denoting the uncoded blocks of user  by
by  , the precoded blocks are
, the precoded blocks are

Second, each user transmits two precoded data blocks in a cycle of 3 slots. Two cooperative transmission schemes are considered for a three-slot cycle, namely, the full-cooperation scheme and the half-cooperation scheme.
3.1. The Full-Cooperation Scheme
In this scheme, the two users superimpose their own data to the data received from the other user. Two blocks from each user, that is,  and
and  are transmitted and recovered in three time slots as follows.
are transmitted and recovered in three time slots as follows.
Slot 
Both users transmit their own data,  and
and  , respectively. These are received as
, respectively. These are received as  +
+  and
and  +
+  , respectively, by the other user.
, respectively, by the other user.
Slot 
The users transmit a weighted combination of their own data  (
( ) and the signal that they received during the previous slot after it has been scaled by
) and the signal that they received during the previous slot after it has been scaled by  (
( ) and mapped from the incoming carriers to outgoing carriers. The amount of power allocated for cooperation by users
) and mapped from the incoming carriers to outgoing carriers. The amount of power allocated for cooperation by users  and
and  is proportional to
is proportional to  and
and  , respectively. The selection of those weights is formulated as an optimization problem in Section 3.5. The transmitted signals of both users, that is,
, respectively. The selection of those weights is formulated as an optimization problem in Section 3.5. The transmitted signals of both users, that is,  and
and  are given by
are given by

Slot 
Both users again transmit  and
and  as their own data, plus the signal that they received during slot
as their own data, plus the signal that they received during slot  . Note that there is a component of
. Note that there is a component of  (
( ) in the received signals by users
) in the received signals by users  (2). In order to eliminate that component, the precoding for that block is modified as
(2). In order to eliminate that component, the precoding for that block is modified as

 can be obtained at each user by correlating the signal that was received in the
can be obtained at each user by correlating the signal that was received in the  th slot with the signal that was transmitted in the
th slot with the signal that was transmitted in the  th time slot. Therefore, the transmitted signals
th time slot. Therefore, the transmitted signals  and
and  can be expressed as
can be expressed as

In the  th slot, the cycle is repeated with two new data blocks. Table 2 shows the transmit signals of each user during three slots.
th slot, the cycle is repeated with two new data blocks. Table 2 shows the transmit signals of each user during three slots.
The signals received at the BS during slots  ,
,  ,
,  over
over  are:
are:



Similarly, the received signals over carriers in  during slots
during slots  are:
are:



Based on (10), (12), and (14), let us form the matrix equation:

where

Similarly, based on (13), (15), and (11), let us form the matrix equation:

where

By observing (16) and (18), and keeping in mind that  and
and  are functions of both
are functions of both  and
and  ,
,  , one can see that cooperation has effectively created two transmission paths for the information blocks. This effect is analogous to employing two transmitters. We should note that interblock precoding was used in [16] to exploit time diversity introduced by time varying channels. Here, even if the channel is completely static, interblock precoding allows us to exploit spatial diversity introduced by cooperation. The proposed scheme with interblock precoding requires on the average 1.5 slots for each data block to achieve the double diversity induced by cooperation. Without interblock precoding, two slots would be required.
, one can see that cooperation has effectively created two transmission paths for the information blocks. This effect is analogous to employing two transmitters. We should note that interblock precoding was used in [16] to exploit time diversity introduced by time varying channels. Here, even if the channel is completely static, interblock precoding allows us to exploit spatial diversity introduced by cooperation. The proposed scheme with interblock precoding requires on the average 1.5 slots for each data block to achieve the double diversity induced by cooperation. Without interblock precoding, two slots would be required.
Combining (16) and (18), the following MIMO problem can be formulated at the receiver:

where

Assuming knowledge of  , recovery of
, recovery of  based on
based on  is discussed in Section 3.4.
is discussed in Section 3.4.
3.1.1. Transmission Energy Adjustment
Let  be the power of one data block transmitted by user
be the power of one data block transmitted by user  without and with cooperation, respectively. For simplicity let us take
without and with cooperation, respectively. For simplicity let us take  and
and  . In the cooperative OFDM scheme, the transmission of
. In the cooperative OFDM scheme, the transmission of  and
and  requires three slots, as opposed to the two slots required in the no-cooperation scheme. To maintain the energy used by the two schemes for the transmission of a block pair at the same level, we need to adjust the transmission power. In the noncooperative case, the transmission of 2 blocks requires energy equal to
requires three slots, as opposed to the two slots required in the no-cooperation scheme. To maintain the energy used by the two schemes for the transmission of a block pair at the same level, we need to adjust the transmission power. In the noncooperative case, the transmission of 2 blocks requires energy equal to  . Under cooperation, the energy spent by user 1 and user 2 to transmit 3 blocks is
. Under cooperation, the energy spent by user 1 and user 2 to transmit 3 blocks is

To ensure that the energy spent is the same in cooperative and noncooperative cases it should hold:  .
.
Since the channel taps are assumed to be zero-mean unit-variance Gaussian random variables, the magnitudes  are i.i.d. Rayleigh distributed, that is,
are i.i.d. Rayleigh distributed, that is,  . Let
. Let  be the average
be the average  over the interuser channel coefficients. It holds
over the interuser channel coefficients. It holds

When  are sufficiently small (23) can be approximated as
are sufficiently small (23) can be approximated as  .
.
3.1.2. Diversity Analysis
It is shown in [13] that for a single user OFDM system, the maximum diversity gain achievable with one transmit antenna is equal to the number of independent fading paths of the channel. Diversity is related to the bit error rate performance [18] and is usually increased by adding more transmitters and receivers. In this section, we follow a similar procedure as in [13] to study the diversity gain achieved by (20) and show that (20) achieves the full spatial diversity available, that is,  without adding more transmitters.
without adding more transmitters.
The probability of  being detected when
being detected when  is transmitted is
is transmitted is

where  ,
,  ,
,  and
and  is the noise variance. Then we have
is the noise variance. Then we have

where  and
and

Let us define

and partition  into two
into two  vectors
vectors  and
and  . Then, (25) can be further rewritten as
. Then, (25) can be further rewritten as

where

and  and
and  are submatrices of the
are submatrices of the  -point DFT matrix corresponding to
-point DFT matrix corresponding to  and
and  .
.
Because  is generally invertible, it is reasonable to assume that
is generally invertible, it is reasonable to assume that  has full rank. Conditioned on the interuser channels
has full rank. Conditioned on the interuser channels  and
and  , the pairwise error probability is [19]
, the pairwise error probability is [19]

where  denotes the
denotes the  th eigenvalue of a matrix in the decreasing order.
th eigenvalue of a matrix in the decreasing order.
It can be seen that for high SNR the decay of the error probability is of the order of  . We should emphasize that interblock precoding is essential in achieving this diversity. Intuitively, using interblock precoding, the data within a block and between blocks can share all the available channels equally, and thus the receiver can obtain the maximum number of copies of those data. This can also been seen analytically as follows. Without interblock precoding, that is,
. We should emphasize that interblock precoding is essential in achieving this diversity. Intuitively, using interblock precoding, the data within a block and between blocks can share all the available channels equally, and thus the receiver can obtain the maximum number of copies of those data. This can also been seen analytically as follows. Without interblock precoding, that is,  , the signal model in (20) becomes
, the signal model in (20) becomes

Since both  and
and  can be partitioned into six
can be partitioned into six  diagonal matrices as seen in (17), (19), the ML decoding algorithm is performed on a pair of
diagonal matrices as seen in (17), (19), the ML decoding algorithm is performed on a pair of  and
and  per subcarrier:
per subcarrier:

where

where  denotes
denotes  and
and  denotes
denotes  . Repeating the diversity analysis as above, we get
. Repeating the diversity analysis as above, we get

Similar to (28), we have

where  ,
,

and  contains the first
contains the first  entries of the column in the
entries of the column in the  -point DFT matrix corresponding to the
-point DFT matrix corresponding to the  th subcarrier in
th subcarrier in  . Since the rank of
. Since the rank of  is two, the maximum rank of
is two, the maximum rank of  is two. Thus, without interblock precoding, the maximum diversity gain that the cooperation scheme could achieve would be two.
is two. Thus, without interblock precoding, the maximum diversity gain that the cooperation scheme could achieve would be two.
To achieve the full diversity for both users we need  . If we choose
. If we choose  as an example, user 1 cannot achieve the maximum diversity
as an example, user 1 cannot achieve the maximum diversity  . However, if the channel of one user is very bad, this user should terminate cooperation to maintain its own signal power at a certain level, that is, set
. However, if the channel of one user is very bad, this user should terminate cooperation to maintain its own signal power at a certain level, that is, set  or
or  to zero. Unlike pure transmit diversity, where we always have a good (wired) channel between the transmitters, cooperation can exhibit the same performance only when the interuser channel is good. In OFDM, where we have multiple carriers, some carriers will enjoy the full diversity gain by cooperation while some carriers will not.
to zero. Unlike pure transmit diversity, where we always have a good (wired) channel between the transmitters, cooperation can exhibit the same performance only when the interuser channel is good. In OFDM, where we have multiple carriers, some carriers will enjoy the full diversity gain by cooperation while some carriers will not.
3.2. The Half-Cooperation Scheme
In the full cooperation scheme, both users are involved in the cooperation. In order to keep the total energy consumed by the full-cooperation scheme equal to that of the no-cooperation scheme, we have to reduce the power assigned to each data block. Therefore, the maximum diversity gain is doubled at the price of SNR. It is expected that, at low SNR, the full-cooperation scheme will yield worse performance in terms of BER than the no-cooperation scheme. One might wonder whether the performance at low SNR can be improved by sacrificing diversity to some extent. Next, we investigate another scheme in which only the strongest of the two users cooperates. In particular, user 1 serves as a relay for user 2, while user 2 does not help user 1. Unlike the full-cooperation scheme, users send their information separately to the BS. Again, three slots are required for two users to transmit two blocks of data as follows.
Slot 
Both users transmit their own data  and
and  , respectively. User 1 receives
, respectively. User 1 receives  from user 2.
from user 2.
Slot 
Both users transmit their own data  and
and  , respectively. At the time of transmission, user 1 receives
, respectively. At the time of transmission, user 1 receives  from user 2.
from user 2.
Slot 
User 2 terminates transmission. User 1 transmits the signal that he received in the previous two slots over  and
and  .
.
In the ( )th slot, the cycle is repeated with two new data blocks. Table 3 shows the transmit signals of each user during the three slots. The received signals at the BS containing user 1's data and user 2's data are, respectively, equal
)th slot, the cycle is repeated with two new data blocks. Table 3 shows the transmit signals of each user during the three slots. The received signals at the BS containing user 1's data and user 2's data are, respectively, equal


where  represents the addictive Gaussian noise on the user-to-BS channel for user 1 in the (
represents the addictive Gaussian noise on the user-to-BS channel for user 1 in the ( )th slot over
)th slot over  .
.
3.2.1. Transmission Energy Adjustment
Under cooperation, the energy spent by user 1 and user 2 to transmit  blocks is:
blocks is:

Similar to the full-cooperation scheme, the average signal power over the interuser channel coefficients  is given by
is given by

When  , (40) can be approximated as
, (40) can be approximated as  . In the full-cooperation scheme,
. In the full-cooperation scheme,  . Therefore, the half-cooperation scheme can save more transmission power for each data block. It is expected that when SNR is relatively low, the half-cooperation scheme can yield better performance than the full-cooperation scheme.
. Therefore, the half-cooperation scheme can save more transmission power for each data block. It is expected that when SNR is relatively low, the half-cooperation scheme can yield better performance than the full-cooperation scheme.
3.2.2. Diversity Analysis
Similar to the scenarios discussed in [13], the maximum diversity gain of user 1 in (37) is  . From the analysis of Section 3.1.2, the maximum diversity gain of user 2 in (38) is
. From the analysis of Section 3.1.2, the maximum diversity gain of user 2 in (38) is  . This indicates that user 1 has to sacrifice its performances for the sake of user 2. On the other hand, the full-cooperation scheme is a win-win situation for both users when the SNR is relatively high.
. This indicates that user 1 has to sacrifice its performances for the sake of user 2. On the other hand, the full-cooperation scheme is a win-win situation for both users when the SNR is relatively high.
Table 1 summarizes the maximum diversity gain of the full-cooperation scheme (FC), the full-cooperation scheme without precoding (FC-no precoding), the half-cooperation scheme (HC), the no-cooperation scheme with precoding (NC) and the no-cooperation scheme without precoding (NC-no precoding).
3.3. Time Division Duplexing
The cooperation scheme described above is strongly dependent on the users being able to both receive and transmit simultaneously. However, in a practical situation this might be difficult. Nevertheless it is possible to effectively achieve full duplex operation by time division duplexing.
In the original scheme both users transmit during the entire duration of time slot  (
( symbols plus the cyclic prefix). However, we can allocate half a time slot for each user to the data vectors
symbols plus the cyclic prefix). However, we can allocate half a time slot for each user to the data vectors  and
and  . During time slot
. During time slot  , user
, user  will first transmit
will first transmit  data symbols plus the cyclic prefix. Next, user
data symbols plus the cyclic prefix. Next, user  will transmit his own
will transmit his own  data symbols plus the cyclic prefix. During each transmission, all the other users will be in receive mode. Therefore, there is no difference between this time division approach (half duplex) and the full duplex one, and the analysis and conclusions hold in this case too.
data symbols plus the cyclic prefix. During each transmission, all the other users will be in receive mode. Therefore, there is no difference between this time division approach (half duplex) and the full duplex one, and the analysis and conclusions hold in this case too.
3.4. Symbol Recovery
The maximum diversity can be best exploited using ML decoding. In general, ML decoding has prohibitively high complexity especially when the number of subcarriers  is large. Here, following the main idea of [13], we implement ML by optimal subcarrier grouping. The set of all subcarriers is divided into
is large. Here, following the main idea of [13], we implement ML by optimal subcarrier grouping. The set of all subcarriers is divided into  equally spaced groups. Each group contains
equally spaced groups. Each group contains  subcarriers. In order to achieve the maximum multipath diversity, it should hold that
subcarriers. In order to achieve the maximum multipath diversity, it should hold that  (see Section 4 for diversity analysis). To reduce the complexity further, we let two users exchange their subcarriers to transmit data in the second slot, that is, in slot
(see Section 4 for diversity analysis). To reduce the complexity further, we let two users exchange their subcarriers to transmit data in the second slot, that is, in slot  , user 1 transmits over
, user 1 transmits over  and receives over
and receives over  , while user 2 transmits over
, while user 2 transmits over  and receives over
and receives over  . By this way, the minimum
. By this way, the minimum  can be reduced to
can be reduced to  to achieve diversity of the order of
to achieve diversity of the order of  . For simplicity, we assume that
. For simplicity, we assume that  is an integer. The sets of subcarriers for two users
is an integer. The sets of subcarriers for two users  and
and  are divided into
are divided into  groups, each group containing
groups, each group containing  equally spaced subcarriers. Let us define
equally spaced subcarriers. Let us define

where  denotes the subcarrier pattern for the
denotes the subcarrier pattern for the  th group;
th group;  represents the transmitted signal of the
represents the transmitted signal of the  th user in the
th user in the  th slot over the
th slot over the  th group of subcarriers;
th group of subcarriers;  denotes the received signal at BS in the
denotes the received signal at BS in the  th slot over the
th slot over the  th group of subcarriers in
th group of subcarriers in  ;
;  denotes the noise at user
denotes the noise at user  over the
over the  th group of subcarriers during the transmission of the data block from user
th group of subcarriers during the transmission of the data block from user  in the
in the  th slot (The
th slot (The  th user represents the BS);
th user represents the BS);  and
and  are the fading coefficients of the channel from the
are the fading coefficients of the channel from the  th user to the
th user to the  th user over the
th user over the  th group of subcarriers in
th group of subcarriers in  and
and  , respectively. If we take the full-cooperation scheme as an example, the model for the received signal by grouping subcarriers can be reduced to
, respectively. If we take the full-cooperation scheme as an example, the model for the received signal by grouping subcarriers can be reduced to

where

By optimal subcarrier grouping, we only perform the precoding on a group of subcarriers.
Let  be an
be an  unitary Vandermonde matrix defined as in [13]. The precoding matrixes
unitary Vandermonde matrix defined as in [13]. The precoding matrixes  and
and  in (6) can be simplified as
in (6) can be simplified as  .
.
3.5. Optimal Allocation of Power during Allocation
In this section, we discuss the optimization of power allocation parameter  and
and  based on the model of (42). We assume that user 1 is the strong user, that is, user 1 has less subcarriers in deep fade as compared to user 2 (weak user). During the cooperation, user 1 will assist user 2, while at the same time, will also receive some help.
based on the model of (42). We assume that user 1 is the strong user, that is, user 1 has less subcarriers in deep fade as compared to user 2 (weak user). During the cooperation, user 1 will assist user 2, while at the same time, will also receive some help.
Let us define  to be the vector of the parameters to be determined. The objective function is defined in terms of the SINR of user 1 and user 2. In order to derive the SINR for the users, we need to separate the data of each user in the model of (42) as
to be the vector of the parameters to be determined. The objective function is defined in terms of the SINR of user 1 and user 2. In order to derive the SINR for the users, we need to separate the data of each user in the model of (42) as

where  and
and  contain the first half and the second half of the columns of
contain the first half and the second half of the columns of  , respectively. On letting
, respectively. On letting  denote the SINR of the
denote the SINR of the  th user at the
th user at the  th subcarrier, we have
th subcarrier, we have

where the numerators of  are linear functions of
are linear functions of  and the denominators are the polynomials of
and the denominators are the polynomials of  .
.
The optimization problem is formulated as follows. We wish to maximize the SINR on the worst subcarriers of the weak user, subject to the constraint that the SINR on all subcarriers of the strong user is above some threshold  , that is,
, that is,

where the last constraint means that user 2 never spends more energy than user 1 when helping user 1. The threshold depends on the applications that user 1 needs to transmit, and is here assumed given. The lower the threshold, the more help user 1 will provide. The advantage for user 1 is that if the user has subcarriers on which the SINR is less than  , the situation on those subcarriers will improve.
, the situation on those subcarriers will improve.
A more standard form of the above problem is

or equivalently,

Since the denominators of  are polynomials of
are polynomials of  , finding the solution of the problem of (48) is not easy. We will proceed by making some simplifying assumptions. Let us assume that the interuser channels are quite good and that the noise at the user end is very small so that
, finding the solution of the problem of (48) is not easy. We will proceed by making some simplifying assumptions. Let us assume that the interuser channels are quite good and that the noise at the user end is very small so that  and
and  are negligible as compared to
are negligible as compared to  and
and  . Since the coefficients of the high orders of
. Since the coefficients of the high orders of  are linear combinations of
are linear combinations of  and
and  , the high orders of
, the high orders of  can be ignored. Therefore, the denominators of
can be ignored. Therefore, the denominators of  can be approximated as a linear function in
can be approximated as a linear function in  . Let
. Let  be represented by
be represented by  . Finding the solution of (48) is based on the following observations.
. Finding the solution of (48) is based on the following observations.
-
(1)
The constraints (a)–(c) are linear so they give rise to the feasible set shown by a polyhedron
 in Figure 1. The irregular pentagon
in Figure 1. The irregular pentagon  and a triangle
and a triangle  are formed by constraints (a) and (b)-(c), respectively.
are formed by constraints (a) and (b)-(c), respectively. -
(2)
With a fixed
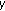 , the
, the  th inequality in the constraint (d) yields a halfspace
th inequality in the constraint (d) yields a halfspace 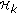 :
: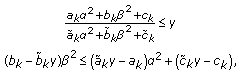 (49)
(49)where
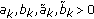 .
. -
(3)
When
 takes the minimum value
takes the minimum value  ,
, 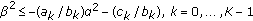 and thus the feasible set is empty. As
and thus the feasible set is empty. As  increases, the dimension of the feasible set increases. There are several different scenarios.
increases, the dimension of the feasible set increases. There are several different scenarios.
-
(a)
If
 ,
,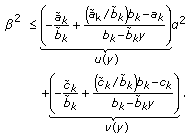 (50)
(50)-
(i)
If
 or
or  , the halfspace
, the halfspace  approaches
approaches  as
as  is increasing in
is increasing in  , and finally
, and finally 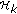 intersects with
intersects with  . Let
. Let  denote the minimum
denote the minimum 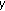 that the
that the 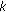 th inequality of the constraint (d) yields. Then this
th inequality of the constraint (d) yields. Then this  is achieved when
is achieved when  touches a vertex of
touches a vertex of  .
. -
(ii)
If
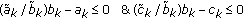 ,
,  and
and  are decreasing functions of
are decreasing functions of 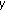 . Therefore, the halfspace
. Therefore, the halfspace 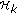 and
and 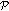 do not intersect within
do not intersect within  .
. -
(iii)
If
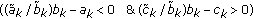 , or
, or 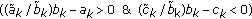 ,
, 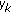 is achieved on a vertex of
is achieved on a vertex of 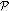 if
if  .
.
-
(i)
-
(b)
If
 does not exist when
does not exist when  , we have to consider the scenario in which
, we have to consider the scenario in which 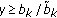 . First, we consider
. First, we consider 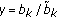 and so
and so  .
.-
(i)
If
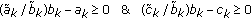 , the intersection of
, the intersection of 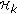 with
with 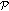 is
is 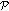 itself. Thus,
itself. Thus,  .
. -
(ii)
If
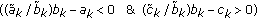 or
or 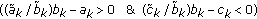 , we have
, we have (51)
(51) -
(iii)
If
 or
or 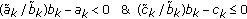 ,
, 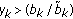 then refer to (c).
then refer to (c).
-
(i)
-
(c)
If
 does not exist when
does not exist when  , we have to consider the scenarios in which
, we have to consider the scenarios in which  and so
and so  . When
. When 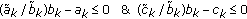 , we can always find a feasible
, we can always find a feasible 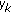 .
.
In conclusion, we know
-
(i)
If
 , any elements in the set
, any elements in the set  can give rise to the minimum
can give rise to the minimum 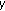 ,
,  . However, this case happens with small probability.
. However, this case happens with small probability. -
(ii)
Otherwise,
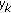 always falls on a vertex of
always falls on a vertex of 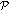 .
.
Since  inequalities of constraint (d) need to be satisfied simultaneously, the optimal
inequalities of constraint (d) need to be satisfied simultaneously, the optimal  is a vertex of
is a vertex of  satisfying
satisfying

where  is the maximum value of the set
is the maximum value of the set  obtained from the
obtained from the  inequalities. Therefore, we can determine the optimal power allocation parameters
inequalities. Therefore, we can determine the optimal power allocation parameters  with the aid of the geometric interpretation of (48). The minimum
with the aid of the geometric interpretation of (48). The minimum  is the maximum value of
is the maximum value of  =
=  ,
,  .
.
4. Simulation Results
In this section, we provide simulation result to illustrate the performance of the proposed full-cooperation (FC) and half-cooperation (HC) schemes. To illustrate the advantages of cooperation in addition to precoding, we compare the two proposed approaches to a noncooperative scheme (NC) that uses the same interblock precoding strategy and is equivalent in terms of power consumption.
We consider an OFDM system with  subcarriers and 4QAM signals. We use the model of [20] to generate channels consisting of two equal power taps with normalized Doppler shift equal to
subcarriers and 4QAM signals. We use the model of [20] to generate channels consisting of two equal power taps with normalized Doppler shift equal to  . The channel is virtually static in order to eliminate temporal diversity due to by channel variation and thus highlight diversity due to cooperation and multipath. The SNR of the interuser channel is fixed at 30 dB. For the interblock precoding, we use
. The channel is virtually static in order to eliminate temporal diversity due to by channel variation and thus highlight diversity due to cooperation and multipath. The SNR of the interuser channel is fixed at 30 dB. For the interblock precoding, we use  unitary matrices and group carriers into blocks of two. Two users exchange their subcarriers as described in Section 3.4.
unitary matrices and group carriers into blocks of two. Two users exchange their subcarriers as described in Section 3.4.
In our simulations, we assign unit power to each OFDM symbol for the noncooperative scheme. The power of each OFDM block in the proposed cooperative schemes is determined by (23) and (40). This guarantees that cooperative and noncooperative schemes consume the same energy during a cycle of three slots. In the following figures and discussion the term SNR refers to the SNR for the noncooperative scheme, that is, the reciprocal of the noise power. We assume  . We force user 1 and user 2 to have
. We force user 1 and user 2 to have  and
and  deep-fading subcarriers, respectively. The variance of nondeep-fading subcarriers is set to
deep-fading subcarriers, respectively. The variance of nondeep-fading subcarriers is set to  while the variance of subcarriers in deep fade is set to
while the variance of subcarriers in deep fade is set to  . We consider three cases where
. We consider three cases where  ,
,  .
.
Figures 2, 3, and 4 compare the BER performances of each user for FC and NC in three cases described above for SNR01 = SNR02. Since our proposed approach of optimizing  and
and  holds only when
holds only when  , we consider the scenarios of relatively small SNR01 and SNR02. Let the threshold in (48) for the SINR of user 2 over all the subcarriers be
, we consider the scenarios of relatively small SNR01 and SNR02. Let the threshold in (48) for the SINR of user 2 over all the subcarriers be  corresponding to
corresponding to  , respectively. In each channel realization, we update the optimal
, respectively. In each channel realization, we update the optimal  and
and  with knowledge of channel coefficients and noise variance. The procedure to determine the optimal
with knowledge of channel coefficients and noise variance. The procedure to determine the optimal  and
and  based on the analysis in Section 3.5 is sketched as follows:
based on the analysis in Section 3.5 is sketched as follows:
-
(1)
We first find the vertices of the feasible sets of
 and
and 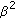 satisfying the constraints (a)–(c) of (48);
satisfying the constraints (a)–(c) of (48); -
(2)
We determine the vertex that gives rise to the the minimum
 for the
for the 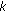 th constraint of (d) in (48), and record the value of
th constraint of (d) in (48), and record the value of 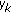 ;
; -
(3)
The optimal solution
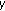 of (48) is the maximum element of the set
of (48) is the maximum element of the set  . Based on that maximum value for
. Based on that maximum value for 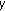 the optimal
the optimal  and
and 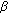 are found via (52).
are found via (52).
Figures 2–4 show that FC can significantly improve the performances of both users at higher SNR.
Figures 5, 6, and 7 show the BER performance of each user for the FC, HC and NC for SNR01 = SNR02 = 5 dB~35 dB. Both  and
and  are fixed to
are fixed to  for HC, while for FC it is taken
for HC, while for FC it is taken  . One can see that HC can significantly improve the performances of user 2 with a negligible penalty on the other user's performance as compared to NC. At low SNR, HC performs slightly better than FC with regards to user 2's performances. When the two users encounter relatively high SNR, the FC scheme can improve the performance of both users. When the antennas are not able to switch from one scheme to another, the FC scheme is always a wise choice regardless of the environment.
. One can see that HC can significantly improve the performances of user 2 with a negligible penalty on the other user's performance as compared to NC. At low SNR, HC performs slightly better than FC with regards to user 2's performances. When the two users encounter relatively high SNR, the FC scheme can improve the performance of both users. When the antennas are not able to switch from one scheme to another, the FC scheme is always a wise choice regardless of the environment.
5. Conclusion
In this paper, we have proposed and compared two precoded schemes with user cooperation for two-user OFDMA systems. By analyzing the pairwise error probability of the proposed system, we have shown that the full-cooperation scheme can double the diversity available to both users without requiring additional transmitters. Therefore, the full-cooperation scheme can improve the BER performance of both users when the SNR of the users towards the receiver is relatively high so that the fading dominates the performance. On the other hand, when the SNR of two users is low, the half-cooperation scheme can achieve slightly better performance than the full-cooperation scheme. Furthermore, the use of interblock precoding, as compared to intrablock precoding, reduces the number of time slots required by the cooperative OFDM system to achieve the maximum diversity induced by cooperation. The extension of the proposed scheme to the multiuser case is not trivial; it involves selecting the users to cooperate with each other, or modifying the proposed scheme to render the cooperation of more than two users feasible. Such extension will be part of future work.
References
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part I: system description. IEEE Transactions on Communications 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part II: implementation aspects and performance analysis. IEEE Transactions on Communications 2003, 51(11):1939-1948. 10.1109/TCOMM.2003.819238
Laneman JN, Wornell GW: Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks. IEEE Transactions on Information Theory 2003, 49(10):2415-2425. 10.1109/TIT.2003.817829
Nosratinia A, Hunter TE, Hedayat A: Cooperative communication in wireless networks. IEEE Communications Magazine 2004, 42(10):74-80. 10.1109/MCOM.2004.1341264
Can B, Yomo H, de Carvalho E: Hybrid forwarding scheme for cooperative relaying in OFDM based networks. Proceedings of IEEE International Conference on Communications (ICC '06), June 2006 10: 4520-4525.
Hunter TE, Nosratinia A: Diversity through coded cooperation. IEEE Transaction on Wireless Communications 2006, 5: 283-289.
Dai L, Gui B, Cimini LJ: Selective relaying in OFDM multihop cooperative networks. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC '07), March 2007 963-968.
Liu KJR, Sadek AK, Su W, Kwasinski A: Cooperative Communications and Networking. Cambridge Univeristy Press, Cambridge, UK; 2009.
Han Z, Himsoon T, Siriwongpairat WP, Liu KJR: Resource allocation for multiuser cooperative OFDM networks: who helps whom and how to cooperate. IEEE Transactions on Vehicular Technology 2009, 58(5):2378-2391.
Weng L, Murch RD: Cooperation strategies and resource allocations in multiuser OFDMA systems. IEEE Transactions on Vehicular Technology 2009, 58(5):2331-2342.
Tepedelenlioglu C, Challagulla R: Low-complexity multipath diversity through fractional sampling in OFDM. IEEE Transactions on Signal Processing 2004, 52(11):3104-3116. 10.1109/TSP.2004.836452
Tepedelenlioglu C: Maximum multipath diversity with linear equalization in precoded OFDM systems. IEEE Transactions on Information Theory 2004, 50(1):232-235. 10.1109/TIT.2003.821987
Liu Z, Xin Y, Giannakis GB: Linear constellation precoding for OFDM with maximum multipath diversity and coding gains. IEEE Transactions on Communications 2003, 51(3):416-427. 10.1109/TCOMM.2003.809791
Petropulu A, Zhang R, Lin R: Blind OFDM channel estimation through simple linear preceding. IEEE Transactions on Wireless Communications 2004, 3(2):647-655. 10.1109/TWC.2003.821140
Gao F, Nallanathan A: Blind channel estimation for OFDM systems via a generalized precoding. IEEE Transactions on Vehicular Technology 2007, 56(3):1155-1164.
Lin R, Petropulu AP: Linear precoding assisted blind channel estimation for OFDM systems. IEEE Transactions on Vehicular Technology 2005, 54(3):983-995. 10.1109/TVT.2005.844681
Ding Y, Uysal M: Multi-relay cooperative OFDM with amplify-and-forward relaying invited paper. Proceedings of IEEE Radio and Wireless Symposium (RWS '09), January 2009, San Diego, Calif, USA 614-617.
Zheng L, Tse DNC: Diversity and multiplexing: a fundamental tradeoff in multiple-antenna channels. IEEE Transactions on Information Theory 2003, 49(5):1073-1096. 10.1109/TIT.2003.810646
Tarokh V, Seshadri N, Calderbank AR: Space-time codes for high data rate wireless communication: performance criterion and code construction. IEEE Transactions on Information Theory 1998, 44(2):744-765. 10.1109/18.661517
Zheng YR, Xiao C: Improved models for the generation of multiple uncorrelated Rayleigh fading waveforms. IEEE Communications Letters 2002, 6(6):256-258. 10.1109/LCOMM.2002.1010873
Yatawatta S, Petropulu AP: A multiuser OFDM system with user cooperation. Proceedings of the 38th Asilomar Conference on Signals, Systems and Computers, November 2004, Pacific Grove, Calif, USA 319-323.
Acknowledgments
This work was supported by the Office of Naval Research under Grant ONR-N-00014-07-1-0500 and the National Science Foundation under Grant CNS-0905425. Preliminary results of this work were presented at the 2004 Asilomar Conference on Signals, Systems, and Computers [21].
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yu, Y., Yatawatta, S. & Petropulu, A. A Precoded OFDMA System with User Cooperation. J Wireless Com Network 2010, 843745 (2010). https://doi.org/10.1155/2010/843745
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/843745
 in Figure
in Figure  and a triangle
and a triangle  are formed by constraints (a) and (b)-(c), respectively.
are formed by constraints (a) and (b)-(c), respectively.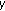 , the
, the  th inequality in the constraint (d) yields a halfspace
th inequality in the constraint (d) yields a halfspace 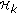 :
: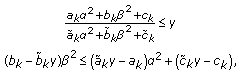
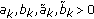 .
. takes the minimum value
takes the minimum value  ,
, 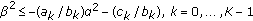 and thus the feasible set is empty. As
and thus the feasible set is empty. As  increases, the dimension of the feasible set increases. There are several different scenarios.
increases, the dimension of the feasible set increases. There are several different scenarios. ,
,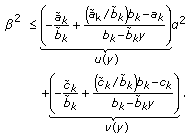
 or
or  , the halfspace
, the halfspace  approaches
approaches  as
as  is increasing in
is increasing in  , and finally
, and finally 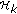 intersects with
intersects with  . Let
. Let  denote the minimum
denote the minimum 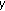 that the
that the 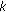 th inequality of the constraint (d) yields. Then this
th inequality of the constraint (d) yields. Then this  is achieved when
is achieved when  touches a vertex of
touches a vertex of  .
.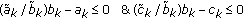 ,
,  and
and  are decreasing functions of
are decreasing functions of 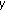 . Therefore, the halfspace
. Therefore, the halfspace 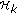 and
and 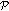 do not intersect within
do not intersect within  .
.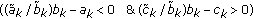 , or
, or 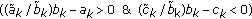 ,
, 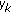 is achieved on a vertex of
is achieved on a vertex of 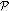 if
if  .
. does not exist when
does not exist when  , we have to consider the scenario in which
, we have to consider the scenario in which 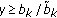 . First, we consider
. First, we consider 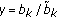 and so
and so  .
.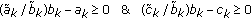 , the intersection of
, the intersection of 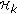 with
with 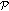 is
is 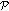 itself. Thus,
itself. Thus,  .
.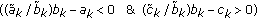 or
or 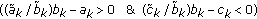 , we have
, we have
 or
or 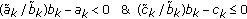 ,
, 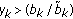 then refer to (c).
then refer to (c). does not exist when
does not exist when  , we have to consider the scenarios in which
, we have to consider the scenarios in which  and so
and so  . When
. When 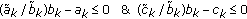 , we can always find a feasible
, we can always find a feasible 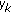 .
.
 , any elements in the set
, any elements in the set  can give rise to the minimum
can give rise to the minimum 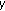 ,
,  . However, this case happens with small probability.
. However, this case happens with small probability.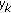 always falls on a vertex of
always falls on a vertex of 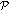 .
. and
and 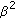 satisfying the constraints (a)–(c) of (48);
satisfying the constraints (a)–(c) of (48); for the
for the 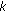 th constraint of (d) in (48), and record the value of
th constraint of (d) in (48), and record the value of 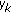 ;
;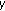 of (48) is the maximum element of the set
of (48) is the maximum element of the set  . Based on that maximum value for
. Based on that maximum value for 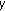 the optimal
the optimal  and
and 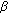 are found via (52).
are found via (52).
 and user 2 has
and user 2 has
 subcarriers in deep fade.
subcarriers in deep fade.

 and user 2 has
and user 2 has
 subcarriers in deep fade.
subcarriers in deep fade.

 and user 2 has
and user 2 has
 subcarriers in deep fade.
subcarriers in deep fade.

 and user 2 has
and user 2 has
 subcarriers in deep fade.
subcarriers in deep fade.

 and user 2 has
and user 2 has
 subcarriers in deep fade.
subcarriers in deep fade.

 and user 2 has
and user 2 has
 subcarriers in deep fade.
subcarriers in deep fade.