- Research Article
- Open access
- Published:
Comparison of Channel Estimation Protocols for Coherent AF Relaying Networks in the Presence of Additive Noise and LO Phase Noise
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 861735 (2010)
Abstract
Channel estimation protocols for wireless two-hop networks with amplify-and-forward (AF) relays are compared. We consider multiuser relaying networks, where the gain factors are chosen such that the signals from all relays add up coherently at the destinations. While the destinations require channel knowledge in order to decode, our focus lies on the channel estimates that are used to calculate the relay gains. Since knowledge of the compound two-hop channels is generally not sufficient to do this, the protocols considered here measure all single-hop coefficients in the network. We start from the observation that the direction in which the channels are measured determines (1) the number of channel uses required to estimate all coefficient and (2) the need for global carrier phase reference. Four protocols are identified that differ in the direction in which the first-hop and the second-hop channels are measured. We derive a sensible measure for the accuracy of the channel estimates in the presence of additive noise and phase noise and compare the protocols based on this measure. Finally, we provide a quantitative performance comparison for a simple single-user application example. It is important to note that the results can be used to compare the channel estimation protocols for any two-hop network configuration and gain allocation scheme.
1. Introduction
Cooperative networks offer diversity, multiplexing, and array gains as in MIMO systems but in a distributed fashion. The spatial diversity, that is inherently available, can be exploited by user cooperation to decrease the outage probability for a given rate, thus making the communication more robust against deep fades [1–5]. Furthermore, coherent beamforming allows for a distributed spatial multiplexing gain [6–9]. For interference networks comprising multiple source-destination pairs, this involves allowing the users to communicate concurrently on the same physical channel.
Note that the relays in these networks are usually not able to decode all data streams due to the large amount of inter-user interference. Instead, they assist the communication by simply forwarding scaled and rotated versions of their received signals, which corresponds to the multiplication with complex-valued gain factors. We refer to this type of forwarding protocol as multiuser AF relaying (e.g., [6]). The relay gains are chosen such that all signals add up coherently at the destination antennas. Global channel knowledge, that is, knowledge of all first-hop and second-hop channel coefficients, is usually required to calculate the gain factors accordingly. It is important to stress that information about the equivalent two-hop (source-relay-destination) channels (treated e.g., in [10–12]) is generally not enough to explicitly compute the relay gains. A gradient-based iterative scheme is required to find the gain factors in this case (e.g., [13]). Examples of papers discussing coherent cooperative gain allocation schemes, where the relay gains are computed from instantaneous, global CSI are [14–18].
Contribution
This work was triggered by the simple fact that the relay gains in coherent AF networks are computed from channel estimates. The quality of these estimates obviously has an impact on the accuracy with which the gain factors can be computed. This in turn determines the degree to which the signals from the relays combine coherently at the destinations and thus immediately affect the system performance. We furthermore observe that the direction in which the channels in a wireless network are measured (The source-relay (first-hop) and the relay-destination (second-hop) channels can be measured either in "forward direction", that is, from sources/relays to relays/destinations, or in "backward direction", that is, from relays/destinations to sources/relays.) (e.g., using training sequences [19]) determines  the number of channel uses required to estimate all coefficients and
the number of channel uses required to estimate all coefficients and  the need for a global phase reference at a certain set of nodes [20]. In the presence of additive noise and LO phase noise, both factors have an impact on the quality of the channel estimates. In this work, we compare four channel estimation protocols that differ in the direction in which the single-hop channel matrices are measured. As a result, the accuracy of the channel estimates obtained by the protocols is different. For symmetry reasons we can constrain ourselves to the discussion of only two of the four protocols. We quantify the quality of the channel estimates and discuss which protocol delivers the most accurate channel estimates and thus allows for the best overall system performance. It turns out that there are situations where one protocol outperforms the other and vice versa.
the need for a global phase reference at a certain set of nodes [20]. In the presence of additive noise and LO phase noise, both factors have an impact on the quality of the channel estimates. In this work, we compare four channel estimation protocols that differ in the direction in which the single-hop channel matrices are measured. As a result, the accuracy of the channel estimates obtained by the protocols is different. For symmetry reasons we can constrain ourselves to the discussion of only two of the four protocols. We quantify the quality of the channel estimates and discuss which protocol delivers the most accurate channel estimates and thus allows for the best overall system performance. It turns out that there are situations where one protocol outperforms the other and vice versa.
The authors of [21] consider a very simple special case of this problem. They investigate the accuracy of a channel estimation protocol (corresponding to protocol B1 in this work) for a two-hop network with a single source-destination pair and multiple AF relays. The gain factors are to be computed from the channel estimates at the relays in a way that all signals combine coherently at the destination antenna. The authors neglect LO phase noise and implicitly assume a perfect carrier phase synchronization between all relays and the destination. In comparison to [21], this work compares four different channel estimation protocols, considers multiple source-destination pairs, takes LO phase noise into account, and drops the assumption of perfect phase synchronization.
Outline
The system model is presented in Section 2. We derive the input/output relation in Section 2.1 and discuss the impact of unknown and random LO phases on the signaling in Section 2.2. Section 3 then motivates the usage of the MSE of the estimated two-hop channels to judge the quality of the channel estimates. The four previously mentioned protocols are derived in Section 4. We will explain how the effort to estimate all channel coefficients in a distributed network depends on the direction in which the channel are measured. A scheme that can provide the relays with a global phase reference was originally presented in [22]. It is shortly revisited in Section 5. Section 6 then discusses the impact of additive noise and relay phase noise on the quality of the channel estimates delivered by the protocols. Finally, we compare the quality of the channel estimates produced by the protocols in Section 7.
Notation 1.
We use bold uppercase and lowercase letters to denote matrices and vectors, respectively. The operators  ,
,  , and
, and  are the matrix transpose, hermitian transpose, and conjugate complex, respectively. We use
are the matrix transpose, hermitian transpose, and conjugate complex, respectively. We use  to denote a convolution and
to denote a convolution and  is the expectation with respect to
is the expectation with respect to  .
.  is the identity matrix of size
is the identity matrix of size  . The expression
. The expression  writes the elements of
writes the elements of  into a diagonal matrix. Finally, vectors with entries that are taken from a normal and a complex normal distribution with mean
into a diagonal matrix. Finally, vectors with entries that are taken from a normal and a complex normal distribution with mean  and variance
and variance  are denoted by
are denoted by  and
and  , respectively.
, respectively.
2. System Model
Consider a distributed wireless network where  sources and the same number of destinations communicate with the help of
sources and the same number of destinations communicate with the help of  linear AF relay nodes. Each source wants to transmit data to a dedicated destination, together forming a source-destination pair. Figure 1 shows the system configuration. For the sake of simplicity, it is assumed that all nodes in the network employ a single antenna only. The extension of this work to multiantenna nodes is straightforward. It is furthermore assumed that the relays are not able to transmit and receive at the same time (half-duplex constraint; e.g., [4]). Consequently, a "transmission cycle" consists of two phases: phase one comprises the "first-hop" transmission from the sources to all relays and phase two the "second-hop" transmission from the relays to the destinations.
linear AF relay nodes. Each source wants to transmit data to a dedicated destination, together forming a source-destination pair. Figure 1 shows the system configuration. For the sake of simplicity, it is assumed that all nodes in the network employ a single antenna only. The extension of this work to multiantenna nodes is straightforward. It is furthermore assumed that the relays are not able to transmit and receive at the same time (half-duplex constraint; e.g., [4]). Consequently, a "transmission cycle" consists of two phases: phase one comprises the "first-hop" transmission from the sources to all relays and phase two the "second-hop" transmission from the relays to the destinations.
The relays shift their received signals to complex baseband, sample them, and store the samples until the end of the first phase. In the second phase, they retransmit scaled and rotated version of their received samples to the destinations. This corresponds to the multiplication of the samples with a complex-valued gain factor at each relay. As long as the sampling theorem is fulfilled, the analog transmit signal can be reconstructed perfectly from the stored samples.
Note that the direct link is not taken into account in this work because it is independent of LO phases of the relays. The quality of its estimates is therefore the same for all four channel estimation protocols. Without going further into details, we assume that the nodes are perfectly synchronized in time.
2.1. Input/Output Relation
All channels are assumed to be mutually independent and frequency flat. They are subject to Rayleigh fading, that is, the channel coefficients are zero-mean complex Gaussian random variables with variance  . The matrices
. The matrices  and
and  are called first-hop and second-hop channel matrix, respectively. The propagation environment is quasistatic, that is, the channels are constant during at least one transmission cycle while different channel realizations are temporally uncorrelated (block fading).
are called first-hop and second-hop channel matrix, respectively. The propagation environment is quasistatic, that is, the channels are constant during at least one transmission cycle while different channel realizations are temporally uncorrelated (block fading).
The relays multiply the signals they receive from the sources with complex-valued gains before retransmission. All gain factors are collected in the diagonal gain matrix  . Let
. Let  denote the vector comprising the transmit symbols of all sources at a certain point in time. They are transmitted over the first-hop matrix channel
denote the vector comprising the transmit symbols of all sources at a certain point in time. They are transmitted over the first-hop matrix channel  to the relays. Their received symbols are stacked in the vector
to the relays. Their received symbols are stacked in the vector

where the vector  comprises AWGN samples. Prior to retransmission,
comprises AWGN samples. Prior to retransmission,  is multiplied with the gain matrix
is multiplied with the gain matrix  . The transmit signals of the relays are then sent over the second-hop matrix channel
. The transmit signals of the relays are then sent over the second-hop matrix channel  to the destination nodes. The vector of received symbols is
to the destination nodes. The vector of received symbols is

where  comprises the AWGN samples at the destinations. The matrix
comprises the AWGN samples at the destinations. The matrix  comprises the coefficients
comprises the coefficients

where  is the channel coefficient from source
is the channel coefficient from source  to relay
to relay  and
and  the channel coefficient from relay
the channel coefficient from relay  to destination
to destination  .
.
2.2. Local Oscillator Phase Offsets
Consider two single-antenna nodes A and B with independent LO. Let  denote the complex-valued coefficient of the frequency-flat equivalent low-pass channel between them. The LO phase offsets of nodes A and B are denoted by
denote the complex-valued coefficient of the frequency-flat equivalent low-pass channel between them. The LO phase offsets of nodes A and B are denoted by  and
and  , respectively. They introduce phase rotations to the signals during the mixing operations, with positive sign when mixing from baseband to passband and with negative sign when mixing from passband to baseband (e.g., [23]). Consequently, the equivalent complex baseband-to-baseband channels from A to B and from B to A are
, respectively. They introduce phase rotations to the signals during the mixing operations, with positive sign when mixing from baseband to passband and with negative sign when mixing from passband to baseband (e.g., [23]). Consequently, the equivalent complex baseband-to-baseband channels from A to B and from B to A are

They are reciprocal, that is,  if A and B are phase synchronous, that is,
if A and B are phase synchronous, that is,  (cf. [20]).
(cf. [20]).
Each terminal in the system shown in Figure 1 employs its own LO. It is thus sensible to assume that their LO phases are mutually independent. Let  ,
,  , and
, and  denote the LO phase offsets of source
denote the LO phase offsets of source  , relay
, relay  , and destination
, and destination  , respectively. If the relay phases stay constant for a transmission cycle, the "equivalent two-hop channel" between source
, respectively. If the relay phases stay constant for a transmission cycle, the "equivalent two-hop channel" between source  and destination
and destination  is
is

where  is defined in (3).
is defined in (3).  in (5) is independent of the LO phases of the relays because their impact on the signal during reception is compensated when the signal is retransmitted (If the relay phases change during the time between reception and retransmission (e.g., due to phase noise), they do not compensate. As a consequence, a phase error is introduced to the signal [24].).
in (5) is independent of the LO phases of the relays because their impact on the signal during reception is compensated when the signal is retransmitted (If the relay phases change during the time between reception and retransmission (e.g., due to phase noise), they do not compensate. As a consequence, a phase error is introduced to the signal [24].).
Note that the way the signals from the relays add up at the destination antennas (constructively or destructively) is independent of both the LO phases of the sources and of the destinations. For this reason  and
and  do not have an impact on the accuracy of the gain factors that are computed from channel estimates. They can thus be chosen to be of any value without changing the result of the analysis. In order to keep the notation simple, we therefore set
do not have an impact on the accuracy of the gain factors that are computed from channel estimates. They can thus be chosen to be of any value without changing the result of the analysis. In order to keep the notation simple, we therefore set  and
and  to zero, that is,
to zero, that is,  for all
for all  . This means that
. This means that  (see (5)).
(see (5)).
3. Performance Measure
Coherent gain allocation schemes compute the relay gains in a way that the signals from all relays combine coherently at the destinations (e.g., [6]). In any practical network, the gain factors are computed from the estimates  and
and  and not
and not  and
and  . This makes
. This makes

the equivalent two-hop coefficients "anticipated" or "desired" by the relays in contrast to the "actual" coefficients  experience by the data symbols. The idea behind coherent relaying is that the relays can adjust
experience by the data symbols. The idea behind coherent relaying is that the relays can adjust  (and in particular its phase) by their choice of
(and in particular its phase) by their choice of  . In the presence of channel estimation errors, we can write
. In the presence of channel estimation errors, we can write

where the estimation error  directly translates into an SINR loss at destination
directly translates into an SINR loss at destination  . A sensible performance measure for the channel estimation protocols considered in this work is consequently how well
. A sensible performance measure for the channel estimation protocols considered in this work is consequently how well  matches
matches  . This is well reflected by the MSE
. This is well reflected by the MSE

which will be used as a figure of merit.
4. Channel Estimation Protocols
In this section, the anticipated equivalent two-hop channel coefficients are derived for four different channel estimation protocols. They differ in the direction in which the single-hop channels  and
and  are measured and can be compared based on two observations.
are measured and can be compared based on two observations.
-
(1)
Number of required channel uses: the effort required to estimate all first-hop and second-hop channel coefficients depends on the direction in which they are measured. In the following, we assume that it takes one channel use to estimate one channel coefficient.
-
(2)
Need for global phase reference: it turns out that for two of the protocols, the gain factors can only be computed correctly if the relays possess a global phase reference.
The channel coefficients in the two-hop network shown in Figure 1 can be measured (e.g., using training sequences or pilot symbols) either in forward direction, that is, from sources/relays to relays/destinations, or in backward direction, that is, from relays/destinations to sources/relays. In order to highlight the impact of the LO phases of the relays, estimation noise is omitted in this section. Measuring the first-hop and second-hop channels in forward direction consequently yields knowledge of the coefficients  and
and  . In contrast to that, estimating the channels in backward direction yields knowledge of
. In contrast to that, estimating the channels in backward direction yields knowledge of  and
and  (see (4)). There are altogether four combinations of directions in which the first-hop and second-hop channel matrices can be measured. The four corresponding protocols are as follows.
(see (4)). There are altogether four combinations of directions in which the first-hop and second-hop channel matrices can be measured. The four corresponding protocols are as follows.
Protocol A1
All channels are measured in forward direction. The anticipated equivalent two-hop channels are in this case given by

Protocol A2
All channels are measured in backward direction. The anticipated equivalent two-hop channels are now

which is the same as for protocol A1.
Protocol B1
For protocol B1 all channel coefficients are measured at the relays. The anticipated equivalent two-hop channels are in this case

If the LO phases of the relays are different, we generally have  . The gain factors can consequently not be computed correctly from
. The gain factors can consequently not be computed correctly from  and
and  . In this case, the relays require a global phase reference. This means that their LO phases have to be equal, that is,
. In this case, the relays require a global phase reference. This means that their LO phases have to be equal, that is,  , for all
, for all  . Equation (11) then becomes
. Equation (11) then becomes

The phase  that enters
that enters  may be random and unknown. As long as it is the same for all relays (due to a global phase reference), it has no impact on the way the signals add up at the destination antennas. Since
may be random and unknown. As long as it is the same for all relays (due to a global phase reference), it has no impact on the way the signals add up at the destination antennas. Since  , (12) implies that the anticipated SINR at destination
, (12) implies that the anticipated SINR at destination  (which is based on
(which is based on  ) is equal to the actual one.
) is equal to the actual one.
Protocol B2
For protocol B2, all channels are measured at the sources and destinations. The anticipated equivalent two-hop channels are

Again, the relays require a global phase reference. Otherwise, the gain factors cannot be computed correctly (cf. Protocol B1). For protocol B2, we get in this case

We have seen that the relays require a global phase reference if the channels are estimated with protocols B1 and B2. This means that an additional effort is necessary compared to A1 and A2. However, it turns out that protocols A1 and A2 require more channel uses in order to estimate all first-hop and second-hop channel coefficients than B1 and B2 if  (see Table 1). The total effort to estimate all channel coefficients in a two-hop network depends on the number of sources, relays, and destinations. Figure 2 shows the required number of channel uses (to estimate all channel coefficients) for all four protocols versus the number of source-destination pairs for
(see Table 1). The total effort to estimate all channel coefficients in a two-hop network depends on the number of sources, relays, and destinations. Figure 2 shows the required number of channel uses (to estimate all channel coefficients) for all four protocols versus the number of source-destination pairs for  . This value of
. This value of  has been shown to be the minimum number of relays that can orthogonalize
has been shown to be the minimum number of relays that can orthogonalize  source-destination pairs [6]. All values in the plot can take only integer numbers. The connecting lines between the points are simply for the sake of a better visualization. It can be seen that protocols B1 and B2 require less channel uses than protocols A1 and A2. In particular, the effort for B1 is by far the least of all protocols if the number of relays is large.
source-destination pairs [6]. All values in the plot can take only integer numbers. The connecting lines between the points are simply for the sake of a better visualization. It can be seen that protocols B1 and B2 require less channel uses than protocols A1 and A2. In particular, the effort for B1 is by far the least of all protocols if the number of relays is large.
Apart from the effort to measure all channel coefficients, the four protocols differ in the quality of the channel estimates they deliver in the presence of noise. In Section 6, we will discuss impact of additive noise and relay phase noise on the quality of the channel estimates. Since the anticipated equivalent two-hop channels are the same for protocols A1 and A2, (see (9) and (10)), it suffices to consider only one of them. Furthermore, (12) and (14) reveal that  . Consequently, the MSE of the anticipated equivalent two-hop channels is the same for protocols B1 and B2. In the following, we will thus confine ourselves to the discussion of protocols A1 and B1. The results then also hold for A2 and B2.
. Consequently, the MSE of the anticipated equivalent two-hop channels is the same for protocols B1 and B2. In the following, we will thus confine ourselves to the discussion of protocols A1 and B1. The results then also hold for A2 and B2.
It is important to realize that in a distributed network, each node can only estimate the channels to itself. For example, using protocol B1, relay  can only estimate the
can only estimate the  th row of the first-hop channel matrix and the
th row of the first-hop channel matrix and the  th column of the second-hop channel matrix. We call this kind of channel knowledge "local CSI". In contrast to that, "global CSI" refers to the knowledge of all channel coefficients. In the two-hop network shown in Figure 1, this means knowledge of the complete first-hop and second-hop channel matrices, that is,
th column of the second-hop channel matrix. We call this kind of channel knowledge "local CSI". In contrast to that, "global CSI" refers to the knowledge of all channel coefficients. In the two-hop network shown in Figure 1, this means knowledge of the complete first-hop and second-hop channel matrices, that is,  and
and  .
.
There exists no channel estimation protocol that yields global CSI at an individual node in a distributed network. In order to obtain global CSI at the relays in Figure 1 (so that they can compute their gain factors locally), all locally estimated channel coefficients have to be disseminated. Since the number of channel coefficients that have to be disseminated is identical for all protocols, the effort is the same in all cases. It has thus no impact on the comparison presented in this work and is omitted in the following considerations.
5. Distributed Phase Synchronization Scheme
In the previous section, we have seen that the gain factors can only be computed correctly from channel estimates obtained with protocols B1 or B2 if the relays are phase synchronous. Two approaches to provide the relays with a global phase reference have been presented in [22] and [25, 26]. The scheme presented in [22] will be used for channel estimation protocol B1 in Section 6 and is therefore shortly revisited in this section. Please refer to [22] for a more detailed description and a comparison to the scheme presented [25, 26]. We again focus on LO phase offsets and omit estimation noise in this section. Furthermore, the LO phases of all relays are assumed to be constant during a transmission cycle.
A single node (source, relay, or destination) in the network is assigned "master" M while all relays are "slaves". Each relay transmits a training sequence to the master node, which in turn retransmits conjugate-complex and time-inverted versions of its received sequences back to the relays. From their received signals, the relays can now obtain knowledge of

where  and
and  are the current LO phases of relay
are the current LO phases of relay  and the master node, respectively. The phase error introduced to
and the master node, respectively. The phase error introduced to  by the LO phases of the relays can be compensated with knowledge of
by the LO phases of the relays can be compensated with knowledge of  . Instead of disseminating
. Instead of disseminating  , each relay
, each relay  has to disseminate
has to disseminate

to all other relays. Together with  , the anticipated equivalent two-hop channel becomes (cf. (11))
, the anticipated equivalent two-hop channel becomes (cf. (11))

It has the same form as (12), where  , and is independent of the LO phases of the relays. Note that knowledge of
, and is independent of the LO phases of the relays. Note that knowledge of  is used to compensate the phase error introduced to
is used to compensate the phase error introduced to  by the channel estimates. This means that the phase synchronization scheme only has to be performed when the channel estimates are updated (and
by the channel estimates. This means that the phase synchronization scheme only has to be performed when the channel estimates are updated (and  has become outdated due to phase noise).
has become outdated due to phase noise).
In the following, we shortly assess the effort required to perform this phase synchronization scheme. Assume to this end that all relays transmit on orthogonal channels to the master node, which again transmits on orthogonal channels back to the relays. This results in a total of  orthogonal channel uses if none of the relay nodes acts as a master node (If a relay acts as master, the number of orthogonal channel uses reduces to
orthogonal channel uses if none of the relay nodes acts as a master node (If a relay acts as master, the number of orthogonal channel uses reduces to  . In the following, we will, however, assume that no relay acts as master node.). It yields the most accurate phase synchronization results (because there is no interference) but also requires the biggest effort. If the transmissions from relays to master node and back are orthogonalized in time, this corresponds to a total of
. In the following, we will, however, assume that no relay acts as master node.). It yields the most accurate phase synchronization results (because there is no interference) but also requires the biggest effort. If the transmissions from relays to master node and back are orthogonalized in time, this corresponds to a total of  timeslots. For a wideband system, orthogonality can instead be achieved in frequency domain, which then only requires a total of
timeslots. For a wideband system, orthogonality can instead be achieved in frequency domain, which then only requires a total of  timeslots. In the following, we will denote the number of channel uses required to perform the phase synchronization scheme by
timeslots. In the following, we will denote the number of channel uses required to perform the phase synchronization scheme by  .
.
The fact that protocols B1 and B2 require a global phase reference at the relays while A1 and A2 do not has to be taken into account when comparing their respective effort. Figure 3 shows the number of timeslots necessary to estimate all channel coefficients and to perform the phase synchronization scheme (for protocols B1 and B2). We plot the two extreme cases  and
and  and see that they lead to extremely different results for B2 and B1. This will be taken into account in the following by using
and see that they lead to extremely different results for B2 and B1. This will be taken into account in the following by using  as a parameter for the comparison.
as a parameter for the comparison.
6. Impact of Noise
Up to now, phase noise and additive noise perturbing the channel estimates have been neglected. Both will, however, degrade the quality of the channel estimates and therefore the performance of any coherent gain allocation scheme. While the impact of estimation noise on all protocols of Section 4 is the same, the impact of phase noise is not. In this section, the impact of relay phase noise and estimation noise on the quality of the channel estimates produced by protocols A1 and B1 is investigated. The result allows for a comparison that states which protocol delivers better channel estimates under which circumstances.
All relays are assumed to employ free running LO. Wiener phase noise is in this case an appropriate model that describes the LO phase fluctuations as sampled Wiener process (e.g., [27]). The severity of the unknown and random phase changes is then a linear function of time. Consequently, the protocols requiring more channel uses to estimate all coefficients suffer more from phase noise than those requiring less channel uses. In order to assess the impact of relay phase noise on the quality of the channel estimates, the notion of "block phase noise" is introduced: the LO phases of the relays stay constant for a single channel use and change randomly afterwards (similar to a block fading channel model). In the Wiener phase noise model, the phase changes are mutually independent, zero-mean Gaussian random variables. Their variance is in the following denoted by  . It is assumed to be the same for all relays.
. It is assumed to be the same for all relays.
In addition to phase noise, additive signal noise perturbs the measurement signal and thus has a degrading impact on the estimates. Let

denote the MMSE estimate of a channel coefficient  , where
, where  is additive noise and
is additive noise and  a scaling factor. The estimation error is given by
a scaling factor. The estimation error is given by  . By the property of the MMSE estimation,
. By the property of the MMSE estimation,  and
and  are uncorrelated and
are uncorrelated and  , where
, where  (e.g., [28]). If
(e.g., [28]). If  and
and  are known to the receiver, it can choose
are known to the receiver, it can choose

 has then the same variance as
has then the same variance as  and thus
and thus  . For a given estimation SNR (denoted by
. For a given estimation SNR (denoted by  ), the noise variance is given by
), the noise variance is given by

In the following, we derive expressions for the perturbed single-hop channel estimates obtained by protocols A1 or B1. These are then used as basis for the subsequent performance comparison of both protocols.
6.1. Single-Hop Channel Estimates: Protocol A1
Channel estimation protocol A1 starts with the sources transmitting their training sequences sequentially so that the relays can estimate their local first-hop channels. Afterwards, the relays sequentially transmit their training sequences so that the destinations can estimate their local second-hop channels. The timeslots at which the nodes transmit their training sequences are given in Table 2. After all channel coefficients are measured, the relays and destinations disseminate their local estimates to all relays so that they can locally compute their respective gain factors. In the following, we derive expressions for the channel estimates as a function of the actual channels and the perturbations (additive estimation noise and phase noise).
 First-Hop Channels. Let
First-Hop Channels. Let  denote the phase offset of relay
denote the phase offset of relay  in timeslot 1. Furthermore, the phase change between timeslots
in timeslot 1. Furthermore, the phase change between timeslots  and
and  is denoted by
is denoted by  ,
,  . Consequently, the phase offset of relay
. Consequently, the phase offset of relay  in timeslot
in timeslot  , that is, while source
, that is, while source  is transmitting its training sequence, is given by
is transmitting its training sequence, is given by

where  . Since all
. Since all  are mutually independent (a property of the Wiener phase noise model), their sum is zero-mean Gaussian with variance
are mutually independent (a property of the Wiener phase noise model), their sum is zero-mean Gaussian with variance  . The estimated channel coefficient between source
. The estimated channel coefficient between source  and relay
and relay  is then given by
is then given by

where  is given in (19) and
is given in (19) and  is AWGN (cf. (18)).
is AWGN (cf. (18)).
 Second-Hop Channels. From timeslot
Second-Hop Channels. From timeslot  until timeslot
until timeslot  , the relays transmit training sequences to the destinations. Let
, the relays transmit training sequences to the destinations. Let  be defined as in (21) for
be defined as in (21) for  . Then the estimated channel coefficients are
. Then the estimated channel coefficients are

where  is AWGN and
is AWGN and

The phase changes  are zero-mean Gaussian with variance
are zero-mean Gaussian with variance  . Furthermore, the scaling factor
. Furthermore, the scaling factor  is assumed to be the same as for the estimation of the first-hop channel coefficients because the channel coefficients and noise samples have the same statistics.
is assumed to be the same as for the estimation of the first-hop channel coefficients because the channel coefficients and noise samples have the same statistics.
6.2. Single-Hop Channel Estimates: Protocol B1
Protocol B1 starts in the same way as A1. The sources sequentially transmit their training sequences so that the relays can estimate their local first-hop channels. Afterwards, phase synchronization as described in Section 5 is performed to provide the required phase reference at the relays. This scheme requires  timeslots, where
timeslots, where  . Finally, the destinations sequentially transmit their training sequences so that the relays can estimate the local second-hop channels in backward direction. The timeslots at which the nodes transmit their training sequences are given in Table 3. For the phase synchronization, all relays transmit their training sequences in timeslots
. Finally, the destinations sequentially transmit their training sequences so that the relays can estimate the local second-hop channels in backward direction. The timeslots at which the nodes transmit their training sequences are given in Table 3. For the phase synchronization, all relays transmit their training sequences in timeslots  to
to  . The master node M then transmits in timeslots
. The master node M then transmits in timeslots  until
until  .
.
 First-Hop Channels: the estimated first-hop channel coefficients are the same as for protocol A1. They are given in (22).
First-Hop Channels: the estimated first-hop channel coefficients are the same as for protocol A1. They are given in (22).
 Phase Synchronization: at timeslot
Phase Synchronization: at timeslot  , the relays start to transmit their training symbols
, the relays start to transmit their training symbols  on orthogonal channels to the master node M. The phase offset of relay
on orthogonal channels to the master node M. The phase offset of relay  at this time is denoted by
at this time is denoted by

where  is the phase offset at timeslot
is the phase offset at timeslot  (cf. (21) for
(cf. (21) for  ) and
) and

is the phase change between timeslots  and
and  due to phase noise. For the phase synchronization scheme, we assume that the average accuracy is equal for all relays. This is realized by the assumption the relay phases stay constant not only for a single channel use, but for
due to phase noise. For the phase synchronization scheme, we assume that the average accuracy is equal for all relays. This is realized by the assumption the relay phases stay constant not only for a single channel use, but for  channel uses. Thus, they remain unchanged for the time it takes all relays to transmit their training sequences to M. Afterwards, the phases change and remain unchanged again for the time the master node retransmits to the relays. The signal that is received at M from relay
channel uses. Thus, they remain unchanged for the time it takes all relays to transmit their training sequences to M. Afterwards, the phases change and remain unchanged again for the time the master node retransmits to the relays. The signal that is received at M from relay  can then be written as
can then be written as

where  is the respective channel coefficient and
is the respective channel coefficient and  additive noise at the master node. The transmission from relays to the master node takes
additive noise at the master node. The transmission from relays to the master node takes  timeslots. At timeslot
timeslots. At timeslot  , the master node starts retransmitting
, the master node starts retransmitting

which is the conjugate complex of its received symbol  . At this time, the LO phase offset of relay
. At this time, the LO phase offset of relay  is
is  , where
, where

is the phase change due to phase noise. Consequently, relay  receives
receives

Multiplication with  and phase estimation yields
and phase estimation yields

where  and
and  . The phase offset
. The phase offset

is due to phase noise and  is due to the additive noise components in (30). In [29] it was shown that for large SNR,
is due to the additive noise components in (30). In [29] it was shown that for large SNR,  is approximately Gaussian. For the following considerations, this assumption is made and we have
is approximately Gaussian. For the following considerations, this assumption is made and we have  and
and  .
.
 Second-Hop Channels: for the estimation of the second-hop channel coefficients, the relay phases stay constant for a single channel use and change independently afterwards. In contrast to protocol A1, the second-hop channels are now estimated in backward direction. This means that the channel coefficients are measured at the relays. Their estimates are given by
Second-Hop Channels: for the estimation of the second-hop channel coefficients, the relay phases stay constant for a single channel use and change independently afterwards. In contrast to protocol A1, the second-hop channels are now estimated in backward direction. This means that the channel coefficients are measured at the relays. Their estimates are given by

The respective relay phases  are
are

where the phase changes  and
and  are given in (26) and (29), respectively. Furthermore,
are given in (26) and (29), respectively. Furthermore,  and
and  for
for  . The variance of
. The variance of  is larger than the variance of
is larger than the variance of  for
for  because it took the master
because it took the master  timeslots to transmit to all relays during the phase synchronization procedure.
timeslots to transmit to all relays during the phase synchronization procedure.
 Disseminated Channel Coefficients: after the first-hop and second-hop channel coefficients have been measured, the estimates have to be disseminated to all relays. The disseminated first-hop and second-hop channel estimates are
Disseminated Channel Coefficients: after the first-hop and second-hop channel coefficients have been measured, the estimates have to be disseminated to all relays. The disseminated first-hop and second-hop channel estimates are  as given in (22) and
as given in (22) and

respectively (cf. (16)). The phase correction term  is the result of the phase synchronization scheme. It is given in (31).
is the result of the phase synchronization scheme. It is given in (31).
6.3. Channel Estimation Error: Equivalent Two-Hop Channels
A sensible performance measure for the channel estimation schemes was found to be how well the anticipated equivalent two-hop channels match the actual ones. In this section, we derive  defined in (8) for protocols A1 and B1, respectively. The main results are (41) and (48).
defined in (8) for protocols A1 and B1, respectively. The main results are (41) and (48).
 Protocol A1: for channel estimation protocol A1, the estimates of the first-hop and second-hop channel coefficients are given in (22) and (23), respectively. The anticipated and the actual equivalent two-hop channel coefficients between source
Protocol A1: for channel estimation protocol A1, the estimates of the first-hop and second-hop channel coefficients are given in (22) and (23), respectively. The anticipated and the actual equivalent two-hop channel coefficients between source  and destination
and destination  are in this case
are in this case


respectively, where  . Note that the gain factors
. Note that the gain factors  in (36) and (37) are the same. The channel estimation error
in (36) and (37) are the same. The channel estimation error  is defined in (7). In order to compute the MSE given in (8) by averaging over the perturbing noise (additive estimation noise and phase noise), the dependence of the gain factors on the channel estimates has to be known explicitly. Since we want to compare the channel estimation protocols independently from a specific gain allocation scheme, we instead fix the channel estimates (and therefore also
is defined in (7). In order to compute the MSE given in (8) by averaging over the perturbing noise (additive estimation noise and phase noise), the dependence of the gain factors on the channel estimates has to be known explicitly. Since we want to compare the channel estimation protocols independently from a specific gain allocation scheme, we instead fix the channel estimates (and therefore also  ) and average over all channel realizations that might have led to these estimates. Let
) and average over all channel realizations that might have led to these estimates. Let

denote the sets of actual and estimated channel coefficients between source  and all relays and between all relays and destination
and all relays and between all relays and destination  . The MSE of the estimated equivalent two-hop channels is then given by
. The MSE of the estimated equivalent two-hop channels is then given by

where

because all channel coefficients are mutually independent. It can be shown that

where  is defined in (36). The proof is included in [30] but is omitted in this work due to space limitation. The gradient of the MSE with respect to the gain factors is
is defined in (36). The proof is included in [30] but is omitted in this work due to space limitation. The gradient of the MSE with respect to the gain factors is  , where
, where  is the vector comprising all
is the vector comprising all  . It can easily be derived from (41) and is useful for gradient-based gain allocations that optimize the relay gains for robustness against channel estimation errors.
. It can easily be derived from (41) and is useful for gradient-based gain allocations that optimize the relay gains for robustness against channel estimation errors.
 Protocol B1: for channel estimation protocol B1, the estimates of the first-hop and second-hop channel coefficients are given in (22) and (35), respectively. They can be written as
Protocol B1: for channel estimation protocol B1, the estimates of the first-hop and second-hop channel coefficients are given in (22) and (35), respectively. They can be written as


For (43) we used (35), (31), (33), and  (cf. (4)). Furthermore,
(cf. (4)). Furthermore,  has the same statistics as
has the same statistics as  . The anticipated and the actual equivalent two-hop channel coefficients between source
. The anticipated and the actual equivalent two-hop channel coefficients between source  and destination
and destination  are given in (36) and (37), respectively. For a noiseless estimation, that is,
are given in (36) and (37), respectively. For a noiseless estimation, that is,  and
and  (cf. (35)), (36) becomes
(cf. (35)), (36) becomes

Again, we fix the channel estimates (and therefore also  ) and average the channel estimation error
) and average the channel estimation error  over all channel realizations that might have led to these estimates. The phase difference
over all channel realizations that might have led to these estimates. The phase difference  between (37) and (44) has to be taken into account when computing
between (37) and (44) has to be taken into account when computing  . It is in this case given by
. It is in this case given by

where

Comparing (46) with (36) and (45) with (7) reveals that the MSE of the estimated equivalent two-hop channel coefficients for protocol B1 can easily be derived from (41). Since

the resulting MSE is found by replacing  in (41) by
in (41) by  :
:

where  is defined in (36). The gradient
is defined in (36). The gradient  can be easily computed from (48).
can be easily computed from (48).
6.4. Channel Estimation Error: Single-Hop Channels
Instead of averaging over all channel and noise realizations, the MSEs in the previous section have been computed for fixed channel estimates. It is not clear how well the actual quality of the estimates is reflected in this measure. In this section, we investigate an alternative measure that is very simple. Since both protocols deliver the same estimates for the first-hop channels, we compare them based on the quality of the second-hop channel estimates.
For protocol A1, the estimated channel coefficient between relay  and destination
and destination  is given in (23). The MSE of the second-hop channel estimate is then
is given in (23). The MSE of the second-hop channel estimate is then

For protocol B1, the estimate of the second hop channel between relay  and destination
and destination  is given in (35). The MSE with respect to the noiseless case is thus
is given in (35). The MSE with respect to the noiseless case is thus

where  is given in (33) and
is given in (33) and  in (31). Equation (50) can be written as
in (31). Equation (50) can be written as

where  and
and  is given in (34), respectively. Taking their mutual dependency into account, we finally get
is given in (34), respectively. Taking their mutual dependency into account, we finally get

Note that  is independent of
is independent of  and we denote
and we denote  ,
,  .
.
7. Performance Comparison
In this section, the quality of the channel estimates produced by protocols A1 and B1 is compared quantitatively. To this end, a simple network is used as an application example. It comprises a single source-destination pair and  relays, where the gain allocation is distributed MRC, that is, the relay gain factors are
relays, where the gain allocation is distributed MRC, that is, the relay gain factors are

The scaling factor  ensures that an average transmit power constraint is met. Since the gain factors are explicit functions of the channel estimates, we can furthermore assess the accuracy with which the approximations in Sections 6.3 and 6.4 judge the performance of the protocols: averaging the squared estimation error over the perturbations (estimation noise and phase noise) delivers reference MSE of the anticipated equivalent two-hop channels in closed-form. They are denoted by
ensures that an average transmit power constraint is met. Since the gain factors are explicit functions of the channel estimates, we can furthermore assess the accuracy with which the approximations in Sections 6.3 and 6.4 judge the performance of the protocols: averaging the squared estimation error over the perturbations (estimation noise and phase noise) delivers reference MSE of the anticipated equivalent two-hop channels in closed-form. They are denoted by  and
and  for protocols A1 and B1, respectively.
for protocols A1 and B1, respectively.
We compare the quality of the channel estimates by computing the ratio of MSE. The reference  will be denoted by "Two-hop MSE (reference)". A value larger than one means that the estimates produced by B1 are more accurate than those produced by A1, a value smaller than one means that B1 delivers more accurate estimates than A1. Note that the number of source-destination pairs and relays in the network has an impact on the quality of the channel estimates. While the estimated first-hop channels are equal for protocols A1 and B1, the MSEs of the second-hop estimates are not. Their MSEs (and thus the quality of their estimates) are equal if
will be denoted by "Two-hop MSE (reference)". A value larger than one means that the estimates produced by B1 are more accurate than those produced by A1, a value smaller than one means that B1 delivers more accurate estimates than A1. Note that the number of source-destination pairs and relays in the network has an impact on the quality of the channel estimates. While the estimated first-hop channels are equal for protocols A1 and B1, the MSEs of the second-hop estimates are not. Their MSEs (and thus the quality of their estimates) are equal if  (cf. (49) and (52)). Although being independent of
(cf. (49) and (52)). Although being independent of  , this point is a function of the destination index
, this point is a function of the destination index  . Increasing the
. Increasing the  while keeping
while keeping  constant is therefore in favor of protocol A1. If the number of relays increases, the relation between
constant is therefore in favor of protocol A1. If the number of relays increases, the relation between  and
and  determines which protocol delivers the better estimates of the second-hop channel coefficients.
determines which protocol delivers the better estimates of the second-hop channel coefficients.
The performance comparison in this section is based on the above-mentioned application example but the results in Sections 6.3 and 6.4 can be used to compare the channel estimation protocols for any two-hop network configuration (e.g., multiuser networks) and gain allocation. We use the ratio of MSE to compare the quality of the estimates obtained by protocols A1 and B1. The ratios of MSE used for performance comparison are as follows.
-
(1)
Section 6.3: in order to compare the quality of the estimates produced by A1 and B1 based on (41) and (48), we average
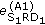 and
and 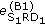 over all channel estimates in
over all channel estimates in  for the case that the gain factors are given in (53). The ratio
for the case that the gain factors are given in (53). The ratio 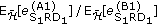 is then denoted by "Fixed estimate MSE".
is then denoted by "Fixed estimate MSE". -
(2)
Section 6.4: since (49) depends on the order in which the relays transmit their training sequences, we perform an averaging over all relays and define
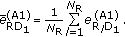 (54)
(54)The ratio
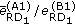 is then denoted by "Second-hop MSE", where
is then denoted by "Second-hop MSE", where  and
and  are given in (49) and (52), respectively.
are given in (49) and (52), respectively.
The dashed, horizontal line in Figures 4–7 indicates the points where the performance of protocols A1 and B1 is equal. The estimation SNR is defined in (20), where  . It is assumed to be the same for both the first-hop and the second-hop channel estimates. In Figure 4, the MSE ratios are plotted versus
. It is assumed to be the same for both the first-hop and the second-hop channel estimates. In Figure 4, the MSE ratios are plotted versus  . For small number of relays, Protocol A1 delivers the more accurate channel estimates. Protocol B1 outperforms A1 in terms of estimation accuracy for large
. For small number of relays, Protocol A1 delivers the more accurate channel estimates. Protocol B1 outperforms A1 in terms of estimation accuracy for large  because the number of channel uses required by A1 to estimate all coefficients increases with
because the number of channel uses required by A1 to estimate all coefficients increases with  whereas B1 is unaffected (see Table 1). Figure 5 shows the MSE ratios versus
whereas B1 is unaffected (see Table 1). Figure 5 shows the MSE ratios versus  . Increasing the number of timeslots required by the phase synchronization scheme leads to a decreasing quality of the channel estimates obtained by protocol B1. Since protocol A1 does not require phase synchronization, its performance is unaffected. In Figure 6, the MSE ratio is depicted versus
. Increasing the number of timeslots required by the phase synchronization scheme leads to a decreasing quality of the channel estimates obtained by protocol B1. Since protocol A1 does not require phase synchronization, its performance is unaffected. In Figure 6, the MSE ratio is depicted versus  . Phase noise degrades the estimates obtained by protocol A1 more than those obtained by B1. The reason for this behavior is that in the present configuration A1 requires more channel uses to estimate all channel coefficients than B1. For large
. Phase noise degrades the estimates obtained by protocol A1 more than those obtained by B1. The reason for this behavior is that in the present configuration A1 requires more channel uses to estimate all channel coefficients than B1. For large  , the performance of both protocols converges because the phases of the channel estimates will asymptotically be uniformly distributed. Furthermore, it can be observed that the comparison based on the results from Section 6.4 slightly overestimates the performance of protocol A1 for large
, the performance of both protocols converges because the phases of the channel estimates will asymptotically be uniformly distributed. Furthermore, it can be observed that the comparison based on the results from Section 6.4 slightly overestimates the performance of protocol A1 for large  . The MSE ratios are shown versus the estimation SNR in Figure 7. The quality of the estimates produced by protocol B1 suffers more from decreasing
. The MSE ratios are shown versus the estimation SNR in Figure 7. The quality of the estimates produced by protocol B1 suffers more from decreasing  than A1. The reason for this behavior is that, apart from the channel coefficients, the phase values have to be estimated for the phase synchronization scheme. This is an additional source of error that degrades performance. However, for large
than A1. The reason for this behavior is that, apart from the channel coefficients, the phase values have to be estimated for the phase synchronization scheme. This is an additional source of error that degrades performance. However, for large  , the impact of additive noise becomes negligible and the fact that protocol A1 suffers more from phase noise than B1 dominates. Protocol B1 thus outperforms A1 at high
, the impact of additive noise becomes negligible and the fact that protocol A1 suffers more from phase noise than B1 dominates. Protocol B1 thus outperforms A1 at high  .
.
Comparing the curves to the respective references ("Two-hop MSE (reference)") shows that the measure in Section 6.3 is very accurate for high-estimation SNR (from about  ). Furthermore, the measure in Section 6.4 is very accurate in medium estimation SNR (
). Furthermore, the measure in Section 6.4 is very accurate in medium estimation SNR ( ) and low-phase noise (
) and low-phase noise ( ). In the respective range of parameters, both measures are able to judge the performance of both channel estimation protocols very well.
). In the respective range of parameters, both measures are able to judge the performance of both channel estimation protocols very well.
8. Conclusions
In this work, we investigated different channel estimation protocols for two-hop AF relaying networks (single-user and multiuser) in the presence of additive estimation noise and relay phase noise. They differ in the direction in which the single-hop links are measured and thus the required effort to estimate all channel coefficients in the network. We used the MSE of the channel estimates as an indicator for the performance of the protocols. This is a sensible measure because computing the gain factors from more accurate channel estimates will on the average lead to better system performance. It was possible to draw conclusions independently of the gain allocation by comparing the MSE of the second-hop estimates only. Finally, we compared the protocols quantitatively for a single-user application example. It is important to note that the results can as well be used to assess the channel estimation protocols for any two-hop network configuration and gain allocation.
References
Laneman JN, Wornell GW: Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks. IEEE Transactions on Information Theory 2003, 49(10):2415-2425. 10.1109/TIT.2003.817829
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part I: system description. IEEE Transactions on Communications 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part II: implementation aspects and performance analysis. IEEE Transactions on Communications 2003, 51(11):1939-1948. 10.1109/TCOMM.2003.819238
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Muhaidat H, Uysal M: Cooperative diversity with multiple-antenna nodes in fading relay channels. IEEE Transactions on Wireless Communications 2008, 7(8):3036-3046.
Wittneben A, Rankov B: Distributed antenna systems and linear relaying for gigabit MIMO wireless. Proceedings of the 60th IEEE Vehicular Technology Conference (VTC '04), September 2004, Los Angeles, Calif, USA 3624-3630.
Morgenshtern VI, Boelcskei H, Nabar RU: Distributed orthogonalization in large interference relay networks. Proceedings of IEEE International Symposium on Information Theory (ISIT '05), September 2005 1211-1215.
Bölcskei H, Nabar RU, Oyman Ö, Paulraj AJ: Capacity scaling laws in MIMO relay networks. IEEE Transactions on Wireless Communications 2006, 5(6):1433-1444.
Dana AF, Hassibi B: On the power efficiency of sensory and ad hoc wireless networks. IEEE Transactions on Information Theory 2006, 52(7):2890-2914.
Patel CS, Stüber GL: Channel estimation for amplify and forward relay based cooperation diversity systems. IEEE Transactions on Wireless Communications 2007, 6(6):2348-2355.
Cui T, Gao F, Nallanathan A: Optimal training design for channel estimation in amplify and forward relay networks. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007 4015-4019.
Gao F, Cui T, Nallanathan A: On channel estimation and optimal training design for amplify and forward relay networks. IEEE Transactions on Wireless Communications 2008, 7(5):1907-1916.
Eşli C, Wagner J, Wittneben A: Distributed gradient based gain allocation for coherent multiuser AF relaying networks. Proceedings of the IEEE International Conference on Communications (ICC '09), June 2009
Berger S, Wittneben A: Cooperative distributed multiuser MSE relaying in wireless ad-hoc networks. Proceedings of the 39th Asilomar Conference on Signals, Systems and Computers, October-November 2005, Pacific Grove, Calif, USA 1072-1076.
Khajehnouri N, Sayed AH: A distributed MMSE relay strategy for wireless sensor networks. Proceedings of the 6th Workshop on Signal Processing Advances in Wireless Communications (SPAWC '05), June 2005 796-800.
Shi H, Abe T, Asai T, Yoshino H: Analyses of achievable gains in half duplex MIMO relaying schemes using multiple relay nodes. IEICE Transactions on Communications 2007, E90-B(9):2541-2551. 10.1093/ietcom/e90-b.9.2541
Guan W, Luo H: Joint MMSE transceiver design in non-regenerative MIMO relay systems. IEEE Communications Letters 2008, 12(7):517-519.
Ding Z, Chin WH, Leung KK: Distributed beamforming and power allocation for cooperative networks. IEEE Transactions on Wireless Communications 2008, 7(5):1817-1822.
Meyr H, Moeneclaey M, Fechtel SA: Digital Communication Receivers: Synchronization, Channel Estimation, and Signal Processing, Wiley Series in Telecommunications and Signal Processing. John Wiley & Sons, New York, NY, USA; 1997.
Berger S, Wittneben A: When do non-regenerative two-hop relaying networks require a global phase reference? Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '09), November-December 2009, Honolulu, Hawaii, USA
Behbahani AS, Eltawil A: On channel estimation and capacity for amplify and forward relay networks. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '08), December 2008 3685-3689.
Berger S, Wittneben A: Carrier phase synchronization of multiple distributed nodes in a wireless network. Proceedings of the 8th IEEE Signal Processing Advances in Wireless Communications (SPAWC '07), June 2007, Helsinki, Finland
Proakis JG: Digital Communications, McGraw-Hill Series in Electrical and Computer Engineering. McGraw-Hill, New York, NY, USA; 2001.
Berger S, Wittneben A: Impact of local-oscillator imperfections on nonregenerative TDD and FDD relaying. Proceedings of Vehicular Technology Conference (VTC '10), May 2010, Taipei, Taiwan
Tu Y-S, Pottie GJ: Coherent cooperative transmission from multiple adjacent antennas to a distant stationary antenna through AWGN channels. Proceedings of the 55th Vehicular Technology Conference (VTC '02), 2002, Birmingham, Ala, USA 1: 130-134.
Barriac G, Mudumbai R, Madhow U: Distributed beamforming for information transfer in sensor networks. Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks (IPSN '04), April 2004 81-88.
Demir A, Mehrotra A, Roychowdhury J: Phase noise in oscillators: a unifying theory and numerical methods for characterization. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications 2000, 47(5):655-674. 10.1109/81.847872
Yoo T, Goldsmith A: Capacity and power allocation for fading MIMO channels with channel estimation error. IEEE Transactions on Information Theory 2006, 52(5):2203-2214.
Berger S, Wittneben A: Impact of noisy carrier phase synchronization on linear amplify- and-forward relaying. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007 795-800.
Berger S: Coherent cooperative relaying in low-mobility multiuser networks, Ph.D. dissertation. ETH, Zurich, Switzerland; 2010. Appendix A1, http://www.nari.ee.ethz.ch/~berger/Appendix_A1.pdf
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Berger, S., Wittneben, A. Comparison of Channel Estimation Protocols for Coherent AF Relaying Networks in the Presence of Additive Noise and LO Phase Noise. J Wireless Com Network 2010, 861735 (2010). https://doi.org/10.1155/2010/861735
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/861735


 .
.

 .
.
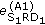 and
and 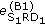 over all channel estimates in
over all channel estimates in  for the case that the gain factors are given in (53). The ratio
for the case that the gain factors are given in (53). The ratio 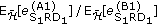 is then denoted by "
is then denoted by "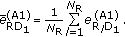
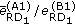 is then denoted by "
is then denoted by " and
and  are given in (49) and (52), respectively.
are given in (49) and (52), respectively.
 for
for
 ,
,
 , and
, and
 .
.

 for
for
 ,
,
 , and
, and
 .
.

 for
for
 ,
,
 , and
, and
 .
.

 for
for
 ,
,
 , and
, and
 .
.