- Research Article
- Open access
- Published:
VLSI Implementation of a Fixed-Complexity Soft-Output MIMO Detector for High-Speed Wireless
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 893184 (2010)
Abstract
This paper presents a low-complexity MIMO symbol detector with close-Maximum a posteriori performance for the emerging multiantenna enhanced high-speed wireless communications. The VLSI implementation is based on a novel MIMO detection algorithm called Modified Fixed-Complexity Soft-Output (MFCSO) detection, which achieves a good trade-off between performance and implementation cost compared to the referenced prior art. By including a microcode-controlled channel preprocessing unit and a pipelined detection unit, it is flexible enough to cover several different standards and transmission schemes. The flexibility allows adaptive detection to minimize power consumption without degradation in throughput. The VLSI implementation of the detector is presented to show that real-time MIMO symbol detection of 20 MHz bandwidth 3GPP LTE and 10 MHz WiMAX downlink physical channel is achievable at reasonable silicon cost.
1. Introduction
Multi-antenna or multi-in and multiout (MIMO) technologies have been widely adopted by the latest wireless standards such as 3GPP LTE and WiMAX to enhance the spectrum efficiency. For MIMO systems, a major challenge is the symbol detection at the receiver. In particular, as channel coding (e.g., Turbo) is used, soft output (the log-likelihood ratio, LLR) must be computed as the input to the channel decoder. Consider a MIMO system with  transmit antennas and
transmit antennas and  receive antennas. Let
receive antennas. Let  be a transmitted vector of length
be a transmitted vector of length  , obtained by mapping a set of information bits onto an
, obtained by mapping a set of information bits onto an  -QAM constellation
-QAM constellation  . Then the received vector of length
. Then the received vector of length  is given by
is given by

where  is an
is an  complex-valued channel matrix which is assumed to be known.
complex-valued channel matrix which is assumed to be known.  is the transmitted symbol vector.
is the transmitted symbol vector.  is noise vector and
is noise vector and  is the received symbol vector. The optimum soft detector is Maximum-A-Posteriori (MAP) detector which computes
is the received symbol vector. The optimum soft detector is Maximum-A-Posteriori (MAP) detector which computes

Here " " means all
" means all  for which the
for which the  th bit of
th bit of  is equal to
is equal to  . Computing (2) requires enumeration of the entire set of possible transmitted vectors. The complexity of doing this is usually not affordable in practice.
. Computing (2) requires enumeration of the entire set of possible transmitted vectors. The complexity of doing this is usually not affordable in practice.
As a trade-off between performance and complexity, various MIMO detection methods such as sphere decoding [1, 2], fixed complexity sphere decoding [3, 4], and MFCSO decoding [5] have been proposed to reach near-MAP performance with lower complexity than MAP. In [6], VLSI implementation of a complexity reduced K-best detector for  MIMO and 16-QAM is presented for WiMAX/WiFi. In [7], VLSI implementation of a soft-output MIMO detector for
MIMO and 16-QAM is presented for WiMAX/WiFi. In [7], VLSI implementation of a soft-output MIMO detector for  MIMO in WLAN is presented. Without QR decomposition unit being included, it consumes 135 kGate with a reduced candidate list. In [8], a K-best detector for
MIMO in WLAN is presented. Without QR decomposition unit being included, it consumes 135 kGate with a reduced candidate list. In [8], a K-best detector for  MIMO is implemented in a Xilinx Virtex-5 FPGA. However, the complexity of sphere decoding grows exponentially with the number of transmit antennas and polynomially in the size of the signal constellation. More importantly, the tree search used in sphere decoding is in principle a sequential procedure which is difficult to parallelize. In [3], a fixed-throughput sphere detector is proposed with fixed complexity and parallelism for hard decision. In [5], a low-complexity near-MAP detection method is proposed for high-order modulation (e.g., 64-QAM). The performance loss from MAP due to the suboptimal search introduced in MFCSO is proven by simulation to be small in [5]. However, in [5], the complexity of MFCSO is only presented in number of arithmetic operations without the silicon cost and processing latency being addressed and no comparison with prior art is made. Most importantly, none of these methods proposed have taken the system specific features of LTE (e.g., OFDMA and H-ARQ) into consideration and are mostly based on very simple channel models (e.g., AWGN). In [9], limited evaluation of MFCSO is carried out with a focus on LTE system.
MIMO is implemented in a Xilinx Virtex-5 FPGA. However, the complexity of sphere decoding grows exponentially with the number of transmit antennas and polynomially in the size of the signal constellation. More importantly, the tree search used in sphere decoding is in principle a sequential procedure which is difficult to parallelize. In [3], a fixed-throughput sphere detector is proposed with fixed complexity and parallelism for hard decision. In [5], a low-complexity near-MAP detection method is proposed for high-order modulation (e.g., 64-QAM). The performance loss from MAP due to the suboptimal search introduced in MFCSO is proven by simulation to be small in [5]. However, in [5], the complexity of MFCSO is only presented in number of arithmetic operations without the silicon cost and processing latency being addressed and no comparison with prior art is made. Most importantly, none of these methods proposed have taken the system specific features of LTE (e.g., OFDMA and H-ARQ) into consideration and are mostly based on very simple channel models (e.g., AWGN). In [9], limited evaluation of MFCSO is carried out with a focus on LTE system.
In this paper, with the aid of more realistic LTE and WiMAX simulation chains and different channel models, several MIMO detection algorithms are applied to LTE and WiMAX systems and with their performance quantitatively evaluated. Second, although the MFCSO detection algorithm proposed by the authors in [5] has a very low detection complexity, under random AWGN channels, it requires relatively strong channel coding to maintain a near-MAP performance in frame error ratio [5]. In this paper, its performance with the aid of H-ARQ is investigated. In order to validate MFCSO from VLSI implementation perspectives, both FPGA and ASIC implementation of an MFCSO detector is presented. Note that most commercial terminals are limited by cost and power consumption, especially the power consumption of the analog part of each antenna chain. According to the LTE and WiMAX standards,  and
and  MIMO schemes are included as a good trade-off between performance gain and complexity (or power consumption). Hence, only these schemes are considered in here. The result is compared with a state-of-the-art soft-output sphere decoding (SSD) [1] and the K-best detector presented in [10] from both performance and cost aspects.
MIMO schemes are included as a good trade-off between performance gain and complexity (or power consumption). Hence, only these schemes are considered in here. The result is compared with a state-of-the-art soft-output sphere decoding (SSD) [1] and the K-best detector presented in [10] from both performance and cost aspects.
The remainder of the paper is organized as follows. In Section 2, the application of MIMO techniques in LTE and WiMAX is presented. Section 3 introduces the linear and MFCSO MIMO detection algorithms. Section 4 addresses the detection flow. The architecture of the detector is addressed in Section 5. The link-level simulation results are presented in Section 6. Section 7 analyzes the implementation complexity, and Section 8 presents the adaptive method used to optimize power efficiency. Section 9 presents both the FPGA-and ASIC-based implementation of the detector. Finally, Section 10 concludes the paper.
2. MultiAntenna in LTE and WiMAX
Wireless standards such as 3GPP LTE and WiMAX have incorporated MIMO transmission schemes to boost the peak data rate. Meanwhile, software-defined radio (SDR) technologies allow both of them to be supported by the same piece of hardware.
3GPP Long-Term Evolution (LTE) is the next generation radio access technology which incorporates Orthogonal Frequency Division Multiple Access (OFDMA) as the multiple access scheme in downlink. MIMO technologies are also mandatory in LTE to achieve the LTE bit-rate targets (e.g 100 Mbit/s peak data rate for downlink). As part of the receiver chain depicted in Figure 1, MIMO symbol detection is a significant challenge for VLSI implementation.
The input to the MIMO detector presented in this paper includes the estimated channel matrix

the received symbol vector  , and the estimated noise variance
, and the estimated noise variance  . The output of the detector is the LLR values of the demodulated bits.
. The output of the detector is the LLR values of the demodulated bits.
In both LTE and WiMAX, spatial multiplexing (SM) and transmit diversity have been adopted as the two major MIMO schemes. SM is a MIMO technique aimed at maximizing the data throughput by exploiting the degrees of freedom in MIMO channels. Since the multiplexing gain is only available for high SNR region, spatial multiplexing is usually used when high SNR is available. STBC/SFBC [11] assumes the channel is stationary among adjacent time intervals or subcarriers so that a single codeword is mapped to these adjacent intervals or subcarriers to benefit from either time or frequency diversity in transmission. The most widely used STBC/SFBC scheme is Alamouti scheme in space or frequency domain. Since STBC/SFBC only requires a linear detector to achieve diversity, the detector design is easier. Note that in this paper, only open-loop MIMO is considered without feedback from the terminal.
2.1. Spatial Multiplexing
Spatial multiplexing is a MIMO technique aimed at maximizing the data throughput by exploiting the degrees of freedom in MIMO channels. Since the multiplexing gain is only available in high SNR region, spatial multiplexing is usually used when high SNR is available. As depicted in Figure 2(a), spatial multiplexing usually requires both  and
and  to be large. In general, the degree of freedom (multiplexing gain) is determined by
to be large. In general, the degree of freedom (multiplexing gain) is determined by  which is the rank of the channel matrix
which is the rank of the channel matrix  . In case
. In case  is badly conditioned (e.g. when line-of-sight occurs,
is badly conditioned (e.g. when line-of-sight occurs,  becomes a singular matrix), the pseudoinversion of
becomes a singular matrix), the pseudoinversion of  in (15) using linear detection will be very difficult which requires very large dynamic range. In other words, the gain of spatial multiplexing heavily depends on the multipath fading. A dual-stream spatial multiplexing scheme is depicted in Figure 2(a) .
in (15) using linear detection will be very difficult which requires very large dynamic range. In other words, the gain of spatial multiplexing heavily depends on the multipath fading. A dual-stream spatial multiplexing scheme is depicted in Figure 2(a) .
2.2. Transmit Diversity
Transmit diversity schemes that exploit the diversity gain of multi-antenna transmission have also been adopted by LTE and WiMAX. The Space-Time Block Coding (STBC) in WiMAX and Space-Frequency Block Coding (SFBC) in LTE [11] are both transmit diversity schemes to transmit data for guaranteed diversity while requiring only a low-complexity symbol detector on the receiver side. In both cases, the Alamouti matrix [12] is used because it is the only full-rate linear STBC (or SFBC) code with a diversity gain of 2. In other words, the transmit diversity schemes considered in this paper are Alamouti schemes in the space and frequency domains. This assumes the channels of either adjacent symbol intervals or subcarriers are identical, so that either time or frequency diversity will be achieved when a single codeword is mapped to different antennas within two adjacent time or frequency intervals. The basic  space-frequency channel matrix is defined as
space-frequency channel matrix is defined as

3. Soft-Output MIMO Detection
The optimum soft-output MIMO detector computes the Log-Likelihood Ratio (LLR) in (2). Commonly the sums in (2) are approximated by their largest terms ("log-max") which requires the solution of problems of the type  , subject to
, subject to  . Since MAP provides the best theoretical performance, it is commonly used as a benchmark when comparing other algorithms
. Since MAP provides the best theoretical performance, it is commonly used as a benchmark when comparing other algorithms

3.1. Linear Detection
In linear detection such as Zero-forcing (ZF) and Minimum Mean Squared Error (MMSE), the receiver symbol vector  is multiplied with a linear filter:
is multiplied with a linear filter:


The correlation between the elements in the noise vector  is neglected and the symbols in
is neglected and the symbols in  are demodulate individually, treating the output of the model (6) as
are demodulate individually, treating the output of the model (6) as  independent scalar channels. Although linear detectors will incur a severe performance loss in slow fading channels [4], they have very low implementation cost compared to more advanced MIMO detection algorithms which makes them suitable for low-cost real-time implementations. As depicted in Figure 3, the linear detection procedure involves two parts: channel preprocessing and symbol demapping. The channel preprocessing procedure mainly consists of matrix multiplication and inversion as shown in (6) and (7).
independent scalar channels. Although linear detectors will incur a severe performance loss in slow fading channels [4], they have very low implementation cost compared to more advanced MIMO detection algorithms which makes them suitable for low-cost real-time implementations. As depicted in Figure 3, the linear detection procedure involves two parts: channel preprocessing and symbol demapping. The channel preprocessing procedure mainly consists of matrix multiplication and inversion as shown in (6) and (7).
3.2. Fixed-Complexity Soft Output (FCSO)
The Layered Orthogonal Lattice Detector (LORD) proposed in [13] and the FCSO MIMO detector presented in [4] are similar and use a suboptimal method to reduce the complexity at the cost of negligible performance loss. A general  MIMO system using 64-QAM is taken as a case study. Here each complex-valued symbol is considered to be one layer and only the top layer is exactly marginalized with the remaining three layers approximately marginalized. The channel-rate processing of FCSO involves the QRD of
MIMO system using 64-QAM is taken as a case study. Here each complex-valued symbol is considered to be one layer and only the top layer is exactly marginalized with the remaining three layers approximately marginalized. The channel-rate processing of FCSO involves the QRD of  rank-reduced channel matrices
rank-reduced channel matrices

which generates an upper triangular matrix  , and a unitary matrix
, and a unitary matrix  so that
so that

Here  QRD is needed for different
QRD is needed for different  .
.
The symbol-rate processing consists of the following steps.
(1) Pick one transmitted symbol  as the top layer. The entire constellation
as the top layer. The entire constellation  is enumerated in the exact marginalization (
is enumerated in the exact marginalization ( in (5)) only for
in (5)) only for  . For the
. For the  candidate
candidate  in
in  , by canceling its effect on the received symbol vector
, by canceling its effect on the received symbol vector  , a new vector
, a new vector

is computed.
(2) By multiplying  with
with  from (9), compute
from (9), compute

(3) Based on  and
and  , using DFE,
, using DFE,  can be estimated using hard decision. From this, compute the Euclidean distance
can be estimated using hard decision. From this, compute the Euclidean distance

and eventually the log-likelihood ratio (LLR). Taking a 64-QAM system as an example, as shown in the following:

the LLR of the six bits that constitute the top-layer symbol can be computed using (12). This involves the computation of 64 different  as shown in (14)
as shown in (14)

3.3. Modified FCSO (MFCSO)
Although the FCSO detector has substantially reduced the complexity compared to MAP detector, further reduction is still needed for a practical implementation with large signal constellations. In the following, further approximations and improvements to FCSO detection, namely Modified FCSO (MFCSO) detector [5], are elaborated. In [4], the entire constellation  is enumerated in the exact marginalization (
is enumerated in the exact marginalization ( in (5)). In this paper, instead of searching the full constellation
in (5)). In this paper, instead of searching the full constellation  , we propose to sum over only a subset
, we propose to sum over only a subset  of constellation points around an initial estimate
of constellation points around an initial estimate  . This initial estimate will be obtained by zero-forcing detection. The size of
. This initial estimate will be obtained by zero-forcing detection. The size of  , denoted by
, denoted by  , is chosen to be 16 and 8 in this paper for the complexity and performance comparisons. In effect, the proposed detector is a further approximation of that in [4], which consists of only partially enumerating the symbols selected for exact marginalization (the set
, is chosen to be 16 and 8 in this paper for the complexity and performance comparisons. In effect, the proposed detector is a further approximation of that in [4], which consists of only partially enumerating the symbols selected for exact marginalization (the set  in (5)).
in (5)).
Similar to FCSO, the channel-rate processing of MFCSO involves computing QRD  times, as shown in (9) and (8). As an overhead compared to FCSO, the coefficient matrix
times, as shown in (9) and (8). As an overhead compared to FCSO, the coefficient matrix

is needed to perform the ZF/MMSE-based initial estimate of  in (16) below. The symbol-rate processing of MFCSO is the following
in (16) below. The symbol-rate processing of MFCSO is the following
(1) Linear detection (ZF/MMSE) is carried out to estimate the initial symbol vector

Here  is the transmitted symbol vector,
is the transmitted symbol vector,  is the
is the  symbol in it.
symbol in it.
(2) For each initially estimated symbol  , a candidate set
, a candidate set  is created.
is created.  contains
contains  lattice points close to
lattice points close to  .
.
(3) For each point  , approximate marginalization is applied to the rest of the layers either via ZF or ZF-DFE. According to (17), a multiplication of
, approximate marginalization is applied to the rest of the layers either via ZF or ZF-DFE. According to (17), a multiplication of  and
and  is needed for each
is needed for each  which is updated proportionally to the size of
which is updated proportionally to the size of  and the symbol rate. However, note that
and the symbol rate. However, note that

where  is an
is an  vector, which can be precalculated at channel rate.
vector, which can be precalculated at channel rate.
(4) Using back substitution [14],  can be estimated from
can be estimated from

(5)  together with
together with  form a complete possible transmitted symbol vector which has an Euclidean distance
form a complete possible transmitted symbol vector which has an Euclidean distance

(6) In total, there will be  different
different  values for each layer, and there will be four layers each being the top layer once. Therefore, for a
values for each layer, and there will be four layers each being the top layer once. Therefore, for a  system,
system,  different
different  values need to be computed. In case
values need to be computed. In case  , there will be 64 different
, there will be 64 different  values which is 1/4 compared to the FCSO proposed in [4].
values which is 1/4 compared to the FCSO proposed in [4].
(7) For the sake of low complexity, instead of MAP detection, the following approximation can be used, so that

As presented in [5], the performance gap between MAP and MFCSO for  MIMO using 64-QAM and 3/4 convolutional coding was proven to be small when
MIMO using 64-QAM and 3/4 convolutional coding was proven to be small when  (0.5 dB when FER=
(0.5 dB when FER= ). The gap increases to 2 dB when
). The gap increases to 2 dB when  . On the other hand, the complexity of the detector when
. On the other hand, the complexity of the detector when  is already feasible for VLSI implementation.
is already feasible for VLSI implementation.
3.4. MFCSO in LTE and WiMAX
As a simplification of the general MFCSO algorithm presented in Section 3.3, a  MFCSO method for SM is elaborated in the following. Considering each complex-valued symbol as one layer, only one of them is exactly marginalized and the other is approximately marginalized (using DFE hard decision). The channel rate processing of MFCSO involves the QR decomposition (QRD) of two
MFCSO method for SM is elaborated in the following. Considering each complex-valued symbol as one layer, only one of them is exactly marginalized and the other is approximately marginalized (using DFE hard decision). The channel rate processing of MFCSO involves the QR decomposition (QRD) of two  channel matrices which are
channel matrices which are  in (3) and
in (3) and

The QRD generates an upper triangular matrix  , and a unitary matrix
, and a unitary matrix  according to (9).
according to (9).
The detection procedure for  SM described in the following text is slightly different from the MFCSO presented in [5].
SM described in the following text is slightly different from the MFCSO presented in [5].
(1) Linear detection in (16) is carried out to estimate the  initial symbol vector
initial symbol vector

Here  is the transmitted symbol vector, within which,
is the transmitted symbol vector, within which,  is the
is the  symbol.
symbol.
(2) For each initially estimated symbol  ,
,  , a candidate set
, a candidate set  is created.
is created.  contains
contains  constellation points close to
constellation points close to  .
.
(3) First  is chosen as the top-layer symbol. In order to perform DFE,
is chosen as the top-layer symbol. In order to perform DFE,

needs to be computed. The same operation is needed once again when  is chosen as the top layer later.
is chosen as the top layer later.
(4) For the  constellation point
constellation point  , its effect on
, its effect on  will have to be canceled out.
will have to be canceled out.

Based on  , the partial Euclidean distance
, the partial Euclidean distance

computed for the top-layer.
(5) DFE is applied to detect the other layer. Using back substitution [14],  can be estimated from
can be estimated from

(6) The estimated  together with
together with  form a complete possible transmitted symbol vector
form a complete possible transmitted symbol vector  , from which an accumulated full Euclidean distance
, from which an accumulated full Euclidean distance

can be computed.
(7) In total, there will be  different
different  computed when
computed when  is chosen as the top layer. Then
is chosen as the top layer. Then  is chosen as the top-layer symbol as well. Based on
is chosen as the top-layer symbol as well. Based on  , and
, and  , the same procedure needs to be done once again to compute another
, the same procedure needs to be done once again to compute another  different
different  . Hence, for the
. Hence, for the  system,
system,  different
different  values need to be computed. They are used to update the LLR values in the end as described in [5].
values need to be computed. They are used to update the LLR values in the end as described in [5].
4. Flow Analysis of MIMO Detection
Independent of the detection method, the processing flow of MIMO symbol detection can always be partitioned into two parts, namely channel-rate processing and symbol-rate processing as depicted in Figure 3.
4.1. Channel-Rate Preprocessing
The channel preprocessing is about the precalculation of equalization coefficient matrices from the estimated channel matrix  . According to (15)), the computation involved in linear detection is mainly matrix manipulation including matrix multiplication and inversion. Here the matrix
. According to (15)), the computation involved in linear detection is mainly matrix manipulation including matrix multiplication and inversion. Here the matrix  can be a complex-valued matrix of arbitrary size. As mentioned in [15], in practice, the size of
can be a complex-valued matrix of arbitrary size. As mentioned in [15], in practice, the size of  is typically between
is typically between  and
and  . Although larger matrices (e.g.,
. Although larger matrices (e.g.,  ) can still be managed [15], the cost of real-time implementation will be much higher. For MFCSO, channel-rate processing includes the QR decomposition in (9). For MFCSO, aside from computing
) can still be managed [15], the cost of real-time implementation will be much higher. For MFCSO, channel-rate processing includes the QR decomposition in (9). For MFCSO, aside from computing  , QR decomposition is also needed according to (9).
, QR decomposition is also needed according to (9).
4.2. Symbol-Rate Processing
The symbol-rate processing in soft-output linear detection [16] is to demap the equalized complex values to soft bits. In case of near-MAP detection methods such as MFCSO, layered processing is involved which requires substantially more computational effort. As described in Section 3.3, the symbol-rate processing in MFCSO involves the multiplication, subtraction, and computing the Euclidean distance based on estimated symbols.
5. Architecture of the MIMO Detector
The block diagram of the MFCSO detector is depicted in Figure 4. The detector contains two major parts, the channel preprocessing unit (ChPU) and the detection unit (DU). As presented in Section 3.3 and [5], it is decided that the candidate set size  for 64-QAM. It allows real-time detection of both
for 64-QAM. It allows real-time detection of both  STBC/SFBC and SM for LTE and WiMAX. Modulation schemes from QPSK to 64-QAM are supported.
STBC/SFBC and SM for LTE and WiMAX. Modulation schemes from QPSK to 64-QAM are supported.
5.1. Channel Preprocessing Unit
The ChPU as depicted in Figure 5 handles channel-rate processing tasks such as computation of  in (15) and the QR decomposition in (9). These are performed every time the estimated channel is updated. The computed coefficient matrices
in (15) and the QR decomposition in (9). These are performed every time the estimated channel is updated. The computed coefficient matrices  will be stored in the coefficient buffer and fed to the LLR demapper as input. As depicted in Figure 5, ChPU contains two Complex-valued Multiply-and-ACcumulate (CMAC), an inverse-square-root unit and a 32-bit register file containing 24 registers. The ChPU is a programmable unit controlled by microcode. The operations supported by the ChPU are listed in Table 1. The method presented in [16] has been used to compute
will be stored in the coefficient buffer and fed to the LLR demapper as input. As depicted in Figure 5, ChPU contains two Complex-valued Multiply-and-ACcumulate (CMAC), an inverse-square-root unit and a 32-bit register file containing 24 registers. The ChPU is a programmable unit controlled by microcode. The operations supported by the ChPU are listed in Table 1. The method presented in [16] has been used to compute  , and the Modified Gram-Schmidt method [14] is used to compute
, and the Modified Gram-Schmidt method [14] is used to compute  and
and  matrices in (9).
matrices in (9).
5.2. Detection Unit
The DU computes the LLR values using the method presented in Section 3 and the Log-Max approximation in (20)

The DU consists of a number of processing elements (PE) as illustrated in Figure 6 which can utilize the parallelism in the MFCSO algorithm. The computed LLR values  can be either directly passed to the channel decoder or combined with previously stored LLR values in the soft-buffer for H-ARQ. Since the processing in DU is at symbol rate which is much higher than the channel-rate processing in ChPU, a fully pipelined architecture is used in DU to allow the computation of 16 different
can be either directly passed to the channel decoder or combined with previously stored LLR values in the soft-buffer for H-ARQ. Since the processing in DU is at symbol rate which is much higher than the channel-rate processing in ChPU, a fully pipelined architecture is used in DU to allow the computation of 16 different  in (27) to be finished within 16 clock cycles. DU is configured by a control register and can bypass the functions defined in Section 3 to only enable MMSE detection with soft output. The MMSE mode can be used in power saving mode to reduce the power consumption with a loss of detection performance. A 16-bit fixed-point datatype with proper scaling is adopted in DU, the output LLR values are quantized to be 6-bit signed integers. The number of PE in the DU is decided at design time according to the processing load and latency analysis. In this paper, it is chosen to be two based on the latency analysis in Section 9.3.
in (27) to be finished within 16 clock cycles. DU is configured by a control register and can bypass the functions defined in Section 3 to only enable MMSE detection with soft output. The MMSE mode can be used in power saving mode to reduce the power consumption with a loss of detection performance. A 16-bit fixed-point datatype with proper scaling is adopted in DU, the output LLR values are quantized to be 6-bit signed integers. The number of PE in the DU is decided at design time according to the processing load and latency analysis. In this paper, it is chosen to be two based on the latency analysis in Section 9.3.
5.3. Memory Subsystem
The MIMO detector itself does not contain memory except the small program memory. In order to store the temporarily computed  ,
,  ,
,  ,
,  , and
, and  which are updated by the channel preprocessor at the channel rate, a coefficient buffer as depicted in Figure 4 is needed. The coefficient memory stores the above values for all data subcarriers (up to 20 MHz bandwidth for LTE and 10 MHz to WiMAX). The FIFO that stores the incoming data to the detector from the channel estimator and the subcarrier demapper is not shown in the figure, neither is the FIFO that passes the computed LLR values to the channel decoder hardware. Note that in case STBC is used, the number of data stored in
which are updated by the channel preprocessor at the channel rate, a coefficient buffer as depicted in Figure 4 is needed. The coefficient memory stores the above values for all data subcarriers (up to 20 MHz bandwidth for LTE and 10 MHz to WiMAX). The FIFO that stores the incoming data to the detector from the channel estimator and the subcarrier demapper is not shown in the figure, neither is the FIFO that passes the computed LLR values to the channel decoder hardware. Note that in case STBC is used, the number of data stored in  memory can be reduced almost by half owing to the Alamouti features of
memory can be reduced almost by half owing to the Alamouti features of  , and no
, and no  and
and  matrices are needed.
matrices are needed.
6. Performance Evaluation
In order to evaluate the performance of various MIMO detection algorithms, simulation is carried out using link-level 3GPP LTE and WiMAX simulators [17, 18]. The simulators are developed using MATLAB and C.
It includes the complete physical layer signal processing such as timing/frequency synchronization, channel estimation, subcarrier demapping, rate-matching, and turbo decoding. H-ARQ based on CRC of coded blocks is also enabled to support chase combine (CC) with up to three retransmissions. The bandwidth is set to be 5MHz in the simulation, the velocity of UE is 3 km/h and the scenario is urban micro [19]. Perfect synchronization and channel estimation are assumed to focus the simulation on detection performance. The Turbo decoder runs at most six iterations with early stopping. The WiMAX simulator [17] also works on 5MHz bandwidth. Two channel coding methods used in the simulation are Reed-Solomon with Convolutional (RS-Conv) and Low-Density Parity-Check (LDPC) coding. Two channel models namely the 3GPP SCME [19] and ITU Pedestrian B (PedB) [17] channel models are used in this paper. It is assumed the channel is quasistatic within one OFDM symbol duration. Note that the 1-TTI latency is introduced for uplink ACK/NACK in the simulation.
6.1. 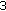 GPP LTE
GPP LTE
Figure 7 shows the block error rate (BLER) of the LTE system with H-ARQ using different detection methods. The blue curves are the BLER of the first transmission while the red ones represent that of the first retransmission in H-ARQ. The figure shows that the BLER of the retransmission is drastically reduced compared to the first transmission which improves the throughput as shown later.
The result in Figures 8 and 9 shows that in case of 64-QAM and the weakest (rate  ) channel coding defined in LTE is used, for
) channel coding defined in LTE is used, for  SM, the FER performance of MAP is always better than that of MFCSO and
SM, the FER performance of MAP is always better than that of MFCSO and  -best. MFCSO achieves lower FER than the
-best. MFCSO achieves lower FER than the  -best (
-best ( ) used in [10] until very high SNR. MMSE has the worst FER performance. Note that in wireless systems, throughput is a more important performance factor than BER or FER because it has a direct effect on the user experience. Figure 9 shows that the gain in throughput brought by MFCSO against MMSE is significant (up to 12.6 Mbits/s, or
) used in [10] until very high SNR. MMSE has the worst FER performance. Note that in wireless systems, throughput is a more important performance factor than BER or FER because it has a direct effect on the user experience. Figure 9 shows that the gain in throughput brought by MFCSO against MMSE is significant (up to 12.6 Mbits/s, or  higher than the one achieved by MMSE). In comparison, the throughput performance degradation caused by the approximation in MFCSO is much smaller (up to 2.5 Mbits/s, or
higher than the one achieved by MMSE). In comparison, the throughput performance degradation caused by the approximation in MFCSO is much smaller (up to 2.5 Mbits/s, or  lower than that achieved by MAP). The much smaller gap in throughput in comparison to that of FER mainly owes to the H-ARQ retransmission with chase combining. The result shows that even with a sub optimal detector (with much lower complexity than the optimal detector) and almost no channel coding, a throughput that is close to the one achievable by MAP detectors can still be reached when H-ARQ is used. The throughput gain of MFCSO over the K-best is as significant as 5 Mbits/s (
lower than that achieved by MAP). The much smaller gap in throughput in comparison to that of FER mainly owes to the H-ARQ retransmission with chase combining. The result shows that even with a sub optimal detector (with much lower complexity than the optimal detector) and almost no channel coding, a throughput that is close to the one achievable by MAP detectors can still be reached when H-ARQ is used. The throughput gain of MFCSO over the K-best is as significant as 5 Mbits/s ( ), when SNR is 26 dB.
), when SNR is 26 dB.
Figures 10 and 11 show the BLER and throughput of  SFBC with two different CQI values (9 and 15). The simulation shows that SFBC reaches
SFBC with two different CQI values (9 and 15). The simulation shows that SFBC reaches  at much lower SNR than SM as depicted in Table 2, though the throughput is half.
at much lower SNR than SM as depicted in Table 2, though the throughput is half.
Figure 12 depicts the achievable throughput using two-level adaptive modulation and coding (AMC). The result shows that when SNR is worse than 10 dB, SFBC achieves both higher throughput and lower BLER than SM even if MAP detector is used.
6.2. WiMAX
The result in Figures 13 and 14 shows that when mild channel coding (e.g., RS-Conv 3/4) is used without H-ARQ in the WiMAX system, MFCSO still achieves near-MAP performance in FER and MAP performance in throughput. It has a gain of more than 9 dB compared to the MMSE detector. The use of stronger code (e.g. LDPC) will bring a gain of 4 dB in throughput compared to RS-Conv. This shows that MFCSO has a very promising performance/complexity trade-off taking the advance of channel coding into consideration. The result also shows that once FER reaches 0.01, any further improvement of FER gives only negligible increase in throughput.
6.3. Impact of Channel Estimation Error
In most of the literatures [1, 3, 5], perfect channel state information (CSI) is assumed which is never true in reality. In [4], channel estimation error is emulated with a randomly generated error constrained by the value of its average power, and the affected FER is plotted. However, how the channel estimation error affects the link-level performance of MIMO detection with the presence of H-ARQ has not been studied according to the best knowledge of the authors. In this paper, based on the least square (LS) channel estimation, the impact of channel estimation error on link-level performance is investigated, which provides a realistic measurement of the achievable performance of the MFCSO detector in a practical system. In this paper, an LTE system with  (coding rate 0.8547, 64-QAM) and open-loop
(coding rate 0.8547, 64-QAM) and open-loop  MIMO scheme is simulated using PedB channel. For comparison purposes, the MFCSO detector is benchmarked against the soft-output sphere decoding (SSD) in [1] and the MAP detector. However, note that no complexity reduction of SSD as used in [1] is applied in this paper, thus, the SSD performance reaches the upper bound. As depicted in Figure 15 and 16, regardless of the channel estimation error, SSD always achieves the same BLER and throughput performance as MAP detection. In Figure 15, the slope of the BLER curve of MFCSO will decrease when SNR reaches 28 dB. Considered from traditional point of view, the BLER performance of MFCSO is significantly worse than SSD and MAP (more than 2 dB). However, as shown in Figure 16, the throughput performance of MFCSO is only negligibly lower (0.3 dB) than that of SSD and MAP. This further proves that MFCSO has a better performance/complexity trade-off when taking system-level impact into consideration. Figure 16 also shows the throughput gap between the case assuming perfect CSI and the one with realistic LS estimated CSI is 1.5 dB in the active region for
MIMO scheme is simulated using PedB channel. For comparison purposes, the MFCSO detector is benchmarked against the soft-output sphere decoding (SSD) in [1] and the MAP detector. However, note that no complexity reduction of SSD as used in [1] is applied in this paper, thus, the SSD performance reaches the upper bound. As depicted in Figure 15 and 16, regardless of the channel estimation error, SSD always achieves the same BLER and throughput performance as MAP detection. In Figure 15, the slope of the BLER curve of MFCSO will decrease when SNR reaches 28 dB. Considered from traditional point of view, the BLER performance of MFCSO is significantly worse than SSD and MAP (more than 2 dB). However, as shown in Figure 16, the throughput performance of MFCSO is only negligibly lower (0.3 dB) than that of SSD and MAP. This further proves that MFCSO has a better performance/complexity trade-off when taking system-level impact into consideration. Figure 16 also shows the throughput gap between the case assuming perfect CSI and the one with realistic LS estimated CSI is 1.5 dB in the active region for  . In principle, channel estimation error will only cause the throughput curve to shift right by 1.5 dB.
. In principle, channel estimation error will only cause the throughput curve to shift right by 1.5 dB.
7. Implementation Considerations
In LTE [11], taking a 5 MHz bandwidth LTE system as an example, up to 7 OFDM symbols need to be processed within one slot (0.5 ms) which contain 1900 data subcarriers. This means that there will be no more than  to finish the detection of each subcarrier on average. Therefore, proper detection methods have to be chosen in order to maximize the data rate at reasonable implementation cost.
to finish the detection of each subcarrier on average. Therefore, proper detection methods have to be chosen in order to maximize the data rate at reasonable implementation cost.
As depicted in (7), for  SM, the MMSE detector needs to compute the inverse of a
SM, the MMSE detector needs to compute the inverse of a  matrix. It has been presented in [16] that the inversion of small matrices can be done using direct inversion which supplies sufficient precision for most of the channels. The FCSO and MFCSO detector involves the search of a number of trellis nodes as depicted in Table 3. The FCSO detector always visits the complete constellation (e.g., 16 for 16-QAM and 64 for 64-QAM), while MFCSO only visits a subset of it (e.g., 9 for 16-QAM and 16 for 64-QAM). Note that MFCSO requires MMSE detection to compute the initial estimate (22) which is an extra cost compared to FCSO. To the knowledge of the author, SSD with complexity reduction [1] has a similar complexity compared to FCSO, which is not analyzed in this paper due to the limited space.
matrix. It has been presented in [16] that the inversion of small matrices can be done using direct inversion which supplies sufficient precision for most of the channels. The FCSO and MFCSO detector involves the search of a number of trellis nodes as depicted in Table 3. The FCSO detector always visits the complete constellation (e.g., 16 for 16-QAM and 64 for 64-QAM), while MFCSO only visits a subset of it (e.g., 9 for 16-QAM and 16 for 64-QAM). Note that MFCSO requires MMSE detection to compute the initial estimate (22) which is an extra cost compared to FCSO. To the knowledge of the author, SSD with complexity reduction [1] has a similar complexity compared to FCSO, which is not analyzed in this paper due to the limited space.
In practice, the hardware is usually implemented taking both the cost and performance issues into consideration. Based on the complexity analysis in Table 6 and the performance analysis in Section 6, MFCSO falls into the favor of the authors to be chosen as the target algorithm for ASIC implementation. Using ST 65 nm CMOS process, while meeting the  constraint, the implemented detector supporting both MMSE and MFCSO for
constraint, the implemented detector supporting both MMSE and MFCSO for  SM and up to 64-QAM modulation occupies less than
SM and up to 64-QAM modulation occupies less than  as proven later.
as proven later.
8. Adaptive Transmission and Detection
As depicted in Table 3, a detector supporting dual-mode MFCSO/MMSE detection consumes 2.5 times the area of the one only supporting MMSE. Hence, the former one is assumed to target high-end users willing to pay more in area and power for performance (e.g., laptops). The MMSE single-mode detector is in favor of low-end users for connectivity with minimum cost (e.g., smartphones). Note that the user cares about latency as well as throughput, and latency is partly determined by the number of retransmissions. Hence, it is also important to keep the retransmissions to a minimum (which requires low FER). Figure 12 shows that with AMC, SM using MFCSO detector always brings higher throughput when SNR is greater than 10 dB. For both types of users, when SNR is worse than 10 dB (as in Figure 12), SFBC is preferred instead of SM. For low-end users, SM can be used when  while SFBC is still preferable (due to the low FER thus fewer retransmissions resulting in low latency) to be used from 10 to 25 dB. For high-end users, SM is preferred when SNR is at least higher than 10 dB. On the other hand, the MMSE mode will consume substantiately lower power than the MFSCO mode, the high-end users might only want to switch to MFCSO-mode when there is enough battery power and high SNR (e.g.,
while SFBC is still preferable (due to the low FER thus fewer retransmissions resulting in low latency) to be used from 10 to 25 dB. For high-end users, SM is preferred when SNR is at least higher than 10 dB. On the other hand, the MMSE mode will consume substantiately lower power than the MFSCO mode, the high-end users might only want to switch to MFCSO-mode when there is enough battery power and high SNR (e.g.,  25 dB). When SNR is very low, SFBC is also preferred due to its robustness (as depicted in Figure 12). The SNR ranges suggested for the mode switching of two types of detector hardware are shown in Table 4. The adaptive scheme brings power efficiency and can supply best-effort performance in an economic way.
25 dB). When SNR is very low, SFBC is also preferred due to its robustness (as depicted in Figure 12). The SNR ranges suggested for the mode switching of two types of detector hardware are shown in Table 4. The adaptive scheme brings power efficiency and can supply best-effort performance in an economic way.
9. Final VLSI Implementation
The implementation of our design is done in two steps. First, for fast prototype and to compare with the prior art in [10], the symbol detector is implemented using Xilinx FPGA. Second, ASIC flow including synthesis, floorplan, placement, and routing is carried out using ST 65 nm process libraries and Synopsys low-power design flow.
9.1. FPGA Prototype
Xilinx ISE and Core Generator were used to synthesize the design based on the Virtex2 xc2v6000 FPGA. The synthesis result is depicted in Table 5. The proposed implementation supports up to 64-QAM as described in Section 9.3. Table 5 shows that it consumes  fewer slices and
fewer slices and  fewer embedded multipliers compared to the K-best detector presented in [10]. Note that the K-best FPGA implementation in [10] only supports the real-time detection of
fewer embedded multipliers compared to the K-best detector presented in [10]. Note that the K-best FPGA implementation in [10] only supports the real-time detection of  QPSK spatial multiplexing in LTE. The FPGA-based detector presented in [8] covers a different antenna configuration, and most importantly the Virtex-5 FPGA used has a different architecture from the Virtex-2 FPGAs, which makes it difficult to make an area comparison.
QPSK spatial multiplexing in LTE. The FPGA-based detector presented in [8] covers a different antenna configuration, and most importantly the Virtex-5 FPGA used has a different architecture from the Virtex-2 FPGAs, which makes it difficult to make an area comparison.
9.2. ASIC Implementation
Table 6 depicts the gate count, and working frequency of the ASIC implementation. In reality, the channel coefficients are updated less frequently than the received symbols, thus, they are saved in the coefficient memory which is not counted in [10]. In order to compare the area consumed by memory and the detector itself, a demo chip including a 172800 bit coefficient memory and a 19200 bit data memory for 5 MHz bandwidth is implemented using Cadence backend flow. As depicted in Figure 17, the total area of the detector is  with half of it consumed by the actual logic (
with half of it consumed by the actual logic ( 0.2
0.2  ) of the detector and the other half by the memory. Note that the microcode memory is implemented as a piece of logic in the chip. The size of the memories depends on the number of subcarriers (or bandwidth) to be supported. The
) of the detector and the other half by the memory. Note that the microcode memory is implemented as a piece of logic in the chip. The size of the memories depends on the number of subcarriers (or bandwidth) to be supported. The  -best detector in [20] supports
-best detector in [20] supports  MIMO and 100 Mbps data rate. As mentioned in Section 3.3, the complexity of MFCSO is proportional to
MIMO and 100 Mbps data rate. As mentioned in Section 3.3, the complexity of MFCSO is proportional to  . Hence, the area of the detection part for
. Hence, the area of the detection part for  will be four times of the presented
will be four times of the presented  solution. Compared to the
solution. Compared to the  figure of a
figure of a  -best detector for
-best detector for  MIMO in 0.13-
MIMO in 0.13- m running at 270 MHz (which is
m running at 270 MHz (which is  without memory in 65-nm according to CMOS scaling), the solution in this paper is
without memory in 65-nm according to CMOS scaling), the solution in this paper is  without memory. Also note that [20] does not include the channel preprocessing part which is expected to give a major contribution in area (it already consumes half of the area of this solution).
without memory. Also note that [20] does not include the channel preprocessing part which is expected to give a major contribution in area (it already consumes half of the area of this solution).
9.3. Processing Throughput
Taking the assumption made in [10], for LTE system with 5 MHz bandwidth, there will be at most 300 data subcarriers to be processed within one OFDM symbol duration which is  . This requires the detection of each data subcarrier to be finished within
. This requires the detection of each data subcarrier to be finished within  . For the FPGA implementation which has a clock frequency of 90 MHz, this amount of time is equal to around 25 clock cycles. Note that the detector can process two subcarriers in parallel which means each subcarrier can be finished within 16 cycles. For
. For the FPGA implementation which has a clock frequency of 90 MHz, this amount of time is equal to around 25 clock cycles. Note that the detector can process two subcarriers in parallel which means each subcarrier can be finished within 16 cycles. For  spatial multiplexing and 64-QAM (12 bits per subcarrier), this corresponds to
spatial multiplexing and 64-QAM (12 bits per subcarrier), this corresponds to  Mbps processing throughput.
Mbps processing throughput.
The ASIC implementation can easily run at a clock frequency of 300 MHz which means 1570 data subcarriers can be computed within  . This corresponds to 225 Mbps processing throughput which allows real-time detection of 20 MHz bandwidth LTE downlink (containing up to 1200 data subcarriers) to be supported. Since the WiMAX 2004 [17] only uses 10 MHz bandwidth, it has a lower peak data rate than LTE, thus can be easily supported.
. This corresponds to 225 Mbps processing throughput which allows real-time detection of 20 MHz bandwidth LTE downlink (containing up to 1200 data subcarriers) to be supported. Since the WiMAX 2004 [17] only uses 10 MHz bandwidth, it has a lower peak data rate than LTE, thus can be easily supported.
Note that the MFCSO detector can be switched to MMSE mode by poweringdown the major part of the DU. The detection in SFBC/STBC transmission schemes is in fact MMSE detection which can be handled by the MMSE mode. Since the MMSE mode will consume substantially less power than the MFCSO mode, the detector is switched to MMSE mode when the terminal enters power-saving mode.
10. Conclusion
In this paper, the VLSI implementation of a fixed complexity near-MAP MIMO detector ASIC is presented for multistandard wireless terminals. It achieves near-MAP throughput during LTE simulations, even with a relatively weak channel code and with high-order modulation (e.g.,  ). Furthermore, based on the adaptive scheme proposed in Section 8, a good performance and power trade-off can be achieved. In comparison to prior art such as the
). Furthermore, based on the adaptive scheme proposed in Section 8, a good performance and power trade-off can be achieved. In comparison to prior art such as the  -best solution in [10], the detector presented achieves better performance and lower silicon cost. The impact of realistic channel estimation on detection performance is also presented.
-best solution in [10], the detector presented achieves better performance and lower silicon cost. The impact of realistic channel estimation on detection performance is also presented.
References
Studer C, Wenk M, Burg A, Bölcskei H: Soft-output sphere decoding: performance and implementation aspects. Proceedings of the 40th Asilomar Conference on Signals, Systems, and Computers (ACSSC '06), November 2006 2071-2076.
Li M, Bougard B, Xu W, Novo D, Van Der Perre L, Catthoor F: Optimizing Near-ML MIMO detector for SDR baseband on parallel programmable architectures. Proceedings of the Conference on Design, Automation and Test in Europe (DATE '08), March 2008 444-449.
Barbero LG, Thompson JS: Rapid prototyping of a fixed-throughput sphere decoder for MIMO systems. Proceedings of the IEEE International Conference on Communications (ICC '06), June 2006 3082-3087.
Larsson EG, Jaldén J: Fixed-complexity soft MIMO detection via partial marginalization. IEEE Transactions on Signal Processing 2008, 56(8):3397-3407.
Wu D, Larsson EG, Liu D: Implementation aspects of fixed-complexity soft-output MIMO detection. Proceedings of the 69th IEEE Vehicular Technology Conference (VTC '09), April 2009
Moezzi-Madani N, et al.: A low-area flexible MIMO detector for WiMAX/WiFi standards. Proceedings of the Conference on Design, Automation and Test in Europe (DATE '10), March 2010, Dresden, Germany 1637-1640.
Cupaiuolo T, et al.: Low-complexity high throughput VLSI architecture of soft-output ML MIMO detector. Proceedings of the IEEE Dessign, Test and Automation in Europe, March 2010, Dresden, Germany
Amiri K, Cavallaro JR, Dick C, Rao RM: A high throughput configurable SDR detector for multi-user MIMO wireless systems. Journal of Signal Processing Systems. In press
Wu D, Eilert J, Liu D: Evaluation of MIMO symbol detectors for 3GPP LTE terminals. Proceedings of the 17th European Signal Processing Conference (EUSIPCO '09), 2009, Glasgow, Scotland
Ketonen J, Juntti M: SIC and K-best LSD receiver implementation for a MIMO-OFDM system. Proceedings of the 16th European Signal Processing Conference (EUSIPCO '08), August 2008
3GPP : Evolved Universal Terrestrial Radio Access (EUTRA): physical channels and modulation. Technical Specifications September 2008., (36.211 V8.4.0):
Alamouti SM: A simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998, 16(8):1451-1458. 10.1109/49.730453
Siti M, Fitz MP: A novel soft-output layered orthogonal lattice detector for multiple antenna communications. Proceedings of the IEEE International Conference on Communications (ICC '06), June 2006 1686-1691.
Golub GH, Van Loan CF: Matrix Computations. 3rd edition. The Johns Hopkins University Press, Baltimore, Md, USA; 1996.
Wu D, Eilert J, Liu D, Wang D, Al-Dhahir N, Minn H: Fast complex valued matrix inversion for multi-user STBC-MIMO decoding. Proceedings of the IEEE Computer Society Annual Symposium on VLSI: Emerging VLSI Technologies and Architectures (ISVLSI '07), March 2007 325-330.
Wu D, Eilert J, Liu D: Implementation of a high-speed MIMO soft-output symbol detector for software defined radio. Journal of Signal Processing Systems. In press
Mehlführer C, Caban S, Rupp M: Experimental evaluation of adaptive modulation and coding in MIMO WiMAX with limited feedback. EURASIP Journal on Advances in Signal Processing 2008., 2008:
Mehlführer C, Wrulich M, Ikuno JC, Bosanska D, Rupp M: Simulating the long term evolution physical layer. Proceedings of the 17th European Signal Processing Conference (EUSIPCO '09), 2009, Glasgow, Scotland
Baum DS, Salo J, Milojevic M, Kyösti P, Hansen J: MATLAB implementation of the interim channel model forbeyond-3G systems (SCME). May 2005.
Chen S, Zhang T, Xin Y: Relaxed K-best MIMO signal detector design and VLSI implementation. IEEE Transactions on Very Large Scale Integration (VLSI) Systems 2007, 15(3):328-337.
Acknowledgments
The work of D. Wu, J. Eilert, R. Asghar, and D. Liu is supported by the Multibase Project from European Commission's 7th Framework in partner with Ericsson AB, Infineon AG, IMEC, Lund University, and KU-Leuven. The authors would like to thank ST Microelectronics for supplying 65nm process, ProfessorErik G. Larsson for discussion on MIMO detection, and Christian Mehlführer and the Christian Doppler Laboratory for Design Methodology of Signal Processing Algorithms at Vienna University of Technology, for contributions on the LTE simulation chain.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu (EURASIP Member), D., Eilert, J., Asghar, R. et al. VLSI Implementation of a Fixed-Complexity Soft-Output MIMO Detector for High-Speed Wireless. J Wireless Com Network 2010, 893184 (2010). https://doi.org/10.1155/2010/893184
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/893184


 .Space-frequency block coding (SFBC),
.Space-frequency block coding (SFBC), 




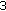 GPP LTE
GPP LTE
 SM, CQI=15), red curves are the BLER of the 1st retransmission of H-ARQ.
SM, CQI=15), red curves are the BLER of the 1st retransmission of H-ARQ.



 SFBC, MMSE).
SFBC, MMSE).

 SFBC, MMSE).
SFBC, MMSE).





