- Research Article
- Open access
- Published:
Flow Oriented Channel Assignment for Multi-radio Wireless Mesh Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 930414 (2010)
Abstract
We investigate channel assignment for a multichannel wireless mesh network backbone, where each router is equipped with multiple interfaces. Of particular interest is the development of channel assignment heuristics for multiple flows. We present an optimization formulation and then propose two iterative flow oriented heuristics for the conflict-free and interference-aware cases, respectively. To maximize the aggregate useful end-to-end flow rates, both algorithms identify and resolve congestion at instantaneous bottleneck link in each iteration. Then the link rate is optimally allocated among contending flows that share this link by solving a linear programming (LP) problem. A thorough performance evaluation is undertaken as a function of the number of channels and interfaces/node and the number of contending flows. The performance of our algorithm is shown to be significantly superior to best known algorithm in its class in multichannel limited radio scenarios.
1. Introduction
There exists considerable interest in deploying wireless mesh networks (WMNs) as a backhaul in support of ubiquitous broadband wireless access for mobile as well as fixed clients [1, 2]. We study an infrastructure WMN, where a collection of stationary wireless mesh routers are interconnected as a multihop backbone to provide clients, network access. As shown in Figure 1, among all mesh routers, some have client connectivity (mesh access points), and some have Internet gateway capability. The mesh backbone then supports multihop flows amongst mesh routers. These flow traffics are aggregated from a group of clients, leading to needed long-term stability for system optimization.
The success of such WMNs largely hinges on their potential for scaling backbone throughput with increasing client density while preserving network coverage. As has already been noted in [3–5], a crucial element in throughput scaling is more effective utilization of available multiple (nonoverlapping) channels. We propose to achieve this by having multiple interfaces per node at incremental hardware cost; for example, note the availability of integrated 802.11 a/b/g transceivers on the same network interface card (NIC). In the future, such integration of multiple transceivers (such as different generations of a successful technology such as 802.11) on a single device will be commonplace, and our work is thus well aligned with this trend.
Channel assignment (CA) is a resource management challenge in such a multiradio multichannel paradigm, whereby a particular channel is now assigned to a specific link and network interface pair. This is a largely underexplored domain with the potential of boosting network throughput as it can mitigate both intra- and interflow interference. Optimal channel assignment would simultaneously involve the choices of routing metric, rate control, power control, and medium access control (MAC). Such an integrated global approach is ambitious and results in very complex systems optimization; typically, only a partial subset of all available resources are used to obtain insight, and our work is no exception.
Various channel assignment algorithms [6–16] which are studied in literature can be classified into packet level, link level and flow level based on their granularity. Packet level algorithms are highly dynamic, where channels are assigned for every packet [6] or every few packets [7]. Channel switching overhead [17] is the major drawback of these algorithms. In flow level algorithms, channels are assigned to several successive links which compose a flow or a set of intersecting flows. In [18], channels are assigned to flows along with the route establishment in a single-radio multichannel network. In [19], links from intersecting flows are assigned the same channels. Flow level algorithms are free of channel switching and are aware of traffic flows however, at the cost of spatial reuse, especially in a dense network. Link level algorithms belong to the most popular category, in which channels are assigned at the granularity of a link. Some optimize link-based metrics, for example, minimizing accumulated interference among links [8, 9] and maximizing weighted sum of simultaneously active links [10]. In networks with stable topology and traffic flows, end-to-end metrics have been shown to be a better suit [13–16]. The performance metric in [13] is the cross-section goodput which is defined as the sum of all useful bandwidth between traffic aggregation nodes and gateway nodes. In [14], the minimum throughput that can be routed from a node to the Internet is maximized. End-to-end throughput optimizations are studied in [15], however, without concrete protocol design. In [16], the authors assume that all links reside in a single collision domain and formulate channel assignment as a game, where players (links) compete for the same pool of channels. Links from a multihop flow form a coalition, and their payoff is the end-to-end flow rate.
Both flow oriented heuristics proposed in this paper are both link level algorithms that maximize aggregate end-to-end flow rates. The flow oriented graph coloring (FOGC) algorithm is designed for the conflict-free case, and it is extended to a general flow oriented channel assignment (FOCA) heuristic for the interference-aware case. Both iterative algorithms identify instantaneous bottlenecks of multihop flows based on previous assignment, routing, and topology information. To resolve congestion at each iteration, they first try to assign a new channel to then bottleneck then optimally allocate link rate among a group of contending flows that share this link by solving a linear programming problem. A simulation example in Figure 2 helps demonstrate the impact of bottleneck and the benefit of resolving congestion. In Figure 2, three flows  ,
,  , and
, and  share a common link
share a common link  . Each node has three NICs, and there are four nonoverlapping channels. Let us assume that
. Each node has three NICs, and there are four nonoverlapping channels. Let us assume that  do not conflict with
do not conflict with  , and vice versa. Operating under conflict-free condition, links
, and vice versa. Operating under conflict-free condition, links  achieve approximately 23 Mbps per channel, while
achieve approximately 23 Mbps per channel, while  has a rate of approximately 10 Mbps per channel. It can be easily shown that a naive algorithm which simply assigns channels to high data rate links suffers from the congestion at bottleneck
has a rate of approximately 10 Mbps per channel. It can be easily shown that a naive algorithm which simply assigns channels to high data rate links suffers from the congestion at bottleneck  even though the overall link rate is maximized. By considering the flow/routing information, a better strategy is to favor the bottleneck even though it has a lower per-link reward. In this simple example, resolving congestion increases the overall network throughput by 100%.
even though the overall link rate is maximized. By considering the flow/routing information, a better strategy is to favor the bottleneck even though it has a lower per-link reward. In this simple example, resolving congestion increases the overall network throughput by 100%.
In particular, the key contribution of this work is threefold:
-
(i)
A generalized optimization model for flow oriented channel assignment in a multiradio multichannel mesh backbone,
-
(ii)
A flow oriented graph coloring (FOGC) algorithm that maximizes the aggregate useful flow rates for conflict-free channel assignment problem,
-
(iii)
A centralized flow oriented channel assignment (FOCA) heuristic for interference-aware cases. It maximizes the aggregate useful flow rates by utilizing cross-layer routing and network topology information.
The remaining of this paper is organized as follows. System model and problem formulation are presented in Section 2. We first introduce and evaluate FOGC algorithm for conflict-free cases in Sections 3 and 4. Then this algorithm is extended to FOCA algorithm in Section 5. Simulation of FOCA is presented in Section 6, followed by concluding remarks in Section 7.
2. System Model and Problem Formulation
We model a wireless mesh backbone consisting of  wireless routers (nodes),
wireless routers (nodes),  active links, and
active links, and  multihop flows. The connection between mobile clients and wireless access points is out of the scope of this paper. The sets of wireless routers, links, channels, and flows are indexed as
multihop flows. The connection between mobile clients and wireless access points is out of the scope of this paper. The sets of wireless routers, links, channels, and flows are indexed as  ,
,  ,
,  and
and  , respectively. Notations
, respectively. Notations  ,
,  ,
,  are used for the
are used for the  th link, the
th link, the  th flow, and the
th flow, and the  th channel, respectively. For convenience, all notations are summarized in Table 1 with additional explanations as follows.
th channel, respectively. For convenience, all notations are summarized in Table 1 with additional explanations as follows.
-
(i)
Channel Assignment Matrix.
 for all
for all  . An element
. An element  denotes that link
denotes that link 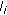 occupies
occupies  of channel
of channel  .
. -
(ii)
Routing Matrix.
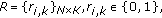 for all
for all  , representing the global routing information. If
, representing the global routing information. If  , flow
, flow 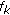 traverses link
traverses link  . A multihop flow
. A multihop flow 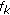 is then defined by the set of links it traverses, that is,
is then defined by the set of links it traverses, that is,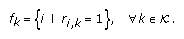 (1)
(1) -
(iii)
NIC Vector
 . An element
. An element 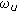 (for all
(for all 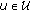 ) is the number of network interface cards on node
) is the number of network interface cards on node  .
. -
(iv)
Interference Matrix.
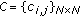 ,
,  for all
for all  , representing the binary symmetric conflicts among links. Entries in
, representing the binary symmetric conflicts among links. Entries in 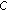 are determined using a binary two-hop interference model that is widely used in graph modeling of wireless networks [10, 14, 20] (whereby links within two hops of each other deemed to be mutually interfering).
are determined using a binary two-hop interference model that is widely used in graph modeling of wireless networks [10, 14, 20] (whereby links within two hops of each other deemed to be mutually interfering). -
(v)
Clique Matrix.
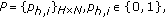 for all
for all  . A clique is a maximum subset of links such that all distinct pairs in this subset would potentially conflict with each other [21]. Assume the total number of cliques is
. A clique is a maximum subset of links such that all distinct pairs in this subset would potentially conflict with each other [21]. Assume the total number of cliques is 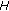 ; each row of
; each row of  , thus represents one of these cliques. Clearly,
, thus represents one of these cliques. Clearly,  depends on network topology, and links within one clique must time share a channel if they are assigned the same one:
depends on network topology, and links within one clique must time share a channel if they are assigned the same one: (2)
(2)where symbol
 denotes component-wise inequality.
denotes component-wise inequality. -
(vi)
Channel Reward.
 for all
for all 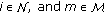 . Reward
. Reward  is the maximum supportable data rate of link
is the maximum supportable data rate of link  when it exclusively uses channel
when it exclusively uses channel 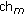 .
. -
(vii)
Achievable Link Rate Vector.
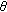 . A rate
. A rate 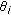 (for all
(for all 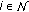 ) is the achievable data rate of
) is the achievable data rate of 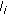 under a given channel assignment decision:
under a given channel assignment decision: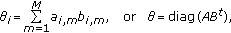 (3)
(3)where diag(
 ) returns a column vector formed from all the diagonal elements.
) returns a column vector formed from all the diagonal elements. -
(viii)
Flow Rate Vector.
 . A rate
. A rate 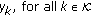 , is the supportable end-to-end rate of flow
, is the supportable end-to-end rate of flow 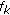 . The total rate of the contending flows traversing a common link cannot exceed the link's rate
. The total rate of the contending flows traversing a common link cannot exceed the link's rate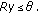 (4)
(4) -
(ix)
Link Rate Allocation Matrix.
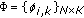 . A flow
. A flow 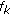 is allowed to use up to
is allowed to use up to  of a link
of a link 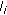 's rate. If
's rate. If 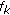 does not traverse
does not traverse 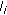 (
( ),
), 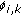 is set to 0. Equation (4) is then expressed in a component-wise way:
is set to 0. Equation (4) is then expressed in a component-wise way: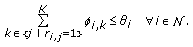 (5)
(5)Both
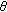 and
and  are hidden variables in the formulation (7) that we will present soon; however, they will act as important roles in both heuristic algorithms.
are hidden variables in the formulation (7) that we will present soon; however, they will act as important roles in both heuristic algorithms. -
(x)
Network Interface Constraint. The total number of channels assigned to links incident to a node cannot exceed the node's NIC number. Channels are assigned to links while NIC constraint resides on nodes. We introduce a network topology-dependent matrix
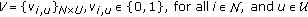 to solve such contradiction. The entry
to solve such contradiction. The entry  denotes that node
denotes that node  is one end of link
is one end of link 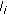 . By mapping the channel assignment results to each wireless router, the NIC constraint is given by:
. By mapping the channel assignment results to each wireless router, the NIC constraint is given by: (6)
(6)where the cardinality function Card(
 ) counts the number of nonzero entries in each column; hence Card(
) counts the number of nonzero entries in each column; hence Card(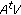 ) is the number of NICs needed at wireless routers.
) is the number of NICs needed at wireless routers. -
(xi)
Flow Oriented Metric.
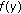 is a continuously differentiable, increasing, and concave utility function of end-to-end flow rates, that is, the aggregated flow rate
is a continuously differentiable, increasing, and concave utility function of end-to-end flow rates, that is, the aggregated flow rate 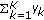 .
.
Given the notations above, the flow oriented channel assignment problem in mesh backbone can be stated as the following convex-cardinality (nonconvex) problem:

The optimization variables are channel assignment decisions  and supportable flow rates
and supportable flow rates  . The routing matrices
. The routing matrices  is the required cross-layer routing information, while matrix
is the required cross-layer routing information, while matrix  and
and  are computed from the topology information. Channel reward
are computed from the topology information. Channel reward  is considered to be a known parameter. If there always exist sufficient NICs per mesh router, the only cardinality (nonconvex) constraint is eliminated, making (7) a convex problem.
is considered to be a known parameter. If there always exist sufficient NICs per mesh router, the only cardinality (nonconvex) constraint is eliminated, making (7) a convex problem.
3. Flow Oriented Graph Coloring Algorithm (FOGC)
In some network systems—such as TDMA-based mesh—conflict-free channel assignment is required. Then assigning each channel becomes a binary decision:

and assignment decisions are mutually exclusive among conflicting links:

Substituting (8) for  and (9) for
and (9) for  in (7), the general formulation is reduced to
in (7), the general formulation is reduced to

When there is no NIC limitation and  is linear, (10) is further reduced to an integer linear programming (ILP) problem by removing the last constraint. Optimal solution for ILP problems can be obtained numerically.
is linear, (10) is further reduced to an integer linear programming (ILP) problem by removing the last constraint. Optimal solution for ILP problems can be obtained numerically.
Several past work have demonstrated the effectiveness of greedy graph coloring algorithms in solving conflict-free resource assignment problems. A greedy solution, Progressive Minimum Neighbor First (PMNF), is proposed in [22] for the unified time/frequency/code domain channel assignment problem. The PMNF is extended to Color-Sensitive Graph Coloring (CSGC) in [20] to solve the channel assignment problem in a multichannel scenario. In the color-sensitive contention graph, vertices are connected via multiple colored edges that represent multiple channels, and colors may have different rewards on different vertices.
Following this color-sensitive graph coloring approach, we present a flow oriented graph coloring (FOGC) algorithm that heuristically solves (10) with the objective function  , where
, where  is the requested end-to-end rate of flow
is the requested end-to-end rate of flow  . FOGC is an iterative algorithm that resolves instantaneous congestion. In each iteration, FOGC first identifies bottleneck links and assigns a new channel to the most critical one. This heuristic process is carefully designed so that the conflict constraint (the 4th constraint) and the NIC constraint (the 5th constraint) in (10) are satisfied. Therefore, the remaining process prior to next iteration is an LP problem that optimally allocat the rate of each link to contending flows that share the link. This iterative algorithm is of low complexity, based on local optimality for each additional assignment.
. FOGC is an iterative algorithm that resolves instantaneous congestion. In each iteration, FOGC first identifies bottleneck links and assigns a new channel to the most critical one. This heuristic process is carefully designed so that the conflict constraint (the 4th constraint) and the NIC constraint (the 5th constraint) in (10) are satisfied. Therefore, the remaining process prior to next iteration is an LP problem that optimally allocat the rate of each link to contending flows that share the link. This iterative algorithm is of low complexity, based on local optimality for each additional assignment.
We use a symbol—vector  —to store the instantaneous bottleneck links1 of all
—to store the instantaneous bottleneck links1 of all  flows. If the end-to-end traffic demand of a flow has already been satisfied, there is no bottleneck for that flow. The superscript on all notations denote the current iteration, that is,
flows. If the end-to-end traffic demand of a flow has already been satisfied, there is no bottleneck for that flow. The superscript on all notations denote the current iteration, that is,  is
is  's value in the
's value in the  th iteration.
th iteration.
Step 0 (initiate  ).
).
Assuming no prior knowledge,

Step 1 (identify bottleneck Links).
There is

where  is the requested rate of
is the requested rate of  . The set of bottleneck links,
. The set of bottleneck links,  , are labeled and sorted in descending order according to their unsatisfied traffic demand. An all-zero vector indicates the end of the algorithm, otherwise the link with the largest label is selected. Future steps may set a label value to zero if the rate of that particular link can not be improved by assigning a new channel.
, are labeled and sorted in descending order according to their unsatisfied traffic demand. An all-zero vector indicates the end of the algorithm, otherwise the link with the largest label is selected. Future steps may set a label value to zero if the rate of that particular link can not be improved by assigning a new channel.
Step 2 (channel assignment strategy (update  to
to )).
)).
Assume that link  connecting nodes
connecting nodes  and
and  is the critical bottleneck selected in Step 1. The channel assignment decision varies according to the number of available NICs on
is the critical bottleneck selected in Step 1. The channel assignment decision varies according to the number of available NICs on  and
and  .
.
-
(1)
If
 and
and  both have free NICs and at least one available channel in common, assign the most beneficial2 available channel in common
both have free NICs and at least one available channel in common, assign the most beneficial2 available channel in common 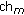 to link
to link  . Eliminate
. Eliminate  from the available channel list of all
from the available channel list of all  's and
's and  's conflicting neighbors.
's conflicting neighbors. -
(2)
Otherwise, redirect to Step 1, set the label value of
 to zero, and reselect a link with the largest label.
to zero, and reselect a link with the largest label.
Step 3 (link rate allocation (solve  )).
)).
Entering with the  th channel assignment matrix
th channel assignment matrix  , we next calculate the link rate allocation matrix
, we next calculate the link rate allocation matrix  and the supportable flow rate vector
and the supportable flow rate vector  via optimally solving the following LP problem:
via optimally solving the following LP problem:

Thus far, we have a new link rate allocation matrix  . Returning to Step 1, we can determine a new set of bottleneck links
. Returning to Step 1, we can determine a new set of bottleneck links  for next iteration. This algorithm terminates when an all-zero label vector appears in Step 1.
for next iteration. This algorithm terminates when an all-zero label vector appears in Step 1.
Since the 4th and 5th constraints in (10) are satisfied in the heuristical process in FOGC, the optimal result from (13) is not necessarily an optimal solution for (10). The following proposition shows that FOGC achieves optimality in a simple single flow case.
Proposition 1.
In the single flow case, FOGC is the optimal channel assignment when channels have identical reward.
Proof.
Assume that  is an optimal channel assignment that assigns a channel to link
is an optimal channel assignment that assigns a channel to link  at its
at its  th operation. It is easy to verify that exchange the sequence of terms in
th operation. It is easy to verify that exchange the sequence of terms in  does not affect its optimality. Let
does not affect its optimality. Let  be the assignment from FOGC algorithm which has exactly the same first
be the assignment from FOGC algorithm which has exactly the same first  assignments as
assignments as  . Here we will show that either
. Here we will show that either  agrees with the optimal assignment on its first
agrees with the optimal assignment on its first  assignments or
assignments or  has already achieved optimality on the
has already achieved optimality on the  th assignment. If
th assignment. If  and
and  , swap
, swap  and
and  in
in  . Then
. Then  has the same first
has the same first  assignments as
assignments as  . If
. If  and
and  , then the flow rate will never increase after the
, then the flow rate will never increase after the  th assignment in
th assignment in  , because
, because  is an instantaneous bottleneck which is never treated again in
is an instantaneous bottleneck which is never treated again in  . Then
. Then  achieves optimality at its
achieves optimality at its  th operation.
th operation.
In the simplest case, FOGC's locally optimal strategy leads to global optimality. In general, FOGC's performance in more complicated scenarios is evaluated through simulation in the following section.
4. Simulation Results of FOGC
Though FOGC algorithm works for any network system where conflict-free assignment is desired and the interference among links can be modeled using distance-based conflict graph, for demonstration purpose, FOGC algorithm is simulated in ring and grid topologies (Figure 3) using ideal two-hop interference model. FOGC is compared with two other algorithms. The baseline is a centralized Link-Based Graph Coloring (LBGC) algorithm which seeks to maximize the overall link rates without routing knowledge. The upper bound is the optimal channel assignment3 (OPT) obtained by exhaustive search. In LBGC, the flows traversing a common link share this link's rate fairly.
In an  node ring, each link only conflicts with adjacent 4 links. Two
node ring, each link only conflicts with adjacent 4 links. Two  -hop flows are randomly generated. Assume that each node has sufficient NICs and the number of available channels is varied from 2 to 8. An immediate observation from Figure 4 is that no end-to-end throughput is obtained when there are less than 3 channels. This is simply due to the conflict-free constraint and the predefined 2-hop interference model. As one can see, FOGC follows OPT closely and outperforms LBGC 120% in the case of 8 channels. This demonstrates that resolving instantaneous bottlenecks is a good greedy heuristic to achieve near optimal performance at low complexity.
-hop flows are randomly generated. Assume that each node has sufficient NICs and the number of available channels is varied from 2 to 8. An immediate observation from Figure 4 is that no end-to-end throughput is obtained when there are less than 3 channels. This is simply due to the conflict-free constraint and the predefined 2-hop interference model. As one can see, FOGC follows OPT closely and outperforms LBGC 120% in the case of 8 channels. This demonstrates that resolving instantaneous bottlenecks is a good greedy heuristic to achieve near optimal performance at low complexity.
In an  grid topology, several source-destination pairs are randomly selected, and the shortest path is randomly selected for each pair. Up to 17, identical channels are provided to three 8-hop flows. As Figure 5 shows, with sufficient NICs, the average end-to-end flow rate scales almost linearly with channel resources in presence of 3 or more channels. When the number of NICs on each node is limited, the per flow throughput would saturate at some stage. This saturation point reveals the resource utilization efficiency of each algorithm. With only 2 NICs, the FOGC almost fully exploits 4 channels and could partially utilize up to 8 channels. Overall, Figure 5 demonstrates that FOGC is superior to LBGC in terms of efficiency in utilizing multiple channels with very limited number of NICs, by using additional routing and network topology information.
grid topology, several source-destination pairs are randomly selected, and the shortest path is randomly selected for each pair. Up to 17, identical channels are provided to three 8-hop flows. As Figure 5 shows, with sufficient NICs, the average end-to-end flow rate scales almost linearly with channel resources in presence of 3 or more channels. When the number of NICs on each node is limited, the per flow throughput would saturate at some stage. This saturation point reveals the resource utilization efficiency of each algorithm. With only 2 NICs, the FOGC almost fully exploits 4 channels and could partially utilize up to 8 channels. Overall, Figure 5 demonstrates that FOGC is superior to LBGC in terms of efficiency in utilizing multiple channels with very limited number of NICs, by using additional routing and network topology information.
5. Flow Oriented Channel Assignment Algorithm (FOCA)
Due to the broadcast nature of wireless communication, the conflict-free assumption is rarely true in practice and should be viewed as a model approximation. The a forementioned graph coloring algorithm FOGC is extended to a general flow oriented channel assignment (FOCA) algorithm to heuristically solve (7). Conflicting links are allowed to time-share the same channel, and in each iteration, apart from assigning a new channel, channel switching mechanism and channel switching propagation are designed to adjust existing assignment decisions.
FOCA has a similar iteration process as FOGC. It first identifies the bottleneck links, then assigns a new channel, or adjusts existing channel assignment to resolve congestion, and prior to entering the next iteration, optimal allocation of link rate to contending flows that share this link is computed by solving an LP problem.
Step 0.
Same as FOGC.
Step 1.
Same as FOGC.
Step 2 (channel assignment strategy (update  to
to )).
)).
Assume that link  connecting nodes
connecting nodes  and
and  is the critical bottleneck selected by Step 1. The channel assignment decision varies according to the number of available NICs on
is the critical bottleneck selected by Step 1. The channel assignment decision varies according to the number of available NICs on  and
and  .
.
-
(1)
At least one free NIC on both
 and
and  : assign a locally least occupied channel to a free NIC on
: assign a locally least occupied channel to a free NIC on  and
and  , respectively.
, respectively. -
(2)
No free NIC on
 at least one free NIC on
at least one free NIC on  (or vice versa): choose locally least occupied channel from
(or vice versa): choose locally least occupied channel from  's channel usage list and have one free NIC of
's channel usage list and have one free NIC of  tuned to that channel to communicate with
tuned to that channel to communicate with  .
. -
(3)
Neither
 nor
nor  has any free NIC:
has any free NIC: -
(a)
 and
and  have at least one common channel4: communicate on a least occupied common channel utilizing the NICs already tuned to that channel.
have at least one common channel4: communicate on a least occupied common channel utilizing the NICs already tuned to that channel. -
(b)
 and
and  have no common channel, and the connectivity between
have no common channel, and the connectivity between  and
and  has already been satisfied: return to Step 1 to set the label of link
has already been satisfied: return to Step 1 to set the label of link 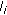 to zero.
to zero. -
(c)
 and
and  have no common channel in use, and the connectivity between
have no common channel in use, and the connectivity between  and
and  is not satisfied: channel switching and channel switching propagation are needed. A least occupied channel is selected from
is not satisfied: channel switching and channel switching propagation are needed. A least occupied channel is selected from  's and
's and  's channel usage list, respectively. Assume they are
's channel usage list, respectively. Assume they are  and
and  , and
, and 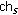 carries a lower traffic load. As Figure 6 shows,
carries a lower traffic load. As Figure 6 shows,  's NIC that originally works on
's NIC that originally works on  is switched to
is switched to  to communicate with
to communicate with  . To preserve
. To preserve  's connection with its own neighbors on
's connection with its own neighbors on 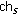 , this switching is propagated to those neighbors, and then to neighbors of those neighbors, and so on.
, this switching is propagated to those neighbors, and then to neighbors of those neighbors, and so on.
-
(a)
At the completion of this step, we have updated the channel assignment matrix  to
to  .
.
Step 3.
Same LP optimization as in FOGC.
6. Simulation Results of FOCA
The flow oriented channel assignment (FOCA) is simulated using random network topologies (Figure 7) in ns-3 [23] simulator because (i) node model is architected to support multiple interfaces, (ii) channel model is architected to support multiple channels in ns-3. Customized functions are implemented to install multi-interface on nodes and bind interfaces to channels according to different channel assignment algorithms5. First, we generate random topologies, multiple source-destination pairs, and one least hop-count path for each pair. This routing information is stored to assist future channel assignments. Then channel assignment algorithm is performed in a centralized manner before data transmission. All results are averaged over multiple runs on multiple random topologies. The FOCA is compared to a unified one-to-one channel assignment, which assigns the  th channel to the
th channel to the  th NIC. The unified algorithm is of zero complexity and performs well when the number of NICs matches with the number of channels. It generates a much better baseline than any random assignment, which is unfortunately always used as an inaccurate benchmark. Another contrast is an empirical traffic load-aware channel assignment (LACA). In [13], LACA, a routing algorithm, as well as the control loop between them are designed. Assumeing a precalculated routing and fixed injected traffic load, the LACA assigns channel resources to links in the decreasing order of the expected link load. The original evaluation metric "cross-section bandwidth" is similar to the end-to-end flow rate in this paper.
th NIC. The unified algorithm is of zero complexity and performs well when the number of NICs matches with the number of channels. It generates a much better baseline than any random assignment, which is unfortunately always used as an inaccurate benchmark. Another contrast is an empirical traffic load-aware channel assignment (LACA). In [13], LACA, a routing algorithm, as well as the control loop between them are designed. Assumeing a precalculated routing and fixed injected traffic load, the LACA assigns channel resources to links in the decreasing order of the expected link load. The original evaluation metric "cross-section bandwidth" is similar to the end-to-end flow rate in this paper.
In real-world applications, the NIC limitation is frequently confronted before the number of channels becomes a limitation. Therefore the multichannel limited-radio scenario performance is the key criteria in evaluating channel assignment algorithms. We first simulate three 5-hop flows in random networks, where each node has only 2 NICs, and vary the number of channels. Similar to the conclusion from Figure 5, in Figure 8, FOCA's throughput saturates at approximately 9 channels and outperforms LACA approximated 50% in the saturated case. Once saturation is reached, increasing the number of channels causes only jitter but not significant increment in flow rate, because now the limitation is insufficient NICs on some bottleneck links. A good channel assignment algorithm will efficiently utilize as many channels as possible with very few NICs by diversifying traffic over as many channels as possible to avoid intra- and inter flow interference. Hence, the saturation point (in terms of the number of channels) and the saturation flow rate in the multichannel limited-radio scenario are of particular interest to system designers.
Next we evaluate the performance when sufficient NICs are provided. Three 5-hop flows are injected in random networks with 6 available channels while the number of NICs per node is varied. As one could see from Figure 9, with sufficient NICs per node, the simplest unified one-to-one channel assignment (baseline) will outperform both FOCA and LACA. The region in which FOCA (LACA) stays above the baseline is FOCA's (LACA's) effective operating region. For example, with these particular parameter settings, LACA should be avoided when there are 4 or more NICs per node, and FOCA is a favorable algorithm only up to 5 NICs per node. Figure 9 clearly justifies that both FOCA and LACA are designed for multichannel limited-radio scenarios.
Scalability is a practical challenge for mesh backbone. We simulate the aggregated flow rate as well as the per flow rate by gradually increasing the number of coexisting 3-hop flows. The random networks simulated have 6 channels and 2 NICs per node. As expected, the per flow throughput in Figure 10 decreases steadily as the number of coexisting flows increases. However, as shown in Figure 11 shows, the aggregated flow throughput increases with diminishing slope till the network becomes saturated. FOCA has a higher saturated aggregate throughput due to its effective resource management. Further increasing the amount of coexisting flows leads to more variance in FOCA than in LACA. Fortunately, no significant aggregate throughput drop is observed, showing that FOCA has the acceptable scalability when network becomes overloaded.
7. Conclusion
The fast deployment of WMNs places stringent requirements on end-to-end rates of the underlying multihop mesh backbone, especially in large scale and dense scenarios. This paper studies the channel assignment problem for a multichannel multiradio mesh backbone. We first presented a general optimization formulation, which is nonconvex due to practical constraints. Then a flow oriented graph coloring (FOGC) greedy algorithm was designed for the conflict-free case, and it was extended to a flow oriented channel assignment (FOCA) heuristic for the general case where interference is considered. Both algorithms identify instantaneous bottlenecks at each additional assignment iteration using routing and network topology information and try to resolve congestion by (i) assigning a new channel, (ii) channel switching (FOCA only), and (iii) optimally allocating link rate to contending flows by solving an LP problem. Simulation not only demonstrated the effectiveness of addressing bottlenecks at each additional iteration but also showed that both FOCA and FOGC can efficiently exploit multiple channels with very limited number of NICs.
Although both heuristics are for a static network, their low complexity as well as the relatively high stability of traffic flows in mesh backbone allow the channel assignment decision to be adapted periodically or once the accumulated changes exceed a certain threshold. While the proposed algorithms pursue local optimality at each additional assignment, this does not lead to global optimality. An option is to extend this heuristic (at cost of additional complexity) by looking several steps ahead, that is, considering more than one critical bottleneck link at each iteration. This framework can be applied towards other utility functions as well.
References
Bruno R, Conti M, Gregori E: Mesh networks: commodity multihop ad hoc networks. IEEE Communications Magazine 2005, 43(3):123-131.
Akyildiz IF, Wang X: A survey on wireless mesh networks. IEEE Communications Magazine 2005, 43(9):S23-S30.
Kyasanur P, So J, Chereddi C, Vaidya NH: Multichannel mesh networks: challenges and protocols. IEEE Wireless Communications 2006, 13(2):30-36. 10.1109/MWC.2006.1632478
Kyasanur P, Vaidya NH: Capacity of multi-channel wireless networks: impact of number of channels and interfaces. Proceedings of the 11th Annual International Conference on Mobile Computing and Networking (MobiCom '05), 2005 43-57.
Vijaykumar R, Das AK, Roy S, Ma H: Multi-radio multi-channel mesh networks. In Wireless Mesh Networking: Architectures, Protocols and Standards. Auerbach; 2006.
So J, Vaidya N: Multi-channel MAC for ad hoc networks: handling multi-channel hidden terminals using a single transceiver. Proceedings of the 5th International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '04)), 2004 222-233.
Bahl P, Chandra R, Dunagan J: SSCH: slotted seeded channel hopping for capacity improvement in IEEE 802.11 ad-hoc wireless networks. Proceedings of the 10th Annual International Conference on Mobile Computing and Networking (MobiCom '04), 2004 216-230.
Ramachandran KN, Belding EM, Almeroth KC, Buddhikot MM: Interference-aware channel assignment in multi-radio wireless mesh networks. Proceedings of the 25th IEEE International Conference on Computer Communications (INFOCOM '06), 2006
Subramanian AP, Gupta H, Das SR: Minimum interference channel assignment in multi-radio wireless mesh networks. Proceedings of the 4th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON '07), 2007 481-490.
Das AK, Alazemi HMK, Vijayakumar R, Roy S: Optimization models for fixed channel assignment in wireless mesh networks with multiple radios. Proceedings of the 2nd Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks (SECON '05), 2005 463-474.
Kyasanur P, Vaidya N: Routing and link-layer protocols for multi-channel multi-interface ad hoc wireless networks. ACM SIGMOBILE Mobile Computing and Communications Review 2006, 10(1):31-43. 10.1145/1119759.1119762
Skalli H, Ghosh S, Das SK, Lenzini L, Conti M: Channel assignment strategies for multiradio wireless mesh networks: issues and solutions. IEEE Communications Magazine 2007, 45(11):86-95.
Raniwala A, Gopalan K, Chiueh T: Centralized channel assignment and routing algorithms for multi-channel wireless mesh networks. ACM SIGMOBILE Mobile Computing and Communications Review 2004, 8(2):50-65. 10.1145/997122.997130
Alicherry M, Bhatia R, Li L: Joint channel assignment and routing for throughput optimization in multi-radio wireless mesh networks. Proceedings of the 11th Annual International Conference on Mobile Computing and Networking (MobiCom '05), September 2005 58-72.
Tang J, Xue G, Zhang W: Cross-layer optimization for end-to-end rate allocation in multi-radio wireless mesh networks. Wireless Networks 2009, 15(1):53-64. 10.1007/s11276-007-0024-y
Gao L, Wang X, Xu Y: Multiradio channel allocation in multihop wireless networks. IEEE Transactions on Mobile Computing 2009, 8(11):1454-1468.
Chereddi C, Kyasanur P, Vaidya NH: Design and implementation of a multi-channel multi-interface network. Proceedings of the 2nd International Workshop on Multi-Hop Ad Hoc Networks: From Theory to Reality (REALMAN '06), 2006 23-30.
So J, Vaidya N: A routing protocol for utilizing multiple channels in multi-hop wireless networks with a single transceiver. University of Illinois at Urbana, Champaign, Ill, USA; 2004.
Vedantham B, Kakumanu S, Lakshmanan S, Sivakumar R: Component based channel assignment in single radio, multi-channel ad hoc networks. Proceedings of the 12th Annual International Conference on Mobile Computing and Networking (MobiCom '06), 2006 378-389.
Peng C, Zheng H, Zhao BY: Utilization and fairness in spectrum assignment for opportunistic spectrum access. Mobile Networks and Applications 2006, 11(4):555-576. 10.1007/s11036-006-7322-y
Huang XL, Bensaou B: On max-min fairness and scheduling in wireless ad-hoc networks: analytical framework and implementation. Proceedings of the 2nd ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '01), October 2001, Long Beach, Calif, USA 221-231.
Ramanathan S: Unified framework and algorithm for channel assignment in wireless networks. Wireless Networks 1999, 5(2):81-94. 10.1023/A:1019126406181
The ns-3 network simulator http://www.nsnam.org
Endnotes
1.In case that a multihop flow has several bottleneck links, one link is randomly selected to break the tie.2. The most beneficial channel is the one which provides the highest reward (data rate).3. Since the complexity of exhaustive search scales exponentially with the number of links and channels, we only present OPT in a ring topology.4. A common channel is the channel that both
 and
and  are using to communicate with neighbors other than each other.5.Simulation code available at http://www.ee.washington.edu/research/funlab/mrmc/index.html.
are using to communicate with neighbors other than each other.5.Simulation code available at http://www.ee.washington.edu/research/funlab/mrmc/index.html.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ye, F., Roy, S. & Niu, Z. Flow Oriented Channel Assignment for Multi-radio Wireless Mesh Networks. J Wireless Com Network 2010, 930414 (2010). https://doi.org/10.1155/2010/930414
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/930414


 for all
for all  . An element
. An element  denotes that link
denotes that link 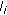 occupies
occupies  of channel
of channel  .
.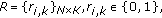 for all
for all  , representing the global routing information. If
, representing the global routing information. If  , flow
, flow 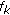 traverses link
traverses link  . A multihop flow
. A multihop flow 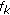 is then defined by the set of links it traverses, that is,
is then defined by the set of links it traverses, that is,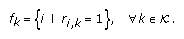
 . An element
. An element 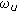 (for all
(for all 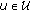 ) is the number of network interface cards on node
) is the number of network interface cards on node  .
.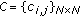 ,
,  for all
for all  , representing the binary symmetric conflicts among links. Entries in
, representing the binary symmetric conflicts among links. Entries in 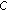 are determined using a binary two-hop interference model that is widely used in graph modeling of wireless networks [
are determined using a binary two-hop interference model that is widely used in graph modeling of wireless networks [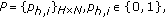 for all
for all  . A clique is a maximum subset of links such that all distinct pairs in this subset would potentially conflict with each other [
. A clique is a maximum subset of links such that all distinct pairs in this subset would potentially conflict with each other [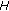 ; each row of
; each row of  , thus represents one of these cliques. Clearly,
, thus represents one of these cliques. Clearly,  depends on network topology, and links within one clique must time share a channel if they are assigned the same one:
depends on network topology, and links within one clique must time share a channel if they are assigned the same one:
 denotes component-wise inequality.
denotes component-wise inequality. for all
for all 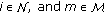 . Reward
. Reward  is the maximum supportable data rate of link
is the maximum supportable data rate of link  when it exclusively uses channel
when it exclusively uses channel 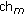 .
.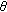 . A rate
. A rate 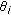 (for all
(for all 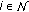 ) is the achievable data rate of
) is the achievable data rate of 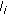 under a given channel assignment decision:
under a given channel assignment decision: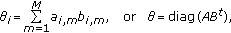
 ) returns a column vector formed from all the diagonal elements.
) returns a column vector formed from all the diagonal elements. . A rate
. A rate 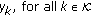 , is the supportable end-to-end rate of flow
, is the supportable end-to-end rate of flow 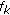 . The total rate of the contending flows traversing a common link cannot exceed the link's rate
. The total rate of the contending flows traversing a common link cannot exceed the link's rate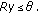
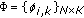 . A flow
. A flow 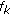 is allowed to use up to
is allowed to use up to  of a link
of a link 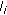 's rate. If
's rate. If 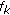 does not traverse
does not traverse 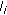 (
( ),
), 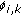 is set to 0. Equation (
is set to 0. Equation (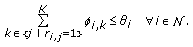
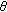 and
and  are hidden variables in the formulation (7) that we will present soon; however, they will act as important roles in both heuristic algorithms.
are hidden variables in the formulation (7) that we will present soon; however, they will act as important roles in both heuristic algorithms.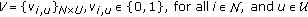 to solve such contradiction. The entry
to solve such contradiction. The entry  denotes that node
denotes that node  is one end of link
is one end of link 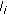 . By mapping the channel assignment results to each wireless router, the NIC constraint is given by:
. By mapping the channel assignment results to each wireless router, the NIC constraint is given by:
 ) counts the number of nonzero entries in each column; hence Card(
) counts the number of nonzero entries in each column; hence Card(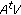 ) is the number of NICs needed at wireless routers.
) is the number of NICs needed at wireless routers.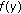 is a continuously differentiable, increasing, and concave utility function of end-to-end flow rates, that is, the aggregated flow rate
is a continuously differentiable, increasing, and concave utility function of end-to-end flow rates, that is, the aggregated flow rate 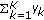 .
. and
and  both have free NICs and at least one available channel in common, assign the most beneficial2 available channel in common
both have free NICs and at least one available channel in common, assign the most beneficial2 available channel in common 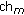 to link
to link  . Eliminate
. Eliminate  from the available channel list of all
from the available channel list of all  's and
's and  's conflicting neighbors.
's conflicting neighbors. to zero, and reselect a link with the largest label.
to zero, and reselect a link with the largest label.


 10 grid topology with three 8-hop flows.
10 grid topology with three 8-hop flows.
 and
and  : assign a locally least occupied channel to a free NIC on
: assign a locally least occupied channel to a free NIC on  and
and  , respectively.
, respectively. at least one free NIC on
at least one free NIC on  (or vice versa): choose locally least occupied channel from
(or vice versa): choose locally least occupied channel from  's channel usage list and have one free NIC of
's channel usage list and have one free NIC of  tuned to that channel to communicate with
tuned to that channel to communicate with  .
. nor
nor  has any free NIC:
has any free NIC:  and
and  have at least one common channel4: communicate on a least occupied common channel utilizing the NICs already tuned to that channel.
have at least one common channel4: communicate on a least occupied common channel utilizing the NICs already tuned to that channel. and
and  have no common channel, and the connectivity between
have no common channel, and the connectivity between  and
and  has already been satisfied: return to Step 1 to set the label of link
has already been satisfied: return to Step 1 to set the label of link 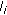 to zero.
to zero. and
and  have no common channel in use, and the connectivity between
have no common channel in use, and the connectivity between  and
and  is not satisfied: channel switching and channel switching propagation are needed. A least occupied channel is selected from
is not satisfied: channel switching and channel switching propagation are needed. A least occupied channel is selected from  's and
's and  's channel usage list, respectively. Assume they are
's channel usage list, respectively. Assume they are  and
and  , and
, and 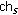 carries a lower traffic load. As Figure
carries a lower traffic load. As Figure  's NIC that originally works on
's NIC that originally works on  is switched to
is switched to  to communicate with
to communicate with  . To preserve
. To preserve  's connection with its own neighbors on
's connection with its own neighbors on 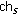 , this switching is propagated to those neighbors, and then to neighbors of those neighbors, and so on.
, this switching is propagated to those neighbors, and then to neighbors of those neighbors, and so on.





 and
and  are using to communicate with neighbors other than each other.5.Simulation code available at
are using to communicate with neighbors other than each other.5.Simulation code available at