- Research Article
- Open access
- Published:
Blind Separation of Two Users Based on User Delays and Optimal Pulse-Shape Design
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 939340 (2010)
Abstract
A wireless network is considered, in which two spatially distributed users transmit narrow-band signals simultaneously over the same channel using the same power. User separation is achieved by oversampling the received signal and formulating a virtual multiple-input multiple-output (MIMO) system based on the resulting polyphase components. Because of oversampling, high correlations can occur between the columns of the virtual MIMO system matrix which can be detrimental to user separation. A novel pulse-shape waveform design is proposed that results in low correlation between the columns of the system matrix, while it exploits all available bandwidth as dictated by a spectral mask. It is also shown that the use of successive interference cancelation in combination with blind source separation further improves the separation performance.
1. Introduction
We consider the problem of multiuser separation in wireless networks via approaches that do not use scheduling. This problem is of interest, for example, when traffic is generated in a bursty fashion, in which case fixed bandwidth allocation would result in poor bandwidth utilization. Lack of scheduling results in collisions, that is, users overlapping in time and/or frequency. To separate the colliding users, one could enable multiuser separation via receive antenna diversity, or code diversity, as in code-division multiple-access (CDMA) systems. However, the former requires expensive hardware since multiple transceiver front ends involve significant cost. Further, the use of multiple antennas might not be possible on small-size terminals or devices. CDMA systems require bandwidth expansion, which requires greater spectral resources, and also introduces frequency-selective fading. In the following, we narrow our field of interest to random-access systems that for the aforementioned reasons cannot exploit antenna diversity, and that are inexpensive in terms of bandwidth. In such systems, the use of different power levels by the users can enable user separation by exploiting the capture effect [1], or successive interference cancellation (SIC) [2]. Different power levels can result from different distances between the users and the destination, or could be intentionally assigned to users in order to facilitate user separation. While the former case, when it arises, makes the separation problem much easier, the latter approach might not be efficient, as low-power users suffer from noise and channel effects. In the following, we focus on the most difficult scenario of separating a collision of equal-power users. Almost equal powers would also result from power control. Power control is widely used, hence this scenario is of practical interest.
A delay-division multiple access approach was proposed in [3], which exploits the random delays introduced by transmitters. The approach of [3] considers transmissions of isolated frames. It requires that users have distinct delays, assumes full channel knowledge at the receiver and exploits the edges of a frame over which users do not overlap. Pulse-shape waveform diversity was considered in [4] to separate multiple users in a blind fashion. In [4], the received signal is oversampled and its polyphase components are viewed as independent mixtures of the user signals. User separation is achieved by solving a blind source separation problem. Although no specifics on waveform design are given in [4], the examples used in the simulations of [4] consider wideband waveforms for the users. However, if large bandwidth is available, then CDMA would probably be a better alternative to blind source separation. Pulse-shape diversity is also employed in [5, 6], addressing situations in which the pulse-shape waveforms have bandwidth constraints.
In this paper we follow the oversampling approach of [4], with the following differences. First, we introduce an intentional half-symbol delay between the two users. Second, both users use the same optimally designed pulse-shape waveform. Third, we use successive interference cancelation in combination with blind source separation to further improve the separation performance.
The paper is organized as follows. In Section 2, we describe the problem formulation. The proposed blind method is presented in Section 3. The Pulse-shape design is derived in Section 4. Simulation results validating the proposed method are presented in Section 5, while concluding remarks are given in Section 6.
Notation 1.
Bold capitals denote matrices. Bold lower-case symbols denote vectors. The superscript  denotes transposition. The superscript
denotes transposition. The superscript  denotes the pseudoinverse.
denotes the pseudoinverse.  denotes the diagonal matrix with diagonal elements the elements of
denotes the diagonal matrix with diagonal elements the elements of  .
.  denotes rounding down to the nearest integer.
denotes rounding down to the nearest integer.  denotes the trace of its argument.
denotes the trace of its argument.  denotes the phase of its argument.
denotes the phase of its argument.
2. Problem Formulation
We consider a distributed antenna system, in which  users transmit simultaneously to a base station. Although much of this paper studies the case
users transmit simultaneously to a base station. Although much of this paper studies the case  , for reasons that will be explained later, we will keep the
, for reasons that will be explained later, we will keep the  user notation throughout. Narrow-band transmission is assumed here, in which the channel between any user and the base station undergoes flat fading. In addition, quasi-static fading is assumed, that is, the channel gains remain fixed during several symbols.
user notation throughout. Narrow-band transmission is assumed here, in which the channel between any user and the base station undergoes flat fading. In addition, quasi-static fading is assumed, that is, the channel gains remain fixed during several symbols.
The transmitted signal of user  is of the form
is of the form

where  is the
is the  th symbol of user
th symbol of user  ;
;  is the symbol period;
is the symbol period;  is a pulse-shaping function with support
is a pulse-shaping function with support  , where
, where  is an integer.
is an integer.
The continuous-time baseband received signal  can be expressed as
can be expressed as

where  denotes the complex channel gain between the
denotes the complex channel gain between the  th user and the base station;
th user and the base station;  denotes the delay of the
denotes the delay of the  th user;
th user;  is the carrier frequency offset (CFO) of the
is the carrier frequency offset (CFO) of the  th user, arising due to relative motion or oscillator mismatch between receive and transmitter oscillators, and
th user, arising due to relative motion or oscillator mismatch between receive and transmitter oscillators, and  represents noise.
represents noise.
Our objective is to obtain an estimate of each user sequence,  , up to a complex scalar multiple that is independent of
, up to a complex scalar multiple that is independent of  . The estimation will be based on the received signal only, while channel gains, CFOs and user delays are assumed to be unknown. During the recovery process, there is permutation ambiguity, that is, the order of the users may be lost and again the user signals will be recovered up to a scalar multiple. However, these are considered to be trivial ambiguities and are inherent in blind estimation problems.
. The estimation will be based on the received signal only, while channel gains, CFOs and user delays are assumed to be unknown. During the recovery process, there is permutation ambiguity, that is, the order of the users may be lost and again the user signals will be recovered up to a scalar multiple. However, these are considered to be trivial ambiguities and are inherent in blind estimation problems.
We should note that typically, in high-speed communication systems, the main lobes of the pulse-shape functions overlap by  [7]. This extended time support allows for better frequency concentration, or equivalently, lower spectral occupancy for the transmission of each symbol. However, it introduces intersymbol interference (ISI). Examining
[7]. This extended time support allows for better frequency concentration, or equivalently, lower spectral occupancy for the transmission of each symbol. However, it introduces intersymbol interference (ISI). Examining  for
for  (see (1)), we note the contribution of the
(see (1)), we note the contribution of the  th symbol, the contribution of symbol
th symbol, the contribution of symbol  due to the main lobe of
due to the main lobe of  , and also contributions of symbols
, and also contributions of symbols  due to the sidelobes of
due to the sidelobes of  , respectively. If
, respectively. If  is a Nyquist pulse and samples are taken at times
is a Nyquist pulse and samples are taken at times  , the overlap does not play any role. However, when we obtain more than one sample during the symbol interval, we expect ISI effects.
, the overlap does not play any role. However, when we obtain more than one sample during the symbol interval, we expect ISI effects.
Sampling the received signal  at times
at times  we obtain
we obtain


where  is the normalized CFO between the
is the normalized CFO between the  th user and the base station,
th user and the base station,  "*" denotes convolution, and
"*" denotes convolution, and  is defined as
is defined as

The  th polyphase component,
th polyphase component,  , can be expressed as
, can be expressed as

Let us form the vector  as
as  . It holds that
. It holds that

where  is a
is a  matrix whose
matrix whose  th row equals
th row equals  ;
;  ; and
; and  . This is a
. This is a  instantaneous multiple-input multiple-output (MIMO) problem. Under certain assumptions, to be provided in the following section, the channel matrix
instantaneous multiple-input multiple-output (MIMO) problem. Under certain assumptions, to be provided in the following section, the channel matrix  is identifiable, and the vector
is identifiable, and the vector  can be recovered up to certain ambiguities. In particular, for each
can be recovered up to certain ambiguities. In particular, for each  , we get
, we get  different versions of
different versions of  , that is,
, that is,  within a scalar ambiguity. The effects of the CFO on the separated signals can be mitigated by using any of the existing single-CFO estimation techniques (e.g., [8–13]), or a simple phase-locked loop (PLL) device [14].
within a scalar ambiguity. The effects of the CFO on the separated signals can be mitigated by using any of the existing single-CFO estimation techniques (e.g., [8–13]), or a simple phase-locked loop (PLL) device [14].
3. Blind User Separation
3.1. Assumptions
The following assumptions are sufficient for user separation.
-
(A1)
Each of the elements of
 , as a function of
, as a function of  , is a zero-mean, complex Gaussian stationary random process with variance
, is a zero-mean, complex Gaussian stationary random process with variance  , and is independent of the inputs.
, and is independent of the inputs. -
(A2)
For each
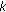 ,
, 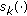 is independent and identically distributed (i.i.d.) with zero mean and nonzero kurtosis, that is,
is independent and identically distributed (i.i.d.) with zero mean and nonzero kurtosis, that is,  The
The  's are mutually independent, and each user has unit transmission power.
's are mutually independent, and each user has unit transmission power. -
(A3)
The oversampling factor
 satisfies
satisfies 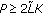 .
. -
(A4)
The channel coefficients
 are nonzero.
are nonzero. -
(A5)
The user delays,
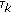 ,
,  in (3) are randomly distributed in the interval
in (3) are randomly distributed in the interval 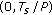 .
. -
(A6)
Either the CFOs are distinct, or the user delays are distinct.
-
(A7)
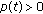 for
for 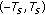 ; and
; and  only for
only for 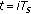 and
and 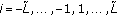 .
.
Under assumption  , it is easy to verify that the rotated input signals
, it is easy to verify that the rotated input signals  are also i.i.d. with zero mean and nonzero kurtosis. Also, the
are also i.i.d. with zero mean and nonzero kurtosis. Also, the  's are mutually independent for different
's are mutually independent for different  's. Assumptions
's. Assumptions  and
and  are needed for blind MIMO estimation based on (7). Assumptions
are needed for blind MIMO estimation based on (7). Assumptions  guarantee that the virtual MIMO channel matrix
guarantee that the virtual MIMO channel matrix  in (7) has full rank with high probability. Assumption
in (7) has full rank with high probability. Assumption  can actually be relaxed. As will be discussed later, (see (18)), the contributions of low-value columns of
can actually be relaxed. As will be discussed later, (see (18)), the contributions of low-value columns of  in (7) can be viewed as noise. This effectively reduces the dimensionality of the problem.
in (7) can be viewed as noise. This effectively reduces the dimensionality of the problem.  and
and  guarantee that
guarantee that  will be nonzero for all allowable values of
will be nonzero for all allowable values of  ,
,  , and
, and  . To see the effect of
. To see the effect of  , let us write the channel matrix
, let us write the channel matrix  as
as

where  is formed by appending
is formed by appending  in (5) for different
in (5) for different  's, that is,
's, that is,

and consider the case in which all users have the same delays, that is,  . If the CFOs are different, A has full column rank. Even if the CFOs are not distinct, the columns of the channel matrix can be viewed as having been drawn independently from an absolutely continuous distribution, and thus the channel matrix has full rank with probability one [15].
. If the CFOs are different, A has full column rank. Even if the CFOs are not distinct, the columns of the channel matrix can be viewed as having been drawn independently from an absolutely continuous distribution, and thus the channel matrix has full rank with probability one [15].
3.2. Channel Estimation and User Separation
One can apply to (7) any blind source separation algorithm (e.g., [16]) to obtain an estimate of the channel matrix,  , which is related to the true matrix as
, which is related to the true matrix as

where  is a column permutation matrix, and
is a column permutation matrix, and  is a complex diagonal matrix. The method of [16] requires fourth-order cumulants of
is a complex diagonal matrix. The method of [16] requires fourth-order cumulants of  . Accordingly, the estimate of the decoupled signals
. Accordingly, the estimate of the decoupled signals  within permutation and diagonal complex scalar ambiguities is
within permutation and diagonal complex scalar ambiguities is

Denoting by  the diagonal element of
the diagonal element of  , which corresponds to the phase ambiguity of user
, which corresponds to the phase ambiguity of user  with delay
with delay  , the separated signals can be expressed as
, the separated signals can be expressed as

At this point, the users' signals have been decoupled, and all that is left is to mitigate the CFO in each recovered signal. This can be achieved with any of the existing single CFO estimation methods, such as [8–12], or [13]. Alternatively, if the CFO is very small, then we can estimate it and at the same time mitigate its effects using a PLL. We should note here that even a very small CFO needs to be mitigated in order to have good symbol recovery. For example, for 4-ary quadrature amplitude modulation (4QAM) signals and without CFO compensation, even if the normalized CFO  is as small as
is as small as  , the constellation will be rotated to a wrong position after
, the constellation will be rotated to a wrong position after  samples.
samples.
If the CFO is large, then a PLL does not suffice, with the severity of the problem depending on the modulation scheme. In this case, the phase of the estimated channel matrix  can be used to obtain a CFO estimate. If
can be used to obtain a CFO estimate. If  for all
for all  , then it can be easily seen that
, then it can be easily seen that  with
with

where  is a
is a  vector with all elements equal to one, and
vector with all elements equal to one, and  . The least-squares estimates of the CFO can be obtained as
. The least-squares estimates of the CFO can be obtained as

where  is the
is the  th element of
th element of  .
.
On noting that the decoupled signals  in (12) are permuted (see (11)) in the same manner as the estimated CFOs in (14), we can use the
in (12) are permuted (see (11)) in the same manner as the estimated CFOs in (14), we can use the  's to compensate for the effect of CFO in the decoupled signals in (12) and obtain estimates of the input signals as
's to compensate for the effect of CFO in the decoupled signals in (12) and obtain estimates of the input signals as

where  with
with  . In order to resolve user permutation and shift ambiguities, one can use user IDs embedded in the data [17].
. In order to resolve user permutation and shift ambiguities, one can use user IDs embedded in the data [17].
Although in theory, under the above stated conditions, the matrix  has full rank for any number of users,
has full rank for any number of users,  , the matrix condition number may become too high when CFOs or delay differences between users become small. As
, the matrix condition number may become too high when CFOs or delay differences between users become small. As  increases, the latter problem will escalate. Further, for large
increases, the latter problem will escalate. Further, for large  , the oversampling factor,
, the oversampling factor,  , must be large. However, as
, must be large. However, as  increases, neighboring pulse-shape function samples will be close to each other, and the condition number of
increases, neighboring pulse-shape function samples will be close to each other, and the condition number of  will increase. Therefore, the shape of the pulse-shape function sets a limit on the oversampling factor one can use and thus on the number of users one can separate. Recognizing that the above are difficult issues to deal with, we next focus on the two-user case. Further, we propose to introduce an intentional delay of
will increase. Therefore, the shape of the pulse-shape function sets a limit on the oversampling factor one can use and thus on the number of users one can separate. Recognizing that the above are difficult issues to deal with, we next focus on the two-user case. Further, we propose to introduce an intentional delay of  between the two users, in addition to any small random delays there exist in the system.
between the two users, in addition to any small random delays there exist in the system.
The performance of user separation depends on the pulse-shape function and also on the location of the samples. Although uniform sampling was described above, non-uniform sampling can also be used, in which case the expressions would require some straightforward modifications. If the samples correspond to a low-value region of the pulse, the corresponding polyphase components will suffer from low signal-to-noise ratio. Also, if the sampling points are close to each other, then the condition number of  will increase. Therefore, one should select the sampling points so that the corresponding samples are all above some threshold and the sampling points are as separated as possible. The effect of pulse-shape and optimal shape design will be discussed in the following section.
will increase. Therefore, one should select the sampling points so that the corresponding samples are all above some threshold and the sampling points are as separated as possible. The effect of pulse-shape and optimal shape design will be discussed in the following section.
4. Pulse-Shape Design
In this section, we first investigate the effects of pulse-shape on the condition number of  . Since the condition number of a matrix increases as the column correlation increases, we next look at the correlation between the columns of
. Since the condition number of a matrix increases as the column correlation increases, we next look at the correlation between the columns of  .
.
Let us partition the channel matrix  into two sub-matrices
into two sub-matrices  and
and  , containing, respectively, the columns of
, containing, respectively, the columns of  corresponding to the main lobe and those corresponding to the sidelobes of the pulse. We can rewrite (7) as follows:
corresponding to the main lobe and those corresponding to the sidelobes of the pulse. We can rewrite (7) as follows:

where

with  as defined in (9). Correspondingly,
as defined in (9). Correspondingly,  , and
, and  . If the sidelobes of the pulse are very low, then
. If the sidelobes of the pulse are very low, then  can be treated as noise and (16) can be written as
can be treated as noise and (16) can be written as

4.1. Pulse Effects
In order to maintain a well-conditioned  , the correlation coefficient between its columns should be low. Let us further divide the matrix
, the correlation coefficient between its columns should be low. Let us further divide the matrix  into
into  and
and  . The elements of
. The elements of  are samples from the decreasing part of the main lobe of the pulse. On the other hand, the elements of
are samples from the decreasing part of the main lobe of the pulse. On the other hand, the elements of  are from the increasing part of the main lobe of the pulse. Thus, the correlation coefficient of
are from the increasing part of the main lobe of the pulse. Thus, the correlation coefficient of  and
and  is smaller than the correlation coefficient of
is smaller than the correlation coefficient of  and
and  , or that of
, or that of  and
and  . Thus, we focus on the effects of the pulse on the column correlations within
. Thus, we focus on the effects of the pulse on the column correlations within  and
and  .
.
Proposition 1.
Let  be a Nyquist pulse that is positive within its main lobe, that is,
be a Nyquist pulse that is positive within its main lobe, that is,  for
for  . We further assume
. We further assume  is an even function with very low sidelobes. For
is an even function with very low sidelobes. For  and
and  (
( ) in
) in  , the absolute value of the correlation coefficient between
, the absolute value of the correlation coefficient between  and
and  is upper bounded as follows:
is upper bounded as follows:

where  ,
,  is the sampling interval, that is,
is the sampling interval, that is,  , and
, and  is given by
is given by

where  denotes the first-order derivative of
denotes the first-order derivative of  .
.
Proof.
See the appendix.
When  is large, the following approximation holds:
is large, the following approximation holds:

Thus, for fixed  and
and  , the correlation coefficient between
, the correlation coefficient between  and
and  decreases with increasing
decreases with increasing  . It can be shown that the same holds for the correlation coefficient between
. It can be shown that the same holds for the correlation coefficient between  and
and  .
.
Because  should be a Nyquist pulse with small sidelobes and
should be a Nyquist pulse with small sidelobes and  for
for  , it should hold that
, it should hold that

where  is small.
is small.
There are additional constraints that the pulse should satisfy, the most important of which is a bandwidth constraint. Most commercial systems, for example, the IEEE 802.11a, IEEE 802.11b, and IEEE 802.11g wireless local-area networks (WLANs) [18], are equipped with a spectral mask that dictates the maximum allowable spectrum, or equivalently, the maximum symbol rate. This leads to a constraint of the form

where  is the Fourier transform of
is the Fourier transform of  , and
, and  denotes the spectral mask.
denotes the spectral mask.
4.2. Optimum Pulse Design
Based on the above constraints and assuming that  satisfies the conditions of Proposition 1, the pulse design problem can be expressed as
satisfies the conditions of Proposition 1, the pulse design problem can be expressed as





The problem of (24a)-(24e) is not easy to solve. Next, we will take steps towards reformulating it into a convex optimization problem. Let  be a vector containing samples of
be a vector containing samples of  taken in
taken in  , with sampling interval
, with sampling interval  , in which case
, in which case  (
( is an integer representing the number of samples in each symbol interval). The objective function (24a) is equivalent to
is an integer representing the number of samples in each symbol interval). The objective function (24a) is equivalent to

where  is of the form
is of the form

As  is an even symmetric function, the Fourier transform of
is an even symmetric function, the Fourier transform of  can be represented as
can be represented as  , where
, where  , with power spectral density (PSD) equal to
, with power spectral density (PSD) equal to  . Hence, the constraint (24b) is equivalent to
. Hence, the constraint (24b) is equivalent to

Because (27) involves an infinite number of constraints, we sample  in the frequency domain:
in the frequency domain:

where  is the number of samples in
is the number of samples in  . In order for (28) to be a good approximation of (27),
. In order for (28) to be a good approximation of (27),  should be on the order of
should be on the order of  [19].
[19].
In the discrete-time domain, (24c) is equivalent to

where  is small and
is small and  with
with  leading zeros.
leading zeros.
Define  , with the
, with the  th element equal to
th element equal to  . Equation (24d) is equivalent to
. Equation (24d) is equivalent to

with  . Hence the problem of (24a)-(24e) can be reformulated as
. Hence the problem of (24a)-(24e) can be reformulated as





Since it involves maximization of a convex function, (31a) is not a convex optimization problem. Letting  ,
,  should be a positive semidefinite matrix of rank
should be a positive semidefinite matrix of rank  . The problem of (31a)–(31e) is equivalent to
. The problem of (31a)–(31e) is equivalent to







However, the constraint of (32g) is not a convex constraint. By dropping it, we obtain a semidefinite relaxation of the primal problem [20]. The resulting convex optimization problem is






As we drop the constraint  , the resulting
, the resulting  might not be of unit rank. In this case, we apply eigen-decomposition to
might not be of unit rank. In this case, we apply eigen-decomposition to  . Let
. Let

where  is the largest eigenvalue of
is the largest eigenvalue of  , and
, and  is the corresponding eigenvector. As
is the corresponding eigenvector. As  , its eigenvalues
, its eigenvalues  for
for  . If
. If

then  can result in a good pulse-shape. If
can result in a good pulse-shape. If  , then it holds that
, then it holds that

which indicates that  in the problem of (24a)–(24e) is maximized. Moreover,
in the problem of (24a)–(24e) is maximized. Moreover,  can guarantee the validity of (31b) and (31c). Also, if
can guarantee the validity of (31b) and (31c). Also, if  and
and  , then
, then

This indicates that the PSD of  will be under the IEEE 802.11 mask. In the same way, we can prove that
will be under the IEEE 802.11 mask. In the same way, we can prove that

which further indicates that  has small sidelobes. Moreover,
has small sidelobes. Moreover,  is small and the validity of (38) implies that
is small and the validity of (38) implies that

which indicates that, if we sample at intervals  , the interference from neighboring symbols can be neglected.
, the interference from neighboring symbols can be neglected.
If  , then it holds that
, then it holds that  . Also, (33e) requires that the
. Also, (33e) requires that the  th element of
th element of  be greater than zero for
be greater than zero for  . Hence,
. Hence,  or
or  for
for  . Thus, within its mainlobe,
. Thus, within its mainlobe,  is greater than zero, or its amplitude becomes very small.
is greater than zero, or its amplitude becomes very small.
5. Simulation Results
5.1. Pulse Design Examples
In this section, we demonstrate the performance of a pulse designed as described in Section 4.2. We take  samples per symbol, that is,
samples per symbol, that is,  , and set
, and set  . Then we obtain
. Then we obtain  and
and  samples in the time and frequency domains, respectively. We take
samples in the time and frequency domains, respectively. We take  to be
to be  . In Figure 1, we show the ratio
. In Figure 1, we show the ratio  of the resulting matrix
of the resulting matrix  at different symbol rates, where
at different symbol rates, where  is the largest eigenvalue of
is the largest eigenvalue of  . One can see that the smallest
. One can see that the smallest  is above
is above  , which means that the condition of (35) is satisfied. Therefore,
, which means that the condition of (35) is satisfied. Therefore,  is a good choice of pulse-shape.
is a good choice of pulse-shape.
For symbol rate  , or equivalently,
, or equivalently,  , the designed time-domain pulse is shown in Figure 2. For comparison, the Isotropic Orthogonal Transform Algorithm (IOTA) pulse [21] is also shown in the same figure. The corresponding PSDs, along with the IEEE 802.11 spectral mask are given in Figure 3. From the figures we can see that the proposed pulse decreases faster than the IOTA pulse within
, the designed time-domain pulse is shown in Figure 2. For comparison, the Isotropic Orthogonal Transform Algorithm (IOTA) pulse [21] is also shown in the same figure. The corresponding PSDs, along with the IEEE 802.11 spectral mask are given in Figure 3. From the figures we can see that the proposed pulse decreases faster than the IOTA pulse within  . The larger the value of
. The larger the value of  , the faster
, the faster  decreases. In Figure 3, one can see that the PSD of the proposed pulse is under the 802.11 mask, while the PSD of the IOTA pulse violates the mask at
decreases. In Figure 3, one can see that the PSD of the proposed pulse is under the 802.11 mask, while the PSD of the IOTA pulse violates the mask at  MHz.
MHz.
For symbol rate  , or,
, or,  , the obtained pulse is given in Figures 4 and 5. We also plot the raised cosine pulse with roll-off factor being equal to
, the obtained pulse is given in Figures 4 and 5. We also plot the raised cosine pulse with roll-off factor being equal to  . One can see that, in the frequency domain, the proposed pulse is under the 802.11 mask, while in the time domain the proposed pulse is narrower. Note that at this symbol rate, the IOTA pulse cannot meet the mask constraint.
. One can see that, in the frequency domain, the proposed pulse is under the 802.11 mask, while in the time domain the proposed pulse is narrower. Note that at this symbol rate, the IOTA pulse cannot meet the mask constraint.
5.2. SER Performance
In this section, we demonstrate the performance of the proposed user separation approach via simulations. We consider a two-user system. The channel coefficients  and
and  are taken to be zero-mean complex with unit amplitude and phase that is randomly distributed in
are taken to be zero-mean complex with unit amplitude and phase that is randomly distributed in  . The CFOs are chosen randomly in the range
. The CFOs are chosen randomly in the range  . The input signals are
. The input signals are  -QAM containing
-QAM containing  symbols. The estimation results are averaged over
symbols. The estimation results are averaged over  independent channels, and
independent channels, and  Monte-Carlo runs for each channel. One user is intentionally delayed by half a symbol and in addition, small delays, taken randomly from the interval
Monte-Carlo runs for each channel. One user is intentionally delayed by half a symbol and in addition, small delays, taken randomly from the interval  , are introduced to each user.
, are introduced to each user.
In our simulations, we combine blind source separation method with SIC [2]. For blind source separation the Joint Approximate Diagonalization of Eigenmatrices (JADE) algorithm was used, which was downloaded from http://perso.telecom-paristech.fr/~cardoso/Algo/Jade/jade.m. We first apply JADE to decouple the users, and then correct the decoupled users' CFOs. Subsequently, the strongest user, that is, the one which shows the best concentration around the nominal constellation is deflated from the received polyphase components to detect the other user. SIC requires that the first user should be detected very well. To achieve this, the sampling points are chosen around the peak of one user signal, so that ISI and interuser interference effects are minimized.
Eliminating CFO effects from the decoupled users can be done via a PLL, if the CFO is small, or a PLL initialized with a good CFO estimate, if the CFO is large as the PLL by itself would not converge in this case. For the latter case, since we sample around the peak of one user, the CFO estimation formula of (14) requires a small modification before it is applied. Let the  sampling points occur at
sampling points occur at  , and let
, and let  be the phase of the channel matrix corresponding to these sampling points. The least-squares estimate of the CFO
be the phase of the channel matrix corresponding to these sampling points. The least-squares estimate of the CFO  can be obtained as
can be obtained as

where  is the
is the  th element of
th element of  .
.
In this experiment, the pulse has time support  . We take
. We take  polyphase components of the received symbols, each consisting of samples taken evenly over the interval
polyphase components of the received symbols, each consisting of samples taken evenly over the interval  , with sampling period
, with sampling period  . In order to sample around the peak of one user, we used the true shift values. However, in a realistic scenario this information would be obtained via synchronization pilots [17].
. In order to sample around the peak of one user, we used the true shift values. However, in a realistic scenario this information would be obtained via synchronization pilots [17].
The symbol error rate (SER) performance at  sec, that is, at symbol rate
sec, that is, at symbol rate  M/sec, using the waveform of Figure 2, is shown in Figure 6 along with the performance corresponding to the IOTA pulse. We can see that the SER of the proposed pulse is lower; there is an approximate
M/sec, using the waveform of Figure 2, is shown in Figure 6 along with the performance corresponding to the IOTA pulse. We can see that the SER of the proposed pulse is lower; there is an approximate  dB SNR advantage over the IOTA result.
dB SNR advantage over the IOTA result.
In Figure 7, we show the SER versus SNR at different symbol rates. First, by taking  sec, or equivalently symbol rate
sec, or equivalently symbol rate  M/sec, we compare the SER performance of the proposed pulses and the raised cosine pulse with roll-off factor 1. As we can see, the performance of the proposed pulse is better. For example, the proposed pulse can achieve
M/sec, we compare the SER performance of the proposed pulses and the raised cosine pulse with roll-off factor 1. As we can see, the performance of the proposed pulse is better. For example, the proposed pulse can achieve  at
at  dB SNR, while the raised cosine pulse needs
dB SNR, while the raised cosine pulse needs  dB SNR to achieve the same SER. In the same figure we show the SER performance of the proposed pulse at symbol rate
dB SNR to achieve the same SER. In the same figure we show the SER performance of the proposed pulse at symbol rate  M/sec. At this rate, the proposed pulse can achieve an SER of
M/sec. At this rate, the proposed pulse can achieve an SER of  at
at  dB SNR.
dB SNR.
In Figure 8, we show SER performance for different values of the oversampling factor,  , at different symbol rates. For
, at different symbol rates. For  , the sampling occurs evenly within the interval
, the sampling occurs evenly within the interval  of each received symbol with sampling period
of each received symbol with sampling period  . One can see that, for symbol rate
. One can see that, for symbol rate  M/sec, when the SNR is higher than
M/sec, when the SNR is higher than  dB, the SER performance improves by increasing
dB, the SER performance improves by increasing  from
from  to
to  . For symbol rates equal to
. For symbol rates equal to  M/sec and
M/sec and  M/sec the SER performance remains almost the same with increasing
M/sec the SER performance remains almost the same with increasing  .
.
In order to demonstrate the effect of the proposed pulse on the condition number of the system matrix, we show in Figure 9 the condition number of  corresponding to the proposed and IOTA pulses, averaged over
corresponding to the proposed and IOTA pulses, averaged over  random channels realizations and with
random channels realizations and with  . In order to make a fair comparison, the CFOs and random delays were set to be the same for both pulses. No noise was added in the data. The estimated
. In order to make a fair comparison, the CFOs and random delays were set to be the same for both pulses. No noise was added in the data. The estimated  's were collected from the JADE output, and their condition numbers were calculated. One can see that the proposed pulse results consistently in lower condition number than the IOTA pulse.
's were collected from the JADE output, and their condition numbers were calculated. One can see that the proposed pulse results consistently in lower condition number than the IOTA pulse.
Next, we show the effect of user delays on performance. As before, one user is delayed by a half-symbol interval, and in addition, a random delay  is added to both users to model random delays introduced at the transmitter. In this experiment, the range for the random delay
is added to both users to model random delays introduced at the transmitter. In this experiment, the range for the random delay  is increased from
is increased from  to
to  . For random delays within
. For random delays within  , in order to prevent the delay difference of two users from being too small, we select the delays so that their difference is no less than a threshold
, in order to prevent the delay difference of two users from being too small, we select the delays so that their difference is no less than a threshold  . The resulting SER performance is shown in Figure 10. When the range of
. The resulting SER performance is shown in Figure 10. When the range of  increases from
increases from  to
to  the performance becomes worse. This is because by increasing the range for the random delay, the signals of the two users overlap by a larger amount, which results in high condition number for the channel matrix
the performance becomes worse. This is because by increasing the range for the random delay, the signals of the two users overlap by a larger amount, which results in high condition number for the channel matrix  . The best performance would be obtained with just the half-symbol delay and no random delays; however, this is not a realistic case.
. The best performance would be obtained with just the half-symbol delay and no random delays; however, this is not a realistic case.
Next, to show the advantage of the intentional half-symbol delay, we consider a case without intentional delay, with random user delays only. The random delays of both users are taken within  . In order to prevent worsening of performance we restricted the smallest delay difference between two users to be no less than
. In order to prevent worsening of performance we restricted the smallest delay difference between two users to be no less than  . We compare the SER performance of the proposed pulse with IOTA and raised cosine pulses at different symbol rates. Firstly, comparing the corresponding curves in Figure 10, one can first see that without the intentional delay the SER performance decreases. In particular, for the proposed pulse in order to achieve SER
. We compare the SER performance of the proposed pulse with IOTA and raised cosine pulses at different symbol rates. Firstly, comparing the corresponding curves in Figure 10, one can first see that without the intentional delay the SER performance decreases. In particular, for the proposed pulse in order to achieve SER  , we need an SNR of
, we need an SNR of  dB and
dB and  dB for symbol rates
dB for symbol rates  M/sec and
M/sec and  M/sec, respectively. Secondly, the SER performance of the proposed pulse is still better than that of IOTA and raised cosine pulses at the corresponding symbol rate.
M/sec, respectively. Secondly, the SER performance of the proposed pulse is still better than that of IOTA and raised cosine pulses at the corresponding symbol rate.
Finally, we show the effect of CFOs on performance (see Figure 12). In order to highlight the effect of the CFOs, SER results were obtained without intentional delay, with random delays taken in the interval  and by setting the delay difference of the two users to be no less than
and by setting the delay difference of the two users to be no less than  . The normalized CFOs were chosen randomly within the range
. The normalized CFOs were chosen randomly within the range  for
for  , and
, and  . For
. For  we restricted the smallest difference between two CFOs to be no less than
we restricted the smallest difference between two CFOs to be no less than  , and for
, and for  , we set no threshold on the CFO difference of the two users. For
, we set no threshold on the CFO difference of the two users. For  , the CFO is quite large, and the PLL by itself is not enough to remove the CFO in the decoupled users. Therefore, we first used the method described in Section 3.2 to estimate the CFOs and then used the PLL to compensate for the residual CFO.
, the CFO is quite large, and the PLL by itself is not enough to remove the CFO in the decoupled users. Therefore, we first used the method described in Section 3.2 to estimate the CFOs and then used the PLL to compensate for the residual CFO.
The quality of the CFO estimates depends on the accuracy of the channel matrix estimate. Since low-magnitude elements of the channel matrix correspond to low values of the pulse, and as such are susceptible to errors, we set a threshold,  , defined as
, defined as  , and for CFO estimation, we only use elements of
, and for CFO estimation, we only use elements of  whose amplitudes are greater than
whose amplitudes are greater than  . In this experiment, we took
. In this experiment, we took  . The CFO effects were eliminated via a PLL initialized with the CFO estimate of (40). One can see that the larger
. The CFO effects were eliminated via a PLL initialized with the CFO estimate of (40). One can see that the larger  gives better performance. It is important to note that the large CFOs involve bandwidth expansion. The percentage of bandwidth expansion can be calculated as
gives better performance. It is important to note that the large CFOs involve bandwidth expansion. The percentage of bandwidth expansion can be calculated as  , where
, where  MHz is the bandwidth of the pulse. For
MHz is the bandwidth of the pulse. For  and
and  , the percentages of bandwidth expansion for symbol rates
, the percentages of bandwidth expansion for symbol rates  M/sec,
M/sec,  M/sec and
M/sec and  M/sec are, respectively,
M/sec are, respectively,  ,
,  , and
, and  .
.
6. Conclusions
A blind  -user separation scheme has been proposed that relies on intentional user delays, optimal pulse-shape waveform design, and also combines blind user separation with SIC. The proposed approach achieves low SER at a reasonable SNR level. Simulation results for the
-user separation scheme has been proposed that relies on intentional user delays, optimal pulse-shape waveform design, and also combines blind user separation with SIC. The proposed approach achieves low SER at a reasonable SNR level. Simulation results for the  case have confirmed that the proposed pulse design leads to SER performance better than that of conventional pulse-shape waveforms. The intentional delay was equal to half a symbol interval, which means that the users still overlap significantly during their transmissions. The use of intentional delay is necessitated by the fact that, although small user delay and CFO differences help preserve the identifiability of the problem, in practice, they may not suffice to separate the users. Also, although the proposed approach can work for any number of users, as the number of users increases, the CFO and delay differences become smaller, which makes the separation more difficult. Based on our experiments, small CFO differences did not affect performance. Although introducing large intentional CFO differences among users could help, that would increase the effective bandwidth. A new ALOHA-type protocol that separates second-order collision based on the ideas described in this paper, along with a software-defined radio implementation can be found in [17].
case have confirmed that the proposed pulse design leads to SER performance better than that of conventional pulse-shape waveforms. The intentional delay was equal to half a symbol interval, which means that the users still overlap significantly during their transmissions. The use of intentional delay is necessitated by the fact that, although small user delay and CFO differences help preserve the identifiability of the problem, in practice, they may not suffice to separate the users. Also, although the proposed approach can work for any number of users, as the number of users increases, the CFO and delay differences become smaller, which makes the separation more difficult. Based on our experiments, small CFO differences did not affect performance. Although introducing large intentional CFO differences among users could help, that would increase the effective bandwidth. A new ALOHA-type protocol that separates second-order collision based on the ideas described in this paper, along with a software-defined radio implementation can be found in [17].
References
Onozato Y, Liu J, Noguchi S: Stability of a slotted ALOHA system with capture effect. IEEE Transactions on Vehicular Technology 1989, 38(1):31-36. 10.1109/25.31132
Tse D, Viswanath P: Fundamentals of Wireless Communication. Cambridge University Press, Cambridge, UK; 2005.
Brandt-Pearce M: Signal separation using fractional sampling in multiuser communications. IEEE Transactions on Communications 2000, 48(2):242-251. 10.1109/26.823557
Zhang Y, Kassam SA: Blind separation and equalization using fractional sampling of digital communications signals. Signal Processing 2001, 81(12):2591-2608. 10.1016/S0165-1684(01)00155-4
Petropulu AP, Olivieri M, Yu Y, Dong L, Lackpour A: Pulse-shaping for blind multi-user separation in distributed MISO configurations. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '08), March-April 2008, Las Vegas, Nev, USA 2741-2744.
Liu X, Oymak S, Petropulu AP, Dandekar KR: Collision resolution based on pulse shape diversity. Proceedings of the IEEE International Workshop on Signal Processing Advances for Wireless Communications (SPAWC '09), June 2009, Perugia, Italy 409-413.
Sklar B: Digital Communications: Fundamentals and Applicatons. Prentice Hall, Upper Saddle River, NJ, USA; 2001.
Ciblat P, Loubaton P, Serpedin E, Giannakis GB: Performance analysis of blind carrier frequency offset estimators for noncircular transmissions through frequency-selective channels. IEEE Transactions on Signal Processing 2002, 50(1):130-140. 10.1109/78.972489
Ghogho M, Swami A, Durrani T: On blind carrier recovery in time-selective fading channels. Proceedings of the 33rd Asilomar Conference on Signals, Systems, and Computers, 1999, Pacific Grove, Calif, USA 1: 243-247.
Gini F, Giannakis GB: Frequency offset and symbol timing recovery in flat-fading channels: a cyclostationary approach. IEEE Transactions on Communications 1998, 46(3):400-411. 10.1109/26.662646
Scott KE, Olasz EB: Simultaneous clock phase and frequency offset estimation. IEEE Transactions on Communications 1995, 43(7):2263-2270. 10.1109/26.392969
Wang Y, Ciblat P, Serpedin E, Loubaton P: Performance analysis of a class of nondata-aided frequency offset and symbol timing estimators for flat-fading channels. IEEE Transactions on Signal Processing 2002, 50(9):2295-2305. 10.1109/TSP.2002.801919
Roman T, Visuri S, Koivunen V: Blind frequency synchronization in OFDM via diagonality criterion. IEEE Transactions on Signal Processing 2006, 54(8):3125-3135.
Wolaver DH: Phase-Locked Loop Circuit Design. Prentice Hall, Englewood Cliffs, NJ, USA; 1991.
Sidiropoulos ND, Giannakis GB, Bro R: Blind PARAFAC receivers for DS-CDMA systems. IEEE Transactions on Signal Processing 2000, 48(3):810-823. 10.1109/78.824675
Cardoso JF, Souloumiac A: Blind beamforming for non-Gaussian signals. IEE Proceedings F 1993, 140(6):362-370.
Liu X, Kountouriotis J, Petropulu AP, Dandekar KR: ALOHA with collision resolution (ALOHA-CR): theory and software defined radio implementation. IEEE Transactions on Signal Processing 2010, 58(8):4396-4410.
IEEE standard 802.11 http://www.ieee802.org/11/
Wu S, Boyd S, Vandenberghe L: FIR filter design via spectral factorization and convex optimization. In Applied and Computational Control, Signals and Circuits. Edited by: Datta BN. Birkhauser, Basel, Switzerland; 1998:215-245.
Sidiropoulos ND, Davidson TN, Luo Z-Q: Transmit beamforming for physical-layer multicasting. IEEE Transactions on Signal Processing 2006, 54(6):2239-2251.
Le Floch B, Alard M, Berrou C: Coded orthogonal frequency division multiplex [TV broadcasting]. Proceedings of the IEEE 1995, 83(6):982-996. 10.1109/5.387096
Acknowledgment
This research was been supported by the National Science Foundation under Grants CNS-09-16947 and CNS-09-05398 and by the Office of Naval Research under Grants N00014-07-1-0500 and N00014-09-1-0342.
Author information
Authors and Affiliations
Corresponding author
Appendix
Proof of Proposition 1
Proof.
We have


On letting  and
and  , the correlation between
, the correlation between  and
and  is equal to
is equal to


Taking the absolute value of (A.2), we have


The last step is due to the fact that  for
for  within the mainlobe, and that both
within the mainlobe, and that both  and
and  are within the interval
are within the interval  . We also have
. We also have


When the number of samples  is large,
is large,  and
and  are close. Applying first-order Taylor series expansion to each component of
are close. Applying first-order Taylor series expansion to each component of  , we have
, we have


On writing


we can approximate  by
by


The correlation between  and
and  is bounded by
is bounded by


And  can be approximated by
can be approximated by


where  . Since
. Since


we obtain


On substituting (A.11) into (A.9), we have


In the last step of (A.12), we assumed that  is large and
is large and  and
and  are small, and also that
are small, and also that  .
.
In the same way  can be approximated as
can be approximated as


Because  is an even function and also has very low sidelobes, (A.13) can be further simplified as
is an even function and also has very low sidelobes, (A.13) can be further simplified as


Substituting (A.12) and (A.13) into (A.8), we have


In this last step, we let


Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, X., Petropulu, A.P., Poor, H.V. et al. Blind Separation of Two Users Based on User Delays and Optimal Pulse-Shape Design. J Wireless Com Network 2010, 939340 (2010). https://doi.org/10.1155/2010/939340
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/939340
 , as a function of
, as a function of  , is a zero-mean, complex Gaussian stationary random process with variance
, is a zero-mean, complex Gaussian stationary random process with variance  , and is independent of the inputs.
, and is independent of the inputs.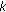 ,
, 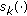 is independent and identically distributed (i.i.d.) with zero mean and nonzero kurtosis, that is,
is independent and identically distributed (i.i.d.) with zero mean and nonzero kurtosis, that is,  The
The  's are mutually independent, and each user has unit transmission power.
's are mutually independent, and each user has unit transmission power. satisfies
satisfies 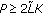 .
. are nonzero.
are nonzero.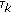 ,
,  in (3) are randomly distributed in the interval
in (3) are randomly distributed in the interval 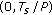 .
.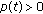 for
for 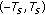 ; and
; and  only for
only for 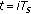 and
and 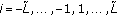 .
.
 for different symbol rates.
for different symbol rates.





 .
.
 .
.
 , with CFOs randomly chosen within the range
, with CFOs randomly chosen within the range  .
.
 .
.
 .
.
 .
.