- Research Article
- Open access
- Published:
Impact of Antenna Correlation on a New Dual-Hop MIMO AF Relaying Model
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 956721 (2010)
Abstract
A novel system model is proposed for the dual-hop multiple-input multiple-output amplify-andforward relay networks, and the impact of antenna correlation on the performance is studied. For a semiarbitrary correlated source-relay channel and an arbitrary correlated relay-destination channel, the complementary cumulative distribution function (CCDF) and the moment-generating function (MGF) approximations of the end-to-end signal-to-noise ratio (SNR) are derived. The outage probability, the average symbol error rate (SER), and the ergodic capacity approximations are also derived. Two special cases are treated explicitly: (1) dual-antenna relay and multiple-antenna destination and (2) uncorrelated antennas at the relay and correlated antennas at the destination. For the first case, the CCDF, the MGF and the average SER of an upper bound of the end-to-end SNR are derived in closed-form. For the second case, the CCDF, the MGF, the average SER, and the moments of SNR are derived in closed-form; as well, the high SNR approximations for the outage probability and the average SER are derived, and the diversity gain and coding gain are developed. Extensive numerical results and Monte Carlo simulation results are presented to verify the analytical results and to quantify the detrimental impact of antenna correlations on the system performance.
1. Introduction
Cooperative relay networks have been the focus of a flurry of research activities and standard deployment [1–5]. The use of multiple antennas at the source, relay, and/or destination of relay networks offers significant performance gains [6–15]. Such cooperative multiple-input multiple-output (MIMO) relaying opens up the possibility of deploying diversity transmission techniques such as beamforming, maximal ratio transmission (MRT), maximal ratio combining (MRC), and transmit antenna selection (TAS) strategies [10–12, 15]. In this paper, a suboptimal yet a simple and efficient system model, which achieves a better trade-off among the hardware cost, complexity, and the performance, is proposed and analyzed for dual-hop MIMO amplify-and-forward (AF) relay networks.
Prior Related Research
The prior work can be divided into two broad categories. The first category deals with multiple-antenna terminals (source, relay, and destination) [6, 10–17]. The second category considers single-antenna terminals only [4, 5, 18–21].
Single-antenna AF relaying over two hops with source and destination using multiple antennas is analyzed in [10, 11, 13]. In these works, beamforming or MRT and MRC technologies are considered. The difference between [11] and [13] is that the former considers independent Rayleigh fading whereas the latter considers independent Nakagami-
fading. In particular, [10] extends [13] to study the effect of antenna correlation at the source and destination. Moreover, in [12], the performance in independent Rayleigh fading is derived for a system, where the source uses TAS and the destination, MRC.
References [6, 15] analyze the performance of dual-hop multibranch cooperative systems with decode-and-forward (DF) relays equipped with multiple receive antennas and a single transmit antenna. However, the source and the destination are single-antenna terminals. In [6], the performance metrics are derived by considering threshold-based MRC and threshold-based selection diversity combining at the relay. Moreover, [15] extends [6] by employing distributed beamforming to achieve improved capacity gains.
In [14, 16, 17], the performance of single-relay system, where the source, the relay, and the destination terminals are equipped with multiple transmit/receive antennas, is analyzed. All these works employ space time block codes. The analysis in [14] considers both DF and AF relaying strategies. In [16], the performance analysis employs random matrix theory. Reference [17] derives the exact outage probability in closed form.
For the sake of completeness, we briefly mention some prior research of the second category dealing with single-antenna two-hop AF relay networks. Their performance over Rayleigh fading is analyzed in [4, 5]. The performance bounds for the multibranch case of such networks over Nakagami-
fading are derived in [18]. Reference [19] derives their performance over nonidentical Nakagami-m fading links. The performance bounds of such networks over generalized Gamma fading channels and nonidentical Weibull fading channels are derived in [20, 22]. In [21], the exact expressions and lower bounds for mixed Rayleigh and Rician fading channels are derived.
Motivation
Although the dual-hop MIMO relay models in [10–12, 15] provide significant performance gains over single-antenna relaying [4, 5, 18–20], the following issues may arise in practical network deployments of such networks. In the emerging cellular dual-hop relay networks, employing multiple antennas at the mobile stations (MS) is strictly limited due to power and space constraints. However, there are no such constrains at the base stations (BS). On the other hand, the hardware cost and complexity associated with the relay should be low compared to a traditional BS. Although relaying can be performed by an MS as well, in this work, an infrastructure (fixed) relay [7] is considered. Such a relay can employ multiple antennas.
In this paper, we consider a practical scenario where a single-antenna MS communicates with a multiple-antenna BS via a fixed relay equipped with multiple antennas. This particular setup is shown in Figure 1. The relay uses selection diversity combining (SDC) for signal reception and uses one transmit antenna for forwarding the amplified signal. Although several other antenna setups are possible for the relay, we focus on this setup for several reasons. First, alternatives such as MRC are more costly; if the relay employs MRC reception, a separate receiver chain is required for each receive antenna, and this requirement increases the cost and complexity. Second, a single transmit antenna at the relay keeps the cost comparable to that of a single antenna relay, which requires only one transmit chain. Although this particular transmit/receive strategy adopted at the relay may not be optimal, it is designed to gain MIMO diversity benefits yet keep the costs/complexity at the relay as low as possible. Finally, from a theoretical point of view, there is no difficulty in analyzing other antenna configurations at the relay, but space limitations prevent us from doing so. The proposed system model may thus readily be used for emerging cellular networks with MIMO relaying, where the use of multiple antennas in a BS is reasonable; however the use of multiple antennas at MS may be strictly limited due to the terminal size and power constraints.
System model: dual-hop MIMO relaying.
Our Contribution
Although MIMO techniques achieve diversity/SNR gains, these gains decrease when there is spatial correlation among the signals received by antenna elements. Therefore, the performance losses due to antenna correlations must be quantified. In this paper, in particularly, we consider the impact of spatial (antenna) correlation on our proposed dual-hop MIMO AF relay network (Figure 1). To the best of our knowledge, the proposed network setup has not been analyzed before, and the differences between our work and [6, 10] are as follows. The setup in [10] studies a multiple-antenna source and single-antenna relay. Moreover, in [10], MRT and MRC are employed at the source and destination whereas our setup employs SDC and MRC at the relay and destination, respectively. Although reference [6] considers a relay identical to ours, the destination is a single-antenna terminal. The relaying strategy in [6] is DF whereas AF relaying is considered here. Further, [6] considers independent fading whereas our work treats consider correlated fading.
In our work, for a semiarbitrary correlated source-relay channel and arbitrary correlated relay-destination channel, we derive integral expressions for the complementary cumulative distribution function (CCDF) and the moment-generating function (MGF) of the end-to-end signal-to-noise ratio (SNR). The numerically efficient Gauss-Laguerre quadrature rule [23] is employed to evaluate the integrals. The outage probability, the average symbol error rate (SER), and the ergodic capacity expressions are also derived. Closed-form expressions are derived for the performance of two special cases of antenna correlation: (
) dual-antenna relay and multiple-antenna destination and (
) uncorrelated antennas at the relay and correlated antennas at the destination. We develop closed-form expressions for the CCDF and the MGF of an upper bound of the SNR for the first case. The average SER is evaluated by using the Gauss-Chebyshev quadrature rule [23]. Exact closed-form expressions are derived for the CCDF, the MGF, the average SER, and the moments of SNR of the second case. In particular, for the second case, the high SNR approximations for the outage probability and the average SER are derived and used to obtain valuable insights such as the diversity and the coding gains. Numerical and Monte Carlo simulation results are provided to analyze the system performance, obtain valuable insights, and validate our analysis. The insights provided by our analysis may well be used for designing of MIMO relay networks.
The rest of this paper is organized as follows. Section 2 presents the system and the channel model. In Section 3, the performance analysis is presented. Section 4 contains the numerical and simulation results. Section 5 concludes the paper, and the proofs are annexed.
Notations
is the Modified Bessel function of the second kind of order
[23, 
]. 
is the Gauss Hypergeometric function [23, 
]. 
denotes the Gaussian Q-function[23, 
]. 
is the 
th-order Marcum
-function [24, equation (
)]. For the sake of brevity, we write 
to denote 
. 
is the 
th-order Modified Bessel function of the first kind [23, 
]. 
is the Exponential integral function [25, 
]. 
denotes the expected value of
over 
. 
and 
are the Frobenius norm and conjugate transpose of 
.
2. System and Channel Model
We consider the dual-hop relay network in Figure 1. The single-antenna source (
) communicates with the destination (
) having 
antennas via an AF relay (
). The relay has 
receive antennas and uses only one antenna among them for forwarding. (Although TAS can be used at the relay for the second time slot, it provides diversity gains only when 
despite the additional CSI feedback requirement (see Remark 1 in Section 3). However, in practice, 
is unlikely even since the relays should usually be more cost/complexity effective than BS.) Half-duplex transmission is assumed. Since we consider a MIMO-enabled infrastructure relay, which is used primarily for extending the network coverage, the direct channel between 
and 
, which is far apart, is not considered assuming heavy shadowing and path loses. Cooperation occurs in two timeslots. In the first timeslot, the source transmits to the relay. In the second timeslot, the relay forwards an amplified version of the source signal to the destination. The relay and destination employ SDC and MRC receptions, respectively. Perfect channel state information is assumed to be available at the relay and destination.
2.1. Source-to-Relay Channel Model
An arbitrary correlation model for the source-to-relay (
) channel appears to be analytically intractable for dual-hop AF relay networks. We instead consider the semiarbitrary correlation model. (The use of the semiarbitrary correlation model simplifies the 
-fold numerical integration [26] in evaluating the CCDF of the SDC output SNR for the 
channel into a single integral [27] and thereby enables the efficient computation of distribution functions of the end-to-end SNR of dual-hop AF relaying.) In other words, the 
single-input multiple-output (SIMO) channel is a semiarbitrary correlated [27] flat Rayleigh fading channel. The 
channel vector is given by 
, where 
is the 
covariance matrix at the relay, and 
is an 
vector with independent Rayleigh fading entries. The 
th element of 
is given by [28, 
]
Thus, 
can be parameterized by a 
vector 
with the 
th element 
.
2.2. Relay-to-Destination Channel Model
The relay-to-destination (
) SIMO channel is an arbitrary correlated [29] flat Rayleigh fading channel. In this case, the 
channel vector is given by 
, where 
is the covariance matrix at the destination, and 
is an 
vector with independent Rayleigh fading entries. 
is constructed according to a practical channel model [30, 31] with the 
th element given by
where 
is the relative antenna spacing between adjacent antennas (measured in number of wavelengths) of the linear array of antennas at the destination, 
is the mean angle of arrival, and 
is the destination angular spread. The actual angle of arrival is given by 
with 
. Such a correlation model may arise in practice in uniform linear antenna arrays, and this model appears to be adequate to describe a real-world scattering environment [30].
2.3. The End-to-End SNR
The received signal vector at the relay can be written as
where 
is the transmit power; 
is the transmitted symbol satisfying 
; 
is the additive white Gaussian noise (AWGN) vector with mean zero and variance 
. The relay employs SDC to obtain the scalar signal as
where 
and 
are the elements of 
and 
is the AWGN at the 
th antenna. In the second timeslot, the signal 
is amplified with the gain 
and forwarded to the destination. The received signal at the destination can be written as
where 
is the relay transmit power factor, 
is the 
AWGN vector satisfying 
, and 
is the receive weight vector for MRC operation [32] given by 
. Next, we expand (5) to obtain the following model for the received signal at the destination:
By using (6), the resulting SNR can be obtained as
The gains of practical channel state information-(CSI-)assisted relays can be defined as in [1, 4]. Thus, by substituting 
into (7), the SNR of the dual-hop system with the practical CSI-assisted relay can be written as follows:
where 
is the instantaneous SNR of the SDC output at the relay in semiarbitrary correlated Rayleigh fading, and 
is the instantaneous SNR of the MRC output at the destination over arbitrary correlated Rayleigh fading. We also define 
and 
as the average of 
and 
, respectively.
We can also consider ideal CSI-assisted relays that invert the 
channel regardless of its fading state [4]. For this case, the relay gain is given by 
, and the SNR 
is given by [4]
Moreover, the 
can be upper bounded as [5, 18]
3. Performance Analysis
This section presents a comprehensive performance analysis of our proposed MIMO relay network model by taking into account the spatial correlation of antenna elements at the MIMO-enabled terminals. The CCDF and the MGF of the end-to-end SNR 
are derived and used to obtain accurate closed-form approximations the outage probability, the average symbol error rate (SER), and the ergodic capacity.
3.1. Statistical Characterization of the End-to-End SNR
An accurate closed-form approximation for the CCDF of the end-to-end SNR in (8) can be derived as (Appendix A)
where 
are the eigenvalues of 
, 
is the determinant of the Vandermonde matrix of the eigenvalues of 
, and 
is the determinant of the matrix 
with 
th row and 
th column removed. The 
th element of 
is given by 
where 
denotes the eigenvalues of 
. Further, 
and 
are the weights and the nodes of the Gauss-Laguerre quadrature rule, respectively. The nodes 
and weights 
can be efficiently computed by using the approach proposed in [33]. Moreover, 
is the number of terms used for the Gauss-Laguerre quadrature rule.
The MGF of the end-to-end SNR is a useful statistic which can be used to analyze a wide range of performance metrics. The MGF of 
can accurately be approximated as follows (Appendix A):
where 
and 
.
3.2. Outage Probability
The outage probability is the probability that the instantaneous SNR 
falls below a predefined SNR threshold 
. Thus, the outage probability 
can readily be obtained by using (11) as follows:
3.3. Average Symbol Error Rate
The average SER is an important performance metric of wireless networks. The conditional error probability (CEP) of the coherent binary frequency-shift keying (C-BFSK) and 
-ary pulse amplitude modulation (PAM) is given as 
[32], where 
and 
are constants dependent on the modulation scheme. For example, the cases 
and 
yield the exact bit error rate of the coherent binary phase-shift keying (BPSK) and C-BFSK, respectively. Further, the SER of 
-ary PAM is given by 
and 
[32]. An accurate closed form average SER approximation can be derived by integrating 
over the PDF of the SNR 
as follows (Appendix B):
where 
and 
.
3.4. Ergodic Capacity
The channel capacity is defined as the maximum data rate at which information can be transmitted across a noisy channel with arbitrary reliability. The ergodic capacity 
is defined as the expected value of the instantaneous maximum mutual information 
between 
and 
. For a dual-hop cooperative relay system operating over two timeslots per burst, 
is given by 
[1]. Then, the ergodic capacity can be expressed as 
By substituting (A.4) into 
and applying the Gauss-Laguerre quadrature rule, an approximation for 
in closed form is obtained as follows:
where 
and 
.
3.5. Special Cases
In this section, two special cases of our proposed system model are analyzed.
3.5.1. Two Receive Antennas at the Relay (
)
)Consider the case where only two receive antennas are at the relay. This case may arise in practise due to the space limitations at the relay or due to the cost factor. In this section, the lower bounds for the outage probability and the average SER are derived in closed form by using the upper bound of the SNR 
in (10).
The CCDF of 
can be written as [34]
When 
, the CCDF of SDC in the equally correlated Rayleigh fading channels given in (A.2) reduces to the well-known result [35, 36]
The CCDF of 
can readily be obtained by using (A.3) and 
as follows:
Then, the closed-form expression for the CCDF of 
can be obtained by substituting (17) and (18) into (16) as follows:
where 
and 
.
The MGF of 
can be derived in closed-form by substituting (19) into (A.5) as follows:
where 
and 
.
With the aid of (19), a lower bound of the outage probability can readily be computed as follows: 
Next, we present an accurate and computationally efficient closed-form approximation for computing a lower bound for the average SER. The CEP of the coherent binary frequency-shift keying (C-BFSK) and 
-ary PAM can be expressed in an alternative form [37] as 
. The average error rate can be obtained in the following form by averaging the alternative CEP expression over the PDF of 
and manipulating it with the variable transformation 
[37]:
We use an accurate and computationally efficient method in [37] which uses the Gauss-Chebyshev quadrature rule [23] to obtain a very compact closed-form expression for (21):
where 
is a positive integer, 
and 
is the remainder term. 
becomes negligible as 
increases [37]. Thus, the lower bound of average SER can be obtained by substituting (20) into (22).
Moreover, for the CEP of the noncoherent binary frequency-shift keying (NC-BFSK) and differential BPSK (D-BPSK) is given in the form [32] 
, with 
and 
for D-BPSK and NC-BFSK, respectively. Now, the average SER of NC-BFSK and D-BPSK can be derived by substituting (19) into 
as follows:
where 
and 
.
3.5.2. Uncorrelated Antennas at the Relay (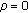
)
)When the antenna spacing at the relay is sufficiently large, the 
channels experience independent Rayleigh fading. In this case, the CCDF of 
can be obtained by substituting 
in (A.4) and by using the identity of the Marcum-
function, 
as follows (Appendix D):
Let us consider an ideal CSI-assisted relay. For this case, the SNR 
is given in (9), and the CCDF of 
can be easily obtained with the aid of (24) as follows:
The PDF of 
and 
can easily be derived by differentiating (24) and (25) with respect to 
and by using 
[38, 
]. However, for the sake of brevity, the PDF results are omitted.
A closed-form expression for the MGF of 
can be derived by substituting (A.4) into (A.5) as shown in Appendix E:
where 
and 
.
By substituting (24) into (B.1), a closed-form expression for the average SER can be derived as follows (Appendix F):
A generalized closed-form expression for the moments of the SNR can be obtained by substituting (25) into 
and evaluating the resulting integral as follows (Appendix G):
The SNR moments can be used to study the higher-order metrics, such as the skewness and the kurtosis that characterize the distribution of 
. The skewness (
), which is a measure of the symmetry of the distribution, can be obtained as 
. The kurtosis (
), which quantifies the degree of peakedness of the distribution, is given by 
. On the other hand, the amount of fading (AoF) is a performance metric which quantifies the severity of the fading that the signal experienced from the source to the destination. The AoF is given by 
.
3.6. High SNR Analysis
This section presents the high SNR analyses for the proposed system model when the antennas at the relay are uncorrelated.
3.6.1. The Outage Probability at High SNR
The behavior of the cumulative distribution function (CDF) of 
for large 
is equivalent to the behavior of 
around 
[39]. By substituting 
and 
into (25) and by expressing the exponential function and the Bessel function in terms of their Taylor series expansions around 
[38, equations (
) and (
)], one obtains the expression with the lowest powers of 
. Now, by collecting the first-order terms, the high SNR approximation (i.e., when 
) for the CDF of the end-to-end SNR (24) can be derived as follows:
where
At high SNR, the outage probability can easily be obtained by substituting (29) into 
.
3.6.2. The Symbol Error Rate at High SNR
The average SER at high SNR can be derived by substituting (29) into 
as follows:
In the high SNR regime, the average SER can be represented by 
, where 
and 
are referred to as the diversity gain and coding gain, respectively [39]. By using (31), 
and 
are given by
respectively.
Remark 1.
The diversity order of the proposed system is given by 
(32). If a single-antenna relay is used, then 
even though the destination is equipped with multiple antennas. Thus, our analysis shows that in order to retain MIMO diversity benefits for dual-hop relay networks with single-antenna sources, the relay should be equipped with multiple antennas.
Remark 2.
In our proposed system model, the relay uses only one transmit antenna for forwarding the amplified signal to the destination. Since the relay is already equipped with multiple antennas, transmit antenna selection (TAS) can also be employed at the relay. If the transmit antenna, which maximizes the end-to-end SNR, is used at the relay, then the diversity order of the system can be written by following (32) as
Thus, the system with TAS guarantees a diversity order of 
whereas the system without TAS provides a diversity order of 
. Hence TAS improves the diversity benefits only when 
. However, when 
, the system with TAS achieves coding gains despite no diversity advantages.
4. Numerical Results
This section presents the numerical and the simulation results for the proposed dual-hop AF MIMO relaying with antenna correlation. Monte Carlo simulation results are provided to verify the accuracy of the analytical derivations presented in Section 3. In computing the Gauss-Laguerre approximation for the outage probability (13), average bit error rate (BER) (14), and ergodic capacity (15), we choose 
to be 25 for 
and 
to be 30 for 
.
4.1. Comparison of Semiarbitrary and Arbitrary Correlation Models for the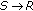 
Channel
ChannelIn Figure 2, the average BER of BPSK for the proposed dual-hop MIMO relay network is plotted by taking into account two correlation models; (i) semiarbitrary correlation (ii) arbitrary correlation for the 
channels. For both these cases, the 
channel is arbitrary correlated. The average BER curves for the former case are plotted by using our closed-form BER approximation (14), whereas the Monte Carlo simulation results are used for the latter case. Figure 2 reveals clearly that the semiarbitrary correlation model agrees well with the arbitrary correlation model for different antenna setups. Thus, our analytical results may well be used to obtain design insights for dual-hop MIMO AF relay networks over arbitrary correlated fading. Figure 2 also verifies that the maximum diversity order is given by the minimum number of antenna at the relay and destination; 
. This fact can also be proved by applying the min-max cut from the 
and from 
[40]. The BER curve corresponding to 
, 
represents the dual-hop relaying with single-antenna terminals. The proposed dual-hop relay network with multiple-antenna relay and destination provides a substantial BER performance gains compared to single-antenna relaying. Moreover, the exact agreement between the analytical curves and the Monte-Carlo simulation points verifies the accuracy of our analysis.
Average BER of BPSK for dual-hop MIMO relaying with antenna correlation at the relay and destination.
. 
, 
, and 
. For 
, 
, and 
, 
is chosen as 
, 
, and 
, respectively.
4.2. Impact of Spatial Correlation on the Average BER
In Figure 3, the impact of antenna correlation at both the relay and destination on the average BER of the BPSK is depicted. Three different correlation effects are obtained by changing 
, 
, and 
. Since 
is the relative antenna spacing between the adjacent antennas in the linear array measured in the number of wavelengths, and 
is the angular spread at the destination, smaller values of 
and 
result in higher antenna correlation at the destination. Moreover, the amount of antenna correlation at the relay can also be changed by changing 
, where 
is a 
vector containing the elements 
and 
of 
semiarbitrary correlation matrix (1). Thus, three correlation scenarios are obtained as (a) high correlation, (b) medium correlation, and (c) low correlation. Figure 3 reveals clearly that the higher correlation effect at both the relay and destination degrades the BER performance significantly.
The impact of antenna correlation at the relay and destination on the average BER of BPSK. (a) High correlation: 
; (b) medium correlation: 
; (c) low correlation: 
. Here, 
, 
, and 
for 
, and 
, and 
, 
for 
.
4.3. Impact of Spatial Correlation on the Outage Probability
In Figure 4, the outage probability is plotted against the correlation coefficient of the 
channels for the low, medium, and high spatial correlation scenarios in the 
channels. Here, the 
channels undergo equally correlated fading. The outage probability performance significantly degrades as the correlation of antennas at the relay increases. Moreover, this figure also shows that the correlation of the antennas at the destination has a considerable impact on the outage probability.
Impact of spatial correlation on the outage probability of dual-hop MIMO relaying.
 dB and 
.
4.4. Impact of Spatial Correlation on the Ergodic Capacity
Figure 5 shows the impact of spatial correlation of antenna elements at relay and the destination on the ergodic capacity for semiarbitrary correlated 
and arbitrary correlated 
channels. Lower antenna spacing (i.e., higher spatial correlation) results in substantial losses in capacity. Figure 5 also reveals that the smaller angular spreads (i.e., higher spatial correlation) degrade the capacity benefits. A higher number of antennas at both the relay and destination increase the capacity benefits of dual-hop systems.
The impact of correlation coefficient of source-to-relay channels and antenna spacing/angular spread at the destination on the ergodic capacity.
 dB. 
. For 
, the 
semiarbitrary correlation matrix is parameterized by 
, 
, 
and 
. For 
,
correlation matrix is parameterized by 
, 
, 
and 
.
4.5. Sensitivity to the Antenna Spacing and Angular Spread
Figure 6 plots the average BER of BPSK against the antenna spacing for three different angular spreads (
, 
, and 
). Here, the 
channel is equally correlated whereas the 
channel is arbitrary correlated. Two different antenna configurations at the relay and destination are considered. Lower antenna spacings and angular spreads at the destination degrade the BER performance considerably. The BER curves seem to be approaching a fixed value once the antenna spacing is increased beyond 2.5 
, regardless of the angular spread.
Impact of antenna spacing/angular spread at the destination on the average BER of BPSK.
 dB, 
, and 
.
4.6. Numerical Results for the Special Cases
This section presents the numerical results for the special cases: (
) dual-antenna relay and (
) uncorrelated antennas at the relay.
4.6.1. Dual-Antenna Relay
In Figures 7 and 8, we analyze the tightness of the lower bounds developed for the average BER and the outage probability for the special case of dual-antenna relay. Both the lower bounds are tighter to the exact curves at moderate-to-high SNR regime. Thus, these bounds may serve as benchmarks for performance analysis of practical systems with practical CSI-assisted relays. In computing the lower bound for average BER by using the MGF approach, we choose 
to be 10 for the Gauss-Chebyshev approximation in (22). The exact agreement between the BER curves evaluated using (22) and Monte Carlo simulation results validates the computational accuracy of our analysis.
Average BER of dual-hop MIMO relaying over correlated Rayleigh fading channels with two antennas at the relay and four antennas at the destination.
, 
, and 
.
Outage probability of dual-hop MIMO relaying over correlated Rayleigh fading channels with two antennas at the relay and three antennas at the destination.
, 
, and 
.
Figures 7 and 8 also reveal that the average BER and the outage probability performance gap between the curves corresponding to high correlation and medium correlation are larger than those of curves corresponding to low correlation and medium correlation. The reason for this performance gap difference is because when 
[32], the effect of antenna correlation at the destination becomes negligible, and the performance degradation is resulted solely by the antenna correlation at the relay. However, when 
, 
, the performance is degraded by antenna correlation at the relay and destination.
4.6.2. Uncorrelated Antennas at the Relay
In Figure 9, the outage probability of dual-hop MIMO relaying with uncorrelated antennas at the relay and correlated antennas at the destination is plotted against the destination angular spread. It shows that the outage probability degrades considerably due to the spatial correlation of antennas at the destination. Higher angular spreads degrade the outage probability performance significantly. Lowering the antenna spacing at the destination adversely impacts the outage probability.
Impact of destination antenna angular spread on the outage probability of dual-hop MIMO relaying with uncorrelated antennas at the relay and correlated antennas at the destination.
 dB, 
, and 
.
Figure 10 shows the average BER performance of dual-hop MIMO relaying with uncorrelated antennas at the relay and correlated antennas at the destination. Figure 10 also shows the high SNR analysis of the average BER for different antenna configurations at the relay and destination. The analytical curves obtained from (27) agree exactly with the Monte Carlo simulation points. The average BER with ideal CSI-assisted relays serves as tight lower bounds or a benchmark for the average BER with practical CSI-assisted relays.
Average BER of dual-hop MIMO relaying over Rayleigh fading channels with uncorrelated antennas at the relay and correlated antennas at the destination.
, 
, 
, and 
.
4.7. Comparison of BER of BPSK for Several Dual-Hop MIMO AF Relay System Models
Figure 11 compares the average BER of BPSK for several dual-hop MIMO AF relaying models over arbitrary correlated fading. These average BER curves are plotted by using Monte-Carlo simulation results. This figure shows that dual-hop relay networks, which use beamforming or TAS at 
and 
channels with MIMO channels (i.e., multiple antennas at each terminal) outperform the networks with SIMO channels (i.e., single-antenna source and the relay uses only a single transmit antenna out of 
in the second timeslot). Further, it shows that although the TAS is performed at the relay for the 
channel, no diversity gains but a coding gain can be achieved over the use of arbitrary single transmit antenna when 
. For dual-hop relay models, which use SDC with SIMO channels for 
and 
, perform relatively well with those which use MRC. Although the proposed model (see BER curve corresponding to [
(SIMO): SDC at 
, 
(SIMO): MRC at 
] in Figure 11) is suboptimal, it achieves most of the MIMO benefits while using only one transmit/receive chain at the relay.
Average BER of several dual-hop MIMO AF relay system models over arbitrary correlated Rayleigh fading channels.
, 
, 
, and 
.
5. Conclusion
A suboptimal yet simple and realistic dual-hop AF MIMO relay network model was developed. The impact of spatial correlation on the performance of the proposed system model over Rayleigh fading was investigated by using a semiarbitrary and arbitrary correlation models for the 
and 
channels, respectively. Accurate closed-form expressions for the CCDF, the MGF, the outage probability, the average symbol error rate, and the ergodic capacity were derived. The performance of two special cases was studied: (
) dual-antenna relay and multiple-antenna destination, and (
) uncorrelated antennas at the relay and correlated antennas at the destination. The high SNR approximations for the outage probability and the average were derived to obtain valuable system design insights such as the diversity order and coding gain. Numerical and Monte Carlo simulation results were presented to investigate the detrimental effect of the antenna correlation on the system performance and to validate our analyses. Our results show that in order to retain MIMO benefits for dual-hop relay networks that consist of single-antenna sources and multiple-antenna destinations, MIMO-enabled relays should be used. Our results may be useful in analyzing practical system scenarios that involve a single-antenna portable device communicating with a multiple-antenna base station via an infrastructure-based fixed relay equipped with multiple antennas.
Appendices
A. Statistical Characterization of the End-to-End SNR
The closed-form approximation for the CCDF of the end-to-end SNR in (8) can be obtained by using the following integral expression [13]:
where 
and 
are the CCDF and probability density function (PDF) of 
and 
, respectively. The CCDF of 
can be written as in [27, 36]
The PDF of 
can be written as in [10]
where 
, 
, 
, 
, and 
are defined in (11). By substituting (A.2) and (A.3) into (A.1), we obtain an integral expression for the CCDF of the SNR as follows:
where 
and 
. No closed-form solution for the double-integral (A.4) appears to be available. However, it is in the form of 
, and, thus, it can be efficiently and accurately approximated by using the Gauss-Laguerre quadrature rule [23] in closed form as in (11).
The MGF of 
can be derived as follows:
The second equality of (A.5) is obtained by integrating by parts and considering that 
. By substituting (A.4) into (A.5), the MGF of 
is obtained as follows:
where 
and 
. Again, one can accurately approximate 
in (A.6) by using the Gauss-Laguerre quadrature rule as in (12).
B. Average Symbol Error Rate
The average SER has the integral representation [31]
By substituting (A.4) into (B.1), the average SER is obtained as follows:
where 
and 
. Since the triple integral (B.2) does not appear amenable to a closed-form solution, we again use the Gauss-Laguerre quadrature rule to obtain an accurate average SER approximation as in (14).
C. MGF of the Upper Bounded SNR with Two Receive Antennas at the Relay
By substituting (19) into (A.5), one gets
where
The integral 
can be solved by substituting 
and by using [41, equations (
) and (
)] as 
where 
, 
, and 
. The integral 
can be solved by using [42, 
] as 
where 
. Substitution of 
and 
into (C.1) yields the desired result given in (20).
D. CCDF of SNR with Uncorrelated Antennas at the Relay
When the 
channel undergoes independent Rayleigh fading, one can obtain the CCDF of 
by letting 
in (A.4) as 
where 
By using the fact that 
[41, equation (
)] and binomial expansion, 
can be simplified to the following form:
By evaluating the integral in (D.1) by using [25, 
], one can obtain the result given in (25).
E. MGF of the SNR with Uncorrelated Antennas at an Ideal CSI-Assisted Relay
By substituting the CCDF of the SNR given in (25) into (A.5), one obtains
where 
The integral 
can be evaluated by using [25, 
] to yield the desired result given in (26).
F. Average SER with Uncorrelated Antennas at an Ideal CSI-Assisted Relay
By substituting (25) into (B.1), one obtains the following:
where 
We solve 
by using [25, 
], and substituting into (F.1), we obtain the desired result given in (27).
G. Moments of SNR with Uncorrelated Antennas at an Ideal CSI-Assisted Relay
By substituting (25) into 
, one obtains
where 
. The desired result in (28) can be obtained by solving 
by using [25, 
].
This section provides sketches of the proofs of some of the results presented in Section 3.
References
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Pabst R, Walke BH, Schultz DC, Herhold P, Yanikomeroglu H, Mukherjee S, Viswanathan H, Lott M, Zirwas W, Dohler M, Aghvami H, Falconer DD, Fettweis GP: Relay-based deployment concepts for wireless and mobile broadband radio. IEEE Communications Magazine 2004, 42(9):80-89. 10.1109/MCOM.2004.1336724
Yanikomeroglu H: Fixed and mobile relaying technologies for cellular networks. Proceedings of the 2nd Workshop on Applications and Services in Wireless Networks (ASWN '02), July 2002 75-81.
Hasna MO, Alouini M-S: End-to-end performance of transmission systems with relays over Rayleigh-fading channels. IEEE Transactions on Wireless Communications 2003, 2(6):1126-1131. 10.1109/TWC.2003.819030
Anghel PA, Kaveh M: Exact symbol error probability of a cooperative network in a rayleigh-fading environment. IEEE Transactions on Wireless Communications 2004, 3(5):1416-1421. 10.1109/TWC.2004.833431
Adinoyi A, Yanikomeroglu H: Cooperative relaying in multi-antenna fixed relay networks. IEEE Transactions on Wireless Communications 2007, 6(2):533-544.
Kim Y, Liu H: Infrastructure relay transmission with cooperative MIMO. IEEE Transactions on Vehicular Technology 2008, 57(4):2180-2188.
Oyman Ö, Laneman JN, Sandhu S: Multihop relaying for broadband wireless mesh networks: from theory to practice. IEEE Communications Magazine 2007, 45(11):116-122.
Fan Y, Thompson J: MIMO configurations for relay channels: Theory and practice. IEEE Transactions on Wireless Communications 2007, 6(5):1774-1786.
Louie RH, Li Y, Suraweera HA, Vucetic B: Performance analysis of beamforming in two hop amplify and forward relay networks with antenna correlation. IEEE Transactions on Wireless Communications 2009, 8(6):3132-3141.
Da Costa DB, Aissa S: Cooperative dual-hop relaying systems with beamforming over nakagami-m fading channels. IEEE Transactions on Wireless Communications 2009, 8(8):3950-3954.
Chen S, Wang W, Zhang X, Zhao D: Performance of amplify-and-forward MIMO relay channels with transmit antenna selection and maximal-ratio combining. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC '09), April 2009
Louie RHY, Li Y, Vucetic B: Performance analysis of beamforming in two hop amplify and forward relay networks. Proceedings of IEEE International Conference on Communications (ICC '08), May 2008 4311-4315.
Muhaidat H, Uysal M: Cooperative diversity with multiple-antenna nodes in fading relay channels. IEEE Transactions on Wireless Communications 2008, 7(8):3036-3046.
Talebi A, Krzymień WA: Multiple-antenna multiple-relay cooperative communication system with beamforming. Proceedings of the 67th IEEE Vehicular Technology Conference (VTC '08), May 2008 2350-2354.
Dharmawansa P, McKay MR, Mallik RK: Dual hop MIMO relaying with orthogonal space-time block codes. Proceedings of IEEE International Conference on Communications (ICC '09), June 2009
Chalise BK, Vandendorpe L: Outage probability analysis of a MIMO relay channel with orthogonal space-time block codes. IEEE Communications Letters 2008, 12(4):280-282.
Ikki S, Ahmed MH: Performance analysis of cooperative diversity wireless networks over Nakagami-m fading channel. IEEE Communications Letters 2007, 11(4):334-336.
Senaratne D, Tellambura C: Unified performance analysis of two hop amplify and forward relaying. Proceedings of IEEE International Conference on Communications, June 2009, Dresden, Germany
Ikki S, Ahmed MH: Performance analysis of dual-hop relaying communications over generalized gamma fading channels. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007 3888-3893.
Suraweera HA, Louie RHY, Li Y, Karagiannidis GK, Vucetic B: Two hop amplify-and-forward transmission in mixed Rayleigh and Rician fading channels. IEEE Communications Letters 2009, 13(4):227-229.
Ikki SS, Ahmed MH: Performance analysis of dual hop relaying over non-identical weibull fading channelsw. Proceedings of the 69th IEEE Vehicular Technology Conference (VTC '09), April 2009
Abramowitz M, Stegun I: Handbook of Mathematical Functions. Dover, New York, NY, USA; 1970.
Nuttall AH: Some integrals involving the QM-function. Naval Underwater Systems Center, New London Lab.; May 1974.
Gradshteyn I, Ryzhik I: Table of Integrals, Series, and Products. 7th edition. Academic Press, San Diego, Calif, USA; 2007.
Zhang QT, Lu HG: A general analytical approach to multi-branch selection combining over various spatially correlated fading channels. IEEE Transactions on Communications 2002, 50(7):1066-1073. 10.1109/TCOMM.2002.800804
Zhang X, Beaulieu NC: Performance analysis of generalized selection combining in generalized correlated Nakagami-m fading. IEEE Transactions on Communications 2006, 54(11):2103-2112.
Tong YL: The Multivariate Normal Distribution. 3rd edition. Spring, New York, NY, USA; 1990.
Zhang QT: Maximal-ratio combining over Nakagami fading channels with an arbitrary branch covariance matrix. IEEE Transactions on Vehicular Technology 1999, 48(4):1141-1150. 10.1109/25.775363
Bölcskei H, Borgmann M, Paulraj AJ: Impact of the propagation environment on the performance of space-frequency coded MIMO-OFDM. IEEE Journal on Selected Areas in Communications 2003, 21(3):427-439. 10.1109/JSAC.2003.809723
McKay MR, Grant AJ, Collings IB: Performance analysis of MIMO-MRC in double-correlated Rayleigh environments. IEEE Transactions on Communications 2007, 55(3):497-507.
Proakis J: Digital Communications. 4th edition. McGraw-Hill, New York, NY, USA; 2001.
Golub GH, et al.: Calculation of Gauss quadrature rules. Stanford University, Stanford, Calif, USA; 1967.
David HA: Order Statistics. John Wiley & Sons, New York, NY, USA; 1981.
Schwartz H, Bennett W, Stein S: Communication Systems and Techniques. McGraw-Hill, New York, NY, USA; 1966.
Chen Y, Tellambura C: Distribution functions of selection combiner output in equally correlated Rayleigh, Rician, and Nakagami-m fading channels. IEEE Transactions on Communications 2004, 52(11):1948-1956. 10.1109/TCOMM.2004.836596
Annamalai A, Tellambura C, Bhargava VK: Efficient computation of MRC diversity performance in Nakagami fading channel with arbitrary parameters. Electronics Letters 1998, 34(12):1189-1190. 10.1049/el:19980863
Gradshteyn I, Ryzhik I: Table of Integrals, Series, and Products. 6th edition. Academic Press, San Diego, Calif, USA; 2000.
Wang Z, Giannakis GB: A simple and general parameterization quantifying performance in fading channels. IEEE Transactions on Communications 2003, 51(8):1389-1398. 10.1109/TCOMM.2003.815053
Yuksel M, Erkip E: Multiple-antenna cooperative wireless systems: a diversity-multiplexing tradeoff perspective. IEEE Transactions on Information Theory 2007, 53(10):3371-3393.
Nuttall AH: Some integrals involving the Q-function. Naval Underwater Systems Center, New London Lab.; 1972.
Erdelyi A, Magnus W, Tricomi FG: Tables of Integral Transforms. Volume 1. Mcgraw-Hill, New York, NY, USA; 1954.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Amarasuriya, G., Tellambura, C. & Ardakani, M. Impact of Antenna Correlation on a New Dual-Hop MIMO AF Relaying Model. J Wireless Com Network 2010, 956721 (2010). https://doi.org/10.1155/2010/956721
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/956721