- Research Article
- Open access
- Published:
A Comparison of Scheduling Strategies for MIMO Broadcast Channel with Limited Feedback on OFDM Systems
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 968703 (2010)
Abstract
We consider a multiuser downlink transmission from a base station with multiple antennas (MIMO) to mobile terminals (users) with a single antenna, using orthogonal frequency division multiplexing (OFDM). Channel conditions are reported by a feedback from users with limited rate, and the base station schedules transmissions and beamforms signals to users. We show that an important set of schedulers using a general utility function can be reduced to a scheduler maximizing the weighted sum rate of the system. For this case we then focus on scheduling methods with many users and OFDM subcarriers. Various scheduling strategies are compared in terms of achieved throughput and computational complexity and a good tradeoff is identified in greedy and semiorthogonal user selection algorithms. In the greedy selection algorithm, users are selected one by one as long as the throughput increases, while in the semiorthogonal approach users are selected based on the channel correlation. An extension of these approaches from a flat-fading channel to OFDM is considered and simplifications that may be useful for a large number of subcarriers are presented. Results are reported for a typical cellular transmission of the long-term evolution (LTE) of 3GPP.
1. Introduction
Next generation wireless cellular systems are expected to support high-quality multimedia services; this motivates the interest in multiantenna (MIMO) systems, where both spatial diversity and multiplexing can be used to increase the achievable throughput. In fact, it has been shown that the downlink capacity of a MIMO system with perfect channel state information (CSI) scales as a linear function of the number of transmit antennas [1]. Although nonlinear dirty paper coding scheme achieves the system capacity, it has a high computational cost [2], and simpler solutions have been investigated. Linear beamforming has been shown [3] to achieve a large part of dirty paper coding capacity; in particular, zero forcing beamforming matched to an opportunistic scheduling is widely used [3].
However, benefits of MIMO are obtained only by a proper scheduling of transmissions, which opportunistically exploits channel conditions in order to increase throughput, while ensuring quality of service (QoS). Several scheduling techniques have been proposed for MIMO single carrier systems on flat fading channels based on various approaches, including clique search [4], maximization of the Frobenius norm of the composite channel matrix [5, 6], user channel orthogonality [7–9], single bit feedback [10], waterfilling [11], tree search [12], evolutionary algorithms [13], and greedy scheduling [14] extended to the case of limited feedback in [15]. In some cases, joint optimization of scheduling and power allocation is performed [4–6, 10, 11, 13], while in other cases only scheduling is considered [7–9, 14]. Moreover, QoS-oriented multiuser scheduling and beamforming have been investigated in [16], in order to conciliate the request of high throughput with low packet delays. An overview of research on cross-layer scheduling for multiuser MIMO single-carrier systems is given in [17]. A similar problem to multiuser MIMO scheduling can be found in other transmission systems, such as multicarrier code- or frequency-division multiple access [18].
In frequency selective channels, single carrier modulation is often replaced by orthogonal frequency division multiplexing (OFDM) due to its efficiency in overcoming multipath fading. In fact, the combination of MIMO and OFDM seems to be the technology of future wireless cellular systems, as it has been proposed for downlink in the long term evolution (LTE) release of 3GPP standard [19, 20]. When MIMO OFDM is considered, scheduling becomes more complex, as the number of resources to be allocated, that is, the number of subcarriers, increases and only suboptimal approaches are viable [12]. Complexity is further increased in a frequency division duplexing system, where CSI is provided to the base station by each user (mobile terminal) through a feedback channel. In fact, due to the limited feedback rate, only a partial CSI is available at the base station and additional processing is required to compensate the channel uncertainty. Some of the scheduling techniques considered for single carrier transmissions can be extended to OFDM. For example, in [21] a scheduling algorithm has been proposed for MIMO OFDM systems which extends method [14] for single-carrier systems: the set of scheduled users on each subcarrier is built in a greedy fashion, by adding one user at a time with the aim of maximizing a weighted sum rate (WSR). In [22] this approach has been further simplified to avoid the need of computing a new beamforming matrix upon the insertion of a new candidate in the set of scheduled users. A further simplification of the scheduling is achieved by computing an estimate on their signal to interference ratio which is then used to exclude users that would not contribute to the WSR, by introducing a threshold to their signal to noise plus interference ratio.
In this paper, we first show that any scheduler maximizing a wide class of utility functions can be reduced to a scheduler maximizing the weighted sum rate, where the weights are suitably chosen according to the utility function. Then we revise scheduling techniques proposed in the literature that maximize the weighted sum rate for a multiuser MIMO OFDM system with limited feedback and compare them in a LTE 3GPP scenario in terms of (i) computational complexity, (ii) memory requirements, and (iii) achievable throughput.
The rest of the paper is organized as follows. In Section 2 we describe the downlink MIMO OFDM system model. In Section 3 a general scheduling method is derived and algorithms [14, 21] are revised. Sections 4 and 5 present, respectively, the user selection and user preselection strategies of [22]. In Section 6 the complexity of the various strategies is investigated. In Section 7 simulation results are illustrated and Section 8 outlines main conclusions.
Notation 1.
Bold upper and lower letters denote matrices and vectors, respectively;  denotes Hermitian operation (transpose complex conjugate), while
denotes Hermitian operation (transpose complex conjugate), while  denotes transpose;
denotes transpose;  is the vector norm, and
is the vector norm, and  stands for expectation.
stands for expectation.
2. System Model
We consider the downlink of a cellular system based on OFDM [23] with  subcarriers. The base station has
subcarriers. The base station has  transmit antennas while
transmit antennas while  users have one antenna each. Transmission is performed in time slots of
users have one antenna each. Transmission is performed in time slots of  OFDM symbols and in each time slot users feedback a partial CSI, which is used by the base station to schedule downlink transmissions. The transmission bandwidth is divided into
OFDM symbols and in each time slot users feedback a partial CSI, which is used by the base station to schedule downlink transmissions. The transmission bandwidth is divided into  resource blocks, each composed of
resource blocks, each composed of  subcarriers. At slot
subcarriers. At slot  , let
, let  be the set of
be the set of  users,
users,  , scheduled for downlink transmission on resource block
, scheduled for downlink transmission on resource block  . We denote as stream the (user, resource block) pair
. We denote as stream the (user, resource block) pair  . Let also
. Let also  be the set of streams scheduled at slot
be the set of streams scheduled at slot  , that is,
, that is,

In our analysis we model the channel as quasi static, that is, it is considered invariant for the duration of one OFDM symbol, and it has the same frequency response on all subcarriers of each resource block. Hence, the frequency response of the MIMO channel on resource block  of OFDM symbol
of OFDM symbol  for all
for all  transmit antennas and all
transmit antennas and all  users is described by the complex
users is described by the complex  channel matrix
channel matrix  , where the
, where the  column channel vector
column channel vector  collects the gains between the
collects the gains between the  antennas of the base station and stream
antennas of the base station and stream  . In general, for OFDM symbol
. In general, for OFDM symbol  , and
, and  are, respectively, the
are, respectively, the  and
and  column vectors of the transmitted and received signals on subcarrier
column vectors of the transmitted and received signals on subcarrier  of resource block
of resource block  . The discrete-time complex baseband transmission model for subcarrier
. The discrete-time complex baseband transmission model for subcarrier  of resource block
of resource block  is given by
is given by

where  is a
is a  complex Gaussian noise vector with i.i.d. components having zero mean and variance
complex Gaussian noise vector with i.i.d. components having zero mean and variance  . The transmit signal is subject to the total power constraint
. The transmit signal is subject to the total power constraint  where
where  is the available power. In order to exploit spatial diversity, the transmit signal is obtained from the
is the available power. In order to exploit spatial diversity, the transmit signal is obtained from the  data signal
data signal  by applying the zero-forcing beamforming matrix
by applying the zero-forcing beamforming matrix  , that is,
, that is,

where  is the power normalization vector which enforces equal stream power as given by
is the power normalization vector which enforces equal stream power as given by

where the expectation is taken only with respect to  , and
, and  is the
is the  th entry of
th entry of  .
.
2.1. Feedback Information
In a frequency division duplexing system, channel state information is provided through a feedback channel; therefore, we assume that matrix  is not perfectly known at the base station while user
is not perfectly known at the base station while user  perfectly estimates the channel vectors once for time slot, that is, when
perfectly estimates the channel vectors once for time slot, that is, when  , to obtain
, to obtain  . As in [24] we adopt a double feedback information for all the users at each slot. In particular, at slot
. As in [24] we adopt a double feedback information for all the users at each slot. In particular, at slot  user
user  feeds back for each resource block
feeds back for each resource block  : (i) a channel direction information (CDI)
: (i) a channel direction information (CDI)  , which ideally tracks the normalized channel vector
, which ideally tracks the normalized channel vector  , namely
, namely

and (ii) a channel quality information (CQI), based on the estimated signal-to-noise plus interference ratio (SNIR) at the receiver for  orthogonal scheduled users evaluated as [24]
orthogonal scheduled users evaluated as [24]

We assume that the feedback channel has a finite rate of  bits per slot and per user and allows zero-delay error-free transmission. The base station builds the matrix
bits per slot and per user and allows zero-delay error-free transmission. The base station builds the matrix

containing the unit-norm reconstructed channel vectors  . Using the partial CSI, base station evaluates an estimate
. Using the partial CSI, base station evaluates an estimate  of the SNIR of stream
of the SNIR of stream  as will be seen in Section 4. Zero-forcing beamforming with equal power distribution among streams is implemented for each resource block, hence the beamforming matrix is
as will be seen in Section 4. Zero-forcing beamforming with equal power distribution among streams is implemented for each resource block, hence the beamforming matrix is

An estimate of the normalized (with respect to the bandwidth) rate achieved by stream  at slot
at slot  is
is

Notation  highlights the fact that rates achieved by different streams are mutually dependent, as (i) more streams allocated simultaneously on the same resource blocks yield interference, and (ii) the total power is distributed among active streams. Performance is evaluated in terms of WSR,
highlights the fact that rates achieved by different streams are mutually dependent, as (i) more streams allocated simultaneously on the same resource blocks yield interference, and (ii) the total power is distributed among active streams. Performance is evaluated in terms of WSR,

with  suitable weights that take into account fairness and QoS constraints.
suitable weights that take into account fairness and QoS constraints.
2.2. Exhaustive Search Scheduling
At each slot, we aim at scheduling the set of streams that maximizes WSR.
This problem can be solved by considering all  possible sets and evaluating the WSR achieved by each candidate set. Unfortunately, this exhaustive search (ES) scheduling has a high computational cost, which becomes infeasible for an increasing number of users and subcarriers. Simpler and suboptimal scheduling methods are investigated in Section 4.
possible sets and evaluating the WSR achieved by each candidate set. Unfortunately, this exhaustive search (ES) scheduling has a high computational cost, which becomes infeasible for an increasing number of users and subcarriers. Simpler and suboptimal scheduling methods are investigated in Section 4.
3. Maximum Utility Scheduler
In order to balance the opportunistic use of channel resources with fairness among users, we consider a multiuser scheduler. We first consider in this section general criteria for the choice of weights of the WSR and we derive the optimum maximum utility scheduler weights for a general utility function. Then we specialize the result for the maximum sum rate scheduler and the proportional fair scheduler.
3.1. General Multiuser Scheduling
Let  be the achievable rate associated with user
be the achievable rate associated with user  , that is,
, that is,  . In the first slot, the average throughput achieved by user
. In the first slot, the average throughput achieved by user  is
is  ,
,  . The estimate of the average throughput achieved by user
. The estimate of the average throughput achieved by user  can be updated as
can be updated as

where  is the set of scheduled users at slot
is the set of scheduled users at slot  . If we aim at achieving an average throughput
. If we aim at achieving an average throughput  for user
for user  , we can define the normalized averaged throughput at slot
, we can define the normalized averaged throughput at slot  as
as

In [25], the following concave and differentiable utility function has been proposed to design schedulers

where  is a fairness parameter to be chosen according to the desired scheduling policy. For example, for
is a fairness parameter to be chosen according to the desired scheduling policy. For example, for  we obtain the proportional fair scheduler (PFS). For
we obtain the proportional fair scheduler (PFS). For  we obtain the utility function of the maximum sum rate scheduler. When
we obtain the utility function of the maximum sum rate scheduler. When  , (13) becomes the utility function of the max-min scheduler.
, (13) becomes the utility function of the max-min scheduler.
In Appendix , we derive the set of users  that maximizes the sum utility
that maximizes the sum utility

The solution is

with weights

where  is the set of all possible streams. Note that for
is the set of all possible streams. Note that for  , (16) boils down to the maximum utility scheduler of [25].
, (16) boils down to the maximum utility scheduler of [25].
3.2. Maximum Sum Rate Scheduling
The maximum sum rate scheduler does not consider the fairness among users ( ) and simply aims at maximizing the achievable sum rate (SR), providing
) and simply aims at maximizing the achievable sum rate (SR), providing  , for
, for  , and
, and

3.3. Proportional Fair Scheduling
The multiuser multicarrier proportional fair scheduling (MMPFS) algorithm [26] is an extension to the OFDM multiuser scenario of the PFS algorithm.
For MMPFS, the average throughput of user  is updated as in (11) with
is updated as in (11) with  , where
, where  is a parameter related to the time over which fairness should be achieved. In [27] it has been shown that proportional fairness, maximizing
is a parameter related to the time over which fairness should be achieved. In [27] it has been shown that proportional fairness, maximizing  , is achieved by scheduling users as
, is achieved by scheduling users as

We observe that for  we can approximate
we can approximate

and MPFS (18) coincides with the maximization of the WSR (15) with weights (16),  and
and  .
.
4. Greedy Scheduling Strategies
Now that we have established that maximizing the weighted sum rate is equivalent to the maximization of a wide set of utility functions, we focus on methods that allow to achieve this goal. In the following we investigate suboptimal solutions to problem (15) for a small number of users  , when the probability of having a fully loaded system is small. In fact, in this scenario power distribution has an important role in selecting the optimal user set. In Section 4.3 we will consider the case of a high number of users
, when the probability of having a fully loaded system is small. In fact, in this scenario power distribution has an important role in selecting the optimal user set. In Section 4.3 we will consider the case of a high number of users  , and in this case a simplification of scheduling is possible. For ease of notation we drop both slot (
, and in this case a simplification of scheduling is possible. For ease of notation we drop both slot ( ) and OFDM symbol (
) and OFDM symbol ( ) index in the remaining of the paper.
) index in the remaining of the paper.
4.1. Multicarrier Greedy (MG)
In [14], a greedy scheduling algorithm in a single-carrier flat-fading system has been proposed, where users are selected one by one as long as the throughput increases and it has been then extended to an OFDM system in [21] and denoted here multicarrier greedy (MG).
The MG algorithm comprises  steps, and at each step we select the stream that maximizes the increase of WSR. Let
steps, and at each step we select the stream that maximizes the increase of WSR. Let  be the set of streams scheduled for transmission at step
be the set of streams scheduled for transmission at step  ,
,  , with the corresponding WSR
, with the corresponding WSR  . Initially we have
. Initially we have  . The stream selected at step
. The stream selected at step  , is
, is

and we set  . The WSR
. The WSR  increases at each step, since stream
increases at each step, since stream  is inserted under the condition that
is inserted under the condition that

When (21) does not hold, the algorithm is stopped,  and
and  . Hence,
. Hence,  is a random variable. Evaluation of the WSR in (20) for the current set of streams is based on the observation that for an equal power allocation across users and resource blocks under constraint (4), using (3), the allocated power to user
is a random variable. Evaluation of the WSR in (20) for the current set of streams is based on the observation that for an equal power allocation across users and resource blocks under constraint (4), using (3), the allocated power to user  and resource block
and resource block  turns out to be [15]
turns out to be [15]

Therefore, a SNIR estimate for stream  with
with  can be computed by scaling with the newly computed transmit power the CQI value, that is,
can be computed by scaling with the newly computed transmit power the CQI value, that is,

where  is given by (6) while
is given by (6) while  is the
is the  th column of the beamforming matrix
th column of the beamforming matrix  for users scheduled at step
for users scheduled at step  . Note that total power
. Note that total power  has been divided by
has been divided by  in order to obtain the per stream power
in order to obtain the per stream power  .
.
4.2. Projection-Based Greedy (PBG)
According to the MG algorithm, the introduction of a new candidate stream  into the set
into the set  at step
at step  decreases the SNIRs (23) for two reasons:
decreases the SNIRs (23) for two reasons:
-
(1)
the power is redistributed among all streams;
-
(2)
beamforming of streams already scheduled on the same resource block is modified.
Due to (a), it is beneficial to perform scheduling jointly among resource blocks rather than separately on each resource block. Due to (b), a new beamforming matrix must be computed for users scheduled on resource block  of the candidate stream. Hence, at each step many beamformers must be designed for each resource block to test (21) and only one candidate stream is then scheduled. In order to reduce the computational complexity, the projection-based greedy (PBG) algorithm [22] assumes that the insertion of a new stream does not significantly alter the SNIR of already scheduled streams. Indeed, this assumption holds as long as the channel vector of the candidate stream is almost orthogonal to channel vectors of previously scheduled streams. Therefore, we update the SNIR estimate of already scheduled streams as follows
of the candidate stream. Hence, at each step many beamformers must be designed for each resource block to test (21) and only one candidate stream is then scheduled. In order to reduce the computational complexity, the projection-based greedy (PBG) algorithm [22] assumes that the insertion of a new stream does not significantly alter the SNIR of already scheduled streams. Indeed, this assumption holds as long as the channel vector of the candidate stream is almost orthogonal to channel vectors of previously scheduled streams. Therefore, we update the SNIR estimate of already scheduled streams as follows

for  , while for the first step we set
, while for the first step we set  . Furthermore, the evaluation of the SNIR for the candidate streams requires only the computation of
. Furthermore, the evaluation of the SNIR for the candidate streams requires only the computation of  instead of the entire beamformer. In particular, if we define
instead of the entire beamformer. In particular, if we define

from (23) we have

In order to compute (25) and the corresponding SNIR (26) of the candidate stream  , it can be observed that its beamforming vector is obtained by the orthogonalization of
, it can be observed that its beamforming vector is obtained by the orthogonalization of  with respect to the normalized channel vector of already scheduled streams on the same resource block. Hence, an orthonormal basis
with respect to the normalized channel vector of already scheduled streams on the same resource block. Hence, an orthonormal basis  is first constructed for the space generated by the channel vectors
is first constructed for the space generated by the channel vectors  of streams in
of streams in  on resource block
on resource block  . Then the beamforming vector for stream
. Then the beamforming vector for stream  would be proportional to
would be proportional to

Now, by imposing  , the identity matrix, it is
, the identity matrix, it is  and we have
and we have

By using (26) and (28), there is no need to determine a new beamformer in correspondence of each candidate stream; instead, only the basis  needs to be updated at each step, and this requires only few vector multiplications. Note that the computation of
needs to be updated at each step, and this requires only few vector multiplications. Note that the computation of  is based on the projection of the candidate vector on the basis, as from the acronym PBG. Once all streams have been scheduled, a beamformer is computed to perform transmission.
is based on the projection of the candidate vector on the basis, as from the acronym PBG. Once all streams have been scheduled, a beamformer is computed to perform transmission.
4.3. Greedy Scheduling Strategies in the High 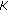 Scenario
Scenario
If  , multiuser diversity provides
, multiuser diversity provides  orthogonal streams on each resource block with very high probability, thus we will have almost always a fully loaded system, that is,
orthogonal streams on each resource block with very high probability, thus we will have almost always a fully loaded system, that is,  . In this case, both MG and PBG algorithms can be simplified without redistributing the available power at each new insertion, and the per stream power (4) becomes
. In this case, both MG and PBG algorithms can be simplified without redistributing the available power at each new insertion, and the per stream power (4) becomes

Scheduling can then be simplified by operating independently on each resource block.
4.4. Multicarrier Semiorthogonal User Selection Algorithm (MSUS)
The semiorthogonal user selection (SUS) scheme [9] can be easily generalized to the OFDM scenario and is here denoted as multicarrier SUS (MSUS). The generalization includes also the maximization of the WSR instead of the SR as considered in [9]. MSUS proceeds by steps now applied separately on each resource block. For resource block  , let
, let  be the initial set containing the indexes of all users. The scheduled stream at step
be the initial set containing the indexes of all users. The scheduled stream at step  is characterized by having maximum CQI, that is,
is characterized by having maximum CQI, that is,

After selecting  streams, the
streams, the  th stream
th stream  is chosen within the set
is chosen within the set

as

where  is a design parameter that sets the maximum correlation allowed between the quantized channel vectors of the selected users. We note that in MSUS we apply
is a design parameter that sets the maximum correlation allowed between the quantized channel vectors of the selected users. We note that in MSUS we apply  single carrier SUS in parallel, one for each resource block. Also in this case the number of steps is random as the algorithm ends when set
single carrier SUS in parallel, one for each resource block. Also in this case the number of steps is random as the algorithm ends when set  is empty. Once users have been scheduled, the total power is equally distributed among the scheduled streams according to (4).
is empty. Once users have been scheduled, the total power is equally distributed among the scheduled streams according to (4).
5. Preselection Methods
In the MG algorithm the WSR  increases at each step and using (9) and (10), condition (21) becomes
increases at each step and using (9) and (10), condition (21) becomes

From (23) we obtain that this condition is satisfied only if the SNIR is high enough to compensate for losses incurred by the insertion of a new scheduled stream, that is, the power redistribution and the beamforming modification, as described by conditions (1) and (2) of Section 4.2. This observation suggests a further simplification of the PBG algorithm, by a-priori excluding the streams whose SNIR is below a certain threshold. Indeed, as for each candidate stream the SNIR (26) must be evaluated, by excluding streams that could never be inserted, the scheduling procedure can be fastened [22].
Note that the idea of preselecting users has been first introduced in [28], by letting users feeding back their CSI and rate request only if the quality of their channel is above a threshold. On the other hand, we use preselection as a technique to simplify scheduling rather than reducing the feedback rate. Moreover, in our case the preselection is not based only on the channel quality but also on the correlation with other users' channels.
5.1. Preselection PBG (PPBG)
We first observe from (28) that  and from (25) we obtain
and from (25) we obtain

Therefore, at step  of PBG there is a minimum value of
of PBG there is a minimum value of  that satisfies (33), denoted
that satisfies (33), denoted  , and we consider for scheduling only streams having SNIR
, and we consider for scheduling only streams having SNIR

As shown Appendix , at high SNR we have

Then by considering only streams  satisfying (35), we decrease the number of comparisons and SINR updates at each step of PBG. In the high
satisfying (35), we decrease the number of comparisons and SINR updates at each step of PBG. In the high  scenario the preselection technique is not feasible; in fact, as illustrated in Appendix ,
scenario the preselection technique is not feasible; in fact, as illustrated in Appendix ,  for
for  , and therefore (35) is verified by all streams.
, and therefore (35) is verified by all streams.
We further note that  is an increasing function of
is an increasing function of  ; hence, streams whose CQI is below the threshold
; hence, streams whose CQI is below the threshold  at step
at step  can be neglected also in the next steps.
can be neglected also in the next steps.
5.2. Simplified Preselection PBG (S-PPBG)
A further simplification in preselection is achieved by neglecting weights  on evaluating
on evaluating  , that is, by considering
, that is, by considering  in (B.2) to yield
in (B.2) to yield

Within PBG methods, we note that this approach becomes optimal when the scheduling objective coincides with the maximization of the SR. However, for the maximization of the WSR, S-PPBG is in general suboptimal.
6. Complexity Analysis
We analyze the worst case complexity of the various approaches, in terms of both computational complexity and memory requirement.
6.1. Computational Complexity
We assume that a comparison yields a computational complexity equal to  complex multiplications (CMUX), while the inversion of an
complex multiplications (CMUX), while the inversion of an  matrix performed by Gaussian elimination methods has complexity
matrix performed by Gaussian elimination methods has complexity  CMUX. The beamforming and
CMUX. The beamforming and  evaluation have therefore complexity
evaluation have therefore complexity

We first observe that all considered algorithms select one stream per step, until at most  streams are allocated on each resource block, thus in general
streams are allocated on each resource block, thus in general  . At step
. At step  ,
,  streams are considered for insertion in
streams are considered for insertion in  . Furthermore, at each step, the per stream power
. Furthermore, at each step, the per stream power  is adapted, due to the insertion of a candidate stream in
is adapted, due to the insertion of a candidate stream in  .
.
6.1.1. MG Complexity
Complexity of the MG algorithm in the low  scenario is given by
scenario is given by

where  denotes the resource block of the stream selected at step
denotes the resource block of the stream selected at step  . The first term in (39) accounts for the selection of the stream with maximum CQI. The remaining terms account for step
. The first term in (39) accounts for the selection of the stream with maximum CQI. The remaining terms account for step  through
through  , with (a) update of SNIR estimate of the
, with (a) update of SNIR estimate of the  already scheduled streams, (b) computation of a new beamformer for each of the
already scheduled streams, (b) computation of a new beamformer for each of the  candidate streams on subcarrier
candidate streams on subcarrier  , (c) evaluation of
, (c) evaluation of  , (d) update of the SNIR estimates, and (e) evaluation of the WSR. Lastly, the algorithm determines the stream which maximizes the WSR at step
, (d) update of the SNIR estimates, and (e) evaluation of the WSR. Lastly, the algorithm determines the stream which maximizes the WSR at step  and checks condition (21).
and checks condition (21).
In the high  scenario complexity becomes
scenario complexity becomes

since now  and no power update is necessary at each step.
and no power update is necessary at each step.
6.1.2. PBG Complexity
Complexity of the PBG in the low  scenario is
scenario is

In fact, the PBG algorithm for each candidate stream on resource block  (a) performs the projection of channel vector on the orthogonal basis and (b) updates the SNIR estimate. At each step, the basis is also updated according to the channel vector of last scheduled stream. At the end, the beamforming matrix is computed according to the set of scheduled streams.
(a) performs the projection of channel vector on the orthogonal basis and (b) updates the SNIR estimate. At each step, the basis is also updated according to the channel vector of last scheduled stream. At the end, the beamforming matrix is computed according to the set of scheduled streams.
In the high  scenario we have
scenario we have

since scheduling can be performed in parallel on all resource blocks.
6.1.3. PPBG Complexity
The complexity of the PPBG in the low  scenario is given by
scenario is given by

It only differs from PBG in the evaluation of  at each step, since it depends on the set of scheduled streams. Similarly, in the high
at each step, since it depends on the set of scheduled streams. Similarly, in the high  scenario we have
scenario we have

6.1.4. S-PPBG Complexity
Applying the S-PPBG algorithm, we have an additional cost due to (35); on the other hand, on resource block  , at each step
, at each step  we exclude a number of streams
we exclude a number of streams  from the set of possible streams.
from the set of possible streams.  takes into account also the scheduled streams. Then at step
takes into account also the scheduled streams. Then at step  we have
we have  candidate streams on resource block
candidate streams on resource block  and in total
and in total  . Complexity becomes
. Complexity becomes

Note that  is a random variables depending on the channel realization. In the high
is a random variables depending on the channel realization. In the high  scenario we still consider power adjustment; otherwise, from (B.2), we could never exclude streams, and then S-PPBG would become PBG. Complexity of S-PPBG in the high
scenario we still consider power adjustment; otherwise, from (B.2), we could never exclude streams, and then S-PPBG would become PBG. Complexity of S-PPBG in the high  scenario becomes
scenario becomes

The MSUS algorithm is equivalent to  SUS algorithms working in parallel. We remind that at each step SUS considers
SUS algorithms working in parallel. We remind that at each step SUS considers  candidate users, where
candidate users, where  is the number of users excluded at step
is the number of users excluded at step  . It is
. It is

6.2. Asymptotic Complexity Analysis
According to complexities required by various scheduling algorithms, we investigate their asymptotic behavior as a function of  . For MG we have
. For MG we have

For PBG and PPBG we have

Both S-PPBG and MSUS perform the exclusion of worse streams. Let  be the percentage of streams excluded at step
be the percentage of streams excluded at step  , for S-PPBG it is
, for S-PPBG it is  while for MSUS
while for MSUS  . Asymptotic expressions are
. Asymptotic expressions are

where  , and
, and  .
.
6.3. Memory Occupation
Lastly we investigate memory requirements of the scheduling algorithms in terms of complex location (CLS) units. We first note that all algorithms store (a) CDI and CQI of all streams, (b) the set of selected streams, and (c) the final beamformers; then a memory occupation of  CLS is common to all algorithms. For MG we have
CLS is common to all algorithms. For MG we have

since MG stores (a)  (or, equivalently,
(or, equivalently,  ), requiring
), requiring  CLS, (b) per user rates (
CLS, (b) per user rates ( CLS as worst case), (c) new beamformer (
CLS as worst case), (c) new beamformer ( CLS), (d) total rate provided by each candidate (
CLS), (d) total rate provided by each candidate ( CLS), and (e) current and last final rates (
CLS), and (e) current and last final rates ( CLS). For PBG and PPBG we have
CLS). For PBG and PPBG we have

as PBG stores (a) the value  , (b) total rate provided by each candidate stream (
, (b) total rate provided by each candidate stream ( CLS), and (c) orthogonal basis (
CLS), and (c) orthogonal basis ( CLS).
CLS).
The S-PPBG memory requirement is given by

with respect to PBG it needs to store also  (
( CLS as worst case).
CLS as worst case).
Finally, for MSUS we have

as MSUS stores (a) correlations of candidate streams and last inserted stream ( CLS), (b) the value of
CLS), (b) the value of  (
( CLS), and (c) the set of total rates of each candidate (
CLS), and (c) the set of total rates of each candidate ( CLS as worst case).
CLS as worst case).
7. Simulation Results
We compare the scheduling algorithms in terms of average sum rate (SR) and complexity requirements. All users are uniformly distributed in a cell of radius 500 m, as in [29]; we consider an average  of 15 dB per resource block at the cell border and path loss is included in the channel model. We assume also a realistic MIMO channel with time, frequency, and spatial correlation among the elements of
of 15 dB per resource block at the cell border and path loss is included in the channel model. We assume also a realistic MIMO channel with time, frequency, and spatial correlation among the elements of  . The channel is modeled as slowly time-variant, frequency selective Rayleigh fading as from the spatial channel model (SCM) [30]. According to the LTE release, we set transmission bandwidth to 2.5 MHz, divided into
. The channel is modeled as slowly time-variant, frequency selective Rayleigh fading as from the spatial channel model (SCM) [30]. According to the LTE release, we set transmission bandwidth to 2.5 MHz, divided into  resource blocks and centered at the carrier frequency of 2 GHz. The base station is equipped with
resource blocks and centered at the carrier frequency of 2 GHz. The base station is equipped with  antennas spaced by 10 wavelength. Scheduling and beamforming are performed once a slot, and each slot is composed of 7 adjacent OFDM symbols. CSI feedback is performed with a variable number of bits using an optimized codebook, as detailed in [31].
antennas spaced by 10 wavelength. Scheduling and beamforming are performed once a slot, and each slot is composed of 7 adjacent OFDM symbols. CSI feedback is performed with a variable number of bits using an optimized codebook, as detailed in [31].
7.1. Performance Comparison
We first compare the SR achieved by MG with ES scheduling using as optimization criterion the maximum sum rate. For complexity reasons simulations have been limited to  resource blocks. To simplify simulations in the ES method, results of both MG and ES in the high
resource blocks. To simplify simulations in the ES method, results of both MG and ES in the high  scenario,
scenario,  , refer to
, refer to  . In fact, we verified that for high
. In fact, we verified that for high  the system is fully loaded with a probability higher then
the system is fully loaded with a probability higher then  ; in this scenario the power granted to each carrier is
; in this scenario the power granted to each carrier is  , and then user selection can be performed independently on each carrier. We consider both the case of perfect CSI at the transmitter and the case of partial CSI obtained by feedback from the receiver, with a feedback rate of 12 bit/user/resource block/slot. We observe that partial CSI provides a loss on SR of 2 up to 3.5 bit/user/resource block/slot, but it does not affect the general behavior of the two algorithms. As we can see from Figure 1, both MG and ES have a very close sum rate for all
, and then user selection can be performed independently on each carrier. We consider both the case of perfect CSI at the transmitter and the case of partial CSI obtained by feedback from the receiver, with a feedback rate of 12 bit/user/resource block/slot. We observe that partial CSI provides a loss on SR of 2 up to 3.5 bit/user/resource block/slot, but it does not affect the general behavior of the two algorithms. As we can see from Figure 1, both MG and ES have a very close sum rate for all  . Hence, in the following we consider MG as performance bound.
. Hence, in the following we consider MG as performance bound.
Figure 2 illustrates the average SR achieved by the scheduling algorithms as a function of the number of users  in the low
in the low  scenario for a feedback rate of 12 bit/user/resource block/slot. We note a negligible loss in performance of the simplified methods. Similarly, simulations in the high
scenario for a feedback rate of 12 bit/user/resource block/slot. We note a negligible loss in performance of the simplified methods. Similarly, simulations in the high  scenario show that MG, PBG, and S-PPBG achieve a SR of 16.40 bit/s/Hz, while MSUS provides 15.40 bit/s/Hz. Overall we observe that the simplified algorithms do not provide SR loss for all
scenario show that MG, PBG, and S-PPBG achieve a SR of 16.40 bit/s/Hz, while MSUS provides 15.40 bit/s/Hz. Overall we observe that the simplified algorithms do not provide SR loss for all  . This is mainly due to the fact that all scheduling methods are based on an opportunistic approach, so they all aim at selecting the best set of orthogonal users. We also note that all algorithms always select the same first stream, whose channel vector in turn determines the choice of the other streams. We underline that the average SR of S-PPBG is very close to that of PBG and MG; moreover, since S-PPBG is an approximation of PPBG, we deduce that also PPBG provides the same SR of S-PPBG. Figure 3 confirms this behavior also with a PFS.
. This is mainly due to the fact that all scheduling methods are based on an opportunistic approach, so they all aim at selecting the best set of orthogonal users. We also note that all algorithms always select the same first stream, whose channel vector in turn determines the choice of the other streams. We underline that the average SR of S-PPBG is very close to that of PBG and MG; moreover, since S-PPBG is an approximation of PPBG, we deduce that also PPBG provides the same SR of S-PPBG. Figure 3 confirms this behavior also with a PFS.
We note also in Figure 3 that preselection applied to PBG provides slightly better performance, despite the fact that it considers a lower number of candidate sets. In fact, preselection aims at excluding from scheduling streams that would not increase the WSR and prevents the scheduler from inserting them for fairness reasons.
Figure 4 reports the average SR versus the feedback rate; we observe that the simplified methods are also robust to quantization error; in fact, for all considered values of feedback rate, PBG and S-PPBG provide the same SR of MG. Note that a feedback rate of 12 bit/user/RB/slot would result in an extremely large feedback overhead for the cases with a high number of users (960 bit/RB/slot for  users), while performance decreases markedly at lower feedback rates.
users), while performance decreases markedly at lower feedback rates.
7.2. Complexity Comparison
Figure 5 shows complexity versus  . For
. For  to
to  the low
the low  complexity expressions are used, while from
complexity expressions are used, while from  to 1024 we use the high
to 1024 we use the high  complexity expressions. We first observe that the complexity ratio between the scheduling algorithms is nearly the same both in the low
complexity expressions. We first observe that the complexity ratio between the scheduling algorithms is nearly the same both in the low  and high
and high  regime. As expected, MSUS and S-PPBG complexity trend is not influenced by the value of
regime. As expected, MSUS and S-PPBG complexity trend is not influenced by the value of  . From Figure 5 we note that for
. From Figure 5 we note that for  , with corresponding fully load probability in the range from
, with corresponding fully load probability in the range from  to
to  , the computational cost of MG is from 2.2 to 18.5 times the cost of PBG, with a factor increasing in
, the computational cost of MG is from 2.2 to 18.5 times the cost of PBG, with a factor increasing in  ; as expected, the preselection technique further reduces complexity by a factor 1.2–1.4 with respect to PBG. We note also that complexity of S-PPBG is only 2.4–2.9 times the complexity of MSUS. As complexity of PPBG is bounded between that of PBG and S-PPBG and these two are very close, we omitted to show PPBG in Figure 5.
; as expected, the preselection technique further reduces complexity by a factor 1.2–1.4 with respect to PBG. We note also that complexity of S-PPBG is only 2.4–2.9 times the complexity of MSUS. As complexity of PPBG is bounded between that of PBG and S-PPBG and these two are very close, we omitted to show PPBG in Figure 5.
In the high  scenario, simulations confirm the analysis; in fact, for
scenario, simulations confirm the analysis; in fact, for  we have
we have  ,
,  ,
,  , and
, and  . We underline that in the high
. We underline that in the high  regime S-PPBG complexity is higher than that of PBG because of the required power distribution; indeed simplification of preselection does not compensate the need of redistributing the total power. On the other hand, we note that the high complexity required by MG is mainly due to the evaluations of the beamformer at each step.
regime S-PPBG complexity is higher than that of PBG because of the required power distribution; indeed simplification of preselection does not compensate the need of redistributing the total power. On the other hand, we note that the high complexity required by MG is mainly due to the evaluations of the beamformer at each step.
Memory requirements, investigated in Section 6, do not prefigure large differences between different methods; for  required memory locations are 35890 for MG, 29682 for PBG, 29730 for S-PPBG, and 33841 for MSUS. Hence, the simplified techniques achieve a reduction of memory requirement with respect to existing algorithms.
required memory locations are 35890 for MG, 29682 for PBG, 29730 for S-PPBG, and 33841 for MSUS. Hence, the simplified techniques achieve a reduction of memory requirement with respect to existing algorithms.
8. Conclusions
This paper has provided an overview of scheduling problems for multiuser downlink MIMO OFDM systems. We first have shown that scheduling according to a wide class of utility functions can be reduced to a scheduling problem aiming at maximizing the weighted sum rate of the system, under a proper choice of the weighting function. Then we have compared scheduling algorithm having as objective the maximization of the weighted sum rate, including greedy algorithms, based on throughput maximization and algorithms based on the semiorthogonality among MIMO channels. Extensions to a OFDM scenario of algorithms originally devised for flat-fading single-carrier systems have been investigated. The comparison has been carried out both in terms of computational complexity and in terms of achievable throughput.
Several insights on the performance of the state of the art scheduling algorithms can be highlighted from the numerical results. Firstly, the MG approach achieves an average sum rate which is very close to the maximum value achieved by ES, over a wide range of cell loads. When compared against MSUS, the proposed MG technique has a gain of about 50% in terms of average sum rate in most network conditions. Moreover, MG requires a significantly lower complexity than that of ES and only 30% additional CMUXs than MSUS. Hence, we believe that MG provides a good trade-off between performance and complexity.
Lastly, limitations in the feedback rate have a severe impact on the performance of all scheduling approaches. Indeed we have seen that all schedulers yield an average sum rate that increases linearly with the number of bits used to feedback the CSI with an increase of about 1 bit/s/Hz for each additional feedback bit.
Appendices
A. Proof of (15)
We aim at solving

From (12) and (11), the problem (A.1) can be rewritten as

where  indicates that user
indicates that user  is scheduled, that is,
is scheduled, that is,  if
if  and
and  otherwise.
otherwise.
Following the derivations of [25] we observe that for all but the scheduled users, the allocated rate at slot  is zero, therefore we have
is zero, therefore we have

Under the assumption  , the following approximation holds
, the following approximation holds

In turn, from (13) the derivative can be written as

Therefore, by inserting (A.5) into (A.4) we obtain (15).
B. Proof of (36)
We observe that condition (33) is equivalent to

where  is the generic candidate stream.
is the generic candidate stream.
In the high SNR scenario, with  , we have
, we have  and from (24), condition (B.1) becomes
and from (24), condition (B.1) becomes

Hence from (B.2), (36) follows. We note that, in the high  scenario, (B.1) becomes
scenario, (B.1) becomes

and  .
.
References
Tse D, Viswanath P: Fundamentals of Wireless Communication. Cambridge University Press, Cambridge, UK; 2005.
Caire G, Shamai S: On the achievable throughput of a multiantenna Gaussian broadcast channel. IEEE Transactions on Information Theory 2003, 49(7):1691-1706. 10.1109/TIT.2003.813523
Yoo T, Goldsmith A: On the optimality of multiantenna broadcast scheduling using zero-forcing beamforming. IEEE Journal on Selected Areas in Communications 2006, 24(3):528-541.
Yoo T, Goldsmith A: Sum-rate optimal multi-antenna downlink beamforming strategy based on clique search. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '05), November-December 2005, St. Louis, Mo, USA 3: 1510-1514.
Shen Z, Chen R, Andrews JG, Heath RW Jr., Evans BL: Low complexity user selection algorithms for multiuser MIMO systems with block diagonalization. IEEE Transactions on Signal Processing 2006, 54(9):3658-3663.
Wang J, Love DJ, Zoltowski MD: User selection for the MIMO broadcast channel with a fadiness constraint. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '07), April 2007, Honolulu, Hawaii, USA 3: 9-12.
Viswanathan H, Kumaran K: Rate scheduling in multiple antenna downlink wireless systems. Proceedings of Allerton Conference on Communication, Control, and Computing, October 2001, Allerton, Ill, USA
Swannack C, Uysal-Biyikoglu E, Wornell GW: Low complexity multiuser scheduling for maximizing throughput in the MIMO broadcast channel. Proceedings of Allerton Conference on Communication, Control, and Computing, October 2004, Allerton, Ill, USA
Yoo T, Jindal N, Goldsmith A: Multi-antenna downlink channels with limited feedback and user selection. IEEE Journal on Selected Areas in Communications 2007, 25(7):1478-1491.
Diaz J, Simeone O, Bar-Ness Y: Sum-rate of MIMO broadcast channels with one bit feedback. Proceedings of IEEE International Symposium on Information Theory (ISIT '06), July 2006, Seattle, Wash, USA 1944-1948.
Kobayashi M, Caire G: An iterative water-filling algorithm for maximum weighted sum-rate of Gaussian MIMO-BC. IEEE Journal on Selected Areas in Communications 2006, 24(8):1640-1646.
Fuchs M, Galdo GD, Haardt M: Low-complexity space-time-frequency scheduling for MIMO systems with SDMA. IEEE Transactions on Vehicular Technology 2007, 56(5):2775-2784.
Jiang M, Rubio F, Wang Y, Gomez J, Yuan D: User selection for maximum sum-rate in multi-user and MISO system with evolutionary algorithm. Proceedings of the 1st International Workshop on Cross Layer Design (IWCLD '07), September 2007, Jinan, China 74-77.
Dimic G, Sidiropoulos ND: On downlink beamforming with greedy user selection: performance analysis and a simple new algorithm. IEEE Transactions on Signal Processing 2005, 53(10):3857-3868.
Trivellato M, Boccardi F, Tosato F: User selection schemes for MIMO broadcast channels with limited feedback. Proceedings of the 65th IEEE Vehicular Technology Conference (VTC '07), April 2007, Dublin, Ireland 2089-2093.
Alexiou A, Reis J, Gameiro A: QoS-based multiuser scheduling in MIMO systems. Proceedings of the 16th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '05), September 2005, Berlin, Germany 2: 837-841.
Anton-Haro C, Svedman P, Bengtsson M, Alexiou A, Gameiro A: Cross-layer scheduling for multi-user MIMO systems. IEEE Communications Magazine 2006, 44(9):39-45.
Trifonov P, Costa E, Filippi A, Schulz E: Adaptive coding in MC-CDMA/FDMA systems with adaptive sub-band allocation. European Transactions on Telecommunications 2004, 15(3):207-214. 10.1002/ett.967
Overview of the 3GPP long term evolution physical layer Motorola, January 2003, http://www.freescale.com/files/wireless_comm/doc/white_paper/3GPPEVOLUTIONWP.pdf
Ekstrom H, Furuskar A, Karlsson J, et al.: Technical solutions for the 3G long-term evolution. IEEE Communications Magazine 2006, 44(3):38-45.
Benvenuto N, Conte E, Tomasin S, Trivellato M: Joint low-rate feedback and channel quantization for the MIMO broadcast channel. Proceedings of Tyrrhenian International Workshop on Digital Communication, September 2007, Ischia Island, Italy
Conte E, Tomasin S, Benvenuto N: Scheduling strategies for multiuser MIMO OFDM systems with limited feedback. Proceedings of the 19th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '08), September 2008, Cannes, France
Hanzo L, Münster M, Chei B, Keller T: OFDM and MC-CDMA for Broadband Multi-User Communications, WLANS and Broadcasting. John Wiley & Sons, New York, NY, USA; 2003.
Jindal N: Finite rate feedback MIMO broadcast channels. Proceedings of Workshop on Information Theory and Its Applications (ITA '06), February 2006, San Diego, Calif, USA
Svedman P, Wilson SK, Cimini LJ Jr., Ottersten B: Opportunistic beamforming and scheduling for OFDMA systems. IEEE Transactions on Communications 2007, 55(5):941-952.
Kountouris M, Gesbert D: Memory-based opportunistic multi-user beamforming. Proceedings of IEEE International Symposium on Information Theory (ISIT '05), September 2005, Adelaide, SC, USA 1426-1430.
Jalali A, Padovani R, Pankaj R: Data throughput of CDMA-HDR a high efficiency-high data rate personal communication wireless system. Proceedings of the 51st Vehicular Technology Conference (VTC '00), May 2000, Tokyo, Japan 3: 1854-1858.
Gesbert D, Alouini M-S: How much feedback is multi-user diversity really worth? Proceedings of IEEE International Conference on Communications, June 2004, Paris, France 1: 234-238.
SCM micro cell and urban canyon model Motorola, January 2003, http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/3GPP_3GPP2_SCM/ConfCall-10-20030130/
Salo J, Galdo GD, Salmi J, et al.: Matlab implementation of the 3GPP spatial channel model. January 2005., (3GPP TR 25.996):http://www.tkk.fi/Units/Radio/scm/
Benvenuto N, Conte E, Tomasin S, Trivellato M: Predictive channel quantization and beamformer design for MIMO-BC with limited feedback. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007, Washington, DC, USA 3607-3611.
Acknowledgment
The authors thank the editor and the reviewers for their comments on the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Conte, E., Tomasin, S. & Benvenuto, N. A Comparison of Scheduling Strategies for MIMO Broadcast Channel with Limited Feedback on OFDM Systems. J Wireless Com Network 2010, 968703 (2010). https://doi.org/10.1155/2010/968703
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/968703
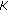 Scenario
Scenario
 .
.

 . Scheduling objective is the maximization of the sum rate.
. Scheduling objective is the maximization of the sum rate.
 . Scheduling objective is proportional fair scheduling.
. Scheduling objective is proportional fair scheduling.

 .
.