- Research Article
- Open access
- Published:
Secure Geographic Routing in Ad Hoc and Wireless Sensor Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 975607 (2010)
Abstract
Security in sensor networks is one of the most relevant research topics in resource constrained wireless devices and networks. Several attacks can be suffered in ad hoc and wireless sensor networks (WSN), which are highly susceptible to attacks, due to the limited resources of the nodes. In this paper, we propose innovative and lightweight localization techniques that allow for intrusion identification and isolation schemes and provide accurate location information. This information is used by our routing protocol which additionally incorporates a distributed trust model to prevent several routing attacks to the network. We finally evaluate our algorithms for accurate localization and for secure routing which have been implemented and tested in real ad hoc and wireless sensor networks.
1. Introduction
Security in sensor networks is one of the most relevant research topics in resource-constrained wireless devices and networks.Many security issues arise from the nature of such networks: nodes are severely limited in key capabilities (such as, transmission power and computing resources), and they operate in an ad hoc mode, requiring the cooperation of other devices to route data packets to their destination. Thus, deploying ad hoc and wireless sensor networks (WSN) in a hostile environment is a challenging task that usually requires the use of different combined techniques at various network levels.
Intruder identification in an ad hoc network is defined as the procedure of identifying the user or host that conducts inappropriate, incorrect, or anomalous activities that threaten the connectivity or reliability of the network or the authenticity of the data traffic flowing through it. Intruder identification is, thus, triggered when the ad hoc network is aware of an attack so as to trace back to the source of the attack. The identification of an intruder should be followed by an isolation procedure that prevents that node to communicate with any other node in the network. Intruders may misbehave maliciously either regarding lower or higher communication layers and can thus be detected either by lower layer schemes (e.g., secure routing protocols) or application layer mechanisms.
In the framework of the FP7-AWISSENET project [1], we have designed and validated a security tool box that efficiently defends against an important subset of the identified attacks. In the paper, we present 2 main innovations, which work cooperatively to respond to attacks in the wireless network: a lightweight solution for accurate localization information based on range-free techniques (for radio access networks where only the RSSI information is available), and an innovative trust-aware routing approach called Ambient Trust Secure Routing (ATSR) protocol which is based on the geographical routing principle and incorporates a distributed trust model to defend against routing attacks. Accurate localization information is necessary both for application layer Intrusion Detection Systems (to identify/locate the intruders) and for secure routing since the proposed location-based routing requires trustable localization information. It is worth pointing out that a geographical routing approach has been adopted to efficiently cope with the large network dimensions of current and emerging WSNs.
The rest of the paper is organised as follows: Section 2 is presenting the general architecture of the wireless networks structure we used for our research and where we tested our solutions. Section 3 is devoted to the accurate localization techniques and algorithms description for range-free techniques, and for robust range-based positioning. In Section 4 we describe the geographical secure routing protocol. In Section 5 we evaluate the algorithms and protocols developed for the wireless networks described in Section 2 based on results from simulation but also experimental work on our real-life test-bed. We end the paper with the conclusions, acknowledgement and references.
2. Security Attacks Tackled and GeneralFramework
A great variety of attacks has been described in the literature on security on ad hoc and wireless sensor networks [2] targeting the different networking operations. The long list of routing attacks [3] includes both easily implementable attacks and more sophisticated attacks. Black/grey-hole attacks (where a malicious node drops all or part of the received traffic) and modification attacks (where a malicious node modifies all or part of the forwarded messages so that the included data are no longer valid) are quite common. On the other hand, a node may falsify the state machine of the routing protocol by replaying stale routing information (replaying attack) or by advertising high quality links to the destination to attract the traffic and then forward it to a colluding adversary node. The first attack category can be efficiently mitigated by implementing a trust management system: each node monitors the behaviour of its neighbours before cooperating with it. The second category can be detected by intrusion detection systems (IDSs) which can be implemented on a subset of the network nodes since it is associated with higher processing and energy requirements. It is stressed that Intrusion Detection Systems are capable of detecting attacks addressing all networking protocols (not only routing) depending on the implemented rules.
The implementation of localization techniques assists in the identification of intruders by intrusion detection systems that mainly target the mitigation of more sophisticated and aggressive attacks addressing the communications protocol state machine. Most intruder identification and isolation schemes which are based on monitoring the network traffic and are lacking localization tools are only effective against a limited subset of attacks like denial of service. On the contrary, the detection of more aggressive attacks like the case of the black-hole intruder (which is trying to deceive the network operation by advertising that it has a fake shortest route to the destination node) or of a wormhole attack (where two malicious nodes create a tunnel to divert network traffic through a private link) requires the implementation of localization tools. In such cases, the possibility of getting information about the position of the network nodes allows a monitoring system to detect inconsistencies between the logical topology of the network and the physical situation of the nodes and then triggers the proper networking actions.
Coming to the routing operation, in our attempt to design a secure routing protocol suitable for large WSNs to meet the market trends for high WSN penetrations, we have opted for a location-based routing protocol. In geographical (i.e., location-based) routing, each node sends its data packet to the neighbour that is closest to the destination for further forwarding. Location-based routing relies on the assumption that each node announces its location in the so-called Beacon message. This requires the existence of GPS equipment on every node, which is a rather costly solution, or the implementation of localization techniques. However, the fact that each node announces its coordinates allows for Sybil attacks: a malicious node may announce a false location (possibly close to the data sink) to attract the traffic and then drop it or process it. The only way to overcome this drawback of geographical routing is to design and implement localization techniques which allow the network nodes to calculate the position of their neighbours and compare it with the one announced in the messages, so that malicious nodes are excluded from any network cooperation.
The proposed secure routing protocol incorporates a distributed trust model which is capable of defending black and grey-hole attacks, modification attacks, as well as attacks targeting the trust model itself (e.g., bad-mouthing attack) based on both direct and indirect trust information as will be detailed in Section 4. It additionally takes into account the remaining energy level of each neighbour so as to perform load balancing and better manage the overall energy resources.
3. Robust Localization for Geographic Routing
3.1. Introduction
Localization techniques for WSNs can be broadly classified into two main categories: range-based and range-free. Range-based approaches assume the availability of accurate measurements directly related to the distances and/or the relative angles between pairs of network nodes. On the other hand, range-free methods only use parameters readily available at the PHY layer level that are only loosely related to the position of the node.
Although there are different magnitudes that can be related to the distance between two nodes that establish a radio link, two of them are especially useful in WSNs: received signal strength (RSS) and signal time-of-arrival (TOA). However, while RSS-related measurements are easy to obtain in standard off-the-shelf IEEE 802.15.4 devices, attaining values of TOA require, either attaching to them some special purpose hardware (such as, ultrasonic transducers) or resorting to different radio interfaces (such as, those described in the IEEE 802.15.4a standard) that would make new devices incompatible at the PHY level with legacy ones. We will, thus, concentrate our attention in techniques that use RSS measurements as the base to achieve localization, either using range-based or range-free approaches.
From the point of view of positioning, two network topologies can be defined: single-hop localization, when all the nodes to be located can independently obtain their locations [4, 5], and multihop or cooperative localization, when unlocated nodes, have do not enough position references and so they have to exchange information between them and consider the localization of the whole network as a global optimization task [6].
Among the range-free approaches found in the literature, some of them try to achieve localization based on simple variables such as, connectivity [7] or hop-count [8], while others use more informative parameters related to signal angle-of-arrival (AOA) [9] or received power [10, 11]. Most of the latter range-free approaches use the so-called received signal strength indicator (RSSI), which is a coarsely quantized value of RSS that can be retrieved from the PHY in most commercial sensor nodes.
We want to remark here that, although there are a number of proposed techniques for range-free techniques, unfortunately only a few of them have been reportedly implemented on real devices and have shown satisfactory performance in realistic environments. This fact makes almost impossible to establish a fair comparison between different approaches. We also miss in the related literature an assessment of both range-based and range-free approaches under a common simulation framework.
In this paper we will consider only single-hop localization techniques. So, to perform the localization process, we will assume that an unknown-position node (UN) is always in the neighbourhood of a sufficient number of anchor nodes (AN) whose positions are known and act as location references. In the sequel we will use the following notation.
-
(i)
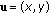 is the position in the plane of the UN.
is the position in the plane of the UN. -
(ii)
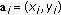 is the position of the i th AN, where
is the position of the i th AN, where  .
. -
(iii)
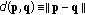 is the Euclidean distance between two arbitrary network nodes at positions p and q.
is the Euclidean distance between two arbitrary network nodes at positions p and q. -
(iv)
 is the RSS in dBm measured at the receiver of node q for a signal transmitted by node p.
is the RSS in dBm measured at the receiver of node q for a signal transmitted by node p.
3.2. Range-Based Positioning
In range-based localization, we assume that there exists a measurement equation, derived from a radio propagation model, which relates distances and measured RSS values, such as, the log-distance path loss model [12]:

where  is the mean received power (in dBm) at a reference distance
is the mean received power (in dBm) at a reference distance  (typically 1 m),
(typically 1 m),  is the path-loss exponent (which depends on the environment), and
is the path-loss exponent (which depends on the environment), and  is the measurement error (represented as a zero-mean Gaussian random variable). Therefore, the additive error in logarithmic scale (dBs) affects distance measurements as a multiplicative random variable (log-normal shadowing).
is the measurement error (represented as a zero-mean Gaussian random variable). Therefore, the additive error in logarithmic scale (dBs) affects distance measurements as a multiplicative random variable (log-normal shadowing).
Now, given N ANs located at known points  in the neighbourhood of the UN
in the neighbourhood of the UN  , which can collect independent RSS measurements
, which can collect independent RSS measurements  for packets sent by the ANs, the maximum likelihood estimation (MLE) of the node position can be obtained from the model (1) as
for packets sent by the ANs, the maximum likelihood estimation (MLE) of the node position can be obtained from the model (1) as

where

Finding the global solution of (2) is a difficult nonlinear optimization problem because of the existence of local minima, so that we will try to find simpler alternatives. For instance, using (1) we can obtain an estimation of the distance between nodes  and
and  as
as

so that we can establish the following overdetermined set of nonlinear equations:

where  are defined in (3). A suboptimal solution of (5) can be obtained if we square and change signs, and then define the new auxiliary variables
are defined in (3). A suboptimal solution of (5) can be obtained if we square and change signs, and then define the new auxiliary variables

because the resulting system of equations

is linear in the unknowns x, y, and  , and thus can be rewritten in vector-matrix form as
, and thus can be rewritten in vector-matrix form as

where  and
and

Now, the least squares (LS) solution to the overdetermined linear system (8) is given as

which gives the estimated position  of the node as the first and second components of vector
of the node as the first and second components of vector  .
.
Notice that the value of  depends on parameters such as, the transmitted power, antenna gain and orientation, and attenuations owing to different elements in the signal path, which are quite difficult to precisely control. So, unless we have a mechanism to perform periodic calibrations of the RSS measurements, and we ensure that the experimental conditions remain stable in time, we will often have to deal with situations in which distances can only be estimated from RSS up to an unknown multiplicative constant
depends on parameters such as, the transmitted power, antenna gain and orientation, and attenuations owing to different elements in the signal path, which are quite difficult to precisely control. So, unless we have a mechanism to perform periodic calibrations of the RSS measurements, and we ensure that the experimental conditions remain stable in time, we will often have to deal with situations in which distances can only be estimated from RSS up to an unknown multiplicative constant

where the constant  should also be estimated from the measurements as a "nuisance" parameter. In this case, the localization protocol should be reversed: anchor nodes obtain RSS values
should also be estimated from the measurements as a "nuisance" parameter. In this case, the localization protocol should be reversed: anchor nodes obtain RSS values  for packets sent by the UN, and then send those measurements back to the node (or to a central processor) to estimate the UN position. So, now the system (8) can be reformulated with an extended vector
for packets sent by the UN, and then send those measurements back to the node (or to a central processor) to estimate the UN position. So, now the system (8) can be reformulated with an extended vector  and
and

Notice that a data-fusion process is implicit in (10), because all the available measurements are combined to achieve the localization of the node.
3.3. Range-Free Techniques
Range-free methods do not rely on the existence of a measurement model. Instead, many of these methods assume a simple monotonicity constraint: for an arbitrary set of three nodes  , the following condition apply:
, the following condition apply:

Notice that, because the transmitted power is assumed unknown, RSSI measurements are not expected to be symmetric, that is, ρ(p,q)≠ ρ(q,p). One of the simplest approaches to the solution of the problem of localizing a node based on the restriction (13) is given by the so-called ROCRSSI algorithm [11], which we briefly outline below.
If we assume the unlocated node u is surrounded by N anchors then, for every anchor a
i
 in the neighbourhood of
in the neighbourhood of  , we will assume that the following RSSI values are available:
, we will assume that the following RSSI values are available:
One anchor to node RSSI:  ,
,
N−1 anchor to anchor RSSIs:  .
.
Now, if we sort the anchor to anchor RSSI measurements as

and we compare the anchor to node RSSI with the sorted anchor to anchor RSSIs so that, for instance,

where  , then, the monotonicity constraint (13) implies that the UN lies on a ring centred around a
i
, with inner radius
, then, the monotonicity constraint (13) implies that the UN lies on a ring centred around a
i
, with inner radius  and outer radius
and outer radius  :
:

The special cases  and
and  should be treated separately: the first one implies that u belongs to the disk
should be treated separately: the first one implies that u belongs to the disk  , while in the second case we can either assume that the node lies in the exterior of a circle
, while in the second case we can either assume that the node lies in the exterior of a circle  or, as suggested in [11], simply discard the measurement to avoid unbounded regions. After repeating the following procedure for all the anchors, the UN is found to be located on the intersection of the rings defined by (16). Then, the final position of the UN is estimated as the centroid of such intersection region.
or, as suggested in [11], simply discard the measurement to avoid unbounded regions. After repeating the following procedure for all the anchors, the UN is found to be located on the intersection of the rings defined by (16). Then, the final position of the UN is estimated as the centroid of such intersection region.
With actual measurements, the condition (13) does not hold for every pair of nodes because the radio channel is usually anisotropic, so that not all the rings (16) have a common intersection. The compromise solution in such cases is to assume the UN to be in the region of the plane where most of the rings intersect. This is equivalent to assume that every anchor "votes" for a given ring as a candidate to hold the UN, and the region of the plane that gets the higher number of votes is finally elected. Such voting strategy has the added benefit of providing a good degree of robustness to some kinds of attacks to the localization process, as we will see in Section 3.4. A simple, yet computationally costly, implementation of the voting approach is given by the grid-scan algorithm [10].
Another important fact to be taken into account is that shadowing effects make the variance of RSS measurements to increase with distance [6]. In our context, it means that the RSSI values obtained from ANs that are far away from the node are suffering from large errors and can be excluded from the localization process. For this reason, we propose a modification of the original ROCRSSI technique which we call "best anchors selection" (BAS)
The BAS method first fixes a maximum number or rings for each AN that can be considered as "reliable", in the sense that RSSI measurements at nodes placed within those rings have relatively low variance. Such number could be obtained, for example, by counting the number of neighbouring anchors that are within a given maximum distance of each AN. For simplicity, let us assume that this number of reliable rings is  , the same for all the ANs. Then, for every anchor a
i
, the same for all the ANs. Then, for every anchor a
i
 in the neighbourhood of
in the neighbourhood of  , and assuming the RSSI measurements obtained from that anchor are ordered as in (14), we can determine a "ring number" r
i
associated to the UN as follows:
, and assuming the RSSI measurements obtained from that anchor are ordered as in (14), we can determine a "ring number" r
i
associated to the UN as follows:
If  , then
, then  ;
;
else, if  for
for  , then
, then  ;
;
else,  .
.
Once the ring numbers  are obtained, we form the set S
K
of ANs for which the condition
are obtained, we form the set S
K
of ANs for which the condition  holds.
holds.

Now, we will use ROCRSSI to obtain an estimation of the position of the UN, provided that at least we can obtain the intersection of two rings.
If  , then apply ROCRSSI algorithm using only ANs in S
K
.
, then apply ROCRSSI algorithm using only ANs in S
K
.
else, apply ROCRSSI using the original set of ANs  .
.
The advantages of the BAS approach over the original ROCRSSI are twofold: first, we get a reduction in localization error because of the exclusion of unreliable measurements, and second, computational complexity is also reduced because we only need to apply the grid-scan algorithm to a subset of the ANs.
3.4. Resilience to Attacks
As it was previously stated, localization of a given node requires the existence of a sufficient number of reference (anchor) nodes whose positions are known; usually, these ANs report their coordinates to other nodes by means of some kind of beacon packets. However, in a hostile environment, some ANs could be compromised by an attacker so that, for instance, they are forced to transmit incorrect beaconing references or to manipulate measurements in order to introduce biases in the computations of their relative distances to other nodes. In such cases, the localization process by means of conventional approaches (for instance, the LS algorithm) gives incorrect results, so that every node within the radio range of a malicious AN is wrongly positioned.
For range-based approaches, a possible solution to mitigate the effects of such kind of attacks is to resort to robust estimation techniques, which are resilient to the effects of outliers [13–16]. However, most of these algorithms are quite complex, and so require too many storage and computational resources to be implemented on most low-cost and low-power devices.
On the other hand, most range-free localization techniques are intrinsically robust to attacks as long as there are more well-behaved anchors than malicious in the vicinity of the UN and provided that these latter nodes do not collude together to defeat the whole localization procedure. This is because positioning is usually based on a "majority decision" taken after considering location information gathered from neighbour nodes that give "scores" to different feasible positions for the node. Additionally, range-free positioning techniques can also be extended to actively detect and counteract fake beacons [17] and to also neutralize more advanced threats to WSNs such as the wormhole and Sybil attacks [9].
4. Trust-Aware Routing
4.1. Introduction
To defend against routing attacks, the realisation of a trust management system has been extensively pursued in the literature. Trust is defined as the confidence of a node  that node
that node  will perform as expected, that is, on the node's
will perform as expected, that is, on the node's  cooperation for the accomplishment of a specific action.
cooperation for the accomplishment of a specific action.
The methods for obtaining trust information and defining each node's trustworthiness are referred to as trust models, and can be classified according to a number of design options [18]. Trust is evaluated upon a number of event types that can be recorded and analysed. Each event type (corresponding to a trust metric) allows the assessment of a specific node behaviour aspect and consequently the detection of a specific attack type. For example, each node  can assess the forwarding behaviour of its neighbour
can assess the forwarding behaviour of its neighbour  by comparing the successfully forwarded packets to the total number of packets that
by comparing the successfully forwarded packets to the total number of packets that  sent to
sent to  . A systematic failure reveals a malicious node, denying its routing tasks. Analysing the collected measurements, either a trust value can be derived (in many cases a ratio of successful over failed events) or distinct trust levels can be distinguished. To improve the reliability of the trust information and efficiently support mobility, reputation exchange schemes have been proposed (e.g., [19]). These schemes however increase the resource consumption while attacks targeting the reputation protocol itself have already been identified: for example, spreading wrong information or behaving differently towards different neighbors, the reputation exchange protocol can be deceived [20].
. A systematic failure reveals a malicious node, denying its routing tasks. Analysing the collected measurements, either a trust value can be derived (in many cases a ratio of successful over failed events) or distinct trust levels can be distinguished. To improve the reliability of the trust information and efficiently support mobility, reputation exchange schemes have been proposed (e.g., [19]). These schemes however increase the resource consumption while attacks targeting the reputation protocol itself have already been identified: for example, spreading wrong information or behaving differently towards different neighbors, the reputation exchange protocol can be deceived [20].
Focusing on location-based routing protocols, interesting trust-based enhancements have been proposed in [21–23]. In all these approaches, a trust management system based on direct evidence is implemented while a reputation exchange mechanism has been introduced in [22] as an optional choice (without any rigorous specification of the relevant protocol). In this work, multipath routing is suggested, sacrificing node and network resources for the transmission of multiple copies of each packet, to increase the probability of reaching the destination. In [23], an interesting approach for extending the network lifetime is proposed, which however consumes significant node resources, since it requires the derivation of the coverage area of each neighbor based on Beacon messages and on exchanging the neighbor lists. In the same work, the packets travel through nodes exceeding a trust threshold. This choice introduces the need for selecting an application-dependent trust threshold and can result in limited connectivity in case nodes fulfilling this condition do not exist. Finally, the authors of [21] have investigated and proposed measures for detecting and defending against flooding attacks at the cost of implementing a rate-shaper on each sensor node which is considered a rather costly solution.
In the sequence we will present an innovative trust-aware routing approach called Ambient Trust Secure Routing (ATSR) protocol which is based on the geographical routing principle and incorporates a distributed trust model which is capable of detecting forwarding, integrity, and bad-mouthing attacks while it additionally extends the network lifetime by considering the neighbours remaining energy during routing decision making.
4.2. The Distributed Trust Model
For the detection of routing attacks in a large WSN, we have designed a fully distributed trust model which mandates that each node combines direct trust information and indirect trust information to define the trustworthiness of all its one-hop distance neighbours. We first present the collection of trust measurements and how the direct trust values are reached and then we proceed to the indirect trust information (reputation) exchange procedure.
One of the most important issues during the trust model design is to define the set of behaviour aspects/metrics against which each node is evaluated. On each sensor node, a trust repository is used to store trust information per neighbour and trust metric. The monitored trust metrics include the following.
-
(i)
Packet Forwarding: To detect nodes that deny to or selectively forward packets, each time a source node transmits a packet for forwarding, it enters the promiscuous mode and overhears the wireless medium to check whether the packet was actually forwarded by the selected neighbour.
-
(ii)
Network Layer Acknowledgements (ACK): To detect nodes that collude with other adversaries (which possibly drop packets) disrupting the network operation, we suggest that each source node waits for a network-layer ACK to check whether its message has successfully reached a higher-layer node (i.e., the base station).
-
(iii)
Packet Precision: Each time a source node transmits a packet for forwarding and then overhears the wireless medium to ensure that the packet was forwarded, it additionally processes it to check the packet's integrity, that is, that no unexpected modification has occurred.
-
(iv)
Reputation Response: To check the sincere execution of the reputation protocol, each node calculates for each neighbour the number of reputation responses received divided by the number of times this neighbour was asked for reputation information. This way, nodes that do not cooperate in the execution of the reputation protocol are assigned lower trust values.
-
(v)
Reputation Validation: To protect against wrong reputations being spread around (bad-mouthing attacks), each time a node
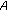 receives a reputation response message from node
receives a reputation response message from node  regarding node
regarding node 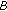 , if node
, if node 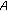 is confident about the direct trust value it has calculated for node
is confident about the direct trust value it has calculated for node 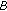 , it compares the received value (i.e., the reputation provided from node
, it compares the received value (i.e., the reputation provided from node  ) with its own direct trust on node
) with its own direct trust on node 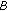 . If the difference exceeds a predefined threshold, then the provided reputation is considered as "wrong reputation"; otherwise, it is a "correct reputation" and node
. If the difference exceeds a predefined threshold, then the provided reputation is considered as "wrong reputation"; otherwise, it is a "correct reputation" and node  is scored accordingly.
is scored accordingly. -
(vi)
Remaining Energy: Systematically selecting a highly trusted node for forwarding the packets may lead to the exhaustion of its energy. Additionally, fixed traffic flows are vulnerable to traffic analysis attacks. In this view, we have enriched our trust model with energy information. In our novel routing protocol, the basic routing message indicating the node availability and position (the Beacon message defined in all location-based routing protocols) is extended to include the "remaining energy" field of the source node based on which the energy-knowledge is built.
Coming to the quantification of trust, for each trust metric m associated with successful/failed interactions, two counters (2-byte wide) are used to store the number of successful/failed interactions, respectively. Based on them, each node i calculates the trust value of each metric  regarding node j (denoted as
regarding node j (denoted as  ) by dividing the number of successfully completed interactions with the number of total (attempted) interactions of type m between i and j. The six trust values are then combined in a weighted sum to produce the total Direct Trust value:
) by dividing the number of successfully completed interactions with the number of total (attempted) interactions of type m between i and j. The six trust values are then combined in a weighted sum to produce the total Direct Trust value:

where  stands for the weight of trust metric m. All weights sum up to 1 so that the total direct trust value ranges from 0 to 1.
stands for the weight of trust metric m. All weights sum up to 1 so that the total direct trust value ranges from 0 to 1.
The exchange of indirect trust information is important mainly for newly initialized nodes or recently arrived nodes (in case of mobility). To trigger the indirect trust exchange process, each node periodically issues a reputation request message. A crucial design issue affecting the produced network load and the consumed node resources is to decide which nodes should be queried for indirect trust evidence. In ATSR, we opted for requesting reputation information from a limited number (four) of neighbors, as a first action towards limiting the introduced overhead. In more detail, the source node randomly selects one node per quadrant so that indirect trust information for all its one-hop neighbours is gathered.
To limit the amount of communicated data (overhead) and economize resources, since the reputation exchange is mainly implemented to assist nodes with no or limited (direct) trust knowledge to reach a more reliable conclusion for the trustworthiness of nodes they are interested in, a requested node provides its opinion for its neighbors only if it is confident about the direct trust value it has calculated. This is decided upon the so-called confidence factor  of node i considering node j, which is calculated based on the following equation:
of node i considering node j, which is calculated based on the following equation:

where noi stands for the Number Of Interactions (noi) between node i and node j. So, following this novel scheme, the requested node scans its trust table and includes in its reputation response message, the direct trust value it has calculated for all neighbors corresponding to confidence factor exceeding a predefined threshold (e.g., above 0.9).
Once node i that transmitted the reputation request message receives the reputation responses, node i calculates the Indirect Trust value for node j,  , by summing up the received values adopting the relevant direct trust as weight factors, so that a reputation provided by a highly trusted node counts more. Finally, the Total Trust (TT) value for a neighbor j is produced combining direct and indirect trust values in the following formula:
, by summing up the received values adopting the relevant direct trust as weight factors, so that a reputation provided by a highly trusted node counts more. Finally, the Total Trust (TT) value for a neighbor j is produced combining direct and indirect trust values in the following formula:

where  is the confidence factor described previously. It is obvious that as the number of interactions (and thus the confidence factor, C) increases, the direct trust value becomes more significant than the reputation information.
is the confidence factor described previously. It is obvious that as the number of interactions (and thus the confidence factor, C) increases, the direct trust value becomes more significant than the reputation information.
4.3. The ATSR Routing Cost Function
The combination of a fully distributed trust management scheme with a geographical routing approach renders the proposed routing solution suitable for large-scale WSNs, since scalability is a dominant feature of all location-based protocols, such as the Greedy Perimeter Stateless Routing-GPSR [24], which rely on local topology information only. Following this approach, each node is characterized by its coordinates and packets are forwarded to the neighbouring node which is the closest to the destination (based on geographical information). Nodes only need to announce their coordinates to their one hop neighbours, through the so-called Beacon messages, which are not further propagated, hence saving node and network resource. Furthermore, the routing table maintained in each node includes only one hop neighbors and its size depends only on the network density (number of nodes in the neighborhood) and not on the overall WSN dimensions.
The objective of our protocol is to choose for forwarding the node that optimizes the following three factors: trust, proximity to the destination, and remaining energy to complete its forwarding task. As regards the distance of each neighbour to the base station, we define the distance metric which is quantified as follows:

where  is the Euclidean distance of neighbour j to the base station and
is the Euclidean distance of neighbour j to the base station and  stands for the sum of the distance of all its
stands for the sum of the distance of all its  neighbors to the base station, which can be calculated based on their coordinates and the coordinates of the base station. Following (21), the shortest distance to the destination maximizes the value.
neighbors to the base station, which can be calculated based on their coordinates and the coordinates of the base station. Following (21), the shortest distance to the destination maximizes the value.
The distance metric  and the total trust value (which has already incorporated the remaining energy value) are summed up in a weighted manner and are used to calculate the Routing Function (
and the total trust value (which has already incorporated the remaining energy value) are summed up in a weighted manner and are used to calculate the Routing Function ( ):
):

where  and
and  represent the significance of distance and trust criterion, respectively, with
represent the significance of distance and trust criterion, respectively, with  +
+  =1. Based on this equation, a routing value for each neighbor is calculated and the node that corresponds to the maximum value is selected for forwarding the packet as it represents a good candidate satisfying an integrated set of requirements: trust, energy, and proximity to the destination.
=1. Based on this equation, a routing value for each neighbor is calculated and the node that corresponds to the maximum value is selected for forwarding the packet as it represents a good candidate satisfying an integrated set of requirements: trust, energy, and proximity to the destination.
4.4. Resilience to Attacks
The proposed trust-aware location-based routing scheme detects and efficiently defends against routing attacks. Due to its location-based operation, nodes cannot advertise "good" links to the destination and thus attract traffic. It is only the location that counts and the trustworthiness of this information is ensured by the implementation of the localization techniques presented in Section 3. Coming to traffic dropping, this selfish behaviour is detected based on the collections of measurements regarding the forwarding behaviour of each neighbour. It is worth stressing that lacking this tool, any location-based routing protocol suffers 100% packet loss for a session, if just one selfish node exists in the path to the destination dropping either part or all the received traffic. Our algorithm, based on the incorporated trust model, detects the selfish nodes and finds alternative paths to the destination as is shown in Section 5. In more detail, the higher the weight factor of forwarding is, the sooner the selfish node is detected. Packet integrity is mainly ensured by encryption techniques, which however require a significant amount of node resources. Our approach allows for integrity attack detections at low implementation cost (as will be shown in Section 5). Finally, the already known attacks concerning the indirect trust exchange are mitigated by monitoring and scoring the neighbours behaviour regarding this operation. It is worth stressing that the reputation exchange protocol consumes node and network resources and thus, the support of mobility can only justify its implementation in state-of-the-art sensor nodes.
The detection of flooding and link spoofing attacks requires the implementation of more sophisticated schemes (e.g., rate controllers and protocol state-machine monitoring) which are not feasible in state-of-the-art nodes. Thus, we assume that intrusion detection systems implemented on a subset of network nodes undertake the responsibility of defending against these attacks. Traffic analysis attacks can be mitigated by realising load balancing techniques. As a first action, taking into account the neighbours remaining energy leads to a certain level of load balancing. In general, the trust-aware routing protocol acts as a first line of defence against routing attacks leaving the second line to a more complicated IDS block.
5. Evaluation Results and Testing
5.1. Testing Environment
To evaluate and validate the designed mechanisms, the localization and trusted routing algorithms were first modelled and assessed using simulation tools and then they were implemented and integrated in the AWISSENET test-bed. The simulation models provided the opportunity of fine-tuning the algorithms and also of evaluating the performance under extreme conditions that rarely happen in real test-beds, as for example, the performance for hundreds or even thousands of nodes. The AWISSENET test-bed includes thirty IRIS sensor nodes [25] running TinyOS v2.1. Part of the test bed set up is shown in Figure 1. An additional test-bed involving 100 nodes is currently undergoing tests. No differences have been observed so far.
5.2. Results
In the sequence, we first present results regarding the performance of the two presented blocks (secure routing and localization module) as different performance metrics apply to each of them and then we discuss the implementation cost which is considered an important evaluation parameter.
5.2.1. Results of Localization
We have conducted some simulations so as to compare both range-based and range-free techniques in terms of localization accuracy and robustness and also to show the computational savings that the BAS approach can provide. The simulated WSN is composed of 50 ANs plus one UN randomly deployed in a square room of 20 m  20 m. Some of the anchors can be "malicious" and report their positions to be 40 m away from their actual locations (although they are not able to forge measurements). For RSS values, we have assumed the log-normal path loss model (1) with path-loss exponent
20 m. Some of the anchors can be "malicious" and report their positions to be 40 m away from their actual locations (although they are not able to forge measurements). For RSS values, we have assumed the log-normal path loss model (1) with path-loss exponent  and standard deviation
and standard deviation  dB as stated in [5]. In range-free methods, we have used a square grid of 50
dB as stated in [5]. In range-free methods, we have used a square grid of 50  50 elements, which implies a spatial resolution of 40 cm in the proposed environment. For the BAS method, we have fixed a number of reliable rings per anchor K = 4.
50 elements, which implies a spatial resolution of 40 cm in the proposed environment. For the BAS method, we have fixed a number of reliable rings per anchor K = 4.
The quality of the position estimation is measured through statistics of the "location error", defined as

where (x,y) and  are the actual and estimated positions, respectively. The location error is characterized by its cumulative distribution function (CDF):
are the actual and estimated positions, respectively. The location error is characterized by its cumulative distribution function (CDF): 
Some results are represented in Figure 2, where we can see that the linearized LS approaches give higher errors when compared with range-free techniques in this environment and also are much more sensitive to location attacks. On the other hand, the MLE method, not surprisingly, gives the overall best performance, but the optimization (2) requires a starting point quite near the optimal solution so as to avoid getting trapped at a local minimum.
Another set of simulations were carried out to show the computational savings of the BAS approach over the conventional ROCRSSI. Notice that, by far, the most computationally demanding step in ROCRSSI is the grid-scan algorithm, whose complexity is proportional to both the size of the grid and the number of rings. In conventional ROCRSSI, the number of processed rings is always equal to the number of anchors in the neighbourhood of the UN, whereas in ROCRSSI-BAS only a subset of the anchors (those considered as "most reliable") are processed, so that a significant reduction in the number of computations is expected.
Figure 3 shows the mean number of processed rings for the same experimental conditions as in the previous simulations and varying the number of anchors. The most remarkable thing we can observe is that the complexity of ROCRSSI-BAS is almost independent of the number of anchors, as opposed to conventional ROCRSSI that always requires a number of computations proportional to N.
We have also experimented range-free localization with real devices. A set of seven IRIS motes [25] were situated at fixed positions inside a room of approximately 9 m  9 m, so that they acted as anchors. Another IRIS node was the UN, and collected RSSI values from the anchors to estimate its own location using ROCRSSI-BAS. The actual positions in centimetres of the anchors (referenced to a corner of the room) were
9 m, so that they acted as anchors. Another IRIS node was the UN, and collected RSSI values from the anchors to estimate its own location using ROCRSSI-BAS. The actual positions in centimetres of the anchors (referenced to a corner of the room) were  , (520,600), (600,600), (680,560), (640,440), (520,440),
, (520,600), (600,600), (680,560), (640,440), (520,440),  , while the UN was located in 46 different positions among the anchors. Figure 4 shows the disposition of the nodes.
, while the UN was located in 46 different positions among the anchors. Figure 4 shows the disposition of the nodes.
The resulting root mean square error (RMSE) of the position estimation for all the positions is 47 cm, which is about one half of the minimum separation between anchors.
5.2.2. Results of Secure Routing
The performance of the proposed ATSR protocol was first assessed through exhaustive simulations using the JSIM open simulation platform. Simulation tests were run for two topologies consisting of 100 and 1000 nodes, respectively, organised on a symmetric grid. To debug and monitor the behaviour of the protocol that was implemented in the IRIS nodes, we developed a custom software tool, based on the Listen library of TinyOS. This tool is capable of showing the remaining energy, node coordinates and ID, as well as the temperature and lighting indications, the types of messages, the routing path (number of hops and node id), the neighboring nodes, and the packet loss indication. The results obtained through this tool were very close to the results obtained from the simulation procedure. Minor deviations were attributed to the message collisions that occurred in the real test-bed environment which were not taken into account by the routing protocol in the simulations.
To evaluate the efficiency of the proposed ATSR protocol in detecting malicious nodes issuing grey-hole attacks, we ran a scenario set for 100 nodes in the network with malicious nodes randomly dropping the received traffic. The scenarios were tested for three different values of the weight vector; namely, ATSR-1 represents the configuration  = 0.3,
= 0.3, = 0.1,
= 0.1, = 0.2,
= 0.2, = 0.2,
= 0.2, = 0.2, and ATSR-2 mandates
= 0.2, and ATSR-2 mandates  = 0.25,
= 0.25, = 0,
= 0, = 0.25,
= 0.25, = 0.25,
= 0.25, = 0.25. The results in terms of packet loss are shown in Figure 5(a), where it is shown that even in the presence of 45% of malicious nodes in the network, ATSR succeeds in detecting the malicious nodes and in defining alternative paths towards the destination with the packet loss remaining below 5%. (Original GPSR which does not consider the node trustworthiness suffers of 74% packet loss for 45% malicious nodes in the network.) The same scenarios were also run for malicious nodes issuing black-hole attacks and the results were even better since black-hole nodes are more easily detected because their forwarding trustworthiness drops very fast. The performance difference among the two scenarios (ATSR-1 and ATSR-2) is rather insignificant. Comparing the
= 0.25. The results in terms of packet loss are shown in Figure 5(a), where it is shown that even in the presence of 45% of malicious nodes in the network, ATSR succeeds in detecting the malicious nodes and in defining alternative paths towards the destination with the packet loss remaining below 5%. (Original GPSR which does not consider the node trustworthiness suffers of 74% packet loss for 45% malicious nodes in the network.) The same scenarios were also run for malicious nodes issuing black-hole attacks and the results were even better since black-hole nodes are more easily detected because their forwarding trustworthiness drops very fast. The performance difference among the two scenarios (ATSR-1 and ATSR-2) is rather insignificant. Comparing the  and
and  values, which mainly target the detection of the packet dropping behaviour, for ATSR-1 and 2, we observe that the reduction of
values, which mainly target the detection of the packet dropping behaviour, for ATSR-1 and 2, we observe that the reduction of  to zero, brings no performance deterioration because ATSR is operating on a hop-by-hop mode.
to zero, brings no performance deterioration because ATSR is operating on a hop-by-hop mode.
Malicious nodes that perform integrity attacks altering either the data messages and/or the control messages do not cause packet loss but affect the validity of the messages. As a result, to evaluate the performance of ATSR in avoiding nodes issuing integrity attacks, we measured the altered packets that travel in the network. In the scenarios tested on this purpose, malicious nodes modify the received and forwarded traffic. The results for different penetrations of the malicious nodes are shown in Figure 5(b) where we also include the number of attacks measured when the nodes implement the original GPSR routing protocol which does not take into account trust information. It is worth stressing that this figure presents the attacks for a fixed simulation time; in real-life, any non-trust-aware routing protocol would allow the cooperation with malicious nodes and the number of altered messages would continuously increase. Instead, adopting ATSR, the number of attacks does not increase since the malicious nodes are detected and no further cooperation with them is attempted. In the same figure, we have included the number of attacks observed when malicious nodes act as grey-hole attackers. The grey-hole attacks measured are higher than the integrity attacks and this is due to the fact that when a node constantly issues integrity attacks, its trust-worthiness drops after only a few interactions, while for grey-hole attackers which randomly drop packets, it takes few more interactions to reveal the adversary nodes.
The proposed ATSR protocol efficiently detects and avoids cooperating with nodes providing wrong trust information during the executing of the reputation exchange protocol. To demonstrate this part of the functionality, we present the relevant results from the AWISSENET test-bed. The topology considered in this test is shown in Figure 6. Node 1 transmits packets towards the base station (node 0). The path initially calculated and followed traverses node 9. However, node 9 is programmed to act maliciously providing wrong trust information (i.e., issuing bad-mouthing attack). Based on the developed tool, we verified that once node 9 is identified as a bad-mouth attacker from node 4, then node 4 black-lists node 9 and never uses it for forwarding messages. Due to the random nature of neighbour selection for asking for reputation information ("round-robin" manner), the time required for the detection of the malicious node depends on the frequency of reputation request message generation. The important conclusion is that once a node is recognized acting maliciously, then it is excluded from future interactions. In the presented TOSSIM run, node 9 was revealed after 53 data messages exchange and from this point on, node 4 selected node 8 as the next-hop neighbour until other reasons (e.g., remaining energy) caused path alteration.
5.2.3. Final Results
The presented localization mechanisms and trusted routing protocol have been successfully integrated in IRIS motes and their proper operation has been extensively verified. The node resources required for the implementation of the localization and trusted routing modules are included in Tables 2 and 1.
Coming to the ATSR module, this was successfully compiled and required 35 Kbytes of ROM and about 3.5 Kbytes of RAM. Table 1 tabulates the resources required for the complete ATSR protocol implementation and also includes the resources required for the trust model alone. It is evident that the trust model implementation consumes resources which however represent a small percentage of the overall trust routing block, proving that the security of the routing procedure can be improved with limited resources.
When combining the localization and trusted routing modules, the resources required for the implementation depend on the network density (which directly affects the number of one-hop neighbours of each node), the dimensions of the grid for the range-free localization algorithm (which affects the precision of the positions), and the maximum allowable size for the data in a packet (TOSH_DATA_LENGTH). Table 2 includes the results for different values of these parameters.
Considering the implementation feasibility one of the major evaluation parameters, within AWISSENET we have integrated the protocols presented in this paper with other modules enhancing security including a distributed Intrusion Detection and a secure service discovery block. Our goal is to shield the WSN against as many attacks as possible. In this respect, the presented algorithms combined provide defence against black-hole, sink-hole, any type of integrity (modification) attack, attacks targeting the trust model (bad-mouthing, conflicting behaviour) attack, and Sybil attack while leaving to the intrusion detection system the responsibility of detecting flooding and higher layers attacks. It is worth stressing that the efficient defence against Sybil attack through the implementation of localization techniques comes at a low cost and obsoletes the need for GPS equipment while at the same time assists the intrusion detection system in the identification and localization of the intruder.
6. Conclusions
In this paper, we described innovative lightweight localization techniques that allow for intrusion identification and isolation schemes and provide accurate location information. We presented the way this information is used by our routing protocol which additionally incorporates a distributed trust model to prevent several routing attacks to the network. Both techniques combined can offer a powerful solution to several attacks in resource wireless constrained networks such as, WSNs, which has been implemented in real wireless motes and evaluated and tested extensively providing promising results based on a reliable and a lower cost/less scare resources consuming solution for WSNs.
The scientific advances can be summarized in 2 areas: better and improved precision localization techniques and secure routing mechanisms.
Focusing on the localization, we implemented range-free RSSI-based localization techniques which provide a simple yet effective way to determine a node position without resorting to expensive equipment or radio interfaces incompatible with existing WSNs. They also do not require a previous calibration of the environment so as to directly correlate RSS measurements to distance values (as range-based or "fingerprinting" approaches do) and are robust to attacks to the localization process. On the other hand, one of their drawbacks is the complexity of the grid-scan algorithm necessary to estimate the position, which can be prohibitively high if the density of anchor nodes is high. For this reason, we have proposed a technique to discard anchors that provide unreliable positioning information so that both an improvement in the accuracy in the localization and a reduction in computational complexity are achieved. The resulting BAS method has been successfully implemented and tested on real devices with encouraging results.
Focusing on the secure routing, we proposed and tested an Ambient Trust Secure Routing (ATSR) protocol which is based on the geographical routing principle and incorporates a distributed trust model to defend against routing attacks which efficiently detects and avoids cooperating with nodes providing wrong trust information during the executing of the reputation exchange protocol, providing an efficient way to tackle several attacks.
The results have been demonstrated in the framework of the project AWISSENET.
References
AWISSENET project, http://www.awissenet.eu/home.aspx
Giruka VC, Singhal M, Royalty J, Varanasi S: Security in wireless sensor networks. Wireless Communications and Mobile Computing 2008, 8(1):1-24. 10.1002/wcm.422
Karlof C, Wagner D: Secure routing in wireless sensor networks: attacks and countermeasures. Ad Hoc Networks 2003, 1(2-3):293-315. 10.1016/S1570-8705(03)00008-8
Sayed AH, Tarighat A, Khajehnouri N: Network-based wireless location: challenges faced in developing techniques for accurate wireless location information. IEEE Signal Processing Magazine 2005, 22(4):24-40.
Patwari N, Hero AO III, Perkins M, Correal NS, O'Dea RJ: Relative location estimation in wireless sensor networks. IEEE Transactions on Signal Processing 2003, 51(8):2137-2148. 10.1109/TSP.2003.814469
Patwari N, Ash JN, Kyperountas S, Hero AO III, Moses RL, Correal NS: Locating the nodes: cooperative localization in wireless sensor networks. IEEE Signal Processing Magazine 2005, 22(4):54-69.
Bulusu N, Heidemann J, Estrin D: GPS-less low-cost outdoor localization for very small devices. IEEE Personal Communications 2000, 7(5):28-34. 10.1109/98.878533
Niculescu D, Nath B: DV based positioning in ad hoc networks. Telecommunication Systems 2003, 22(1–4):267-280.
Lazos L, Poovendran R: SeRLoc: secure range-independent localization for wireless sensor networks. Proceedings of the ACM Workshop on Wireless Security (WiSe '04), October 2004 21-30.
He T, Huang C, Blum BM, Stankovic JA, Abdelzaher T: Range-free localization schemes for large scale sensor networks. Proceedings of the 9th Annual International Conference on Mobile Computing and Networking (MobiCom '03), September 2003 81-95.
Liu C, Wu K, He T: Sensor localization with ring overlapping based on comparison of received signal strength indicator. Proceedings of the IEEE International Conference on Mobile Ad-Hoc and Sensor Systems, October 2004 516-518.
Rappaport TS: Wireless Communications, Principles and Practice. 2nd edition. Prentice-Hall, Upper Saddle River, NJ, USA; 2002.
Sun B, Osborne L, Xiao Y, Guizani S: Intrusion detection techniques in mobile ad hoc and wireless sensor networks. IEEE Wireless Communications 2007, 14(5):56-63.
Li Z, Trappe W, Zhang Y, Nath B: Robust statistical methods for securing wireless localization in sensor networks. Proceedings of the 4th International Symposium on Information Processing in Sensor Networks (IPSN '05), April 2005 91-98.
Liu D, Ning P, Du WK: Attack-resistant location estimation in sensor networks. Proceedings of the 4th International Symposium on Information Processing in Sensor Networks (IPSN '05), April 2005 99-106.
García-Otero M, Álvarez-García F, Casajús-Quirós FJ: Securing wireless sensor networks by using location information. Proceedings of the 16th International Conference on Systems, Signals and Image Processing (IWSSIP '09), June 2009
Wu K, Liu C, Pan J, Huang D: Robust range-free localization in wireless sensor networks. Mobile Networks and Applications 2007, 12(5-6):392-405. 10.1007/s11036-008-0041-9
Theodorakopoulos G, Baras JS: On trust models and trust evaluation metrics for ad hoc networks. IEEE Journal on Selected Areas in Communications 2006, 24(2):318-328.
Ganeriwal S, Balzano LK, Srivastava MB: Reputation-based framework for high integrity sensor networks. ACM Transactions on Sensor Networks 2008, 4(3):1-37.
Sun Y, Han Z, Ray Liu KJ: Defense of trust management vulnerabilities in distributed networks. IEEE Communications Magazine 2008, 25(2):112-119.
Pirzada AA, McDonald C: Trusted greedy perimeter stateless routing. Proceedings of the 15th IEEE International Conference on Networks (ICON '07), November 2007, Adelaide, Australia 206-211.
Kang KD, Liu K, Abu-Ghazaleh N: Securing geographic routing in wireless sensor networks. Proceedings of the 9th Annual NYS Cyber Security Conference: Symposium on Information Assurance, June 2006, Albany, NY, USA
Hung K-S, Lui K-S, Kwok Y-K: A trust-based geographical routing scheme in sensor networks. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '07), March 2007, Hong Kong 3125-3129.
Karp B, Kung HT: GPSR: greedy perimeter stateless routing for wireless networks. Proceedings of the Annual International Conference on Mobile Computing and Networking (MobiCom '00), August 2000, Boston, Mass, USA 243-254.
CROSSBOW technology, http://www.xbow.com
Acknowledgments
The work presented in this paper was partially supported by the EU-funded FP7 211998 AWISSENET project [1] athe ARTEMIS projects SMART (100032) and SIMPLE (100261), and the spanish national project AMURA (TEC2009-14219-C03-01).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
García-Otero, M., Zahariadis, T., Álvarez, F. et al. Secure Geographic Routing in Ad Hoc and Wireless Sensor Networks. J Wireless Com Network 2010, 975607 (2010). https://doi.org/10.1155/2010/975607
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/975607
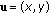 is the position in the plane of the UN.
is the position in the plane of the UN.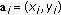 is the position of the i th AN, where
is the position of the i th AN, where  .
.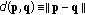 is the Euclidean distance between two arbitrary network nodes at positions p and q.
is the Euclidean distance between two arbitrary network nodes at positions p and q. is the RSS in dBm measured at the receiver of node q for a signal transmitted by node p.
is the RSS in dBm measured at the receiver of node q for a signal transmitted by node p. receives a reputation response message from node
receives a reputation response message from node  regarding node
regarding node 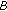 , if node
, if node 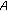 is confident about the direct trust value it has calculated for node
is confident about the direct trust value it has calculated for node 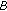 , it compares the received value (i.e., the reputation provided from node
, it compares the received value (i.e., the reputation provided from node  ) with its own direct trust on node
) with its own direct trust on node 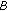 . If the difference exceeds a predefined threshold, then the provided reputation is considered as "wrong reputation"; otherwise, it is a "correct reputation" and node
. If the difference exceeds a predefined threshold, then the provided reputation is considered as "wrong reputation"; otherwise, it is a "correct reputation" and node  is scored accordingly.
is scored accordingly.




