- Research Article
- Open access
- Published:
COMAS: A Cooperative Multiagent Architecture for Spectrum Sharing
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 987691 (2010)
Abstract
Static spectrum allocation is a major problem in recent wireless network domains. Generally, these allocations lead to inefficient usage creating empty spectrum holes or white spaces. Thus, some alternatives must be ensured in order to mitigate the current spectrum scarcity. An effective technology to ensure dynamic spectrum usage is cognitive radio, which seeks the unutilized spectrum portions opportunistically and shares them with the neighboring devices. However, since users generally have a limited knowledge about their environment, we claim that cooperative behavior can provide them with the necessary information to solve the global issues. Therefore, in this paper, we develop a novel approach for spectrum allocation using a multiagent system that enables cognitive radio devices to work cooperatively with their neighboring licensed (or primary user) devices in order to utilize the available spectrum dynamically. The fundamental aspect of our approach is the deployment of an agent on each device which cooperates with its neighboring agents in order to have a better spectrum sharing. Considering the concurrent, distributed, and autonomous nature of the proposed approach, Petri nets are adopted to model the cooperative behaviors of primary and cognitive radio users. Our simulation results show that the proposed solution achieves good performance in terms of spectrum access, sustaining lower communication overhead.
1. Introduction
The deployment of modern day wireless devices follows the static spectrum usage, where spectrum is assigned to a licensed user for longer durations. This static spectrum assignment is considered to be extremely favorable in order to avoid the device-level collisions; however, it leads to radio spectrum shortage problem creating empty spectrum holes. According to [1], in both rural and urban areas, spectrum usage can go as low as 10–15%, resulting in huge amount of spectrum to be wasted. As a result, the newly arriving unlicensed devices are forced to use unlicensed bands leading to inefficient and crowded spectrum utilizations.
Cognitive radio (CR), firstly coined by Mitola [2], is considered to be an efficient technology to enable dynamic and opportunistic spectrum sharing. Generally, a CR (or secondary) user senses the nearby empty spectrum portions and is capable of sharing them with the neighboring devices, without interrupting the working of licensed (or primary) users. It continuously monitors the environmental radio frequency (RF) signals and alters its transmission and reception parameters in order to better perform its functions. However, one of the key issues in CR networks is to avoid device level collisions and interferences while maintaining efficient spectrum usage. We argue that a noncooperative node can cause harmful interference to its neighbors and hence can reduce the overall spectrum usage.
One effective solution to enable interdevice cooperation and information exchange is multiagent system [3]. Basically, a multiagent system (MAS) is composed of groups of autonomous agents working together by having frequent interactions with each other, in order to solve the tasks which are beyond the capabilities of a single agent [4]. Each agent works dynamically to fulfill its user needs and has partial knowledge and imperfect information about the nearby environment. In addition, an efficiently designed CR device, with an agent embarked on it, is capable of interacting with neighboring radios to form a dynamic and collaborative network and provides a rationale to conceptualize new spectrum sharing techniques for CR networks. This rationale is particularly attractive and equally important to create spectrum sharing solutions that can work in dynamic, distributed, and open wireless networks domains.
Therefore, in this paper, an MAS-based approach is proposed, where the primary and secondary users are equipped with agents. The secondary user (SU) agents coexist and cooperate with the legacy PU agents using the message-passing and decision-making mechanisms of contract net protocol (CNP) [5]. The whole environment is ad hoc with the frequent changes in the neighborhoods of primary and secondary users. Moreover, in order to capture the agents' interactions under mobile conditions, Petri net (PN) modeling is used [6]. The graphical and analytical nature of PN allows us to visualize the detailed feasibility analysis of agents' internal behaviors when they have to make spectrum sharing deals/agreements. While passing through several cooperative stages, we study the interagent message exchange in order to make cooperative decisions. In this context, our previous works [7, 8] have focused on proposing a cooperative spectrum sharing framework and analyzing its behavior. Unlike our previous contributions, in this paper we deploy our primary and secondary users according to Poisson distributions [9] and monitor their arrivals and departures under ad hoc conditions. These distributions help us in identifying the exponential time periods (or holding times) for which the users utilize the available spectrum.
The rest of the paper is organized as follows. Prior works related to dynamic spectrum sharing are summarized in Section 2. Section 3 formulates the problem statement. In Section 4, we propose our cooperative framework. Petri net model along with some important properties of our design is presented in Section 5. Section 6 depicts simulation results. Finally, Section 7 concludes our paper with the future perspectives.
2. Related Work
In the recent past, several dynamic spectrum sharing approaches have been proposed using different techniques such as game theory and auctions and medium access control protocols. In fact, some researchers have also drawn their focus towards multiagent-based approaches for spectrum sharing. In [10], an MAS is used for managing spectrum resources across several wireless LANs (WLANs), collocated in a geographical area. Each access point (AP) located in a WLAN contains an agent which interacts with the neighboring AP agents (located in other WLANs) to form an MAS. The internal architecture of an agent consists of two parts: predictive parameter estimation, which generates parameter estimates using the signal characteristics received from WLAN environments, andresource management optimization, which decides the suitable spectrum bands to be selected. The proposed approach is explained conceptually, but none of the analysis and experiments are shown. On the contrary, the works proposed in [11, 12] consider market-based auctions for dynamic spectrum sharing. The SUs working as consumer agents submit their bids to the PUs (or auctioneer agents) which shows their willingness for spectrum sharing. The auctioneer agents then share the spectrum based on the received bids. The ultimate aim of using auctions is to provide an incentive for SUs to maximize their spectrum usage (and hence the utility), while allowing network to achieve Nash Equilibrium. However, considering the competitive nature of market-based approaches, it is hard to develop agents with unselfish behaviors.
According to Weib and sen [13], agents should have the ability to learn from their past states in order to better perform their following actions/moves. This MAS learning can provide significant contribution to spectrum allocation in CR networks, if the devices have the knowledge of their past sharing patterns and neighborhood movements. In vicinity, the solutions based on MAS learning are presented in [14, 15]. Basically, the SUs periodically share the relative traffic information on the sensed channels (they are likely to be used in near future), with the neighboring devices. Based on this information exchange, multiagent learning (i.e., delay sensitive and Q-learning) algorithms are proposed which allow the CR users to dynamically and autonomously optimize their transmission power on a selected channel and to avoid the inter-device interferences. Conversely, sometimes these learning algorithms can create a situation, where the agents have weak assumptions about other agents' spectrum usage making the task of getting accurate information more difficult.
A different cooperative approach named DSAP (dynamic spectrum access protocol) is presented in [16]. This approach is based on the concept of centralized server which is responsible for leasing spectrum to the requesting users in a small geographical region. The server also maintains a global view of the network's channel conditions through a series of frequent information exchanges with its clients. However, centralized server can become a huge bottleneck in diverse network conditions.
Game-theoretical solutions are considered to be a perfect match of nature for dynamic spectrum allocations. Mostly, in these approaches [17, 18], to efficiently utilize the scarce spectrum resource, PUs adopt the roles of the leaders, by selecting a subset of neighboring SUs and granting them spectrum access. In return, SUs work as the followers, by paying PUs the relative price for spectrum utilization and maximizing their utilities in terms of spectrum access for a specific time period. Yet, each user focuses on maximizing its individual usage without taking into account the others, showing selfish behaviors. As a result, in order to allow players to work interdependently, cooperative games are proposed [19, 20]. In cooperative games, the SUs' transmission powers and spectrum usage are common knowledge, and their utility functions are chosen in order to maximize the global utility. At the same time, cooperative approaches require a feedback from each player to be sent to the centralized server about its utility function, increasing the overall algorithmic complexity.
A local bargaining approach is presented in [21], where the CR users self-organize into small bargaining groups. The group formation process starts by the initiator CR node, sending a group formation request to its neighbors for a subset of spectrum portions. The interested neighbors acknowledge the request, and the bargaining group is formed ensuring minimum spectrum allocation to each group member. The experimental results prove that local bargaining performs similar to greedy approach [22] incurring less communication overhead.
Aside from local bargaining and game-theoretical approaches, some authors suggest that the spectrum sharing problems are similar to MAC issues [23], where several users try to access the same channel and their access should be coordinated with the neighboring users to avoid interferences. In MAC-based spectrum sharing [24, 25], when an SU is using a specific channel, both the transmitter and the receiver synchronize themselves by sending a busy tone signal through the associated control channel, such that the signal interferences should be avoided. Nevertheless, sending frequent busy tones can interrupt the neighboring devices, because each time they have to stop their normal working flow in order to listen to the busy tone on the control channel.
Our proposed approach is different from the above as we consider a framework where PU agents are working together with the SUs in order to enable dynamic spectrum allocations. The agents' internal behaviors are cooperative and unselfish, which allow them to help maximizing each others' utility functions. To the best of our knowledge, the idea of deploying a cooperative MAS over CR networks under ad hoc conditions along with the modeling of users' spectrum sharing process using Petri nets and detailing their internal message structures has not been previously addressed. Therefore, we think that our work will provide a novel contribution to the current dynamic spectrum access literature.
3. Problem Description
Before formulizing our problem statement, let us consider an ad hoc network scenario in Figure 1(a scenario of two PUs and one SU is shown just as an example for depicting the deployment of cooperative agents under ad hoc network setting). The figure depicts an emergency situation during an accident in a very remote area, where the user is in a noncovered zone (i.e., the radio resources at this moment are not available) or the radio access technology requires an energy that the terminal (a mobile, a laptop, or a PDA) does not own. In this case, an SU should observe the nearby PUs (PU1 and PU2) and sense their transmission signals to identify the available spectrum bands. Then, its agent can cooperate with the conforming primary user agents to make dynamic spectrum sharing agreements.
We now formulize our problem. Let  be a directed network consisting of a set of mobile nodes N such that
be a directed network consisting of a set of mobile nodes N such that  and a set of directed arcs
and a set of directed arcs  . Each directed arc
. Each directed arc  connects a secondary user
connects a secondary user  to a primary user
to a primary user  . Similarly, we can denote the directed arc
. Similarly, we can denote the directed arc  to connect
to connect  to
to  . The secondary users are cooperating with the neighboring primary users to have a spectrum sharing agreement. We assume that
. The secondary users are cooperating with the neighboring primary users to have a spectrum sharing agreement. We assume that  is the amount of spectrum that a secondary user "
is the amount of spectrum that a secondary user " " is desiring to get from a primary user "
" is desiring to get from a primary user " ". Similarly,
". Similarly,  is the amount of time for which "i" wants to utilize the spectrum, and
is the amount of time for which "i" wants to utilize the spectrum, and  is the price it is willing to pay to "
is the price it is willing to pay to " ". On the other hand, for a primary user "j", s
ji
is the amount of spectrum it is willing to share with "
". On the other hand, for a primary user "j", s
ji
is the amount of spectrum it is willing to share with " ",
",  is the respected time limit, and
is the respected time limit, and  is the price it is expecting to get after sharing its spectrum. We can formulate the above model for each secondary user "
is the price it is expecting to get after sharing its spectrum. We can formulate the above model for each secondary user " " as follows:
" as follows:

subject to

Similarly, for primary users,

subject to


where  and
and  are the lower and upper bounds of available spectrum of "
are the lower and upper bounds of available spectrum of " ". This means that "
". This means that " " cannot ask for an amount of spectrum above this limit.
" cannot ask for an amount of spectrum above this limit.
4. Cooperative Spectrum Allocation Framework
In this section, we explain the internal architectures of primary and secondary users along with their working behaviors. Basically, our design (as shown in Figure 2) is based on five different interlinked parts that embody the working of our cooperative approach:
-
(i)
dynamic spectrum sensor,
-
(ii)
spectrum characterizer,
-
(iii)
secondary user interface,
-
(iv)
agent's knowledge module, and
-
(v)
agent's cooperation module.
The working of these modules is described, in the following. Obviously, the primary user does not contain the cognitive radio module, while the agent module is common in both the primary and secondary users. Note that, in essence, spectrum sensing and characterizing is beyond the scope of our work; thus, our focus will be on agent module which is the key functionary to enable cooperation between primary and secondary users.
4.1. Dynamic Spectrum Sensor
The function of dynamic spectrum sensor (DSS) is the sensing of radio spectrumholes by continuously monitoring the neighboring PU signals. Several techniques such as PU's weak signal and its energy detection [26] and cooperative detection [27] can be used to perform spectrum sensing. For DSS, it is also necessary that the sensing is performed by considering a real-time dynamic environment, because it is not obvious at what time a spectrum band is occupied or when it is free. Thus, all the factors such as PU's signal power with the respected noise, spectrum traffic (by calculating the number of current users and taking into account the application type), sampling time, and intervals must be kept in consideration.
4.2. Spectrum Characterizer
Spectrum characterizing can be considered as a subfunction of spectrum sensing. Basically, our spectrum characterizer (SC) module functions as to arrange/divide the spectrumholes information (received through DSS) according to capacity. In a simple way, to create a capacity-based descending ordered list of neighboring PUs, SC uses the Shannon Theorem:

where C is the capacity in bits per second, B is the bandwidth measured in hertz and SNR is the respected signal-to-noise ratio in watts. For more details, the complete derivation and formulation of the above equation is found in [28].
4.3. Secondary User Interface
The third part, secondary user interface (SUI) sends a request message to the agent module, whenever a user wants to have a portion of spectrum (for internet surfing, watching high quality videos, etc.). The message is of the form req ( ), where
), where  is the amount of spectrum needed by the SU depending upon its application in use, for a time duration
is the amount of spectrum needed by the SU depending upon its application in use, for a time duration . In reality, the user's request depends upon the application to be used. For example, if a user runs a Skype-based multimedia application on its PDA or cell phone on daily bases, then each time this application is executed, its request for spectrum utilization will remain the same.
. In reality, the user's request depends upon the application to be used. For example, if a user runs a Skype-based multimedia application on its PDA or cell phone on daily bases, then each time this application is executed, its request for spectrum utilization will remain the same.
4.4. Agent's Knowledge Module
Agent's knowledge module (AKM) gets PUs' characterization information from SC module which serves as a motivation for agents that subsets of neighbors having unutilized spectrum portions are available. This list is not permanent, rather it is updated and maintained on regular time intervals. Secondary user's AKM (or SU-AKM) also gets the req message from SUI module, and, based on the inputs from both the modules, it prepares a call for proposal (CfP) message:

where SUID is the secondary user's ID (or its agent's identification) and it is used to help PU to reply back to the corresponding SU,  is the amount of spectrum needed by the SU,
is the amount of spectrum needed by the SU,  is the desired time limit (or holding time) for the spectrum utilization, and
is the desired time limit (or holding time) for the spectrum utilization, and  is the deadline to receive the PUs' responses (proposals). Parallel to CfP creation, SU-AKM maintains the neighboring PUs' information that is received via frequent interactions between the agents, along with a list of previously received proposals (if there exist any). This information includes the leaving and joining of neighboring nodes in a network and their current spectrum status, and it helps an SU to create a more precise CfP. Uniformly, the PU-AKM module functions almost in the same manner by maintaining the neighboring SUs' arrivals and departures information and a list of their previous spectrum demands.
is the deadline to receive the PUs' responses (proposals). Parallel to CfP creation, SU-AKM maintains the neighboring PUs' information that is received via frequent interactions between the agents, along with a list of previously received proposals (if there exist any). This information includes the leaving and joining of neighboring nodes in a network and their current spectrum status, and it helps an SU to create a more precise CfP. Uniformly, the PU-AKM module functions almost in the same manner by maintaining the neighboring SUs' arrivals and departures information and a list of their previous spectrum demands.
4.5. Agent's Cooperation Module
Agent's cooperation module (ACM) manages the cooperation between primary and secondary users. After the reception of a CfP message from SU-AKM, the SU-ACM sends the received CfP to the neighboring and currently available PU agents. The PUs are considered to be available if they still exist in the corresponding SU's neighborhood with their spectrum portions. Besides, SU-ACM also performs the main decision for an SU by selecting the appropriate proposal. In much the same way, PU-ACM chooses the most suitable CfP for a PU and sends the proposal in response. Finally, the appropriate agreement for both the primary and secondary users is the one which is profitable and maximizes their utility values.
On average, the utility for a PU is the price paid by SU agents for their spectrum utilization divided by the amount of spectrum it has shared for the respected time period. An SU agent's utility is represented as its spectrum usage for the required time divided by the corresponding price paid to the PUs.
Accordingly, Figures 3 and 4 delineate the behavioral working of secondary and primary users, respectively. Both the behaviors show the same characterizing, analyzing, sending, receiving, and deciding steps mentioned before. The spectrum sharing process for an SU starts by getting the characterization results and the user requirements and continues until the sending of CfPs and receiving of the proposals. The process ends either by having an agreement or disagreement. For a PU, the process follows the same pattern by first analyzing the received CfPs, sending the proposals as responses, and finally ending the process either by receiving an accept or a reject message from the conforming SU.
5. Petri Net Model for the Cooperative Approach
Petri Net (PN) [6] is a graphical tool for the formal description of the flow of activities in complex systems. Generally, PNs are used to represent the logical interactions among nodes, devices, and parts of a system. Their discrete and distributed nature makes them highly suitable to model interagent interactions and capture the dynamics of decentralized environments. A simple PN model is shown in Figure 5. Basically, it contains two types of nodes, namely, a set of places  and a set of transitions
and a set of transitions  . A place is represented by a circle, and a transition can be shown by a bar (or a box). Further, a PN consists of a set of inputs
. A place is represented by a circle, and a transition can be shown by a bar (or a box). Further, a PN consists of a set of inputs  , outputs
, outputs  , and the markings
, and the markings  (assignment of tokens to the places). The marking of a PN is a vector, the components of which are positive integer values. The dimension of this vector is equal to the number of places. A token (represented by a small filled circle) is moved from one place to another when a transition is fired. For example, in Figure 5, firing of transitions
(assignment of tokens to the places). The marking of a PN is a vector, the components of which are positive integer values. The dimension of this vector is equal to the number of places. A token (represented by a small filled circle) is moved from one place to another when a transition is fired. For example, in Figure 5, firing of transitions  ,
,  ,
,  , and
, and  can allocate several resources from one agent to another, and these firings can be represented by removal of tokens from input places and their addition to the output places.
can allocate several resources from one agent to another, and these firings can be represented by removal of tokens from input places and their addition to the output places.
A simple PN with initial marking
 [
29
].
[
29
].
5.1. Modeling Spectrum Sharing Agreement/Disagreement Using PN
A cooperative spectrum sharing model between a primary and a secondary user is a five-tuple  , where
, where  is the finite set of places,
is the finite set of places,  is a finite set of transitions,
is a finite set of transitions,  and
and  are the input and output functions which specify the input and output places of transitions, and
are the input and output functions which specify the input and output places of transitions, and  is the set of markings such that
is the set of markings such that  and
and  denote the sets of initial and final markings, after firing all the transitions. We also denote by
denote the sets of initial and final markings, after firing all the transitions. We also denote by
-
(i)
 the set of input places p of a transition
the set of input places p of a transition  :
: 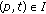 ;
; -
(ii)
 the set of output places p of a transition
the set of output places p of a transition  :
: 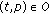 ;
; -
(iii)
 the set of input transitions t of a place
the set of input transitions t of a place 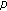 :
:  ;
; -
(iv)
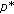 the set of output transitions t of a place
the set of output transitions t of a place 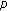 :
: 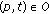 .
.
Places represent several states of primary and secondary users during a spectrum sharing agreement/disagreement. A transition  is enabled when an event is about to occur (e.g., a CfP is ready to be sent), and it is fired when the event occurs (i.e., a CfP has been successfully sent). Firing a transition will remove token(s) from each *
is enabled when an event is about to occur (e.g., a CfP is ready to be sent), and it is fired when the event occurs (i.e., a CfP has been successfully sent). Firing a transition will remove token(s) from each * and will add them to
and will add them to  *. Formally, firing transitions consists of transforming the
*. Formally, firing transitions consists of transforming the  into
into  as follows [29]:
as follows [29]:

The cooperation process of an SU with two neighboring PUs to make a spectrum sharing agreement is shown in Figure 6, while the description of various states and transitions is summarized in Tables 1 and 2. The spectrum sharing process starts with places p
1
, p
4
, and p
5
, where  is ready to send CfPs and PU1 and PU2 are ready to receive them. Firing transition t
1
removes a token from place p
1
and adds it to
is ready to send CfPs and PU1 and PU2 are ready to receive them. Firing transition t
1
removes a token from place p
1
and adds it to  ,
,  , and
, and  . Thus, when transition
. Thus, when transition  is fired, the CfPs are sent from
is fired, the CfPs are sent from  to PU1 and PU2. Both the tokens from p
2
and p
3
enable transitions
to PU1 and PU2. Both the tokens from p
2
and p
3
enable transitions  and
and  , and firing of these two transitions adds one token each to
, and firing of these two transitions adds one token each to  and
and  , showing the reception of CfPs by PU1 and PU2. Similarly, the remainder of the message passing process follows the same pattern (of tokens removal and addition), where
, showing the reception of CfPs by PU1 and PU2. Similarly, the remainder of the message passing process follows the same pattern (of tokens removal and addition), where  accepts PU1 for spectrum sharing and it rejects PU2 due to its unsatisfactory proposal. The states and transitions involved in these message exchanges are
accepts PU1 for spectrum sharing and it rejects PU2 due to its unsatisfactory proposal. The states and transitions involved in these message exchanges are

After the reception of an accept message, the spectrum sharing is started between  and PU1, and it continues until the spectrum is completely utilized and the respected price is paid. A successful spectrum sharing contains the rest of the states and transitions of Figure 6. The primary users will behave in the same manner when they have to deal with multiple CfPs at a time. Moreover, if a secondary user receives more than one proposal which is equally satisfactory, then the decision will be made on the FIFO bases. Finally, Table 3 depicts the initial and final markings of tokens after firing all the transitions. It is clear that the value of M
f
becomes "3" only when a spectrum portion is shared or the price is paid.
and PU1, and it continues until the spectrum is completely utilized and the respected price is paid. A successful spectrum sharing contains the rest of the states and transitions of Figure 6. The primary users will behave in the same manner when they have to deal with multiple CfPs at a time. Moreover, if a secondary user receives more than one proposal which is equally satisfactory, then the decision will be made on the FIFO bases. Finally, Table 3 depicts the initial and final markings of tokens after firing all the transitions. It is clear that the value of M
f
becomes "3" only when a spectrum portion is shared or the price is paid.
5.2. Some Definitions
By analyzing our proposed model along with Tables 1 and 2, we can conclude the following few definitions.
Definition 1.
For a secondary user  , the Petri net
, the Petri net  , for an empty part of the spectrum
, for an empty part of the spectrum  for time
for time  , is a working model if and only if the movement from initial marking M
osi
to final marking M
fsi
, after firing all transitions, results in the maximization of its utility function
, is a working model if and only if the movement from initial marking M
osi
to final marking M
fsi
, after firing all transitions, results in the maximization of its utility function  such that
such that  , where
, where  is the corresponding price
is the corresponding price  that is asked to pay for its spectrum utilization. Similarly, for a primary user
that is asked to pay for its spectrum utilization. Similarly, for a primary user  , a Petri net
, a Petri net  , for an empty spectrum portion
, for an empty spectrum portion  with the associated price
with the associated price  , the movement from initial marking M
opj
to final marking M
fpj
, results in the maximization of its utility function U
puj
such that
, the movement from initial marking M
opj
to final marking M
fpj
, results in the maximization of its utility function U
puj
such that  . Both the primary and secondary users work cooperatively to maximize each other's utility functions. Especially, the primary users send the proposals which are in their own profit as well as of the requesting secondary users.
. Both the primary and secondary users work cooperatively to maximize each other's utility functions. Especially, the primary users send the proposals which are in their own profit as well as of the requesting secondary users.
Definition 2.
A Petri net  , for an empty part of the spectrum s, is said to be unsuccessful if moving from M
os
to M
fs
results in no change in the utility functions of both the participating secondary and primary users such that
, for an empty part of the spectrum s, is said to be unsuccessful if moving from M
os
to M
fs
results in no change in the utility functions of both the participating secondary and primary users such that

In our proposed model, the PN between SUi and PU2 proved to be unsuccessful, because, after performing all the cooperation steps, the utility functions of both of the users remain unchanged, resulting in spectrum sharing disagreement.
5.3. Behavioral Properties
To verify the efficiency of our approach, we provide the behavioral properties of the proposed PN model. These properties, when interpreted in the context of the modeled system, allow the system designer to understand the working of the considered network. By behavioral properties we mean the properties which are dependent on all the markings of a PN; that is, the initial and final markings are interlinked. Thus, we provide here the most important behavioral properties such as reachability, boundness, and liveness [30].
Reachability
In order to find out the reachability of the proposed model, it is necessary to locate a sequence of events or transitions which would transform an initial marking to a final marking by representing the required functioning behavior of the network. This transformation is similar to real networks, where a sequence of steps (i.e., sending and receiving of messages, accepting requests) would allow the network to achieve its required goals. The reachability also indicates the presence of the real network-related facts, which reflect the behavior of participating nodes. For our proposed model in Figure 6, let  be the initial marking for a state
be the initial marking for a state  , then the final marking
, then the final marking  reachable from
reachable from  can be written as
can be written as

where  is the vector containing the firings related to
is the vector containing the firings related to  .
.  can be denoted as
can be denoted as

Here,  and
and  are the number of tokens added and consumed from
are the number of tokens added and consumed from  . For all
. For all  , (11) can be written as
, (11) can be written as

where  and
and  are the initial and final marking sets for all
are the initial and final marking sets for all  and
and  is a vector containing all
is a vector containing all  related to all
related to all  .
.
Reachability is very important for our proposed model as it helps us in calculating the final markings reachable from initial markings and shows the flow of tokens from place to place. To prove this property from our proposed PN let us give an example. As mentioned before, Table 3 shows all the initial and final markings with the addition and subtraction of tokens for Figure 6. From this table, we can calculate  and
and  as follows:
as follows:

Using (14), equation (13) becomes

Thus, in our PN, the addition of vector V with initial marking set  enables us to reach the final marking set
enables us to reach the final marking set  .
.
Boundness
A place  of a PN model is said to be
of a PN model is said to be  -bounded if the number of tokens in
-bounded if the number of tokens in  always remain less than or equal to
always remain less than or equal to  ; that is,
; that is,  , where
, where  an integer value >0 and
an integer value >0 and  are the number of tokens in place
are the number of tokens in place  .
.  is always bounded when it is
is always bounded when it is  -bounded. Boundness is an important property in order to check the design errors in a PN model. For instance, some tokens may permanently stay in places and create serious bottlenecks for the whole PN. In Figure 6, boundness holds for all the places as the number of tokens in each place is within
-bounded. Boundness is an important property in order to check the design errors in a PN model. For instance, some tokens may permanently stay in places and create serious bottlenecks for the whole PN. In Figure 6, boundness holds for all the places as the number of tokens in each place is within  , where
, where  .
.
In contrast to reachability which is verified using marking sets, boundness can be easily verified using coverability graph [29]. Coverability graph represents all the possible markings of a PN model in the form of a simple tree where  represents the root node, all the markings reachable from
represents the root node, all the markings reachable from  are the nodes, and the arcs represent the firing of transitions. Therefore, for simplicity, we construct a coverability graph in Figure 7 for the initial part of Figure 6 that is, for states
are the nodes, and the arcs represent the firing of transitions. Therefore, for simplicity, we construct a coverability graph in Figure 7 for the initial part of Figure 6 that is, for states  and transitions
and transitions  . From the graph, we notice that states
. From the graph, we notice that states  are 1-bounded and state
are 1-bounded and state  is 2-bounded. Thus, the graph remains
is 2-bounded. Thus, the graph remains  -bounded for all the states, and value of
-bounded for all the states, and value of  never becomes 0. Boundness can similarly be verified for all the remaining states and transitions of Figure 6.
never becomes 0. Boundness can similarly be verified for all the remaining states and transitions of Figure 6.
Coverability graph for some states and transitions of Figure 6.
Liveness
Definition A.
In wireless networks, different tasks are performed at several time instances and similar is the case with Petri net models, where many transitions are ready to fire at distinct times. Generally, a PN is live when there exists at least one transition  which is ready to be fired at a particular time instance. Formally,
which is ready to be fired at a particular time instance. Formally,

where  is the time instance and
is the time instance and  is the function indicating either a transition t is ready to fire or not [31]. Our PN remains live during a spectrum sharing process because at least one
is the function indicating either a transition t is ready to fire or not [31]. Our PN remains live during a spectrum sharing process because at least one  always remains ready to be fired. For example, when PU1 and PU2 receive the CfPs, the transitions
always remains ready to be fired. For example, when PU1 and PU2 receive the CfPs, the transitions  and
and  are in their ready states and they are fired when PU1 and PU2 send their proposals to SUi. Then, at the next time instance, transition
are in their ready states and they are fired when PU1 and PU2 send their proposals to SUi. Then, at the next time instance, transition  is ready to fire and is fired when SUi sends its responses to PU1 and PU2 and similar is the case with the other transitions. Thus, the PN remains live for the whole process of spectrum sharing.
is ready to fire and is fired when SUi sends its responses to PU1 and PU2 and similar is the case with the other transitions. Thus, the PN remains live for the whole process of spectrum sharing.
Definition B.
A PN is said to be live if and only if, from any node in its reachability graph, it is possible to find a directed path having this node as origin. In other words, the PN is live when each node of its directed graph is the origin of at least one arc. If we consider the coverability graph of Figure 7, we notice that each node contains at least one arc as origin; thus, this coverability graph is live. Likewise, for the proposed PN model of Figure 6, we can clearly see that each transition contains at least one arc to reach its next state until the spectrum sharing process arrives to its end. Therefore, we can conclude that the proposed PN is live.
6. Experimental Results
6.1. Setup
In this section, we present various numerical results to evaluate the working of the proposed cooperative approach, based on the following simulation setup. Multiple sets of primary and secondary users are randomly placed according to Poisson distribution [9] in a noiseless and mobile ad hoc network with the continuous change in their neighborhoods. The SUs cooperate with the PUs in order to make spectrum sharing deals/agreements. According to the studies presented in [17, 32], we set the elapsed simulation time  to 90 minutes. All the simulations are conducted in Java Application Development Environment (JADE) [33], over a PC with 2.4 GHZ dual processor and 4 GB memory.
to 90 minutes. All the simulations are conducted in Java Application Development Environment (JADE) [33], over a PC with 2.4 GHZ dual processor and 4 GB memory.
The parameter selection is shown in Table 4. As mentioned in [34], we set the bandwidth of each spectrum portion to 3.75 MHz. The simulation is conducted for a total of 10 runs (i.e.,  ) (we have also verified our simulation with different values of elapsed time for several runs (i.e.,
) (we have also verified our simulation with different values of elapsed time for several runs (i.e.,  , 30, 40, 50, …), and nevertheless the agents behaviors remain the same), and the average values are taken for plotting the graphs. According to [35], the fractional percentage of the time for which the spectrum is being used by the PUs (or holding time) in an urban environment follows the exponential distribution with mean μ
p
and is measured as approximately 40 to 45%; thus, we set the mean spectrum usage of PUs to 40%. Considering the capacity of a single machine, the maximum number of primary and secondary users is 100 in total. Moreover, the rates λ
p
and λ
s
denote the Poisson distributions of primary and secondary users. For simplicity, we fix the value of λ
s
to 5 and compare our parameters at various values of λ
p
(i.e.,
, 30, 40, 50, …), and nevertheless the agents behaviors remain the same), and the average values are taken for plotting the graphs. According to [35], the fractional percentage of the time for which the spectrum is being used by the PUs (or holding time) in an urban environment follows the exponential distribution with mean μ
p
and is measured as approximately 40 to 45%; thus, we set the mean spectrum usage of PUs to 40%. Considering the capacity of a single machine, the maximum number of primary and secondary users is 100 in total. Moreover, the rates λ
p
and λ
s
denote the Poisson distributions of primary and secondary users. For simplicity, we fix the value of λ
s
to 5 and compare our parameters at various values of λ
p
(i.e.,  , 4, and 5). This variation factor helps us in understanding the behaviors of SUs when they have to deal with different numbers of PUs. Additionally, during a simulation run of 90 minutes, we also observe distinct values of our parameters over five different time intervals of 18 minutes each, ensuring that the parameters can be compared across several time instants. We calculate a primary user's utility as the price paid by SUs for spectrum utilization divided by the amount of spectrum it has shared for the respected time period. Likewise, a secondary user's utility is represented as its spectrum usage for the required time divided by the price paid by the PUs. Finally, the number of nonallocated spectrum portions measures the overall percentage of spectrum deficit (
, 4, and 5). This variation factor helps us in understanding the behaviors of SUs when they have to deal with different numbers of PUs. Additionally, during a simulation run of 90 minutes, we also observe distinct values of our parameters over five different time intervals of 18 minutes each, ensuring that the parameters can be compared across several time instants. We calculate a primary user's utility as the price paid by SUs for spectrum utilization divided by the amount of spectrum it has shared for the respected time period. Likewise, a secondary user's utility is represented as its spectrum usage for the required time divided by the price paid by the PUs. Finally, the number of nonallocated spectrum portions measures the overall percentage of spectrum deficit ( ).
).
6.2. Obtained Results
Firstly, we show the histograms of PUs' spectrum usage at several values of λ p in Figure 8. All three histograms depict the spectrum usage probability of PUs at different instances of time. At early stages, this probability is high, but, later, the spectrum is mostly unutilized, and, thus, the SUs can have a higher percentage of successful spectrum sharing agreements during these periods.
Successful Agreements
We now plot the average number of successful spectrum sharing agreements between primary and secondary users. By a successful agreement, we mean that an SU has utilized the assigned spectrum according to its requirement. Formally for an agreement  ,
,

And, if we denote a successful agreement by  , we can write the summation as
, we can write the summation as

where  represents the number of successful agreements and
represents the number of successful agreements and  and
and  are the time values for which spectrum is being utilized and requested by the secondary user. Of course, due to the cooperative nature of agents, the secondary user pays the agreed price (for its spectrum utilization) to the respected primary user.
are the time values for which spectrum is being utilized and requested by the secondary user. Of course, due to the cooperative nature of agents, the secondary user pays the agreed price (for its spectrum utilization) to the respected primary user.
Figures 9(a) and 9(b) show three curves of  plotted using several numbers of SUs (
plotted using several numbers of SUs ( ) at various time values. From the figures, the differences in
) at various time values. From the figures, the differences in  at
at  , 4, and 5 are clearly observable. For small
, 4, and 5 are clearly observable. For small  , the values of
, the values of  are marginally the same, because most of the PUs are busy during the early time periods and it is difficult for SUs to find the required PUs with the available spectrum portions. When
are marginally the same, because most of the PUs are busy during the early time periods and it is difficult for SUs to find the required PUs with the available spectrum portions. When  reaches higher values with simulation time greater than 50 minutes, the distinction between
reaches higher values with simulation time greater than 50 minutes, the distinction between  is much clearer. This distinction also shows that fewer successful agreements are made when
is much clearer. This distinction also shows that fewer successful agreements are made when  , because the number of available PUs are less. But, when we increase λ
p
to 4 and 5, the values of
, because the number of available PUs are less. But, when we increase λ
p
to 4 and 5, the values of  almost reach their maximum positions. Furthermore, we can observe that for bigger values of λ
p
, the cooperation between the primary and secondary users is still very effective, as more SUs have made successful spectrum sharing agreements.
almost reach their maximum positions. Furthermore, we can observe that for bigger values of λ
p
, the cooperation between the primary and secondary users is still very effective, as more SUs have made successful spectrum sharing agreements.
Percentage Utility
Figure 10 compares the average percentage utility of SUs at different time values. Particularly, the utilities are within 20 to 55% when  , while they can reach 70% (80% resp.) when
, while they can reach 70% (80% resp.) when  (
( resp.). The graph is in conjunction with Figures 8 and 9, where at, time values greater than 50 minutes, the SUs can find more available PUs for spectrum sharing. Moreover, it is noticeable that the utility values can augment up to 80% (with
resp.). The graph is in conjunction with Figures 8 and 9, where at, time values greater than 50 minutes, the SUs can find more available PUs for spectrum sharing. Moreover, it is noticeable that the utility values can augment up to 80% (with  ) showing higher efficiency in terms of spectrum utilization. Nevertheless, complete satisfaction is not achieved, considering that the environment is ad hoc and the PUs are hesitant to share their spectrum portions for longer time durations. In contrast, Figure 11 shows that the average percentage utility of PUs is almost 90% for all three values ofλ
p
, since the PUs are always less (or equal) in number compared to SUs and there is relatively a higher chance that they can easily find SUs to share their unutilized spectrum.
) showing higher efficiency in terms of spectrum utilization. Nevertheless, complete satisfaction is not achieved, considering that the environment is ad hoc and the PUs are hesitant to share their spectrum portions for longer time durations. In contrast, Figure 11 shows that the average percentage utility of PUs is almost 90% for all three values ofλ
p
, since the PUs are always less (or equal) in number compared to SUs and there is relatively a higher chance that they can easily find SUs to share their unutilized spectrum.
We now compare the average percentage utility values of primary and secondary users achieved through simulations to the optimal value. Optimal value can be achieved when the average percentage utilities of primary and secondary users are fully satisfied (i.e., 100%). Figure 12 summarizes the results. We observe that the values achieved through experiments are very close to the optimal value and they can reach almost 90% showing good utility-based performance of our approach.
Another way of showing above results is to compare the number of SUs with spectrum demands and those which are served in the end. For this depiction, we fix the maximum number of SUs to 50 and observe the results for different values of PUs, in Figure 13. Served SUs are those which have completely obtained the required spectrum. In all the three comparisons, even though a large amount of SUs have been completely served, still a percentage of them remains unsuccessful. Thus, under ad hoc situations, despite the fact that the primary and secondary users are equal in numbers, the results are not fully achieved.
Communication Cost
The number of cooperation messages for successful spectrum sharing agreements determines the average communication cost ( ). Formally,
). Formally,

where  is the number of messages sent and received for a successful agreement
is the number of messages sent and received for a successful agreement  such that
such that  .
.
Different values of  along with several numbers of successful agreements are plotted in Figure 14. In the figure, the value of
along with several numbers of successful agreements are plotted in Figure 14. In the figure, the value of  is initially 4, but it climbs to an average of 8 messages per agreement. This increasing pattern in
is initially 4, but it climbs to an average of 8 messages per agreement. This increasing pattern in  is directly relational to number of PUs (
is directly relational to number of PUs ( ); that is, when the available PUs in an SU's neighborhood are less in number, the message exchange between the users is not high. Similarly, when
); that is, when the available PUs in an SU's neighborhood are less in number, the message exchange between the users is not high. Similarly, when  increases, the SUs can find more PUs in their neighborhood causing
increases, the SUs can find more PUs in their neighborhood causing  to increase. However, the values of
to increase. However, the values of  are not very high, showing the communication efficiency of our approach.
are not very high, showing the communication efficiency of our approach.
Explicitly Awarded Spectrum Sharing Agreements
Another important novelty of our approach is the ability of PUs to make explicit agreements with the neighboring SUs. The necessity of explicit agreements arrives in situations, where the corresponding PU's spectrum portion is in utilization at the time of CfP reception and therefore its current spectrum status is set to "busy." In our approach, the PUs can still send their explicit proposals to SUs when they get unoccupied. Each PU maintains a list of recent CfPs(stored in its cache), and, accordingly, it sends the proposal to the most suitable one whose deadline is not yet expired. In relation, Figure 15 delineates the percentage of explicitly awarded spectrum sharing agreements. It is clearly envisaged that almost 10 to 20% of the agreements have been explicitly awarded by the PUs.
Spectrum Deficit
Figure 16 depicts the percentage spectrum deficit ( ). One important reason to draw this graph is to see whether the values of
). One important reason to draw this graph is to see whether the values of  increase with large numbers of agents. This observation also shows the performance degradation of the whole system with an increased amount of traffic. In the corresponding figure, initially the values of
increase with large numbers of agents. This observation also shows the performance degradation of the whole system with an increased amount of traffic. In the corresponding figure, initially the values of  are within 60–80%, because at these stages most of the PUs are occupied. Later, the values of
are within 60–80%, because at these stages most of the PUs are occupied. Later, the values of  continue to decrease on a steady pace, as more PUs become available. Still, there is not a rapid degradation in overall system performance, showing the efficiency of our proposed solution.
continue to decrease on a steady pace, as more PUs become available. Still, there is not a rapid degradation in overall system performance, showing the efficiency of our proposed solution.
Comparison with Other Approaches
Finally, we compare our solution to greedy algorithm [22], cooperative local bargaining [21], and dynamic spectrum access protocol (DSAP) [16]. In greedy algorithm, most of the PUs are self-interested, and they are hesitant to share the available spectrum, until they get the highest offer maximizing their individual utility. Local bargaining is cooperative, where the users exchange messages and they self-organize into bargaining groups for spectrum sharing. DSAP is based on the concept of centralized licensed server which is responsible for leasing spectrum to the requesting users. Thus, we compare our approach to three different solutions showing greedy, cooperative, and centralized behaviors, respectively. All the solutions are implemented under our ad hoc scenario, and the users are deployed according to Poisson processes with  and
and  .
.
Figures 17(a) and 17(b) compare the average achieved utility values by the SUs and the communication cost associated with successful agreements, respectively. We notice that the utility values and communication cost for greedy approach is very high considering the selfish nature of the neighboring PUs. Consequently, most of the time SUs receive unsatisfactory proposals, and several messages are wasted. The local bargaining approach is limited to one-to-one bargaining, where an SU can bargain with only one PU at a time. Thus, local bargaining achieves similar utility to greedy approach at a reduced communication cost. Considering DSAP, the users exchange several kinds of messages including discover, offer, request, acknowledge, and reclaim, and so forth making its communication cost higher. However, due to its centralized nature, where several users cooperate with only one primary user for their spectrum assignments, DSAP behaves similar to our approach in terms of communication cost with lesser utility. On the other hand, our approach shows improvements in utility values compared to all three approaches incurring slightly higher communication cost than local bargaining.
7. Conclusion and Future Perspectives
In this paper, a cooperative approach to enable dynamic spectrum sharing is presented. The solution is based on multiagent cooperation, where the primary and secondary users exchange bilateral messages to make spectrum sharing agreements in an ad hoc manner. The behavioral modeling of our approach based on Petri nets proves its efficiency for dynamic and distributed environments. Experimental results show that, compared to greedy, bargaining, and centralized solutions, our cooperative solution works very effectively without having higher communication cost.
One important area of our future research corresponds to unlicensed spectrum sharing, where the spectrum can be viewed as an open "pool," and all the devices are of equal rights and priorities, that is, none of the devices have exclusive license for spectrum usage. The unlicensed devices (using multiagent system) can form necessary coalitions in order to maximize spectrum usage and minimize interferences. We are also planning to develop mathematical models for our approach to analyze its working with large numbers of agents.
References
Mchenry M: Spectrum white space measurements. New America Foundation Broadband Forum, June 2003
Mitola J: Cognitive radio: an integrated agent architecture for software defined radio, Ph.D. thesis. KTH Royal Institute of Technology, Stockholm, Sweden; 2000.
Sycara KP: Multiagent systems. AI Magazine 1998, 19(2):79-92.
Durfee EH, Lesser V: Negotiating task decomposition and allocation using partial global planning. Distributed Artificial Intelligence Journal 1989, 2: 229-244.
Smith RG: The contract net protocol: high-level communication and control in a distributed problem solver. IEEE Transactions on Computers 1980, 29(12):1104-1113.
Hsieh FS: Developing cooperation mechanism for multi-agent systems with Petri nets. Engineering Applications of Artificial Intelligence 2009, 22(4-5):616-627. 10.1016/j.engappai.2009.02.006
Mir U, Merghem-Boulahia L, Gaïti D: A cooperative multiagent based spectrum sharing. Proceedings of the 6th Advanced International Conference on Telecommunications (AICT '10), May 2010, Barcelona, Spain 124-130.
Mir U, Merghem-Boulahia L, Gaïti D: Multiagent based spectrum sharing using Petri nets. Proceedings of International Workshop on Artificial Intelligence and Distributed Systems (PAAMS '10), 2010, Salamanca, Spain
Kingman JFC: Poisson Processes. Clarendon Press, England, UK; 1993.
Jiang X, Howitt I, Raja A: Cognitive radio resource management using multi-agent systems. Proceedings of the 4th Annual IEEE Consumer Communications and Networking Conference (CCNC '07), January 2007, Las Vegas, Nev, USA 1121-1127.
Tonmukayakul A, Weiss MBH: An agent-based model for secondary use of radio spectrum. Proceedings of the 1st IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '05), November 2005, Baltimore, Md, USA 467-475.
Kloeck C, Jaekel H, Jondral F: Multi-agent radio resource allocation. Mobile Networks and Applications 2006, 11(6):813-824. 10.1007/s11036-006-0051-4
Weib G, Sen S: Adaptation and Learning in Multiagent Systems. Springer, Berlin, Germany; 1996.
Li H: Multi-agent Q-learning of channel selection in multi-user cognitive radio systems: a two by two case. Proceedings of IEEE International Conference on Systems, Man, and Cybernetics, 2009, San Antonio, Tex, USA 1395-1422.
Shiang HP, van der Schaar M: Delay-sensitive resource management in multi-hop cognitive radio networks. Proceedings of the 3rd IEEE Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '08), October 2008, Chicago, Ill, USA 120-131.
Brik V, Rozner E, Banerjee S, Bahl P: DSAP: a protocol for coordinated spectrum access. Proceedings of the 1st IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '05), November 2005, Baltimore, Md, USA 611-614.
Niyato D, Hossain E: Competitive pricing for spectrum sharing in cognitive radio networks: dynamic game, inefficiency of nash equilibrium, and collusion. IEEE Journal on Selected Areas in Communications 2008, 26(1):192-202.
Liu M, Ahmad SHA, Wu Y: Congestion games with resource reuse and applications in spectrum sharing. Proceedings of International Conference on Game Theory for Networks (GameNets '09), May 2009, Istanbul, Turkey 171-179.
Ghosh C, Agrawal DP, Rao MB: Channel capacity maximization in cooperative cognitive radio networks using game theory. ACM Mobile Computing and Communications 2009, 13: 2-13.
Hamdi K, Letaief KB: Cooperative communications for cognitive radio networks. Proceedings of the 8th Annual Postgraduate Symposium. Convergence of Telecommunications, Networking and Broadcasting, 2007, Liverpool, UK 878-893.
Cao L, Zheng H: Distributed spectrum allocation via local bargaining. Proceedings of the 2nd Annual IEEE Communications Society Conference on Sensor and AdHoc Communications and Networks (SECON '05), September 2005, Santa Clara, Calif, USA 475-486.
Zheng H, Peng C: Collaboration and fairness in opportunistic spectrum access. Proceedings of IEEE International Conference on Communications (ICC '05), May 2005, Seoul, Korea 3132-3136.
Kumar S, Raghavan VS, Deng J: Medium access control protocols for ad hoc wireless networks: a survey. Ad Hoc Networks 2006, 4(3):326-358. 10.1016/j.adhoc.2004.10.001
Wang H, Qin H, Zhu L: A survey on MAC protocols for opportunistic spectrum access in cognitive radio networks. Proceedings of International Conference on Computer Science and Software Engineering (CSSE '08), December 2008 214-218.
Sengupta S, Chatterjee M, Mainak K: Dynamic spectrum access in cognitive radio based tactical networks. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC '09), April 2009, Budapest, Hungary 1343-1348.
Zhang W, Mallik RK, ben Letaief K: Optimization of cooperative spectrum sensing with energy detection in cognitive radio networks. IEEE Transactions on Wireless Communications 2009, 8(12):5761-5766.
Qi C, Wang J, Li S: Weighted-clustering cooperative spectrum sensing In cognitive radio context. Proceedings of the WRI International Conference on Communications and Mobile Computing (CMC '09), January 2009 102-106.
Clancy TC: Dynamic spectrum access in cognitive radio networks, Ph. D. dissertation. University of Maryland, College Park, Md, USA; 2006.
Proth J-M, Xie X: Petri Nets: A Tool for Design and Management of Manufacturing Systems. John Wiley & Sons, West Sussex, UK; 1996.
Murata T: Petri nets: properties, analysis and applications. Proceedings of the IEEE 1989, 77(4):541-580. 10.1109/5.24143
Liu Z: Performance analysis of stochastic timed petri nets using linear programming approach. IEEE Transactions on Software Engineering 1998, 24(11):1014-1030. 10.1109/32.730548
Xing Y: Cognitive radio networks: learning, games and optimization, Ph.D. thesis. Stevens Institute of Technology, Hoboken, NJ, USA; 2006.
Kim D, Le L, Hossain E: Joint rate and power allocation for cognitive radios in dynamic spectrum access environment. IEEE Transactions on Wireless Communications 2008, 7(12):5517-5527.
McHenry MA: NSF spectrum occupancy measurements project summary. August 2005.
Acknowledgment
This effort is partly sponsored by the technologies for terminals in opportunistic radio applications (TEROPP) Project of French National Research Agency (ANR) under Grant no. ER502-505E and is also partly supported by the Higher Education Commission (HEC), Pakistan.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mir, U., Merghem-Boulahia, L. & Gaïti, D. COMAS: A Cooperative Multiagent Architecture for Spectrum Sharing. J Wireless Com Network 2010, 987691 (2010). https://doi.org/10.1155/2010/987691
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/987691





 the set of input places p of a transition
the set of input places p of a transition  :
: 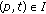 ;
; the set of output places p of a transition
the set of output places p of a transition  :
: 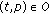 ;
; the set of input transitions t of a place
the set of input transitions t of a place 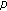 :
:  ;
;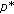 the set of output transitions t of a place
the set of output transitions t of a place 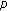 :
: 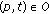 .
.










