- Review Article
- Open access
- Published:
List Decoding of Generalized Reed-Solomon Codes by Using a Modified Extended Key Equation Algorithm
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 212136 (2011)
Abstract
This work presents a modified extended key equation algorithm in list decoding of generalized Reed-Solomon (GRS) codes. A list decoding algorithm of generalized Reed-Solomon codes has two steps, interpolation and factorization. The extended key equation algorithm (EKE) is an interpolation-based approach with a lower complexity than Sudan's algorithm. To increase the decoding speed, this work proposes a modified EKE algorithm to perform codeword checking prior to such an interpolation process. Since the evaluation mapping is engaged in encoding, a codeword is not generated systematically. Thus, the transmission information is not directly obtained from a received codeword. Therefore, the proposed algorithm undertakes a matrix operation to obtain the transmission information once a received vector has been checked to be error-free. Simulation results demonstrate that the modified EKE algorithm in list decoding of a GRS code provides low complexity, particularly at high signal-to-noise ratios.
1. Introduction
Reed-Solomon (RS) codes are currently used in a wide variety of applications, ranging from data storage systems, mobile communications, to satellite communications. The third-generation (3G) wireless standard utilizes RS codes as outer codes. For CDMA2000 high-rate broadcast packet data air interface [1], they are expected to be adopted as outer codes in concatenated coding schemes for future fourth-generation (4G) wireless systems.
Algorithms for hard decision decoding of RS codes are typically classified into two well-known types, namely, syndrome-based decoding and interpolation-based decoding. Well-developed algorithms in the first category include the Peterson-Gorenstein-Zierler algorithm [2], Berlekamp-Massey algorithm [2, 3], Euclidean algorithm [2, 3], frequency domain algorithm [2, 3], and step-by-step algorithm [4–7]. Algorithms in the second category include the Welch-Berlekamp algorithms [8, 9] and list decoding algorithms [10–12], as Koetter-Vardy algorithm [13] is also a list decoding algorithm but with soft decision approaching.
Sudan's algorithm [10] decodes GRS codes in two steps involved, namely, interpolation and factorization. An interpolation is performed on a received word  , producing a nonzero bivariate polynomial
, producing a nonzero bivariate polynomial  with at least
with at least  points
points  , such that
, such that  and
and  . Factorization is then performed on
. Factorization is then performed on  , yielding linear factors (or called
, yielding linear factors (or called  -root polynomials)
-root polynomials)  . The codewords are then generated from these distinct factors
. The codewords are then generated from these distinct factors  via an evaluation mapping. A decoded codeword
via an evaluation mapping. A decoded codeword  is chosen if the Hamming distance between
is chosen if the Hamming distance between  and
and  is
is  or less.
or less.
Because solving these interpolation equations of Sudan's algorithm with a naïve Gaussian elimination requires the time complexity  , an EKE algorithm has been presented to decrease this complexity [12]. The EKE algorithm employs generalized Berlekamp-Massy algorithm (or the Feng-Tzeng algorithm in [14]) that obtains the shortest recurrence that generates a given sequence, and the time complexity of EKE to solve these interpolation equations is
, an EKE algorithm has been presented to decrease this complexity [12]. The EKE algorithm employs generalized Berlekamp-Massy algorithm (or the Feng-Tzeng algorithm in [14]) that obtains the shortest recurrence that generates a given sequence, and the time complexity of EKE to solve these interpolation equations is  .
.  represents a design parameter, typically a small constant, which is an upper bound on the size of the list of decoded codewords.
represents a design parameter, typically a small constant, which is an upper bound on the size of the list of decoded codewords.
Guruswami and Sudan (GS) presented an improvement on Sudan's algorithm [11], by introducing a multiplicity  at each interpolation point. A nonzero
at each interpolation point. A nonzero  polynomial exists that interpolates the points
polynomial exists that interpolates the points  ,
,  with multiplicity
with multiplicity  , and is formed by
, and is formed by  , where
, where  , and the expression of
, and the expression of  denotes the number of ways to choose
denotes the number of ways to choose  from
from  . In comparison with Sudan's work, the GS algorithm provides more
. In comparison with Sudan's work, the GS algorithm provides more  linear homogeneous equations in interpolation, thus improving the decoding correction distance. Increasing
linear homogeneous equations in interpolation, thus improving the decoding correction distance. Increasing  improves the decoding performance but also increases the required complexity. The asymptotical decoding correction fraction is given by
improves the decoding performance but also increases the required complexity. The asymptotical decoding correction fraction is given by  , and the code rate
, and the code rate  is given by
is given by  . The increase in decoding capability is substantial, especially for low-rate GRS codes.
. The increase in decoding capability is substantial, especially for low-rate GRS codes.
Koetter and Vardy [13] extended the GS algorithm by incorporating the soft information received from a channel into the interpolation process. With a complexity that is a polynomial of the code length, the Koetter-Vardy (KV) algorithm can achieve a substantial coding gain over the GS algorithm. For instance, at a frame-error-rate (FER) of  , the KV algorithm can achieve a coding gain of about 1 dB over the GS algorithm, for a (255, 144) GRS code transmitted over an additive white Gaussian noise (AWGN) channel using 256-QAM modulation [13].
, the KV algorithm can achieve a coding gain of about 1 dB over the GS algorithm, for a (255, 144) GRS code transmitted over an additive white Gaussian noise (AWGN) channel using 256-QAM modulation [13].
However, those approaches have a drawback, that is codeword checking is absent during decoding. In other words, regardless of whether the received sequence is correct or not, the decoding algorithm proceeds to decode it. This work overcomes this drawback by presenting a modified EKE algorithm with codeword checking. Additionally, a matrix operation is also proposed to obtain the transmission information from the received codeword. As in syndrome-based decoding, if the syndrome vector is all-zero, then the decoding process is terminated and the received sequence is output as a decoded codeword. The rest of this paper is organized as follows. Section 2 introduces the EKE algorithm. Section 3 then presents the modified EKE algorithm with the proposed codeword checking method and the matrix operation to obtain the transmission information from the received codeword. Finally, simulations and conclusions are presented in Section 4.
2. Extended Key Equation Algorithm
Consider an evaluation mapping  and
and  . A codeword in an
. A codeword in an  GRS code over GF(
GRS code over GF( ) is generated as
) is generated as

where the information vector is  , the generator matrix is
, the generator matrix is

and  is a primitive element in GF(
is a primitive element in GF( ).
).
The term  is the upper bound of the number of consistent codewords, which are at Hamming distance
is the upper bound of the number of consistent codewords, which are at Hamming distance  from any received word. For an
from any received word. For an  GRS code, Sudan's algorithm corrects any error pattern of up to
GRS code, Sudan's algorithm corrects any error pattern of up to  errors for
errors for

where  denotes the smallest nonnegative integer holding the following equation:
denotes the smallest nonnegative integer holding the following equation:

Assuming that  , the value of
, the value of  becomes
becomes

Let  be a field, and let
be a field, and let  represent the set of all polynomials of degree
represent the set of all polynomials of degree  in the variable
in the variable  over
over  . Sudan's algorithm consists of the following steps.
. Sudan's algorithm consists of the following steps.
-
(1)
Find a nonzero bivariate polynomial
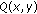 over
over  with at least
with at least  points
points  , such that
, such that  and
and  , for a received vector
, for a received vector  .
. -
(2)
Output all polynomials
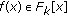 for which
for which 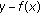 is a factor of
is a factor of  and
and  for at least
for at least  locators
locators  .
.
In [2, 3], for an  RS code, the error-locator polynomial
RS code, the error-locator polynomial  and the error-evaluator polynomial
and the error-evaluator polynomial  are computed in the following key equation (KE):
are computed in the following key equation (KE):

In [12], based on the linear factors of bivariate polynomials  where the polynomial arithmetic is carried out modulo a power of
where the polynomial arithmetic is carried out modulo a power of  in Sudan's algorithm, an EKE algorithm is derived as follows:
in Sudan's algorithm, an EKE algorithm is derived as follows:

where  ,
,  , and
, and  are polynomials that satisfy certain degree constraints and
are polynomials that satisfy certain degree constraints and  are syndrome polynomials computed as follows:
are syndrome polynomials computed as follows:


Furthermore, the above equation can be obtained as follows:

which is denoted as

Let

where  and
and  . After these polynomials
. After these polynomials  ,
,  , have been computed in (11) by using the Feng-Tzeng algorithms [14] or a similar algorithm mentioned in [12], the polynomial
, have been computed in (11) by using the Feng-Tzeng algorithms [14] or a similar algorithm mentioned in [12], the polynomial  is obtained as follows:
is obtained as follows:

and satisfies

A design parameter  in [12] is an upper bound on the size of the list of decoded codewords. For code rate
in [12] is an upper bound on the size of the list of decoded codewords. For code rate  , from (4), the value of
, from (4), the value of  is determined by the following range:
is determined by the following range:

The EKE algorithm employs the Feng-Tzeng algorithm [14] to decode GRS codes. The dimensions of the  -matrix in (11) are
-matrix in (11) are  by
by  . Since the Feng-Tzeng algorithm is run column by column in a matrix, therefore the column length dominates the decoding complexity. Reducing the column length lowers the complexity of locating the smallest set of linear dependent coefficients. The algorithm of [12] requires the solving of
. Since the Feng-Tzeng algorithm is run column by column in a matrix, therefore the column length dominates the decoding complexity. Reducing the column length lowers the complexity of locating the smallest set of linear dependent coefficients. The algorithm of [12] requires the solving of  homogeneous linear equations in (11) and then finding the corresponding coefficients of
homogeneous linear equations in (11) and then finding the corresponding coefficients of  in (14). Hence, the time complexity is
in (14). Hence, the time complexity is  , which is less than the time complexity of
, which is less than the time complexity of  of Sudan's algorithm. Consequently, the EKE algorithm is more attractive than the algorithm of [10].
of Sudan's algorithm. Consequently, the EKE algorithm is more attractive than the algorithm of [10].
3. Modified Extended Key Equation Algorithm
Since the polynomial  is associated with a codeword
is associated with a codeword  , which has zeros
, which has zeros  [15], a parity-check matrix for
[15], a parity-check matrix for  is given by [16, 17]
is given by [16, 17]

Theorem 1.
For a received vector  , codeword checking
, codeword checking  is equal to the computation of
is equal to the computation of  , which is
, which is

where  denotes the matrix transpose.
denotes the matrix transpose.
Proof.
For computing the value of  in (9), a different element
in (9), a different element  should yield a different result for
should yield a different result for  . Consequently, the value of
. Consequently, the value of  can be simplified as
can be simplified as

Equation (9) becomes

For the vector  , the calculation of each
, the calculation of each  can be denoted as follows:
can be denoted as follows:

and the vector  becomes
becomes

Theorem 2.
The codeword checking  is checked to be all-zero, and then the transmission message is given by
is checked to be all-zero, and then the transmission message is given by

where  is the last
is the last  -tuple of
-tuple of  and
and  is a
is a  matrix such that
matrix such that  is a systematical matrix.
is a systematical matrix.
Proof.
The proof is quite trivial. In the expression of (1),

Then,

Example 1.
For a (7, 3) GRS code over GF(23) generated by the polynomial  , a codeword
, a codeword  is given by the evaluation mapping provided as the transmission message
is given by the evaluation mapping provided as the transmission message  . If the codeword is transmitted over an error-free channel, then
. If the codeword is transmitted over an error-free channel, then  is checked to be all-zero by (17) and the transmission message is computed by (22) as follows:
is checked to be all-zero by (17) and the transmission message is computed by (22) as follows:

where

With the above theorems, the list decoding algorithm [12] of an  ,
,  GRS code is adjusted as follows.
GRS code is adjusted as follows.
-
(1)
Perform codeword-checking,
 , for a received vector
, for a received vector 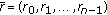 . If
. If  is an all-zero vector, then output the corresponding message vector
is an all-zero vector, then output the corresponding message vector  determined as
determined as 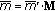 , where a vector
, where a vector  is the last
is the last  -tuple of
-tuple of 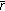 . Then, go to step 5.
. Then, go to step 5. -
(2)
Perform the EKE interpolation:
-
(a)
compute the syndrome polynomials in parallel:
 and
and 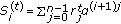 and
and  ,
, -
(b)
find polynomial polynomials
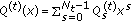 , where
, where  , by the Feng-Tzeng algorithm such that
, by the Feng-Tzeng algorithm such that  ,
,  ,
, -
(c)
form the bivariate polynomial
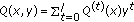 , and then obtain the polynomial
, and then obtain the polynomial  satisfying
satisfying  ,
, 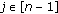 .
.
-
(a)
-
(3)
Perform the factorization on the bivariate polynomial
 by employing the reconstruction algorithm [12] to find the
by employing the reconstruction algorithm [12] to find the  -root polynomials
-root polynomials 
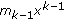 .
. -
(4)
Generate the corresponding codeword
 for each polynomial
for each polynomial 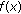 . Output the message vectors
. Output the message vectors 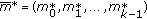 of the codewords
of the codewords  with the Hamming distance to
with the Hamming distance to  equal to
equal to  or less.
or less. -
(5)
Terminate decoding
4. Simulations and Conclusions
Figure 1 displays the decoding performance of listing decoding [12] with the modified EKE algorithm as a (255, 223, 33) GRS code and a (255, 239, 17) GRS code are transmitted with BPSK signaling over AWGN channels. Figure 2 illustrates the probability of the EKE algorithm being executed in such a listing decoding. Those simulations demonstrate that codeword checking has little effect on decoding at low signal-to-noise ratios. However, the modified EKE algorithm provides lower decoding complexity when the signal-to-noise is high. At a block error rate (BER) of  , the probabilities of the EKE algorithm being utilized in list decoding of these two GRS codes are 0.98 and 0.75, respectively. This work presents a modified EKE algorithm, incorporating codeword checking and a matrix operation, which obtains the transmission information from the received codeword. The computation of codeword checking does not increase the complexity of the original EKE algorithm, because it is an item in the original decoding process. The proposed EKE algorithm is beneficial when the signal-to-noise ratio is high.
, the probabilities of the EKE algorithm being utilized in list decoding of these two GRS codes are 0.98 and 0.75, respectively. This work presents a modified EKE algorithm, incorporating codeword checking and a matrix operation, which obtains the transmission information from the received codeword. The computation of codeword checking does not increase the complexity of the original EKE algorithm, because it is an item in the original decoding process. The proposed EKE algorithm is beneficial when the signal-to-noise ratio is high.
References
Agashe P, Rezaiifar R, Bender P: CDMA2000® high rate broadcast packet data air interface design. IEEE Communications Magazine 2004, 42(2):83-90.
Wicker SB: Error Control Systems for Digital Communication and Storage. Prentice Hall, New York, NY, USA; 1995.
Lin S, Costello DJ Jr.: Error Control Coding. 2nd edition. Prentice Hall, New York, NY, USA; 2004.
Peterson WW, Weldon EJ: Error-Control Codes. 2nd edition. MIT Press, Cambridge, Mass, USA; 1972.
Massy JL: Step-by-step decoding of Bose-Chauhuri-Hocquenghem codes. IEEE Transactions on Information Theory 1965, 11(4):580-585. 10.1109/TIT.1965.1053833
Wei SW, Wei CH: High-speed decoder of Reed-Solomon codes. IEEE Transactions on Communications 1993, 41(11):1588-1593. 10.1109/26.241736
Chen TC, Wei CH, Wei SW: Step-by-step decoding algorithm for Reed-Solomon codes. IEE Proceedings Communications 2000, 147(1):8-12. 10.1049/ip-com:20000149
Welch L, Berlekamp ER: Error correction for algebraic block codes. U.S. Patent 4 633 470, 1983
Fedorenko SV: A simple algorithm for decoding Reed-Solomon codes and its relation to the Welch-Berlekamp algorithm. IEEE Transactions on Information Theory 2005, 51(3):1196-1198. 10.1109/TIT.2004.842738
Sudan M: Decoding of Reed Solomon codes beyond the error-correction bound. Journal of Complexity 1997, 13(1):180-193. 10.1006/jcom.1997.0439
Guruswami V, Sudan M: Improved decoding of reed-solomon and algebraic-geometry codes. IEEE Transactions on Information Theory 1999, 45(6):1757-1767. 10.1109/18.782097
Roth RM, Ruckenstein G: Efficient decoding of Reed-Solomon codes beyond half the minimum distance. IEEE Transactions on Information Theory 2000, 46(1):246-257. 10.1109/18.817522
Koetter R, Vardy A: Algebraic soft-decision decoding of Reed-Solomon codes. IEEE Transactions on Information Theory 2003, 49(11):2809-2825. 10.1109/TIT.2003.819332
Feng GL, Tzeng KK: A generalization of the Berlekamp-Massey algorithm for multisequence shift-register synthesis with applications to decoding cyclic codes. IEEE Transactions on Information Theory 1991, 37(5):1274-1287. 10.1109/18.133246
MacWilliams FJ, Sloane NJ: The Theory of Error Correcting Codes. North Holland, Amsterdam, The Netherlands; 1977.
McEliece RJ: The Theory of Information and Coding. 2nd edition. Cambridge University Press, Cambridge, UK; 2002.
Pellikaan R, Wu XW: List decoding of q-ary Reed-Muller codes. IEEE Transactions on Information Theory 2004, 50(4):679-682. 10.1109/TIT.2004.825043
Acknowledgment
The authors would like to thank the National Science Council of the Republic of China, Taiwan, for financially supporting this research under Contract no. NSC 97-2221-E-212-005.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hu, TH., Chang, MH. List Decoding of Generalized Reed-Solomon Codes by Using a Modified Extended Key Equation Algorithm. J Wireless Com Network 2011, 212136 (2011). https://doi.org/10.1155/2011/212136
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/212136
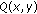 over
over  with at least
with at least  points
points  , such that
, such that  and
and  , for a received vector
, for a received vector  .
.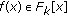 for which
for which 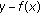 is a factor of
is a factor of  and
and  for at least
for at least  locators
locators  .
. , for a received vector
, for a received vector 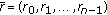 . If
. If  is an all-zero vector, then output the corresponding message vector
is an all-zero vector, then output the corresponding message vector  determined as
determined as 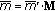 , where a vector
, where a vector  is the last
is the last  -tuple of
-tuple of 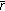 . Then, go to step 5.
. Then, go to step 5. and
and 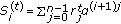 and
and  ,
,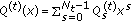 , where
, where  , by the Feng-Tzeng algorithm such that
, by the Feng-Tzeng algorithm such that  ,
,  ,
,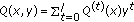 , and then obtain the polynomial
, and then obtain the polynomial  satisfying
satisfying  ,
, 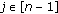 .
. by employing the reconstruction algorithm [
by employing the reconstruction algorithm [ -root polynomials
-root polynomials 
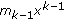 .
. for each polynomial
for each polynomial 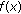 . Output the message vectors
. Output the message vectors 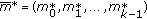 of the codewords
of the codewords  with the Hamming distance to
with the Hamming distance to  equal to
equal to  or less.
or less.
