- Research Article
- Open access
- Published:
Lower Bound of Energy-Latency Tradeoff of Opportunistic Routing in Multihop Networks
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 265083 (2011)
Abstract
Opportunistic networking aims at exploiting sporadic radio links to improve the connectivity of multihop networks and to foster data transmissions. The broadcast nature of wireless channels is an important feature that can be exploited to improve transmissions by using several potential receivers. Opportunistic relaying is thus the first brick for opportunistic networking. However, the advantage of opportunistic relaying may be degraded due to energy increase related to having multiple active receivers. This paper proposes a thorough analysis of opportunistic relaying efficiency under different realistic radio channel conditions. The study is intended to find the best tradeoff between two objectives: energy and latency minimizations, with a hard reliability constraint. We derive an optimal bound, namely, the Pareto front of the related optimization problem, which offers a good insight into the benefits of opportunistic routings compared with classical multihop routing schemes. Meanwhile, the lower bound provides a framework to optimize the parameters at the physical layer, MAC layer, and routing layer from the viewpoint of cross layer during the design or planning phase of a network.
1. Introduction
Opportunistic networking refers to all techniques which provide advantages from the use of spontaneous radio links in mobile ad-hoc networks (MANETs) [1]. In classical networking instead, the link between pairwise node is distinguished as being connected or not. This kind of classification relies on the traditional layered design of networking: the PHY and MAC layers ensure a perfect connection of some preselected links and the routing layer selects the path from these links.
However, in practice, due to the complexity of wireless environment and possible movement of nodes or surrounding objects, a network is an evolving process with unstable links and always remaining in an intermediate state, that is, partially connected, as presented in [2–5]. Moreover, these works have shown that unreliable links can be effectively exploited to improve the performance of the MAC or routing layer. More specifically, opportunism may improve the performance of multihop routing by selecting one relay according to its instantaneous linking status. Additionally, in our previous work [6], we quantified how unreliable links can improve the connectivity of Wireless Sensor Networks (WSNs) by exploiting the broadcast nature of the wireless medium, where all nodes are assumed to be simultaneously active and to try to receive a packet.
Opportunistic forwarding techniques, for example, [7, 8], exploit the same principle, that is, unreliable links, to improve multihop transmissions. The idea of opportunistic forwarding is that at each hop, a set of next-hop relay candidates which have successfully received a packet compete for acting as a relay. During the relay-selection phase, a priority is assigned to each relay candidate according to a predefined metric, for example, the geographical closeness of the relay candidate to the destination [9] as shown in Figure 1.
The objective of this paper consists of the evaluation of the maximal efficiency that can be achieved with such opportunistic routing schemes, namely, finding an optimal set of forwarding nodes to balance energy cost and the transmission delay. The efficiency of opportunistic communications can be evaluated from different viewpoints. For multihop networks, we identify three important performance parameters: the end-to-end reliability, the end-to-end delay (referred to as latency hereafter), and the energy consumption. Accordingly, to evaluate opportunistic communications fairly, we introduce a multiobjective optimization framework [10]. Due to the fundamentality of reliability, we consider it as a hard constraint in this paper. The use of acknowledged transmissions allows to fulfill this constraint, at least from a theoretical point of view. The other two constraints, that is, energy and latency, are considered as two competing objective functions that should be simultaneously minimized.
Several previous works on opportunistic routings, such as [7, 9, 11–13], provide the analysis of energy and latency performances. In [7, 11], energy and latency performances of a routing scheme called GeRaF are analyzed, and the effects of node density, traffic load, and duty cycle are evaluated. The simulations in [12] show the impacts of node density, radio channel quality and traffic rate on the energy consumption at each node, the average delay of packet and the goodput of opportunistic protocol. It is concluded that the benefit of opportunistic scheme is about 10% decrease in power and 40% reduction in delay. Whereas these analysis are based on an unrealistic disc link model [5, 6], which relies on the definition of a reception threshold level and is not well adapted to the research of opportunistic communications due to the neglect of propagation phenomena, for example, fading and shadowing. Furthermore, the energy efficiency of the protocol CAGIF [13] is studied in a fading channel, where the whole set of neighbor nodes try to receive packets from the source node, which may degrade energy performance. In order to improve the energy efficiency, an efficient selection mechanism of relay nodes is proposed in [9], rather than choosing all the neighbors as relay candidates. Simulation results of [9] in a shadowing channel indicate that the energy efficiency is greatly improved.
However, in the aforementioned studies, a fixed transmission power is considered, and the number of relay candidates is chosen according to a given routing policy, without providing any proof of optimality. Therefore, these studies are insufficient to determine whether the relative low performances of opportunistic routing are intrinsic to this kind of routing or due to the specific protocol (relay selection policy, fixed power choice, etc.).
Concerning this question, we propose in this paper to analyze the lower bound of the energy-latency tradeoff for opportunistic communications under a hard end-to-end reliability constraint. To obtain this bound, we consider the size of candidate cluster and the transmission power as variables of the optimization problem. Firstly, we do not focus on the relay selection mechanism here but on the two following issues: what is the best set of relay candidates and what is the performance of the optimized set of candidates? Then, according to the theoretical analysis, we propose an opportunistic routing protocol to reach the best performance of a network.
With regard to the routing policy, we assume that for a given cluster, only the candidate closest to the destination is selected to forward the packet. Such a strategy obviously relies on the assumption that each node has the full knowledge of the position of itself and the destination. Once a node has a packet to send, it appends the locations of itself and the intended relay cluster to the packet and then broadcasts it. The relay candidates which successfully receive the packet (solid nodes in Figure 1) assess their own priorities of acting as relay, based on how close they are to the destination. The best relay which is the closest to the destination forwards the packet, as shown in Figure 1. In contrast with the the aforementioned schemes, this scheme utilizes an optimized candidate cluster, instead of all active neighbors, to receive the packet for the purpose of saving energy and taking advantage of the spatial diversity.
The main contributions of this paper are the following.
-
(i)
A general framework for evaluating the maximal efficiency of the opportunistic routing principle is provided. Energy and latency are compromised under an end-to-end reliability constraint.
-
(ii)
The Pareto front of energy-latency tradeoff is derived in different scenarios. A closed-form expression of energy-latency tradeoff, when the number of relay candidates is fixed, and an algorithm to find the optimal number of relay candidates are proposed. The simulation results verify the correctness of this lower bound in a 2-dimension Poisson distributed network. The numerical analysis show that opportunistic routing is inefficient in an Additive White Gaussian Noise (AWGN) channel; however, it is efficient in Rayleigh block fading and Rayleigh fast fading channels on the condition of a small-size cluster.
-
(iii)
The lower bound of energy efficiency and its corresponding maximal delay are derived.
-
(iv)
An opportunistic protocol is proposed to minimize energy consumption under a delay constraint.
The remaining part of this paper is organized as follows: Section 2 describes the models and metrics used in this paper. In Section 3, the lower bound of energy-delay tradeoff of one-hop transmission is deduced, and the lower bound of energy efficiency is obtained for the delay-tolerant applications. The result about one-hop transmission is extended to the scenario of multihop transmissions in Section 4, and the gain of opportunistic communications on the energy efficiency is analyzed. In Section 5, the lower bounds proposed are applied to optimize the physical parameters of a network. In Section 6, a novel opportunistic protocol is introduced, and the simulation results using this protocol verify the theoretical analysis. Section 7 discusses the significance of these results and gives some conclusions.
2. Models and Metrics
This section introduces the problem formulation by modeling wireless links, energy consumption, and transmission delay. Two metrics are proposed and referred to as mean energy distance ration per bit ( ) and mean delay distance ratio (
) and mean delay distance ratio ( ). For the readability, all parameters used in this paper are described in Table 1. The values of parameter about nodes are obtained from the datasheet of [14].
). For the readability, all parameters used in this paper are described in Table 1. The values of parameter about nodes are obtained from the datasheet of [14].
2.1. System Model
In this paper, the nodes in a network are assumed to be independently and randomly distributed according to a random Poisson process of density  . The probability of finding
. The probability of finding  nodes in a region
nodes in a region  follows a two-dimensional Poisson distribution
follows a two-dimensional Poisson distribution

with  , where
, where  is the surface of
is the surface of  ,
,  represents the exponential function.
represents the exponential function.
We consider the case of a source node  forwarding a packet to a sink/destination node
forwarding a packet to a sink/destination node  .
.  is one of
is one of  's neighbors which is closer to
's neighbors which is closer to  than
than  .
.
In addition, each  is associated with a pair,
is associated with a pair,  , where
, where  , as detailed in (9), is the link probability between
, as detailed in (9), is the link probability between  and
and  and
and  is the effective transmission distance given by
is the effective transmission distance given by

where  and
and  are the Euclidian distance between
are the Euclidian distance between  and
and  and that between
and that between  and
and  , respectively.
, respectively.
 is aware of its own location and those of its neighbors and the destination
is aware of its own location and those of its neighbors and the destination  and gets their link probability
and gets their link probability  s, such that
s, such that  can select a set of forwarding candidates among its neighbors according to some kind of priority, for example, the distance to the destination node. Let
can select a set of forwarding candidates among its neighbors according to some kind of priority, for example, the distance to the destination node. Let  denote the forwarding candidate set, which includes all the nodes involved in the local collaborative forwarding. The number of nodes in
denote the forwarding candidate set, which includes all the nodes involved in the local collaborative forwarding. The number of nodes in  is
is  .
.
2.2. Energy Consumption Models
According to the previous assumptions, the energy consumption for transmitting one packet  is composed of three parts: the energy consumed by the transmitter
is composed of three parts: the energy consumed by the transmitter  , by the receiver
, by the receiver  , and by the acknowledgment packet exchange
, and by the acknowledgment packet exchange 

In this work, these energy consumption components are expressed according to the models proposed in [15]


We further assume that the same transmission scheme is used for data and acknowledgment transmissions, which allows another assumption that the acknowledgment energy is a fraction of the data transmission one

where  represents the length's ratio between ACK and data packets. We also assume that an ACK packet is much smaller than a data packet [17], that is,
represents the length's ratio between ACK and data packets. We also assume that an ACK packet is much smaller than a data packet [17], that is,  .
.
Therefore, the energy consumption per bit defined by  is given by
is given by

where  and
and  stand, respectively, for the radio emission energy and the circuit energy per node. Both are obtained by identifying (4)–(6) into(3)
stand, respectively, for the radio emission energy and the circuit energy per node. Both are obtained by identifying (4)–(6) into(3)

where  . The related parameters are described in Table 1.
. The related parameters are described in Table 1.
2.3. Realistic Unreliable Link Models
As claimed in the introduction, transmission errors play an important role in reliable communications. Hence, we consider herein the radio link probability as the metric of link quality, which is derived from the packet error rate (PER) according to [17]

where  is the PER obtained according to a signal to noise ratio (SNR)
is the PER obtained according to a signal to noise ratio (SNR)  .
.  is the SNR between nodes
is the SNR between nodes  and
and  , which derives from the classical attenuation model in [15]
, which derives from the classical attenuation model in [15]

where  denotes the transmission distance between nodes
denotes the transmission distance between nodes  and
and  ,
,  for the sake of simplicity. Refer to Table 1 for other parameters.
for the sake of simplicity. Refer to Table 1 for other parameters.
PER may have various forms depending on the transmission technology (modulation, coding, diversity, etc.). The unreliable link models are approximated for AWGN and Rayleigh block fading channels, respectively, as follows (refer to [17] for more details): in AWGN channels,

in Rayleigh fast fading channels,

and in Rayleigh block fading channels,

where  and
and  rely on the modulation type and order; for example, for Multiple Quadrature Amplitude Modulation (MQAM),
rely on the modulation type and order; for example, for Multiple Quadrature Amplitude Modulation (MQAM),  and
and  . For BPSK,
. For BPSK,  and
and  .
.
Meanwhile, according to the opportunistic relaying principle, the successful transmission means that at least one node receives the packet correctly. Therefore, for  forwarding nodes whose sequence is based on the protocol priority, the probability of a successful transmission is
forwarding nodes whose sequence is based on the protocol priority, the probability of a successful transmission is

where  is the link probability between
is the link probability between  and node
and node  as defined in (9).
as defined in (9).
To ensure reliable transmissions, a retransmission procedure with an acknowledgment mechanism is adopted. Assuming a simple infinite retransmission scheme until success, the average transmissions number  is the sum of a geometric series
is the sum of a geometric series

where  is the number of transmissions,
is the number of transmissions,  and
and  are the successful transmission probability of data packet and ACK packet, respectively, calculated by (14).
are the successful transmission probability of data packet and ACK packet, respectively, calculated by (14).
For the sake of simplicity, however, the ACK packet failures will be neglected (i.e.,  ), which is based on the three following points: Firstly, ACK packets are supposed to be much smaller than data packets. For instance, for ACK and data packet lengths of 26 and 320 bytes, respectively, a successful data transmission probability of 80% corresponds to an ACK transmission probability of 98%. Secondly, data and ACK packets are supposed to experience the same channel state [18]. Thirdly, a more efficient coding scheme can be used for ACK packets to improve its reliability if necessary. Under this assumption,
), which is based on the three following points: Firstly, ACK packets are supposed to be much smaller than data packets. For instance, for ACK and data packet lengths of 26 and 320 bytes, respectively, a successful data transmission probability of 80% corresponds to an ACK transmission probability of 98%. Secondly, data and ACK packets are supposed to experience the same channel state [18]. Thirdly, a more efficient coding scheme can be used for ACK packets to improve its reliability if necessary. Under this assumption,  can be approximated by
can be approximated by

where  stands for
stands for  for simplification.
for simplification.
2.4. Mean Energy Distance Ratio Per Bit (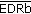 )
)
The energy efficiency definition is not unique and relies on the applicative framework [15]. In this paper, we focus our work on periodic monitoring applications which suggest that a good metric is the energy per correctly received bit. Moreover, since the energy cost increases monotonically with the transmission distance, the mean Energy Distance Ratio per bit ( ) metric (in
) metric (in  ) as proposed in [16] is relevant and represents the energy consumption for transmitting one bit over one meter. According to the definition of
) as proposed in [16] is relevant and represents the energy consumption for transmitting one bit over one meter. According to the definition of  , we have
, we have

where  is the expected transmission distance for opportunistic communication. The effective distance depends on the retransmission priority policy. After ordering the nodes
is the expected transmission distance for opportunistic communication. The effective distance depends on the retransmission priority policy. After ordering the nodes  from the first priority to the last one, the average effective distance becomes
from the first priority to the last one, the average effective distance becomes

The substitution of (7), (16), and (18) into (17) leads to

It should be noticed that this metric integrates all physical and link layers parameters, so that we can use this metric to analyze the joint PHY/MAC efficiency.
2.5. Mean Delay Distance Ratio (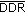 )
)
The delay of a packet to be transmitted over one hop,  , is defined as the sum of three delay components. The first component is the queuing delay during which a packet waits for being transmitted,
, is defined as the sum of three delay components. The first component is the queuing delay during which a packet waits for being transmitted,  . The second component is the transmission delay that is equal to
. The second component is the transmission delay that is equal to  . The third component is
. The third component is  . Note that we neglect the propagation delay because the transmission distance between two nodes is usually short in multihop networks.
. Note that we neglect the propagation delay because the transmission distance between two nodes is usually short in multihop networks.
Furthermore, a reliable one-hop transmission will suffer from the delay caused by retransmissions. According to (16), the mean delay of a reliable one-hop transmission is

Since delay raises with the increase of the distance between the source node and the destination node, we propose a new delay metric, the Delay Distance Ratio ( ), which is defined as
), which is defined as

Note that  includes all factors of physical and link layers also, so
includes all factors of physical and link layers also, so  and
and  are the effective metrics to measure the effect of these parameters on the energy efficiency and the delay of a network.
are the effective metrics to measure the effect of these parameters on the energy efficiency and the delay of a network.
3. Energy-Delay Tradeoff for One-HopTransmission
In this section, we analyze the energy-latency tradeoff under the reliability constraint in the scenario of one-hop transmission. The optimal transmission power and the optimal number of receivers will be analyzed and the closed-form expression of lower bound of energy-delay tradeoff is obtained.
The energy-delay tradeoff of one-hop transmission can be abstracted as a constrained optimization problem

where ddr refers to the delay constraint. Consequently, minimizing the energy consumption under a delay constraint can be achieved by finding the three parameters  for one-hop transmission, where
for one-hop transmission, where  is the optimal transmission power,
is the optimal transmission power,  is the optimal number of opportunistic relay candidates,
is the optimal number of opportunistic relay candidates, is the optimal transmission distance for each relay candidate.
is the optimal transmission distance for each relay candidate.
This is a mixed integer nonlinear programming (MINLP) problem that can be solved using a branch-and-bound algorithm [19], but it is time consuming. We propose in the following an alternative which relies on an analytic solution when the size of the forwarding set is constant. A simple iterative procedure is then proposed to find the optimal size.
3.1. Energy-Delay Tradeoff for a Given Number of Receivers
According to (10), the real transmission distance is related to the SNR with  . The effective distance is upper bounded by the physical distance and depends on the position of the forwarding node with respect to the S-D line. In the following, we assume that the physical and effective distances are equal, which means that the forwarding nodes are located in the vicinity of the S-D line. Under this approximation, (19) and (21) are converted to functions of
. The effective distance is upper bounded by the physical distance and depends on the position of the forwarding node with respect to the S-D line. In the following, we assume that the physical and effective distances are equal, which means that the forwarding nodes are located in the vicinity of the S-D line. Under this approximation, (19) and (21) are converted to functions of  and
and  as follows:
as follows:


where  and
and

First, we consider the scenario where  is fixed.
is fixed.
Theorem 1.
When  is constant, the lower bound of energy-delay tradeoff represented by (24) and (23) is achieved if and only if the SNR vector
is constant, the lower bound of energy-delay tradeoff represented by (24) and (23) is achieved if and only if the SNR vector  is equal to
is equal to

Proof.
Refer to Appendix A.
The lower bound of energy-delay tradeoff is thus characterized by:

where  and
and  are constant. The priority between energy and delay is balanced with the transmission power
are constant. The priority between energy and delay is balanced with the transmission power  .
.
From this bound, according to (24), the optimal transmission power for a given delay constraint,  , is derived as
, is derived as

Next, we show how to obtain  . For a given set of nodes having fixed SNRs, exploiting (18) leads to the following theorem.
. For a given set of nodes having fixed SNRs, exploiting (18) leads to the following theorem.
Theorem 2.
For a given set of  forwarding nodes whose corresponding
forwarding nodes whose corresponding  is
is  , respectively,
, respectively,  is minimized with respect to
is minimized with respect to  if and only if the
if and only if the  are ordered in an increasing order such that the higher priority is given to the node with the smaller
are ordered in an increasing order such that the higher priority is given to the node with the smaller  .
.
Proof.
Refer to Appendix B.
Then, we have to find the SNR values  that minimize
that minimize  , according to Theorem 2. Due to computational complexity and for the sake of simplicity, we assume that all the forwarding nodes are located in the same area and thus that all
, according to Theorem 2. Due to computational complexity and for the sake of simplicity, we assume that all the forwarding nodes are located in the same area and thus that all  are equal to an optimal value
are equal to an optimal value  . This means that the
. This means that the  receivers have the same effective transmission distance
receivers have the same effective transmission distance  and are deployed around the line between a source node and a destination node as shown in Figure 2. In this way,
and are deployed around the line between a source node and a destination node as shown in Figure 2. In this way,  can be approximated by
can be approximated by 

Figure 3 shows the exact value of minimum  and its approximation
and its approximation  under the same condition. Note that the difference between the exact value and the approximation is very small. Therefore, we use
under the same condition. Note that the difference between the exact value and the approximation is very small. Therefore, we use  to analyze the lower bound of tradeoff between
to analyze the lower bound of tradeoff between  and
and  in the following.
in the following.
The minimum value of  is available by its first derivative with respect to
is available by its first derivative with respect to  , leading to
, leading to

where  is the derivation of
is the derivation of  with respect to
with respect to  .
.
It should be noticed that the whole lower bound of the energy-delay tradeoff is obtained for the same SNR value at the receivers. Furthermore, note that this SNR constraint can be achieved for different couples of transmission power and effective distance parameters. In other words, to satisfy the optimal SNR constraint, the internode distance and the power transmission should be selected jointly according to a desired tradeoff constraint between delay and energy.
Equation (30) implies that the optimal SNR strongly relies on the function  . Thus, we should consider different channels to obtained the closed-form expression of its lower bound. First, we focus on AWGN, Rayleigh fast fading and Rayleigh block fading channels, then, a general solution of obtaining
. Thus, we should consider different channels to obtained the closed-form expression of its lower bound. First, we focus on AWGN, Rayleigh fast fading and Rayleigh block fading channels, then, a general solution of obtaining  is given for all other scenarios.
is given for all other scenarios.
Substituting (11), (12), and (13) into (30), respectively, yields  in the different kinds of channels.
in the different kinds of channels.
3.1.1. AWGN

where  is the branch of the Lambert W function satisfying
is the branch of the Lambert W function satisfying  [20].
[20].
3.1.2. Rayleigh Block Fading Channel

3.1.3. Rayleigh Fast Fading Channel

Substituting  ,
,  and
and  into (29), respectively, yields
into (29), respectively, yields  in the three kinds of channels.
in the three kinds of channels.
3.1.4. Other Scenarios
Contrarily to the above-mentioned cases, in many practical situations, the closed-form expression of or
or  . Then, a numeric approach can be used.
. Then, a numeric approach can be used.
The first problem may hold when the expression of link probability is not known. In this case, the value of  has to be approached with an iterative approximation algorithm.
has to be approached with an iterative approximation algorithm.
A second limit may be encountered for estimating a closed-form expression of even if the link probability is known. For example, when a coding scheme is employed, the link probability is more complex, and a closed-form expression of
even if the link probability is known. For example, when a coding scheme is employed, the link probability is more complex, and a closed-form expression of  is untractable. In this case, a sequential quadratic programming (SQP) algorithm (see for instance [21]) can be adopted to solve the optimization problem of minimizing
is untractable. In this case, a sequential quadratic programming (SQP) algorithm (see for instance [21]) can be adopted to solve the optimization problem of minimizing  . Then, approximated values of
. Then, approximated values of  and
and  are obtained.
are obtained.
3.2. Optimal Number of Receivers
In the previous subsection, the lower bound of energy delay tradeoff is obtained for a fixed number of receivers. In this subsection, we analyze how to select the optimal number of receivers for a given ddr.
Theorem 3.
 is convex with respect to
is convex with respect to  .
.
Proof.
Refer to Appendix C.
Theorem 3 proves that a global minimum exists. In addition, since the optimal power  is known explicitly with (28) under a delay constraint ddr, the minimum value of
is known explicitly with (28) under a delay constraint ddr, the minimum value of  for a given delay constraint ddr can be obtained by searching the optimal number of receivers. The following algorithm addresses this optimization.
for a given delay constraint ddr can be obtained by searching the optimal number of receivers. The following algorithm addresses this optimization.
3.3. Lower Bound of Energy-Delay Tradeoff
The proposed algorithm offers a method to achieve  under a delay constraint ddr. Then, substituting
under a delay constraint ddr. Then, substituting  into (27) and (28), the lower bound of energy-delay tradeoff for one-hop transmission with opportunistic communications is
into (27) and (28), the lower bound of energy-delay tradeoff for one-hop transmission with opportunistic communications is

3.4. Minimum Energy Consumption
In the previous section, we found the lowest point existed in each curve of lower bound of energy-delay tradeoff in three kinds of channels. For delay-tolerant applications, the minimum energy consumption point is very important, that is, the lowest point on the curve of lower bound of energy-delay tradeoff. In the following subsection, we will derive this point.
In this subsection, as to the lowest point, we derive the lower bound of energy efficiency and corresponding energy-optimal transmission power and distance without the delay constraints.
3.4.1. Optimal Transmission Power
Assuming  is constant, in order to get the minimum value of
is constant, in order to get the minimum value of  , it is obvious that we should minimize
, it is obvious that we should minimize  and
and  at the same time in (23). Letting
at the same time in (23). Letting  , we have
, we have  . Then, employing Lagrange algorithm, we have
. Then, employing Lagrange algorithm, we have

Solving the above equation, we obtain

which is the optimal transmission power minimizing  .
.
Substituting (8) into (36) yields

where  is the transmission duration of a packet. Since
is the transmission duration of a packet. Since  generally, the first part of (37) can be neglected. Thus, we get
generally, the first part of (37) can be neglected. Thus, we get

It should be noted that  is tightly related to
is tightly related to  , so that we should apply Algorithm 1 to find the optimal number of receivers
, so that we should apply Algorithm 1 to find the optimal number of receivers  which is tightly related to the modulation, the type of channel of a network. Then, substituting
which is tightly related to the modulation, the type of channel of a network. Then, substituting  into (38) yields
into (38) yields

Algorithm 1: Search the optimal number of receivers  .
.
 ,
,  ,
,  , ddr
, ddr
while  do
do
Calculate 

if  then
then
 ,
, 
return 
else
 ,
, 
end if
end while
Meanwhile, (39) also shows that the characteristics of the amplifier have a strong impact on  . When the efficiency of the amplifier is high, that is,
. When the efficiency of the amplifier is high, that is,  ,
,  reaches its maximum value. As well, it is clear that when the environment of transmission deteriorates, namely,
reaches its maximum value. As well, it is clear that when the environment of transmission deteriorates, namely,  increases,
increases,  decreases correspondingly. However,
decreases correspondingly. However,  is independent of
is independent of  .
.
3.4.2. Lower Bound of 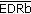 and Its Corresponding Delay
and Its Corresponding Delay
The lower bound of  is obtained by substituting (29) and (39) into(23)
is obtained by substituting (29) and (39) into(23)

Based on this result, we can set the transmission power of node according to (39) to minimize the total energy consumption for the delay-tolerant applications. Note that; this value is the threshold of transmission power, this is to say, the transmission power of nodes should not be smaller than this value; otherwise, a network system will be running in an inefficient state as shown on the right side curve of the lowest point in Figure 4.
Moreover, on the basis of (24) and  , the corresponding delay of the lowest point; that is, maximal mean delay is obtained
, the corresponding delay of the lowest point; that is, maximal mean delay is obtained

where  is the distance between a source node and a destination node.
is the distance between a source node and a destination node.
3.4.3. Minimum Mean Transmission Distance
By  ,
,  and (10), we obtain the minimal mean transmission distance:
and (10), we obtain the minimal mean transmission distance:

This distance shows the minimal distance between a source node and a destination node; otherwise, too small hop distance results in more energy consumption or too many hops, namely, too much delay.
3.4.4. Energy-Delay Tradeoff in Different Channels
According to the analysis in previous subsections, we obtain  and
and  under a delay constraint ddr, then we have the lower bound of energy-delay tradeoff for one-hop transmission with opportunistic communication on the basis of (34). Because (
under a delay constraint ddr, then we have the lower bound of energy-delay tradeoff for one-hop transmission with opportunistic communication on the basis of (34). Because ( ,
,  ,
,  ) tightly depends on the function of link probability,
) tightly depends on the function of link probability,  , we analyze the lower bound of energy-delay tradeoff in three different channels mentioned in this section.
, we analyze the lower bound of energy-delay tradeoff in three different channels mentioned in this section.
Figure 4 shows the lower bound of energy-delay tradeoff and the corresponding optimal transmission power and the optimal number of receivers. It should be noticed that the lowest point exists in each curve; this is to say, there is the most energy saving point without the delay constraints for each channel, and the corresponding mean delay is the maximum mean delay of a pair of nodes. In Section 3.4, we have analyzed the most energy saving point in detail. The left side of the lowest point shows the energy consumption increases with the decrease of the delay constraint which coincides with our intuition. However, in the right of the lowest point, the energy consumption increases with the increase of the delay because both the transmission power and the number of receives are too small which results in very small hop distance, that is, the increase of the hop number. Certainly, this work state should be avoided in practice.
Note that the optimal number of receivers corresponding to the lowest point in each curve is 2 in Rayleigh block fading and fast fading channels and is 1 in an AWGN channel. The result implies that too many nodes will lead to the waste of energy; this is to say, we should avoid acting all neighbor nodes as the relay candidates. In addition, the optimal number of receivers raises with the decrease of delay limit. As for the corresponding optimal transmission power, it is not monotonically decreased as we saw in traditional P2P communications. Conclusively, it is clear that the transmission power and the number of relay candidates should be adjusted correctly according to a delay constraint in order to avoid too much energy consumption. Algorithm 1 and (28) provide the approach to calculate the optimal transmission power and a distributed algorithm to select the optimal relay candidates will be introduced in Section 6.
Though the lower bound on the energy-delay tradeoff is derived in linear networks, it will be shown by simulations in the following Section 6 that this bound is proper for 2-dimensional Poisson distributed networks.
4. Energy-Delay Tradeoff of MultihopTransmissions
In this section, we extend the result of the one-hop transmission case developed in Section 3 to the scenarios of multihop transmission. Meanwhile, the effect of physical parameters on lower bound of energy-delay tradeoff and the energy efficiency gain of opportunistic communication are analyzed.
4.1. Lower Bound of Energy-Delay Tradeoff
The lower bound of energy-delay tradeoff can be abstracted as an optimization problem

where  and
and  are the end-to-end energy consumption and delay between a source node and a destination node.
are the end-to-end energy consumption and delay between a source node and a destination node.
In order to obtain the lower bound of energy-latency tradeoff of multihop transmission, the theorems about equivalent distance transmission are introduced as follows.
Theorem 4.
In a homogeneous network, a source node  sends a packet of
sends a packet of  bits to a destination node
bits to a destination node  using
using  hops in opportunistic communication mode. The
hops in opportunistic communication mode. The  relaying clusters are located around
relaying clusters are located around  line, as shown in Figure 2, and each cluster has the same number of relay candidates
line, as shown in Figure 2, and each cluster has the same number of relay candidates  . The distance between
. The distance between  and
and  is
is  . The length of each hop is
. The length of each hop is  , respectively, and the average
, respectively, and the average  is denoted as
is denoted as  . The minimum mean total energy consumption
. The minimum mean total energy consumption  is obtained if and only if
is obtained if and only if 

Proof.
Refer to Appendix D.
Theorem 5.
On the same assumption as Theorem 4, the mean delay of one-hop transmission is referred to as  . The minimum mean end-to-end delay
. The minimum mean end-to-end delay  is given by
is given by

if and only if  .
.
Proof.
Refer to Appendix E.
Based on Theorems 4 and 5, we conclude that regarding a pair of source and destination nodes with a given number of hops, the single scenario, which minimizes both mean energy consumption and mean transmission delay, is that each hop with uniform distance along a linear path. As a result, the optimization about energy and delay for a single hop will bring the optimization of the same performance for the multihop transmission. Hence, the results about the lower bound of energy-delay tradeoff in Section 3 can be used directly in multihop transmissions.
Theorems 4 and 5 hold in a specific deployment of a set of sensors. However, this condition would probably fail due to some obstacles like walls. In this case, two approaches can be adopted.
-
(1)
The model can be adapted locally. The pathloss function can be adapted in different areas. For instance, in the case of a very dense wireless sensors deployment, a subset of nodes can decide to remain active only under local estimation of the pathloss properties.
-
(2)
A statistical shadowing can be added to take into account the discrepancy between local reality and the theoretical model. This point out of the scope of the paper. While, this approach is proposed by another team in a paper extending our contribution [22].
4.2. The Gain of Opportunistic Communication
We analyze the energy efficiency gain of opportunistic communications compared with traditional P2P communications in this subsection. The benefit of opportunistic communication in terms of energy efficiency, as shown in Figure 5, is measured with the energy gain defined as:

where the  is the optimal
is the optimal  with a delay constraint ddr in traditional point-to-point communications, which is obtained according to the approach proposed in [17], and
with a delay constraint ddr in traditional point-to-point communications, which is obtained according to the approach proposed in [17], and  is referred to as the optimal
is referred to as the optimal  with the same delay constraint using opportunistic communications obtained by (34).
with the same delay constraint using opportunistic communications obtained by (34).
Figure 5 provides an example in three kinds of channel and the physical parameters are shown in Table 1. In this example, the gain of opportunistic communications decrease from 25% to 0% with the increase of the delay constraint. The gain becomes 0 when the delay constraint is greater than 0.11 ms/m which implies that the opportunistic communication has changed to the traditional P2P communication which coincides with the result in Figure 4, where the optimal number of receiver becomes 1 for the corresponding delay constraint. In other words, when the delay constraint is greater than a threshold, the traditional P2P communication is more energy efficient than the opportunistic communication in an AWGN channel.
In Rayleigh block fading and Rayleigh fast fading channels, the gain of opportunistic communications is always greater than 0, which reveals the opportunistic communication outperforms the traditional P2P communication in these two kinds of channel, where opportunistic routings benefit from the effect of diversity and can improve the energy efficiency, while the gain decreases with the increase of the delay constraint.
According to these results, it can be concluded that opportunistic communications are more energy efficient for Rayleigh block fading channels than for AWGN channels.
5. Effect of Physical Layer Parameters
The closed-form expression on energy-delay tradeoff provides the framework to evaluate the energy-delay performance of a network according to its parameters of physical layer, MAC layer, and routing layer. This framework can be used in the following applications.
(1) Performance Evaluation
During the design or planning phase of a network, these results of performance evaluation provide the basis of the choice of sensor node and the choice of routing and MAC protocols.
(2) Benchmark of Performance
Regarding the design of a protocol, the best performance of a network can be obtained using this framework which can act as the benchmark of performance in order to measure the performance of a protocol and to adjust the parameters of the protocol.
(3) Parameter Optimization
Likewise in the design phase of a network, we can optimize the parameters such as transmission power according to the request of performance of a network on the basis of the framework.
In this subsection, on the basis of (34), the effects of coding scheme and the type of modulation on the lower bound of energy-delay tradeoff are studied, as the examples of the applications of parameter optimization.
(a) Coding
Coding can reduce the probability of bit or block error but introduces more bits resulting to more energy consumption. What is the benefit of coding in the viewpoint of energy-delay tradeoff will be revealed in the following part in three kinds of channels. Here, Hamming code  is used as an example. The results in Figure 6 indicate that this kind of coding brings some benefit in both energy and delay in a Rayleigh fast fading channel; however, it introduces more energy and delay in AWGN and Rayleigh block fading channels. Therefore, it is dependent on the type of channel to decide if coding should be used.
is used as an example. The results in Figure 6 indicate that this kind of coding brings some benefit in both energy and delay in a Rayleigh fast fading channel; however, it introduces more energy and delay in AWGN and Rayleigh block fading channels. Therefore, it is dependent on the type of channel to decide if coding should be used.
(b) Modulation
High-order modulation brings high BER but reduces the transmission time and energy when in the same symbol rate due to the increase of bit rate. The effect of modulation on the lower bound of energy-delay tradeoff in three kinds of channel is shown in Figure 7. We note that the optimal modulation scheme is different in each kind of channel, while it is independent of the delay constraint.
Besides the above three parameters, the other parameters such as circuitry power, strength of fading, transmit rate or the integration of several parameters can be analyzed also according to the different applications because this framework includes every parameter in physical layer. On the basis of these analysis results, we can adjust the parameters to obtain the best performance of a network.
6. Simulations
The purpose of this section is to verify the theoretical analysis of the lower bound on the energy-delay tradeoff and the energy efficiency in a 2-dimensional Poisson distributed network by simulations although these theoretical results are obtained in a linear network using approximation approach. First, we introduce a novel opportunistic protocol on the basis of the theoretical analysis.
6.1. Opportunistic Protocol
The analysis in Section 3 reveals that the transmission power and the number of receivers should be configured as the corresponding optimal values in order to approach the lower bound of energy-delay tradeoff. While. Algorithm 1 proposed in Section 3 requires the acknowledgment of global network parameters, which can not be directly applied to distributed networks. Consequently, an algorithm in distributed manner is introduced based on the algorithm proposed in [9] and the analysis in Section 3.
The containing property in Lemma 3.4 proposed in [9] shows that a straightforward way to find an optimal set containing  nodes is to add a new node into the optimal node set containing
nodes is to add a new node into the optimal node set containing  nodes. Furthermore, when a local minimum
nodes. Furthermore, when a local minimum  is found, it is the global minimum according to Theorem 3. Based on this idea, a distributed algorithm for finding the optimal receiver set at each hop in order to minimize the energy consumption and satisfy the delay constraint ddr is proposed in Algorithm 2.
is found, it is the global minimum according to Theorem 3. Based on this idea, a distributed algorithm for finding the optimal receiver set at each hop in order to minimize the energy consumption and satisfy the delay constraint ddr is proposed in Algorithm 2.
Algorithm 2: Search the optimal set of receivers.
 ,
,  , ddr
, ddr
while  do
do
for each node  do
do
 ;
;
Sorting the nodes in 
according to their effective transmission distance;

if  then
then
 ;
; 
end if
end for
if  then
then
 ;
; 
else
return 
end if
end while
In Algorithm 2,  is the set of neighbor nodes of a source node,
is the set of neighbor nodes of a source node,  is the set of nodes selected to receive the packet from the source node.
is the set of nodes selected to receive the packet from the source node.
Next, we introduce the process of this protocol.
-
(1)
Search the forward candidates according to Algorithm 2.
-
(2)
Assign a priority to each node according to its effective transmission distance.
-
(3)
Transmit the data packet including the information of relay candidates ID and theirs corresponding priorities.
-
(4)
Nodes in the set of relay candidates try to receiver packet.
-
(5)
A node which receives the packet correctly calculates the backoff time according to the priority and waits for the ACK packet from the nodes with the priority higher than that of itself.
-
(6)
If a node does not receive any ACK packet, it broadcasts its ACK packet and then is ready to transmit the received packet to next hop or destination. If a node receives an ACK packet, the received data packet is dropped from its queue.
-
(7)
The source node waits for the ACK packet from one of forwarding candidates. If an ACK packet is received, the source node removes the packet from the buffer; otherwise, it is ready to retransmit the data packet.
6.2. Simulation Setup
In the simulations, the lower bounds of energy-delay tradeoff and  are evaluated in an area
are evaluated in an area  of surface
of surface  using the simulator Wsnet [23]. The nodes are uniquely deployed according to Poisson distribution.
using the simulator Wsnet [23]. The nodes are uniquely deployed according to Poisson distribution.
All the other simulation parameters concerning a node are listed in Table 1. The distance between the source and the destination nodes is 1000 m. The source node transmits only one data packet of 320 bytes to the destination with BPSK modulation. The size of ACK packet is 26 bytes. For every hop, the transmitter will retransmit the data packet until the data packet is received by the next relay node; this is to say, there is no limit for the number of retransmissions in order to ensure the reliability. The opportunistic protocol proposed in Section 6.1 is employed to simulations. A simulation will be repeated for 1000 times in each different configuration.
The network model used in the simulations assumes the following statements.
-
(i)
After the initial phase, the network is geographical aware; that is, each node knows the position of itself, the sink node and all the neighbor nodes in the network.
-
(ii)
Each node in the network has the same fixed transmission power.
6.3. Results and Analysis
In order to analyze the variety of energy-delay tradeoff with the increase of node density, the simulations are run in three cases: 200, 400, and 800 nodes in the simulation area. The transmission power of each node is configured as the optimal transmission power derived from (28).
Figure 8 provides the simulation results which are compared with the theoretical lower bound of energy-delay tradeoff in a Rayleigh block fading channel. The comparison reveals that the simulation results approach to the theoretical lower bound with the increase of the node density, because the distance between pairwise relay node achieved from the routing scheme is more and more near the optimal transmission distance at each hop when the node density increases. The corresponding mean number of receivers in each hop shown in Figure 9 also verify this phenomenon because the mean number of receivers reduces with the increase of node density. And we can deduce that the lower bound can be reached when the node density is high enough. Hence, it is concluded that the theoretical lower bound on  is adequate for a 2-dimensional Poisson network although its derivation is based on a linear network using an approximation method. Furthermore, these results imply that unreliable links play an important role in energy saving.
is adequate for a 2-dimensional Poisson network although its derivation is based on a linear network using an approximation method. Furthermore, these results imply that unreliable links play an important role in energy saving.
7. Conclusions
In this paper, an unreliable link model is firstly integrated into our energy model using the specific metrics for energy efficiency and delay:  ,
,  . By minimizing
. By minimizing  for AWGN, Rayleigh block fading and Rayleigh fast fading channels with and without delay constraint, we have shown that the channel state impacts the optimal number of receivers in a cluster. Meanwhile, the corresponding optimal transmission power and the optimal transmission range are obtained. The energy-delay tradeoff for one-hop and multihop transmissions are analyzed and compared with the tradeoff given by traditional P2P communications. The main conclusion is that opportunistic communications exploiting spatial diversity are beneficial for Rayleigh fast fading and the Rayleigh block fading channels.
for AWGN, Rayleigh block fading and Rayleigh fast fading channels with and without delay constraint, we have shown that the channel state impacts the optimal number of receivers in a cluster. Meanwhile, the corresponding optimal transmission power and the optimal transmission range are obtained. The energy-delay tradeoff for one-hop and multihop transmissions are analyzed and compared with the tradeoff given by traditional P2P communications. The main conclusion is that opportunistic communications exploiting spatial diversity are beneficial for Rayleigh fast fading and the Rayleigh block fading channels.
Appendices
A. The Lower Bound of Energy-Delay Tradeoff
Proof.
Without loss of generality, let us introduce a new function  and let
and let  is the minimum value of
is the minimum value of  and
and  , then we get
, then we get

where  .
.
If (A.1) are not the equations providing the lower bound of energy-delay tradeoff, then we assume that there exists another value of  ,
,  by which the lower bound of energy-delay tradeoff can be obtained
by which the lower bound of energy-delay tradeoff can be obtained


Notice that according to this assumption, we can deduce that  when
when  .
.
Considering  , we have
, we have

Substituting (A.4) into (A.2) yields

Therefore, this assumption leads to a contradiction. Finally, we can conclude that (24) and (23) is the lower bound of energy-delay tradeoff when the minimum value of  is available.
is available.
B. Minimum G Function
Refer to the Theorem 2. For a given  nodes whose corresponding
nodes whose corresponding  is
is  , the minimum value of
, the minimum value of  can only be obtained by giving the higher relay priority to the node whose
can only be obtained by giving the higher relay priority to the node whose  is smaller.
is smaller.
Proof.
Let us introduce a new function  . It can easily be seen that maximizing the value of
. It can easily be seen that maximizing the value of  leads to minimizing
leads to minimizing  . Next, we prove this theorem by maximizing
. Next, we prove this theorem by maximizing  .
.
When  , the maximum value of
, the maximum value of  can be gotten directly. Then, we assume it holds for
can be gotten directly. Then, we assume it holds for  where the relationship between is
where the relationship between is  and its corresponding priority is
and its corresponding priority is  . Therefore, the theorem will be proved if we can show that it holds for
. Therefore, the theorem will be proved if we can show that it holds for  .
.
Without loss of generality, we may assume  is the SNR of the
is the SNR of the  node and
node and  . Here, there are three scenarios for assigning the priority of the
. Here, there are three scenarios for assigning the priority of the  node,
node, :
:  ,
,  and
and  .
.
When  ,
,

When  ,
,

The difference between  and
and  is
is

Because  when
when  , we can obtain that
, we can obtain that  .
.
When  , using the similar method, the same result is obtained.
, using the similar method, the same result is obtained.
Thus, we conclude that the theorem holds.
C. Proof of  Convexity
Convexity
Refer to Theorem 3.  is a convex function with respect to
is a convex function with respect to  .
.
Proof.
According to the definition of concave, the theorem will be proved if we can show:  where
where  . Then, we will proof this condition holds.
. Then, we will proof this condition holds.

with

where  and
and  .
.
Obviously, (C.1) is great than 0 if  and
and  . Regarding
. Regarding  , it is easily concluded that
, it is easily concluded that  . Next, we proof
. Next, we proof  .
.
When  , we have
, we have  . Meanwhile,
. Meanwhile,

so,  is a monotonic decreasing function. Thus,
is a monotonic decreasing function. Thus,  for all
for all  .
.
Finally, it is evident to see that  is a convex function.
is a convex function.
D. Minimum Energy Consumption inMultihop Transmissions
Proof.
The mean energy consumption for each hop of index  is set to
is set to  . Since each hop is independent from the other hops, the mean total energy consumption is
. Since each hop is independent from the other hops, the mean total energy consumption is  . Hence, the problem of finding the minimum mean total energy consumption can be rewritten as
. Hence, the problem of finding the minimum mean total energy consumption can be rewritten as

Set

where  is the Lagrange multiplier.
is the Lagrange multiplier.
According to the method of the Lagrange multipliers, we obtain

Equation (D.3) shows that the minimum value of  is obtained in the case:
is obtained in the case:  . Moreover, in a homogeneous linear network, the properties of each node are identical. Therefore,
. Moreover, in a homogeneous linear network, the properties of each node are identical. Therefore,

Because

we deduce  is a monotonic increasing function of
is a monotonic increasing function of  when the pathloss exponent follows
when the pathloss exponent follows  . Therefore, the unique solution of (D.3) is
. Therefore, the unique solution of (D.3) is  . Finally, we obtain
. Finally, we obtain

E. Minimum Mean Delay in MultihopTransmissions
Proof.
The theorem can be proved in the same way as shown for Theorem 4. This theorem is valid if and only if  is a monotonic increasing function of
is a monotonic increasing function of  which holds with the attenuation model in (10)
which holds with the attenuation model in (10)

where  and
and  are the first and second derivative of (14) with respect to
are the first and second derivative of (14) with respect to  . Because
. Because  and
and  in case of
in case of  in many practical scenarios, (E.1) is great than 0. Thus,
in many practical scenarios, (E.1) is great than 0. Thus,  is a monotonic increasing function with respect to
is a monotonic increasing function with respect to  .
.
References
Pelusi L, Passarella A, Conti M: Opportunistic networking: data forwarding in disconnected mobile ad hoc networks. IEEE Communications Magazine 2006, 44(11):134-141.
Ganesan D, Krishnamachari B, Woo A, Culler D, Estrin D, Wicker S: Complex behavior at scale: an experimentalstudy of low-power wireless sensor networks. 2003.
Woo A, Culler DE: Evaluation of efficient link reliability estimators for low-power wireless networks. Computer Science Division, University of California; 2003.
Zhao J, Govindan R: Understanding packet delivery performance in dense wireless networks. In Proceedings of the1st International Conference on Embedded Networked Sensor Systems, 2003, Los Angeles, Calif, USA. ACM Press; 1-13.
Zamalloa MZ, Bhaskar K: An analysis of unreliability and asymmetry in low-power wireless links. ACM Transactions on Sensor Networks 2007., 3(2):
Gorce J-M, Zhang R, Parvery H: Impact of radio link unreliability on the connectivity of wireless sensor networks. Eurasip Journal on Wireless Communications and Networking 2007, 2007:-16.
Zorzi M, Rao RR: Geographic random forwarding (GeRaF) for ad hoc and sensor networks: energy and latency performance. IEEE Transactions on Mobile Computing 2003, 2(4):349-365. 10.1109/TMC.2003.1255650
Biswas S, Morris R: Exor: opportunistic multi-hop routing for wireless networks. In Proceedings of The Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, 2005, Philadelphia, Pa, USA. ACM; 133-144.
Kai Z, Wenjing L, Jie Y, Brown DR III: On geographic collaborative forwarding in wireless ad hoc and sensor networks. Proceedinsg of the 2nd Annual International Conference on Wireless Algorithms, Systems, and Applications (WASA '07), August 2007 11-18.
Jaffrès-Runser K, Gorce J-M, Ubéda S: Multiobjective QoS-oriented planning for indoor wireless LANs. Proceedinsg of the IEEE 64th Vehicular Technology Conference (VTC '06), September 2006 1-5.
Shah RC, Wiethölter S, Wolisz A, Rabaey JM: Modeling and analysis of opportunistic routing in low traffic scenarios. Proceedings of the 3rd International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt '05), April 2005 294-304.
Shah RC, Wiethölter S, Wolisz A, Rabaey JM: When does opportunistic routing make sense? Proceedings of the 3rd IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom '05), March 2005 350-356.
Zhang L, Soong B-H: Energy efficiency analysis of channel aware geographic-informed forwarding (CAGIF) for wireless sensor networks. IEEE Transactions on Wireless Communications 2008, 7(6):2033-2038.
Micaz datasheet http://www.xbow.com
Karl H, Willig A: Protocols and Architectures for Wireless Sensor Networks. John Wiley and Sons, New York, NY, USA; 2005.
Gao JL: Analysis of energy consumption for ad hoc wireless sensor networks using a bit-meter-per-joule metric. 2002.
Zhang R, Gorce JM, Jaffrès-Runser K: Energy-delay bounds analysis in wireless multi-hop networks with unreliableradio links. ARES /INRIA; 2008.
Cerpa A, Wong J, Kuang L, Potkonjak M, Estrin D: Statistical model of lossy links in wireless sensor networks. Proceedings of The 4th International Symposium on Information Processing in Sensor Networks (IPSN '05), 2005
Li D, Sun X: Nonlinear Integer Programming. Springer, New York, NY, USA; 2006.
Corless RM, Gonnet GH, Hare DEG, Jeffrey DJ, Knuth DE: On the lambertw function. Advances in Computational Mathematics 1996, 5(4):329-359.
Ravindran A, Ragsdell KM, Reklaitis GV: Engineering Optimization. 2nd edition. John Wiley & Sons, New York, NY, USA; 2006.
Predojev T, Alonso-Zarate J, Dohler M: Energy-delay tradeoff analysis in embedded m2m networks with channelcoding. Proceedings of the 21st Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '10), 2010
Acknowledgments
This work was funded by the French ANR project BANET, "Body Area Networks and Technologies", and by the French Ministry of Industry through the European ITEA2 Geodes Project, and by INRIA.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, R., Gorce, JM., Berder, O. et al. Lower Bound of Energy-Latency Tradeoff of Opportunistic Routing in Multihop Networks. J Wireless Com Network 2011, 265083 (2011). https://doi.org/10.1155/2011/265083
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/265083

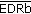 )
)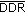 )
)

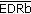 and Its Corresponding Delay
and Its Corresponding Delay
 -
- tradeoff and corresponding parameters in different channels. AWGN channelRayleigh block fading channelRayleigh fast fading channel
tradeoff and corresponding parameters in different channels. AWGN channelRayleigh block fading channelRayleigh fast fading channel



 -
- tradeoff in different node densities
tradeoff in different node densities
 Convexity
Convexity