- Research Article
- Open access
- Published:
A Near-Optimum Multiuser Receiver for STBC MC-CDMA Systems Based on Minimum Conditional BER Criterion and Genetic Algorithm-Assisted Channel Estimation
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 351494 (2011)
Abstract
The implementation of efficient baseband receivers characterized by affordable computational load is a crucial point in the development of transmission systems exploiting diversity in different domains. This would be a crucial point in the future development of 4G systems, where space, time, and frequency diversity will be combined together in order to increase system throughput. In this framework, a linear multiuser detector for MC-CDMA systems with Alamouti's Space-Time Block Coding (STBC), which is inspired by the concept of Minimum Conditional Bit Error Rate (MCBER), is proposed. The MCBER combiner has been implemented in adaptive way by using Least-Mean-Square (LMS) optimization. The estimation of Channel State Information (CSI), necessary to make practically feasible the MCBER detection, is aided by a Genetic Algorithm (GA). The obtained receiver scheme is near-optimal, as both LMS-based MCBER and GA-assisted channel estimation perform closely to optimum in fulfilling their respective tasks. Simulation results evidenced that the proposed receiver always outperforms state-of-the-art receiver schemes based on EGC and MMSE criterion exploiting the same degree of channel knowledge.
1. Introduction
Future mobile communications standards will be required to provide high performance in terms of data rate, capacity, and quality of service. For this reason, the efficient exploitation of diversity in different domains (time, space, frequency) will be an issue. Multicarrier modulations [1] and Multiple-Input Multiple-Output (MIMO) space-time coding [2] are among the enabling technologies of future diversity-based high-capacity wireless communications. As claimed by Ahmadi in [3], next-generation mobile WiMAX technology will be based on Orthogonal Frequency Division Multiple Access (OFDMA), supported by Time-Division Duplexing (TDD) or Frequency-Division Duplexing (FDD), and advanced multiantenna systems, exploiting novel space-time coding schemes. OFDM and OFDMA apparently dominate the panorama of multicarrier modulations in wireless standards. However, in these last years, the spread-spectrum extension of OFDM, namely, Multicarrier CDMA (MC-CDMA), is raising a renewed interest. MC-CDMA is intrinsically more robust than OFDMA over frequency-selective channels. MC-CDMA transmits a user's symbol in parallel over a subcarrier set. Therefore, for the same number of subcarriers, MC-CDMA obtains a frequency diversity gain with respect to OFDMA. The price to be paid is an increasing amount of multiuser interference (MUI) due to the overlap of different symbols over the same subcarrier set. The adoption of low-complexity multiuser detection makes MC-CDMA a valuable competitor with OFDMA with some clear advantages in terms of anti-multipath resilience, in particular in mobile environments. It is worth to mention a recent work [4] that considers the evolution of High-Speed Packet Access (HSPA) from single-carrier DS/CDMA (HSPA currently adopts a PHY-layer scheme rather similar to Wideband CDMA of UMTS) to Multicarrier CDMA. Such an evolution is motivated by the synergies of HSPA with 3GPP Long-Term Evolution (LTE), which considers OFDMA and Single-Carrier FDMA (SC-FDMA) as preferential PHY-layer options. MC-CDMA may become a competitor also in future WiMAX standardization. Very recently, Aldhaheri and Al-Qahtani presented in [5] a novel MC-CDMA transmission scheme for fixed and mobile WiMAX. The performance improvement attainable by MC-CDMA with respect to the conventional OFDMA is relevant, in particular when the speed of the terminal is very high.
In such a framework, multiantenna systems, space-time coding, and multicarrier CDMA can be regarded as key technologies for future broadband wireless networking. In [6], it is shown that MC-CDMA with Space-Time Block Coding (STBC) can jointly exploit diversity in space and frequency domains in order to counteract multipath fading effects and, therefore, to provide performances quite close to the single-user bound. As it happens in Single-Input Single-Output (SISO) MC-CDMA, multiuser detection (MUD) plays a key role in improving system performances.
Theoretically optimum nonlinear maximum likelihood detection is characterized by an unsustainable computational complexity (exponentially growing with the number of users). For this reason, suboptimum linear MUD strategies should be investigated. Minimum Mean Square Error- (MMSE-) MUD techniques have been proposed for STBC MC-CDMA systems in [7]. Although MMSE is a good choice in order to provide a simple implementation of adaptive receivers (Least-Mean-Square (LMS) and Recursive-Least-Squared (RLS) implementations are allowed), it is intrinsically suboptimal because it minimizes the Mean Squared Error between the received signal and the noiseless signal pattern. This results in a maximization of the Signal-to-Noise plus Interference Ratio (SINR), rather than in the minimization of the Bit Error Rate (BER) that is the expected target of an efficient receiver. The Minimum Bit Error Rate (MBER) criterion for multiuser detection has been successfully applied to DS-CDMA [8], MC-CDMA [9], and SDMA [10]. Partial equalization and adaptive Threshold Orthogonality Restoring (TORC) based on BER minimization have been also proposed for MC-CDMA in [11, 12]. The potential advantages of implementing linear MBER MUD in STBC MC-CDMA context can be easily explained. STBC MC-CDMA is a transmission methodology, where diversity is obtained both in space and in frequency domain. The diversity gain, increased with respect to the conventional SISO case, is obtained at the price of an increased system complexity. In our opinion, the exploitation of the "full potential" of STBC MC-CDMA techniques can be obtained only by means of optimized multiuser detection approaches. In such a perspective, the investigation of MBER strategies can be regarded as a step ahead towards the computationally affordable signal detection optimization also in the STBC MC-CDMA case. The application of MBER reception to STBC MC-CDMA is not straightforward and should be investigated by carefully taking into account tight requirements in terms of ease of implementation and reduced computational effort. An example of application of MBER criterion to STBC MC-CDMA MUD has been shown in [13]. The unknown probability density function (PDF) of the decision variable has been expressed in closed, but approximated, form by using the Parzen windows methodology. Then, the LMS criterion has been applied in order to adaptively implement the MBER receiver. The MBER-MUD approach of [13] does not require Channel State Information (CSI) knowledge and is characterized by a moderate computational complexity. Despite these favorable features, the multiuser receiver of [13] is quite far from optimality, in particular when the number of users increases.
In this paper, we are proposing a near-optimum multiuser detector for STBC MC-CDMA transmission systems based on the Minimum Conditional Bit Error Rate (MCBER) and on Genetic Algorithm- (GA-) assisted channel estimation. The design of MCBER-MUD and GA-assisted channel estimation for STBC MC-CDMA is motivated by the basic requirements of implementing an actual receiver scheme (that, therefore, cannot assume the ideal CSI knowledge) characterized by affordable computational load and near-optimal performance. MCBER-MUD criterion has been successfully applied in [14] to DS/CDMA systems and in [15] to SISO MC-CDMA systems. MCBER-MUD is a slight modification of the original MBER-MUD criterion that allows reducing the computational complexity to a linear order with the number of users without significant losses in BER performances with respect to theoretically optimum ML-MUD. The STBC scheme considered in the present paper is the well-known Alamouti's scheme [16] characterized by ease of concept and implementation, computational efficiency and performance very close to theoretical bounds when employed in multipath fading channels. The practical implementation of the proposed MCBER detector relies on an adaptive optimization strategy based on the concept of deterministic gradient. In particular, we considered LMS to derive the MCBER solution in numerical iterative form. Such a choice has been motivated by the necessity of testing a computationally tractable algorithm like gradient descent, widely employed in practical MUD implementations. In this framework, it is worth citing a very recent paper [17], where another LMS-based adaptive receiver has been proposed for MC-CDMA systems with Alamouti's STBC. Such receiver is based on a modified MSE cost function and an improved LMS optimization strategy. The convergence rate is increased with respect to conventional LMS receiver. We think that our approach represents a step ahead with respect to [17], as it tries to minimize the system BER instead of minimizing the MSE between the filter output and the expected symbol belonging to the STBC block. The explicit BER minimization is conceptually closer to optimality than partial equalization and TORC of [11, 12], whose performance is lower bounded by that of MMSE receiver exploiting ideal CSI knowledge.
It is known from the literature that formal MBER and MCBER criteria require CSI knowledge to work. Therefore, the problem of channel estimation should be adequately considered in the perspective of the provision of a technically viable solution. Searching for reliable and computationally efficient adaptive channel estimation, we decided to propose a Genetic Algorithm- (GA-) assisted semi adaptive MMSE channel estimation. The idea of exploiting a GA-based approach in order to efficiently implement channel estimation has been suggested by the promising results achieved in [18]. In this work, Genetic Algorithm has been considered for near-optimal channel estimation applied to STBC MC-CDMA with MMSE multiuser detection. Substantially, the effectiveness of the GA-based approach has been assessed by comparing BER performance of the Wiener solution to MMSE-MUD, obtained by using the ideally known channel matrices and that one obtained by using estimated channel matrices. The maximum performance loss due to nonideal channel estimation was only 1 dB. On the other hand, results shown in [18] evidenced that iterative LMS-based MMSE-MUD may provide unsatisfactory performance, in particular when the interference load increases.
The paper is organized as follows. Section 2 contains the description of the system model. Section 3 details the implementation of the proposed near-optimal receiver based on MCBER and GA-assisted channel estimation. Section 4 shows some selected simulation results aimed at assessing the effectiveness of the proposed approach by means of a thorough comparison with other state-of-the-art receivers. Moreover, some considerations about computational complexity and parameterization both of MCBER reception and GA-assisted channel estimation are sketched at the end of Section 4. Finally, paper conclusions are drawn in Section 5.
2. STBC MC-CDMA System Description
In the present dealing, we consider a synchronous multiuser MC-CDMA system using Alamouti's Space Time Block Coding [16]. A block scheme of such a transmission system is drawn in Figure 1. Two consecutive data symbols of the generic user  related to the generic
related to the generic  th modulation period
th modulation period  are mapped to two transmitting antennas according to the code matrix
are mapped to two transmitting antennas according to the code matrix  , whose elements are given by [16]
, whose elements are given by [16]

The superscript operator ( ) denotes the complex conjugate. The matrix of (1) represents Alamouti's STBC block. Alamouti's scheme exhibits some clear advantages. Essentially, it makes available a space diversity gain also for mobile terminals only by exploiting transmit diversity [16]. The most economic and advantageous Alamouti's configuration considers two transmit antennas (installed at base station or access point) and a single antenna mounted at the receiver side [16]. Such a configuration is considered in our paper, where the focus is on the development of cost-effective mobile terminals. Without losing generality, we suppose to consider binary antipodal BPSK symbols therefore,
) denotes the complex conjugate. The matrix of (1) represents Alamouti's STBC block. Alamouti's scheme exhibits some clear advantages. Essentially, it makes available a space diversity gain also for mobile terminals only by exploiting transmit diversity [16]. The most economic and advantageous Alamouti's configuration considers two transmit antennas (installed at base station or access point) and a single antenna mounted at the receiver side [16]. Such a configuration is considered in our paper, where the focus is on the development of cost-effective mobile terminals. Without losing generality, we suppose to consider binary antipodal BPSK symbols therefore,  . The encoder outputs are transmitted during two consecutive transmission periods, each one of duration equal to
. The encoder outputs are transmitted during two consecutive transmission periods, each one of duration equal to  . During the first transmission period (i.e.,
. During the first transmission period (i.e.,  ), two symbols
), two symbols  and
and  are modulated by two separate Inverse Fast Fourier Transform- (I-FFT-) based multicarrier transmitters using a unique Hadamard-Walsh sequence
are modulated by two separate Inverse Fast Fourier Transform- (I-FFT-) based multicarrier transmitters using a unique Hadamard-Walsh sequence  , where
, where  is the number of subcarriers employed for spreading. Finally, the RF-converted Multicarrier Spread Spectrum (MC-SS) signals are simultaneously transmitted by antenna 1 and antenna 2, respectively. In the same way, during the successive transmission period (i.e.,
is the number of subcarriers employed for spreading. Finally, the RF-converted Multicarrier Spread Spectrum (MC-SS) signals are simultaneously transmitted by antenna 1 and antenna 2, respectively. In the same way, during the successive transmission period (i.e.,  ), the symbol
), the symbol  is transmitted by antenna 1, and the symbol
is transmitted by antenna 1, and the symbol  is transmitted by antenna 2, respectively. The complex conjugate operator disappears, as we are considering real symbols. In order to make the notation more compact in the multiuser case, we define two vectors of symbols
is transmitted by antenna 2, respectively. The complex conjugate operator disappears, as we are considering real symbols. In order to make the notation more compact in the multiuser case, we define two vectors of symbols  and, similarly,
and, similarly,  together with the orthonormal code matrix C as
together with the orthonormal code matrix C as

The received signal samples acquired at two consecutive symbol periods after the FFT-based coherent demultiplexing can be expressed as follows:

where  and
and  are
are  vectors,
vectors,  (with
(with 
 ) is the Additive Gaussian Noise vector (all vector components are independent and identically distributed with zero mean and variance
) is the Additive Gaussian Noise vector (all vector components are independent and identically distributed with zero mean and variance  ), and
), and  (with
(with  ) is the
) is the  diagonal channel matrix, where
diagonal channel matrix, where  is the complex channel coefficient related to subcarrier
is the complex channel coefficient related to subcarrier  and to the transmit antenna
and to the transmit antenna  . We reasonably assume that fading is flat over each subcarrier and almost time-invariant during two consecutive transmission periods (i.e., the coherence time is much greater than the symbol period).
. We reasonably assume that fading is flat over each subcarrier and almost time-invariant during two consecutive transmission periods (i.e., the coherence time is much greater than the symbol period).
3. The Design of the Near-Optimum STBC MC-CDMA Linear Multiuser Receiver Based on Conditional BER Minimization and GA-Assisted Channel Estimation
3.1. Design Motivations
As remarked in [1], in order to cope with the dramatic increase in demand of high-speed wireless connections, there is an urgent demand of flexible, efficient, and computationally affordable transceivers. The design of attractive wireless transceivers hinges on a range of contradictory factors. Given a certain wireless channel, it is always possible to design a transmission scheme capable of increasing transmission integrity at the cost of more sophisticated signal processing. Alternatively, transmission integrity may be increased without increasing system complexity, provided that, for example, channel coding/interleaving delay can be further extended. It is also realistic to increase the system integrity by invoking a more robust but lower throughput modulation scheme. In such a case, the integrity is increased without spending in terms of system complexity, just in terms of bandwidth expense. In this paper, we adopted a transmission scheme characterized by intrinsic robustness against multipath channel impairment (i.e., STBC MC-CDMA). Transmission integrity should be guaranteed without increasing too much system complexity, considering also that we have decided to exploit only transmit diversity in order to keep the mobile terminal cheaper. In order to solve the tradeoff between integrity and complexity, we design an innovative STBC MC-CDMA receiver architecture based on the integration of (a) Minimum-Conditioned BER linear MUD and (b) Genetic Algorithm-assisted channel estimation. In the following part of this section, we shall detail and motivate both the adopted linear MUD criterion and the channel estimation strategy based on evolutionary optimization.
3.2. LMS-Based MCBER Multiuser Detector
In this sub-section, we shall describe the Minimum Conditional Bit-Error-Rate criterion for STBC MC-CDMA linear multiuser detection. A generic linear multiuser detector generates two decision variables based on the linear combination of the received signal samples. Thus, the (scalar) decision variables for the user  , denoted by
, denoted by  and
and  , related to the
, related to the  th modulation period can be expressed as follows:
th modulation period can be expressed as follows:

where  and
and  are the
are the  -elements vectors of receiver gains employed by the generic
-elements vectors of receiver gains employed by the generic  th user in order to recombine the baseband output of the FFT-based demodulation stage. The operator (
th user in order to recombine the baseband output of the FFT-based demodulation stage. The operator ( ) denotes the scalar product. As we are considering a BPSK modulation, the couple of bits contained in a single STBC block can be estimated by observing the real part of
) denotes the scalar product. As we are considering a BPSK modulation, the couple of bits contained in a single STBC block can be estimated by observing the real part of  and
and  , respectively. Conditioned on the transmitted bit vectors
, respectively. Conditioned on the transmitted bit vectors  and
and  , assuming the perfect knowledge of the channel matrices
, assuming the perfect knowledge of the channel matrices  and
and  the random variables
the random variables  and
and  are Gaussian-distributed with mean values as follows:
are Gaussian-distributed with mean values as follows:

and variance  .
.
To make the derivation of the probability of error easier, we can refer to the so-called sign-adjusted decision variables [10] defined as follows:  and
and  . These new decision variables are Gaussian-distributed as well with mean values
. These new decision variables are Gaussian-distributed as well with mean values  and
and  and variances
and variances  and
and  , respectively. It is clear that the correct block detection event happens if and only if
, respectively. It is clear that the correct block detection event happens if and only if  . Thus, the probability to have an error in the STBC block transmitted by user
. Thus, the probability to have an error in the STBC block transmitted by user  can be written as follows:
can be written as follows:

As  and
and  are independent random variables, we obtain
are independent random variables, we obtain

We can analytically compute the single probabilities of (7), conditioned on the bit vectors  and
and  as follows:
as follows:

where  is the conventional Gaussian error function. The calculation of the probability of error conditioned on
is the conventional Gaussian error function. The calculation of the probability of error conditioned on  and
and  is straightforward:
is straightforward:

Assuming that the two symbols contained in an STBC block have the same probability of error, the third term in (9) is negligible with respect to the first two ones. Thus, a good approximation of (9) is given by

By considering that the  possible transmitted bit vectors are independent and equiprobable, the average probability of error for the
possible transmitted bit vectors are independent and equiprobable, the average probability of error for the  th user can be written as
th user can be written as

The theoretical MBER criterion would lead to the computation of the couple of receiver gain vectors  minimizing the average probability of error of (11). The computational complexity of this detector is exponential in the number of users
minimizing the average probability of error of (11). The computational complexity of this detector is exponential in the number of users  , so its practical application becomes unfeasible as
, so its practical application becomes unfeasible as  increases. An alternative near-optimum linear detection criterion forecasts the minimization of the conditional probability of error [14, 15]. The Minimum Conditional BER (MCBER) can be expressed, in the considered STBC MC-CDMA case, as follows:
increases. An alternative near-optimum linear detection criterion forecasts the minimization of the conditional probability of error [14, 15]. The Minimum Conditional BER (MCBER) can be expressed, in the considered STBC MC-CDMA case, as follows:

The BER is conditioned in (12) only to the symbols not transmitted by the  th user in its own STBC block and is thus averaged with respect to all the possible combinations of the
th user in its own STBC block and is thus averaged with respect to all the possible combinations of the  th user's symbols. In our case, Alamouti's block is
th user's symbols. In our case, Alamouti's block is  sized; therefore, the number of possible symbol combinations is
sized; therefore, the number of possible symbol combinations is  . Dua et al. claim in [14] that the Minimum Conditional BER (MCBER) adaptive MUD has a convergence rate comparable to MBER-MUD with a marginally low degradation in terms of bit error rate and affordable computational burden linearly increasing with users' number. Formally, the following optimization problem must be solved:
. Dua et al. claim in [14] that the Minimum Conditional BER (MCBER) adaptive MUD has a convergence rate comparable to MBER-MUD with a marginally low degradation in terms of bit error rate and affordable computational burden linearly increasing with users' number. Formally, the following optimization problem must be solved:

Note that the couple of vectors  minimizing (13) are different from
minimizing (13) are different from  minimizing (11). In [14], it is pointed out that no closed-form expression for MBER solution has to be found. The same fact is verified for MCBER solution. For this reason, a numerical solution has to be investigated. A possible solution is to exploit the Least-Mean-Square (LMS) algorithm based on the concept of gradient descent. LMS updating of the receiver weights is done iteratively along the negative gradient of the error probability surface, along both directions
minimizing (11). In [14], it is pointed out that no closed-form expression for MBER solution has to be found. The same fact is verified for MCBER solution. For this reason, a numerical solution has to be investigated. A possible solution is to exploit the Least-Mean-Square (LMS) algorithm based on the concept of gradient descent. LMS updating of the receiver weights is done iteratively along the negative gradient of the error probability surface, along both directions  and
and  . The updating rule at
. The updating rule at  th iteration is given by:
th iteration is given by:

where  is the step-size parameter and
is the step-size parameter and  and
and  represent the gradient along the two directions
represent the gradient along the two directions  and
and  , respectively. For the first iteration (namely,
, respectively. For the first iteration (namely,  ), the following initialization has been chosen:
), the following initialization has been chosen:  . This is a reasonable choice, commonly used in the literature dealing with adaptive detection of MC-CDMA signals (see, e.g., [9]).
. This is a reasonable choice, commonly used in the literature dealing with adaptive detection of MC-CDMA signals (see, e.g., [9]).
The LMS implementation of the MCBER detector can be obtained straightforwardly by using the updating rule of (11) combined with the gradient expressions reported in the following (mathematical details are omitted for the sake of brevity):

As far as data symbols transmitted by users  are concerned, we define the vectors
are concerned, we define the vectors  and
and  in which the elements
in which the elements  and
and  represent the symbol decisions performed by user
represent the symbol decisions performed by user  . The choice of exploiting the symbol decisions taken by users
. The choice of exploiting the symbol decisions taken by users  instead of using random symbols has been considered in order to improve the convergence of the adaptive optimization algorithm (as already noted in [14]).
instead of using random symbols has been considered in order to improve the convergence of the adaptive optimization algorithm (as already noted in [14]).
3.3. The Proposed GA-Assisted Channel Estimation
In a realistically implemented receiver, the channel matrices  and
and  are not deterministically known, as assumed in Section 3.2, but they should be replaced by their estimates
are not deterministically known, as assumed in Section 3.2, but they should be replaced by their estimates  and
and  . It is clear that the estimation of CSI strongly impacts on MCBER receiver performance. The theoretical near-optimality of MCBER criterion may be seriously impaired by unreliable channel estimation. In this paper, we considered the GA-assisted MMSE channel estimation for STBC MC-CDMA system already presented in [18]. Such a channel estimation strategy, applied to the ideal MMSE multiuser detection, demonstrated itself very robust and near-optimal, clearly outperforming state-of-the-art techniques based on gradient descent. Genetic algorithms have a 20-year history of successful applications in telecommunications, signal processing, and electromagnetic fields due to some basic features, useful to solve complex problems with reasonable computational effort [19].
. It is clear that the estimation of CSI strongly impacts on MCBER receiver performance. The theoretical near-optimality of MCBER criterion may be seriously impaired by unreliable channel estimation. In this paper, we considered the GA-assisted MMSE channel estimation for STBC MC-CDMA system already presented in [18]. Such a channel estimation strategy, applied to the ideal MMSE multiuser detection, demonstrated itself very robust and near-optimal, clearly outperforming state-of-the-art techniques based on gradient descent. Genetic algorithms have a 20-year history of successful applications in telecommunications, signal processing, and electromagnetic fields due to some basic features, useful to solve complex problems with reasonable computational effort [19].
-
(1)
The convergence to the optimal solution is theoretically guaranteed (provided that a proper parameterization of the GA procedure is set), avoiding that solution be trapped in local minima.
-
(2)
The GA-based procedure can dynamically adapt itself to time-varying system conditions, because a new population of individuals is computed at each new generation.
Such features make advantageous the use of the so-called evolutionary optimization strategies (among which GAs are classified) to find practical solutions to optimization problems characterized by nonlinear cost functions and heavy computational burden (a highlighting example is shown in [20], where the inverse scattering problem is dealt with in electromagnetism). Standard GA implementations [19] represent feasible solutions as a set of individuals (called population). The cost function to be minimized (or maximized) is called fitness function. In our case, the fitness function is the following MMSE metric that must be minimized with respect to the estimated channel matrices  and
and  :
:

At each iteration (namely, generation), the genetic operators of crossover and mutation are applied on selected chromosomes with probabilities  and
and  , respectively, in order to generate new solutions belonging to the search space. The population generation terminates when a satisfactory solution has been produced or when a fixed number of generations have been completed (see Figure 2).
, respectively, in order to generate new solutions belonging to the search space. The population generation terminates when a satisfactory solution has been produced or when a fixed number of generations have been completed (see Figure 2).
The block diagram of the complete MCBER MUD receiver with GA-assisted channel estimation is shown in Figure 3. In order to make channel estimation robust and adaptive with respect to channel variations, we adopted a GA-assisted MMSE strategy articulated into two steps.
-
(1)
Training-Aided Step. during this step, an
 bit-length binary training sequence
bit-length binary training sequence  is transmitted in the form of header for each user
is transmitted in the form of header for each user 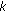 . The bits of the training sequence are organized in
. The bits of the training sequence are organized in  consecutive pairs, each one corresponding to a pair of symbols transmitted in two consecutive signaling periods. In such a way, the vectors of known bits
consecutive pairs, each one corresponding to a pair of symbols transmitted in two consecutive signaling periods. In such a way, the vectors of known bits  and
and  are employed to compute the MSE metric. The training step is repeated with a period approximately equal to the coherence time of the channel. The GA optimizer computes at each signaling period the estimated channel matrices using a selected parameterization in terms of generation number
are employed to compute the MSE metric. The training step is repeated with a period approximately equal to the coherence time of the channel. The GA optimizer computes at each signaling period the estimated channel matrices using a selected parameterization in terms of generation number  , population size
, population size 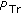 , crossover, and mutation probabilities
, crossover, and mutation probabilities 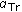 and
and 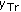 , respectively. The footer
, respectively. The footer  means that the GA parameterization is related to the training step.
means that the GA parameterization is related to the training step. -
(2)
Decision-Directed Adaptive Step: the output of the training step is the channel matrices
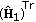 and
and 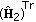 obtained by the GA-based optimizer parameterized in such a way to "learn" the channel in reliable way. During a coherence time period, the stochastic values of the channel coefficients acting over each subcarrier are strongly correlated. By this, a decision-directed adaptive updating step should be reasonably forecast. In the present dealing, the decision-directed updating step is performed by the GA, working with a different parameterization. The GA-based updating procedure is initialized by the solution computed during the training-aided step. During a symbol period, a single iteration is performed by the GA, and a single generation of individuals is produced. The symbols employed in this step to fill the data vectors
obtained by the GA-based optimizer parameterized in such a way to "learn" the channel in reliable way. During a coherence time period, the stochastic values of the channel coefficients acting over each subcarrier are strongly correlated. By this, a decision-directed adaptive updating step should be reasonably forecast. In the present dealing, the decision-directed updating step is performed by the GA, working with a different parameterization. The GA-based updating procedure is initialized by the solution computed during the training-aided step. During a symbol period, a single iteration is performed by the GA, and a single generation of individuals is produced. The symbols employed in this step to fill the data vectors 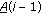 and
and  are the estimated symbols decided at the previous signaling period, that is,
are the estimated symbols decided at the previous signaling period, that is, 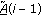 and
and  . In such a step, crossover and mutation operators do not work, because only a GA generation runs. This updating procedure is "light," but this is reasonable because only small variations of the channel amplitude and phase are to be tracked during the coherence period. Moreover, in such a way, the effects of possible symbol errors on channel estimation are conveniently reduced.
. In such a step, crossover and mutation operators do not work, because only a GA generation runs. This updating procedure is "light," but this is reasonable because only small variations of the channel amplitude and phase are to be tracked during the coherence period. Moreover, in such a way, the effects of possible symbol errors on channel estimation are conveniently reduced.
In order to make our approach clearer to the reader, we can summarize the whole GA-assisted channel estimation procedure as follows (the flowchart of the procedure has been shown in Figure 4).
-
(i)
At time
 the GA-based procedure is initialized by a constant-value population. In particular, the identity matrices have been chosen for initialization.
the GA-based procedure is initialized by a constant-value population. In particular, the identity matrices have been chosen for initialization. -
(ii)
The training-aided step begins. The
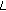 -bit known training sequence is transmitted, and the estimated channel matrices are computed by minimizing the cost function of (13). The GA parameterization is chosen as
-bit known training sequence is transmitted, and the estimated channel matrices are computed by minimizing the cost function of (13). The GA parameterization is chosen as  ,
,  ,
, 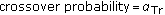 , and
, and 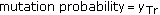 .
. -
(iii)
The training-aided step ends with the computation of the channel matrices at the time
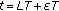 (
( is the execution time of the GA-based optimization procedure expressed in number of bit periods). Now, the GA switches to the decision-directed adaptive modality.
is the execution time of the GA-based optimization procedure expressed in number of bit periods). Now, the GA switches to the decision-directed adaptive modality. -
(iv)
At the beginning of the adaptive step, the GA is initialized with the channel matrices computed at the end of (ii), and the GA parameters are reassigned as follows: generation number
 , population size
, population size 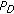 , crossover probability
, crossover probability 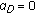 , and mutation probability
, and mutation probability 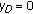 . The footer
. The footer 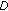 means that the GA parameterization is related now to the decision-directed adaptive step. The GA procedure produces a single population of individuals that are quite close to the one chosen during the previous signaling interval. Such kind of population is stochastically generated in Gaussian way, imposing to the Gaussian generator an updating standard deviation
means that the GA parameterization is related now to the decision-directed adaptive step. The GA procedure produces a single population of individuals that are quite close to the one chosen during the previous signaling interval. Such kind of population is stochastically generated in Gaussian way, imposing to the Gaussian generator an updating standard deviation  that actually is a system parameter. Such a parameter is linked to the Doppler spread and to the signal-to-noise ratio. An explicit mathematical link is very difficult to be obtained, but, as thumb rule, we can say that it needs to be increased as SNR and Doppler spread increase.
that actually is a system parameter. Such a parameter is linked to the Doppler spread and to the signal-to-noise ratio. An explicit mathematical link is very difficult to be obtained, but, as thumb rule, we can say that it needs to be increased as SNR and Doppler spread increase. -
(v)
The decision-directed updating step ends at the time
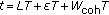 , where
, where 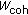 is the coherence time-window of the channel (expressed in number of bits). The GA is reinitialized with the channel matrices computed at the end of the coherence time-window and reparameterized in order to start again with the training-aided step (ii).
is the coherence time-window of the channel (expressed in number of bits). The GA is reinitialized with the channel matrices computed at the end of the coherence time-window and reparameterized in order to start again with the training-aided step (ii).
4. Experimental Results
4.1. Simulation Results
The performances of the proposed STBC MC-CDMA receiver are evaluated by means of intensive simulation trials (performed in MATLAB-SIMULINK 7.5 environment) in a Rayleigh fading channel fixing the following parameters: number of subcarriers  , transmission data rate
, transmission data rate  Kb/s, coherence bandwidth of the channel 2.1 MHz, and Doppler spread of the channel 100 Hz. We considered two test cases: the most theoretical case related to the MCBER detector exploiting the ideal CSI knowledge and the more realistic case related to the MCBER detector supported by the GA-assisted channel estimation. In such a way, we shall be able to test the effectiveness of the channel estimation strategy adopted together with the impact of nonideal channel estimation on MCBER performances.
Kb/s, coherence bandwidth of the channel 2.1 MHz, and Doppler spread of the channel 100 Hz. We considered two test cases: the most theoretical case related to the MCBER detector exploiting the ideal CSI knowledge and the more realistic case related to the MCBER detector supported by the GA-assisted channel estimation. In such a way, we shall be able to test the effectiveness of the channel estimation strategy adopted together with the impact of nonideal channel estimation on MCBER performances.
In order to verify the effectiveness of the proposed approach, we considered other state-of-the-art receivers for comparison, namely,
-
(i)
the ideal MMSE MUD receiver exploiting ideal CSI knowledge [7];
-
(ii)
the LMS adaptive implementation of MMSE receiver [7];
-
(iii)
the single-user Equal-Gain Combining (EGC) receiver [7];
-
(iv)
the MMSE MUD receiver supported by the GA-assisted channel estimation [18].
As lower bound, we considered the BER curve obtained by Maximal Ratio Combining (MRC) detection in the single-user case (i.e., the optimal single-user detection, supposing the absence of multiuser interference). In our simulations, we considered three different scenarios including  ,
,  , and
, and  users. The GA optimizer has been parameterized as follows: (i) training-aided step
users. The GA optimizer has been parameterized as follows: (i) training-aided step  ,
,  ,
,  ,
,  ,
,  , (ii) decision-directed adaptive step
, (ii) decision-directed adaptive step  . As the Jakes channel model has been adopted for simulation, the channel coherence time window approximately equals about 1800 bits. Therefore, the overhead due to the insertion of the training sequence equals to less than 1.8%.
. As the Jakes channel model has been adopted for simulation, the channel coherence time window approximately equals about 1800 bits. Therefore, the overhead due to the insertion of the training sequence equals to less than 1.8%.
The corresponding BER curves versus  are shown for all the tested receivers in Figures 5, 6, and 7, respectively. It can be seen that in all scenarios the proposed LMS-based MCBER detector with and without ideal CSI knowledge clearly outperforms both EGC detector and LMS-based MMSE adaptive detector that exhibit a nasty error floor as the number of users increases. Moreover, the proposed MCBER detector exploiting ideal CSI knowledge yields performances that are better than those ones of ideal MMSE detector. Such a last improvement is clearly evident for
are shown for all the tested receivers in Figures 5, 6, and 7, respectively. It can be seen that in all scenarios the proposed LMS-based MCBER detector with and without ideal CSI knowledge clearly outperforms both EGC detector and LMS-based MMSE adaptive detector that exhibit a nasty error floor as the number of users increases. Moreover, the proposed MCBER detector exploiting ideal CSI knowledge yields performances that are better than those ones of ideal MMSE detector. Such a last improvement is clearly evident for  and
and  users, whereas it becomes slighter for
users, whereas it becomes slighter for  users. In general, for an increasing number of users, BER curves related to ideal MMSE and MCBER tend to become closer to each other and more distant with respect to the single-user bound. Such behaviour is not unexpected. As number of users
users. In general, for an increasing number of users, BER curves related to ideal MMSE and MCBER tend to become closer to each other and more distant with respect to the single-user bound. Such behaviour is not unexpected. As number of users  increases, the global detection noise (including AWGN and multiuser interference) is getting more and more Gaussian-distributed, and, therefore, optimizing the receiver with respect to the MMSE provides very close results to optimizing on BER. Moreover, the single-user bound curve depicted in Figures 5–7 is a lower bound also on theoretically optimum ML detection as it does not take into account the presence of the multiuser interference. In case of increasing number of users, it is getting more and more difficult for a linear receiver to approach the single-user bound.
increases, the global detection noise (including AWGN and multiuser interference) is getting more and more Gaussian-distributed, and, therefore, optimizing the receiver with respect to the MMSE provides very close results to optimizing on BER. Moreover, the single-user bound curve depicted in Figures 5–7 is a lower bound also on theoretically optimum ML detection as it does not take into account the presence of the multiuser interference. In case of increasing number of users, it is getting more and more difficult for a linear receiver to approach the single-user bound.
Focusing our attention on the effectiveness of the GA-assisted channel estimation applied in such an MCBER-MUD framework, we can see from Figures 5–7 that the MCBER detector supported by nonideal channel estimation performs very close to MCBER detector exploiting the ideal channel knowledge for  and
and  users. The effects of nonideal channel estimation are more evident for higher number of users (
users. The effects of nonideal channel estimation are more evident for higher number of users ( ) and therefore in the presence of higher level of multiuser interference. In this last case, the MCBER receiver with GA-assisted channel estimation performs a bit less than MMSE receiver with ideal CSI knowledge but better than the MMSE using the same algorithm for channel estimation. In our opinion, the most relevant fact able to confirm the correctness of our analysis is that the proposed MCBER detector always outperforms MMSE MUD when working together in the same conditions of "channel knowledge."
) and therefore in the presence of higher level of multiuser interference. In this last case, the MCBER receiver with GA-assisted channel estimation performs a bit less than MMSE receiver with ideal CSI knowledge but better than the MMSE using the same algorithm for channel estimation. In our opinion, the most relevant fact able to confirm the correctness of our analysis is that the proposed MCBER detector always outperforms MMSE MUD when working together in the same conditions of "channel knowledge."
In Figure 8, some results have been shown about the variance of the channel estimation error (EEV). One can note that such a variance, computed on the overall channel coefficients, is decreasing with  and exhibits satisfactory values (i.e., lower than 10-2 for
and exhibits satisfactory values (i.e., lower than 10-2 for  dB for
dB for  ,
,  , and
, and  users). As expected (and already evidenced by BER curves of Figures 5–7), EEV increases with the number of users, because MUI increases.
users). As expected (and already evidenced by BER curves of Figures 5–7), EEV increases with the number of users, because MUI increases.
4.2. Computational Complexity Considerations and Algorithmic Parameterization
As far as computational issues are concerned, the current literature claims that MCBER criterion has a computational order which is linear with the number of users [14]. In such a case, the computational effort would be reduced with respect to the ideal MMSE detector (which is  [7]), and it would be comparable with the LMS-based adaptive implementation of MMSE (which is linear again). In our opinion, the reduction of the computational complexity is one of the main advantages yielded by the proposed approach. In fact, the MCBER criterion is theoretically closer to optimality than MMSE, and simulation results shown in Figures 5–7 confirm this claim. But the developed adaptive MCBER-MUD algorithm is also less demanding from a computational viewpoint than ideal MMSE, despite requiring the same knowledge of the channel state information.
[7]), and it would be comparable with the LMS-based adaptive implementation of MMSE (which is linear again). In our opinion, the reduction of the computational complexity is one of the main advantages yielded by the proposed approach. In fact, the MCBER criterion is theoretically closer to optimality than MMSE, and simulation results shown in Figures 5–7 confirm this claim. But the developed adaptive MCBER-MUD algorithm is also less demanding from a computational viewpoint than ideal MMSE, despite requiring the same knowledge of the channel state information.
About computational complexity of the GA-assisted channel estimator we can say that GA requires a number of elementary operations to derive a solution that is equal to  [19]. Thus, the computational burden required during the training-aided step is of the order of
[19]. Thus, the computational burden required during the training-aided step is of the order of  elementary operations to be executed during an execution time window
elementary operations to be executed during an execution time window  , where
, where  . The value assigned to
. The value assigned to  mainly depends on the computational power of the signal-processing device employed. During the decision-directed adaptive step, the computational requirement of the GA is reduced to
mainly depends on the computational power of the signal-processing device employed. During the decision-directed adaptive step, the computational requirement of the GA is reduced to  elementary operations to be executed during an STBC modulation period. Such a computational requirement is comparable with that one involved in state-of-the-art STBC channel estimation algorithms (see [18] for the comparison).
elementary operations to be executed during an STBC modulation period. Such a computational requirement is comparable with that one involved in state-of-the-art STBC channel estimation algorithms (see [18] for the comparison).
In order to conclude this section, we provide now some notes about algorithmic parameterization. The step-size parameter  of both LMS-based algorithms (MMSE and MCBER) has been chosen empirically for each scenario in order to minimize the overall BER over the various
of both LMS-based algorithms (MMSE and MCBER) has been chosen empirically for each scenario in order to minimize the overall BER over the various  values. From the parameters selection phase, we noted that LMS-based MCBER detector is characterized by a reduced sensitivity to parameterization with respect to state-of-the-art LMS-based MMSE MUD. Indeed, fixing the number of users
values. From the parameters selection phase, we noted that LMS-based MCBER detector is characterized by a reduced sensitivity to parameterization with respect to state-of-the-art LMS-based MMSE MUD. Indeed, fixing the number of users  , the step-size
, the step-size  is substantially invariant with respect to
is substantially invariant with respect to  values. On the other hand, LMS-based MMSE multiuser detector would require a different value of
values. On the other hand, LMS-based MMSE multiuser detector would require a different value of  for each
for each  in order to provide satisfactory BER performances. As far as the parameterization of the GA-based optimizer is concerned, we must say that formal methodologies targeted to find an optimal parameterization of genetic procedures are not available. In the literature, there are only some interesting heuristic analyses like the one proposed by Tsoy in [21]. So GA parameters have been selected by means of explicitly devoted simulation trials, performed by keeping into account the major guidelines pointed out in [21] that basically are the following two: (a) the population size should be sufficiently large in order to have a conveniently dimensioned space search, and (b) the number of generations should be appropriately assigned in dependence of the population size. In fact, in case of large population, too strict limit for the search time can force algorithm to stop without having enough time to realize its search possibility. At the end of the simulation trials devoted to parameterization, we found numerical values for generation number, population size, crossover, and mutation probabilities (shown in Section 4.1) that have assured the best tradeoff between achieved results and computational load. In particular, we assumed an intermediate
in order to provide satisfactory BER performances. As far as the parameterization of the GA-based optimizer is concerned, we must say that formal methodologies targeted to find an optimal parameterization of genetic procedures are not available. In the literature, there are only some interesting heuristic analyses like the one proposed by Tsoy in [21]. So GA parameters have been selected by means of explicitly devoted simulation trials, performed by keeping into account the major guidelines pointed out in [21] that basically are the following two: (a) the population size should be sufficiently large in order to have a conveniently dimensioned space search, and (b) the number of generations should be appropriately assigned in dependence of the population size. In fact, in case of large population, too strict limit for the search time can force algorithm to stop without having enough time to realize its search possibility. At the end of the simulation trials devoted to parameterization, we found numerical values for generation number, population size, crossover, and mutation probabilities (shown in Section 4.1) that have assured the best tradeoff between achieved results and computational load. In particular, we assumed an intermediate  equal to 15 dB as reference value, and we derived by simulations the best parameterization for this value. Then, we observed by other simulations that the GA parameterization chosen for the reference
equal to 15 dB as reference value, and we derived by simulations the best parameterization for this value. Then, we observed by other simulations that the GA parameterization chosen for the reference  is "very close to the best" also for higher and lower
is "very close to the best" also for higher and lower  . The reduced sensitivity to parameterization of GA procedures, already observed in [18], is again confirmed.
. The reduced sensitivity to parameterization of GA procedures, already observed in [18], is again confirmed.
5. Conclusions
In this paper, a novel receiver scheme has been investigated for MC-CDMA systems using Alamouti's space-time block coding. In particular, we considered a Minimum Conditional Bit-Error-Rate (MCBER) MUD linear receiver in order to reduce the computational complexity without significant performance degradations with respect to the formal MBER criterion. In the perspective of a real receiver deployment, an adaptive LMS-based implementation of the MCBER detector has been integrated with a robust and computationally affordable channel estimation assisted by a genetic optimizer. The proposed MCBER approach always allows improving BER performances with respect to other state-of-the-art linear detectors working with the same degree of channel knowledge. It is worth noting that the performance improvement with respect to MMSE-MUD strategies is achieved by spending a reduced computational effort, linearly increasing with the number of users. Numerical results evidenced that BER curves of MCBER and ideal MMSE are getting closer as the number of users approaches the maximum allowable value. This behaviour is intrinsic to the linear multiuser detection and fully motivated by the nature of the MCBER criterion adopted.
Future research activities might concern the utilization of evolutionary optimization algorithms (e.g., GA, Particle Swarm Optimization (PSO), etc.) to provide a numerical solution to the MCBER problem instead of the proposed LMS-based solution. Also the adoption of PSO-assisted channel estimation, instead of GA-assisted one, may represent an interesting topic for future research.
References
Hanzo L, Yan LL, Kuan EL, Yen K: Single and Multi-Carrier DS-CDMA. Wiley, Chichester, UK; 2003.
Tse D, Visvanath P: Fundamentals of Wireless Communications. Cambridge University Press, Cambridge, Mass, USA; 2005.
Ahmadi S: An overview of next-generation mobile WiMAX technology. IEEE Communications Magazine 2009, 47(6):84-98.
Johansson K, Bergman J, Gerstenberger D, Blomgren M, Wallén A: Multi-carrier HSPA evolution. Proceedings of the 69th IEEE Vehicular Technology Conference (VTC '09), April 2009, Barcelona, Spain 1-5.
Aldhaheri RW, Al-Qahtani AH: Performance analysis of fixed and mobile WiMAX MC-CDMA-based system. Proceedings of the 7th International Symposium on Wireless Communications Systems (ISWCS '10), September 2010, York, UK 436-440.
Juntti M, Vehkapera M, Leinonen J, Li Z, Tujkovic D, Tsumura S, Hara S: MIMO MC-CDMA communications for future cellular systems. IEEE Communications Magazine 2005, 43(2):118-124.
Auffray JM, Helard JF: Performance of multicarrier CDMA technique combined with space-time block coding over Rayleigh channel. Proceedings of the 7th IEEE International Symposium on Spread Spectrum Techniques and Applications, September 2002, Prague, Czech Republic 2: 348-352.
Chen S, Samingan AK, Mulgrew B, Hanzo L: Adaptive minimum-BER linear multiuser detection for DS-CDMA signals in multipath channels. IEEE Transactions on Signal Processing 2001, 49(6):1240-1247. 10.1109/78.923306
Yi SJ, Tsimenidis CC, Hinton OR, Sharif BS: Adaptive minimum bit-error-rate multi-user detection for asynchronous MC-CDMA systems in frequency selective Rayleigh fading channels. Proceedings of the 14th IEEE Personal, Indoor and Mobile Radio Communications Conference (PIMRC '03), September 2003, Beijing, China 2: 1269-1273.
Chen S, Livingstone A, Hanzo L: Minimum bit-error rate design for space—time equalization-based multiuser detection. IEEE Transactions on Communications 2006, 54(5):824-832.
Conti A, Masini B, Zabini F, Andrisano O: On the down-link performance of multi-carrier CDMA systems with partial equalization. IEEE Transactions on Wireless Communications 2007, 6(1):230-239.
Masini BM, Conti A: Adaptive TORC detection for MC-CDMA wireless systems. IEEE Transactions on Communications 2009, 57(11):3460-3471.
D'Orazio L, Sacchi C, Fedrizzi R, De Natale FGB: An adaptive minimum-BER approach for multi-user detection in STBC-MIMO MC-CDMA systems. Proceedings of the 50th IEEE Annual Global Telecommunications Conference (GLOBECOM '07), November 2007, Washington, DC, USA 3427-3431.
Dua A, Desai UB, Mallik RK: Minimum probability of error-based methods for adaptive multiuser detection in multipath DS-CDMA channels. IEEE Transactions on Wireless Communications 2004, 3(3):939-948. 10.1109/TWC.2004.827759
Dayal PM, Desai UB, Mahanta A: Minimum conditional probability of error detection for MC-CDMA. Proceedings of the IEEE International Symposium on Spread Spectrum Techniques and Applications (ISSSTA '04), September 2004, Sydney, Australia 51-55.
Alamouti SM: A simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998, 16(8):1451-1458. 10.1109/49.730453
Seo B, Ahn W-G, Jeong C, Kim H-M: Fast convergence LMS adaptive receiver for MC-CDMA systems with space-time block coding. IEEE Communications Letters 2010, 14(8):737-739.
D'Orazio L, Sacchi C, Donelli M, De Natale FGB: MMSE multi-user detection with GA-assisted channel estimation for STBC MC-CDMA mobile communication systems. Proceedings of the 10th IEEE International Symposium on Spread Spectrum Techniques and Applications (ISSSTA '08), August 2008, Bologna, Italy 182-187.
Goldberg DE: Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley, Reading, Mass, USA; 1999.
Rocca P, Massa A: Evolutionary-based optimization techniques for inverse scattering—a review. Proceedings of the 28th Progress in Electromagnetics Research Symposium (PIERS '10), July 2010, Cambridge, Mass, USA
Tsoy YR: The influence of population size and search time limit on genetic algorithm. Proceedings of the 7th Korea-Russia International Symposium on Science and Technology (KORUS '03), June-July 2003, Uslan, Korea 3: 181-187.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
D'Orazio, L., Sacchi, C., Donelli, M. et al. A Near-Optimum Multiuser Receiver for STBC MC-CDMA Systems Based on Minimum Conditional BER Criterion and Genetic Algorithm-Assisted Channel Estimation. J Wireless Com Network 2011, 351494 (2011). https://doi.org/10.1155/2011/351494
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/351494


 bit-length binary training sequence
bit-length binary training sequence  is transmitted in the form of header for each user
is transmitted in the form of header for each user 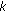 . The bits of the training sequence are organized in
. The bits of the training sequence are organized in  consecutive pairs, each one corresponding to a pair of symbols transmitted in two consecutive signaling periods. In such a way, the vectors of known bits
consecutive pairs, each one corresponding to a pair of symbols transmitted in two consecutive signaling periods. In such a way, the vectors of known bits  and
and  are employed to compute the MSE metric. The training step is repeated with a period approximately equal to the coherence time of the channel. The GA optimizer computes at each signaling period the estimated channel matrices using a selected parameterization in terms of generation number
are employed to compute the MSE metric. The training step is repeated with a period approximately equal to the coherence time of the channel. The GA optimizer computes at each signaling period the estimated channel matrices using a selected parameterization in terms of generation number  , population size
, population size 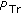 , crossover, and mutation probabilities
, crossover, and mutation probabilities 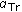 and
and 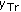 , respectively. The footer
, respectively. The footer  means that the GA parameterization is related to the training step.
means that the GA parameterization is related to the training step.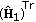 and
and 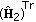 obtained by the GA-based optimizer parameterized in such a way to "learn" the channel in reliable way. During a coherence time period, the stochastic values of the channel coefficients acting over each subcarrier are strongly correlated. By this, a decision-directed adaptive updating step should be reasonably forecast. In the present dealing, the decision-directed updating step is performed by the GA, working with a different parameterization. The GA-based updating procedure is initialized by the solution computed during the training-aided step. During a symbol period, a single iteration is performed by the GA, and a single generation of individuals is produced. The symbols employed in this step to fill the data vectors
obtained by the GA-based optimizer parameterized in such a way to "learn" the channel in reliable way. During a coherence time period, the stochastic values of the channel coefficients acting over each subcarrier are strongly correlated. By this, a decision-directed adaptive updating step should be reasonably forecast. In the present dealing, the decision-directed updating step is performed by the GA, working with a different parameterization. The GA-based updating procedure is initialized by the solution computed during the training-aided step. During a symbol period, a single iteration is performed by the GA, and a single generation of individuals is produced. The symbols employed in this step to fill the data vectors 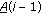 and
and  are the estimated symbols decided at the previous signaling period, that is,
are the estimated symbols decided at the previous signaling period, that is, 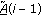 and
and  . In such a step, crossover and mutation operators do not work, because only a GA generation runs. This updating procedure is "light," but this is reasonable because only small variations of the channel amplitude and phase are to be tracked during the coherence period. Moreover, in such a way, the effects of possible symbol errors on channel estimation are conveniently reduced.
. In such a step, crossover and mutation operators do not work, because only a GA generation runs. This updating procedure is "light," but this is reasonable because only small variations of the channel amplitude and phase are to be tracked during the coherence period. Moreover, in such a way, the effects of possible symbol errors on channel estimation are conveniently reduced.
 the GA-based procedure is initialized by a constant-value population. In particular, the identity matrices have been chosen for initialization.
the GA-based procedure is initialized by a constant-value population. In particular, the identity matrices have been chosen for initialization. -bit known training sequence is transmitted, and the estimated channel matrices are computed by minimizing the cost function of (13). The GA parameterization is chosen as
-bit known training sequence is transmitted, and the estimated channel matrices are computed by minimizing the cost function of (13). The GA parameterization is chosen as  ,
,  ,
, 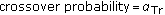 , and
, and 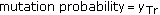 .
.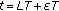 (
( is the execution time of the GA-based optimization procedure expressed in number of bit periods). Now, the GA switches to the decision-directed adaptive modality.
is the execution time of the GA-based optimization procedure expressed in number of bit periods). Now, the GA switches to the decision-directed adaptive modality. , population size
, population size 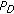 , crossover probability
, crossover probability 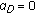 , and mutation probability
, and mutation probability 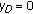 . The footer
. The footer 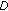 means that the GA parameterization is related now to the decision-directed adaptive step. The GA procedure produces a single population of individuals that are quite close to the one chosen during the previous signaling interval. Such kind of population is stochastically generated in Gaussian way, imposing to the Gaussian generator an updating standard deviation
means that the GA parameterization is related now to the decision-directed adaptive step. The GA procedure produces a single population of individuals that are quite close to the one chosen during the previous signaling interval. Such kind of population is stochastically generated in Gaussian way, imposing to the Gaussian generator an updating standard deviation  that actually is a system parameter. Such a parameter is linked to the Doppler spread and to the signal-to-noise ratio. An explicit mathematical link is very difficult to be obtained, but, as thumb rule, we can say that it needs to be increased as SNR and Doppler spread increase.
that actually is a system parameter. Such a parameter is linked to the Doppler spread and to the signal-to-noise ratio. An explicit mathematical link is very difficult to be obtained, but, as thumb rule, we can say that it needs to be increased as SNR and Doppler spread increase.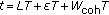 , where
, where 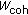 is the coherence time-window of the channel (expressed in number of bits). The GA is reinitialized with the channel matrices computed at the end of the coherence time-window and reparameterized in order to start again with the training-aided step (ii).
is the coherence time-window of the channel (expressed in number of bits). The GA is reinitialized with the channel matrices computed at the end of the coherence time-window and reparameterized in order to start again with the training-aided step (ii).

 yielded by the LMS-based MCBER (with ideal CSI knowledge and GA-assisted channel estimation), EGC (with ideal CSI knowledge), LMS-based MMSE and ideal MMSE (with ideal CSI knowledge and GA-assisted channel estimation) multiuser detectors for
yielded by the LMS-based MCBER (with ideal CSI knowledge and GA-assisted channel estimation), EGC (with ideal CSI knowledge), LMS-based MMSE and ideal MMSE (with ideal CSI knowledge and GA-assisted channel estimation) multiuser detectors for
 subcarriers and
subcarriers and
 users.
users.

 yielded by the LMS-based MCBER (with ideal CSI knowledge and GA-assisted channel estimation), EGC (with ideal CSI knowledge), LMS-based MMSE and ideal MMSE (with ideal CSI knowledge and GA-assisted channel estimation) multiuser detectors for
yielded by the LMS-based MCBER (with ideal CSI knowledge and GA-assisted channel estimation), EGC (with ideal CSI knowledge), LMS-based MMSE and ideal MMSE (with ideal CSI knowledge and GA-assisted channel estimation) multiuser detectors for
 subcarriers and
subcarriers and
 users.
users.

 yielded by the LMS-based MCBER (with ideal CSI knowledge and GA-assisted channel estimation), EGC (with ideal CSI knowledge), LMS-based MMSE and ideal MMSE (with ideal CSI knowledge and GA-assisted channel estimation) multiuser detectors for
yielded by the LMS-based MCBER (with ideal CSI knowledge and GA-assisted channel estimation), EGC (with ideal CSI knowledge), LMS-based MMSE and ideal MMSE (with ideal CSI knowledge and GA-assisted channel estimation) multiuser detectors for
 subcarriers and
subcarriers and
 users.
users.

 measured for
measured for  subcarriers,
subcarriers,  ,
,  , and
, and  users.
users.