- Research Article
- Open access
- Published:
Efficient Key Agreements in Dynamic Multicast Height Balanced Tree for Secure Multicast Communications in Ad Hoc Networks
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 382701 (2011)
Abstract
Alterations and unpredictability of the network topology in mobile ad hoc networks (MANETs) are less capable of ensuring the security of multicast data transmissions than in conventional networks. Despite the recent development of many key agreement protocols for MANETs, to our knowledge, only a few secure multicast data transmissions have been integrated into the key agreement. This study proposes a dynamic multicast height balanced group key agreement (DMHBGKA) that allows a user in a multicast group to efficiently and dynamically compose the group key and securely deliver multicast data from a multicast source to the other multicast group users in wireless ad hoc networks. The hierarchical structure of the proposed key agreement partitions the group members into location-based clusters capable of reducing the cost of communication and key management when member joins or leave networks. Moreover, based on elliptic curve Diffie-Hellman (ECDH) cryptography key management, the proposed scheme not only provides effective and efficient dynamic group key reconstructions and secures multicast data transmissions but also fits the robustness of the wireless networks and lowers overhead costs of security management.
1. Introduction
As an emerging paradigm of wireless communication for mobile nodes, ad hoc networks have received considerable attention in recent years due to a rapid expansion of wireless devices and the interest in mobile communications. In an ad hoc network [1–3], mobile nodes want to communicate with each other, but have no fixed links like a wire infrastructure network. While acting as a router, each node is responsible for discovering dynamically other nodes in a transmission range [4]. The emergence of ad hoc networks poses a challenge for maintaining the security of a group multicast since mobile ad hoc networks differ from conventional wired networks. Security is thus a priority concern in wireless networks, especially for security-sensitive applications. Computer security attributes of confidentiality, integrity, availability, authentication, and nonrepudiation are crucial to protect communications in ad hoc networks. Moreover, the network topology of an ad hoc network changes frequently and unpredictably, explaining why security is extremely challenging in routing and multicasting. In practice, establishing a trusted entity referred to as a certification authority (CA) by using a single node in ad hoc networks is a rather complex task. For an unavailable or compromised CA due to a vulnerable network structure, the entire secure communication cannot access the public keys of other nodes [5–8].
Many security protection schemes have been developed for an individual multicast group. Some schemes address single-security-level group communications by using Diffie-Hellman algorithm extending contributory key management and logical key hierarchy [9]. While describing how a multicast group user can compose a group key, this study presents a hierarchical group key management to multicast data from a multicast source to the remaining multicast members securely. We hypothesize that capable of acquiring the measures, that is, latitude, longitude, and altitude, from global positioning system (GPS) mobile nodes have a hierarchical structure. Additionally, group members are partitioned into location-based clusters to reduce the cost of key management. Moreover, encryption and decryption operations are presented for secure multicast communications.
The rest of this paper is organized as follows. Section 2 introduces the related security aspects of secure multicast communications in ad hoc networks. Section 3 then presents a secure multicast key agreement. Next, Section 4 introduces the proposed dynamic multicast height balanced group key agreement (DMHBGKA) scheme and the process of rekeying for participating and departing nodes. Additionally, Section 5 discusses secure multicast communication operations. Section 6 summarizes the simulation and analytical results for the proposed scheme. Conclusions are finally drawn in Section 7, along with recommendations for future research.
2. Related Security Aspects of Secure Multicast Communications in Ad Hoc Networks
The role of multicasting as a scalable solution for group communication in MANETs has ushered in the development of many group key management approaches. While those schemes normally focus on improving security and reducing the size of group keys, forward and backward confidential information should also be provided for multicast applications whenever a user joins or leaves the system. Kim et al. [7] developed a tree-based group key agreement scheme by using a binary tree infrastructure to compute and update a group key efficiently. That study also completed secure and distributed protocols by exploiting the group Diffie-Hellman (GDH) key exchange. Vasudevan and Sukumar [10] developed a scalable secure multicast algorithm by using a multiserver approach when the data encryption key (DEK) had to be changed. To minimize the rekeying cost, their schemes utilize the dynamic split and merge with a low overhead cost, where a physical server splits and merges its traffic into multiple groups, with each group served by a dedicated server. Wang et al. [11] developed a hybrid group key management scheme with a two-level structure where the group users are subdivided into clusters, subsequently reducing the rekeying cost as key updating. While developing a scheme that ensures key and data authenticity among group members, Chiang and Huang [12] demonstrated the data confidentiality of group messages with the properties of forward and backward confidential information. The group key is established collaboratively by combining the keys of all authenticated members, which assists in maintaining the communication and computation transparency among group members. Chaddoud et al. [13] divided group members into several operation units to perform microkey management. Compared with the logical key hierarchy (LKH), the above schemes can more significantly reduce the overload of the key server and provide more efficient key management for a secure wireless multicast. However, the above schemes lack efficient key management mechanisms for members to participate in or leave MANETs dynamically.
Despite the considerable attention paid to grouping or clustering issues for reducing traffic overhead and broadcast storm problems of MANETs, reducing the rekeying costs in key updating and increasing the key management efficiency have seldom been addressed in group key management schemes that focus on clustering issues. Clustering algorithms for MANETs have been developed to reduce communication costs between mobile nodes. Even numerous mobile nodes require only a few cluster headers to manipulate wireless communications.
Our previous work developed a key-distribution graph model by using the Prüfer decoding algorithm for secure multicast communications in MANETs [12]. A key graph is a directed acyclic graph  with two nodes, that is, leaf nodes (
with two nodes, that is, leaf nodes ( -nodes) representing multicast-user nodes and
-nodes) representing multicast-user nodes and  -nodes representing keys [13]. Each
-nodes representing keys [13]. Each  -node representing a multicast-user node has one outgoing edge associated with the individual key of each user node. Each
-node representing a multicast-user node has one outgoing edge associated with the individual key of each user node. Each  -node has one or more incoming and outgoing edges. If only having incoming edges and no outgoing edge, a
-node has one or more incoming and outgoing edges. If only having incoming edges and no outgoing edge, a  -node is a root of the key graph.
-node is a root of the key graph.  -node denotes a group key held by each user in
-node denotes a group key held by each user in  . Moreover, a key-distribution graph specifies a secure group
. Moreover, a key-distribution graph specifies a secure group  as follows:
as follows:
-
(1)
each multicast-user node in
 corresponds to a unique
corresponds to a unique  -node,
-node, -
(2)
each individual key corresponds to a unique
 -node,
-node, -
(3)
the group key
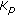 has a direct path from all
has a direct path from all  -nodes.
-nodes.
For instance, the key graph in Figure 1 specifies the following secure group:
 ,
,
 ,
,
 .
.
3. Secure Multicast Key Agreement
This section introduces multicast key management schemes and maintenance concepts that provide location-based multicast secure communications by using elliptic curve Diffie-Hellman agreement and geographic position information to deliver packets to multicast trees securely.
3.1. Elliptic Curve Diffie-Hellman Key Management Agreement
Since MANETs have limited resources, many security schemes provide high security level functions, such as asymmetric key and public key infrastructure (PKI), but they need a lot of resources; therefore, mobile networks cannot perform the security functions very well. To date, several studies have adopted elliptic curve Diffe-Hellman- (ECDH-) based security methods for networks, such as the studies by Sklavos and Zhang [14], Szczechowiak et al. [15], and Liu and Ning [16]. Sklavos and Zhang developed a hardware design and architecture for elliptic curve cryptography (ECC). Szczechowiak et al. investigated the ECC boundary and proved that public key cryptography was practical for wireless networks. Liu and Ning generated an implementation library and an executable package for ECC.
This session briefly introduces the ECC and ECDH schemes [17] for implementation in this study. Table 1 compares the security levels of common cryptographic key lengths. Smaller key size 160-bit in the ECC performs comparable security levels to 1024-bit RSA. The ECC has efficient operation and is indeed practicable for wireless networks with limited resources.
An elliptic curve is topologically equivalent to a torus over a finite field GF (a Galois field of order  ), as shown in Figure 2 and comprises a set of finite points
), as shown in Figure 2 and comprises a set of finite points  , where coordinates
, where coordinates  ,
,  are integers and satisfy
are integers and satisfy

The coefficients  are elements in
are elements in  , since the field
, since the field  (
( prime) is generally adopted in cryptographic applications, such that the elliptic curve in (1) can be translated into
prime) is generally adopted in cryptographic applications, such that the elliptic curve in (1) can be translated into 

where  and
and  belong to
belong to  . Considering two points on curve
. Considering two points on curve  and
and  , and a point at infinity
, and a point at infinity  , where
, where  , points
, points  ,
,  and
and  satisfy the following rules:
satisfy the following rules:
(1) ,
,
(2) ,
,
(3) on the curve, where
on the curve, where  ,
,  , where
, where

However, given points  and
and  on the curve, if the discrete logarithm of
on the curve, if the discrete logarithm of  to base
to base  , denoted as
, denoted as  , is large, then calculating the value of
, is large, then calculating the value of  where
where  is infeasible. The ECC requires the elliptic curve discrete logarithm problem being simple to solve.
is infeasible. The ECC requires the elliptic curve discrete logarithm problem being simple to solve.
The elliptic curve Diffie-Hellman (ECDH) is a variant of the Diffie-Hellman (DH) key agreement protocol, using elliptic curve cryptography that allows two parties to establish a shared secret key (session key) over an insecure channel. Two parties then exploit this key to encrypt subsequent communications using a symmetric key scheme. The ECDH with 160-bit key lengths provides the same security level to a 1024-bit DH secret sharing protocol [15, 16]. However, the original DH protocol needs a key of at least 1024 bits to achieve adequate security; therefore, it requires high CPU and memory capabilities to perform exponential operations. Unfortunately, mobile nodes with limited resources have insufficient power to handle the overhead. Therefore, ECDH is quite suited for MANETs.
Consider the case in ECDH, where mobile node  wants to establish a shared key with node
wants to establish a shared key with node  , as shown in Figure 3. The public parameters (a prime
, as shown in Figure 3. The public parameters (a prime  , a base point
, a base point  as a generator in Diffe-Hellman, coefficients
as a generator in Diffe-Hellman, coefficients  and
and  , and elliptic curve
, and elliptic curve  ) must first be set. Additionally, each party must have an appropriate key pair for elliptic curve cryptography, comprising an ECC private key
) must first be set. Additionally, each party must have an appropriate key pair for elliptic curve cryptography, comprising an ECC private key  (a randomly selected integer) and a public key
(a randomly selected integer) and a public key  (where
(where  ). Let a node key pair of
). Let a node key pair of  denote
denote  , and a node key pair of
, and a node key pair of  denote
denote  . Each party must have the other party's public key. Node
. Each party must have the other party's public key. Node  calculates
calculates  , while node
, while node  calculates
calculates  . Both parties calculate the shared key as
. Both parties calculate the shared key as  . The protocol is secure because it reveals nothing (except public keys, which are not secret), and because no party can calculate the private key of the other unless it can solve the Diffie-Helman problem (DHP) [18]. ECDH scheme is suited for ad hoc networks with limited resources. Each node only needs a few operations to achieve compatible security levels on RSA or Diffee-Hellman. This study exploits ECDH on group-based key managements and secure data transmission mechanisms and proposes a dynamic multicast height balanced group key agreement to achieve effective and efficient key synchronization, even though nodes dynamically participate in and depart from the wireless network.
. The protocol is secure because it reveals nothing (except public keys, which are not secret), and because no party can calculate the private key of the other unless it can solve the Diffie-Helman problem (DHP) [18]. ECDH scheme is suited for ad hoc networks with limited resources. Each node only needs a few operations to achieve compatible security levels on RSA or Diffee-Hellman. This study exploits ECDH on group-based key managements and secure data transmission mechanisms and proposes a dynamic multicast height balanced group key agreement to achieve effective and efficient key synchronization, even though nodes dynamically participate in and depart from the wireless network.
3.2. The Clustering Scheme for Choosing Cluster Head
This section describes the selection steps for cluster headers in the location-based multicluster architecture shown in Figures 4 and 5. The clustering scheme partitions a large group into a hierarchy of recursively organized subgroups based on a distributed geographic hashing method. A mobile node wanting to join a multicast group takes  and
and  coordinates as inputs of a hash function and then outputs a unique region ID. This node subsequently sends a HELLO message, including the region ID,
coordinates as inputs of a hash function and then outputs a unique region ID. This node subsequently sends a HELLO message, including the region ID,  and
and  coordinates. In the same region, the fact that each node with a unique ID realizes
coordinates. In the same region, the fact that each node with a unique ID realizes  and
and  coordinates of its one-hop neighbors allows it to determine which one has the shortest distance to the center of the wireless network area. The node with the shortest distance is selected as a cluster head and then broadcasts a cluster message to the remaining nodes. Following the clustering phases, the system determines 16 clusters in this system, that is,
coordinates of its one-hop neighbors allows it to determine which one has the shortest distance to the center of the wireless network area. The node with the shortest distance is selected as a cluster head and then broadcasts a cluster message to the remaining nodes. Following the clustering phases, the system determines 16 clusters in this system, that is,  . Each cluster head subsequently exploits the proposed DHBGKA scheme to generate a group key
. Each cluster head subsequently exploits the proposed DHBGKA scheme to generate a group key  for each cluster member to ensure secure multicast communications.
for each cluster member to ensure secure multicast communications.
4. Dynamic Multicast Height Balanced Tree
In ad hoc networks, mobile nodes join or leave networks dynamically, necessitating that the system performs group key reconstructions frequently. This work presents a dynamic multicast height balanced group key agreement (DMHBGKA) to achieve dynamic multicast key management. The DMHBGKA tree has the following attributes.
-
(1)
DMHBGKA tree is a special binary search tree in which the subtrees of each node differ in height by at most one. Additionally, each subtree is a DMHBGKA tree, as shown in Figure 6.
-
(2)
Balance factor (BF) denotes the height difference of left and right subtrees, while
 , where
, where 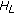 denotes the height of a left subtree, and
denotes the height of a left subtree, and 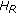 denotes the height of a right subtree.
denotes the height of a right subtree. -
(3)
A node joining or leaving networks leads to a tree unbalance. The proposed DMHBGKA scheme adjusts procedures to rebalance the tree. The procedures are classified into categories of left rotation (LL), left-right rotation (LR), right rotation (RR), and right-left (RL) rotations. The procedure is adjusted as follows.
Step 1.
According to the binary search tree rule, place (or remove) the new joining (or leaving) node in (or from) the correct place, depending on its ID (MAC or IP address).
Step 2.
Calculate the BF of each node, which belongs to  . If not, the DMHBKA tree loses balance.
. If not, the DMHBKA tree loses balance.
Step 3.
Adopt LL, RR, LR, and RL mechanisms to perform unbalanced adjustments.
Step 4.
Reconstruct the balanced DMHBGKA tree.
A node joins or leaves the networks. The time complexity associated with searching the target node is  (
( denotes the number of nodes); the system only needs to modify the link point of the data structure and thus takes
denotes the number of nodes); the system only needs to modify the link point of the data structure and thus takes  time complexity. As the DMHBGKA tree is unbalanced, in a worst case scenario, the adjusting procedure must move a leaf node from the bottom to the root position and at most takes
time complexity. As the DMHBGKA tree is unbalanced, in a worst case scenario, the adjusting procedure must move a leaf node from the bottom to the root position and at most takes  . Given that the DMHBGKA tree is effective and efficient for dynamic mobile networks, this study exploits DMHBGKA to manage the dynamic group as described in detail in the following.
. Given that the DMHBGKA tree is effective and efficient for dynamic mobile networks, this study exploits DMHBGKA to manage the dynamic group as described in detail in the following.
4.1. Dynamic Multicast Height Balanced Group Key Agreement—DMHBGKA
First, based on the node's ID (MAC or IP), this study utilizes the binary search tree algorithm to locate the node in the DMHBGKA tree, as shown in Figure 7. The system then performs ECDH key management agreement from leaf nodes to the root node. Initially, leaf nodes 1 and 3 perform ECDH to obtain the session key  . Nodes 1 and 3 as well as their parent node 2 then calculate the subgroup key
. Nodes 1 and 3 as well as their parent node 2 then calculate the subgroup key  cooperatively. Next, nodes 5 and 7 perform ECDH to obtain the session key
cooperatively. Next, nodes 5 and 7 perform ECDH to obtain the session key  . Nodes 5 and 7 as well as their parent node 6 calculate the subgroup key
. Nodes 5 and 7 as well as their parent node 6 calculate the subgroup key  cooperatively. By using the same procedure, nodes 2 and 6 obtain
cooperatively. By using the same procedure, nodes 2 and 6 obtain  and then deliver it to node 4. Root node 4 then determines the group key
and then deliver it to node 4. Root node 4 then determines the group key  for this tree. Consequently, the root node 4 unicasts securely the group key to each node.
for this tree. Consequently, the root node 4 unicasts securely the group key to each node.
Figure 8 shows that new nodes 8 and 9 join the system. According to the DMHBKA agreement, nodes 8 and 9 are located in the right subtree, and then the adjusting procedure is performed to maintain the tree balance. The group key is subsequently calculated as  . If the root node leaves, as shown in Figure 9, the system selects the largest ID node from either the left subtree or the smallest ID node from the right subtree to replace the root node. Nodes 1 and 2 subsequently leave, with the system performing the adjustment procedure and recalculating the new group key as
. If the root node leaves, as shown in Figure 9, the system selects the largest ID node from either the left subtree or the smallest ID node from the right subtree to replace the root node. Nodes 1 and 2 subsequently leave, with the system performing the adjustment procedure and recalculating the new group key as  in Figure 9.
in Figure 9.
The proposed mechanism identifies the joining or leaving node in O(log  ), and only needs to recalculate the key value from the part of the joining (leaving) node subtree without recalculating the entire tree, thus saving a tremendous amount of operational time. The proposed approach is effective and efficient, and the DMHBGKA algorithm is shown in Algorithms 1 and 2:
), and only needs to recalculate the key value from the part of the joining (leaving) node subtree without recalculating the entire tree, thus saving a tremendous amount of operational time. The proposed approach is effective and efficient, and the DMHBGKA algorithm is shown in Algorithms 1 and 2:
4.2. Interregion Key Exchange Agreement
As the multicast data cross different regions, this study proposes a region key mechanism to secure the transmitted data between regions. For instance, the multicast path is region 1→region 5→region 9→region 13, as shown in Figure 10. Each pair of root nodes must calculate the interregion key between them using the ECDH agreement. Following calculations, this study derives the interregion key  for
for  in region 1 and
in region 1 and  in region 5. The interregion key
in region 5. The interregion key  is for
is for  in region 5 and
in region 5 and  in region 9. The interregion key
in region 9. The interregion key  is for
is for  in region 9 and
in region 9 and  in region 13. Subsequently, the source node and destination node exploit the group and interregion keys to perform secure multicast communications.
in region 13. Subsequently, the source node and destination node exploit the group and interregion keys to perform secure multicast communications.
5. Secure Multicast Communications
This section describes the secure operations for multicast communications in MANETs. Figure 10 presents a multicast group and tree, and a multicast source node  allocated on region 1 is assumed here to want to transfer data to all multicast members which are drawn in dotted circles. For simplicity, a description is made of the encryption and decryption operation of secure multicast from multicast source node
allocated on region 1 is assumed here to want to transfer data to all multicast members which are drawn in dotted circles. For simplicity, a description is made of the encryption and decryption operation of secure multicast from multicast source node  to destination node
to destination node  , that is, one of the multicast members in region 13.
, that is, one of the multicast members in region 13.
This work assumes that the multicast tree is generated by the multicast source and the path from multicast source to destination node  is known. To distinguish between the cluster groups, this study transfers the entire range of the wireless network into a geographical position. The cluster headers are responsible for the secure multicast backbone transmission.
is known. To distinguish between the cluster groups, this study transfers the entire range of the wireless network into a geographical position. The cluster headers are responsible for the secure multicast backbone transmission.
When the multicast source node  wants to transfer multicast data to the destination node
wants to transfer multicast data to the destination node  ,
,  is located in region 1 and belongs to the cluster header node
is located in region 1 and belongs to the cluster header node  . First, secure communications must be ensured between node
. First, secure communications must be ensured between node  and the cluster header node
and the cluster header node  belonging to the multicast backbone network.
belonging to the multicast backbone network.
To ensure data integrity issues, this study adopts hash message authentication code (HMAC) functions to generate HMAC(data) and aggregate HMAC(data) with original multicast data as [data∣HMAC(data)]. Secure multicast communication procedures are described in detail as follows:

 .
.
Initially,  and
and  cooperatively calculate their session key
cooperatively calculate their session key  along the multicast backbone, and then
along the multicast backbone, and then  encrypts the [data∣HMAC(data)] using
encrypts the [data∣HMAC(data)] using  as EKK 1 K 25 P[data∣HMAC(data)]. Additionally, the member node is located in the same region and has the same group key GK1 =
as EKK 1 K 25 P[data∣HMAC(data)]. Additionally, the member node is located in the same region and has the same group key GK1 =  . Therefore, the multicast resource node
. Therefore, the multicast resource node  located in region 1, as shown in Figure 10, encrypts [EKK 1 K 25 P[data∣HMAC(data)]] using GK1 to ensure the security of transmitted data in region 1. This operation ensures that the nodes in adjacent regions 0, 2, 4, 5, and 6 cannot decrypt the encrypted data from the multicast source node.
located in region 1, as shown in Figure 10, encrypts [EKK 1 K 25 P[data∣HMAC(data)]] using GK1 to ensure the security of transmitted data in region 1. This operation ensures that the nodes in adjacent regions 0, 2, 4, 5, and 6 cannot decrypt the encrypted data from the multicast source node.
Subsequently,  sends the encrypted data to the next node
sends the encrypted data to the next node  . After receiving the data,
. After receiving the data,  decrypts the encrypted data EKGK1[EKK 1 K 25 P[data∣HMAC(data)]] using GK1. Subsequently,
decrypts the encrypted data EKGK1[EKK 1 K 25 P[data∣HMAC(data)]] using GK1. Subsequently,  encrypts the [EKK 1 K 25 P[data∣HMAC(data)]] using GK1 again, and deliveries them to the cluster head
encrypts the [EKK 1 K 25 P[data∣HMAC(data)]] using GK1 again, and deliveries them to the cluster head 

 .
.
Once the encrypted data are received, since  and
and  are located in the same region and have the same group key GK1.
are located in the same region and have the same group key GK1.  can decrypt the encrypted data. Subsequently,
can decrypt the encrypted data. Subsequently,  must deliver the data to cluster head
must deliver the data to cluster head  in region 5. Since the transmission data cross different regions, thus
in region 5. Since the transmission data cross different regions, thus  and
and  cooperatively calculate the interregion key
cooperatively calculate the interregion key  , and then
, and then  encrypts
encrypts  using RK1,5 as
using RK1,5 as  . Subsequently,
. Subsequently,  sends the encrypted data to the backbone cluster head
sends the encrypted data to the backbone cluster head 

 .
.
 receives the transmitted data and decrypts them using RK1,5. Subsequently,
receives the transmitted data and decrypts them using RK1,5. Subsequently,  encrypts the received data using
encrypts the received data using  as
as  , and sends them to the next cluster head
, and sends them to the next cluster head  . By repeating the above procedures, the encrypted data are transmitted to cluster head
. By repeating the above procedures, the encrypted data are transmitted to cluster head  allocated in region 13.
allocated in region 13.
The cluster head  is responsible for transmitting the received data to the destination node
is responsible for transmitting the received data to the destination node  . Since
. Since  ,
,  and
and  are located in the same region; therefore, they have the same group key.
are located in the same region; therefore, they have the same group key.  adopts the group key
adopts the group key  to encrypt the received data and transmits the encrypted data to the intermediate node
to encrypt the received data and transmits the encrypted data to the intermediate node 

 .
.
Upon receiving the transmitted data,  decrypts the encrypted data using GK13, encrypts the results using GK13, and sends the encrypted data to the destination node
decrypts the encrypted data using GK13, encrypts the results using GK13, and sends the encrypted data to the destination node 

 .
.
Upon receiving the encrypted data,  decrypts them using GK13 and session key
decrypts them using GK13 and session key  , and verifies the integrity of HMAC(data). If any changes take place during the transmissions, the receiving node detects the modifications immediately by verifying the HMAC. Thus, the proposed secure multicast schemes satisfy the following security analyses.
, and verifies the integrity of HMAC(data). If any changes take place during the transmissions, the receiving node detects the modifications immediately by verifying the HMAC. Thus, the proposed secure multicast schemes satisfy the following security analyses.
-
(1)
Confidentiality and Authentication
During the data transmission, this study exploits the group and interregion keys to encrypt the multicast data. Only the node with the same group or interregion keys can decrypt the transmitted data. The other nodes are not aware of the group and interregion keys; therefore, cannot decrypt the encrypted data. Thus, the scheme can ensure that the data transmission is confidential and authentic.
-
(2)
Data Integrity and Accuracy
This study employs message authentication code (HMAC) to verify the integrity of transmitted data. During the transmission, each node calculates HMAC, and the receiver verifies the integrity of HMAC. Since HMAC is an irreversible operation, given a random number  , no ways can compute
, no ways can compute  such that
such that  . Moreover, when
. Moreover, when  , then
, then . Therefore, if any nodes modify the transmitted data during transmissions, the receiver detects the unmatched HMAC instantly and recognizes the tampered data.
. Therefore, if any nodes modify the transmitted data during transmissions, the receiver detects the unmatched HMAC instantly and recognizes the tampered data.
6. Analyses
6.1. Communication Cost Evaluation
The communication cost of ad hoc networks is an immensely complex problem [19]. The main complicity arises when attempting to consider irregular geographical distribution and any sources of interference (such as maintaining clusters, bandwidth, CPU, memory, and network traffic). This study adopts hop counts to evaluate communication costs, because this is the most widely used measure. In the proposed cluster-based models, it is logical to assume that ad hoc networks have  mobile nodes and are located on a 2D coordinate. These mobile nodes are allocated on the intersections as shown in Figure 11. This study attempts to compute the min-hop-count for any two nodes in the proposed model, for simplicity the following terms are defined.
mobile nodes and are located on a 2D coordinate. These mobile nodes are allocated on the intersections as shown in Figure 11. This study attempts to compute the min-hop-count for any two nodes in the proposed model, for simplicity the following terms are defined.
 : denotes a mobile node allocated on coordinate (a, b).
: denotes a mobile node allocated on coordinate (a, b).
 : represents the minimal hop count between node
: represents the minimal hop count between node  and
and  .
.
AVMinhop: is the average minimal node-hop-count for any two nodes in this model.
AVCBMinhop: denotes the average minimal cluster-hop- count for any two clusters in this model.
A: is a set containing  or
or  .
.
B: is a set containing  or
or 

 : represents the number of
: represents the number of  grids in the model, where
grids in the model, where  ,
,  .
.
Generally,  represents the sum of Minhop between two nodes, which is parallel to the
represents the sum of Minhop between two nodes, which is parallel to the  -axis. Meanwhile,
-axis. Meanwhile,  represents the sum of Minhop between two nodes, which is parallel to the
represents the sum of Minhop between two nodes, which is parallel to the  -axis. Furthermore, Bab represents the number of grids
-axis. Furthermore, Bab represents the number of grids  in an
in an  model. Finally,
model. Finally,  is the Minhop sum of all diagonal line pair nodes belonging to a grid
is the Minhop sum of all diagonal line pair nodes belonging to a grid  . From the aforementioned terminologies, the following equations are established:
. From the aforementioned terminologies, the following equations are established:

From (5), The AVMinhop is determined to be  as follows:
as follows:

Applying (6), the cluster distribution model determined and the AVCBMinhop can be calculated for any two clusters. The cluster model is assumed to be denoted as an  model, and moreover to satisfy three conditions.
model, and moreover to satisfy three conditions.
-
(1)
Each cluster domain has the same number.
-
(2)
Every cluster domain has
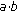 nodes; these nodes lie on
nodes; these nodes lie on  grid, and every intersection is only allocated a node.
grid, and every intersection is only allocated a node. -
(3)
The gateways between two clusters are located on the boundary lines.
For clarity, an example is presented for explanatory purposes. Let the ad hoc networks be represented by a  model, while the cluster domain is a
model, while the cluster domain is a  model, each cluster allocates eight nodes, and the double bold lines represent one cluster domain as shown in Figure 12. The above model shows that the system is divided into eight cluster domains. This study realizes that cluster Ch1 comprises of node set
model, each cluster allocates eight nodes, and the double bold lines represent one cluster domain as shown in Figure 12. The above model shows that the system is divided into eight cluster domains. This study realizes that cluster Ch1 comprises of node set  , and each cluster
, and each cluster  (
( ) has eight nodes. The gateway nodes between clusters Ch1 and Ch3 are the node set
) has eight nodes. The gateway nodes between clusters Ch1 and Ch3 are the node set  , which indicates the boundary between two rectangles. In an
, which indicates the boundary between two rectangles. In an  network model with an
network model with an  cluster model,
cluster model,  divides
divides  and
and  divides
divides  . Since each cluster can be treated as a node, which represents a cluster head, then the set of all clusters can be represented as a
. Since each cluster can be treated as a node, which represents a cluster head, then the set of all clusters can be represented as a  network model, and AVCBMinhop can be computed the same as AVMinhop. From (6),
network model, and AVCBMinhop can be computed the same as AVMinhop. From (6),  . For a
. For a  network model and a
network model and a  cluster model, then from (6),
cluster model, then from (6),  , and the average minimum cluster-hop-count for any two clusters AVCBMinhop is
, and the average minimum cluster-hop-count for any two clusters AVCBMinhop is

The ratio of the communication cost between any two cluster heads and any two nodes is  . Generalizing this equation under the
. Generalizing this equation under the  network model and the
network model and the  cluster model, and it becomes
cluster model, and it becomes

where  . Generally, (8) is lower than 1. This calculation result implies that the cluster-based average minimum cluster-hop-count is below the normal-based minimum node-hop-count. That is, the cluster-based model outperforms the normal node-based model.
. Generally, (8) is lower than 1. This calculation result implies that the cluster-based average minimum cluster-hop-count is below the normal-based minimum node-hop-count. That is, the cluster-based model outperforms the normal node-based model.
Considering the additional communication costs of node-based  and cluster-based
and cluster-based  , the node-based communication costs of two neighboring nodes are assumed to be
, the node-based communication costs of two neighboring nodes are assumed to be  , in which case the costs of cluster-based two neighbor clusters will be
, in which case the costs of cluster-based two neighbor clusters will be  . The
. The  denotes the nodes passing through between two neighbor clusters, which generally is
denotes the nodes passing through between two neighbor clusters, which generally is  . Since two clusters could pass through a gateway node or even multiple nodes when communicating with each other, the
. Since two clusters could pass through a gateway node or even multiple nodes when communicating with each other, the  depends on the position of the cluster head and the cluster topology. Equation (8) then is generalized to be equivalent to
depends on the position of the cluster head and the cluster topology. Equation (8) then is generalized to be equivalent to

If  , then regardless of the values of
, then regardless of the values of  and
and 

Furthermore, where 
 , (9) is
, (9) is

(1)When  . Equation (11) is
. Equation (11) is  .
.
(2)When  . Then
. Then  , and
, and  , (11) is
, (11) is  .
.
(3)When  . Then
. Then  , and
, and  , (11) is
, (11) is  .
.
From the result of the derivation,  (ratio of
(ratio of 
 ) shows that the cluster-based approach outperforms the normal node-based one, at least in situations where the proposed model achieves better communication costs.
) shows that the cluster-based approach outperforms the normal node-based one, at least in situations where the proposed model achieves better communication costs.
6.2. Computational Costs of DMHBGKA
This section evaluates the performances of DMHBKA, tree-based group Diffie-Hellman (TGDH) and group Diffie-Hellman (GDH). Table 3 summarizes the computational costs for several operations.
Key Operations
As a node leaves or joins the multicast tree dynamically, the entire system must reconstruct the group key. However, the operation only affects a specific portion of the subtree of the joining (leaving) node. Therefore, in a worst case scenario, for a leaf node joining or leaving the tree, the system recalculates the group key at most  times, where
times, where  denotes the height of the tree. The system normally recalculates the new group key for
denotes the height of the tree. The system normally recalculates the new group key for  times, where
times, where  denotes the level of the joining (leaving) node. Generally, the system recalculates the group key from the inserted (deleted) node position at level
denotes the level of the joining (leaving) node. Generally, the system recalculates the group key from the inserted (deleted) node position at level  to the root node. Therefore, the number of exponential operations is
to the root node. Therefore, the number of exponential operations is  . However, in the GDH scheme, each node must recalculate its partial group key, thus taking more key operations than DMHBKA and TGDH do.
. However, in the GDH scheme, each node must recalculate its partial group key, thus taking more key operations than DMHBKA and TGDH do.
Node Operations
The average search time for the joining (or leaving) node in the DMHBGKA tree is . Moreover, the system must only modify the data structure of the link point for a joining (or leaving) node, and therefore, it takes
. Moreover, the system must only modify the data structure of the link point for a joining (or leaving) node, and therefore, it takes  time complexity. Additionally, the number of multicast member nodes in the DMHBGKA tree is at most
time complexity. Additionally, the number of multicast member nodes in the DMHBGKA tree is at most  and the minimum is Fab
and the minimum is Fab . Nevertheless, GDH identifies a specific node at most
. Nevertheless, GDH identifies a specific node at most  and the minimum is 1.
and the minimum is 1.
Communications
Data communication for a group key requires  rounds, while a node joins because each node sends one message from its level
rounds, while a node joins because each node sends one message from its level  to the root node. The root node then broadcasts the group key to each node in the tree. The total number of messages is
to the root node. The root node then broadcasts the group key to each node in the tree. The total number of messages is  . Although DMHBGKA broadcasts more rounds than GDH and TGDH do, the message size is significantly lower than that of GDH and TGDH.
. Although DMHBGKA broadcasts more rounds than GDH and TGDH do, the message size is significantly lower than that of GDH and TGDH.
6.3. Group Key Agreement Performance Evaluation
In this study, each node only conserves a session key to encrypt/decrypt data, and exploits a hash function, such as HMAC-160 or RIPEMD-160, to verify the integrity of transmitted data. However, hash functions and session key operations consume few resources during secure data transmissions. Consequently, the plain operations are highly suited for MANETs.
Additionally, several analyses of various key cryptosystems are performed. The experiments are implemented on a Windows XP platform with a 3.2-GHz Celeron(R) CPU, 1-GB of memory, and a GNU C/C++ Library. The nodes move within a fixed region area 1500 m × 1500 m, and node mobility is simulated based on a random waypoint mobility model. Each node moves toward a randomly selected location at a speed uniformly distributed between 0 and max_speed and then pauses for a configured time, before selecting another random location and repeating the process. The mobile nodes pause time has value of (0, 30 s, 60 s, 120 s, 300 s, and 600 s), with 0 representing constant mobility and 600s indicating a stationary network. In a simulated network of nodes (25, 50, 75, 100, and 150), simulations are for constant node speeds of (0 m/s, 5 m/s, 10 m/s, 15 m/s, and 20 m/s), using the above pause time, and where every node has performed several ECDH operations. The mobile node calculates a point multiplication in 0.18 s on SEC-160 curve [20] and 5.2 s to establish a session key on ECDH in the prime field. Key synchronization time and data transmission time on interregion infrastructures are evaluated. Moreover, the proposed ECDH secure multicast data transmission session is also simulated to measure the performance on interregion mode. Table 2 lists the simulation parameters.
The key length of a security level is expressed as the pair  , where
, where  denotes the private key length in DMHBGKA, and
denotes the private key length in DMHBGKA, and  denotes the private key length in DH/RSA [21]. DMHBGKA requires only multiplication operations whereas DH and GDH [22, 23] must perform exponential operations. Therefore, DMHBGKA takes much less computing time than DH and GDH. Results in Figure 13 indicate that DMHBGKA needs a shorter synchronization time than DH and GDH in
denotes the private key length in DH/RSA [21]. DMHBGKA requires only multiplication operations whereas DH and GDH [22, 23] must perform exponential operations. Therefore, DMHBGKA takes much less computing time than DH and GDH. Results in Figure 13 indicate that DMHBGKA needs a shorter synchronization time than DH and GDH in  and
and  . Additionally, Figure 13 describes the estimated synchronization time of the group key for DMHBGKA, DH and GDH schemes. According to this figure, DMHBGKA takes less time than DH and GDH to achieve group key convergence. Figure 14 compares the two regions in terms of the synchronization time of the interregion key. Simulation results indicate that the DMHBGKA schemes outperform GDH and DH ones. This advantage is owing to that each cluster head is responsible for its cluster member key controller. Therefore, each pair of the cluster heads must only exchange their own group keys, making it possible to synchronize the new interregion key between two clusters without recalculating keys of all members in two clusters. Figure 15 indicates that cluster schemes outperform noncluster schemes in terms of synchronization time of the group key. This study divides all members into cluster-2, cluster-4, and cluster-8 structures. The simulation increases the number of cluster members from 1 to 32 sequentially, which is accompanied by implementing a group key. According to Figure 15, the convergent time increases with the number of cluster members. Moreover, cluster-8 performs the best in terms of reconstructing the group key.
. Additionally, Figure 13 describes the estimated synchronization time of the group key for DMHBGKA, DH and GDH schemes. According to this figure, DMHBGKA takes less time than DH and GDH to achieve group key convergence. Figure 14 compares the two regions in terms of the synchronization time of the interregion key. Simulation results indicate that the DMHBGKA schemes outperform GDH and DH ones. This advantage is owing to that each cluster head is responsible for its cluster member key controller. Therefore, each pair of the cluster heads must only exchange their own group keys, making it possible to synchronize the new interregion key between two clusters without recalculating keys of all members in two clusters. Figure 15 indicates that cluster schemes outperform noncluster schemes in terms of synchronization time of the group key. This study divides all members into cluster-2, cluster-4, and cluster-8 structures. The simulation increases the number of cluster members from 1 to 32 sequentially, which is accompanied by implementing a group key. According to Figure 15, the convergent time increases with the number of cluster members. Moreover, cluster-8 performs the best in terms of reconstructing the group key.
Figure 16 shows the resynchronization time of the group key for adding or removing a node. Simulation results indicate that the DMHBGKA scheme takes less resynchronization time for nodes joining or leaving than DH and GDH since the point multiplication takes considerably less time than exponential operations. Furthermore, DMHBGKA must only recalculate the partial key from the place of a joining or leaving node to the root node, yet it does not need to recalculate keys of all members, subsequently achieving synchronization efficiently.
Figure 17 compares DMHBGKA, DH, and GDH schemes in terms of secure multicast data transmission time. Simulation results indicate that the DMHBGKA scheme performs better than other ones in terms of passing through nodes.
7. Conclusions and Future Work
This study presents a dynamic height balance group key agreement (DMHBGKA) scheme to ensure secure multicast data transmissions. The proposed scheme achieves the same security level as RSA and Diffe-Hellman do with shorter keys. Additionally, the proposed scheme performs very well for dynamic nodes joining or leaving. Simulation results indicate that in addition to consuming less system key synchronization time than other methods do, the proposed DMHBGKA scheme is also highly feasible for implementing constrained environments such as ad hoc networks.
Additionally, this study provides resilient and scalable mechanisms for dynamic group key management. The proposed scheme replaces exponential operations with point multiplications when performing ECDH, thus reducing the CPU overhead significantly. Therefore, the proposed scheme is highly promising for dynamic key operations in large-scale ad hoc networks. This study also presents a node in the multicast group, capable of exploiting the interregion key to deliver multicast messages securely from the multicast source to the internodes of the multicast tree. In addition to integrating the DMHBGKA scheme into secure multicast data transmissions, the proposed scheme provides secure communications among regions. Furthermore, the proposed approach utilizes ECDH key operations and a rapid hash function for secure multicast data transmission and data integrity verification, respectively, thus eliminating the requirement for complex operations on mobile nodes. Analytical results indicate that the proposed DMHBGKA scheme outperforms other methods in terms of rekeying performances, computation and communication costs, and overhead. Importantly, the proposed schemes are efficient and scalable for numerous mobile nodes in ad hoc networks.
Algorithm 1: DMHBGKA_Insert (int value, point current).
{
if( current == null ) // insert null node
{ current = new DMHBGKA_Node(value, null, null); }
else if(value < current.value) // less than current node value/
{ current.left = DMHBGKA _Insert(value, current.left);
if(height(current.left) - height(current.right) == 2)
// unbalance occurs//
{if(value < current.left.value)
{current = Rotate_Left_Child(current); //LR
Groupkey_Reconstruction( rootnode, current) //from current node to root }
else
{current = Doublerotate_With_Left_Child(current); //LL
Groupkey_Reconstruction( rootnode, current) //from current node to root//}
}
}
else if(value > current.value)// it is greater than current node//
{current.right = DMHBGKA _Insert(value, current.right);
if(height(current.right) - height(current.left) == 2)
// there is an imbalance//
{ if(value > current.right.value)
{current = Rotate_Right_Child(current); //RL
Groupkey_Reconstruction( rootnode, current) //from current node to root// }
else
{current = doublerotate_Right_Child(current); //RR
Groupkey_Reconstruction( rootnode, current) //from current node to root// }
}
}
current.height = Math.max(height(current.left),
height(current.right)) + 1;
return current;
}
Algorithm 2: DMHBGKA_Remove (int del_val, point node).
{
if( node == null)
{System.out.println(del_val +"Not found in DMHBGKA Tree n"); return null;}
n"); return null;}
else
{ // search for del_val to be deleted//
if(node.value < del_val)
{node.right = DMHBGKA _Remove( del_val, node.right); }
else if( node.value > del_val)
{ node.left = DMHBGKA _Remove( del_val, node.left);}
// del_val found, delete if a descendant is null //
else if( node.left == null)
{ node = node.right;}
else if( node.right == null)
{node = node.left; }
//no descendant is null, rotate on heavier side//
else if( height( node.left ) > height( node.right ))
{ node = Rotate_Right_Child(node); //RL
node.right = DMHBGKA _Remove( del_val, node.right );
Groupkey_Reconstruction( rootnode, current) //from current node to root//}
else
{ node = Rotate_Left_Child( node ); //LR
node.left = DMHBGKA _Remove( del_val, node.left );
Groupkey_Reconstruction( rootnode, current) //from current node to root//}
//reconstruct weight information //
if( node != null )
{node.height = height( node.left ) + height( node.right );}
}
return node;
}
References
Das SM, Pucha H, Hu YC: Distributed hashing for scalable multicast in wireless ad hoc networks. IEEE Transactions on Parallel and Distributed Systems 2008, 19(3):347-362.
Rong B, Chen HH, Qian YI, Lu K, Hu RQ, Guizani S: A pyramidal security model for large-scale group-oriented computing in mobile ad hoc networks: the key management study. IEEE Transactions on Vehicular Technology 2009, 58(1):398-408.
He W, Huang Y, Sathyam R, Nahrstedt K, Lee WC: SMOCK: a scalable method of cryptographic key management for mission-critical wireless ad-hoc networks. IEEE Transactions on Information Forensics and Security 2009, 4(1):140-150.
Basagni S, Chlamtac I, Syrotiuk VR, Talebi R: On-demand location aware multicast (OLAM) for ad hoc networks. Proceedings of IEEE Wireless Communications and Networking Conference, September 2000 1323-1328.
Wang NC, Fang SZ: A hierarchical key management scheme for secure group communications in mobile ad hoc networks. Journal of Systems and Software 2007, 80(10):1667-1677. 10.1016/j.jss.2006.12.564
Yang P, Zheng S: Security management in hierarchical ad hoc network. Proceedings of the International Conferences on Info-Tech and Info-Net, October 2001 642-649.
Kim Y, Perrig A, Tsudik G: Tree-based group key agreement. ACM Transactions on Information and System Security 2004, 7(1):60-96. 10.1145/984334.984337
Wong CK, Gouda M, Lam SS: Secure group communications using key graphs. IEEE/ACM Transactions on Networking 2000, 8(1):16-30. 10.1109/90.836475
Manulis M: Contributory group key agreement protocols, revisited for mobile ad-hoc groups. Proceedings of the 2nd IEEE International Conference on Mobile Ad-Hoc and Sensor Systems (MASS '05), November 2005 811-818.
Vasudevan V, Sukumar R: Scalable secure multicast using multi server approach for wireless environments. Proceedings of the International Conference on Control Automation, Communication and Energy Conservation (INCACEC '09), June 2009
Wang Y, Le PD, Srinivasan B: Hybrid group key management scheme for secure wireless multicast. Proceedings of the 6th IEEE/ACIS International Conference on Computer and Information Science (ICIS '07), July 2007 346-351.
Chiang TC, Huang YM: Group keys and the multicast security in ad hoc networks. Proceedings of the International Conference on Parallel Processing Workshops, October 2003 385-390.
Chaddoud G, Chrisment I, Schaff A: Secure multicast survey. Proceedings of the 16th Word Computer Congress, August 2000 49-56.
Sklavos N, Zhang X: Wireless Security and Cryptography: Specifications and Implementations. CRC Press, Boca Raton, Fla, USA; 2007.
Szczechowiak P, Oliveira LB, Scott M, Collier M, Dahab R: NanoECC: testing the limits of elliptic curve cryptography in sensor networks. Proceedings of the 5th European Conference on Wireless Sensor Networks (EWSN '08), February 2008 305-320.
Liu AN, Ning P: TinyECC: a configurable library for elliptic curve cryptography in wireless sensor networks. Proceedings of the International Conference on Information Processing in Sensor Networks (IPSN '08), April 2008 245-256.
Haodong W, Bo S, Qun L: Elliptic curve cryptography-based access control in sensor networks. International Journal of Security and Networks 2006, 1(3-4):127-137.
Diffie W, Hellman ME: New directions in cryptography. IEEE Transactions on Information Theory 1976, 22(6):644-654. 10.1109/TIT.1976.1055638
Basagni S, Chlamtac I, Farago A: A generalized clustering algorithm for peer-to-peer networks. Proceedings of the Workshop on Algorithmic Aspects of Communication, July 1997 1-15.
Certicom Research : Standards for Efficient Cryptography–SEC 1. Recommended Elliptic Curve Domain Parameters September 2000.
Du W, Deng J, Han YS, Chen S, Varshney PK: A key management scheme for wireless sensor networks using deployment knowledge. Proceedings of the 23rd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '04), March 2004 586-597.
Ateniese G, Steiner M, Tsudik G: New multiparty authentication services and key agreement protocols. IEEE Journal on Selected Areas in Communications 2000, 18(4):628-639. 10.1109/49.839937
Amir Y, Kim Y, Nita-Rotaru C, Tsudik G: On the performance of group key agreement protocols. Proceedings of the 22nd International Conference on Distributed Systems, July 2002 463-464.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lin, HY., Chiang, TC. Efficient Key Agreements in Dynamic Multicast Height Balanced Tree for Secure Multicast Communications in Ad Hoc Networks. J Wireless Com Network 2011, 382701 (2011). https://doi.org/10.1155/2011/382701
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/382701
 corresponds to a unique
corresponds to a unique  -node,
-node, -node,
-node,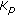 has a direct path from all
has a direct path from all  -nodes.
-nodes.

 .
.


 , where
, where 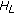 denotes the height of a left subtree, and
denotes the height of a left subtree, and 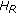 denotes the height of a right subtree.
denotes the height of a right subtree.





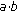 nodes; these nodes lie on
nodes; these nodes lie on  grid, and every intersection is only allocated a node.
grid, and every intersection is only allocated a node.
 ad hoc networks,
ad hoc networks,  cluster domain.
cluster domain.



