- Research Article
- Open access
- Published:
Full-Diversity Space-Time Error Correcting Codes with Low-Complexity Receivers
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 653506 (2011)
Abstract
We propose an explicit construction of full-diversity space-time block codes, under the constraint of an error correction capability. Furthermore, these codes are constructed in order to be suitable for a serial concatenation with an outer linear forward error correcting (FEC) code. We apply the binary rank criterion, and we use the threaded layering technique and an inner linear FEC code to define a space-time error-correcting code. When serially concatenated with an outer linear FEC code, a product code can be built at the receiver, and adapted iterative receiver structures can be applied. An optimized hybrid structure mixing MMSE turbo equalization and turbo product code decoding is proposed. It yields reduced complexity and enhanced performance compared to previous existing structures.
1. Introduction
Space-time block (STB) code designs have recently attracted considerable attention, since they improve the reliability of communication systems over fading channels. Tarokh et al. [1] developed some criteria for designing STB codes (for the high SNR regime), in order to minimize the pairwise error probability. Among the resulting proposed schemes (based on these criteria), orthogonal space-time block (OSTB) codes, introduced by Alamouti [2] and generalized by Tarokh et al. [3], are attractive due to their low optimal decoding complexity. Their practical use is limited to the Alamouti scheme (two transmit antennas) as their rate decreases rapidly with an increase in the number of transmit antennas, and they cannot achieve the MIMO system capacity. Hassibi and Hochwald proposed the linear dispersion codes (LDCs) [4] that maximize the mutual information between transmitted and received signals in order to achieve the maximum ergodic capacity of the equivalent MIMO system.
Then full rate and full diversity STB codes were designed. The application of the threaded layering principle yielded the threaded algebraic space-time (TAST) codes [5]. Belfiore et al. added a nonvanishing determinant constraint [6–8] to achieve the optimal diversity/multiplexing tradeoff [9] and defined the perfect space-time block codes [10, 11].
However, in any transmission system the forward error correction coding is used in conjunction with interleaving. All the above STB codes deal with the forward error correcting code as an independent entity of the transmitter scheme. A joint design of FEC, modulation, and space-time scheme was considered in [1], in order to construct the space-time trellis codes (STTCs) that provide maximum diversity and maximum coding gain. STTCs exhibit higher coding gains than STB codes, but due to their trellis nature, the optimal decoding has a high computational cost incompatible with a practical implementation.
An interesting method to design full diversity space-time block codes with an error correction capability has been developed in [12–14]. In the current paper, these codes are referred as space-time error correcting codes (STECCs) in order to stress on their ability to correct errors due to the transmission. We name also concatenated STECC the serial concatenation of a STECC and an outer linear FEC code. In [12], a binary rank criterion has been introduced in order to construct full diversity STECCs for binary phase shift keying (BPSK) modulation. A generalization of this criterion to design full diversity STECCs with higher spectral efficiency using quadrature amplitude modulation (QAM), has been considered in [14]. But, since the generalized rank criterion implies that the error correcting code must be defined over a finite field where its dimension depends on the modulation order, the construction of full diversity STECCs for higher-order modulations cannot be realized in practice using this approach. In [13], an unified construction of STECCs achieving the optimal rate-diversity tradeoff [15] from binary error correcting codes for different types and orders of modulation has been presented. Independently, an explicit construction of concatenated STECCs for 2 transmit antennas based on explicit linear combinations of FEC codewords has been presented in [16]. Thanks to the linearity of FEC codes, it has been shown in [17] that STECCs seem more adapted than other STB codes to be concatenated with linear forward error correcting codes.
The contributions of this paper are as follows.
-
(i)
Compared to [16], a theoretical analysis of STECC is given resulting in the design of full diversity STECCs for two transmit antennas.
-
(ii)
It is proved that a product code can be reconstructed from a concatenated STECC. An optimized hybrid receiver associating a turbo equalizer (interference canceller) based on the minimum mean square error (MMSE) criterion and a turbo product code decoder is proposed, yielding reduced complexity and enhanced performance.
In Section 2, we describe the system model and show through theoretical analysis the suboptimality of STECCs proposed in [16] for 2 transmit antennas. In Section 3, we apply the threaded layering principle and the binary rank criterion to design full transmit diversity STECCs. In Section 4, considering STECCs concatenated to an outer FEC code, we first show how a product code can be reconstructed at the receiver. Then we combine the turbo equalization and turbo product code decoding principles to develop an adapted receiver with reduced complexity and enhanced performance. In Section 5, we present simulation results and finally, we give our conclusions in Section 6.
Notations
Column vectors (resp., matrices) are denoted by boldface lower (resp., capital) case letters. Superscripts  and
and  stand for transpose and conjugate transpose, respectively.
stand for transpose and conjugate transpose, respectively.  represents the
represents the  identity matrix.
identity matrix.  ,
,  , and
, and  denote, respectively, the ring of rational integers, the field of complex numbers and the ring of complex integers.
denote, respectively, the ring of rational integers, the field of complex numbers and the ring of complex integers.  (resp.,
(resp.,  ) denotes the
) denotes the  matrix having all its elements equal to 0 (resp., 1). Subscripts of matrices indicate their dimensions.
matrix having all its elements equal to 0 (resp., 1). Subscripts of matrices indicate their dimensions.
2. System Model
We first recall the usual criteria applied to design space-time codes for a MIMO system with  transmit antennas and
transmit antennas and  receive antennas considering a transmission over a nonfrequency selective block fading channel. We assume that the channel state information (CSI) is known at the receiver. In the second part, we give a theoretical analysis of the family of rectangular STECCs presented in [16] for
receive antennas considering a transmission over a nonfrequency selective block fading channel. We assume that the channel state information (CSI) is known at the receiver. In the second part, we give a theoretical analysis of the family of rectangular STECCs presented in [16] for  transmit antennas to show that they do not achieve full transmit diversity.
transmit antennas to show that they do not achieve full transmit diversity.
The  received signal matrix can then be expressed as
received signal matrix can then be expressed as

where  is the
is the  transmitted space-time error correcting codeword,
transmitted space-time error correcting codeword,  is the
is the  channel matrix with independent and identically distributed (i.i.d.) zero-mean complex circular Gaussian entries and
channel matrix with independent and identically distributed (i.i.d.) zero-mean complex circular Gaussian entries and  is the
is the  i.i.d. zero-mean complex circular Gaussian noise.
i.i.d. zero-mean complex circular Gaussian noise.
2.1. Space-Time Code Design Criteria
Let us assume a coherent scenario and an optimal maximum likelihood STB code detection. The pairwise error probability (PEP) is defined as the probability of estimating a codeword  at the receiver while
at the receiver while  has been sent. To minimize the pairwise error probability, the space-time code must fulfill the following constraints [18].
has been sent. To minimize the pairwise error probability, the space-time code must fulfill the following constraints [18].
-
(i)
The Rank Criterion. Maximize the minimum rank
 of the matrix
of the matrix 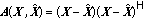 .
. -
(ii)
The Determinant Criterion. Maximize the minimum product of the nonzero eigenvalues, (
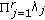 ), of the matrix
), of the matrix 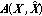 . This criterion maximizes the coding gain.
. This criterion maximizes the coding gain.
The maximum diversity advantage in this context is  . Space-time codes that achieve such a diversity are called full diversity space-time codes [1, 18].
. Space-time codes that achieve such a diversity are called full diversity space-time codes [1, 18].
2.2. Definition of a STECC
A STECC is a space-time code defined as an  symbol matrix based on the modulation of
symbol matrix based on the modulation of  basic binary matrices
basic binary matrices  , which can be grouped to form a binary matrix
, which can be grouped to form a binary matrix  where each entry is a binary
where each entry is a binary  -tuple so that
-tuple so that  is the modulation efficiency. Matrix
is the modulation efficiency. Matrix  is a spatial rearrangement of a FEC codeword of
is a spatial rearrangement of a FEC codeword of  .
.  is called the inner code. Its length is equal to
is called the inner code. Its length is equal to  .
.
2.3.  STECCs: Theoretical Analysis
STECCs: Theoretical Analysis
We consider, in this subsection, the family of rectangular STECCs proposed in [16] and we verify that they do not fulfill the preceding criteria, and thus do not achieve full diversity.
The  STECC in [16] is defined from an one-half coding rate systematic block code of length
STECC in [16] is defined from an one-half coding rate systematic block code of length  . Its codewords are given by
. Its codewords are given by

where  ,
,  , represent the information bits and
, represent the information bits and  stands for the mod-2 addition. Let
stands for the mod-2 addition. Let  (
( ) be the binary matrix associated to a space-time error correcting codeword. It is defined as [16]
) be the binary matrix associated to a space-time error correcting codeword. It is defined as [16]

where  ,
,  , represents an information binary
, represents an information binary  -tuple. Assuming a
-tuple. Assuming a  -ary quadrature amplitude modulation (
-ary quadrature amplitude modulation ( -QAM) where
-QAM) where  , the STECC codeword which corresponds to
, the STECC codeword which corresponds to  is defined by
is defined by

where  ,
,  , represents the
, represents the  -QAM symbol associated to the
-QAM symbol associated to the  th binary
th binary  -tuple denoted by
-tuple denoted by  and
and  represents the
represents the  -QAM symbol associated to the binary
-QAM symbol associated to the binary  -tuple denoted by
-tuple denoted by  . To prove that the rank criterion is not realized, we verify that it is possible to find two STECC codewords such that their difference matrix has a rank of 1 inferior to the maximum possible rank
. To prove that the rank criterion is not realized, we verify that it is possible to find two STECC codewords such that their difference matrix has a rank of 1 inferior to the maximum possible rank  .
.
Let  , thus
, thus

Let  thus
thus  . Let us denote by
. Let us denote by  and
and  the STECC codewords associated to
the STECC codewords associated to  and
and  , respectively. If
, respectively. If  is odd, then the difference matrix
is odd, then the difference matrix  has all entries of the second row equal to 0. In the other case (
has all entries of the second row equal to 0. In the other case ( is even), all the columns of
is even), all the columns of  are equal. Therefore, for all values of
are equal. Therefore, for all values of  , the difference matrix has a rank equal to
, the difference matrix has a rank equal to  and as a consequence this family of STECCs does not achieve a full transmit diversity.
and as a consequence this family of STECCs does not achieve a full transmit diversity.
Furthermore, if we consider the minimum Hamming distance ( ) of the basic binary code defined in (2), one can see that
) of the basic binary code defined in (2), one can see that  and for
and for  ,
,  . For example, the Hamming weight of this basic binary codeword matrix
. For example, the Hamming weight of this basic binary codeword matrix  for all
for all  is equal to 4. As a consequence, inner FEC codes defined for
is equal to 4. As a consequence, inner FEC codes defined for  will not enable to increase the maximum time diversity achieved by the STECC.
will not enable to increase the maximum time diversity achieved by the STECC.
In the following, we focus only on the cases  and
and  in order to illustrate the construction of full diversity STECCs.
in order to illustrate the construction of full diversity STECCs.
3. Full-Diversity STECCs
To determine the maximum rate that can be realized when a full spatial diversity is achieved, we need to define the optimal rate-diversity tradeoff [13] which can be characterized by the following equation:

where  is the modulation symbol rate per channel use (p.c.u.), the quantity
is the modulation symbol rate per channel use (p.c.u.), the quantity  is termed the transmit diversity gain, and
is termed the transmit diversity gain, and  is the extension degree of the transmission symbol set drawn from the modulation symbol set. In our construction, a transmission symbol is drawn from a constellation set, thus
is the extension degree of the transmission symbol set drawn from the modulation symbol set. In our construction, a transmission symbol is drawn from a constellation set, thus  . Moreover, a full transmit diversity is quantified by
. Moreover, a full transmit diversity is quantified by  , therefore the optimal rate-diversity tradeoff implies a maximum rate of one modulation symbol p.c.u., that is, a full diversity STECC has a maximum rate equals to
, therefore the optimal rate-diversity tradeoff implies a maximum rate of one modulation symbol p.c.u., that is, a full diversity STECC has a maximum rate equals to  . As a consequence, we use for the construction
. As a consequence, we use for the construction  -rate inner codes.
-rate inner codes.
As the maximum rate of the inner code is determined, it is important to note that in the following for  and
and  , the selected inner codes have the maximum of the minimum Hamming distance for a combination of
, the selected inner codes have the maximum of the minimum Hamming distance for a combination of  transmit antennas and
transmit antennas and  time periods.
time periods.
3.1. Full-Diversity STECC Designs
In order to realize the full spatial diversity, we recall that the binary rank criterion is a sufficient but not necessary condition to guarantee a full spatial diversity [12]. We apply the unified construction proposed in [13] to ensure a full spatial diversity for high-order modulations.
In [12], the authors prove that if every nonzero codeword of a linear binary code matrix has a maximum rank over the binary field  , then for a binary phase shift keying (BPSK) transmission, the STECC achieves full spatial diversity, that is,
, then for a binary phase shift keying (BPSK) transmission, the STECC achieves full spatial diversity, that is,  . Moreover, it is demonstrated in [13] that if a STECC achieves full spatial diversity for BPSK transmission then using the Lu and Kumar construction (unified construction), we can obtain a full diversity STECC for high-order modulations based on full rank linear binary code matrices.
. Moreover, it is demonstrated in [13] that if a STECC achieves full spatial diversity for BPSK transmission then using the Lu and Kumar construction (unified construction), we can obtain a full diversity STECC for high-order modulations based on full rank linear binary code matrices.
It yields a sufficient but not necessary condition on the linear binary inner code matrix to guarantee full diversity STECCs.
3.2. Threaded Layering Approach
To maximize the STECC diversity, we consider the threaded layering approach [5]. We assume rectangular STECCs of size  . To design full diversity STB code, the threaded layering approach consists in splitting information symbols into disjoint threads. The threads must be active over the
. To design full diversity STB code, the threaded layering approach consists in splitting information symbols into disjoint threads. The threads must be active over the  transmission intervals. For each layer (thread) and at each transmission interval, symbols of this layer are transmitted. Threads use equally often the transmit antennas. To ensure a maximum diversity, each thread must achieve a maximum diversity when symbols corresponding to the other threads are put to zero and threads must be transparent to each other. This can be realized by affecting weighting numbers to each thread such that resulting threads span disjoint algebraic subspaces. These numbers are "Diophantine number".
transmission intervals. For each layer (thread) and at each transmission interval, symbols of this layer are transmitted. Threads use equally often the transmit antennas. To ensure a maximum diversity, each thread must achieve a maximum diversity when symbols corresponding to the other threads are put to zero and threads must be transparent to each other. This can be realized by affecting weighting numbers to each thread such that resulting threads span disjoint algebraic subspaces. These numbers are "Diophantine number".
In the case of STECCs, linear combinations are applied on binary elements which greatly relaxes the constraints to achieve full diversity STECCs. The number of threads is taken equal to the number of transmit antennas. The threaded layering set  is defined, for
is defined, for  , by
, by

where  denotes the mod-
denotes the mod- operation. Table 1 shows the threaded layering for
operation. Table 1 shows the threaded layering for  and
and  structures using 2 threads. We associate the information symbols (resp., redundancy symbols) to the first layer (resp., second layer). Let us denote by
structures using 2 threads. We associate the information symbols (resp., redundancy symbols) to the first layer (resp., second layer). Let us denote by  the information symbol vector and by
the information symbol vector and by  the vector associated to the redundancy symbols.
the vector associated to the redundancy symbols.  is an integer permutation matrix such that the STECC, built up from
is an integer permutation matrix such that the STECC, built up from  ,
,  , and a diophantine number, achieves a full spatial diversity (
, and a diophantine number, achieves a full spatial diversity ( must also keep properties of STECCs defined in (6), i.e., each entry of a space-time codeword matrix is composed of one modulation symbol).
must also keep properties of STECCs defined in (6), i.e., each entry of a space-time codeword matrix is composed of one modulation symbol).
Table 1 The threaded layering in coherent scenario using 2 layers. The numbers refer to thread indexes. The vertical and horizontal axes correspond to the spatial and temporal dimensions, respectively.
3.2.1.  Full-Diversity STECC
Full-Diversity STECC
In this case, it was verified in [19] that a full diversity STECC can be defined by

where  , whatever
, whatever  and
and  (to ensure an energy efficiency). As the determinant of the difference codeword matrix depends on the value of
(to ensure an energy efficiency). As the determinant of the difference codeword matrix depends on the value of  , thus to maximize the coding gain we must carefully select the diophantine number. In [19], it was proved that
, thus to maximize the coding gain we must carefully select the diophantine number. In [19], it was proved that  is the optimal value for 4-QAM and 16-QAM. In this paper, by applying the binary rank criterion and the unified construction of [13] we verify that a full spatial diversity can be achieved without the necessity of a diophantine number (
is the optimal value for 4-QAM and 16-QAM. In this paper, by applying the binary rank criterion and the unified construction of [13] we verify that a full spatial diversity can be achieved without the necessity of a diophantine number ( ). For
). For  , (the same result can be obtained for the other possible 3-tuple) the associated linear binary code matrix is defined by
, (the same result can be obtained for the other possible 3-tuple) the associated linear binary code matrix is defined by

It clearly appears that the first and the second row of  are linearly independent over the binary field
are linearly independent over the binary field  . Thus for a BPSK transmission, the STECC constructed from
. Thus for a BPSK transmission, the STECC constructed from  achieves a full spatial diversity. Therefore, using the unified construction presented in [13], the STECC built up from this linear binary code matrix ensures a full spatial diversity for any order QAM modulation. We also note that this construction can be extended to phase shift keying (PSK) and pulse amplitude (PAM) modulations.
achieves a full spatial diversity. Therefore, using the unified construction presented in [13], the STECC built up from this linear binary code matrix ensures a full spatial diversity for any order QAM modulation. We also note that this construction can be extended to phase shift keying (PSK) and pulse amplitude (PAM) modulations.
3.2.2. 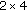 Full-Diversity STECC
Full-Diversity STECC
The inner code corresponds to the extended Hamming code. Due to the fact that the all-one vector is a codeword, the binary rank criterion is false whatever the spatial arrangement into a  binary matrix. We thus apply the threaded layering approach.
binary matrix. We thus apply the threaded layering approach.
The binary  matrix is
matrix is

and the associated space-time error correcting codeword is

To ensure full diversity diophantine number  is chosen such that
is chosen such that  and
and  . In that case, the maximization of the coding gain yields an optimum value for
. In that case, the maximization of the coding gain yields an optimum value for  depending of the modulation order. However, in practice the STECC will be serially concatenated to an outer FEC and it was shown in [20] that the asymptotic global coding gain is independent of the choice of the parameter
depending of the modulation order. However, in practice the STECC will be serially concatenated to an outer FEC and it was shown in [20] that the asymptotic global coding gain is independent of the choice of the parameter  provided that
provided that  and
and  . In [21], we proposed a way to construct full diversity
. In [21], we proposed a way to construct full diversity  STECCs defined from an inner half-rate invertible linear binary codes.
STECCs defined from an inner half-rate invertible linear binary codes.
4. Receiver Structures
This section aims at designing reduced complexity and efficient receivers for concatenated STECCs. A maximum likelihood receiver for the concatenated STECC has a prohibitive complexity, and cannot be implemented in practice. We thus consider lower complexity receivers consisting of the cascade of elementary devices and based on the exchange of reliability information from a device to its neighbour in an iterative manner.
For the sake of generality, we consider the unified construction of Lu and Kumar [13] which encompasses, from a decoding point of view, the  STECCs presented in the previous section (as the diophantine number can be viewed as a rotation of the second thread versus the first one, it does not appear at the decoding stage). We first show how a product code can be built from the concatenated STECC. Hybrid receivers combining both MMSE turbo equalization (successive interference cancellation) and turbo product code decoding will be designed.
STECCs presented in the previous section (as the diophantine number can be viewed as a rotation of the second thread versus the first one, it does not appear at the decoding stage). We first show how a product code can be built from the concatenated STECC. Hybrid receivers combining both MMSE turbo equalization (successive interference cancellation) and turbo product code decoding will be designed.
4.1. Reconstruction of a Product Code from a Concatenated STECC
As mentioned previously to achieve the optimal rate-diversity tradeoff (6) thus the maximum rate of inner codes are necessarily equal to  in order to ensure a full diversity STECC. We consider systematic linear binary inner codes. Thus, to construct a full diversity STECC we need
in order to ensure a full diversity STECC. We consider systematic linear binary inner codes. Thus, to construct a full diversity STECC we need  binary
binary  -tuples
-tuples  ,
,  that correspond to the information sequences and
that correspond to the information sequences and  binary
binary  -tuples that correspond to the redundancy sequences. Thus for
-tuples that correspond to the redundancy sequences. Thus for  the redundancy sequences can be written as
the redundancy sequences can be written as

where  , and
, and  stands for mod-2 addition. It can be space-time formatted to provide space-time codes achieving full spatial diversity using the threaded layering approach presented in the previous section or the unified construction [13].
stands for mod-2 addition. It can be space-time formatted to provide space-time codes achieving full spatial diversity using the threaded layering approach presented in the previous section or the unified construction [13].
Let  be a linear FEC code (outer code), where
be a linear FEC code (outer code), where  denotes the code length and
denotes the code length and  its dimension. For the concatenated STECC,
its dimension. For the concatenated STECC,  ,
,  represent
represent  information codewords and for
information codewords and for  ,
,  , is a linear combination of codewords
, is a linear combination of codewords  defined by (12). After applying a sophisticated space-time formatter, we obtain
defined by (12). After applying a sophisticated space-time formatter, we obtain  space-time error correcting codewords
space-time error correcting codewords  ,
,  to be transmitted. The transmitter scheme is represented in Figure 1. An interleaver is used to protect the information against burst errors, and to benefit from the time diversity.
to be transmitted. The transmitter scheme is represented in Figure 1. An interleaver is used to protect the information against burst errors, and to benefit from the time diversity.
A product code is defined as a serial concatenation of two FEC codes denoted  and
and  . It consists in placing information bits in a
. It consists in placing information bits in a  array.
array.  is applied to encode rows of the array and the columns of the resulting
is applied to encode rows of the array and the columns of the resulting  array are encoded using
array are encoded using  . The
. The  obtained array is a codeword of the product code
obtained array is a codeword of the product code  . Its minimum Hamming distance is the product of minimum Hamming distances of elementary constituent codes. In the case of concatenated STECCs, the
. Its minimum Hamming distance is the product of minimum Hamming distances of elementary constituent codes. In the case of concatenated STECCs, the  FEC codewords
FEC codewords  ,
,  , form a product code represented as
, form a product code represented as

where the inner code (resp., outer code) is applied along columns (resp., rows). We note that the linear outer FEC has no constraints on its rate neither on its length. Moreover, the information rate of the inner code can be increased by reducing the spatial diversity of the STECC according to the optimal rate-diversity tradeoff [13].
When full diversity algebraic STB codes (like the perfect STB codes, LDCs, …) are serially concatenated with linear FEC codes, the maximum order of diversity that can be achieved is equal to  where
where  is the minimum Hamming distance of the outer code. For concatenated full diversity STECCs, the maximum diversity order is equal to
is the minimum Hamming distance of the outer code. For concatenated full diversity STECCs, the maximum diversity order is equal to  , where
, where  is the minimum Hamming distance of the inner code. Thus, concatenated STECCs are better adapted to a serial concatenation with linear outer forward error correcting codes.
is the minimum Hamming distance of the inner code. Thus, concatenated STECCs are better adapted to a serial concatenation with linear outer forward error correcting codes.
4.2. Turbo Product Code Decoding for Concatenated STECC
The existence of a product code for concatenated STECCs enables a better information exchange between the inner code decoder, the outer code decoder and the STECC detector through the application of turbo product code decoding principles [22].
As it is summarized in Figure 2, the turbo product code decoding is based on the reliability information exchange between two elementary soft input soft output (SISO) decoders: the inner one and the maximum a posteriori (MAP) FEC decoder. Each elementary decoder benefits from two inputs: the soft values (intrinsic information) delivered by a detector, and the previous elementary decoder extrinsic information (a priori information). So as to ensure the convergence, weighting coefficients  (
( ) are applied to the a priori information generated by the FEC decoder.
) are applied to the a priori information generated by the FEC decoder.
Assuming a nonfrequency selective block fading channel and perfect synchronization, at each receive antenna, the observation is the superposition of attenuated symbols simultaneously transmitted from transmit antennas and a circular complex Additive White Gaussian Noise. To detect the symbols transmitted from a given antenna, one has to take into account the interference of symbols corresponding to the other antennas. Maximum likelihood detection is possible but its complexity may be high and depends on the modulation order. Linear equalization such as successive interference cancellation enables to reduce the computation cost [23–25]. It consists in providing the equalizer with the estimation of the interfering symbols and cancelling it in the observation. The equalizer consists of a feedforward filter and a feedback filter that can be optimized so as to minimize the mean square error at its output (in such case it is referred as MMSE interference canceller). In [17], we proposed for the concatenated STECC an iterative receiver structure composed by a MAP symbol detector over one symbol duration, which takes a priori soft information from the SISO turbo product code decoder. This structure exploits the channel diversity. But unfortunately, the complexity of MAP detector remains high especially for high-order modulations. To reduce the complexity of the detector, we propose an hybrid structure mixing the MMSE interference canceller and the turbo product code decoder. The resulting receiver scheme is given in Figure 3. The MMSE interference canceller does not take into account the STECC existence. It considers each symbol duration independently of the others and assumes that each received sample only depends on symbols simultaneously transmitted. It thus works as if symbols were transmitted using a spatial multiplexing scheme. The time correlation between transmitted symbols is taken into account in the product code decoder.
Complexity Analysis
In the MMSE turbo equalizer presented in [25], the MMSE interference canceller is the same as the one used in this paper. It is followed by an inner code decoder to take into account the STECC structure, an outer code decoder and another inner code decoder before going back to the equalizer. The structure proposed in this paper, based on the turbo product code decoding algorithm, has a lower complexity since one iteration consists of only one inner code decoding instead of two. Nevertheless, it outperforms the receiver given in [25] thanks to the identification of a turbo product code and to an optimization of the extrinsic information exchange (see Figure 3).
At the detection stage, the MMSE interference canceller is a linear filter, thus its complexity is determined by the size of matrices to be inverted. Moreover, the proposed receiver structure deals with concatenated STECCs as a spatial multiplexing scheme concatenated with an outer product code. Therefore, the MMSE interference canceller must invert a square matrix of dimension  at each iteration. An
at each iteration. An  STECC detection thus requires
STECC detection thus requires  inversions of matrices of size
inversions of matrices of size  , that can be carried out in parallel. Considering a similar transmitter and receiver scheme involving an usual
, that can be carried out in parallel. Considering a similar transmitter and receiver scheme involving an usual  full rate algebraic STB code (like perfect STB code, LDC, TAST code), we need one inversion of a matrix of size
full rate algebraic STB code (like perfect STB code, LDC, TAST code), we need one inversion of a matrix of size  . Indeed, at the receiver, an algebraic STB code is equivalent to a spatial multiplexing scheme with
. Indeed, at the receiver, an algebraic STB code is equivalent to a spatial multiplexing scheme with  receive antennas and
receive antennas and  transmit antennas. Concatenated STECCs thus enable lower complexity receivers compared to linear dispersion codes concatenated to the same outer code.
transmit antennas. Concatenated STECCs thus enable lower complexity receivers compared to linear dispersion codes concatenated to the same outer code.
5. Simulation Results
In this section, different transmission schemes are compared via simulations. Furthermore, we evaluate the performance of the iterative receiver structure based on the turbo product code decoding algorithm with a MMSE interference canceller versus the first MMSE turbo equalizer [25].
For our simulations, we consider  transmit antennas using a QAM Gray-mapped constellation over a Rayleigh nonfrequency selective block fading channel, constant over
transmit antennas using a QAM Gray-mapped constellation over a Rayleigh nonfrequency selective block fading channel, constant over  symbol durations, and
symbol durations, and  receive antennas. The channel is also assumed to be perfectly estimated at the receiver. For the outer FEC code, we use an half-rate convolutional code which is decoded using the SISO BCJR algorithm [26]. The inner code is maximum likelihood decoded according to the rules given in [25]. Plotted curves correspond to the convergence state of the iterative process.
receive antennas. The channel is also assumed to be perfectly estimated at the receiver. For the outer FEC code, we use an half-rate convolutional code which is decoded using the SISO BCJR algorithm [26]. The inner code is maximum likelihood decoded according to the rules given in [25]. Plotted curves correspond to the convergence state of the iterative process.
5.1. Performance of the 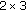 Full-Diversity STECC
Full-Diversity STECC
Figure 4 compares the performance of the  full diversity STECC with those of the
full diversity STECC with those of the  STECC [16] and the Alamouti scheme [2], without concatenation with an outer code.
STECC [16] and the Alamouti scheme [2], without concatenation with an outer code.
In that case, a maximum likelihood (ML) detection is considered at the receiver and as space-time error correcting codewords (resp., Alamouti space-time codewords) are independent from each others, the BER performance remains the same for every  multiple of
multiple of  (resp., 2). One can see that the BER slope of the
(resp., 2). One can see that the BER slope of the  full diversity STECC for
full diversity STECC for  and
and  is equal to
is equal to  , which confirms the full spatial diversity of this structure. On the other hand, as it was expected by the theoretical analysis in the Section 2.3, the BER slope of the
, which confirms the full spatial diversity of this structure. On the other hand, as it was expected by the theoretical analysis in the Section 2.3, the BER slope of the  STECC is equal to
STECC is equal to  which means that this transmission scheme cannot fully exploit the transmit diversity. For
which means that this transmission scheme cannot fully exploit the transmit diversity. For  a gain of 5.3 dB is achieved at a BER of
a gain of 5.3 dB is achieved at a BER of  with the full spatial diversity STECC. Moreover, the full diversity STECC performs 0.5 dB worse compared to the Alamouti scheme which is satisfactory as it is obtained without taking into account the outer FEC code. When
with the full spatial diversity STECC. Moreover, the full diversity STECC performs 0.5 dB worse compared to the Alamouti scheme which is satisfactory as it is obtained without taking into account the outer FEC code. When  , the full diversity STECC benefits from the additional time diversity of the channel. For a
, the full diversity STECC benefits from the additional time diversity of the channel. For a  , the gain over the Alamouti scheme is equal to 0.5 dB.
, the gain over the Alamouti scheme is equal to 0.5 dB.
5.2. Optimization of the Concatenated STECC Iterative Receivers
In Figure 5, we compare the performance of the MMSE interference canceller with a SISO turbo product code decoder versus that of the MMSE turbo equalizer [25] for the concatenated  full diversity STECC. Simulations are carried out for
full diversity STECC. Simulations are carried out for  (roughly quasifast fading channel) and
(roughly quasifast fading channel) and  (slow fading channel), respectively, in order to observe the influence of the time diversity on the performance of the receiver structures. In addition to the computation cost reduction per iteration (one inner decoding instead of two per iteration), the hybrid scheme enables a SNR gain for a same BER value. Another advantage of product code identification is the stopping criterion [22] that can be applied to stop the iterative process as soon as a product codeword is detected, yielding a power consumption saving.
(slow fading channel), respectively, in order to observe the influence of the time diversity on the performance of the receiver structures. In addition to the computation cost reduction per iteration (one inner decoding instead of two per iteration), the hybrid scheme enables a SNR gain for a same BER value. Another advantage of product code identification is the stopping criterion [22] that can be applied to stop the iterative process as soon as a product codeword is detected, yielding a power consumption saving.
For a  and for
and for  (resp.,
(resp.,  ) a gain roughly equal to 0.9 dB (resp., 0.8 dB) is offered by the proposed iterative receiver with respect to the existing one. This hybrid receiver scheme is thus selected.
) a gain roughly equal to 0.9 dB (resp., 0.8 dB) is offered by the proposed iterative receiver with respect to the existing one. This hybrid receiver scheme is thus selected.
5.3. Performance of Concatenated Full-Diversity STECCs
We compare for  and
and  the performance of the concatenated
the performance of the concatenated  full diversity STECC with the concatenated
full diversity STECC with the concatenated  STECC [16] in order to further highlight the advantage of optimizing STECCs from a space-time point of view.
STECC [16] in order to further highlight the advantage of optimizing STECCs from a space-time point of view.
In Figure 6, we compare the performance of the concatenated full diversity STECC versus the concatenated STECC for  (the time duration to transmit one STECC codeword) and
(the time duration to transmit one STECC codeword) and  using 4-QAM Gray-mapped constellation. The higher the coherence time (
using 4-QAM Gray-mapped constellation. The higher the coherence time ( ), the more significant the spatial diversity effect on performance. For a BER =
), the more significant the spatial diversity effect on performance. For a BER =  and for
and for  the proposed transmission scheme outperforms by 0.6 dB the one presented in [16]. The gain increases with
the proposed transmission scheme outperforms by 0.6 dB the one presented in [16]. The gain increases with  . Indeed for
. Indeed for  and
and  (resp.,
(resp.,  ), the gain becomes equal to 2.6 dB for a BER of
), the gain becomes equal to 2.6 dB for a BER of  (resp., 1.7 dB for a
(resp., 1.7 dB for a  ). Note that the computation cost at the receiver side is the same for both schemes.
). Note that the computation cost at the receiver side is the same for both schemes.
Figure 7 shows the effect of the error correction capability of the outer code on the performance measured in terms of BER. We consider a slow fading channel ( ). At a
). At a  and using the
and using the  -rate convolutional code
-rate convolutional code  as an outer code, a gain of 0.9 dB is offered by exploiting the spatial diversity. At the same BER and taking into account the
as an outer code, a gain of 0.9 dB is offered by exploiting the spatial diversity. At the same BER and taking into account the  -rate convolutional code
-rate convolutional code  as an outer code, the gain achieved by the concatenated full diversity STECC with respect to the suboptimal-diversity concatenated STECC is reduced to 0.7 dB. When the error correction capability of the FEC outer code increases, the time diversity becomes more influent than spatial diversity on performance. Concatenated STECCs exploit efficiently the time diversity. Furthermore, considering the scheme with the outer code
as an outer code, the gain achieved by the concatenated full diversity STECC with respect to the suboptimal-diversity concatenated STECC is reduced to 0.7 dB. When the error correction capability of the FEC outer code increases, the time diversity becomes more influent than spatial diversity on performance. Concatenated STECCs exploit efficiently the time diversity. Furthermore, considering the scheme with the outer code  , the gain observed in Figure 7 for
, the gain observed in Figure 7 for  is less than the gain observed in Figure 6 for
is less than the gain observed in Figure 6 for  . The information length is indeed higher in the scheme with
. The information length is indeed higher in the scheme with  .
.
5.4. Puncturing
A drawback of concatenated STECCs is their low coding rate. However, puncturing can be used to increase the system throughput. Unfortunately, puncturing the inner code induces a degradation of the transmit diversity. In order to guarantee a full spatial diversity, we apply puncturing on the outer code. We consider  -rate and
-rate and  -rate punctured convolutional codes generated from the half-rate parent convolutional code
-rate punctured convolutional codes generated from the half-rate parent convolutional code  .
.
In Figure 8, the outer code is punctured so as to get a coding rate of  . For a BER of
. For a BER of  and
and  , the gain of the full diversity scheme compared to the suboptimal one is equal to 1.2 dB. In Figure 9, the outer code coding rate is
, the gain of the full diversity scheme compared to the suboptimal one is equal to 1.2 dB. In Figure 9, the outer code coding rate is  . For a BER of
. For a BER of  , the full diversity scheme outperforms the suboptimal one by 4 dB.
, the full diversity scheme outperforms the suboptimal one by 4 dB.
The outer code puncturing yields a decrease of its error-correction capability and thus a lower exploitation of the available time diversity. Maximization of the space-diversity is all the more essential.
6. Conclusion
In this paper, we have presented the construction of space-time codes with error correction capability and we have optimized the receiver in case of serial concatenation with an outer FEC code.
The application of both binary rank criterion, associated to the Lu and Kumar unified construction, and threaded layering technique yields a systematic procedure for developing full diversity STECCs. When concatenated with an outer FEC code, an equivalent product code can be constructed at the receiver side enabling an hybrid iterative receiver combining both MMSE turbo equalization and turbo product code decoding. Compared to equivalent linear dispersion codes, STECCs are better adapted for a serial concatenation with an outer FEC code and the optimized receiver exhibits a lower computation cost, associated to a better convergence state and a simple stopping criterion yielding power consumption saving.
References
Tarokh V, Seshadri N, Calderbank AR: Space-time codes for high data rate wireless communication: performance criterion and code construction. IEEE Transactions on Information Theory 1998, 44(2):744-765. 10.1109/18.661517
Alamouti SM: A simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998, 16(8):1451-1458. 10.1109/49.730453
Tarokh V, Jafarkhani H, Calderbank AR: Space-time block codes from orthogonal designs. IEEE Transactions on Information Theory 1999, 45(5):1456-1467. 10.1109/18.771146
Hassibi B, Hochwald BM: High-rate codes that are linear in space and time. IEEE Transactions on Information Theory 2002, 48(7):1804-1824. 10.1109/TIT.2002.1013127
El Gamal H, Damen MO: Universal space-time coding. IEEE Transactions on Information Theory 2003, 49(5):1097-1119. 10.1109/TIT.2003.810644
Oggier F, Belfiore JC, Viterbo E: Cyclic division algebras: a tool for space-time coding. Foundations and Trends in Communications and Information Theory 2007, 4(1):1-95. 10.1561/0100000016
Liao H, Xia XG: Some designs of full rate space-time codes with nonvanishing determinant. IEEE Transactions on Information Theory 2007, 53(8):2898-2908.
Wang G, Xia XG: On optimal multilayer cyclotomic space-time code designs. IEEE Transactions on Information Theory 2005, 51(3):1102-1135. 10.1109/TIT.2004.842630
Zheng L, Tse DNC: Diversity and multiplexing: a fundamental tradeoff in multiple-antenna channels. IEEE Transactions on Information Theory 2003, 49(5):1073-1096. 10.1109/TIT.2003.810646
Belfiore JC, Rekaya G, Viterbo E: The Golden code: a 2 × 2 full-rate space-time code with nonvanishing determinants. IEEE Transactions on Information Theory 2005, 51(4):1432-1436. 10.1109/TIT.2005.844069
Oggier F, Rekaya G, Belfiore JC, Viterbo E: Perfect space-time block codes. IEEE Transactions on Information Theory 2006, 52(9):3885-3902.
Hammons AR, Gamal HE: On the theory of space-time codes for PSK modulation. IEEE Transactions on Information Theory 2000, 46(2):524-542. 10.1109/18.825816
Lu HF, Kumar PV: A unified construction of space-time codes with optimal rate-diversity tradeoff. IEEE Transactions on Information Theory 2005, 51(5):1709-1730. 10.1109/TIT.2005.846403
Liu Y, Fitz MP, Takeshita OY: A rank criterion for QAM space-time codes. IEEE Transactions on Information Theory 2002, 48(12):3062-3079. 10.1109/TIT.2002.805074
Lu HF, Kumar PV: Rate-diversity tradeoff of space-time codes with fixed alphabet and optimal constructions for PSK modulation. IEEE Transactions on Information Theory 2003, 49(10):2747-2751. 10.1109/TIT.2003.817469
Lalam M, Amis K, Leroux D: Space-time error correcting codes. IEEE Transactions on Wireless Communications 2008, 7(5):1472-1476.
Hassan MS, Amis K: Turbo product code decoding for concatenated space-time error correcting codes. Proceedings of the 20th IEEE Personal, Indoor and Mobile Radio Communications Symposium (PIMRC '09), September 2009, Tokyo, Japan
Vucetic B, Yuan J: Space-Time Coding. Willey, New York, NY, USA; 2003.
Hassan MS, Amis K: Multilayer space-time error correcting codes. Proceedings of the 6th International Symposium on Wireless Communication Systems (ISWCS '09), September 2009, Sienna, Italy 318-322.
Hassan MS, Amis K: Constellation labeling optimization for iteratively decoded concatenated multilayer space-time error correcting codes. Proceedings of the 5th International Conference on Wireless and Mobile Communications (ICWMC '09), August 2009, Cannes, France 196-199.
Hassan MS, Amis K: Construction of full diversity space-time codes based on half-rate invertible linear binary codes. Proceedings of the 6th International Symposium on Turbo Codes and Iterative Information Processing (ISTC '10), September 2010, Brest, France 117-121.
Pyndiah RM: Near-optimum decoding of product codes: block turbo codes. IEEE Transactions on Communications 1998, 46(8):1003-1010. 10.1109/26.705396
Tüchler M, Koetter R, Singer AC: Turbo equalization: principles and new results. IEEE Transactions on Communications 2002, 50(5):754-767. 10.1109/TCOMM.2002.1006557
Laot C, Le Bidan R, Leroux D: Low-complexity MMSE turbo equalization: a possible solution for EDGE. IEEE Transactions on Wireless Communications 2005, 4(3):965-974.
Lalam M, Amis K, Leroux D: Iterative decoding of space-time error correcting codes. Proceedings of the 18th Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007
Bahl LR, Cocke J, Jelinek F, Raviv J: Optimal decoding of linear codes for minimizing symbol error rate. IEEE Transactions on Information Theory 1974, 20(2):284-287.
Acknowledgments
The authors would like to thank Orange Labs for supporting their research. Part of the content of this manuscript has been published in IEEE ISWCS 2009 and in IEEE PIMRC 2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hassan, M., Amis, K. Full-Diversity Space-Time Error Correcting Codes with Low-Complexity Receivers. J Wireless Com Network 2011, 653506 (2011). https://doi.org/10.1155/2011/653506
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/653506
 of the matrix
of the matrix 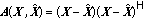 .
.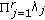 ), of the matrix
), of the matrix 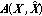 . This criterion maximizes the coding gain.
. This criterion maximizes the coding gain. STECCs: Theoretical Analysis
STECCs: Theoretical Analysis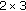 Full-Diversity STECC
Full-Diversity STECC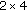 Full-Diversity STECC
Full-Diversity STECC


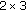 Full-Diversity STECC
Full-Diversity STECC

 full diversity STECC. 1530 informations bits.
full diversity STECC. 1530 informations bits.  .
.  .
.
 .
.  .
.
 information bits.
information bits.  .
.
 information bits.
information bits.  . Outer code: the
. Outer code: the  -rate punctured
-rate punctured  .
.
 information bits.
information bits.  . Outer code: the
. Outer code: the  -rate punctured
-rate punctured  .
.