- Research Article
- Open access
- Published:
Towards a Collision-Free WLAN: Dynamic Parameter Adjustment in CSMA/E2CA
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 708617 (2011)
Abstract
Carrier sense multiple access with enhanced collision avoidance (CSMA/ECA) is a distributed MAC protocol that allows collision-free access to the medium in WLANs. The only difference between CSMA/ECA and the well-known CSMA/CA is that the former uses a deterministic backoff after successful transmissions. Collision-free operation is reached after a transient state during which some collisions may occur. This paper shows that the duration of the transient state can be shortened by appropriately setting the contention parameters. Standard absorbing Markov chain theory is used to describe the behaviour of the system in the transient state and to predict the expected number of slots to reach the collision-free operation. The paper also introduces CSMA/E2CA, in which a deterministic backoff is used two consecutive times after a successful transmission. CSMA/E2CA converges quicker to collision-free operation and delivers higher performance than CSMA/ECA, specially in harsh wireless scenarios with high frame-error rates. The last part of the paper addresses scenarios with a large number of contenders. We suggest dynamic parameter adjustment techniques to accommodate a varying (and potentially high) number of contenders. The effectiveness of these adjustments in preventing collisions is validated by means of simulation.
1. Introduction
Wireless local area networks (WLANs) are a popular choice as a last-hop connection to the Internet. Many consumer devices support the IEEE 802.11 standard [1] and share the radio channel to access the Internet wirelessly. As the number of wireless devices with data to transmit increases, the likelihood that two or more of these devices simultaneously transmit also increases. If a collision between two simultaneous transmissions occurs, the intended receiver of the transmission may not be able to decode the information that has been sent. In some practical scenarios such as conference rooms, the number of collisions may render the wireless network unusable. This paper explores an approach that can reduce the number of collisions and may even allow for collision-free operation of the network.
In the remainder of the paper, we assume the familiarity of the reader with the IEEE 802.11 standard and the related terminology. The focus of the paper is on the medium access control (MAC) layer of the protocol and, in particular, on the distributed coordination function (DCF) and the more recent enhanced distributed channel access (EDCA). Both approaches heavily rely on carrier sense multiple access with collision avoidance (CSMA/CA). This has proven to be a lightweight, robust, and effective protocol in infrastructure scenarios in which a number of nearby stations connect to an access point for Internet access.
A downside of CSMA/CA is that only a fraction of the channel time is devoted to successful transmissions, while the remainder is wasted in the form of collisions and empty channel. Section 2 reviews previous research efforts aimed to increase the efficiency of the protocol, that is, the fraction of channel time devoted to successful transmissions. The emphasis is placed on CSMA with enhanced collision avoidance (CSMA/ECA), a subtle modification to CSMA/CA that uses a deterministic backoff after successful transmissions to avoid collisions. CSMA/ECA reaches collision-free operation after a transient state. We proceed in Section 3 by showing that if the minimum and maximum contention window are set to the same value, the duration of the transient state is reduced. The transition to collision-free operation can be modelled as an absorbing Markov chain. Standard Markov chain theorems can be used to estimate the expected number of slots required to reach the collision-free operation. These analytical results are validated by means of simulation. Section 4 suggests using a deterministic backoff for two consecutive times after a successful transmission. This variation is called CSMA/E2CA, and we study the absorption process to show that its quicker than in the original CSMA/ECA. More importantly, CSMA/E2CA proves to be more resilient in harsh wireless conditions, where the frame error rates are high. A limitation of CSMA/E2CA is that the number of contenders that can operate in a collision-free fashion is limited. Section 5 deals with dynamic parameter adjustment in a CSMA/E2CA network to accommodate a varying (and potentially large) number of contenders. The possibility of using a deterministic backoff for several consecutive times after a successful transmission in briefly discussed in Section 6. Finally, Section 7 concludes the paper.
2. Related Work
Since Abramson's team seminal design and deployment of the Aloha wireless network [2, 3], the MAC protocols have evolved to achieve higher efficiency, which is defined as the fraction of channel time devoted to successful transmissions. By dividing channel time into slots, slotted Aloha may double the efficiency of the original protocol under certain conditions (such as fixed packet length equal to the slot size) [4–6]. In Reservation Aloha [7], a station that successfully transmits obtains a reservation for a slot that follows a deterministic number of slots later.
In WLANs, it is possible to substantially reduce the duration of empty slots thanks to the fact that the propagation times are short, and thus, we can quickly determine that a slot is empty by simply sensing the channel. Shortening the duration of empty slots increases the efficiency of the MAC protocol. This is the idea underlying CSMA/CA. An additional performance improvement can be obtained when the aggressiveness of the contending stations is adjusted as a function of the number of contending stations [8]. Channel observation and advanced filtering techniques can be used to obtain an accurate estimate of the number of contenders and adjust the contention parameters accordingly [9]. It is even possible to get close to the optimal efficiency of CSMA/CA without any knowledge of the number of contenders. Since optimal collision probability is an invariant that does not depend on the number of contenders, control theory and a feedback loop can be used to adjust the contention parameters [10].
Unfortunately, the optimal efficiency of CSMA/CA is still far from one. In other words, a substantial amount of channel time is still wasted in the form of empty slots and collisions. One of the latest research trends in MAC protocols for WLANs is the use of learning protocols. These protocols are executed in a distributed fashion, but they are not completely random. On the contrary, they try to gather information about other stations' intentions to transmit in order to schedule their own transmissions in a way that reduces the chances of collisions. A reduction in the number of collisions results in significant performance gains, and these protocols may even achieve collision-free operation.
A first example of these protocols is the enhanced backoff algorithm (EBA) introduced in [11], which proposes that each station announces its backoff intentions in a special header to avoid collisions. A caveat is that currently deployed hardware would discard EBA packets, since these are not IEEE 802.11 compliant and thus backward compatibility is compromised.
If the stations use a deterministic backoff after successes, it is not longer required to include a header explicitly stating the backoff intentions. Moreover, when all the stations use the same deterministic backoff after successes, the system naturally converges to a collision-free operation in which the stations transmit in a round-robin deterministic fashion. We call this variant of CSMA/CA that uses a deterministic backoff after successes CSMA/ECA (this idea was initially presented with the name of learning binary exponential backoff or L-BEB) [12].
ZeroCollision [13] is a MAC protocol that also converges to a collision-free mode of operation. The operation of ZeroCollision is similar to Reservation Aloha. The slots are grouped in rounds, each round containing  slots, and the stations keep track of the status of each slot (either busy or empty). A station that successfully transmits in the
slots, and the stations keep track of the status of each slot (either busy or empty). A station that successfully transmits in the  th slot (
th slot ( ) obtains an implicit reservation for that slot. If this station has more packets to transmit, it will use again the
) obtains an implicit reservation for that slot. If this station has more packets to transmit, it will use again the  th slot in the next transmission round. Those stations that have no reservation, transmit randomly in any of the slots that were empty in the previous round.
th slot in the next transmission round. Those stations that have no reservation, transmit randomly in any of the slots that were empty in the previous round.
An insightful comparison between CSMA/ECA and ZeroCollision is presented in [14]. ZeroCollision converges quicker to the collision-free operation and CSMA/ECA presents a behaviour that is more similar to current CSMA/CA. This similarity may ease the implementation of CSMA/ECA. The results in this reference also show that ZeroCollision is superior to CSMA/ECA in the presence of channel errors. Additionally, the cited paper also extends both protocols to converge quicker to collision-free operation, to deliver higher performance in lossy channels, and to operate in a collision-free fashion in the presence of a large number of stations. The names of these extended protocols are L-ZC, L-MAC, A-L-ZC, and A-L-MAC. Furthermore, the concept of stickiness is introduced. We will revisit this concept in Section 4 as a means to substantially improve the performance of CSMA/ECA.
Figure 1 provides an example of the operation of CSMA/CA, CSMA/ECA, and ZeroCollision. In each case, there are six different stations contending for the channel. A transmission by one of the stations is represented as a ball in the figure. We use different filling patterns for balls belonging to different stations. The bins represent the slots. Even though all bins are depicted as being equal for convenience, busy slots are substantially longer than empty slots in reality.
In the figure, it can be observed that CSMA/CA uses a random backoff before each transmission attempt, and it never converges to collision-free operation. CSMA/ECA uses a deterministic backoff after successful transmissions and a random backoff otherwise. The value of the deterministic backoff is constant for all stations,  , which is equal to the expectation of the random backoff which is used in CSMA/CA. Note that
, which is equal to the expectation of the random backoff which is used in CSMA/CA. Note that  is also the maximum number of stations that can contend in a collision-free fashion. For this reason, we sometimes refer to
is also the maximum number of stations that can contend in a collision-free fashion. For this reason, we sometimes refer to  as the capacity of the system.
as the capacity of the system.
In the figure, we can see that at some point, all the CSMA/ECA stations successfully transmit and the system operates in a deterministic and collision-free fashion. A property of CSMA/ECA is that a station that has successfully transmitted in its last transmission attempt never collides with another station that has also succeeded in its last transmission attempt.
In our ZeroCollision example, we also use a schedule size  in order to ease comparison with CSMA/CA. In ZeroCollision, a station that successfully transmits does not collide in its next transmission attempt. Consequently, ZeroCollision converges quicker to collision-free operation.
in order to ease comparison with CSMA/CA. In ZeroCollision, a station that successfully transmits does not collide in its next transmission attempt. Consequently, ZeroCollision converges quicker to collision-free operation.
The idea of using a deterministic backoff after successful transmissions is also presented in [15], where it is called semirandom backoff (SBR). This reference studies the convergence to collision-free operation, the collision probability, and the performance in presence of hidden terminals. Delay measures are also presented and many other performance issues are explored. It is concluded that SBR performs equal or better than the random backoff in all possible scenarios.
The focus of the present paper is on single-hop WLAN communications. The broad idea of learning MAC protocols, stickiness, and convergence to a collision-free schedule has been studied in the context of wireless multihop networks in [16–18].
The remainder of this paper deals with CSMA/ECA. We have studied several aspects of CSMA/ECA in our previous work. In particular, the performance of CSMA/ECA for rigid flows, elastic flows, and a combination of both is assessed by means of simulation in [19]. An analytical model that captures the behaviour of the protocol for both saturated and nonsaturated scenarios is presented in [20]. The efficacy of CSMA/ECA in providing traffic differentiation is demonstrated in [21]. In [22], the coexistence of CSMA/ECA with the legacy protocol is studied. This last reference also presents a preliminary study of the duration of the transient state. Finally, a possible solution to the problem of accommodating a large number of stations in a collision-free fashion in infrastructure WLAN is presented in [23]. The present paper, reviews and substantially extends [23].
In this paper, unless otherwise stated, we will rely on the following assumptions.
-
(i)
The ideal channel does not introduce errors. The presence of errors is considered in Section 4.
-
(ii)
There is no capture effect; that is, a collision always results in failure.
-
(iii)
All the stations are in the same collision domain, and we have perfect carrier sensing. Imperfect carrier sense is considered in [15].
-
(iv)
All the stations have the same priority. Traffic prioritization is considered in [15, 21].
-
(v)
(v)All the stations are saturated, which means that they always have a packet ready to be transmitted. The presence of nonsaturated stations is studied in [19].
-
(vi)
All the stations are synchronized to the channel slots.
The current paper presents the following contributions that extend and complement previous work.
-
(i)
We study the particular case in which the minimum contention window is equal to the maximum contention window (
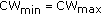 ). We show that this configuration reduces the duration of the transient state.
). We show that this configuration reduces the duration of the transient state. -
(ii)
We make use of standard absorbing Markov chain theory to estimate the average number of slots required to reach collision-free operation.
-
(iii)
We suggest the use of a deterministic backoff for two consecutive times after a successful transmission. In other words, the stations will keep using a deterministic backoff until two consecutive packet losses occur. We call the protocol CSMA/E2CA, and we show that this approach further reduces the duration of the transient state.
-
(iv)
We show that CSMA/E2CA clearly outperforms CSMA/CA and CSMA/ECA in scenarios in which packet losses occur.
-
(v)
We revisit the idea of dynamic parameter adjustment initially presented in [23]. We enhance it by incorporating a hysteresis margin to prevent the oscilation of the contention parameter, and we propose an alternative implementation using integer arithmetic.
3. Parameter Setting and Analytical Model
CSMA/ECA is an attractive contention protocol, because it is very similar to the pervasive CSMA/CA and can achieve collision-free operation. In [22], it is explained that the pseudocode description of CSMA/ECA and CSMA/CA differ in a single line. This makes it very easy to try CSMA/ECA in any simulator, and, in principle, it should be also easy for the manufacturers to switch to the new protocol. The fact that the two protocols are so similar allows for the smooth coexistence of CSMA/ECA and CSMA/CA stations and would allow CSMA/ECA devices to pass WiFi certification tests.
The value of the deterministic backoff after successes in CSMA/ECA is computed as a function of the minimum contention window ( ) as
) as

where  is the ceiling operator,
is the ceiling operator,  is the expectation operator, and
is the expectation operator, and  is the uniform random distribution. In our previous work, we have already shown that using the parameter adjustment possibilities of the latest version of the standard, it is possible to attain traffic differentiation [21] and accommodate a large number of contenders [23] by adjusting
is the uniform random distribution. In our previous work, we have already shown that using the parameter adjustment possibilities of the latest version of the standard, it is possible to attain traffic differentiation [21] and accommodate a large number of contenders [23] by adjusting  . In the following, we will show that we can reduce the time required to reach collision free operation by using a smaller maximum contention window, in particular
. In the following, we will show that we can reduce the time required to reach collision free operation by using a smaller maximum contention window, in particular  . Since the transient state can be seen as an stochastic (trial-and-error) search for a collision free schedule, setting
. Since the transient state can be seen as an stochastic (trial-and-error) search for a collision free schedule, setting  can be intuitively interpreted as reducing the time between trials which results in a faster search. We will show that this is indeed the case.
can be intuitively interpreted as reducing the time between trials which results in a faster search. We will show that this is indeed the case.
The doubling of the contention window after each unsuccessful transmission is called binary exponential backoff (BEB) and its purpose is to reduce the transmission probability of the stations when collisions occur. When the number of stations is large, the role of BEB is to reduce the aggressiveness of the stations to reduce the number of collisions. It was pointed out in [24] that when there are alternative means available to adjust the contention window, BEB simply decreases the fairness and the overall efficiency of an IEEE 802.11e network. The same argument applies if CSMA/ECA is used.
In a CSMA/CA+BEB network (e.g., a IEEE 802.11 network), a station that collides is doubly penalized. First, its payload is not delivered, and second, it has to wait for a longer time before the next transmission attempt. In CSMA/ECA+BEB, a station that collides is triply penalized, because the stations that randomly select their backoff perceive a higher collision probability than those that select their backoff deterministically.
Furthermore, BEB unnecessarily increases the number of slots required for the system to reach collision-free operation. This can be readily observed in Figure 2 that depicts the number of slots required for the system to converge when a given number of stations simultaneously join the contention. To obtain this results, we have used a minimum contention window  and a deterministic backoff after successes
and a deterministic backoff after successes  . The number of contending stations
. The number of contending stations  (
( ) is represented in the
) is represented in the  axis.
axis.
The first two curves are obtained by means of simulation. (We have used custom simulators in  . The simulators only implement the MAC layer and assume that the stations are saturated and in the same collision domain. The channel is ideal and does not introduce errors. The plots represent average values. The standard deviation is below 1% of the plotted value. Source code is available upon request.) In the first one, we use different values for the minimum and maximum contention window (
. The simulators only implement the MAC layer and assume that the stations are saturated and in the same collision domain. The channel is ideal and does not introduce errors. The plots represent average values. The standard deviation is below 1% of the plotted value. Source code is available upon request.) In the first one, we use different values for the minimum and maximum contention window ( and
and  ), while in the second one, the same value is used for both contention windows (
), while in the second one, the same value is used for both contention windows ( ). It can be observed that using the same value reduces the number of slots required for the system to reach collision-free operation. In the remainder of the paper, unless otherwise stated, we will not use BEB (e.g., we will set the maximum contention window to the same value of the minimum contention window).
). It can be observed that using the same value reduces the number of slots required for the system to reach collision-free operation. In the remainder of the paper, unless otherwise stated, we will not use BEB (e.g., we will set the maximum contention window to the same value of the minimum contention window).
When the minimum and maximum contention windows are equal, the system can be modeled as an absorbing Markov chain, and it is possible to compute the expected number of slots required to reach the collision-free operation.
To model the system, we divide the sequence of slots in groups of  slots, and we will refer to each group as a step. This is exactly what we have done in Figure 1 to ease representation. In the figure, slots ranging from 0 to 15 belong to the first step, and those between 16 and 31 belong to the second step. We assume that all the stations transmit once in each step (this is a modelling approximation, since it is not satisfied in the real system). Furthermore, we define the state of the system as the number of successful transmissions in each step.
slots, and we will refer to each group as a step. This is exactly what we have done in Figure 1 to ease representation. In the figure, slots ranging from 0 to 15 belong to the first step, and those between 16 and 31 belong to the second step. We assume that all the stations transmit once in each step (this is a modelling approximation, since it is not satisfied in the real system). Furthermore, we define the state of the system as the number of successful transmissions in each step.
Then, we can model the transition process as an absorbing time-homogeneous Markov chain whose state space is

with initial state  and a stable state
and a stable state  , where
, where  is the number of contenders.
is the number of contenders.
The details to compute the transition matrix  of this Markov chain are provided in [22]. We reproduce here a simple example from that paper in which the number of contenders is
of this Markov chain are provided in [22]. We reproduce here a simple example from that paper in which the number of contenders is  , and the deterministic backoff after successes is
, and the deterministic backoff after successes is  .
.

 is a square matrix of size
is a square matrix of size  . The last row contains only zeros with the exception of the last column which is one. This property characterizes the system as an absorbing Markov chain. It means that when the last state
. The last row contains only zeros with the exception of the last column which is one. This property characterizes the system as an absorbing Markov chain. It means that when the last state  is reached, the system transits to
is reached, the system transits to  with probability 1 that is, the state
with probability 1 that is, the state  is absorbing. Closed form expressions for the computation of
is absorbing. Closed form expressions for the computation of  can be found in [15].
can be found in [15].
In the following, we will closely follow the discussion on absorbing Markov chains presented in [25]. The proofs of the theorems we need can be found in Chapter 11 of this reference.
The canonical representation of our transition matrix is the following:

where  is a 1-by-1 identity matrix,
is a 1-by-1 identity matrix,  is a 1-by-
is a 1-by- zero matrix,
zero matrix,  is a nonzero
is a nonzero  -by-1 matrix, and
-by-1 matrix, and  is a
is a  -by-
-by- matrix. The rows and columns that belong to the transient (TR.) and absorbing (ABS.) states are indicated in the equation.
matrix. The rows and columns that belong to the transient (TR.) and absorbing (ABS.) states are indicated in the equation.
The following theorem guarantees that the collision-free mode of operation will be eventually reached.
Theorem 1.
In an absorbing Markov chain, the probability that the process will be absorbed is 1.
Then, we compute the fundamental matrix  for our system.
for our system.
Theorem 2.
For an absorbing Markov chain the matrix  has an inverse
has an inverse  and
and  . The
. The  -entry
-entry  of the matrix
of the matrix  is the expected number of times the chain is in state
is the expected number of times the chain is in state  , given that it starts in state
, given that it starts in state  . The initial state is counted if
. The initial state is counted if  .
.
The relationship between the fundamental matrix  and the number of steps to absorption is stated in the next theorem.
and the number of steps to absorption is stated in the next theorem.
Theorem 3.
Let  be the expected number of steps before the chain is absorbed, given that the chain starts in state
be the expected number of steps before the chain is absorbed, given that the chain starts in state  , and let
, and let  be the column vector whose
be the column vector whose  th entry is
th entry is  . Then,
. Then,

where  is a column vector all of whose entries are 1.
is a column vector all of whose entries are 1.
Now,  is the expected number of steps to absorption assuming that all the stations simultaneously join the contention. To obtain the expected number of slots to absorption, we have to multiply the number of steps by
is the expected number of steps to absorption assuming that all the stations simultaneously join the contention. To obtain the expected number of slots to absorption, we have to multiply the number of steps by  , which is the number of slots in each step. In Figure 2, these analytical results are compared with the simulation results. It can be observed that our model can be used to predict the expected duration of transient state when
, which is the number of slots in each step. In Figure 2, these analytical results are compared with the simulation results. It can be observed that our model can be used to predict the expected duration of transient state when  .
.
There is a small gap between the analytical and simulation curve in Figure 2 when the number of slots to absorption is low. The explanation lies in the aforementioned modeling assumption that all the stations transmit exactly once in each of the steps. The results that we obtained are in agreement with the ones presented in [15, Table II].
4. CSMA/E2CA and Performance in the Presence of Errors
One of the shortcomings of CSMA/ECA when compared to ZeroCollision is that it takes longer for CSMA/CA to reach the collision-free operation. In this section, we suggest a simple idea to dramatically accelerate the convergence of CSMA/ECA.
In ZeroCollision, a station that successfully transmits in its last transmission attempt will not collide in its next transmission attempt. The reason is that every station keeps track of the other station's successful transmissions and intelligently schedules the next transmission attempt to avoid a collision with those stations that deterministically choose their transmission slot for their next transmission attempt.
Our aim is to shorten the transient state without requiring that each station keeps track of the other stations' successes. Our idea relies on the concept of stickiness introduced in [14]. This reference suggests that a station sticks (with a given probability) to a given slot after suffering a collision. Our proposal is that a station chooses a deterministic backoff for two consecutive times after a successful transmission. Then, a single collision (or channel error) is not enough to move a station from the deterministic mode of operation to the random mode of operation. Suffering two consecutive collisions or channel errors is an unlikely event.
We call the protocol that uses a deterministic backoff for two consecutive times after each successful transmission CSMA/E2CA. This behaviour is exemplified in Figure 3. Take as an example the transmission in slot 11, which is a ball filled with horizontal lines. This station successfully transmits and then it suffers a collision in its next transmission attempt in slot 27. Despite this collision, the station chooses a deterministic backoff again. In our example, the station succeeds in the next transmission attempt in slot 43, and therefore, it keeps using a deterministic backoff. Had the station suffered a new collision in the next transmission attempt in slot 43, it would have used a random backoff in the following transmission attempt. In CSMA/E2CA, a station that suffers two consecutive unsuccessful transmission attempts switches to the random mode of operation.
The stickiness of CSMA/E2CA allows for a quicker convergence to collision-free operation as can be observed in Figure 4. This figure compares simulation results for the average number of slots to absorption in CSMA/ECA and CSMA/E2CA. Stickiness can reduce the expected number of slots to convergence by orders of magnitude when the number of contenders  has a value that is close or equal to the capacity
has a value that is close or equal to the capacity  .
.
In the remainder of this section, we will compare four protocols, namely, CSMA/CA, CSMA/CA + BEB, CSMA/ECA, and CSMA/E2CA. In a first round of simulation, we will use an ideal channel that does not drop packets. This will set the upper bound for the performance of each of the protocols. We opted for measuring the number of empty, success, and collision slots. These measures can be translated to throughput for a given IEEE 802.11 physical flavor (e.g., 11a, 11b, 11g, or 11n) and a given packet length distribution.
The simulations last for 106 slots, and the transitory is taken into account. This is an important detail, since performance in the transient state is traded off for performance in the steady state. Those simulations with a large number of contenders present a higher performance in the steady state but are penalized by longer transient states.
Figure 5 shows the fraction of empty slots. Empty slots are usually very short, and therefore, the performance penalty incurred for having large fraction of empty slots is substantially less than the one caused by collisions. Collisions are depicted in Figure 6. This figure shows that both CSMA/ECA and CSMA/E2CA effectively prevent collisions for a number of contenders lower than  . For the particular case of a number of contenders equal to
. For the particular case of a number of contenders equal to  , the transient state is very long for CSMA/ECA, and therefore, we can observe that the number of collisions is relatively high. Finally, the number of successful slots is presented in Figure 7.
, the transient state is very long for CSMA/ECA, and therefore, we can observe that the number of collisions is relatively high. Finally, the number of successful slots is presented in Figure 7.
From the results, it can be observed that CSMA/ECA and CSMA/E2CA consistently outperform the other two protocols. The difference between CSMA/ECA and CSMA/E2CA in ideal channel conditions is obvious only for a large number of contenders.
For the next simulations round, we will consider a channel that introduces errors. When a single station transmits in a given slot, that packet is dropped with probability equal to 10%. The station is not able to differentiate between packet drop and collision, and therefore, it will react as if a collision has occurred.
Figure 8 shows the fraction of empty slots of the four protocols in a lossy channel. Figure 9 shows the fraction of collisions and Figure 10 the fraction of successful transmissions. The fraction of packet drops is not shown, since it is equal to a 10% of successful transmissions.
From the results, we can conclude that CSMA/CA presents a behaviour that is very similar to the one we have observed in the ideal channel. This is not the case of CSMA/ECA that presents an impaired behaviour, because it cannot differentiate between channel errors and collisions. This problem is partly alleviated by CSMA/E2CA. Nevertheless, if we want to obtain collision-free operation after a short transient state, the number of competing stations has to be around one half of the capacity of the system. As an example, for a deterministic value after successes  , we can accommodate up to
, we can accommodate up to  stations before the number of collisions starts to grow. If we expect that a number of stations much larger than 8 is going to be simultaneously backlogged (with a packet ready to send), then mechanisms that dynamically adjust the contention parameter should be considered. This is the subject ot the next section.
stations before the number of collisions starts to grow. If we expect that a number of stations much larger than 8 is going to be simultaneously backlogged (with a packet ready to send), then mechanisms that dynamically adjust the contention parameter should be considered. This is the subject ot the next section.
5. Dynamic Parameter Adjustment in CSMA/E2CA
In the previous sections, we have studied the performance of CSMA/ECA in scenarios in which the number of active contenders was below the deterministic backoff value used after successful transmissions. This is the situation that is most often encountered in current deployments, in which the number of stations registered to a single access point is moderate, and only a fraction of those stations are contending for the channel.
Nevertheless, it would be desirable that a contention protocol for future WLANs was scalable enough to accommodate an arbitrarily large number of contenders. In the present section, we discuss the dynamic parameter adjustment of CSMA/ECA to accommodate a changing (and potentially high) number of contenders.
The idea of adjusting the  parameter in CSMA/ECA was initially presented in [23]. In the current paper, we review that initial approach, justify its convenience, and present additional results. Our approach relies on the existence of a central entity (access point) that can detect whether the channel slots are empty or busy and computes and distributes the value for
parameter in CSMA/ECA was initially presented in [23]. In the current paper, we review that initial approach, justify its convenience, and present additional results. Our approach relies on the existence of a central entity (access point) that can detect whether the channel slots are empty or busy and computes and distributes the value for  . There are alternative proposals that do not require the existence of such central entity and, therefore, are appropriate for distributed scenarios [14].
. There are alternative proposals that do not require the existence of such central entity and, therefore, are appropriate for distributed scenarios [14].
In an infrastructure deployment, the access point sends beacon intervals approximately every 100 ms. This beacon frames include control information such as the  to be used by the contending stations. For convenience, we will define a beacon interval as the time that elapses between two beacon transmissions. In our approach, we adjust the
to be used by the contending stations. For convenience, we will define a beacon interval as the time that elapses between two beacon transmissions. In our approach, we adjust the  in such a way that the fraction of busy slots (
in such a way that the fraction of busy slots ( ) between two beacon frames is a value around
) between two beacon frames is a value around  .
.
In fact, we accept that the fraction of busy slots takes values between 1⁄ 8 and 1⁄ 2. These particular values are tied to the fact that according to the standard, the minimum contention window has to be a power of two (minus one). If the fraction of busy slots exceeds 1⁄ 2 (i.e., it takes a value between 1⁄ 2 and 1), then the doubling of the contention window would desirably halve the fraction of the busy slots to a value between 1⁄ 4 and 1⁄ 2, which is within our acceptable range.
The wide range of acceptable values provides a hysteresis margin that prevents the oscillation of the  value in use. Table 2 in [23] provides an example that shows that even when collision-free operation is reached, the exact number of success, collision, and empty slots may change from one beacon interval to the next. The hysteresis margin prevents that these little changes trigger an update of the
value in use. Table 2 in [23] provides an example that shows that even when collision-free operation is reached, the exact number of success, collision, and empty slots may change from one beacon interval to the next. The hysteresis margin prevents that these little changes trigger an update of the  value. Notice that decreasing the
value. Notice that decreasing the  value may originate several collisions and move the system from the steady-state collision-free operation to the transient state. For this reason, the reduction of the
value may originate several collisions and move the system from the steady-state collision-free operation to the transient state. For this reason, the reduction of the  value should be prevented unless it is strictly necessary (i.e., unless the fraction of busy slots is very low).
value should be prevented unless it is strictly necessary (i.e., unless the fraction of busy slots is very low).
The recursive equations that regulate the behaviour of the system as described in the previous paragraphs are the following:

where  is an index on the beacon interval and
is an index on the beacon interval and  is the minimum contention window used in the
is the minimum contention window used in the  th beacon interval.
th beacon interval.
The minimum contention window is initially set to its default value. Then, after 100 ms, the new minimum contention window is computed as a function of the previous value and the measured fraction of busy slots during the last beacon interval. The new value for  is conveyed in the subsequent beacon frame. As in [10], we take the design decision to prevent that the minimum contention window takes values below the default value defined in the standard.
is conveyed in the subsequent beacon frame. As in [10], we take the design decision to prevent that the minimum contention window takes values below the default value defined in the standard.
In (6), we make use of the truncate ( ) function that takes the integer part of its argument and discards the decimals. For implementation simplicity, it would be desirable to avoid floating-point operations. The pseudocode in Algorithm 1 can be used to adjust the value of
) function that takes the integer part of its argument and discards the decimals. For implementation simplicity, it would be desirable to avoid floating-point operations. The pseudocode in Algorithm 1 can be used to adjust the value of  using integer arithmetic. We double
using integer arithmetic. We double  when the fraction of busy slots is large, and we halve
when the fraction of busy slots is large, and we halve  if the measured fraction is small.
if the measured fraction is small.
Algorithm 1: adaption in CSMA/ECA.
adaption in CSMA/ECA.
 Initialize
Initialize .
. 
(1)  ;
;
(2) While true do
 Measure the number of empty and
Measure the number of empty and
busy slots in the beacon interval

(3) measure(empty, busy);
-
(4)
if

-
(5)
if

-
(6)
 ;
; -
(7)
if

-
(8)
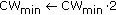 ;
;
Our suggested mechanism does not aim at filling every slot with a successful transmission. On the contrary, we advocate for leaving a large fraction of slots empty. The fraction of empty slots in steady state operation will be a number between 1⁄ 2 and 7⁄ 8. In the results presented at the end of this section, we will see that this large number of empty slots does not severely penalize performance. The rationale for leaving a large number of slots empty is twofold. First, it guarantees quick converge to collision-free operation after any disrupting event, such as an interference burst. Second, the fraction of empty slots would prevent the starvation of legacy terminals if they were present.
As in [23], we will stress our protocol by simulating a scenario in which a large number of contenders simultaneously join the network with ideal channel conditions. In [23], we presented results for a number of contenders equal to 20. In the present work, we present results for various numbers of contenders up to 100. There are two additional differences to take into account when comparing the present results with our previous work. In the present paper, we have used CSMA/E2CA, and we have set  , while in [23], we used CSMA/ECA and
, while in [23], we used CSMA/ECA and  .
.
The results are presented in Figure 11. We plot the channel efficiency in each of the first ten beacon intervals of operation. Channel efficiency is defined as the fraction of time devoted to successful packet transmissions. Since we are evaluating the contention mechanism, the only inefficiencies we take into account are empty and collision slots.
For these experiments, we have assumed that the stations are saturated. They transmit data to the access point using IEEE 802.11b 11 Mbps data rate. The size of data packets is 1500 bytes and all the contenders simultaneously join the network at time 0. We take measures every beacon interval (100 ms) and plot average values across 5000 simulations. The 95% confidence intervals are plotted in the figure even though they are so small that they are hardly visible.
It can be observed in the figure that our suggested approach quickly reacts and adapts the contention parameter to deliver high performance in less than a second, regardless of the number of simultaneous contenders. A careful observer will detect some crossings between the lines in the figure. The explanation lies in the hysteresis margins that we use: the fraction of empty slots are not necessary equal for the different number of contenders.
It is worth noting that the channel efficiency of CSMA/E2CA with parameter adjustment can be increased to any value arbitrarily close to one. This can be achieved by increasing the length of successful slots. Since the length of empty slots is constant, and there are no collision slots after the transient state, the fraction of time devoted to successful transmissions will increase as we increase the duration of a successful transmission. This can be readily achieved using the frame aggregation tools provided by the IEEE 802.11n standard amendment [26].
6. Degree of Stickiness
Throughout the paper, we have considered the CSMA/E2CA protocol that uses a deterministic backoff for two consecutive times after each successful transmission. We can define the degree of stickiness as the number of deterministic backoffs used after each successful transmission. As an example, the degree of stickiness of CSMA/E2CA is two. It is reasonable to consider the possibility of using a deterministic backoff for several (even infinite) times after each successful transmission. Let us discuss the drawbacks of using a large degree of stickiness.
Even in the idealistic scenario considered in the current paper, two stations that have successfully transmitted in their last attempt can collide in their following attempt if there has been a reduction of the  value. The
value. The  value may be reduced if there is a large number of stations that leave the contention, as it has been explained in the previous section. If such reduction occurs, two stations using a large degree of stickiness may suffer a large number of collisions before switching to a random behaviour to search for a collision-free schedule.
value may be reduced if there is a large number of stations that leave the contention, as it has been explained in the previous section. If such reduction occurs, two stations using a large degree of stickiness may suffer a large number of collisions before switching to a random behaviour to search for a collision-free schedule.
In a more realistic scenario, clock drifts may occur. As a result, the different stations may no longer be perfectly synchronized and may not decrement their counters exactly at the same time. If this is the case, two stations that have successfully transmitted in their last transmission attempt can still suffer a collision in their next transmission attempt. Again, if the network uses a large degree of stickiness, it will take several collisions for the stations to switch to a random behaviour to look for a collision-free schedule.
7. Conclusion
In this paper, we have reviewed previous work on learning MAC protocols and, in particular, on CSMA/ECA. We have presented a model that computes the number of slots required to reach collision-free operation, and we have introduced a modification that results in a shorter transitory. Specifically, we advocate for the use of a deterministic backoff for two consecutive times after each successful transmission, and we name this improved protocol CSMA/E2CA. Then, we present extensive simulation results that highlight the benefit of using CSMA/E2CA, specially in those channels that are prone to packet errors.
With static parameter configuration, there is a limit on the number of contenders that can operate in a collision-free fashion in a CSMA/E2CA network. We revisit our previous work on dynamic parameter adjustment for CSMA/ECA to offer a centralized and easy to implement parameter adjustment mechanism for CSMA/E2CA. Finally, we run simulations in which a large number of contenders simultaneously join the network and show that our approach quickly reacts to adjust the contention parameter and deliver high performance for any number of simultaneous contenders.
References
“Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY), Specifications” ANSI/IEEE Std. 802.11, 2007
Abramson N: THE ALOHA SYSTEM: another alternative for computer communications. In Proceedings of the AFIPS Fall Joint Computer Conference, 1970, New York, NY, USA. ACM; 281-285.
Abramson N: The alohanet-surfing for wireless data. IEEE Communications Magazine 2009, 47(12):21-25.
Rom R, Sidi M: Multiple Access Protocols: Performance and Analysis. Springer, New York, NY, USA; 1990.
Roberts L: ALOHA packet system with and without slots and capture. ACM SIGCOMM Computer Communication Review 1975, 5(2):42.
Tanenbaum A: Computer Networks. 1988.
Crowther W, Rettberg R, Walden D, Ornstein S, Heart F: A system for broadcast communication: reservation-ALOHA. Proceedings of 6th Hawaii International Conference on System Sciences (HICSS '73), January 1973, Honolulu, Hawaii, USA 596-603.
Calì F, Conti M, Gregori E, Aleph P: Dynamic tuning of the IEEE 802.11 protocol to achieve a theoretical throughput limit. IEEE/ACM Transactions on Networking 2000, 8(6):785-799. 10.1109/90.893874
Toledo AL, Vercauteren T, Wang X: Adaptive optimization of IEEE 802.11 DCF based on Bayesian estimation of the number of competing terminals. IEEE Transactions on Mobile Computing 2006, 5(9):1283-1296.
Patras P, Banchs A, Serrano P: A control theoretic approach for throughput optimization in IEEE 802.11e EDCA WLANs. Mobile Networks and Applications 2009, 14(6):697-708. 10.1007/s11036-008-0121-x
Choi J, Yoo J, Choi S, Kim C: EBA: an enhancement of the IEEE 802.11 DCF via distributed reservation. IEEE Transactions on Mobile Computing 2005, 4(4):378-390.
Barcelo J, Bellalta B, Cano C, Oliver M: Learning-BEB: avoiding collisions in WLAN. Proceedings of the 14th Eunice Open European Summer School, September 2008
Lee J, Walrand J: Design and analysis of an asynchronous zero collision MAC protocol. http://arxiv.org/abs/0806.3542
Fang M, Malone D, Duffy K, Leith D: Decentralised Learning MACs for Collision-free Access in WLANs. http://arxiv.org/abs/1009.4386
He Y, Yuan R, Sun J, Gong W: Semi-random backoff: towards resource reservation for channel access in wireless LANs. Proceedings of the 17th IEEE International Conference on Network Protocols (ICNP '09), October 2009, Princeton, NJ, USA 21-30.
Yi Y, de Veciana G, Shakkottai S: MAC scheduling with low overheads by learning neighborhood contention patterns. IEEE/ACM Transactions on Networking 2010, 18(5):1637-1650.
Singh S, Acharya PAK, Madhow U, Belding-Royer EM: Sticky CSMA/CA: implicit synchronization and real-time QoS in mesh networks. Ad Hoc Networks 2007, 5(6):744-768. 10.1016/j.adhoc.2006.12.008
Lin CR, Gerla M: Asynchronous multimedia multihop wireless networks. Proceedings of the 16th IEEE Annual Conference on Computer Communications (INFOCOM '97), April 1997 118-125.
Barcelo J, Bellalta B, Sfairopoulou A, Cano C, Oliver M: CSMA with enhanced collision avoidance: a performance assessment. Proceedings of the IEEE Vehicular Technology Conference (VTC '10), 2010
Barcelo J, Bellalta B, Cano C, Sfairopoulou A, Oliver M: Carrier sense multiple access with enhanced collision avoidance: a performance analysis. Proceedings of the ACM International Wireless Communications and Mobile Computing Conference (IWCMC '09), June 2009 733-738.
Barcelo J, Bellalta B, Cano C, Sfairopoulou A, Oliver M, Zuidweg J: Traffic prioritization for carrier sense multiple access with enhanced collision avoidance. Proceedings of the 2nd International Workshop on Multiple Access Communications (MACOM '09), June 2009
Barcelo J, Lopez-Toledo A, Cano C, Oliver M: Fairness and convergence of CSMA with enhanced collision avoidance. Proceedings of the EEE International Conference on Communications (ICC '10), 2010
Barcelo J, Bellalta B, Cano C, Sfairopoulou A, Oliver M: Dynamic parameter adjustment in CSMA/ECA. Proceedings of the 3rd International Workshop on Multiple Access Communications (MACOM '10), September 2010, Barcelona, Spain
Banchs A, Vollero L: Throughput analysis and optimal configuration of 802.11e EDCA. Computer Networks 2006, 50(11):1749-1768. 10.1016/j.comnet.2005.07.008
Grinstead C, Snell J: Introduction to Probability. American Mathematical Society; 1997.
“Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY), Specifications; Amendment 5: Enhancements for Higher Throughput” IEEE Std. 802.11n, 2009
Acknowledgments
The present paper is the extended version of a MACOM workshop paper. The authors benefited from the feedback and discussion in the workshop. The authors are specially indebted with N. Abramson for his clarifications regarding Aloha and with D. Malone for providing recent and valuable references. This work has been partially supported by the Spanish Government under Projects nos. TEC2008-0655/TEC (GEPETO, Plan Nacional I+D) and CSD2008-00010 (COMONSENS, Consolider-Ingenio Program).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Barcelo, J., Bellalta, B., Cano, C. et al. Towards a Collision-Free WLAN: Dynamic Parameter Adjustment in CSMA/E2CA. J Wireless Com Network 2011, 708617 (2011). https://doi.org/10.1155/2011/708617
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/708617

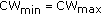 ). We show that this configuration reduces the duration of the transient state.
). We show that this configuration reduces the duration of the transient state.










 ;
;
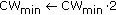 ;
;