- Research Article
- Open access
- Published:
An Efficient Method for Proportional Differentiated Admission Control Implementation
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 738386 (2011)
Abstract
The admission control mechanism inspired in the framework of proportional differentiated services has been investigated. The mechanism provides a predictable and controllable network service for real-time traffic in terms of blocking probability. Implementation of proportional differentiated admission control is a complicated computational problem. Previously, asymptotic assumptions have been used to simplify the problem, but it is unpractical for real-world applications. We improve previous solutions of the problem and offer an efficient nonasymptotic method for implementation of proportional differentiated admission control.
1. Introduction
Efficient implementation of admission control mechanisms is a key point for next-generation wireless network development. Actually, over the last few years an interrelation between pricing and admission control in QoS-enabled networks has been intensively investigated. Call admission control can be utilized to derive optimal pricing for multiple service classes in wireless cellular networks [1]. Admission control policy inspired in the framework of proportional differentiated services [2] has been investigated in [3]. The proportional differentiated admission control (PDAC) provides a predictable and controllable network service for real-time traffic in terms of blocking probability. To define the mentioned service, proportional differentiated service equality has been considered and the PDAC problem has been formulated. The PDAC solution is defined by the inverse Erlang loss function. It requires complicated calculations. To reduce the complexity of the problem, an asymptotic approximation of the Erlang B formula [4] has been applied. However, even in this case, the simplified PDAC problem remains unsolved.
In this paper, we improve the previous results in [3] and withdraw the asymptotic assumptions of the used approximation. It means that for the desired accuracy of the approximate formula an offered load has to exceed a certain threshold. The concrete value of the threshold has been derived. Moreover, an explicit solution for the considered problem has been provided. Thus, we propose a method for practical implementation of the PDAC mechanism.
The rest of the paper is organized as follows. In the next section, we give the problem statement. In Section 3, we first present a nonasymptotic approximation of the Erlang B formula. We then use it for a proportional differentiated admission control implementation and consider some alternative problem statements for an admission control policy. In Section 4, we present the results of numerous experiments with the proposed method. Section 5 is a brief conclusion.
2. Problem Statement
Let us consider the concept of admission control inspired in the framework of proportional differentiated services. In the above paper [3], whose notation we follow, PDAC problem is defined as

Here,
-
(i)
 : is a number of traffic classes.
: is a number of traffic classes. 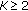 ;
; -
(ii)
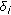 : is the weight of class
: is the weight of class  . This parameter reflects the traffic priority. By increasing the weight, we also increase the admittance priority of corresponding traffic class;
. This parameter reflects the traffic priority. By increasing the weight, we also increase the admittance priority of corresponding traffic class; -
(iii)
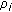 : is the offered load of class
: is the offered load of class  traffic;
traffic; -
(iv)
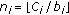 ,
,  is an allotted partition of the link capacity,
is an allotted partition of the link capacity, 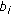 is a bandwidth requirement of class
is a bandwidth requirement of class  connections, and
connections, and  is the largest integer not greater than
is the largest integer not greater than  ;
; -
(v)
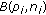 : is the Erlang loss function, that is, under the assumptions of exponential arrivals and general session holding times [5], it is the blocking probability for traffic of class
: is the Erlang loss function, that is, under the assumptions of exponential arrivals and general session holding times [5], it is the blocking probability for traffic of class 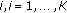 .
.
It needs to find  taking into account known
taking into account known  and the restriction imposed by given link capacity,
and the restriction imposed by given link capacity,  :
:

Let us remark that variations of  imply a discrete changing of the function
imply a discrete changing of the function  . Hence, it is practicably impossible to provide the strict equality in (1). It is reasonable to replace (1) by an approximate equality as follows:
. Hence, it is practicably impossible to provide the strict equality in (1). It is reasonable to replace (1) by an approximate equality as follows:

But, even in this case, the above problem is difficult and complex combinatorial problem. For its simplification, the following asymptotic approximation has been used [3]. If the capacity of link and the offered loads are increased together:

and  , then the Erlang loss function
, then the Erlang loss function

can be approximated by

Taking into account the PDAC problem, the authors of [3] consider the limiting regime when

and  . Under these conditions, the asymptotic approximation of the Erlang B formula has been used and (1) has been replaced by simplified equations as follows:
. Under these conditions, the asymptotic approximation of the Erlang B formula has been used and (1) has been replaced by simplified equations as follows:

In practice, the limited regime (7) is not appropriate. But the simplification (8) can be used without the conditions (7). Actually, the approximation (6) can be applied without the condition (4). We prove it below.
3. Offered Technique
3.1. Approximate Erlang B Formula
We assert that for the desired accuracy of the approximation (6) an offered load has to exceed a certain threshold. The concrete value of the threshold is given by the following theorem.
Theorem 1.
For any small  , if
, if

then

Proof.
Here and below, we use the following designation:

Assume that  . First, we rewrite the Erlang B formula
. First, we rewrite the Erlang B formula

Remark that

Taking into account properties of geometrical progression, we have

Hence

To prove the second inequality of the theorem, we use the following upper bound of the Erlang loss function [6]:

Transform this as follows:

It implies

We have  . Hence,
. Hence,

Thus, for any  such that
such that

it follows that

From the inequality (20), we obtainthe condition (9).
The proof is completed.
Note that the approximate formula (6) can provide the required accuracy  in the case of
in the case of  . Actually, if
. Actually, if  , then the required accuracy is reached for
, then the required accuracy is reached for  . Thus, the condition (9) is sufficient but not necessary. It guarantees the desired accuracy of the approximation for any small
. Thus, the condition (9) is sufficient but not necessary. It guarantees the desired accuracy of the approximation for any small  and
and  .
.
3.2. PDAC Solution
Assume that the solution  of the PDAC problem satisfies inequalities
of the PDAC problem satisfies inequalities  . Let us derive an analytical solution for the PDAC problem under the condition (8). Without reducing generality, assume that
. Let us derive an analytical solution for the PDAC problem under the condition (8). Without reducing generality, assume that  and
and  . Indeed, if
. Indeed, if  , then we define new weights
, then we define new weights  . Thus, the condition (8) can be reformulated as follows:
. Thus, the condition (8) can be reformulated as follows:

According to the transitivity property, any solution of the PDAC problem under condition (8) is also a solution of the PDAC problem under condition (22). Therefore,

Using the equality (2), we get

where

Thus, the formulas (23)–(25) provide the implementation of proportional differentiated admission control.
It is clear that for some values  , we can obtain
, we can obtain  in (24) or
in (24) or  in (23). Therefore, the problem is unsolvable and PDAC implementation is impossible for the given parameters.
in (23). Therefore, the problem is unsolvable and PDAC implementation is impossible for the given parameters.
More precisely, if  , then we have from (24)
, then we have from (24)

Using the following equality:

we derive

From the inequality  , we can write
, we can write

Therefore,

By substituting the expressions (24) for the  into (30), we get after some manipulations the following inequality:
into (30), we get after some manipulations the following inequality:

Note that the problem (22) has been formulated under the condition

Actually, it implies

Thus, the region of acceptability for PDAC problem (22) is defined by

It follows from the theorem that the approximation (6) is applicable even for  and any small
and any small  if
if  . In spite of this fact, the solution above cannot be useful for small values of the ratio
. In spite of this fact, the solution above cannot be useful for small values of the ratio  . In this case, the loss function
. In this case, the loss function  is sensitive to fractional part dropping under calculation
is sensitive to fractional part dropping under calculation  . For example, if
. For example, if  kb/s,
kb/s,  , and we obtain
, and we obtain  kb/s, then the approximate value of the blocking probability is about 0.004. But
kb/s, then the approximate value of the blocking probability is about 0.004. But  and
and  . Thus, the offered approximate formula is useful if the ratio
. Thus, the offered approximate formula is useful if the ratio  is relatively large.
is relatively large.
3.3. Alternative Problem Statements
Let  be the number of channel assigned for class
be the number of channel assigned for class  traffic,
traffic,  . Each class
. Each class  is characterized by a worst-case loss guarantee
is characterized by a worst-case loss guarantee  [7, 8].
[7, 8].
Consider the following optimization problem:

Assume that for all  . It is well known that the Erlang loss function
. It is well known that the Erlang loss function  is a decreasing function of
is a decreasing function of  [9], that is,
[9], that is,  if
if  . Therefore, the optimal solution
. Therefore, the optimal solution  of the problem (35) satisfies the mentioned condition
of the problem (35) satisfies the mentioned condition

If we designate  , then we get
, then we get

Thus, the optimization problem (35) is reduced to the problem (1).
Assume the approximation (6) is admissible. Therefore, the method from previous subsection is supposed to be used, but the optimal solution of the problem (35) can be computed by inverting the formula (36). Taking into account the approximation, we get

Note that in practice the solution  is not usually integer; thus, it has to be as follows:
is not usually integer; thus, it has to be as follows:

We now consider the optimization of routing in a network through the maximization of the revenue generated by the network. The optimal routing problem is formulated as


where  is a fixed number of channels for class
is a fixed number of channels for class  traffic and
traffic and  is a revenue rate of class
is a revenue rate of class  traffic. Obviously, the Erlang loss function
traffic. Obviously, the Erlang loss function  is an increasing function of
is an increasing function of  . Therefore, the optimal solution
. Therefore, the optimal solution  of the problem (40), (41) satisfies the following condition:
of the problem (40), (41) satisfies the following condition:

Hence, the problem (40), (41) can be reduced to the problem (1) as well. Under the approximation, the optimal solution takes the form

and the maximal total revenue is

4. Performance Evaluation
Let us illustrate the approximation quality. The difference  is plotted as a function of offered load in Figure 1. If the number of channel
is plotted as a function of offered load in Figure 1. If the number of channel  is relatively small then high accuracy of approximation is reached for heavy offered load. Let us remark that heavy offered load corresponds to high blocking probability. Generally, this situation is abnormal for general communication systems, but the blocking probability
is relatively small then high accuracy of approximation is reached for heavy offered load. Let us remark that heavy offered load corresponds to high blocking probability. Generally, this situation is abnormal for general communication systems, but the blocking probability  decreases if the number of channels
decreases if the number of channels  increased relative accuracy
increased relative accuracy  . Let us designate
. Let us designate  . If the approximation (2) is admissible for
. If the approximation (2) is admissible for  then it is also admissible for any
then it is also admissible for any  . In Figure 2, the behavior of losses function
. In Figure 2, the behavior of losses function  according to different
according to different  is shown. Thus, the provided approximation is attractive for a performance measure of queuing systems with a large number of devices.
is shown. Thus, the provided approximation is attractive for a performance measure of queuing systems with a large number of devices.
Next, we consider a numerical example to evaluate the quality of a PDAC implementation based on the proposed method. Assume that  Mb/s,
Mb/s,  kb/s,
kb/s,  . In average, there are 1000 channels per traffic class. Following the theorem above, we conclude that the blocking probability can be replaced by the approximation (6) with accuracy about 0.01. Using (23)–(25), find a solution of the simplified PDAC problem and calculate the blocking probability for the obtained values. The results are shown in the Table 1.
. In average, there are 1000 channels per traffic class. Following the theorem above, we conclude that the blocking probability can be replaced by the approximation (6) with accuracy about 0.01. Using (23)–(25), find a solution of the simplified PDAC problem and calculate the blocking probability for the obtained values. The results are shown in the Table 1.
Note that  Mb/s and three channels per 128 kb/s have not been used. We get
Mb/s and three channels per 128 kb/s have not been used. We get

It is easy to see that

If  , and other parameters are the same then
, and other parameters are the same then

If an obtained accuracy is not enough, then the formulas (23)–(25) provide efficient first approximation for numerical methods.
5. Conclusion
In this paper, a simple nonasymptotic approximation for the Erlang B formula is considered. We find the sufficient condition when the approximation is relevant. The proposed result allows rejecting the previously used limited regime and considers the proportional differentiated admission control under finite network resources. Following this way, we get explicit formulas for PDAC problem. The proposed formulas deliver high-performance computing of network resources assignment under PDAC requirements. Thus, an efficient method for proportional differentiated admission control implementation has been provided.
References
Yilmaz O, Chen IR: Utilizing call admission control for pricing optimization of multiple service classes in wireless cellular networks. Computer Communications 2009, 32(2):317-323. 10.1016/j.comcom.2008.11.001
Dovrolis C, Stiliadis D, Ramanathan P: Proportional differentiated services: delay differentiation and packet scheduling. IEEE/ACM Transactions on Networking 2002, 10(1):12-26. 10.1109/90.986503
Salles RM, Barria JA: Proportional differentiated admission control. IEEE Communications Letters 2004, 8(5):320-322. 10.1109/LCOMM.2004.827384
Jagerman DL: Some properties of the Erlang loss function. Bell System Technical Journal 1974, 53(3):525-551.
Bertsekas D, Gallager R: Data Networks. 2nd edition. Prentice Hall, Englewood Cliffs, NJ, USA; 1992.
Harrel A: Sharp bounds and simple approximations for the Erlang delay and loss formulas. Management Sciences 1988, 34(8):959-972. 10.1287/mnsc.34.8.959
Christin N, Liebeherr J, Abdelzaher T: Enhancing class-based service architectures with adaptive rate allocation and dropping mechanisms. IEEE/ACM Transactions on Networking 2007, 15(3):669-682.
Koo J, Shakhov VV, Choo H: An Enhanced RED-Based Scheme for Differentiated Loss Guarantees, Lecture Notes in Computer Science. Volume 4238. Springer, New York, NY, USA; 2006.
Haring G, Marie R, Puigjaner R, Trivedi K: Loss formulas and their application to optimization for cellular networks. IEEE Transactions on Vehicular Technology 2001, 50(3):664-673. 10.1109/25.933303
Shakhov VV: An efficient method for proportional differentiated admission control implementation. Proceedings of the 3rd International Workshop on Multiple Access Communications (MACOM '10), September 2010, Barcelona, Spain 91-97.
Acknowledgments
This research was supported in part by MKE and MEST, Korean government, under ITRC NIPA-2010-(C1090-1021-0008), FTDP(2010-0020727), and PRCP(2010-0020210) through NRF, respectively. A preliminary version of this paper was presented at MACOM 2010, Spain (Barcelona) [10]. The present version includes additional mathematical and numerical results.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shakhov, V., Choo, H. An Efficient Method for Proportional Differentiated Admission Control Implementation. J Wireless Com Network 2011, 738386 (2011). https://doi.org/10.1155/2011/738386
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/738386
 : is a number of traffic classes.
: is a number of traffic classes. 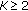 ;
;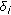 : is the weight of class
: is the weight of class  . This parameter reflects the traffic priority. By increasing the weight, we also increase the admittance priority of corresponding traffic class;
. This parameter reflects the traffic priority. By increasing the weight, we also increase the admittance priority of corresponding traffic class;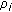 : is the offered load of class
: is the offered load of class  traffic;
traffic;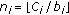 ,
,  is an allotted partition of the link capacity,
is an allotted partition of the link capacity, 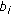 is a bandwidth requirement of class
is a bandwidth requirement of class  connections, and
connections, and  is the largest integer not greater than
is the largest integer not greater than  ;
;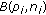 : is the Erlang loss function, that is, under the assumptions of exponential arrivals and general session holding times [
: is the Erlang loss function, that is, under the assumptions of exponential arrivals and general session holding times [ .
.

 according to different values of
according to different values of
 .
.